1. Introduction
There are several methods to estimate and reconstruct missing rainfall data (Kashani and Dinpashoh, 2012). The most common methods are the use of satellites (Githungo et al., 2016; Ekeu-wei et al., 2018; Phoeurn and Ly, 2018), climate models (Singh and Xiaosheng, 2019) and statistical programs (Kim and Pachepsky, 2010; Serrano-Notivoli et al., 2017a). However, despite their utility, satellites provide limited coverage and, in most cases, they have very coarse resolutions that limit local applications. Similarly, climate models are useful but are limited by their spatial scale and are often quite expensive to be developed (Reinoso, 2016). Methods of artificial intelligence, such as artificial neural networks (ANN) and support vector machines (SVM) (Mileva-Boshkoska and Stankovski, 2007; Mwale et al., 2012; Hasan et al., 2015) have a complex mathematical formulation. Therefore, their application demands greater efforts with respect to linear methods, and also requires intensive calculations with a high computational cost. Statistical imputation methods are the most common technique and can be classified as deterministic, stochastic or random, and those based on artificial intelligence (Campozano et al., 2015). Among the statistical methods, the deterministic approach is the most common procedure due to its robustness, simplicity of implementation and high degree of computational efficiency (Campozano et al., 2015). Deterministic weighted methods belong to the spatial interpolation techniques; they represent an adequate approach for the imputation of missing data in daily precipitation series and have received greater acceptance and applicability (Teegavarapu and Chandramouli, 2005; Ahrens, 2006; Kim and Pachepsky, 2010; Chen and Liu, 2012).
Several important studies have already been published regarding the use of deterministic weighted methods for the estimation and reconstruction of missing rainfall data. The inverse distance weighting method (IDW) is the most widely used approach for the estimation of missing data in hydrology and geographical sciences (Xia et al., 1999; Eischeid et al., 2000; Teegavarapu and Chandramouli, 2005; Lee and Kang, 2015). However, despite its usefulness, several authors have presented improvements to the IDW method by incorporating other mathematical approaches that enhance its results. For example, Teegavarapu and Chandramouli (2005) used a data-based approach to impute missing precipitation values. Furthermore, these authors proposed improvements to the IDW method by replacing the weighting value with the correlation coefficient. This new method was called the coefficient of correlation weighting (CCW) method. Results indicate that CCW is far superior to the traditional IDW in estimating the missing rainfall records. Wagner et al. (2012) applied seven methods to compare various spatial interpolation approaches applied to precipitation, which included deterministic methods such as the Thiessen polygon and statistics and geostatistical approaches (ordinary kriging, regression-inverse distance weighting and regression-kriging). The methods tested by these authors showed that the best performing were those based on regression analysis. However, the application of these models in precipitation estimates showed that they may cause negative results that do not correspond to the physics of the phenomenon (the minimum amount of daily rainfall is zero), and should be readjusted to zero (González Hidalgo et al., 2002; Teegavarapu, 2012). Geostatistical estimation methods based on theoretical foundations (particularly kriging) are based on showing the proportion in which the variance between points in space changes and is expressed in a semi-variogram. However, this procedure is limited because it relies on a certain amount of data to produce a reliable and adequate variogram (Toro-Trujillo et al., 2015). Regardless of having a high number of points to interpolate, some authors argue that kriging does not show improvements with respect to the IDW method (Wagner et al., 2012).
In another relevant study, Teegavarapu et al. (2009) applied genetic algorithms (GA) and a distance weighting method to estimate missing precipitation data. These authors concluded that GA provided more accurate estimates over the distance weighting method. Chang et al. (2006) applied GA to search the most suitable order of distances in the variable-order inverse distance method; their results show that the variability of the order of distances is small when the topography of rainfall stations is uniform. This study also confirmed that the variable-order inverse distance method is more suitable than the arithmetic average method and the Thiessen polygons method in describing the spatial variation of rainfall. Suhaila et al. (2008) modified the coefficient of the CCW method and proposed a new weighting method using the correlation coefficient with the inverse distance weighting method (CIDW). Their results show that the modified methods presented better performance in the estimation of missing rainfall data when compared to previous versions in terms of three evaluation measures.
Another relevant study conducted by Lo (1992) added the proportion of distance to altitude, while Chang et al. (2005) added the inverse of these two parameter products in the IDW method. Seyyednejad et al. (2012) proposed to use each of these parameters separately in the numerator, denominator or together as coefficients in the IDW method. These studies have clearly improved deterministic imputation methods that allow for the estimation of missing rainfall values. However, none of the existing methods can be considered to be applicable globally, since the accuracy of these methods are usually affected by different factors that go far beyond the selected interpolation process itself. Specifically, the selection of the best method for estimating missing precipitation data may vary from region to region depending on rain patterns and spatial distributions (de Silva et al., 2007). The selection of the best approach should take into account the topographic and orographic effects of rainfall (Sivapragasam et al., 2015).
In this work, two new generalized weighted methods are proposed. The first method is able to recover the weighting functions of the normal ratio method weighted with correlations (NRWC) (Young, 1992) and a normal ratio modified with the inverse distance method (NRIDW) that uses a new weighting function that combines the weight functions of the NRWC and IDW together with an altitude factor. The second method being proposed generates weighting functions that are reported in the literature, such as CCWM, IDW, CIDW and the relation of altitude with the weighted method of the inverse distance (HIDW). This new method constitutes a generalization of previous methods with the improvement of adding the altitude factor. We believe that both proposals are new contributions to the literature, particularly because the weighting coefficients are determined in an objective manner, minimizing the difference between estimated and observed rainfall data. The two new methods can be classified as optimal interpolation methods with several parameters that need to be optimized to obtain the best results. This optimization was addressed by using inherently continuous algorithms. The metaheuristic adaptation of the covariance matrix (CMA-ES) (Hansen et al., 2003) was used in all of the weighting functions that are needed to find optimal exponents. This method offers better performance than previously reported GA (Hansen et al., 2011; Arsenault et al., 2013). In addition, to test the two new methods, 11 weighted methods were compared in terms of reliability of the precipitation estimates generated. The two new methods are shown to provide an improvement because they include an optimal parameter estimation mechanism for the imputation of daily rainfall records. An automatic procedure is developed that allows to completely rebuild the time-series while preserving its statistical properties. The methods were tested in the study region of Tabasco, a southern Mexican state that is known because of its high rainfall rates. A set of rainfall records covering 32 years between 1980 and 2012 was used to test and validate the new methodology.
2. Methods
2.1 Historical application of deterministic methods to fill missing data in time series
Several existing weighted methods that pertain to spatial interpolation techniques are presented in the following subsection. The methods examined include the modified CCWM, CIDW, and NRIDW, as well as the HIDW. The main difference between these interpolation methods is the way in which the weighting factors (W i ) are estimated. The general formulation to represent these methods was proposed by Li and Heap (2014) and has the following form:
where
Suhaila et al. (2008) proposed several modifications to the existing calculation methods for estimating the missing rainfall values in Petaling Jaya, Malaysia. The first method, which modified the CCW method, consisted in changing the weighting function of the latter (Teegavarapu and Chandramouli, 2005),
by
where r it represents the correlation coefficient of the daily precipitation data between the target station t and the i-th neighboring station; N is the length of the precipitation time series and p is a parameter between 2 and 6. The second method was the CIDW. Here, advantage is taken because the IDW is influenced by the minimum distances between the target station and the neighboring stations. In addition, the correlation factor can also contribute positively to improve the estimates of the missing values of rainfall, considering that the neighboring stations would have greater correlation with the target station. Thus, the weighting factor of this method is given by
where d it represents the distance between the target station t and the i-th neighboring station. Finally, they combine the best proposed NR method (Young, 1992), which is the NRWC, whose weighting function is
With the weighting function of the IDW method it is called modified NRIDW, and its weighting function is
Suhaila et al. (2008) concluded that the proposed methods presented better performance in the estimation of the missing rainfall data, in comparison with their previous versions in terms of three evaluation measures. Lo (1992) added the proportion of distance to altitude, while Chang et al. (2005) added the inverse of these two parameter products in the IDW method. Seyyednejad et al. (2012)) proposed to use each of these parameters separately in the numerator, denominator or together as coefficients in the IDW method. Thus, more general models (HIDW) than those proposed by Lo (1992) and Chang et al. (2005) are obtained; its weighting function is
where h it represents the altitude difference between the target station t and the i-th neighboring stations.
Table I shows a summary of the previously reported imputation methods that were tested and compared to our methods in our study (we included abbreviations and references).
Table I List of the 9 deterministic imputation methods with their respective code.
| # | Impute method | Code | Reference |
| 1 | Classical normal ratio method | NR | (Paulhus and Kohler, 1952) |
| 2 | Normal ratio method weighted with correlations | NRWC | (Young, 1992) |
| 3 | Inverse distance weighting method | IDWM | (Teegavarapu and Chandramouli, 2005; Chang et al., 2006; Moeletsi et al., 2016) |
| 4 | Weighted correlation coefficient method | CCW | (Suhaila et al., 2008; Ford and Quiring, 2014) |
| 5 | Modification to the weighted correlation coefficient method | CCWM | (Suhaila et al., 2008) |
| 6 | Normal ratio modified with inverse distance method | NRIDW | (Suhaila et al., 2008) |
| 7 | Modified correlation coefficient with inverse distance method | CIDW | (Suhaila et al., 2008) |
| 8 | Inverse distance weighting of normal ratio with correlation | NRIDC | (Azman et al., 2015) |
| 9 | Relation of the height with the weighted method of the inverse distance | HIDW | (Seyyednejad et al., 2012) |
2.2 New methods to estimate missing rainfall data
Two new imputation methods based on the NRIDW and CIDW are applied in this study. These two new approaches are distinguished by the inclusion of free parameters (several parameters that need to be optimized to obtain the best results) and by the consideration of the altitude factor. The search for optimal parameters is conducted by using heuristic and metaheuristic techniques, since these methods allow obtaining a solution that is close to the optimum, in a computationally acceptable time. These algorithms can be used in the search for solutions of any optimization problem. In our work, the optimal parameters are computed by means of the adaptation strategy of the covariance matrix (CMA-ES) (Hansen et al., 2003). The optimization algorithm was implemented using the R software with the “cmaes” and “parma” libraries (Trautmann et al., 2011; Ghalanos, 2016). CMA-ES offers a better performance (Hansen et al., 2011) as compared with the optimization technique based on particle clouds (PSO) (Du and Swamy, 2016), as well as with GA (Tsangaratos et al., 2019).
The altitude-rainfall relationship has been investigated previously by (Hevesi et al., 1992a, b), who used cokriging to incorporate elevation into the mapping of the spatial variability of rainfall. They reported a significant correlation (0.75) between average annual precipitation and elevation recorded in 62 stations in Nevada and southeastern California. Another relevant study conducted by al-Ahmadi and al-Ahmadi (2013) analized the relationships between annual and seasonal rainfall and the altitude of the terrain. These authors used 180 rainfall stations with 35 yrs of monthly records from 1971 to 2005 in Saudi Arabia, applying the global ordinary least square (OLS) and local geographically weighted regression (GWR) methods. Their results show that using the GWR method they obtained coefficients of determination higher than 0.64 between altitude and annual, winter, spring, summer, and fall rainfalls. Sadeghi et al. (2017) evaluated rainfall distribution and the effect of elevation as a secondary variable to interpolate rainfall in Iran using several geostatistical techniques such as kriging, co-kriging, IDW, radial basis function, global polynomial interpolation, and local polynomial interpolation. These authors concluded that the rain amount is immediately influenced by elevation and also that the result of co-kriging has a direct correlation with elevation changes. According to Goovaerts (2000), precipitation tends to increase with increasing elevation, mainly because of the orographic effect of mountainous terrain, which causes the air to be lifted vertically, and the condensation occurs due to adiabatic cooling. These studies have shown that the amount and distribution of rainfall is directly affected by elevation. This is why several methods for the imputation of rainfall have included the altitude as a critical component. Our two proposed generalizations (shown below) continue that trend and include an altitude factor.
2.2.1 Generalization of the modified normal ratio with the inverse distance method (GNRIDW)
The weighting function of the NRIDW method is a combination of the weighting functions of the NRWC and IDW methods (see Eq. ENT#091;6ENT#093;). Usually q = 2 is taken as the default value in the weighting factor related to the IDW method (d it ); however, although q=2 is the most commonly used value (Teegavarapu and Chandramouli, 2005; Boke, 2017) there is no theoretical justification for preferring this value over others (Bajjali, 2018). Therefore, other possible values for q should be investigated as well. Given the above-mentioned and considering the altitude as one of the factors that may affect the rainfall records, the following modification to the NRIDW method is proposed:
where r it , d it , and h it represent the correlation coefficient, the distance and the altitude difference between the target station t and the i-th neighboring stations, respectively.
If s = q = 0 is set in Eq. (8), the weighting function of the NRWC method is recovered (compare with Eq. ENT#091;5ENT#093;). If, instead, s = 0 and q = 2, the weighting function of the NRIDW method is obtained (compare with Eq. ENT#091;6ENT#093;). Therefore, this proposal constitutes a generalization of both the NRWC and NRIDW methods. Finally, it is emphasized that the parameters q and s belong to ℝ+ and their values are determined according to the solutions of the following optimization problem:
where Z
i
is the i-th observed rainfall value,
2.2.2 Generalization of the modified correlation coefficient with the inverse distance weighting method (GCIDW)
In line with the above reasoning, the CIDW method can be generalized as well. Let us considerer the q exponent of the IDW as a parameter to be optimized and, as before, let us add the altitude factor. As a result, a generalization of CIDW is obtained in which the weighting factors are given as follows:
where r it , d it and h it represent the correlation coefficient, the distance and the altitude difference between the target station t and the i-th neighboring stations. In this proposal, unlike the previous one, there are three parameters (p, q and s) whose spatial domain is ℝ+. To obtain different combinations of the parameters we can retrieve some of the methods described above. For example, if s = q = 0 is set in Eq. (9), the weighting function of the CCWM method is recovered (compare with Eq. 3), whereas, if s = p = 0, the weighting function of the IDW method is obtained. Besides, if p = 0 we retrieve the weighting function of the HIDW method (compare with Eq. ENT#091;7ENT#093;). Finally, if s = 0 and q = 2, the weighting function of the CIDW method is obtained (compare with Eq. ENT#091;4ENT#093;).
Given that in both of the methods being proposed the weighting coefficients W i are determined in a direct way by solving the optimization problem given in Eq. (9), our proposals can be classified as optimal interpolation methods with several parameters to be optimized.
2.3 Study area
In order to apply the different imputation methods and to illustrate how the two new proposed procedures work, we have chosen the state of Tabasco, which is located in the southern region of Mexico. Tabasco is bordered by the states of Chiapas, Campeche, Quintana Roo and Yucatán (see Fig. 1), which are considered the wettest region in the country. Tabasco extends from the coastal plain of the Gulf of Mexico to the mountain ranges of northern Chiapas. Geographically it is located between 17º 15’-18º 39’ N, and 91º 00’-94º 17’ W. It is bounded to the north by the Gulf of Mexico and the state of Campeche, to the south by the state of Chiapas, to the east by the Republic of Guatemala and to the west by the state of Veracruz (Fig. 1). Tabasco has an area of 25 267 km2, representing 1.3% of the Mexican territory. The major part of the state is a plain surface with a few elevations to the south of the state (5.84% of the total state’s area) (Sosa Cabrera, 2010), which are relatively low in relation to the average sea level (400-900 masl). The territory of Tabasco is located in a tropical zone close to the Gulf of Mexico, which results in a warm climate with only small temperature variations throughout the year. The yearly average temperature is 27 ºC, with an average range of variation of 18.5 to 36ºC. The historical yearly average rainfall in the state is of 2184.6 mm, which is the highest annual precipitation in Mexico. The highest rainfall zone is in the mountain range in the south-center part of the state, with precipitation values above 4000 mm yr-1, while the rest of the state has recorded precipitation values in the range of 1200 to 2500 mm yr-1.
2.4 Climatological database
The state of Tabasco has 83 meteorological stations. However, after a careful analysis of their records, the following problems were found: i) some stations were not useful because the data was collected at different time scales (days, months and years) and ii) some stations with daily rainfall records did not have enough information. Only stations with a minimum of 30 yrs of uninterrupted rainfall information, as recommended by the World Meteorological Organization (WMO, 2011) were chosen. The period from January 1, 1980 to December 31, 2012 was chosen to conduct this investigation. Since there is not a well-established criterion of what to consider as an acceptable percentage of missing data in a time series dataset (Dong and Peng, 2013), an assumption was made to consider datasets with daily rainfall with at most 25% of missing data. This approach allowed to have a more reliable dataset, even though rainfall time series with higher percentages of missing data have been considered in other studies (Malek et al., 2010; Campozano et al., 2015; Toro-Trujillo et al., 2015). Table II shows a summary of the main features of the selected weather stations, which cover 82% of Tabasco’s municipalities (14 of 17). The information was obtained through the Climate Computing Program (Clicom) system of the National Meteorological Service (http://clicom-mex.cicese.mx). None of the weather stations selected had a complete dataset.
Table II Characteristics of the selected stations.
| Station | Country | Long (W) | Lat (N) | Alt (masl) | MD (%) | Period | Max | Mean | Std. | VC | S | K |
| 27002 | Centla | 92.8 | 18.417 | 3 | 12.71 | 1969-2016 | 300 | 3.920 | 12.588 | 3.211 | 6.987 | 81.330 |
| 27004 | Tenosique | 91.493 | 17.449 | 14 | 2.22 | 1948-2016 | 190 | 6.303 | 15.400 | 2.443 | 4.106 | 22.623 |
| 27006 | Balancán | 91.275 | 17.638 | 50 | 2.81 | 1967-2016 | 280 | 4.672 | 12.639 | 2.705 | 5.585 | 52.496 |
| 27007 | Cárdenas | 93.619 | 18.001 | 12 | 15.23 | 1961-2016 | 360 | 5.694 | 17.365 | 3.050 | 6.768 | 75.527 |
| 27008 | Cárdenas | 93.376 | 18.001 | 25 | 12.24 | 1955-2016 | 300 | 5.686 | 16.425 | 2.888 | 6.234 | 61.613 |
| 27009 | Comalcalco | 93.22 | 18.247 | 15 | 19.51 | 1965-2016 | 274 | 4.801 | 15.082 | 3.142 | 6.154 | 56.439 |
| 27011 | Tacotalpa | 92.798 | 17.613 | 20 | 10.21 | 1950-2016 | 269 | 7.70 | 19.35 | 2.513 | 4.520 | 29.630 |
| 27015 | Huimanguillo | 93.942 | 17.837 | 7 | 24.90 | 1965-2016 | 207 | 6.569 | 16.485 | 2.510 | 4.149 | 23.338 |
| 27019 | Jalapa | 92.812 | 17.723 | 14 | 1.41 | 1970-2016 | 310 | 7.115 | 18.879 | 2.653 | 4.866 | 34.161 |
| 27021 | Balancán | 91.293 | 17.757 | 29 | 20.04 | 1969-2016 | 201.2 | 5.418 | 14.518 | 2.679 | 4.602 | 30.757 |
| 27030 | Macuspana | 92.605 | 17.757 | 11 | 0.68 | 1948-2016 | 265 | 6.404 | 16.509 | 2.578 | 4.532 | 29.318 |
| 27034 | Paraíso | 93.212 | 18.396 | 6 | 8.84 | 1949-2016 | 339 | 4.501 | 14.584 | 3.240 | 7.131 | 82.448 |
| 27036 | Cunduacán | 93.176 | 18.067 | 15 | 3.14 | 1970-2016 | 350 | 5.433 | 15.387 | 2.832 | 6.438 | 73.218 |
| 27037 | Centro | 93.879 | 17.854 | 21 | 2.14 | 1948-2016 | 306.4 | 5.680 | 15.312 | 2.696 | 5.258 | 44.671 |
| 27039 | Cunduacán | 93.279 | 17.997 | 23 | 5.22 | 1948-2016 | 268.5 | 5.487 | 15.386 | 2.804 | 5.494 | 46.127 |
| 27040 | Balancán | 91.158 | 17.792 | 44 | 3.28 | 1948-2016 | 273.8 | 4.518 | 12.503 | 2.767 | 5.834 | 55.724 |
| 27042 | Tacotalpa | 92.777 | 17.461 | 44 | 4.85 | 1962-2016 | 343.9 | 9.836 | 23.111 | 2.350 | 4.670 | 32.974 |
| 27044 | Teapa | 92.953 | 17.549 | 51 | 1.24 | 1960-2015 | 301.2 | 8.988 | 20.527 | 2.284 | 4.131 | 25.608 |
| 27047 | Tenosique | 91.427 | 17.472 | 22 | 24.00 | 1921-2015 | 213 | 5.823 | 15.746 | 2.704 | 4.742 | 30.459 |
| 27050 | Centla | 92.6 | 18.384 | 2 | 5.40 | 1948-2015 | 247 | 4.264 | 13.181 | 3.091 | 6.764 | 70.298 |
| 27054 | Centro | 92.928 | 17.997 | 24 | 5.86 | 1948-2015 | 340 | 5.386 | 15.283 | 2.838 | 5.776 | 55.439 |
| 27060 | Centro | 93.768 | 17.974 | 11 | 12.64 | 1972-2016 | 320 | 5.439 | 15.601 | 2.868 | 5.543 | 47.752 |
| 27061 | Teapa | 92.92 | 17.513 | 86 | 16.41 | 1972-2016 | 396.4 | 10.519 | 23.230 | 2.208 | 4.080 | 26.783 |
| 27070 | Tacotalpa | 92.75 | 17.381 | 63 | 1.64 | 1974-2016 | 317 | 8.842 | 20.741 | 2.346 | 4.366 | 28.835 |
| 27075 | Cárdenas | 93.566 | 18.111 | 10 | 10.23 | 1972-2016 | 334 | 6.297 | 18.346 | 2.914 | 5.887 | 53.335 |
| 27076 | Cárdenas | 93.497 | 18.111 | 13 | 24.02 | 1972-2016 | 365 | 6.292 | 19.518 | 3.102 | 7.141 | 74.564 |
| 27077 | Cárdenas | 93.625 | 18.066 | 12 | 13.46 | 1972-2016 | 360 | 5.850 | 18.561 | 3.173 | 5.638 | 48.432 |
| 27078 | Cárdenas | 93.499 | 18.021 | 19 | 6.16 | 1972-2016 | 310 | 4.871 | 15.133 | 3.107 | 6.693 | 73.289 |
| 27084 | Nacajuca | 93.018 | 18.166 | 10 | 6.84 | 1979-2016 | 267 | 4.860 | 14.199 | 2.922 | 5.768 | 49.995 |
Alt: altitude given in masl; MD: percentage of missing data; Std.: standard deviation; VC: variation coefficient; S: skewness; K: kurtosis. The values of the statistical parameters are calculated based on the daily records.
The standard deviation in the state varied between 12.503 and 23.230 mm day-1. These ranges were recorded in very contrasting zones: the lower range corresponds to weather station 27040, located in the municipality of Balancán, to the west-northwest of the state, with an annual precipitation range between 1500 and 2000 mm, while the highest daily precipitation range was found in meteorological station 27061, located in the municipality of Teapa to the center-south of the state (highest rainfall area), with annual ranges above 2500 mm. The Pearson’s linear correlation coefficient between the standard deviation and the daily mean values of rainfall was 0.934. Therefore, both variables are related positively, which means high values of precipitation are associated with high variability (Sokol Jurkoviç and Pasariç, 2013). This relationship allows us to obtain a variation coefficient that homogenizes the variation between all the meteorological stations. In all the weather stations, asymmetric values greater than or equal to 4.080 were obtained, therefore, the rainfall data-set have a positive biased distribution, that is, the distribution of precipitation data tends to be concentrated towards the left rather than towards the right of the mean. Finally, it can be observed that the kurtosis coefficient of the daily rainfall distribution has a minimum of 22.623, implying that in all the meteorological stations there is a visible concentration of rainfall values in the central area of the distribution. As a result, all of the distributions are leptokurtic (Hood et al., 2007).
In order to provide a better perspective on the behavior of rainfall, the calculation of the correlations between the amount of daily rainfall with all possible pairs of the selected weather stations was carried out. At the same time, the distances between the geographical locations of the selected stations was also computed. Figure 2 shows the correlations of the rainfall plotted against the distance, given in kilometers. Weather stations that are separated by distances beyond 140 km have low correlation values (lower than 0.30) and have a low degree of linear association. On the other hand, nearby weather stations have more similar rainfall behaviors than pairs of geographically distant weather stations. DeGaetano (2001) suggests that weather stations that are geographically close to each other should be grouped, because it provides an idea of the spatial structure of the variables under study. Cluster analysis is one of the most common used techniques to identify groups of homogeneous climates (DeGaetano, 2001). Given that the data satisfies the assumption of the existence of spatial correlations between the amount and the frequency of rainfall between neighboring weather stations, the choice of the latter technique was applied in our study. The above analysis is supported by the results shown in figure 2, where a negative relationship between the correlation of daily rainfall amounts and the distance between weather stations is evident.
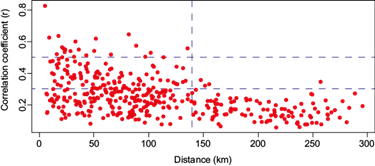
Fig. 2 Correlations between the climatological stations of Tabasco. Here the correlations between the amounts of daily rainfall with all possible pairs of the selected weather stations are calculated, as well as the distances between the geographical locations of the selected stations. Both quantities are shown in a scatter chart.
2.5 Methodology to test the proposed methods
Taking into account that the spatial clustering of observation sites is a common practice in climatology (DeGaetano, 2001; Teegavarapu, 2012), and that empirical methods use weather stations with similar rainfall patterns (Xia et al., 1999; Teegavarapu and Chandramouli, 2005; Ramos-Calzado et al., 2008; Suhaila et al., 2008; Campozano et al., 2015), the hypothesis being tested here is that missing rainfall data in a target station can be imputed by considering the daily rainfall dataset of several neighboring weather stations. The procedure followed to evaluate our hypothesis can be summarized as follows:
The first step is to carry out a cluster’s analysis through the K-means grouping method, in order to define the geographic regions with homogeneous properties.
Then, it is necessary to choose a data-set without missing data in each one of the clusters.
After that we chose a number N of similar neighboring weather stations with respect to the given target station.
Then, for each target station and in each cluster, we applied a number of existing (previously selected) imputation methods.
The above item is complemented by applying two new proposals (not found in the literature) for the imputation of missing data.
Then, following a well-established criterion (mean absolute error ENT#091;MAEENT#093;), we evaluated and chose the best method (optimum parameters) among the ones used in the former items.
Finally, an iterative algorithm was evaluated in each of the target weather stations, which applies the best imputation method (among the ones considered here) in each cluster.
These steps are described in more detail in the following sections.
2.5.1 Non-hierarchical cluster analysis
Cluster analysis is one of the statistical techniques frequently used in meteorology and climatology to group stations in regions with homogeneous climates (Gong and Richman, 1995; DeGaetano, 2001). In this study, the K-mean grouping algorithm (Teegavarapu, 2014; Mohammadrezapour et al., 2018; Reddy et al., 2018;) is used to identify spatial groups of the aforementioned weather stations (see Fig. 1). This allowed for the visualization of the spatial structure of rainfall and to perform an efficient search of neighboring weather stations that are closest to the target station. In order to validate the cluster’s structure, five techniques were used: 1) the elbow method, 2) the TraceW index (Milligan and Cooper, 1985), 3) the Hartigan index (Hartigan, 1975), 4) the Krzanowski index (Krzanowski and Lai, 1988), and 5) the gap statistics (Tibshirani et al., 2001). In order to evaluate the stability of the clusters, the algorithm described by Hennig (2007) was used, which was implemented using the “fpc” software package using R (Hennig, 2015). The stability evaluation of the clusters is based on the use of the Jaccard coefficient (Guha et al., 1999), while the plausible variations in the initial dataset are obtained by bootstrap resampling (Effron and Tibshirani, 1993).
2.5.2 Selection of similar neighboring stations
In all spatial interpolation schemes, the selection and amount of similar neighboring weather stations are very important factors that influence the results of the interpolations (Eischeid et al., 2000). There are many ways to select neighboring weather stations. Some are based on the correlation coefficient (Young, 1992; Eischeid et al., 1995, 2000), while in others the proximity between neighboring weather stations is represented by means of a statistical distance approach (Ahrens, 2006; Ramos-Calzado et al., 2008). According to Eischeid et al. (2000) adding more than four neighboring stations does not significantly improve the results of the interpolation and sometimes worsen the estimates. In this work, a criterion of no more than four neighboring stations was selected as the distance between stations.
2.5.3 Evaluation of the estimation methods performance
There is no agreement in the literature as to what is the best interpolation method that can be applied in all the disciplines that attempt to fill missing data in a time series. This is because the precision of these methods is usually affected by different factors beyond the selected interpolation process itself (Li and Heap, 2008). In particular, the selection of the best method for estimating missing rainfall data may vary from region to region depending on rainfall patterns and spatial distributions (de Silva et al., 2007). Therefore, it is crucial to choose the most appropriate interpolation method for each meteorological station in a given study area. A trivial way in which this task can be achieved, is by evaluating every selected interpolation method in each target station. In this way it is apparent to identify the method that provides the best estimates. Usually spatial interpolation methods produce numerical errors associated with the estimation. Therefore, a way to compare the performance of these methods is through using measures that quantify the committed error. In this regard, MAE is the most natural measure to calculate the average error (Willmott and Matsuura, 2005). The aforementioned error measure is given by
where n is the total number of observations,
2.5.4 Iterative algorithm
In this subsection we describe the iterative procedures used in order to establish reasonable imputed values for daily rainfall. Below we describe, first, the process to find the optimal estimation method and its parameters, and then, the algorithm for the estimation of missing data is presented.
2.5.4.1 Methodology to find the optimal estimation method
We begin by grouping the set X={x 1 ,x 2 ,…,x n } of d--dimensional, n weather stations through using the K-mean method within a group of K clusters, C={c k , k = 1,2,…,K}.. Then, for the k-th cluster in the set C, c k a dataset is selected where there are no missing values. The next step is to determine the number of neighboring weather stations by considering the Euclidean distance criterion:
where d ij is the Euclidean distance between the i-th and the j-th stations that belong in the cluster c k . These are represented in the space of the variables by the vectors
respectively. The variables we consider in this work are the longitude and the latitude in their UTM coordinates. Subsequently, each of the aforementioned methods shown in Table I, are evaluated. The CMA-ES optimization method was used to find optimal parameters-exponents of all weighted methods, including our proposals. For each parameter to be optimized, a search space located within the interval (10-8,50), was considered. In order to avoid falling into a local minimum, 50 iterations are performed, and the average absolute error is calculated. Finally, the optimal method for each destination station is the one that provides the absolute minimum of MAE.
2.5.4.2 Algorithm for estimating missing data
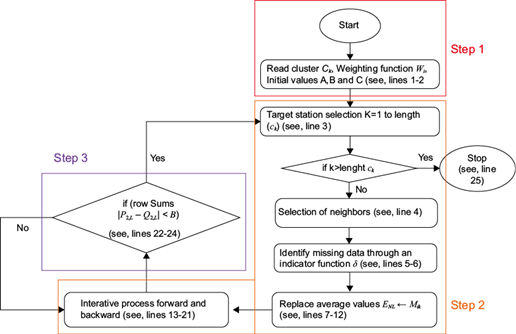
The purpose of the iterative algorithm described below (Fig. 3) is to establish reasonable imputed values for daily rainfall. Moreover, for the i-th target station belonging in the c k cluster, the weight-function W i (obtained through the methodology described in the subsection above) is required.
Firstly, the algorithm requires initial parameters. Line 1 introduces the weighting functions that are associated with the i-th stations belonging in the c k cluster. Then, line 2 introduces a series of initial values: A defines the maximum number of iterations to be considered, B defines the tolerance with which to work and C represents the initial value of a given counter.
Secondly, an iterative procedure is applied to each cluster from line 3 to line 21. In line 4, for each one of the x i target stations belonging in the cluster c k , the distance from the neighboring stations is calculated by using Eq. (10). Considering each one of the distances, the four neighboring stations corresponding to each one of the x i target stations are chosen. Then, the missing data is identified by using the δ indicator function, that is, δ = 1 if the daily rainfall data in x i is missing and δ = 0 otherwise. Line 6 assigns the original data matrix D NL , where N represents the whole set of available data in the study for every target station, and L represents the cluster length c k to a new matrix E NL . This is done in order to preserve the original data and not to lose them in the imputation process. From line 7 to line 12, the missing data is replaced by the average monthly rainfall, considering the historical behavior for each one of the target stations x i . We first calculate the average M ik monthly rainfall matrix for each one of the target stations x i . Then, for the lacking j in the original data E NL , corresponding to the month i in the target station k, the missing j is replaced by the monthly average in M ik . Finally, line 12 rewrites the data matrix that will be imputed and we name it F NL . From line 13 to 21, the main process for imputation of missing data is performed. In this part of the algorithm we start by reading the best method and its parameters (obtained in the subsection Methodology to find the optimal estimation method), the data of the x i target stations, the data of the x j , j ≠ i neighboring stations, as well as the different weighting functions W i associated with each one of the x i target stations. Then, only the missing data are estimated, that is, the data corresponding to a value of the function δ ≠ i. The mean value calculated in the previous stage is replaced by the values obtained when using the optimal methods. So far what has been done is a forward procedure where more than one neighboring station has been selected in order to estimate the missing values in one or in more than one target stations. Line 21 repeats the process started on line 16 but in an inverse manner. Therefore, a backward procedure is now being considered. It is possible that at the beginning of these processes great differences arise, but with the passage of the iterations the process eventually stabilizes.
Finally, the stop criterion is verified in lines 22 to 25. In lines 22 and 23, two descriptive statistics are computed: the mean and the variance per column for two consecutive iterations. These are saved in matrices P 2,L and Q 2,L , respectively. The first row of both matrices is composed by the arithmetic means, while in the second row the variances are found. In order to establish the stopping criterion, we evaluate whether the sum of each row of | P 2,L - Q 2,| is less than 10-13. Therefore, there are no significant differences between the data set with missing values and the complete data set.
In order to provide greater clarity of the iterative algorithm to estimate missing rainfall data, the flow diagram is presented in figure 4.
3. Results and discussion
3.1 Validation of the clusters’ structure
The validation and stability of the structure of the clusters is analyzed in figure 5a, which shows that clusters incorporate much information that results in high values of variance. As shown in this figure, there is a rapid decay until a point k = 4. From this k-value on, the marginal gain drops drastically and the total sum of the squared errors within the clusters tends to change slowly. As a result, an arm-like structure with an “elbow” is observed at the point k = 4. The optimal number of clusters corresponds, precisely, to the position of the elbow. However, the elbow method is heuristic and may or may not work always. For this reason, four different methods were also tested to compute the optimal k value; i.e., optimal number of clusters. Figure 5b shows the gap statistic method. This procedure compares the total within intra-cluster variation for different values of k with their expected values under a null reference distribution of the data. The optimal number of clusters is the value that maximizes the gap statistics. This means that the clustering structure is far away from the random uniform distribution of points (Tibshirani et al., 2001). This plot shows the statistics by number of clusters (k) with standard errors drawn with vertical segments and the optimal value of k marked with a vertical dashed blue line. According to this observation k = 4 is the optimal number of clusters in the data.
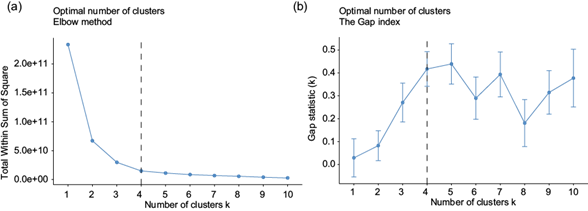
Fig. 5 Sum of squared error against number of clusters (scree plot). (a) Gap statistic. (b) Optimal number of clusters (k = 4).
Table III shows the results of comparing the TraceW, Hartigan and Krzanowski indices used to find the optimal k-value. In this way, five different methods were applied to estimate the optimal number of clusters. It is evident from these results that, in coincidence with the results of the elbow method, the optimal selection for k was 4.
Table III Values of the indices for data partitions in the state of Tabasco.
| Indices | Cluster number | Index value |
| TraceW(k) | 4 | 32255292808 |
| H(k) | 4 | 31.6603 |
| KL(k) | 4 | 10.3271 |
By analyzing the stability of the structure composed of four clusters, the following stability values were obtained: 0.9208770, 0.9051905, 1.0000000 and 1.0000000, respectively. It can therefore be seen that the four clusters are stable. This means that there is a high probability that all of these clusters represent the true structure in the data. Unlike our work, Teegavarapu (2014) carried out the estimation of missing precipitation data using optimal proximity metric-based imputation, nearest-neighbor classification and cluster-based interpolation methods. In this study different cluster sizes were experimented. A total of six clusters resulted in the best performance measures.
3.2 Application and evaluation of the different imputation methods
In order to evaluate the performance of 11 imputation methods (nine from previous studies and two new methods proposed here) of the four clusters, a data-set was selected without the presence of missing values. The comparison between the observed and imputed values was quantified using the MAE. The CMA-ES algorithm was employed in all of the weighting functions in order to find the optimal exponents.
Figure 6 shoes the behavior of the MAE for each one of the 11 allocation methods evaluated. The weather stations 27006, 27008, 27030 and 27054 were randomly selected to test these methods. The vertical axis represents the MAE, while the horizontal axis represents each of the methods mentioned in Table I. The new methods proposed here are identified by the numbers 10 and 11 in the above-mentioned figure. In weather stations 27006 and 27030 the method that shows the minimum MAE is the normal ratio, with values of 5.236 and of 5.498 mm day-1, respectively. In both cases the GCIDW proposal (the one identified through the number 11 in the figure) turns out to be the second-best selection. On the other hand, in the stations 27008 and 270054, the methods 9-11 (which incorporate the altitude factor in the weighting functions) present very similar results, although method 11’ shows the minimum MAE. Therefore, the new proposals presented in this paper, show better performance than the remaining methods considered.
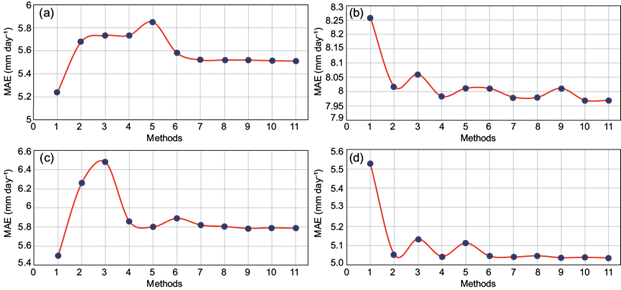
Fig. 6 Mean absolute error of the 11 deterministic imputation methods (Table I.). (a) station 27006, (b) station 27008, (c) station 27030 and (d) station 27054.
The values of MAE for each one of the 11 allocation methods evaluated is shown in Table IV, as well as the mean rank obtained by each imputation method according to the Friedmann test (Lee and Kang, 2015). In the last row, the symbol > denotes that the difference between one or more methods is statistically significant. For instance, {method1a} > {method2b} > {method3bc, method4c} indicates that the method 1 is significantly better than methods 2, 3 and 4. In addition, method 2 is significantly better than method 4, while method 3 does not differ significantly than methods 2, and 4 since it has common bc letters. Finally, method 3, despite not having differences with method 2 is placed next to method 4 since its average ranges are greater than those obtained by method 2 and more like those obtained by method 4.
Table IV Friedman test with MAE values.
| Station | NR | NRWC | CCW | NRIDW | IDW | CCWM | CIDW | NRIDC | HIDW | GNRIDW | GCIDW |
| 27002 | 4.58136(1) | 4.83451(8) | 4.96807(9) | 5.00777(10) | 5.15598(11) | 4.71146(7) | 4.70947(5) | 4.70949(6) | 4.70946(3) | 4.70946(3) | 4.70946(3) |
| 27004 | 6.77994(10) | 6.10653(5.5) | 6.16849(7) | 7.51878(11) | 6.32066(8.5) | 6.09563(4) | 6.08595(3) | 6.08093(2) | 6.32066(8.5) | 6.10653(5.5) | 6.07163(1) |
| 27006 | 5.23647(1) | 5.67940(8) | 5.73487(9) | 5.73614(10) | 5.85213(11) | 5.58435(7) | 5.52095(5) | 5.52142(6) | 5.51980(4) | 5.51524(3) | 5.51171(2) |
| 27007 | 6.34189(9) | 6.09271(3.5) | 6.18950(7) | 6.30211(8) | 6.37237(10.5) | 6.05466(2) | 6.11884(5) | 6.13374(6) | 6.37237(10.5) | 6.09271(3.5) | 6.04016(1) |
| 27008 | 8.25795(11) | 8.01815(9) | 8.05966(10) | 7.98298(5) | 8.01101(7.5) | 8.01078(6) | 7.98051(4) | 7.97959(3) | 8.01101(7.5) | 7.96975(2) | 7.96922(1) |
| 27009 | 6.40267(11) | 6.26948(9) | 6.35378(10) | 6.17743(6) | 6.26834(7.5) | 6.15654(1.5) | 6.16437(3) | 6.16509(4) | 6.26834(7.5) | 6.17518(5) | 6.15654(1.5) |
| 27011 | 7.01162(1) | 7.55082(11) | 7.49064(10) | 7.40102(8) | 7.35470(6) | 7.47037(9) | 7.36369(7) | 7.31915(4) | 7.35466(5) | 7.28865(3) | 7.20960(2) |
| 27015 | 7.95846(10) | 7.45377(3) | 7.48694(7) | 8.20322(11) | 7.60466(9) | 7.45438(4) | 7.46059(5) | 7.46128(6) | 7.58492(8) | 7.44972(1) | 7.44988(2) |
| 27019 | 6.15505(7) | 6.50947(8) | 6.70646(10) | 6.63368(9) | 6.81568(11) | 5.87313(4) | 5.86839(3) | 5.86729(2) | 6.00239(6) | 5.93986(5) | 5.86557(1) |
| 27021 | 6.42263(11) | 6.25919(9) | 6.28160(10) | 6.18465(5) | 6.22970(6.5) | 6.25370(8) | 6.16238(3) | 6.17260(4) | 6.22970(6.5) | 6.15686(2) | 6.14868(1) |
| 27030 | 5.49057(1) | 6.24662(10) | 6.46559(11) | 5.84851(8) | 5.78529(5) | 5.88026(9) | 5.80920(7) | 5.79325(6) | 5.77303(2.5) | 5.77951(4) | 5.77303(2.5) |
| 27034 | 4.79522(6) | 4.78950(5) | 4.85699(7) | 5.10866(11) | 4.99321(10) | 4.78209(4) | 4.92023(9) | 4.90330(8) | 4.72684(1.5) | 4.75235(3) | 4.72684(1.5) |
| 27036 | 6.33703(11) | 5.92331(4) | 5.94339(5) | 5.99212(8) | 6.11030(9.5) | 5.92106(1.5) | 5.99035(7) | 5.98986(6) | 6.11030(9.5) | 5.92271(3) | 5.92106(1.5) |
| 27037 | 6.13804(9) | 5.32788(7) | 5.68747(8) | 6.14029(10) | 6.17238(11) | 5.26160(4) | 5.32653(6) | 5.32557(5) | 5.25829(3) | 5.25275(2) | 5.25078(1) |
| 27039 | 6.19450(1) | 6.29664(5) | 6.34208(6) | 6.73254(11) | 6.42501(9.5) | 6.29204(3) | 6.38629(8) | 6.38101(7) | 6.42501(9.5) | 6.29424(4) | 6.28707(2) |
| 27040 | 5.08625(1) | 5.35654(8) | 5.38551(9) | 5.51924(11) | 5.48610(10) | 5.35309(7) | 5.21965(3) | 5.22774(5) | 5.32263(6) | 5.22181(4) | 5.21821(2) |
| 27042 | 6.98728(11) | 6.43215(9) | 6.67242(10) | 6.29520(8) | 6.28697(7) | 6.26032(3) | 6.26488(4) | 6.27846(5) | 6.28578(6) | 6.25526(2) | 6.25303(1) |
| 27044 | 5.42147(11) | 4.06819(8) | 4.82861(10) | 4.24727(9) | 4.03553(3) | 4.04552(6) | 4.06398(7) | 4.02684(1) | 4.03553(3) | 4.03769(5) | 4.03553(3) |
| 27047 | 7.93838(8) | 7.64081(6.5) | 7.57245(5) | 8.55550(11) | 7.52067(2.5) | 7.52067(2.5) | 8.40706(10) | 8.31264(9) | 7.52067(2.5) | 7.64081(6.5) | 7.52067(2.5) |
| 27050 | 4.23082(1) | 4.34225(10) | 4.34457(11) | 4.27002(6) | 4.27301(7) | 4.34123(9) | 4.26911(5) | 4.27618(8) | 4.25479(4) | 4.24716(3) | 4.24713(2) |
| 27054 | 5.52828(11) | 5.05456(8) | 5.13519(10) | 5.04497(5) | 5.11411(9) | 5.04601(6) | 5.04123(4) | 5.04756(7) | 5.03795(2) | 5.03950(3) | 5.03697(1) |
| 27060 | 5.82079(11) | 5.10067(7) | 5.41674(8) | 5.07405(6) | 5.75415(9.5) | 5.03720(4) | 5.02729(3) | 5.02691(2) | 5.75415(9.5) | 5.07345(5) | 5.02561(1) |
| 27061 | 6.23225(11) | 4.50914(9) | 5.69481(10) | 4.25795(8) | 4.23449(6) | 4.22712(4) | 4.23210(5) | 4.23722(7) | 4.22547(2) | 4.22699(3) | 4.22537(1) |
| 27070 | 7.13218(11) | 6.82955(9) | 7.07248(10) | 6.70350(8) | 6.61122(2.5) | 6.65384(7) | 6.61371(4) | 6.60310(1) | 6.61122(2.5) | 6.62048(5.5) | 6.62048(5.5) |
| 27075 | 8.41981(11) | 7.65928(6) | 7.75188(7) | 7.89028(10) | 7.86985(9) | 7.62878(3) | 7.65905(5) | 7.65235(4) | 7.77776(8) | 7.61372(2) | 7.61337(1) |
| 27076 | 7.54194(11) | 7.17438(3.5) | 7.26591(5) | 7.34792(8) | 7.41980(9.5) | 7.16741(1.5) | 7.29444(7) | 7.28799(6) | 7.41980(9.5) | 7.17438(3.5) | 7.16741(1.5) |
| 27077 | 8.33861(1) | 8.52334(6.5) | 8.54961(8) | 8.64898(11) | 8.57721(9.5) | 8.40869(3) | 8.42298(5) | 8.41384(4) | 8.57721(9.5) | 8.52334(6.5) | 8.33910(2) |
| 27078 | 6.68910(1) | 6.88344(7) | 7.02124(9) | 6.94311(8) | 7.21660(11) | 6.84699(2.5) | 6.85039(5) | 6.85037(4) | 7.17412(10) | 6.87759(6) | 6.84699(2.5) |
| 27084 | 5.18968(11) | 4.89849(4.5) | 4.98309(8) | 4.93012(7) | 5.12807(9.5) | 4.88829(3) | 4.92240(6) | 4.87912(2) | 5.12807(9.5) | 4.89849(4.5) | 4.81314(1) |
| Ranking | 7.28 | 7.14 | 8.48 | 8.52 | 8.22 | 4.67 | 5.28 | 4.83 | 6.09 | 3.74 | 1.76 |
{GCIDWa,GNRIDWa}>{CCWMb,NRIDCb,CIDWb}>{HIDWbc,NRWCbc,NRbc,IDWc,CCWc,NRIDWc}
Lower ranking implies that the method is better. Equal letters a, b, c, d mean that the methods belong to the same homogenous subgroup. Different superscripts imply that the methods belong to different homogeneous subgroups. Superscript represents the range obtained for each method by meteorological station. If there are tied values, it is assigned to each tied value the average of the ranges that would have been assigned without ties.
The results presented in Table IV show that the calculations of MAE when applying the GCIDW method with the exception of one case (weather station 27070) were always between the three lowest values (see superscript values). Therefore, GCIDW obtained the smallest mean rank. Besides, there is a significant difference between all the methods evaluated (significant p-value equal to 0.000). The MAE values in this work were similar to those obtained by other researchers (Deraisme et al., 2001; Suhaila et al., 2008; Qian et al., 2010; Seyyednejad et al., 2012; Serrano-Notivoli et al., 2017b). In particular, the MAE values are between 4 and 8.6 mm with an average value close to 6 mm. Overall, performance results show that CCWM is superior compared to other methods found in the literature. Similar results were obtained by Azman et al. (2015) when they estimated missing rainfall data in Pahang using spatial interpolation weighting methods, probably due to the fact that the used stations were in the same cluster, and it indicates a strong relationship between all the stations.
To identify which method or methods are significantly different, the Nemenyi post hoc test (Pohlert, 2014) was performed. The results indicated there are three well-defined homogeneous subgroups (see last row in Table IV.), with the proposed method (GCIDW) being statistically significantly better than the other methods compared. Therefore, GCIDW can be considered the best method to estimate missing rainfall data among the methods analyzed. In Table V the optimal method for all of the stations within each cluster is presented. The proposed imputation methods resulted optimal in 13 of the 29 stations analyzed (this represents approximately 44.83% of the weather stations). In order of priority, NR, CCWM, NRIDC and HIDW were found in 9, 4, 2 and 1 stations, respectively.
Table V Selection of the optimal method for all stations within each cluster.
| Membership | Station | Optimal method | MAE | p | q | s |
| Cluster 1 | 27007 | 11 | 6.040 | 6.33 | 6.91·10-9 | 0.214 |
| 27008 | 11 | 7.969 | 2.23 | 1.24 | 5.97·10-9 | |
| 27015 | 10 | 7.45 | 2.62·10-9 | 2.18·10-1 | - | |
| 27037 | 11 | 5.251 | 3.95 | 1.18·10-9 | 2.89 | |
| 27039 | 1 | 6.194 | - | - | - | |
| 27060 | 11 | 5.026 | 6.4 | 3.85·10-9 | 0.386 | |
| 27075 | 11 | 7.613 | 2.41 | 1.72·10-9 | 1.27 | |
| 27076 | 5 | 7.167 | 2.86 | - | - | |
| 27077 | 1 | 8.339 | - | - | - | |
| 27078 | 1 | 6.689 | - | - | - | |
| Cluster 2 | 27002 | 1 | 4.581 | - | - | - |
| 27009 | 5 | 6.157 | 8.323 | - | - | |
| 27034 | 9 | 4.727 | 1.96 | 3.36 | - | |
| 27036 | 5 | 5.921 | 1.784 | - | - | |
| 27050 | 1 | 4.231 | - | - | - | |
| 27054 | 11 | 5.037 | 1.116 | 3.61 | 1.098 | |
| 27084 | 11 | 4.813 | 18.283 | 5.96·10-9 | 6.137 | |
| Cluster 3 | 27004 | 11 | 6.072 | 30.5 | 10.776 | 0.278 |
| 27006 | 1 | 5.236 | - | - | - | |
| 27021 | 11 | 6.149 | 3.99 | 1.263 | 10-4 | |
| 27040 | 1 | 5.086 | - | - | - | |
| 27047 | 5 | 7.521 | 10-4 | - | - | |
| Cluster 4 | 27011 | 1 | 7.012 | - | - | 9.42·10-9 |
| 27019 | 11 | 5.866 | 14.5 | 3.17 | 9.42 | |
| 27030 | 1 | 5.491 | - | - | - | |
| 27042 | 11 | 6.253 | 3.8 | 1.16 | 2.56·10-9 | |
| 27044 | 8 | 4.027 | 9.94·10-9 | - | - | |
| 27061 | 11 | 4.225 | 7.93 | 4.67·10-10 | 0.529 | |
| 27070 | 8 | 6.603 | 1.36·10-9 |
Considering the large number of stations, it would be impractical and difficult to examine in detail a box diagram or an error histogram for each weather station. In Table VI a series of basic statistics that synthesize and highlight the performance of each of the optimal methods for the original and imputed series, is shown. For all of the stations the basic statistics between both series are very similar. Regarding the arithmetic mean of daily rainfall, it is computed that, for the most part, values corresponding to the imputed series are slightly below the values of the observed series. The same happens for scattering statistics. The form statistics shows that the imputed series presents a positive biased distribution with a high concentration of rainfall values in the central zone of the distribution. Considering the results of Table VI, it can be concluded that the proposed iterative process allowed imputation of the missing data without significantly altering the distribution of the precipitation time series. Therefore, the imputed series of rainfall data does not present significant differences with respect to the original series.
Table VI Performance statistics for the original and imputed series.
| Membership | Station | Series | Mean | STD | VC | S | K |
| Cluster 1 | 27007 | Original | 5.694 | 17.365 | 3.050 | 6.768 | 75.527 |
| imputed | 5.560 | 16.758 | 3.014 | 6.811 | 76.970 | ||
| 27008 | Original | 5.686 | 16.425 | 2.888 | 6.234 | 61.613 | |
| imputed | 5.617 | 16.097 | 2.866 | 6.203 | 61.018 | ||
| 27015 | Original | 6.569 | 16.485 | 2.510 | 4.149 | 23.338 | |
| imputed | 6.264 | 15.686 | 2.504 | 4.354 | 25.960 | ||
| 27037 | Original | 5.680 | 15.312 | 2.696 | 5.258 | 44.671 | |
| imputed | 5.650 | 15.306 | 2.709 | 5.251 | 44.322 | ||
| 27039 | Original | 5.487 | 15.386 | 2.804 | 5.494 | 46.127 | |
| imputed | 5.450 | 15.252 | 2.799 | 5.527 | 46.516 | ||
| 27060 | Original | 5.439 | 15.601 | 2.868 | 5.543 | 47.752 | |
| imputed | 5.397 | 15.361 | 2.846 | 5.526 | 47.220 | ||
| 27075 | Original | 6.297 | 18.346 | 2.914 | 5.887 | 53.335 | |
| imputed | 6.231 | 18.073 | 2.901 | 5.852 | 52.796 | ||
| 27076 | Original | 6.292 | 19.518 | 3.102 | 7.141 | 74.564 | |
| imputed | 6.133 | 18.257 | 2.977 | 7.131 | 77.017 | ||
| 27077 | Original | 5.850 | 18.561 | 3.173 | 5.638 | 48.432 | |
| imputed | 5.798 | 17.846 | 3.078 | 5.697 | 50.146 | ||
| 27078 | Original | 4.871 | 15.133 | 3.107 | 6.693 | 73.289 | |
| imputed | 4.859 | 14.838 | 3.054 | 6.714 | 74.634 | ||
| Cluster 2 | |||||||
| 27002 | Original | 3.920 | 12.588 | 3.211 | 6.987 | 81.330 | |
| imputed | 3.947 | 12.132 | 3.074 | 6.985 | 83.146 | ||
| 27009 | Original | 4.801 | 15.082 | 3.142 | 6.154 | 56.439 | |
| imputed | 4.713 | 14.562 | 3.089 | 6.586 | 67.426 | ||
| 27034 | Original | 4.501 | 14.584 | 3.240 | 7.131 | 82.448 | |
| imputed | 4.534 | 14.324 | 3.159 | 7.049 | 81.585 | ||
| 27036 | Original | 5.433 | 15.387 | 2.832 | 6.438 | 73.218 | |
| imputed | 5.440 | 15.284 | 2.809 | 6.411 | 73.007 | ||
| 27050 | Original | 4.264 | 13.181 | 3.091 | 6.764 | 70.298 | |
| imputed | 4.339 | 13.022 | 3.001 | 6.697 | 69.929 | ||
| 27054 | Original | 5.386 | 15.283 | 2.838 | 5.776 | 55.439 | |
| imputed | 5.409 | 15.124 | 2.796 | 5.759 | 55.272 | ||
| 27084 | Original | 4.860 | 14.199 | 2.922 | 5.768 | 49.995 | |
| imputed | 4.794 | 14.189 | 2.960 | 6.222 | 61.476 | ||
| Cluster 3 | 27004 | Original | 6.303 | 15.400 | 2.443 | 4.106 | 22.623 |
| imputed | 6.342 | 15.443 | 2.435 | 4.091 | 22.386 | ||
| 27006 | Original | 4.672 | 12.639 | 2.705 | 5.585 | 52.496 | |
| imputed | 4.657 | 12.521 | 2.689 | 5.602 | 53.069 | ||
| 27021 | Original | 5.418 | 14.518 | 2.679 | 4.602 | 30.757 | |
| imputed | 5.243 | 13.645 | 2.603 | 4.755 | 33.368 | ||
| 27040 | Original | 4.518 | 12.503 | 2.767 | 5.834 | 55.724 | |
| imputed | 4.519 | 12.420 | 2.748 | 5.802 | 55.484 | ||
| 27047 | Original | 5.823 | 15.746 | 2.704 | 4.742 | 30.459 | |
| imputed | 5.756 | 14.634 | 2.542 | 4.784 | 32.302 | ||
| Cluster 4 | 27011 | Original | 7.70 | 19.35 | 2.513 | 4.52 | 29.63 |
| imputed | 7.79 | 18.89 | 2.425 | 4.47 | 29.56 | ||
| 27019 | Original | 7.115 | 18.879 | 2.653 | 4.866 | 34.161 | |
| imputed | 7.173 | 18.962 | 2.643 | 4.855 | 33.868 | ||
| 27030 | Original | 6.404 | 16.509 | 2.578 | 4.532 | 29.318 | |
| imputed | 6.423 | 16.488 | 2.567 | 4.523 | 29.263 | ||
| 27042 | Original | 9.836 | 23.111 | 2.350 | 4.670 | 32.974 | |
| imputed | 9.638 | 22.877 | 2.374 | 4.719 | 33.577 | ||
| 27044 | Original | 8.988 | 20.527 | 2.284 | 4.131 | 25.608 | |
| imputed | 8.985 | 20.488 | 2.280 | 4.126 | 25.554 | ||
| 27061 | Original | 10.519 | 23.230 | 2.208 | 4.080 | 26.783 | |
| imputed | 10.229 | 23.011 | 2.249 | 4.199 | 27.749 | ||
| 27070 | Original | 8.842 | 20.741 | 2.346 | 4.366 | 28.835 | |
| imputed | 8.819 | 20.701 | 2.347 | 4.366 | 28.790 |
Finally, the inclusion of the factor that measures the difference in altitude between the target station and the neighboring stations, as well as the optimization of the parameters corresponding to the correlation exponents, p, distance, q and altitude, s, contributed significantly to the computation of better estimates of missing rainfall values.
4. Conclusions
In this work we have proposed two new generalized weighting methods and a methodology to fill missing data through using the optimal method and parameters. In these procedures we have incorporated the altitude difference between the target station and the neighboring stations, as a new variable. The performance of each method was quantified by the MAE. For all of the weight-functions required to find optimal exponents, the metaheuristic adaptation of the covariance matrix (CMA-ES) was employed. The results of this process show that the proposed methods are optimal at 44.83%, followed by the classical normal ratio method with approximately 31%.
The weather stations of the state of Tabasco were clustered through the K-mean procedure, which is based on the Euclidean distance. In our analysis, UTM coordinates were used in order to locate the weather stations representing each east coordinate as a value on the x-axis and each north coordinate as a value on the y-axis. In order to validate the amount of clusters, five methods were employed: (1) elbow method, (2) gap statistics, (3) TraceW index, (4) Hartigan index, and (5) Krzanowski and Lai index. The first two are graphic methods and in all cases the same results were computed. The study on the validity of the optimal number of clusters ends up with the stability study by using an algorithm based on the bootstrap method. All of the stability indices ensured that the four clusters obtained represent the true structure of the dataset.
Choosing the optimal procedure for the analysis of missing data is a huge task, since a particular method can provide optimal estimates only for certain situations. In this regard, when analyzing missing data, our research shows that it is necessary to apply more than one alternative to evaluate each case and decide which method should be the optimal. In terms of performance, one of our proposals, specifically the GCIDW, yields better results in estimating missing rainfall data than those commonly used in literature. The numerical and graphical results computed by comparing the statistics of the original rainfall series with the imputed series show that there are no significant differences between the two series. Therefore, complete daily rainfall databases were obtained without significant statistical differences for the analyzed period (1980-2012). This procedure can be used in future research such as, for instance, multifractal rainfall analysis. The new methods proposed in this work represent new tools not only for the treatment of rainfall missing data in the specific stations analyzed, but they can be safely applied to any other set of weather stations anywhere.











 nueva página del texto (beta)
nueva página del texto (beta)