Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Educación química
versión impresa ISSN 0187-893X
Educ. quím vol.19 no.3 Ciudad de México jul. 2008
Cómo se diseña
¡Un tetraedro en mi bolsa!
A tetrahedron in my bag!
Aarón Pérez-Benítez y Rosa Elena Arroyo-Carmona*
* Centro de investigación de la Facultad de Ciencias Químicas. Benemérita Universidad Autónoma de Puebla. 14 Sur y Av. San Claudio. Col. San Manuel. Puebla, Pue. C.P. 72570. Dirección electrónica: aronper@siu.buap.mx
Recibido: 18 de septiembre de 2007.
Aceptado: 19 de enero de 2008.
Abstract
The construction of a physical model of a tetrahedron starting from a plastic bag is presented. The model can be applied in the learning-teaching of symmetry and stereochemistry of simple molecules possessing atoms with a tetrahedral arrangement of their valence shell's electron pairs, such as oxygen in water, nitrogen in ammonia and carbon in methane.
Enclosing balls, a tetrahedral skeletal model or simple air in the tetrahedral bag is possible to achieve different applications of the model, including the funny and harmless explosion of the bag.
Keywords: Threedimensional model, VSEPR, tetrahedral geometry, homemade model.
Justificación
A pesar de que el tetraedro es bastante frecuente en la vida cotidiana, una buena parte de la población, incluyendo a muchos estudiantes de nivel superior y medio superior, ignora o ha olvidado no sólo sus características geométricas, sino también su nombre correcto (Arroyo-Carmona, 2005). Por ejemplo, es común escuchar frases como: "déme un jugo de triangulito", "es un triángulo" o "la pirámide", para referirse a un producto en empaque tetraédrico o a una forma tetraédrica.1
Al respecto, al buscar en la red dos productos alimenticios que se comercializan en empaques tetraédricos, en sus portales electrónicos a ambos empaques se les menciona como... ¡"triangulares"! (figura 1: Cooperativa, 2007; Lucas, 2007).

Así, con el fin de contribuir a mejorar la enseñanza-aprendizaje de la geometría tetraédrica se presenta la construcción rápida y sencilla de un tetraedro a partir de una bolsa de plástico.
Objetivos
— Contribuir a mejorar la enseñanza-aprendizaje de la geometría espacial.
— Describir la construcción rápida y sencilla de un tetraedro a partir de una bolsa de plástico.
— Proponer variantes del modelo con aplicación a la enseñanza de la geometría, la estereoquímica y la simetría de moléculas tetraédricas sencillas.
Aspectos básicos de la geometría tetraédrica
La palabra tetraedro proviene del griego tetra que significa cuatro y hedra que significa base o asiento. Es un poliedro regular que se conoce desde la antigüedad y forma parte de los denominados sólidos platónicos. Sus características geométricas más importantes se resumen en la tabla 1 (Jackson, 2007).

El tetraedro en la química
Existe una enorme cantidad de moléculas tetraédricas derivadas de distintos elementos de la tabla periódica y los maestros de química (y sobre todo los de química orgánica) nos referimos a ellas sin hacer notar a los estudiantes que existen de dos tipos: las que contienen un átomo en el centro del tetraedro y las que no. La diferencia entre unas y otras es la conectividad que tienen los átomos que se encuentran en los vértices, pues mientras que en las primeras dichos átomos se encuentran enlazados entre sí (e.g. el fósforo blanco, figura 2a: Image, 2007; Henderson, 2000), en las segundas sólo se hallan enlazados con el átomo central (e.g. el metano, figura 2b; Reboiras, 2006).

Este hecho que parece tan sencillo es, sin embargo, motivo de confusión para algunos estudiantes de los cursos preliminares de química general y de química orgánica, pues cuando por primera vez oyen hablar de moléculas tetraédricas piensan que hay enlaces a lo largo de las aristas del tetraedro cuando en realidad no los hay.
En contraste, en otros casos en los que el profesor usa modelos de varillas para ilustrar moléculas tetraédricas con átomo central, muchos estudiantes no alcanzan a percibir la forma tetraédrica u otras características propias del tetraedro, tales como la ubicación de sus elementos de simetría con relación a sus vértices y aristas.
En estos casos se antoja usar los modelos moleculares tridimensionales más apropiados para cada fin, pero éstos usualmente están fuera del alcance económico de la mayoría de los estudiantes o no existen modelos especializados para ilustrar el tópico en cuestión. Por estas razones en este artículo se presenta la manera de construir un tetraedro a partir de una bolsa de polietileno, modelo al que pueden hacérsele distintos agregados como: dibujarle los símbolos estereográficos del grupo puntual Td, meterle pelotas o un modelo tetraédrico de varillas o simplemente llenarlo con aire.
Construcción del modelo
Un tetraedro inflable a partir de una bolsa de plástico. (Edad recomendada: niños de 9 años en adelante).
a) Materiales y herramientas
1 bolsas de polietileno de 15 cm de ancho.
1 trozo de pajilla o popote de plástico de 7 cm de largo.
25-30 cm de cinta adhesiva transparente.
1 tijeras.
1 regla.
b) Procedimiento
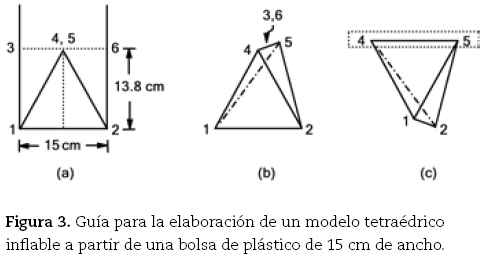
1. Trace una línea paralela al fondo de la bolsa a 13.8 cm de altura y corte sobre ella (figura 3 a).
2. Abra la bolsa separando los puntos 4 y 5 y vuélvala a cerrar juntando 3 y 6. Note que 3 y 6 están marcados naturalmente por el doblez natural de la bolsa, por lo que al juntarlos se definen automáticamente los puntos 4 y 5 (figura 3a-b).
4. Sobre una mesa fije el trozo de cinta adhesiva. Para ello pegue una punta a la mesa, extiéndala en sentido inverso y pegue el otro extremo doblándole la punta. Después de esta operación la cinta habrá quedado con la parte adhesiva boca arriba, a excepción de las puntas.
5. Pegue la boca de la bolsa previamente doblada como se indicó en el paso 2, empleando la mitad del ancho de la cinta adhesiva (figura 3 c).
6. Para pegar la parte complementaria de la boca, gire 180° la bolsa, cuidando de que no se hagan pliegues en ella. Presione firmemente con los dedos para que quede bien sellada la bolsa y corte los sobrantes de la cinta.
8. Con un bolígrafo haga un pequeño orificio a la bolsa e insértele el popote, el cual debe de quedar bien ajustado al orificio para que el aire no se salga. Sople a través del popote y cuando la bolsa haya alcanzado el máximo de su volumen doble el popote y péguelo con un trocito de cinta adhesiva. El modelo terminado se presenta en la figura 4a.
Para construir este tipo de modelo a partir de una bolsa de otro tamaño se requiere obviamente de recalcular mediante el teorema de Pitágoras, la nueva altura a la que deberá cortarse la bolsa. En la tabla 2 se presentan algunos ejemplos.

Agregados y aplicaciones del modelo
a) Un modelo que ilustra las caras y aristas del tetraedro. (Edad recomendada: niños de 9 años en adelante)
Para ilustrar las características externas del poliedro, antes de pegar la bolsa, pinte las aristas 1-2; 1-3; 2-6; 3-6; 1-4 y 2-4 con tinta permanente. Alternativamente puede construirse un tetraedro con seis popotes de 14 cm (según se describe en la literatura: Pérez-Benítez, 1991) e introducirse en la bolsa antes de cortarla y sellarla (figura 4b).
b) Un modelo que ilustra los elementos de simetría del grupo puntual Td (nivel de estudios recomendado: medio superior en adelante).
Para el estudio de la simetría Td trace los segmentos (1-3; 1-2 y 2,6); (3-6; 4-a); (1-4; 1-c; 4-c) y (2-3; 3-4; 4-2) por ambos lados de la bolsa. Estos segmentos representarán los seis planos de simetría (cada uno conteniendo una arista). Asimismo, la posición de los cuatro ejes C3 (cada uno conteniendo un vértice), de los tres ejes C2 (cada uno bisecando pares de aristas opuestas) y de los tres ejes S4 (colineales con los ejes C2) pueden marcarse usando los símbolos estereográficos correspondientes (figura 5b; Quinkert, 1996).
c) Un modelo inflable y con vértices numerados, útil para determinar la quiralidad de un centro estereogénico tetraédrico. (Material didáctico recomendado para los cursos de estereoquímica orgánica de nivel licenciatura)
Para determinar la quiralidad de un centro estereogénico tetraédrico puede obviarse la posición de éste y marcarse únicamente los vértices del tetraedro con los números 1-4. Dichos números corresponderán a las prioridades de los sustituyentes, las cuales se determinan de acuerdo con las reglas de Cahn, Ingold y Prelog (Cahn, 1956). Dado que estos números pueden arreglarse en el espacio de dos maneras distintas se recomienda elaborar dos modelos: uno indicando la disposición de los sustituyentes 1-2-3 en sentido de las manecillas del reloj (figura 6) y el otro en contrasentido. Esta aplicación se describe con amplitud en la literatura (Arroyo-Carmona, 2003).

d) Un modelo que representa a una molécula sencilla cuyo átomo central posee pares de electrones de valencia arreglados tetraédricamente. (Recomendado para la enseñanza-aprendizaje de la teoría de repulsiones de pares de electrones en la capa de valencia, VSEPR, desde el nivel medio hasta el superior).2
De acuerdo a la teoría VSEPR, si un átomo central contiene cuatro pares de electrones en su capa de valencia, éstos se disponen tetraédricamente para disminuir al mínimo sus repulsiones electrostáticas. Los casos que pueden presentarse son: AX4E0, AX3E1 y AX2E2, los cuales producen geometrías moleculares tetraédrica, piramidal y angular, respectivamente (tabla 3).

Construcción del modelo
Siga los pasos antes mencionados para la construcción del tetraedro inflable, pero antes de sellar la bolsa introduzca cuatro esferas de unicel de 4.5 cm y una de 5 cm. Acomode las esferas procurando que ocupen el menor espacio posible para poder sellar la bolsa. Una vez sellada desplace las esferas iguales hasta los vértices del tetraedro y la más grande al centro.
Las esferas deben colorearse previamente con pinturas base agua para representar al átomo central (esfera grande, color X), a los pares de electrones libres (esferas pequeñas, color Y) y a los pares de electrones de enlace (esferas pequeñas, color Z). El número de esferas coloreadas X o Y dependerá del caso de molécula que se quiera representar. Se sugieren los ejemplos de la tabla 3. El modelo terminado que representa al agua (especie química A2X2E2) se presenta en la figura 7.

e) Modelos que representan especies químicas tetraédricas sin átomo central. (Recomendado para la enseñanza-aprendizaje de la geometría tetraédrica de sólidos inorgánicos en los cursos de química inorgánica de nivel licenciatura)
Para representar una molécula tetraédrica sin átomo central como el fósforo blanco, P4 (Henderson, 2000), introduzca cuatro esferas de unicel de 4 cm de diámetro en una bolsa de 10 x 20 cm. Acomode dos esferas en el fondo de la bolsa y las otras dos en forma alternada. Presione las esferas para que ocupen el menor espacio posible. Posteriormente corte la bolsa y séllela como se indicó en el procedimiento general. El modelo terminado se presenta en la figura 8a.

Para modelar otras especies químicas tetraédricas sin átomo central como el cúmulo Au20 (Li, 2003), proceda de la misma manera pero empleando 20 esferas de unicel de 3 cm para una bolsa de 14 x 20 cm (figura 8b).
f) Modelo tetraédrico de varillas dentro de una bolsa tetraédrica de plástico. (Recomendado para la enseñanza-aprendizaje de la geometría de moléculas con átomo central tetraédrico como el metano, CH4 (Reboiras, 2006), en un curso de estereoquímica orgánica de nivel licenciatura)
Si tiene un modelo tetraédrico de varillas o palillos, mida la distancia entre dos vértices, y consiga o elabore una bolsa de esa medida. Introdúzcalo dentro de la bolsa haciendo coincidir sus vértices; recorte y selle la bolsa.
Si no dispone del modelo de palillos entonces elabore uno de la siguiente manera (figura 9):
a) Para una bolsa de 15 cm de arista, recorte dos popotes de 18.4 cm y engrápelos por su parte central formando ángulos de 90° (figura 9a).
b). Doble los popotes formando dos "V's" en planos perpendiculares y una invertida con respecto a la otra (figura 9b). Este ensamble adquirirá rigidez al introducirlo en la bolsa tetraédrica si se hacen coincidir los vértices de ambos modelos. El modelo terminado se presenta en la figura 9 c.
Conclusión
Debido a que la geometría tetraédrica es harto frecuente en la química es necesario que los estudiantes alcancen un alto grado de visualización espacial con ayuda de un modelo que les permita posteriormente operar mentalmente este tipo de moléculas. Los modelos que se presentan en este trabajo han sido elaborados en una sesión de laboratorio de 2 horas y posteriormente se usaron con bastante éxito en un curso de química orgánica básica, para la enseñanza-aprendizaje de la simetría y la quiralidad de moléculas tetraédricas y como apoyo para establecer la dirección del momento dipolar molecular de moléculas tipo AXmEn (donde m + n = 4) como resultado de su geometría (Moore, 2002b).
La elaboración del modelo en su versión más simple fue probada con niños de quinto y sexto grado de educación elemental durante la XIV Semana Nacional de Ciencia y Tecnología. Algunos niños se divirtieron haciendo estallar el modelo y otros decidieron desinflarlo, plegarlo y llevárselo a casa (figura 10a). Una versión rápida del modelo puede elaborarse en cuestión de segundos sin ningún otro material que la bolsa misma, simplemente enrollando la boca de la bolsa (dispuesta como se indica en el inciso "a") hasta una altura tal que, grosso modo, las cuatro aristas que se van formando igualen en tamaño a la del fondo y la boca de la bolsa (figura 10b).

Para estudiantes de licenciatura o posgrado, la lectura de este artículo puede complementarse con el sitio virtual interactivo "MolArch+ Graphics" en donde pueden visualizarse diversos ejemplos de moléculas tetraédricas con y sin átomo central (Immel, 2007).
Bibliografía
Arroyo-Carmona, R. E.; Fuentes López, H.; Méndez-Rojas, M. Á. y Pérez-Benítez, A. La geometría: ¡Un pie que cojea en la enseñanza de la estereoquímica; Educ. quím., 16 (Núm. Extraord.), 184-190, 2005. [ Links ]
Arroyo-Carmona, R. E.; Pérez-Benítez, A. Modelos tridimensionales para la enseñanza de la quiralidad en átomos tetraédricos, Educ. quím., 14(1), 31-35, 2003. [ Links ]
Brown, W. H., Foote, C. S.; Brent L. I. Organic Chemistry, Belmont, CA: Thomson Brooks/Cole, 2005, p. 24. [ Links ]
Cahn, R. S.; Ingold, C. K. y Prelog, V. The specification of asymmetric configuration in organic chemistry, Experientia, XII(3), 81, 1956. [ Links ]
Henderson, W. Main Group Chemistry, Tutorial chemistry texts, 3. Cambridge, UK: Royal Society of Chemistry, 2000, p. 24. [ Links ]
Li, J.; Li, X.; Zai, H.-J.; Wang, L.-S. Au20: A tetrahedral cluster, Science, 293, 864, 2003. [ Links ]
Maier, G.; Neudert, J.; Wolf, O.; Pappusch, D.; Sekiguchi, A.; Tanaka, M.; Matsuo, T., J. Am. Chem. Soc., 124, 13919-13826, 2002. [ Links ]
Mislow, K. M. Introduction to Stereochemistry, Mineola, N.Y.: Dover Publications, 2002. Cap. 1. [ Links ]
Moore, J. W.; Stanitsky, C. L.; Jurs, P. C. Chemistry: The Molecular Science, Fort Worth: Harcourt College Publishers, 2002, (a) p. 387; (b) p. 405. [ Links ]
Pérez-Benítez, A.; González-Vergara, E. Un tetraedro o un tetraedro alargado a partir de un popote y un cordel, Educ. quím., 2(4), 198-200, 1991. [ Links ]
Quinkert, G. Aspects of Organic Chemistry: Structure, Basel: Verlag Helvetica Chimica Acta, 1996. [ Links ]
Reboiras, M. D. Química: la ciencia básica, Madrid: Thomson, 2006, p. 1048. [ Links ]
Recursos electrónicos citados
Cooperativa de Trabajadores Pascual. En línea: <http://www.pascual.com.mx/index_home.html>. Última consulta: 8 de septiembre de 2007.
Image: White phosphorous molecule.jpg - Wikipedia, the free encyclopedia. En línea: <http://en.wikipedia.org/wiki/Image:White_phosphrous_molecule.jpg>. Última consulta: 1 de diciembre de 2007.
Immel, S. "MolArch+ Graphics". En línea: <http://csi.chemie.tu-darmstadt.de/ak/immel/script/redirect.cgi?filename=http://csi.chemie.tu-darmstadt.de/ak/immel/tutorials/symmetry/index3.html>. Última consulta: 8 de septiembre de 2007. [ Links ]
Jackson, F.; Weisstein, E. W. "Tetrahedron" From MathWorld-A Wolfram Web Resource. En línea: <http://mathworld.wolfram.com/Tetrahedron.html>. Última consulta: 6 de septiembre de 2007. [ Links ]
Lucas.com.mx. En línea: <http://www.lucasworld.com/index_prin-inv.asp> Última consulta: 8 de septiembre de 2007.
1 Éstas y otras ideas alternativas sobre los cuerpos geométricos más comunes se han podido identificar en diversos sectores y niveles de estudio de la población escolar durante talleres de divulgación científica en los que ha participado el autor.