Introduction
The issue of how exchange rate volatility influences agricultural trade has been broadly analyzed in empirical literature. Following the Bretton Woods exchange rate system collapse in the early 1970s, there has been increasing concern within research about the effects of exchange rate variability on primary commodity prices. Worth mentioning among the pioneer papers trying to assess such effects is Rindler and Yandle’s (1972) work. They proposed a comparative static single-commodity model in order to analyze the impact of exchange rate changes on the price of a specific primary commodity. The authors estimated price-elasticity coefficients and concluded that it is desirable to consider a range of possible elasticities in order to gather conclusive evidence about these effects. On the other hand, Gilbert (1989) measured the impact of exchange rates and debt of developing countries on commodity prices. The author used the Rindler and Yandle (1972) model in his analysis and applied an error correction model. He concluded that the interaction between dollar appreciation and less developed countries’ (LDC) dollar-denominated debt were responsible for the low real level of commodity prices. Similarly, research done by Dornsbuch (1985) and Beenstock (1988) found long-run elasticities of dollar commodity prices with respect to changes in dollar exchange rate. However, according to Gilbert (1989), the elasticities from Dornsbuch (1985) and Beenstock (1988) are quite large because they used an inappropriate exchange rate index and ignored the effects of LDC indebtedness on dollar commodity prices.
Considering the law of one price, Gilbert (1991) applied a static partial equilibrium model, following Ridler and Yandle (1972), to analyze the impact of exchange rate changes on primary commodity prices. He concluded that although commodity price behavior appears to be consistent with Rindler and Yandle’s (1972) model, there was evidence that for some commodities the sensitivity of exchange rate changes was greater than that found in other papers; a significant amount of commodities had lower elasticities than expected. He also concluded that LDC exchange rates should be taken into consideration for this type of analysis given that anomalous results may be obtained if exchange rates from these countries are ignored. This is because a significant amount of LDCs are either primary commodity producers or related to primary commodity exports-imports. On the other hand, Erdal et al. (2012) analyzed the Real Effective Exchange Rate Volatility (REERV) for Turkey. They found a positive long-term relationship between REERV and agricultural exports yet a negative long-term relationship between REERV and agricultural imports.
Most of the literature on the above issue concluded that exchange rate changes do have an impact on commodity prices. In this regard, it is worth mentioning that these conclusions have been mainly supported by econometric models. Another part of the literature has gone further to study the same relationships for second order processes, i.e. for the variability of both exchange rates and commodity prices. The motivation to do that comes mainly in the light of analyzing the high volatility observed in exchange rates after the collapse of the Breton Woods system and the observed effects on commodity prices. Additionally, Kofman and Viaene (1991) studied commodity price behavior, taking into account futures and forward markets for both currencies and commodities. They emphasized the importance of the correlation between exchange rates and commodity prices based upon forward and futures markets clearing conditions, commodity supply-and-demand shocks and monetary shocks. In a related paper, Jumah and Kunst (2001) found that exchange rate volatility has a positive impact on futures prices of agricultural commodities.1
Exchange rate volatility and its impact on exports and trade flows of industrialized and developing countries have also been studied in several papers. Most of this research has found a positive relationship between exchange rate volatility and international trade (International Monetary Fund (IMF), 1984; Giovannini, 1988; Franke, 1991; Karemera et al., 2011). In this regard and using an error-correction model, Asseery and Peel (1991) found that there is a positive relationship between exchange rate volatility and exports from developed countries, except in the case of the United Kingdom. Using a similar model, Chowdhury (1993) showed a negative relationship between exchange rates and G-7 trade flows. Also, Cushman (1988) showed that real exchange rate volatility had significant negative effects on U.S. trade flows. McKenzie (1999) summarized that despite exhaustive attempts to model these relationships, there is no conclusive evidence. Along the same line, Jaramillo-Villanueva and Sarker (2017) also found a negative relationship between the real exchange rate and powdered milk imports.
Previous works related to the effects of exchange rate volatility on U.S. agricultural trade flows are relatively scarce. Pick (1990) showed that exchange rate volatility adversely affects U.S. agricultural exports, a result that is consistent with the literature related to exchange rate volatility and trade of other non-agricultural sectors. Along the same lines, Babula et al. (1995) showed that exchange rate fluctuations have had a significant negative impact on U.S. corn exports. However, it appears to be moderated in the post-1985 period; other studies that have shown similar conclusions include Anderson and Garcia (1989) and Maskus (1986). Likewise, such studies as the one by Chambers and Just (1979) estimated the effects of exchange rates on agricultural trade but did not include the volatility issue in detail. Additional research projects on this topic (Langley et al., 2000; Miranowski, 2000; Shane and Liefert, 2000; Kafe and Kennedy, 2015; Asteriou et al., 2016) have shown that exchange rate volatility affects agricultural trade, which again is consistent with the majority of the previous works in the specialized literature.
Despite the fact that there is a significant amount of work related to the topic of exchange rate volatility impact on agricultural trade, to the best of our knowledge, no works at present analyze the impact of exchange rate variability on corn exports from Mexico to the U.S. and wheat exports from the U.S. to Mexico. This situation is of particular importance due to the switch in exchange rate regime that Mexico underwent in 1994, going from fixed to floating, and the exchange rate crises in Mexico in 1994 and 2008. The former was due to a local financial crisis and the latter to a global one. In addition, since the North American Free Trade Agreement (NAFTA) went into effect, policy adequacies in Mexico have placed more importance on the agricultural sector and its foreign trade as part of a new Mexican economic model advocating free trade. These changes included liberalization of agricultural commodity prices (including corn and wheat) and hedging programs for agricultural producers and traders against price volatility (Aserca, 2002). This encourages finding a response to the relevant question: Do exchange rate crises in a developing country, in particular Mexico, have a statistically significant influence on exports of corn and imports of wheat?
To address this issue, agricultural trade between Mexico and the U.S. was considered for the aforementioned commodities by means of an econometric model following Langley et al. (2000). In addition, for analysis robustness, a Factor-Augmented Vector Autoregression (FAVAR) model was applied.
It is important to point out that from 1990 until mid-2001, corn exports from Mexico to the U.S. represented approximately 96 percent of total Mexican corn exports, and Mexican wheat imports from the U.S. comprised approximately 90 percent of total Mexican wheat imports (Aserca, 2002). The major differences between the two commodities can be analyzed to explain the trade between Mexico and the U.S. Although NAFTA proposes reductions in tariffs and quotas for both commodities, the volume of corn Mexico exported surpassed that of the wheat it imported during and after the Mexican 1994 crisis. Under NAFTA there were significant reductions in tariffs and quotas for corn trade among NAFTA countries.2 On the other hand, the drop in tariffs and quotas was on average smaller in the case of wheat. The NAFTA regulations went into effect in 1994, when the agreement began. NAFTA could possibly have encouraged corn producers to increase corn exports from Mexico to the U.S. at a higher rate than wheat exports from the U.S. to Mexico.
In contrast to wheat, Mexican corn consumption and production have been relatively stable, even during the 1994 economic crisis (Sagar, 1999). The fact that almost two-thirds of corn is consumed by humans (it is an important part of the Mexican diet) could have encouraged farmers to choose to produce corn instead of other grains used for feeding livestock i.e., barley, sorghum and oats (Sagar, 1999). For example, if a corn producer was not able to export corn, then there were relatively higher opportunities to sell it on the domestic market given that domestic demand had been relatively stable during the 1980s and 1990s (Sagar, 1999) and continues so to more recent times.
The fact that most of the Mexican wheat is used as an intermediary input for wheat-related final products, v.g., bread, flour and pastry, is a reason behind the fact that wheat imports from the U.S. were not as large as Mexican corn exports during the 1990s (Sagar, 1999). In other words, if the demand for bread, flour and pastry does not change, then there is no reason to expect external factors (such as exchange rate volatility) to influence wheat-traded quantities (Kehoe, 2000). Differences between corn and wheat trading quantities exist because the use of each of the commodities in Mexico differs. Wheat is mostly used as an intermediate good, while corn is principally used as a final product for human consumption (the most common example is tortillas, which for many Mexicans is a substitute for bread). Thus, NAFTA regulations and demand-side variables (like consumption) differ for each of the commodities in question, so they must be studied with those differences in mind.3
I. Exchange rate volatility and the export model
An export model including exchange rate volatility (risk term) will be presented in this section. This model is useful in analyzing the relationship between exchange rate volatility and exports for the agricultural commodities under study. Following Asseery and Peel (1991) and Langley et al. (2000), the export function is given using an Error Correction Model (ECM).
Equation (1) is the levels equation to be estimated in order to obtain the residuals, which are subsequently included in the ECM, in equation (2). For both equations, Xt stands for the agricultural commodity exports, Pt is the cash price4 of the agricultural commodity in Mexican pesos, and Yt refers to real national income in the U.S. and Mexico (according to the commodity being analyzed) which is a proxy variable for foreign income. Vt is the real exchange rate volatility which is the conditional standard deviation5 calculated from a GARCH(1,1), and et-1 are the lagged residuals from the cointegrating (the levels) stated in (1) and are error terms satisfying the usual assumptions.
The procedure to estimate ECM coefficients, according to Engle and Granger (1987), is as follows. First, the dependent contemporaneous variable is regressed against the independent contemporaneous variables (excluding the risk term) in an ordinary least squares (OLS) regression in order to obtain the series of residuals. Once the series of residuals are obtained, stationarity tests are carried out on them to validate whether the variables are cointegrated. If the residual series are stationary i.e., I(0), then the variables are cointegrated. Secondly, after proving that the variables in the regression are cointegrated, a second regression is carried out including the risk term (Vt) and the lagged residuals, which represent the ECM. The coefficient of the lagged residual term is expected be negative, statistically significant and less than one, indicating that it will converge. As explained in Brooks (2008), a negative coefficient (lagged residual term) will imply that if the difference between the logarithm of the dependent and independent variables is positive in one period, then the dependent variable will fall (because of the negative sign) during the next period in order to restore equilibrium and vice versa.
For a robustness analysis, an impulse-response function was carried out using the Cholesky variance decomposition methodology. As explained above, a Factor-Augmented Vector Autoregression (FAVAR) model was used to estimate the relevant coefficients. This type of model makes it possible to study the statistical relationship between the analyzed variables, having them interacting in a system of equations in which all variables are endogenous and relatively highly correlated. FAVAR was introduced to the literature by Bernanke et al. (2005) and is widely used to estimate impulse-response functions, especially when there is relatively high correlation between the variables. In general terms, the FAVAR can be stated as follows. It is assumed that the joint dynamics (Ft ', Yt '), where Ft is a vector of non-observable factors of dimension K×1 and Y t represents an economic indicator (prices, real activity, etc.), can be represented in the following transition equation:
where
The above equation cannot be estimated directly, because the Ft factors are non-observable. However, it is possible to get relevant non-observable factors using the principal components method. Assuming that Xt is related to both non-observable Ft factors and observable Yt variables, then it is possible to state the following equation:
where
The procedure for estimating Mexican corn exports and wheat imports involves several steps in the FAVAR method. First, standard methodology is followed to obtain the principal components.6 Subsequently, standard procedure leads to the FAVAR estimate (Bernanke et al., 2005). Model specification takes into account the main components of the relevant series and includes the exchange rate, Mexican corn exports and wheat imports. The second moments of the aforementioned series, expressed as the square of the first differences in each series, are also included in the specification. This improves the estimates, since for this type of econometric models it is more appropriate to capture second moments. With the FAVAR model, it is then possible to estimate Mexican corn exports to the U.S. and U.S. wheat exports to Mexico and analyze their reaction to exchange rate volatility via impulse-response functions.
Given the cointegration relationship previous to ECM application, long-term variable dynamics may be captured using the proposed estimation procedure, while ECM specification captures the short-term dynamics of the variables in a causal relationship. Any deviation from the long-term relationship between the variables will be ‘corrected’ by the error-correction term, as the resulting negative estimated coefficient will be subtracted when the previous value is positive and added when negative, moving towards a long-term equilibrium relationship. In addition, any high correlation between the analyzed variables will be dealt with by the FAVAR. As explained in the literature, application of that type of factor model will help compensate for any misspecification problems through high correlation between the explanatory variables. Analysis of the variables being studied and their descriptive statistics led to the methodology choice. Since other methods that show such statistical relationships mainly emphasize short-term statistical relationships, the one applied here was selected in order to include long-term equilibrium relationships with cointegration, as well.
II. Data description
Monthly agricultural commodity data on Mexican corn exports and U.S. wheat exports are from the U.S. Department of Agriculture (USDA).7
Price data for the agricultural commodities consist of monthly averages (taken from daily data) of corn and wheat spot prices. Data for the foreign income proxy variable, i.e. monthly real disposable personal income in the U.S. (billions of chained 2009 USD) and Mexico (2008 base year) were obtained from the fed and the Central Bank of Mexico, respectively.8 Real exchange rate data were taken from daily peso-USD nominal exchange rates and the Mexican consumer price index (CPI), both from the Central Bank of Mexico. The sample period encompasses 27.5 years from January 1990 to July 2017, bringing the sample size to 330 monthly observations. The sample period was chosen to cover sufficient data before and after the 1994 and 2008 Mexican exchange rate crises. In addition, the Mexican Federal Government only regulated Mexican corn prices prior to 1990 (Sagar, 1999), so world corn prices (as the ones used in this research) do represent a reliable proxy for Mexican corn prices. Unfortunately, to date no corn or wheat producer prices are available in Mexican pesos for this period. However, considering that in 1990 the prices for both commodities were “liberalized”, i.e., no longer regulated by the Mexican government, the grain prices obtained at the USDA represent an acceptable proxy for international corn and wheat prices.
Excluding the real exchange rate, variables are seasonally adjusted because the commodities have seasonal components that depend on their production cycle. Seasonal adjustments were carried out using a ratio to moving average performed in the econometric package EViews 9.0 and explained in more detail below. Let series x t be a filtered function of yt . The first step is to compute the monthly centered moving average of y t as follows,
The next step is to compute the ratio:
The seasonal index im for month m is the average value of rt using only m monthly observations. It follows that seasonal indices are adjusted to obtain one when the mentioned indices are multiplied by each other. This is obtained by computing the seasonal factors (the scaling factor s), which are the ratio of the specific seasonal index (im ) to the geometric mean indices,
The interpretation of s is that, relative to the adjusted series, the series yt is a factor si in period i. Dividing yt by the seasonal factors si , the seasonally adjusted series can be obtained.
The seasonal adjustment procedure was carried out for the monthly corn exports from Mexico to the U.S. and wheat exports from the U.S. to Mexico, as well as for the price data. The proxy variables for foreign income, i.e., monthly real industrial production in the U.S. and Mexico were seasonally adjusted according to the data source. The scaling factors for the exports and the price data can be seen in the appendix of this research.
III. Real exchange rate and the exchange rate risk term estimation
Figure 1 depicts the logarithm of the real Mexican peso-USD exchange rate. The late 1994 and 2008 shocks can clearly be observed, the former related to the 1994 Mexican financial crisis (Tequila effect) and the latter to the 2008-2009 Global Financial (subprime) Crisis. After the 1994 crisis, the real exchange rate appreciated up to 2001, after which a sustained depreciation of the Mexican currency is seen until 2009. Subsequent to 2009, the Mexican peso recovered, yet starting in 2014, it has persistently depreciated.
The Mexican peso-USD exchange rate volatility is estimated with a GARCH(1,1) model as in Bollerslev (1986), Taylor (1985) and Engle (1982). The results of applying the GARCH(1,1) model using monthly exchange rate values can be observed in Table 1. The meaning of the coefficients is the same as expressed previously in section 2. Coefficients a1 and b1 are both observed to be positive, statistically significant, and their sum is less than one. These results satisfy the condition that the sum of the ARCH and GARCH terms must be positive and less than or equal to one as expected for a well-specified GARCH model. The tests on the residuals were generally satisfactory. The correlograms of the standardized squared residuals only gave two significant Ljung-Box statistics (Q2), which are relatively few. This parsimonious specification gave the most consistent estimates when compared to other higher order specifications.9
Table 1 Volatility Estimates of the Monthly Real Mexican Peso-USD Exchange Rate
| GARCH(1, 1) | Real Mexican peso-U.S. dollar exchange rate |
|---|---|
| α2 | 5.10 x 10-6 (3.89 x 10-6) 1.3116 |
| α1 | 0.1025** (0.0470) 2.1781 |
| β1 | 0.8270** (0.0739) 11.1851 |
| L | 8795.3480 |
| Q(12) | 33.68 |
| Q2(12) | 5.84 |
| N | 320 |
Standard errors are shown in brackets. Boldface shows the z-statistic. L represents the log likelihood. The rows showing Q(12) and Q 2(12) are the Ljung-Box statistic for standardized residuals and standardized squared residuals respectively, which has a c2 distribution with 21 degrees of freedom. The critical value is 21 at the 5-percent level. N represents the sample size. The sample size consists of monthly data from January 1990 to July 2017, for a total of 330 monthly observations.
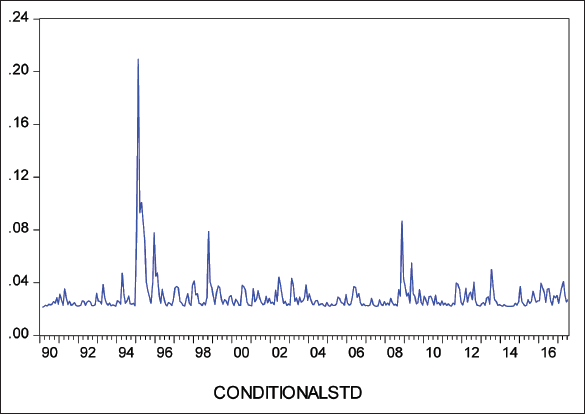
Figure 2 depicts the real Mexican peso-USD exchange rate risk measure (conditional standard deviation) estimated from the GARCH(1, 1) equation (Table 1). In Figure 2, ‘conditional STD’ represents the daily conditional standard deviation of the daily real Mexican peso-USD exchange rate. This figure shows that the conditional volatility estimate was relatively stable from January 1990 until December 1994, when a shock occurred. Again the aforementioned shock is related to the 1994 Mexican Financial Crisis. Before mid- December 1994 (prior to the shock), the Mexican peso exchange rate system was pegged to the USD, but after mid-December 1994 (early during the shock) it became a floating exchange rate system. Stability followed until 2008, when Mexico experienced another significant peak (a second major currency crisis).
IV. Analysis and discussion of the empirical results
Tables 2-6 show the results of estimating the above equations (1)-(2) for corn exports from Mexico to the U.S. and wheat exports from the U.S. to Mexico, respectively. Tables 2 and 4 show the estimates of the long-run (cointegration) equations, and Tables 3 and 5 show the ECM estimates. It is important to point out that daily volatility was transformed to monthly averages in order to include them as the risk term (Vt). Thus, all the variables in the ECM are measured in the same time frequency, which is monthly.
Table 2 Long-Run Equation Estimates of Mexican Corn Exports to the U.S. for the Whole Period under Study
| Underlying coefficient | Corn exports |
|---|---|
| α0 | -99.6315 (26.2951)** -3.7890 |
| α1 | 1.4178 (0.6225)** 2.2775 |
| α2 | 10.8676 (3.3991)** 3.1972 |
| Adj.
R2 DW ARCH White Chow N |
0.2814 1.9717 0.1742 2.3459 0.6332 330 |
Standard errors are shown in brackets. (**) indicates the coefficient is statistically significant at 5-percent confidence level; (*) indicates the coefficient is statistically significant at a 10-percent confidence level. Boldface = t-statistic. Adj. R2 = adjusted coefficient of determination. DW = Durbin Watson statistic. ARCH is the F-Form of the Lagrange Multiplier test for 1st order autoregressive conditional heteroskedasticity in the residuals. White = White Heteroskedasticity Test F-statistic. Chow = Chow test for stability of the parameters, Chow Breakpoint (2008:10). N = sample size. The sample size consists of monthly data from January 1990 to July 2017.
Table 3 Error-Correction-Model (ECM) Estimates of Mexican Corn Exports to the U.S. for the Whole Period under Study
| Underlying coefficient | Corn exports |
|---|---|
| α0 | 0.3296 (1.0321) 0.3194 |
| α1 | 1.1803 (3.1119) 0.3793 |
| α2 | 6.7682 (32.3774) 0.2090 |
| Φ | -6.4595 (23.2417) -0.2779 |
| ϑ | -0.9983 (0.0870)** -11.4764 |
| Adj. R2 | 0.4897 |
| DW | 2.0074 |
| ARCH | 0.1724 |
| White | 1.2901 |
| Chow | 0.2997 |
| N | 330 |
(**) indicates the coefficient is statistically significant at a 5-percent confidence level; (*) indicates the coefficient is statistically significant at a 10-percent confidence level. Boldface = t-statistic. Adj. R2 = adjusted coefficient of determination. DW = Durbin Watson statistic. ARCH is the F-Form of the Lagrange Multiplier test for 1st order autoregressive conditional heteroskedasticity in the residuals. White = White Heteroskedasticity Test F-statistic. Chow = Chow test for stability of the parameters, Chow Breakpoint (2008:10). N = sample size. The sample size consists of monthly data from January 1990 to July 2017, for a total of 330 observations.
Table 4 Long-Run Equation Estimates of U.S. Wheat Exports to Mexico for the Whole Period under Study
| Underlying coefficient | Wheat exports U.S. to Mexico |
|---|---|
| α0 | -162.2059 (18.3301)** -8.8492 |
| α1 | 0.8287 (0.4192)* 1.9768 |
| α2 | 8.1974 (0.8599)** 9.5327 |
| Adj.
R2 DW LM ARCH N |
0.4325 1.1615 10.6848 48.9465 330 |
Standard errors are shown in brackets. (**) indicates the coefficient is statistically significant at a 5-percent confidence level; (*) indicates the coefficient is statistically significant at a 10-percent confidence level. Boldface = t-statistic. Adj. R2 = adjusted coefficient of determination. DW = Durbin Watson statistic. LM = is the F-Form of the Lagrange Multiplier test for 1st order serial correlation in the residuals. ARCH is the F-Form of the Lagrange Multiplier test for 1st order autoregressive conditional heteroskedasticity in the residuals. N = sample size. The sample size consists of monthly data from January 1990 to July 2017. A seasonal dummy variable for the month of May is included in this regression.
Table 5 Error-Correction-Model (ECM) Estimates of U.S. Wheat Exports to Mexico for the Whole Period under Study
| Underlying coefficient | Wheat exports U.S. to Mexico |
|---|---|
| α0 | -0.3900 (0.3260) -1.1961 |
| α1 | -2.2935 (1.1726)* -1.9558 |
| α2 | 7.6189 (4.0542)* 1.8793 |
| Φ | 9.5094 (7.3087) 1.3011 |
| ϑ | -0.6633 (0.0774)** -8.5697 |
| Adj. R2 | 0.3774 |
| DW | 1.5292 |
| LM | 1.3667 |
| ARCH | 4.4516 |
| N | 330 |
(**) indicates the coefficient is statistically significant at a 5-percent confidence level; (*) indicates the coefficient is statistically significant at a 10-percent confidence level. Boldface = t-statistic. Adj. R2 = adjusted coefficient of determination. DW = Durbin Watson statistic. LM = is the F-Form of the Lagrange Multiplier test for 1st order serial correlation in the residuals. ARCH is the F-Form of the Lagrange Multiplier test for 1st order autoregressive conditional heteroskedasticity in the residuals. N = sample size. The sample size consists of monthly data from January 1990 to July 2017. A seasonal dummy variable for the month of May is included in this regression.
Table 6 Long-Run Equation Estimates of Mexican Corn Exports to the U.S. Before and After the 2008 Mexican Exchange Rate Crisis
| Underlying coefficient | Corn exports from Mexico to the U.S. before the crisis |
Corn exports from Mexico to the U.S. after the crisis |
|---|---|---|
| α0 | 52.0580 (154.7670) 0.3364 |
-56.8589 (9.5698)** -5.9415 |
| α1 | -4.4860 (5.8207) -0.7707 |
-0.4226 (0.3087) -1.3690 |
| α2 | -2.3451 (19.2372) -0.1219 |
7.5752 (0.9885)** 7.6636 |
| Adj. R 2 | 0.0137 | 0.4874 |
| DW | 2.0751 | 1.1255 |
| ARCH | 0.6115 | 1.8115 |
| White | 0.9822 | 0.5478 |
| N | 226 | 105 |
Standard errors are shown in brackets. (**) Indicates the coefficient is statistically significant at a 5-percent confidence level; (*) indicates the coefficient is statistically significant at a 10-percent confidence level. Boldface = t-statistic. Adj. R2 = adjusted coefficient of determination. DW = Durbin Watson statistic. ARCH is the F-Form of the Lagrange Multiplier test for 1st order autoregressive conditional heteroskedasticity in the residuals. White = White Heteroskedasticity Test F-statistic. N = sample size. The subsample sizes contain monthly data from January 1990 to October 2008 for the subperiod before the 2008 crisis and from November 2008 to July 2017 for the subperiod after the 2008 crisis.
The unit root tests carried out for the second stage of the estimation procedure in the ECM were the Augmented Dickey-Fuller and Phillips-Perron tests. As expected, the relevant series reveal rejection of the null hypothesis of a unit root, thus indicating they were stationary. It can be observed from Tables 3 and 5 that in the case of corn, the coefficients in question, i.e., the coefficients of the relative price, real foreign income and exchange rate risk, are not statistically significant. The coefficients of relative price and real foreign income are only statistically significant in the case of wheat. For both commodities, the lagged residuals (θ) are statistically significant and negative, as expected (Brooks, 2008). By including the lagged residuals, the aforementioned coefficients indicate how the average speed of adjustment for each of the commodity exports could be different depending on whether the adjustment was made in response to the relative price, real foreign income or real exchange rate volatility.
Figure 3 shows the relevant impulse-response functions of the aforementioned model, showing the response of corn and wheat exports to exchange rate volatility impulses.
After conducting structural break tests, as in Andrews-Quandt (1992) and (1969) and Bai and Perron (1998) methodologies, to analyze the impact of the 2008 For the Mexican financial crisis on Mexican corn exports and U.S. wheat exports, the data was partitioned into two subperiods. The subperiod before the 2008 crisis encompasses from January 1990 until October 2008, and the subperiod after the 2008 crisis covers from November 2008 until July 2017. Equations (1)-(2) above were then re-estimated in order to analyze any major differences during the sub-periods, with results appearing in Tables 7-10.
Table 7 Error-Correction-Model (ECM) Estimates of Mexican Corn Exports to the U.S. Before and After the 2008 Mexican Exchange Rate Crisis
| Underlying coefficient | Corn exports from Mexico to the U.S. before the crisis |
Corn exports from Mexico to the U.S. after the crisis |
|---|---|---|
| α0 | -0.1909 (2.1990) -0.0868 |
-0.1182 (1.5045) -0.0786 |
| α1 | -8.4417 (12.3178) -0.6853 |
-0.8335 (0.8682) -0.9600 |
| α2 | 2.5108 (52.9889) 0.0473 |
7.6750 (16.9799) 0.6526 |
| Φ | 8.8412 (62.1233) 0.1423 |
2.6562 (29.8524) 0.0889 |
| ϑ | -1.0616 (0.1377)** -7.7096 |
-0.5637 (0.1098)** -5.1352 |
| Adj. R2 | 0.5504 | 0.2964 |
| DW | 1.9901 | 1.9663 |
| ARCH | 0.8349 | 2.5987 |
| White | 0.6132 | 2.3417 |
| N | 226 | 105 |
(**) indicates the coefficient is statistically significant at a 5-percent confidence level; (*) indicates the coefficient is statistically significant at a 10-percent confidence level. Boldface = t-statistic. Adj. R2 = adjusted coefficient of determination. DW = Durbin Watson statistic. ARCH is the F-Form of the Lagrange Multiplier test for 1st order autoregressive conditional heteroskedasticity in the residuals. White = White Heteroskedasticity Test F-statistic. N = sample size. The subsample sizes contain monthly data from January 1990 to October 2008 for the subperiod before the 2008 crisis and from November 2008 to July 2017 for the subperiod after the 2008 crisis.
Table 8 Long-Run Equation Estimates of U.S. Wheat Exports to Mexico Before and After the 2008 Mexican Exchange Rate Crisis
| Underlying coefficient | Wheat exports from U.S. to Mexico before the crisis |
Wheat exports from U.S. to Mexico after the crisis |
|---|---|---|
| α0 | -292.0199 (62.3508)** -4.6835 |
-97.8748 (22.0050)** -4.4478 |
| α1 | -3.1625 (1.2099)** -2.6136 |
0.5884 (0.3638)* 1.6170 |
| α2 | 14.6202 (2.9971)** 4.8782 |
5.1629 (1.0284)** 5.0203 |
| Adj. R2 | 0.2895 | 0.3428 |
| DW | 1.4593 | 1.1001 |
| LM | 3.0077 | 10.4524 |
| ARCH | 1.5577 | 3.2738 |
| N | 226 | 105 |
(**) indicates the coefficient is statistically significant at a 5-percent confidence level; (*) indicates the coefficient is statistically significant at 10-percent confidence level. Boldface = t-statistic. Adj. R2 = adjusted coefficient of determination. DW = Durbin Watson statistic. ARCH is the F-Form of the Lagrange Multiplier test for 1st order autoregressive conditional heteroskedasticity in the residuals. N = sample size. The subsample sizes contain monthly data from January 1990 to October 2008 for the subperiod before the 2008 crisis and from November 2008 to July 2017 for the subperiod after the 2008 crisis.
Table 9 Error-Correction-Model (ECM) Estimates of U.S. Wheat Exports to Mexico Before and After the 2008 Mexican Exchange Rate Crisis
| Underlying coefficient | Wheat exports from U.S. to Mexico before the crisis |
Wheat exports from U.S. to Mexico after the crisis |
|---|---|---|
| α0 | -0.1659 (0.6126) -0.2708 |
0.4235 (1.3199) 0.3208 |
| α1 | -6.3046 (2.5547)** -2.4678 |
-0.8216 (0.9414) -0.8727 |
| α2 | 15.2393 (8.2972)* 1.8367 |
4.4601 (3.5288) 1.2639 |
| Φ | 5.9478 (17.2442) 0.3449 |
-8.5610 (26.2743) -0.3258 |
| ϑ | -0.7753 (0.1370)** -5.6589 |
-0.5835 (0.1039)** -5.6155 |
| Adj. R2 | 0.4330 | 0.2721 |
| DW | 1.2768 | 2.2153 |
| LM | 21.2904 | 3.0891 |
| ARCH | 0.9474 | 1.3516 |
| N | 58 | 79 |
(**) indicates the coefficient is statistically significant at a 5-percent confidence level; (*) indicates the coefficient is statistically significant at a 10-percent confidence level. Boldface = t-statistic. Adj. R2 = adjusted coefficient of determination. DW = Durbin Watson statistic. ARCH is the F-Form of the Lagrange Multiplier test for 1st order autoregressive conditional heteroskedasticity in the residuals. N = sample size. The subsample sizes contain monthly data from January 1990 to October 2008 for the subperiod before the 2008 crisis and from November 2008 to July 2017 for the subperiod after the 2008 crisis.
Table 10 Scaling Factors (Seasonal Adjustment of Exports and Price Variables)
| Month | Mexican corn exports | U.S. wheat exports | Corn spot prices | Wheat spot prices |
|---|---|---|---|---|
| 1 | 2.4014 | 0.9337 | 1.0181 | 1.0454 |
| 2 | 1.5619 | 0.9531 | 1.0343 | 1.0290 |
| 3 | 1.5357 | 1.0637 | 1.0670 | 1.0334 |
| 4 | 0.8598 | 0.9341 | 1.0539 | 1.0262 |
| 5 | 0.8731 | 0.6135 | 1.0670 | 1.0508 |
| 6 | 0.5853 | 0.7999 | 1.0205 | 0.9749 |
| 7 | 0.7520 | 0.9942 | 0.9833 | 0.9490 |
| 8 | 0.3051 | 1.2424 | 0.9497 | 0.9565 |
| 9 | 0.3449 | 1.1737 | 0.9097 | 0.9706 |
| 10 | 1.2583 | 1.0012 | 0.9386 | 0.9966 |
| 11 | 1.4038 | 1.0356 | 0.9783 | 0.9969 |
| 12 | 2.8246 | 1.5322 | 0.9936 | 1.0217 |
Scaling factors for the seasonal adjustment of each variable in the study. The sample size contains 330 monthly observations from January 1990 to July 2017.
It can be observed from Table 8 that in the case of corn, the coefficients of relative price, real foreign income and exchange rate volatility are not statistically significant for either subperiod, before and after the 2008 Mexican crisis. Only the lagged residuals are statistically significant. On the other hand, in the case of wheat, the relative price and real foreign income coefficients were statistically significant for the subperiod before the 2008 Mexican crisis; however, the exchange rate volatility term was not statistically significant in any of the subperiods. It can be observed from the diagnostic tests applied to the ECM residuals (Tables 8 and 10) that there are no problems of misspecification.
The differences between the results of both commodities are difficult to justify from economic arguments. However, some major differences may be emphasized between these commodities and the data presented in section 3. In the case of corn, the export volumes were smaller in magnitude compared to wheat. This could explain why the relative price and real foreign income coefficients had a statistically significant influence on wheat but not on corn.
There is relatively high correlation between the Mexican and U.S. real foreign income variable, with correlation coefficients of 0.7207 for the period before the crisis and 0.9613 for the period after the crisis. However, this coefficient was only statistically significant in the case of wheat. Overall, these results are not consistent with the existent literature, which has shown impacts of exchange rate volatility on agricultural trade (Mohanty and Peterson, 1999; and Langley et al., 2000).10 However, these results are consistent with that part of the literature that says that exchange rate volatility does not influence agricultural trade. Specifically, it is consistent in the case of wheat. According to data from Sagar (1999), most of the Mexican wheat that is imported from the U.S. is used as an input for other goods i.e. bread, flour, pastry, etc. If the demand for the final product does not change, as expected in the case of wheat-related products, then there is no reason to expect a significant shift in demand caused by exchange rate volatility (Kehoe, 2000).
Finally, Figure 2 shows that the exchange rate volatility is very similar to a 0-1 crisis dummy variable having several months of 1995 and 2008 values equal to one and zero otherwise. Therefore, a similar approach was used, with an ECM, but this time excluding some months of 1995 and 2008. In other words, excluding those observations may look like a dummy variable. The results do not change qualitatively from those reported in Tables 2-9 and show that exchange rate volatility did not influence the export quantities of the two commodities analyzed, even when omitting the four main months of the crisis (January through April 1995) from the econometric tests. Thus, for this time frame, there is no statistical evidence in the Mexican case that exchange rate volatility influenced the observed export (import) quantities for the two commodities. That is, a demand-side measure did not influence the export quantities of the commodities. This motivated the use of a supply-side measure to examine whether supply-side factors affected the corn quantities exported.
It is worth mentioning that we chose corn exports from Mexico to the United States, since the majority of Mexican corn exports go to that country. According to Sagar figures and due to NAFTA considerations, they represent a significant percentage. On the other hand, we did not focus on corn imports to Mexico from the United States, since in recent years Mexico has been the world’s second largest importer of this ‘commodity’, which shows that its demand is highly inelastic. It is thus difficult to obtain a causal relationship between exchange rate volatility and corn imports, due to the inelastic demand of the latter. Also, considering that the United States is the world’s leading corn exporter, the fraction that Mexico takes from it is a relatively smaller percentage. From a relative point of view, the fraction of exports from Mexico to the U.S. is considerably higher than vice versa. And the fact that exports from Mexico are relatively elastic can show a more significant causal relationship. Furthermore, Mexico imports primarily white corn, though the data in our study is for total corn, which includes yellow corn. The idea of having a causal relationship between exchange rate volatility and agricultural exports from Mexico to the U.S. is mainly related to productivity uncertainty in Mexico due to financial volatility, and Bahmani-Oskooee and Hegerty (2009) also found a causal relationship. We leave the possibility of analyzing Mexican corn imports for future research.
Conclusions
The results presented show that exchange rate volatility had no impact on Mexican corn exports to the U.S. or on U.S. wheat exports to Mexico for the whole sample period studied. The same applies to the subperiods before and after the 2008 Mexican exchange rate crisis. Failure of finding any statistically significant influence of exchange rate volatility on corn and wheat exports from the ECM provides statistical evidence to conclude that both corn exports from Mexico to the U.S. and wheat exports from the U.S. to Mexico were unaffected by either the 1994 and 2008 Mexican exchange rate crises or by the switch in the exchange rate regime in December 1994 (from a pegged to a floating system for the peso-USD exchange rate). This was consistent throughout the study for the whole sample period and the subsample periods before and after the 1994 and 2008 exchange rate crises. These results are also consistent with the part of the specialized literature that argues that exchange rate volatility does not affect agricultural trade.











 nueva página del texto (beta)
nueva página del texto (beta)