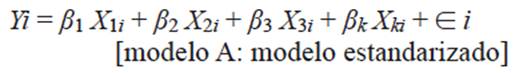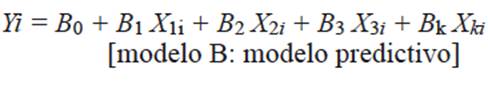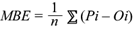INTRODUCCIÓN
La contaminación atmosférica es la modificación de la composición del aire por la presencia de algún contaminante, siendo el material particulado (PM, por sus siglas en inglés) en sus diversos tamaños el más común. El PM es cualquier sustancia (excepto agua pura) en estado sólido o líquido que se encuentra en la atmósfera, con tamaños microscópicos y submicroscópicos. En el aire el PM se clasifica según su diámetro aerodinámico equivalente en partículas totales suspendidas (PTS, hasta 100 µm de diámetro), PM10 (fracción gruesa, hasta 10 µm), PM2.5 (fracción fina, hasta 2.5 µm) y PM1 (fracción superfina, hasta 1 µm) (Seinfeld y Pandis 2016). La exposición de la salud humana a los contaminantes particulados ha sido extensamente investigada y asociada con incrementos en la morbilidad y mortalidad (Pope y Dockery 2006). La Organización Mundial para la Salud (OMS) advierte que las evidencias epidemiológicas señalan que un aumento de 10 μg/m3 en la concentración de PM10 está asociado a un aumento de alrededor del 1 % en la mortalidad (OMS 2005). Las fracciones que representan mayor riesgo para la salud son las más pequeñas, ya que por su reducido tamaño pueden penetrar directamente en las regiones más profundas del sistema respiratorio, y pueden ser tóxicas, cancerígenas, mutagénicas y teratogénicas (Pope et al. 1995).
Por lo antes expuesto, algunos investigadores han profundizado en el análisis, medición y correlaciones del PM. Diversos autores han establecido relaciones multivariantes para predecir la concentración de PM en función de parámetros ambientales; por ejemplo, Baek et al. (1997) realizaron una estimación cuantitativa de las contribuciones de fuentes a las concentraciones de partículas suspendidas en zonas urbanas, suburbanas e industriales en Corea del Sur. Estos autores emplearon técnicas de análisis de componentes principales y análisis de regresión múltiple por etapas para identificar y cuantificar las principales fuentes que influyen en las PTS. Los resultados indicaron que las principales clases de fuentes que contribuyen a las PTS ambientales en Corea son las resuspendidas del suelo y las procedentes de quema de combustible, vehículos de motor y aerosoles secundarios.
Por su parte, Silva et al. (2003) realizaron un estudio de modelamiento de la contaminación atmosférica por partículas en Santiago de Chile para la predicción de PM10. Estos autores usaron datos de la estación de muestreo de Pudahuel (comuna de Santiago) para el periodo 1998-2000 y emplearon técnicas multivariantes y esquemas de regresión adaptativa multivariante. Los autores definieron como variables independientes la concentración de PM10 a diferentes horas, temperatura, humedad relativa y velocidad del viento. Las variables predictoras que mejor explicaron la varianza de la PM10 fueron las concentraciones puntuales de PM10: pm0 (PM10 a las 00:00 LT), pm6 (PM10 a las 06:00 LT) y pm18 (PM10 a las 18:00 LT), así como las variables meteorológicas.
Chaloulakou et al. (2003) aplicaron redes neuronales y modelos de regresión múltiple para la predicción de PM10 en Atenas, Grecia. Los autores concluyeron que los predictores primarios de los modelos estadísticos son parámetros meteorológicos, resaltando que la incorporación de un término de concentración retardado de PM10 conduce a la mejora del poder predictivo de los modelos.
Botero et al. (2004) desarrollaron un modelo estadístico para la evaluación de la calidad del aire con el fin de evaluar las condiciones ambientales y de contaminación por PM en Cali, Colombia. Las variables seleccionadas fueron velocidad del viento en la noche, temperatura media, radiación solar y amplitud de la temperatura. Los autores concluyeron que el clima es uno de los factores que influyen en la presencia de la contaminación por PM.
Cassidy et al. (2007) aplicaron modelos de regresión múltiple de partículas y de monóxido de carbono (CO) usando características ambientales en Baguio City, Filipinas, y encontraron relaciones estadísticamente significativas entre la concentración de PM en el aire y el tráfico vehicular en horas de la madrugada. También obtuvieron una relación estadísticamente significativa entre la presencia de CO y el tráfico en horas pico de la mañana y de la tarde. Además, estos modelos sugieren que el tráfico y el viento en Baguio City afectaban significativamente la concentración de contaminantes.
Ramos-Herrera et al. (2010) realizaron un estudio estadístico sobre la correlación entre contaminantes atmosféricos y variables meteorológicas en la zona norte de Chiapas, México. Los autores aplicaron análisis de RLM para predicción de PM10. Las variables significativas en el modelo fueron temperatura, humedad relativa y dirección del viento.
El objetivo de esta investigación es obtener un modelo lineal multivariante para la predicción de PM1 a partir de variables ambientales, meteorológicas y eventualidades físicas en una región intertropical del centro-norte de Venezuela, localizada en el Valle de Sartenejas en la Gran Caracas.
MATERIALES Y MÉTODOS
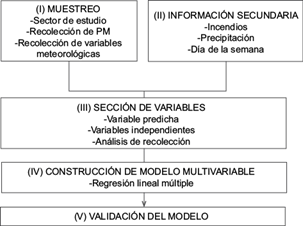
La figura 1 muestra los pasos seguidos en la metodología de investigación, los cuales incluyen: 1) muestreo de PM y variables meteorológicas, 2) recopilación de información secundaria, 3) selección de la variable dependiente y de las variables independientes, 4) construcción del modelo multivariante y 5) validación del modelo.
Muestreo de material particulado y meteorología
Localizada en una región continental intertropical en el norte-centro de Venezuela, la Gran Caracas es una gran urbe ubicada al sur del parque nacional El Ávila, formación montañosa perteneciente a la Cordillera de la Costa. La Gran Caracas está conformada por Caracas y otras ciudades satélites. Ocupa un área de 4704 km2 y tiene 4.25 millones de habitantes (INE 2018). Esta urbe está cruzada por vías rápidas que presentan alto tráfico vehicular en horas críticas y con un número importante de industrias pequeñas y medianas.
Al suroeste de la Gran Caracas se encuentra el Valle de Sartenejas (Fig. 2), a una altitud entre 1200 y 1400 msnm. Este valle ocupa un área de 96 ha, de las cuales 40 ha pertenecen al campus de la Universidad Simón Bolívar. La universidad está rodeada de 255 ha de áreas naturales, de las cuales 45 ha son plantaciones con alta densidad de bosque de pinos; el resto corresponden a bosque nativo, matorrales secundarios y una zona importante de sabana con arbustos diversos y escasos pinos que presentan alta incidencia de incendios (GBUSB 2018a). El Valle de Sartenejas tiene un microclima más fresco que el de la Gran Caracas y habitualmente presenta mayor frecuencia de lluvias.
El campus universitario cuenta con una estación de muestreo de material particulado que opera junto con una estación meteorológica, llamadas en conjunto AireUSB. Esta estación está instalada en la azotea de uno de los edificios del campus a una altura de 9 m, para asegurar que el material particulado sea representativo del aire del sector (coordenadas UTM 10.412352 y -66.883558 m). El sector se percibe poco contaminado por estar rodeado de espacios naturales, a pesar de que a una distancia aproximada de 2 km al suroeste se encuentra una autopista con alto tránsito vehicular, pues es la vía de salida de la Gran Caracas hacia el occidente del país, y a una distancia 3.5 km al noreste se emplaza una zona industrial-residencial. La vía de acceso a la universidad presenta alto tráfico vehicular en horas críticas (Fig. 2).
Para la recolección del PM en sus diferentes tamaños se empleó un muestreador de alto volumen (Hi-Vol, por sus siglas en inglés), el cual es recomendado por la Agencia de Protección Ambiental de los Estados Unidos (USEPA, por sus siglas en inglés) para la recolección de PTS cuando se opera con grandes volúmenes de aire (EPA 1999a). El equipo se calibró siguiendo las instrucciones del manual de operación, el cual se basa en procedimientos de la USEPA para medición de PM de aire exterior con equipos de alto volumen.
Al Hi-Vol se le acopló un impactador en cascada (ImpC) modelo Inc. Series 230 (Tisch Environmental). En el ImpC las partículas de PTS se segregan según su diámetro aerodinámico en seis rangos de tamaños, por medio de cinco bandejas de aluminio ranuradas que dividen las PTS en los siguientes rangos: bandeja 1, > 7.2 μm; bandeja 2, 7.2-3.0 μm; bandeja 3, 3.0-1.5 μm; bandeja 4, 1.5-0.95 μm, y bandeja 5, 0.95-0.49 μm. En el fondo del ImpC se coloca como bandeja 6 un filtro < 0.49 μm. Se usaron filtros de fibra de vidrio.
Se destaca que una de las ventajas de usar un impactador en cascada es la posibilidad de combinar las fracciones recolectadas en las diferentes bandejas según el objetivo de la investigación (Ehrlich et al. 2007, Srivastava et al. 2008, Campos et al. 2015).
Antes de cada muestreo los filtros se someten a un tratamiento térmico en una estufa a temperatura de 120 ºC por 24 h. Luego se estabilizan en un desecador por 24 h más, y posteriormente se pesan de forma independiente en condiciones de humedad y temperatura ambiente conocidas. Para determinar la masa de material particulado en cada filtro, éstos se pesan antes y después de cada muestreo (Fig. 3). La concentración de material particulado se calcula como la masa total de partículas recolectadas dividida entre el volumen de aire muestreado (en μg/m³). El volumen total de aire muestreado se calcula a partir del flujo medido y el tiempo de muestreo. Este valor se corrige a condiciones conocidas de presión y temperatura (WMO 1978, Lodge 1988, EPA 1999b).
Se tomaron muestras de material particulado cada seis días del 23 de agosto de 2014 al 29 de octubre de 2015 para un total de 85 muestras, durante la época de lluvia y de sequía. Del 23 de agosto al 28 de octubre de 2014 el muestreo se realizó por 24 h cada seis días; del 3 de noviembre de 2014 al 24 de septiembre de 2015 el muestreo se realizó por 48 h cada seis días a partir del encendido del equipo, y del 29 de septiembre al 29 de octubre el muestreo fue de 72 h cada seis días a partir del encendido del equipo. Las fechas reportadas corresponden al día de encendido del equipo. El ajuste del periodo de muestreo se debió a que la masa del PM recolectada por los filtros resultaba estar justo en el umbral mínimo de detección de la balanza disponible, lo cual motivó que se incorporaran los periodos de muestreo de 48 y 72 h, los cuales posteriormente se normalizaron a concentraciones de 24 h, tomando en cuenta tiempo de recolección y volumen de aire.
El cuadro I presenta la concentración promedio de PM de cada bandeja del impactador para cada periodo de muestreo (24, 48 y 72 h), la desviación estándar de las mismas, el valor máximo y mínimo de concentración de cada bandeja, y la cantidad de muestras recolectadas, las descartadas y las utilizadas en esta investigación. En dicho cuadro se observa que las mayores concentraciones tienden a presentarse en las bandejas 6 y 2. De un total de 85 muestras recolectadas se descartaron 21 por manejo inadecuado o contaminación de las muestras y/o problemas operativos con los equipos, resultando un total de 64 muestra útiles: 59 para la construcción del modelo y cinco reservadas para la validación.
CUADRO I CONCENTRACIÓN DE MATERIAL PARTICULADO POR BANDEJA DEL IMPACTADOR Y CANTIDAD DE MUESTRAS RECOLECTADAS Y ANALIZADAS
| Bandeja 6 (< 0.49 μm) |
Bandeja 5 (0.95-0.49 μm) |
Bandeja 4 (1.5-0.95 μm) |
Bandeja 3 (3.0-1.5 μm) |
Bandeja 2 (7.2-3.0 μm) |
Bandeja 1 (> 7.2 μm) |
|
| Tiempo de muestreo | 24 h | |||||
| Concentración PM (μg /m3) | 10.41 | 3.46 | 3.48 | 3.92 | 9.97 | 4.71 |
| Desviación estándar (μg/m3) | 4.90 | 2.14 | 2.52 | 2.65 | 4.21 | 2.62 |
| Concentración máx. (μg /m3) | 18.43 | 6.67 | 7.52 | 10.34 | 18.76 | 11.39 |
| Concentración mín. (μg /m3) | 2.62 | 0.27 | 0 | 1.35 | 5.23 | 2.55 |
| Muestras recolectadas | 12 | 12 | 12 | 12 | 12 | 12 |
| Muestras descartadas | 3 | 3 | 3 | 3 | 3 | 3 |
| Muestras útiles | 9 | 9 | 9 | 9 | 9 | 9 |
| Tiempo de muestreo | 48 h | |||||
| Concentración PM (μg /m3) | 11.13 | 4.28 | 5.50 | 7.26 | 13.25 | 7.00 |
| Desviación estándar (μg/m3) | 8.13 | 4.05 | 5.50 | 5.54 | 10.29 | 5.82 |
| Concentración máx. (μg /m3) | 39.31 | 25.25 | 34.10 | 25.68 | 51.49 | 30.83 |
| Concentración mín. (μg /m3) | 0.15 | 0.52 | 0.82 | 1.53 | 0.53 | 0.72 |
| Muestras recolectadas | 66 | 66 | 66 | 66 | 66 | 66 |
| Muestras descartadas | 16 | 16 | 16 | 16 | 16 | 16 |
| Muestras útiles | 50 | 50 | 50 | 50 | 50 | 50 |
| Tiempo de muestreo | 72 h | |||||
| Concentración PM (μg /m3) | 6.11 | 3.13 | 3.13 | 4.80 | 9.03 | 4.83 |
| Desviación estándar (μg/m3) | 1.85 | 1.00 | 0.97 | 1.63 | 2.52 | 1.20 |
| Concentración máx. (μg /m3) | 7.84 | 4.77 | 4.54 | 6.81 | 12.76 | 6.53 |
| Concentración mín. (μg /m3) | 3.28 | 2.21 | 1.95 | 2.93 | 6.44 | 3.31 |
| Muestras tomadas | 7 | 7 | 7 | 7 | 7 | 7 |
| Muestras descartadas | 2 | 2 | 2 | 2 | 2 | 2 |
| Muestras útiles | 5 | 5 | 5 | 5 | 5 | 5 |
| Total de muestras útiles usadas | 64 | |||||
En la estación de muestreo AireUSB los datos meteorológicos fueron recolectados con un equipo Davis Instruments 2010, que operó las 24 h del día durante el tiempo de muestreo (agosto de 2014-octubre de 2015). El periodo de toma de datos para la velocidad y dirección del viento fue de 1 h, para la ocurrencia de lluvia fue diariamente y para el resto de las variables meteorológicas cada 10 min. Luego de un análisis se descartaron algunos datos meteorológicos. En el cuadro II se resume la cantidad de datos meteorológicos esperados y los disponibles.
CUADRO II CANTIDAD DE DATOS POR VARIABLE METEOROLÓGICA
| Variable | Tiempo de muestreo | Núm. días de muestreo | Periodo toma de muestra | Datos recolectados | Datos esperados | Datos disponibles |
| Radiación solar | 23/8/2014-29/10/2015 | 435a | 10 min | 6 datos por hora | 122.985 | 12.910b |
| Humedad relativa | 122.646 | |||||
| 121.286 | ||||||
| Temperatura | 119.981 | |||||
| Velocidad del viento | 60 min | 1 dato por hora | 19.992 | 15.628 | ||
| Dirección del viento | 19.992 | 7.797 | ||||
| Ocurrencia de lluvia | 24 h | 1 dato por día | 435 | 391 |
aÚltimo día de encendido del equipo para recolectar muestras por 72 h, por lo que el número de días de recolección de datos de las variables meteorológicas se consideró hasta el 1 de noviembre de 2015; bla radiación solar se mide sólo en el horario de luz solar (06:00 a 18:00 LT).
A partir del análisis de los registros meteorológicos puede conocerse que la temperatura promedio mensual en el Valle de Sartenejas durante el periodo de estudio varió de 19.7 a 22.8 ºC. La temperatura mínima se mantuvo en el rango de 15.4-18.5 ºC y la máxima fue de 25.0 a 28.0 ºC. La humedad relativa varió de 73 a 81 % y la radiación solar de 250 a 347 cal/cm2. La velocidad del viento promedio fue de 1.57 m/s con 37 % de vientos de calma. Los valores de dirección del viento se descartaron por estar incompletos (Cuadro II).
La estación meteorológica La Mariposa, administrada por el Instituto Nacional de Meteorología e Hidrología (INAMEH), ubicada en las coordenadas UTM 10.40417 y -66.92500 m, a 5.6 km del Valle de Sartenejas, publica registros horarios de velocidad y dirección del viento para 2015. La figura 4 muestra la rosa de vientos en la estación La Mariposa. En ella se observan vientos prevalentes del este con máximos en el este-noreste y sureste, velocidades prevalentes entre 2.5 y 3.5 m/s con 21 % de vientos de calma. En el estudio meteorológico presentado por Goldbrunner (1984) para el periodo 1951-1970 se indica que el viento dominante en Caracas provenía del este con predominio de vientos del sureste, mostrando un máximo en la dirección este-sureste, velocidad predominante de 2 m/s y 44.3 % de vientos de calma.
Esta estación también ha publicado registros mensuales de precipitación y temperatura para el periodo 1970-2000 (MINAMB 2006). La figura 5 muestra el climograma de la estación La Mariposa para el periodo 1970-2000, en el cual se observa una clara época de lluvia (mayo-noviembre) y otra de sequía (diciembre-abril), mostrando un máximo de lluvias en octubre (125 mm) y un mínimo en febrero (10.6 mm). Este comportamiento corresponde al descrito por Goldbrunner (1984) para el periodo 1951-1970 en Caracas.
Información secundaria
La información secundaria consiste en el histórico mensual de precipitación, ocurrencia de incendios, día de inicio del muestreo y días laborables durante el muestreo. El histórico mensual de la precipitación es el promedio de la precipitación mensual acumulada en la estación meteorológica La Mariposa para el periodo 1970-2000, con 328 datos de un total de 360 esperados. La ocurrencia de incendios forestales en los alrededores de la estación AireUSB se obtuvo por medio de los informes técnicos de los bomberos de la Universidad Simón Bolívar y de la agrupación BosquesUSB. Se conoce que durante agosto de 2014 y noviembre de 2015 se reportaron ocho incendios forestales en las zonas verdes aledañas a la universidad (GBUSB 2018b). Las variables día de inicio de muestreo y días laborales se establecieron a partir del calendario; para el caso de días laborales se indica si los días muestreados coinciden con algún día del fin de semana o días festivos.
Selección de variables: dependiente e independientes
La variable dependiente (VP) se define como la concentración de material particulado superfino (PM1) recolectado por la suma de la masa obtenida en los filtros de las bandejas 5 y 6. Esta masa corresponde al PM cuyo diámetro aerodinámico es menor a 0.95 µm, el cual es referido en esta investigación como PM1. Esta variable se mide en una escala continua (valores de 0 a infinito). En el cuadro III se describe la variable dependiente.
CUADRO III DESCRIPCIÓN DE VARIABLE DEPENDIENTE PARA EL ANÁLISIS MULTIVARIADO
| Variable (código) | Material particulado superfino (PM1) |
| Valores Tipo de variable | 0-infinito Continua |
| Unidades | μg/m3 |
| Definición | Concentración de material particulado en el aire con diámetro aerodinámico ≤ 1 µm |
| Definición operacional | Suma de masa neta en μg de los filtros de la bandeja 5 (0.95-0.49 μm) y la bandeja 6 (< 0.49 μm) del ImpC entre el volumen de aire en m3 |
El marco de referencia para la selección de variables independientes se estableció a partir de publicaciones producto de investigaciones similares (Baek et al. 1997, Chaloulakou et al. 2003, Silva et al. 2003, Botero et al. 2004, Cassidy et al. 2007, Ramos-Herrera et al. 2010). La concentración de PM en la atmósfera está relacionada con las concentraciones de otros tamaños de partículas (llamadas variables ambientales), la velocidad y dirección de viento, la radiación solar, la humedad relativa, la temperatura y la precipitación (llamadas variables meteorológicas) y con el tráfico vehicular y la ocurrencia de incendios (llamadas variables de eventos particulares). La selección de variables independientes que se incluye en un modelo es discrecional, pero siempre se basa en los conocimientos físicos y químicos del comportamiento del PM en la atmósfera.
Se seleccionaron once variables independientes: dos ambientales, cinco meteorológicas y cuatro relacionadas con eventos particulares. El detalle de las mismas se presenta en el cuadro IV.
CUADRO IV DESCRIPCIÓN DE VARIABLES INDEPENDIENTES PARA EL ANÁLISIS MULTIVARIADO
| Variables ambientales: material particulado (PM) | ||||||
| Variable (código) | PMcuasifino (PM3.0-0.95) | PMcuasigrueso (PM25-3.0) | ||||
| Valores Tipo de variable | 0-infinito Continua | |||||
| Unidades | μg/m3 | |||||
| Definición | Concentración de material particulado en el aire con diámetro aerodinámico de 3.0 a 0.95 μm | Concentración de material particulado en el aire con diámetro aerodinámico ≥ 3.0 μm. | ||||
| Definición operacional | Suma de masa neta en μg de los filtros de la bandeja 3 (3.0-1.5 μm) y la bandeja 4 (1.5-0.95 μm) del ImpC, entre el volumen de aire en m3 | Suma de la masa neta en μg de los filtros de bandeja 1 (> 7.2 μm) y bandeja 2 (entre 7.2-3.0 μm) del ImpC, entre el volumen de aire en m3. | ||||
| Variables meteorológicas | ||||||
| Variable (código) | Histórico de precipitación (Precip) | Temperatura (Temp ºC) | Velocidad del viento (Wv) | |||
| Valores Tipo de variable | 0-infinito Continua | |||||
| Unidades | mm | ºC | m/s | |||
| Definición | Histórico del promedio mensual de precipitación acumulada como indicador de época de lluvia/sequía, señalando intensidad de precipitación mensual | Cantidad de energía calorífica acumulada en el aire en un momento y lugar determinados | Magnitud del vector velocidad con la que el aire se mueve horizontalmente sobre la superficie de la tierra | |||
| Definición operacional | Promedio de la precipitación mensual acumulada en la estación La Mariposa para el periodo 1970-1999 | Temperatura promedio horaria en la estación meteorológica AireUSB para el periodo de muestreo | Medida horaria de velocidad del viento en la estación meteorológica AireUSB para el periodo de muestreo | |||
| Variable (código) | Humedad relativa (HR %) | Radiación solar (Rad) | ||||
| Valores Tipo de variable | 0-100 Continua | 0-infinito Continua | ||||
| Unidades | % | W/m2 | ||||
| Definición | Relación porcentual entre la cantidad de vapor de agua real que contiene el aire y la que necesita para saturarse a la misma temperatura | Emisión de energía por parte del sol en forma de radiaciones electromagnéticas, cuantificada en unidad de irradiación | ||||
| Definición operacional | Media horaria de humedad relativa en la estación meteorológica AireUSB para el periodo de muestreo | Media horaria de radiación solar en la estación meteorológica AireUSB para el periodo de muestreo | ||||
| Variables relacionadas con eventos particulares | ||||||
| Variable (código) | Ocurrencia de incendios (IncFor) | Ocurrencia de lluvia (Lluvia SI) | Día de inicio muestreo (Día) | |||
| Valores Tipo de variable | 0 ó 1 Discreta | |||||
| Unidades | n/a | |||||
| Definición | Fuego que afecta vegetación en zonas forestales, por causas naturales o inducidas, no controladas | Ocurrencia de lluvia durante el muestreo de partículas | Día de la semana en el que se inicia el muestreo de partículas | |||
| Definición operacional | Ocurrencia de incendio forestal en cercanías a la estación de muestreo AireUSB, documentado por BomberosUSB y/o BosquesUSB; si el incendio coincide con la fecha de muestreo de partículas, la variable toma el valor de 1 | Ocurrencia de lluvia reportado en la estación meteorológica AireUSB; si la lluvia coincide con fecha de muestreo de partículas, la variable toma el valor de 1 | Día de la semana de encendido de equipo para muestreo de partículas | |||
| Variable (código) | Día laboral (DiaLab) | |||||
| Valores Tipo de variable | 0-1 Discreta | |||||
| Unidades | n/a | |||||
| Definición | Los días laborables son de lunes a viernes. Los días no laborables son sábados domingos y feriados | |||||
| Definición operacional | Si el periodo de muestreo coincide con un día del fin de semana o un día festivo, la variable toma el valor de 0 | |||||
USB: Universidad Simón Bolívar
Se utiliza el análisis de correlación de Pearson (r) entre la VP y las VI con la intención de identificar aquellas VI relacionadas de forma significativa (p < 0.1) con la variable dependiente (PM1). Para corroborar la correlación entre dos variables de diferente escala se aplica adicionalmente la prueba t de Student: VP medida en una escala continua y VI medidas en escala discreta (ocurrencia de incendios, ocurrencia de lluvia, día de inicio del muestreo y día laboral).
Construcción del modelo multivariante
El análisis de RLM es una técnica estadística utilizada para estudiar la relación entre un conjunto de más de dos variables independientes (VI), el cual tiene el propósito de averiguar en qué medida la variable dependiente (VP) puede explicarse por las VI. Si se asume una VP (denotada como Yi), su mejor predictor lineal a partir de otras VI (Xi) tendrá la siguiente forma (Peña 2002, Cohen et al. 2003):
donde β 0 , β 1 ,... β k - B 0 , B 1 , B 2 ,…B k son parámetros fijos desconocidos; X 1i ,...,X ki son variables independientes cuyos valores son fijados por el investigador, y ∈ i es una variable aleatoria inobservable (error aleatorio).
El modelo A permite identificar qué variable tiene la contribución más importante sobre la varianza total (Cohen et al. 2003). Los coeficientes β están basados en puntuaciones típicas y son directamente comparables entre sí. Indican la cantidad de cambio que se producirá en la VP por cada cambio de una unidad en la correspondiente variable independiente (manteniendo constantes el resto de VI). Una variable tiene tanta más importancia en la ecuación de regresión cuanto mayor sea, en valor absoluto, el coeficiente de regresión estandarizado (β) (Cohen et al. 2003).
El modelo B se construye con coeficientes no estandarizados B de cada variable. El coeficiente B indica el cambio medio que corresponde a la VP por cada unidad de cambio de la variable independiente. Los coeficientes no estandarizados B se leen en las mismas unidades físicas en las cuales se mide cada variable.
La RLM se basa en una serie de supuestos que la base de datos debe cumplir para que el modelo pueda considerarse válido. Estos supuestos son la escala de medida (la VP debe ser una variable en escala continua); el número de variables (debe haber al menos dos VI en la base de datos); el tamaño de muestra o la cantidad de VI (se debe contar con al menos 10 datos de cada VI); la linealidad (debe existir una relación lineal entre la VP y cada una de las VI por separado, y entre la VP y las VI colectivamente, lo cual se prueba con correlaciones); la independencia de los errores (se debe tener independencia de las observaciones o, lo que es igual, independencia de los residuos); la normalidad (los datos deben ser normales, lo cual se prueba analizando el histograma de los residuos o el gráfico de probabilidad P-P acumulada observada/esperada según la normal); la homocedasticidad (significa que la varianza de la distribución de probabilidad del error [€] es constante para todos los valores de la variable independiente, lo cual se prueba usando el diagrama de dispersión de pronósticos tipificados por residuos tipificados); la multicolinealidad (dos o más VI no deben tener una correlación mayor a r > 0.9), y los valores atípicos (la base de datos no debe mostrar más del 5 % de datos atípicos, celdas vacías o datos perdidos) (Cohen et al. 2003).
Validación del modelo
El indicador de error de sesgo promedio (MBE, por sus siglas en inglés) se usa para validar los resultados del modelo contra datos experimentales. El indicador MBE representa el grado de correspondencia entre una predicción media (Pi) y una observación media (Oi) y se utiliza para describir si un modelo sobrestima (valor positivo) o subestima (valor negativo) una observación (ecuación 3). Valores bajos de MBE son aceptados (Moustris et al. 2010). Para la validación del modelo se tomaron las muestras de PM recolectadas para el periodo de 72 h, reservadas para tal fin.
donde n es el número de puntos de datos, Oi el dato observado y Pi el dato predicho.
RESULTADOS
La figura 6 muestra la correlación de Pearson (r) entre la VP y las VI indicando el valor p de cada correlación. Para interpretar la magnitud de las correlaciones de Pearson se siguieron las pautas propuestas por Ratner (2011). Se seleccionaron las seis variables independientes que obtuvieron correlaciones con p < 0.1, señaladas con asterisco en la figura 6.

Fig. 6 Correlaciones entre la variable dependiente y las variables independientes. *Correlación con p < 0.1; **correlación con p < 0.01
Las concentraciones de los tres rangos de PM (PM1 [PM < 0.95 μm], PMcuasifino [PM3.0-0.95] y PMcuasigrueso [PM25-3.0]) se midieron en simultáneo, en el mismo equipo y separadas por el ImpC, con el mismo tratamiento y las mismas condiciones meteorológicas. Por lo anterior se esperaría que la correlación entre ellas sea significativa y positiva. Las PM1 y las PMcuasifinas son partículas que provienen de fuentes similares, principalmente de origen antrópico (quema de combustibles fósiles) y están relacionadas con la condensación de aerosoles que podrían ser removidas por precipitaciones (Lundgren y Paulus 1975, Whitby y Cantrell 1976). Estos dos rangos de tamaños de partículas presentaron una correlación positiva y significativa (r > 0.7; p < 0.01). Las PMcuasigruesas mayoritariamente provienen de fuentes naturales asociadas a la resuspensión de polvos, compuestos orgánicos naturales, aerosoles marinos, polen y algún tipo de emisiones antrópicas, y además, este tamaño de partículas podría sufrir deposición seca (Lundgren y Paulus 1975, Whitby y Cantrell 1976). Esta diferencia entre PM1 y PMcuasigruesas ocasiona que la correlación entre ellas sea menor a la anterior (r > 0.5; p < 0.01). Se destaca que la correlación no es suficientemente elevada para esperar multicolinealidad entre estas VI.
Las altas temperaturas del aire conducen a sistemas atmosféricos de alta presión que se mueven lentamente, cielos claros y soleados característicos de condiciones atmosféricas estables con aire subsistente, lo que produce acumulación de contaminantes en el aire y provoca mayor concentración de los mismos (Taheri y Sodoudi 2016). La correlación entre PM1 y la temperatura (r ~ 0.34; p < 0.01) muestra una relación lineal positiva moderada (usando como referencia a Ratner [2011]), lo cual indica que a mayor temperatura habrá mayor concentración de PM1.
Al analizar el efecto de la lluvia sobre la concentración de PM1 se observa que, cuando ocurren episodios puntuales de lluvia, disminuye la concentración de PM dejando un aire temporalmente libre de contaminantes por efecto de la deposición húmeda del material particulado. La correlación entre el PM1 y ocurrencia de lluvia resultó ser de r < -0.30; p < 0.1, lo cual implica una relación lineal negativa débil (Ratner 2011). Este valor de correlación débil podría deberse a que se trata de un material particulado muy pequeño que tiende a permanecer más tiempo suspendido en el aire.
Es importante destacar que la variable ocurrencia de lluvia (Lluvia SI) mide cuando este evento sucede o no, sin considerar la intensidad del mismo, en tanto que el histórico del promedio mensual de precipitación acumulada (Precip) considera la intensidad promedio de la precipitación acumulada de cada mes durante el periodo 1970-2000. La correlación entre Precip y el PM1 resultó ser positiva y moderada (r > 0.359; p < 0.01) lo cual significa que la concentración de PM1 disminuiría en la época de sequía y aumentaría en la de lluvia, contrariamente al comportamiento esperado. Este resultado sugiere que la distribución de la precipitación histórica mensual entre 1970 y 2000 podría no ser representativa de la distribución de la intensidad mensual de la precipitación durante el 2015.
El acumulado de la precipitación anual en 2015 (839 mm) fue menor en 4.65 % que el acumulado anual del promedio histórico para 1970-2000 (880 mm). Por su parte, el patrón de distribución de intensidad de la precipitación mensual en 2015 no corresponde con el patrón del comportamiento histórico, presentando precipitaciones abundantes en épocas que históricamente son de sequía y escasas en épocas históricas de lluvia, lo cual explica el resultado de la correlación obtenida. La figura 7 muestra el climograma de 2015 para la estación La Mariposa. En ella se evidencia un comportamiento anómalo de la distribución de la intensidad mensual de la precipitación al compararlo con el histórico (Fig. 5). Este comportamiento anómalo se verifica al aplicar la prueba t de Student para una muestra. Esta prueba contrasta si la media de la precipitación ocurrida cada mes durante el periodo 1970-2000 difiere de una constante especificada por la intensidad de la precipitación ocurrida en ese mes para 2015 (Cuadro V).
CUADRO V COMPARACIÓN DE LA MEDIA DE PRECIPITACIÓN HISTÓRICA ACUMULADA MENSUAL DEL PERIODO 1970-2000 CON LA DE 2015 USANDO LA PRUEBA t de STUDENT PARA UNA MUESTRA
| MES | ENE* | FEB* | MAR* | ABR* | MAY* | JUN* | JUL* | AGO* | SEP* | OCT* | NOV** | DIC* |
| a | 13.31 | 10.59 | 19.15 | 46.72 | 96.41 | 119.44 | 114.15 | 122.86 | 97.40 | 125.04 | 79.90 | 34.99 |
| b | 286.86 | 116.74 | 116.74 | 88.90 | 0.672 | 9.36 | 19.64 | 24.11 | 31.38 | 40.28 | 49.09 | 55.45 |
a: 1970-2000; b: 2015; *p < 0.000; **p <0.001
La correlación entre PM1 y ocurrencia de incendios forestales presentó una relación lineal positiva moderada (r > 0.5; p < 0.01). La ocurrencia de incendios forestales en las proximidades de la estación de muestreo aumenta la cantidad de PM suspendido en el aire, lo cual es congruente con lo esperado. Adicionalmente, también se estudió la correlación entre incendios con PMcuasifino y PMcuasigrueso (r = 0.406, p < 0.01 y r = 0.383, p < 0.01, respectivamente), mostrando una influencia moderada positiva una ante la presencia de PM en el aire tanto en fracciones finas como cuasigruesas.
Debido a que la ocurrencia de incendios (IncFor) y Lluvia SI son variables discretas con correlación estadísticamente significativa hacia la VP, pero con correlaciones moderada y débil, respectivamente, se realiza una comparación de las medias usando la prueba t de Student para muestras independientes con α ≤ 0.05. Los resultados de esta prueba se presentan en el cuadro VI, donde se resaltan en letras negritas las medias que probaron ser estadísticamente diferentes entre sí (p < 0.05), evidenciando que las medias entre las dos variables independientes y la dependiente son diferentes. Esto significa que los valores de ocurrencia de incendios forestales y de lluvia influyen sobre los valores de concentración de PM1. Este resultado ayuda a aclarar la relación moderada y baja obtenida en el análisis de correlación de Pearson.
CUADRO VI COMPARACIÓN DE MEDIAS ENTRE VARIABLE DEPENDIENTE Y VARIABLES INDEPENDIENTES DISCRETAS USANDO LA PRUEBA t de STUDENT
| Variables independientes | Variable dependiente | |||
| (PM1, µg/m3) | ||||
| Media | Desviación estándar | Media (ocurrencia sí = 1) | Media (ocurrencia no = 0) | |
| Incendios forestales | 15.18 | 10.07 | 30.07 | 13.17 |
| Ocurrencia lluvia | 12.31 | 16.88 | ||
Construcción del modelo de regresión lineal múltiple para PM1
Se construyó un modelo de regresión lineal usando solamente las seis variables que se relacionan de forma significativa con PM1 (p < 0.1) y 52 observaciones (se descartaron siete observaciones para un mejor cumplimiento de los supuestos de la RLM). El cuadro VII muestra el modelo que mejor explica la varianza de PM1 con el menor número de VI. Al modelo se le comprobaron los supuestos de homocedasticidad, independencia de los errores y normalidad para verificar que los datos cumplieran con los criterios mínimos para ser utilizados en las predicciones. La varianza de PM1 se explica en más de un 75 % (R2 ajustado = 0.759; p < 0.000) a partir de tres VI: PMcuasifino (PM3.0-0.95), precipitación histórica mensual (histórico del promedio mensual de precipitación acumulada) e IncFor. El análisis mostró que la RLM tenía valores R2 significativos, siendo este resultado similar al encontrado por Thomas y Jacko (2007)), quienes reportan un R2 no ajustado de 80 % para una regresión lineal relacionada con predicción de PM2.5 a través de cuatro VI. Asimismo, resultó ser mayor al R2 ajustado publicado por Nazif et al. 2016) para un análisis de regresión lineal que predice PM10 a partir de diferentes combinaciones de VI.
CUADRO VII RESUMEN DEL MODELO MULTIVARIANTE*
| Variables (código) | B | β | t de Student | Valor de p |
| (Constante) | 3.273 | 3.297 | 0.01 | |
| PMcuasifino (PM3.0-0.95) | 0.572 | 0.667 | 9.167 | 0.00 |
| Precipitaciones históricas (Precip) | 0.059 | 0.311 | 4.390 | 0.00 |
| Incendios forestales (IncFor) | 6.811 | 0.244 | 3.449 | 0.01 |
Variable dependiente = material particulado [PM1]. N = 52 observaciones (siete filas eliminadas para un mejor cumplimiento de los supuestos de la RLM), R2 = 0.7728, R2 ajustado = 0.759, F = 54.43, p = 0.000. Al modelo se le comprobaron los supuestos de la RLM: homocedasticidad, independencia de los errores y normalidad. La base de datos se manejó hasta encontrar el mayor valor de R2 ajustado con el mayor número de observaciones que cumplieran los supuestos de la RLM
Con la información del cuadro VII se construyen el modelo A (ecuación 4) y el modelo B (ecuación 5). El modelo A sólo indica la importancia relativa de cada variable.
Respecto de este modelo, se tiene que:
Al aumentar la concentración de PMcuasifino (PM3.0-0.95) aumenta la concentración de PM1, lo que coincide con los resultados obtenidos en el análisis correlacional. Esta variable es la de mayor importancia al momento de predecir la concentración de PM1 (véase β en el cuadro VII).
La asociación entre IncFor y PM1 señala que al ocurrir los primeros se agrega un valor de 0.244 unidades al valor predicho de la PM1.
El signo positivo de la variable que mide el comportamiento histórico del promedio mensual de precipitación acumulada, muestra que los meses con mayor registro histórico de precipitaciones se asocian con mediciones mayores de PM1. Este resultado lo explica la variación en la distribución de la intensidad de la precipitación mensual de 2015, como ya se mencionó en el análisis correlacional.
El modelo B o modelo predictivo se usa cuando la intención es predecir la concentración de PM1:
En este modelo, el coeficiente que acompaña a la variable PM3.0-0.95 indica que si el resto de las variables se mantuvieran constantes, a un aumento de una unidad en la variable PM3.0-0.95 le correspondería, en promedio, un aumento de 0.572 veces la PM1 (en μg/m3). El mismo análisis se aplica para las otras dos variables.
Validación del modelo predictivo
En el cuadro VIII se presentan los valores medidos y predichos con el modelo B de PM1 usando datos reservados para la validación, así como el valor de MBE para el modelo predictivo. El valor de MBE igual a -1.5 µg/m3 revela que el modelo subestima la concentración de PM1, por lo cual la información que arroja el modelo sobre la concentración promedio de PM1 para una región intertropical en el centro-norte de Venezuela resulta menor que el valor que reportaría el equipo (cuando el modelo prediga una concentración de PM1, el valor medido será siempre mayor). Esta información es de gran utilidad en los casos en que valores obtenidos por el modelo resulten cercanos a valores considerados no seguros para la salud.
CUADRO VIII VALIDACIÓN DEL MODELO PREDICTIVO
| Fecha de medición | 29/sep/15 | 04/oct/15 | 19/oct/15 | 24/oct/15 | 29/oct/15 | MBE (µg/m3) |
| Valor medido (µg/m3) | 42.3 | 26.8 | 39.3 | 19.1 | 35.3 | -1.5 |
| Valor predicho (µg/m3) | 33.8 | 23.1 | 27.3 | 17.7 | 23.2 |
MBE: indicador de error de sesgo promedio, por sus siglas en inglés
Aún no hay un consenso unificado sobre los valores máximos aceptables para el MBE. La literatura indica que entre más cercano a cero sea el valor de MBE mejor será el modelo predictivo. Se comparó el resultado del MBE obtenido (-1.5 µg/m3) con el de estudios similares para predecir contaminantes atmosféricos: los valores de MBE calculados por Corani y Barazzetta (2004) para modelos de predicción de PM10 en Milán variaron de -2.46 a 2.34 µg/m3, los cuales son mayores que el obtenido en esta investigación. Los resultados mostrados por Moustris (2010) para modelos predictivos con NO2, CO, SO2, y O3 resultaron menores a la unidad (-0.771 y 0.615 µg/m3). Los resultados de Dutot et al. (2007) para O3 resultaron comparativamente elevados (-13 y 11 µg/m3). Los modelos diseñados en esta investigación representan los primeros resultados obtenidos en predicciones de PM1 en Venezuela para un área continental intertropical.
CONCLUSIONES
Con la información obtenida a través de la investigación de campo y de fuentes secundarias se logró construir una matriz de datos de variables ambientales, meteorológicas y de eventualidades físicas capaces de predecir el comportamiento de las partículas finas (PM1). Las variables se obtuvieron usando un modelo de RLM que permite estimar concentraciones promedio de PM1 a partir de tres VI: concentración de PMcuasifino (3.0 a 0.95 µm), histórico del promedio mensual precipitación acumulada y ocurrencia de incendios (forestales) en el sector de estudio. El modelo obtenido para predicción de PM1 es válido para aplicarse a la base de datos históricos del promedio mensual de precipitación acumulada de la estación La Mariposa y no es dependiente de valores de precipitación actual medidos en el lugar de muestreo, dando libertad de usar el modelo en futuras investigaciones con datos históricos públicos de precipitación.
El modelo de RLM diseñado explica el 75.9 % de la varianza, es estadísticamente significativo para p < 0.000, cumple con los requisitos de validez de una RLM y presenta un indicador de MBE igual a -1.5 µg/m3, por lo que se establece que el modelo subestima la concentración de PM1.











 nueva página del texto (beta)
nueva página del texto (beta)