INTRODUCTION
This article proposes a simplified method that combines economic input-output life cycle assessment (EIO-LCA) with employment location quotients (LQ). With this combination, we determined the lifecycle emissions (direct and total emissions), with consumption and production-based approach, caused by the electricity use of the 80 economic sectors of the Mexican state of Puebla during 2013.
One hundred and ninety-four countries signed the Paris Agreement of the United Nations Framework Convention on Climate Change (UNFCCC), agreeing to measure and reduce their contribution to global climate change (UNFCCC 2016). This commitment is significant for Mexico since it was the 12th highest contributor to the world’s total carbon dioxide equivalent (CO2e) emissions in 2013, reaching 669 million metric tons (Mmt) of CO2e (WRI 2020).
To fulfill the mandate, Mexico has published its Nationally Determined Contributions (NDCs), requiring a 50 % reduction of 2000’s greenhouse gas (GHG) emissions by 2050 (Semarnat 2013), with an initial target of reducing emissions by 22 % by 2030 (Semarnat 2015). The Mexican General Law of Climate Change establishes dispositions to address climate change effects and regulates mitigation and adaptation actions (DOF 2012). It also highlights the importance of maintaining transverse cooperation among the federal, state and municipal governments for climate change mitigation and adaptation actions. Although the national-level mandates to reduce GHG emissions and carbon footprints (CF), meeting targets also resides within the states (DOF 2012).
A first step in complying with the Paris Agreement requires that states/regions have a proper emission accounting system. Such systems are expensive and resource-intensive in terms of data requirements that are not always available for subnational regions. In this work, we propose a simplified method to determine the CF of a state or region by requiring relatively minimum effort but still gives insight into climate change policies’ effectiveness and can help a state/region strategize to meet mitigation targets.
According to the International Energy Agency (IEA 2016), energy production generated two-thirds of the global GHG emissions (or 30 175 Mmt CO2e) in 2013, and 25 % out of these emissions was attributed to the electricity and heat production sector (IPCC 2014). It is similar for Mexico, for which 66 % (around 490 Mmt CO2e) of the total GHG emissions in 2013 were generated by the energy production sector, which includes electricity production, petroleum refining, solid fuel manufacturing, and other energy industries (INECC 2013). Consequently, national and state-wide GHG mitigation strategies tend to focus on the energy sector because of its significant contribution to the region’s CF. It is essential to propose practical and reliable approaches to account for GHG emissions to measure, benchmark, and evaluate progress towards the emission reduction goals. Furthermore, the Paris Agreement recommends that regional GHG emission reduction measures go beyond the regional impacts externalization and contribute to global impact reduction. In other words, the GHG accounting method should include direct emissions and the indirect emissions that take place elsewhere as a result of the consumption of the state/region; this is most often referred to as a lifecycle approach.
Here we present a simplified accounting method for GHG emissions at the state level, combining economic input-output (EIO), national tables, and lifecycle assessment (LCA). LCA is a cradle-to-grave analysis technique to measure environmental impacts of a product’s life (Muralikrishna and Manickam 2017). When combined with EIO, we can determine the materials and energy resources needed by the various sectors of an economy and the environmental emissions resulting from its economic activities (GDI 2016). EIO-LCA studies are possible thanks to publicly available input-output (IO) tables compiled by national statistic offices or collaborative projects such as Eora1, which developed a multi-region IO database of 187 countries, covering from 1990 to 2013 (Lenzen et al. 2013). LQ can be used as proxies to downscale national IO tables to regional or state levels, as explained by Miller and Blair (2009).
There are previous studies that employ EIO-LCA to quantify GHG emissions at the regional and national levels. For example, at the regional level, EIO-LCA was used to estimate GHG intensities through the lifecycle of wind energy farms in Indiana, USA. Showing wind energy production is not entirely GHG emission-free if all lifecycle stages are contemplated (Kumar et al. 2016). A simplified EIO-LCA study analyzed nine economic sectors of Penghu Island, Taiwan, and determined that the transportation and communication sectors are the highest contributors to the island’s CF (Trappey et al. 2013). At a national level, an EIO-LCA of Japan was performed to examine the effect of a wind power generation system on the environment, the energy sector, and the economy, demonstrating the economic ripple effects of adding new sectors related to power generation to the Japanese IO table. It also determined that for industries like “iron & steel” and “power & heat supply”, the impacts of the wind power system manufacture, construction and operation are large (Nagashima et al. 2016). However, the combined use of EIO-LCA with LQ, both known methods, have not been used to quantify the CF at a state level.
This paper uses the EIO-LCA coupled with LQ to determine the CF of a region or state, specifically Puebla. We have chosen this Mexican state as a case study to illustrate the method and how it can help understand the effectiveness of GHG mitigation strategies in the power generation sector. We propose this method as an easy alternative to resource-intensive bottom-up approaches for GHG accounting. We also show how this type of analysis helps determine which strategies best suit the reduction of CF. The presented method allows us to quantify the CO2e emissions caused by Puebla’s electricity use with two perspectives: (1) a consumption-based approach, and (2) a production-based approach.
Although the CF tool has a common use, the literature inquiries about the absence of a clear definition generally accepted (Wiedmann and Minx 2008). The CF can be defined as an environmental impact indicator representing the amount of GHG emitted into the atmosphere derived from the production and consumption of goods and services, i.e., derived from anthropogenic activities (Peandey et al. 2011). CF is considered one of the most relevant tools for quantifying GHG emissions (Čuček et al. 2014). Countries and their sub-regions (states and municipalities in Mexico’s case) account for their CF through the inventories of their GHG emissions.
In the present article, we estimate the CF caused by the use of electricity by 80 sectors of Puebla’s economy. Such electricity use is assumed to have been driven by the final demand (household consumption, government capital creation, plus exports) of the region.
A relevant contribution of applying EIO-LCA and LQ to estimate the CF of a Mexican state due to its electricity consumption is that there are no previous studies that assess the regional CF in such a simplified way in Latin-American countries. Therefore, the presented method can represent an alternative way to estimate local emissions in an accessible way using relatively few resources and data.
The first advantage of using an EIO-LCA approach over a pure LCA is that it will not be necessary to delimit the system’s study boundary, given that, by default, the boundary is the entire economy to be studied. The second advantage is that, by using the EIO-LCA, the common truncation error of a pure LCA can be overcome (Ward et al. 2017). However, regarding the above-explained LCA modeling process, the EIO-LCA methods are more appropriate as a screening tool. Rather than the central model needed to respond to the objectives of the LCA task, i.e., the EIO-LCA model serves to identify where the highest impacts throughout a whole system occur (Matthews et al. 2019).
The main difference between an EIO and an EIO-LCA model is that the first one focuses on carrying out a detailed analysis of the production and final consumption chain and between industries in a particular territory, in economic terms, without involving the environmental impacts caused by the economy to the studied region. In contrast, the EIO-LCA uses the advantages of an EIO by quantifying the environmental impact of the studied economy.
IO analysis (Leontief 1941) is the most commonly used tool to assess macroeconomics’ environmental impacts. A relevant item of discussion in emission evaluation systems is how emissions’ responsibility is attributed within the IO. Some studies differentiate between two ways of assigning responsibility: the production approach and the consumption approach (Peters 2008, Soeren et al. 2013). A study that uses the production perspective would attribute emissions to a goods or services producer, whereas the consumption perspective would attribute them to the consumer’s responsibility. This attribution is not trivial and has significant consequences in policymaking (Chávez and Ramaswami 2013).
The consumption-based approach allocates the emissions according to the economy’s final demand, including household expenditures, government expenditures, and business capital investments (Chávez and Ramaswami 2013), determining the ripple effect that final demand has throughout an economy. GHG emissions are allocated to the final consumers through this approach rather than producers (BSI 2013). Total consumption-based emissions can be divided into two fractions: (i) the emissions issued by each sector to satisfy its own final demand (known as final demand emissions), and (ii) the emissions that result from intermediate production/consumption, which are referred to as indirect emissions.
On the other hand, the production approach quantifies the direct emissions associated with the production of the goods or service as well as downstream and upstream emissions incurred by the production of other s ectors. These production emissions are typically referred to as direct emissions or lifecycle emissions (BSI 2013) and can also be calculated through bottom-up process-based lifecycle analysis. Regardless of the approach, ultimately, consumption-based emissions and production-based emissions are equal.
To illustrate these definitions, consider the following example of a steel-production plant located within Puebla’s boundaries. Regarding a production perspective, the direct emissions are those coming out of the production plant regardless of whether that steel is consumed inside or outside Puebla. Whereas, from a consumption-based approach, the total emissions assigned to the plant are those related to the products used to meet steel’s final demand, which is the sum of final consumption (households, government, and capital) and exports. Final demand emissions are those directly related to the steel consumed inside Puebla’s boundaries plus exported steel. While indirect emissions would be those that other sectors have emitted to produce the inputs needed by the plant to satisfy steel’s final demand, such as iron ore or coal. Together, final demand emissions and indirect emissions would be the total consumption-based emissions allocated to that steel plant.
In the following sections, we present the case study (section 2), explain how we apply the EIO-LCA and LQ methods to estimate Puebla’s CF due to its electricity consumption (section 3), discuss our results (section 4), and draw conclusions (section 5). We propose this method as an easy alternative to resource-intensive bottom-up approaches for GHG accounting. Also, we show how this type of analysis helps determine which strategies are best suited for reducing the CF.
CASE STUDY: ELECTRICITY PRODUCTION AND USE IN PUEBLA, MEXICO
The state of Puebla is located in the south-central area of Mexico, with a total population of 5.8 million and a density of 160 inhabitants per km² in 2013. Its 72/28 % urban/rural distribution is similar to the national average (78/22 %) (INEGI 2020). It holds the highest number of climate change vulnerable communities in Mexico (23 % of the national total [99/480]) (Inafed 2017), which already suffer droughts, frosts and extreme precipitation (INECC 2019). The 2017-2018 Puebla’s development plan (SFA 2017) states the commitment of the regional government to ensure access to affordable, sustainable, and modern energy for Puebla’s inhabitants as a strategy to curb the environmental impacts of the power generation, transmission and supply (PGT&S) sector. Puebla is one of five in 32 states with a climate change law (Gobierno del Estado de Puebla 2013) and a climate change program in line with the Mexican Clean Development Mechanism (Gobierno de la República 2015). However, Puebla has not yet developed an updated and disaggregated GHG emission inventory, and must consequently rely on national data information services. This has made it impossible to establish quantitative regional mitigation goals related to the electricity sector.
Electricity is the second most used energy source in Mexico (Sener 2017), and the sector growth rate (4 %) doubled the Mexican gross domestic product (GDP) growth between 2006 to 2016 (WB 2017). Mexico aims to generate 35 % of its electricity with clean energy sources by 2024 (Sener 2016) compared with 18 % as of 2010 (IRENA 2018). In 2013, Puebla consumed about 4 % of the total national electricity (583 GWh) and produced 1.7 % of the total national electricity demand (450 GWh) (Sener 2018).
According to the World Bank’s statistics (WB 2018), Puebla contributed 4 % of the Mexican GDP (USD $1.274 trillions in 2013) (INEGI 2018a), being the seventh most significant contributor to the Mexican economy (INEGI 2014). By 2011, Puebla’s GDP was mainly generated by tertiary sectors (63 %), followed by secondary sectors (33 %) and primary production activities (only 4 %) (INEGI 2013a). We focus our analysis on quantifying the CF derived from the state’s 80 commercial and industrial sectors’ lifecycle use. The 80 economic sectors are the same ones listed in the Eora’s Mexican input-output table (IOT) (see Table S1 in the supplementary materials). It assumed that the national and regional economy has the same number of sectors. The commercial and industrial sectors represented 77 % of Mexico’s total electricity consumption in 2015, according to the IEA (2016).
METHODOLOGY AND DATA
We applied an EIO method that uses location quotients (LQs) to quantify the PGT&S of Puebla’s sectors, thereby determining the CF of its 80 economic sectors’ electricity use during 2013. The followed steps are summarized in figure 1, whereas table I summarizes the primary data sources.
TABLE I DATA SOURCES.
| Data | Source |
| IO data of Mexico | EORA (EORA-MRIO 2014) |
| Complementary IO data of Mexico | OECD input-output tables database (OECD 2017) |
| Electricity consumption statistics of Mexico | International Energy Agency (IEA 2018) |
| Miscellaneous | Ministry of Environment and Natural Resources (Semarnat) |
| Energy use and production statistics of Mexico | Ministry of Energy (Sener) and Mexican Energy Regulatory Commission (CRE) |
| National Emissions Inventory | National Institute of Ecology and Climate Change (INECC 2013) |
| Miscellaneous | National Institute of Statistics and Geography (INEGI) |
Seeking to have a more precise intensity vector for the PGT&S sector, we calibrated it by extracting it from the national inter-industrial transactions matrix (Z N ) (directly obtained from Eora) by following the next steps:
Translating the PGT&S vector from ‘000 USD to kilowatt-hours (kWh) by using the tariff paid by the industrial and commercial sectors per kWh, which is 0.11 US$/kWh for heavy industries, 0.17 US$/kWh for service sectors and 0.14 US$/kWh (average tariff) for the rest of the sectors (Sener 2018).
Calculating the share of the 80 analyzed sectors in Mexico’s final electricity consumption.
Recalculating the electricity consumption vector with the International Energy Agency (IEA 2017) data on total electricity use in Mexico.
Inserting the new vector in the Mexican transactions matrix, replacing the original vector.
Once Z N was calibrated, we calculated the national GDP as explained in the Scottish government IO methodology guide (SG 2011). Secondly, we used the contribution to the GDP of each sector to calculate each component of the national technical coefficient matrix (A N ij) and the Leontief inverse matrix (L N ), as explained by Miller and Blair (2009).
Subsequently, we estimated the LQs as per Miller and Blair (2009) from the Mexican Economic Information Bank’s employment statistics (INEGI 2018a) using equation 1, and it was possible to downscale from A N ij to Puebla’s technical coefficient matrix (A ij p) by following equations 2 and 3.
where LQ p refers to Puebla’s LQ factor; Ei p and E p are the employment in sector i and total employment in Puebla, respectively, and Ei N and E N are the employment in sector i and total employment in the whole nation (Deng et al. 2014).
INEGI’s employment statistics of Puebla were aggregated from 114 economic sectors to 80 by following the North American Industry Classification System (NAICS) (US Census Bureau 2017), so we could calculate the employment LQs corresponding to the each of the 80 sectors registered in the Eora’s Mexican IO table. The resulting LQ values are shown in table S2 in the supplementary materials. As suggested by Miller and Blair (2009), LQ factors lower than one were multiplied by the corresponding raw of the A N ij to obtain A p ij. Using A p ij, we obtained Puebla’s Leontief inverse matrix (L p ) as per Miller and Blair (2009).
By using Puebla’s households consumption statistics (ENGASTO) (INEGI 2013b) and the percentage of Puebla’s exports within the national total (INEGI 2018b), it was possible to scale the national total final consumption and exports to a regional level. Although it is known that final consumption is integrated by household, government, and capital consumption, Mexican household consumption represented 90 % of the total final consumption in 2013. Puebla’s final demand (y p ) was calculated according with equation 4 :
where hc p is Puebla’s household consumption vector, and ex p is Puebla’s exports vector.
With L p and y p we calculated Puebla’s total output vector (x p ), as shown in equation (7). To convert the PGT&S vector from monetary units to physical units, we used the electricity prices vector (p j ) (equation 5).
Later, we estimated the emission factor of electricity production (0.47 kgCO2e/kWh) by using the direct factors by energy source reported by Santoyo-Castelazo et al. (2011) and the national electricity grid-mix reported by the Mexican Ministry of Energy (CEE 2013) as shown in table II. We assumed that Puebla’s electricity grid-mix was the same as the Mexican one.
TABLE II MEXICAN ELECTRICITY GRID-MIX AND ELECTRICITY EMISSION FACTORS.
| Energy source | Electricity grid-mix* (%) | Electricity emission factors (e) | |
| Direct emission factor by energy source** (kgCO2e) | kg CO2e/kW h | ||
| Natural gas | 50 | 0.42 | 0.21 |
| Oil | 16 | 0.81 | 0.13 |
| Hydraulic | 14 | 0 | 0 |
| Carbon | 13 | 0.99 | 0.13 |
| Eolic and geothermal | 3 | 0 | 0 |
| Nuclear | 3 | 0 | 0 |
| Diesel | 1 | 0.72 | 0 |
| Total | 100 | - | 0.47 |
With the use of the estimated emission factor (e), we converted the PGT&S vector (in physical units) into a national electricity impact one (b), as shown in equation 5 (more information about how b was transformed to impact matrix (b̂) can be found in the “Electricity impact matrix calculation” section of the supplementary materials.
Vector b represents the environmental impact inflicted by the electricity demand of the region caused by total production. Each element of this vector was estimated following equation 5. The obtained values are shown in table S1 in the supplementary materials.
where b j is the jth element of the impact vector b (kgCO2e/$USTO, where TO is the total output); z PGT&S,j is the jth element of the inter-industrial transaction vector for sector PGT&S ($US); x j is the jth element of the total output row ($US); e is the electricity emission factor (kgCO2e/kWh), and p j is the jth element of the electricity prices vector ($US/kWh).2
When extracting the electricity consumption and the total output of this sector from Mexico’s IOT-Eora 2013 and comparing those values with those obtained from INEGI’s IOT 2013, we observed that INEGI reports a lower electricity consumption and a higher total output equal to US$3,256,646,153 thousand and US$36,746,7723 thousand, respectively (INEGI 2013c). Therefore, these two values were used to obtain the intensity value of this sector.
Considering that the inverse Leontief matrix depends on the technical coefficient matrix (see equation 6), L p shows the direct and indirect requirements by a unit of final demand, by sector (Miller and Blair 2009). Then we calculated the electricity CF matrix, as shown in the following equations:
where L p is Puebla’s Leontief inverse matrix ($TO/$FD, where FD is the final demand); Aij p is Puebla’s technical coefficient matrix; I is an identity matrix; x p is Puebla’s total output vector ($USTO), and y p is Puebla’s final demand vector ($USFD).
From a production-based approach, direct emissions (d p ) for each sector were calculated as:
where d p is the direct emissions vector, b is the national electricity impact vector, calculated previously in equation (5), and x̂ is the x diagonal matrix.
Whilst with a consumption-based approach, we obtained the total emissions needed to face Puebla’s final demand:
where Puebla’s total emissions (T p ) are determined as the product of three factors: b̂ is the national electricity impact diagonal matrix; L p is Puebla’s Leontief inverse matrix, and ŷ p is Puebla’s final demand diagonal matrix.
To extract the part of the emissions caused by intermediate transactions, we calculated a modified inverse Leontief matrix (L p mod):
where L p is Puebla’s Leontief inverse matrix ($TO/ $FD); I is an identity matrix; L p mod is the modified inverse Leontief matrix, which replaced the L p in equation 9 to obtain the indirect emission (I p nd) as shown in equation 11.
Lastly, the final demand emissions (fd CO2 e p ) were calculated following equation 12:
RESULTS AND DISCUSSION
To better understand the contribution of each of Puebla’s economic sectors to its electricity CF, we quantified emissions with a production-based perspective (direct emissions) and with a consumption-based perspective (total emissions). In Puebla, as a result of industrial and commercial electricity use, 15.07 Mmt CO2e were emitted in 2013. These emissions represented approximately 3 % of the total national CO2e emissions caused by Mexico’s industrial and commercial electricity use (508 Mmt CO2e [INECC 2013]) while it represented 63 % of Puebla’s total industrial emissions (24 Mmt CO2e [INECC 2013]).
The highest emitter analyzed through the production-based approach was the food and beverage preparation services sector (F&B), with a total of 7.45 Mmt direct CO2e emissions (49 % of Puebla’s total direct emissions). This sector represented 4 % of Puebla’s total output (US$TO) and 2 % of Puebla’s GDP. The second highest contributor was the business support services (Buss) sector, which emits 3.44 Mmt direct CO2e (23 % of Puebla’s direct emissions). This sector contributed 3 % of Puebla’s total output and 2 % of Puebla’s GDP. The F&B and Buss sectors had high-intensity values: 693 and 252 kgCO2e/$TO, respectively, indicating a potential opportunity for improving their efficiency. For example, we infer that the F&B sector uses refrigerators and other machinery with low efficiency.
Interestingly, sectors with highest contributions to the GDP, such as trade and real estate services, which accounted for 25 % of GDP (see table III), were not the highest CO2e emitters. These two sectors were responsible for less than 0.05 % of the total direct production-based emissions. Figure 2 shows how this trend applies to the five sectors with highest emissions (with the potential exception of the educational services sector [Edu]). Thus, sectors with high contributions to Puebla’s GDP were the lowest emitters, as reflected by their low-intensity factors. This trend seems to indicate that mitigation strategies to reduce CO2e emissions are best targeted to sectors with high-intensity factors (such as F&B and Buss) rather than those with the highest total output (such as trade, real estate services and building).
TABLE III HIGHEST CONTRIBUTORS TO PUEBLA’S GDP.
| Contribution to GDP (%) | Direct emissions in Mmt CO2e (% of total direct emissions) | Intensity value (kg CO2e/$TO) | |
| Trade | 15 | 6.45E-05 (0.0004 %) | 0.0011 |
| Real estate services | 10 | 5.15E-6 (0 %) | 0.0003 |
| Educational services | 5 | 7.78E-01 (5.15 %) | 146 |
| Building | 5 | 3.87E-03 (0.0257 %) | 3.22 |
| Food industry | 4 | 7.93E-06 (0.0001 %) | 0.0009 |
| Total | 38 | 7.82E-01 (5.18 %) | - |
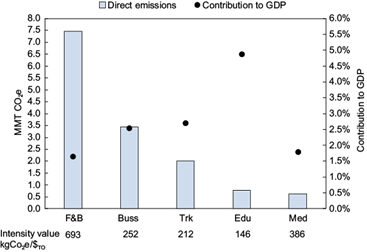
Fig. 2 Highest direct emitters (production approach). Direct emissions (bars) in Mmt CO2e. Dots indicate the contribution of each sector to Puebla’s GDP (in %). Emission intensity values are shown at the bottom of each sector (in kg CO2e/$TO). Sectors: Food and beverage preparation services (F&B), Business support services (Buss), Trucking (Trk), Educational services (Edu), Outpatient medical services and related services (Med).
To better understand the total consumption-based emissions behavior, we calculated the intensity value in terms of final demand (in US dollars) for the five sectors shown in figure 3, obtaining intensities in kgCO2e/$FD. Each intensity value is shown at the bottom of each sector’s bar in figure 3.
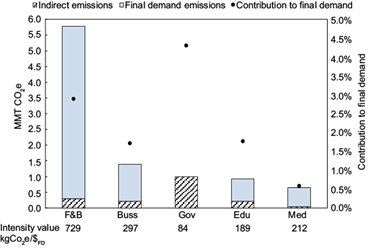
Fig. 3 Highest total emitters (consumption approach). Solid bars: indirect emissions, pattern bars: final demand emissions; both make up total emissions (in Mmt CO2e). Dots indicate each sector’s contribution to Puebla’s final demand (in %). Emission intensity values are shown at the bottom of each sector (in kg CO2e/$FD). Sectors: Food and beverage preparation services (F&B), Business support services (Buss), Government activities (Gov), Educational services (Edu), Outpatient medical services and related services (Med).
Similarly, the F&B and Buss sectors were the highest contributors to Puebla’s total electricity CO2e emissions when analyzed with a consumption-based perspective, as shown in figure 3 (5.78 and 1.39 Mmt CO2e, respectively). To identify whether the consumption-based emissions were caused mainly by final demand (households, government, business, and exports) or by indirect inter-sectoral interactions, we disaggregated into final-demand emissions and indirect emissions (figure 3). Almost all consumption-based emissions of the F&B sector were caused by final demand emissions (95 %); in other words, those emissions were caused by Puebla’s residents consumption of food and beverages. Like the F&B sector, the Buss sector total consumption-based emissions were mainly composed of its final demand emissions (85 %). These two sectors were the highest emitters from both production-based and consumption-based perspectives in absolute and relative terms and presented very similar intensities using both approaches.
Other sectors such as Edu and outpatient medical and related services (Med) presented a similar trend in the composition of their total consumption-based emissions: more than 85 % of their emissions were final-demand emissions. Therefore, it seems that the intensity value plays a more significant role than inter-sectorial interactions, which suggests that mitigation strategies of CO2e emissions would be more efficient if targeted to reducing intensity values rather than to entire supply chains.
However, for the government activities (Gov) sector, which had a higher contribution to indirect emissions, mitigation strategies aimed to decrease the electricity consumption of its suppliers could be more appropriate. The Gov sector was mainly supplied by credit institutions and the financial (C&F) and the trucking (Trk) sectors, according to Puebla’s Leontief matrix. These two sectors had relatively high-intensity values (198 and 212 kg CO2e/$TO, respectively). Furthermore, the Trk sector was a high direct emitter (production-based approach) but not a high total emitter (consumption-based approach). The Trk sector suppliers had very low-intensity values, i.e., the timber industry (3.88E-03 kg CO2e/$TO); this might indicate that mitigation strategies aimed to reduce Gov emissions would be very effective if targeted to reduce the Trk intensity value.
Climate change mitigation strategies targeted at power generation and electricity use often rely on “greening” the electricity mix. However, a closer inspection of the consumption-based and production-based emissions resulting from electricity use shows more potentially effective ways of reducing the CF. Sener (2017) states that by 2024 Mexico will generate 35 % of its electricity by renewable resources. Based on the current renewable rate of 21 % (Sener 2017), this decarbonization of the electricity mix would reduce the emission factor from 0.47 to 0.41 kg CO2e/kWh (see Table S3 in the supplementary materials). Assuming that the rest of the variables remain constant, total industrial and commercial electricity use emissions decreased 13 %, from 15.07 to 13.15 Mmt CO2e.
By contrast, reducing the intensity factor of the F&B sector would result in more significant emission savings. An accurate study of exactly how the intensity factor of 693 kg CO2e/$TO could be diminished by improving the processes with more efficient technologies is out of the scope of this study. Still, an approximation of what is possible can be determined using the Carnegie Mellon EIO-LCA online tool (GDI 2016). We determined an intensity factor of 250 kg CO2e/$TO for F&B in the USA, based on 2007 producer prices. To improve the efficiency of the F&B sector from 693 to 250 kg CO2e/$TO led to a 31 % reduction of Puebla’s total CO2e emissions, from 15.07 to 10.31 Mmt CO2e.
CONCLUSIONS
In this paper, we combine EIO-LCA and LQ to quantify the CF due to the electricity use of a state/regional economy in a relatively simple way. We illustrate this method by performing a CF of the industrial and commercial electricity use in the Mexican state of Puebla. The highest contributors to Puebla’s CO2e emissions due to its electricity use were the F&B and Buss sectors, both from a production-based and consumption-based perspective.
The results show that with a production-based approach, the most influential factor of CO2e emissions is the intensity value, as was illustrated with the F&B, Buss, Trk, and Med sectors. In the case of Puebla, an analysis of consumption-based emissions helped identify that its intensity value primarily influences each sector’s final demand emissions. The most effective reduction measures should be focused on improving technology that consumes electricity. The exception was the Gov sector, which consumption-based emissions were mostly indirect.
The used method was suitable to point out the efficacy of mitigation strategies. Under this context, our results show that decarbonizing the electricity matrix by 35 % (by 2024) will be insufficient to achieve the mitigation goal of a 22 % reduction by 2030 and 50 % by 2050 (Semarnat 2015). Technology improvements related to energy efficiency in sectors with high-intensity factors result in a significant decrease in CF, as shown in the F&B sector.
This article shows that policies focused on mitigating the electrical CF at the national level might not always be the same as those needed to be applied at a sub-national level for each economic sector. It can be said that with the proposed methodology and analysis, it is possible to identify (i) sectors that consume the highest electricity at the regional level, and (ii) each economic sector’s electricity efficiency throughout its production chains. Therefore, the resulting information can provide relevant inputs for climate policy design and aid the design of tailor-made mitigation actions according to each sector’s characteristics and needs.
With the obtained results, we can conclude that Puebla’s CF on account of its electrical usage represented approximately 8 % of Mexico’s CF resulting from its electricity consumption during 2013. In turn, this represented about 43 % of the industry’s emissions derived from Puebla’s energy consumption. It was also possible to identify that the F&B sector had much lower emissions in that state than in the whole of Mexico. This fact could be attributed not only to the difference in geographical scale but mainly to the indirect requirements of this sector, which mostly come from the oil and gas extraction sector at a national level (according to Mexico’s Leontief inverse matrix of 2013). The latter has an intensity factor of 613 kg CO2e /$TO while, at Puebla’s level, the F&B sector inputs come mainly from the Gov sector (according to the 2013 Puebla’s Leontief inverse matrix), which has an intensity value of 84 kg CO2e /$TO. Therefore, it can be said that difference in the classification of the highest emitters between Mexico and Puebla is due to the Leontief’s total requirements matrix or inverse matrix and the final demand of the studied economy.
Likewise, our analysis allows us to identify that the most influential drivers of direct emissions variation in each of Puebla’s 80 economic sectors depend primarily on the intensity value of their electricity consumption within their production chain. Therefore, we can conclude that the most appropriate mitigation measures for Puebla’s economic sector with highest direct emissions according to its electricity consumption should be focused on the efficiency of this usage in its productive chains. On the other hand, the most influential variables of indirect emissions were the inter-industrial interactions and each sector’s final demand, which means that to mitigate indirect emissions, some of the most appropriate mitigation measures should be focused on modifying the economic structure of the region (e.g., migrating from a linear to a circular economic model). An example of mitigation measures could be consumer awareness campaigns involving households, government, and private companies regarding final demand emissions.
Summarizing, with the proposed methodology and analysis, it is possible to identify (i) sectors that consume the highest amount of electricity on a national and regional level, and (ii) the electrical efficiency of each economic sector along with its production chains. In this context, the proposed methodology and our results offer relevant information for decision-makers at a state level to implement mitigation actions focused mainly on the production chains’ energy efficiency according to the particular characteristics of each economic sector. These mitigation actions, complementary to the energy matrix decarbonization, are crucial to aid Mexico in meeting its commitments to the Paris Agreement.
Finally, we would like to point out three significant advantages of the proposed methodology. Firstly, it can be accomplished with few resources, since many IO tables are available at the country level and require standard statistical data at the state level. Secondly, it helps identify which sectors are the highest emitters both directly and indirectly. And thirdly, it helps evaluating the efficiency of decarbonization strategies to better strategize towards mitigation targets.











 nueva página del texto (beta)
nueva página del texto (beta)



