Introducción
El sistema hidrográfico en Valle del Mezquital recibe aproximadamente 56.60 m3 s-1 de agua residual proveniente de la Ciudad de México, 94% de esta agua se utiliza en la irrigación de cultivos en el Valle de Tula, estado de Hidalgo (Comisión Nacional del Agua [Conagua], 2013). El caudal de agua residual generado en la Ciudad de México es desalojado por la red de drenaje: gran canal-interceptor poniente-emisor central, y se conduce hacia el estado de Hidalgo. Durante su recorrido, se vierte en la laguna de Zumpango y en las presas Requena, Endhó, Rojo Gómez & Vicente Aguirre; de estos cuerpos de agua, una parte se deriva hacia canales de riego y se utiliza en la irrigación de cultivos agrícolas. El agua residual finalmente se drena por el río Tula hacia el río Moctezuma, y sigue su curso por el río Pánuco hasta desembocar en el Golfo de México, cerca de Tampico, Tamaulipas (Lesser-Carrillo, Lesser-Illades, Arellano-Islas & González-Posadas, 2011; López-García et al., 2016; Ontiveros-Capurata, Diakite-Diakite, Álvarez-Sánchez & Coras-Merino, 2013; Velázquez-Machuca, Ortega-Escobar, Martínez-Garza, Kohashi-Shibata & García-Calderón, 2002).
Se ha encontrado que el agua residual contiene nutrientes que pueden utilizarse por los cultivos y materia orgánica que puede mejorar algunas propiedades físicas en el suelo (Rascón-Alvarado, Peña-Cervantes, López-Cervantes, Cantú-Sifuentes & Narro-Farías, 2008; Zamora, Rodríguez, Torres & Yendis, 2008). Virto, Bescansa, Imaz & Enrique (2007), al utilizar agua residual proveniente de la industria agroalimentaria, concluyeron que no afectó la calidad de un suelo con elevada concentración de sulfato de calcio CaSO4 ( 2H2O), lo cual indica que el calcio contenido en el suelo o adicionado en el agua de riego disminuye el riesgo de sodificación del suelo (López-García et al., 2016).
El efecto del agua residual aplicada mediante el riego en las propiedades del suelo depende de su concentración y tipo de iones, su conductividad eléctrica (CE), relación de adsorción de sodio (RAS) y el tipo de suelo irrigado. Suelos con alta concentración de calcio disminuyen el efecto dispersante del ión sodio contenido en el agua residual utilizada en la irrigación (Virto et al., 2007).
Otros estudios han demostrado que el agua de origen residual contiene elementos potencialmente tóxicos para los organismos acuáticos (Robledo-Zacarías et al., 2017); por otra parte, los metales pesados, adicionados al suelo mediante el riego, se acumulan en la capa arable de los suelos agrícolas (Siebe, 1994) y pueden ser absorbidos y acumulados en las plantas (Vázquez-Alarcón, Justin-Cajuste, Siebe-Grabach, Alcántar-González & de la Isla de Bauer, 2001). Cifuentes, Blumenthal, Ruiz-Palacios, Bennett & Peasey (1994) y Cifuentes et al. (2000) encontraron que el contacto con el agua de origen residual afectó la salud de la población; en este mismo sentido, Robledo-Zacarías et al. (2017) coincidieron en que el agua residual, vertida en los cuerpos receptores, representa un riesgo alto para la salud humana y para el ambiente, pues se han encontrado farmacéuticos y drogas en el agua residual, lo que ocasiona efectos tóxicos (aún en baja concentración) en los organismos acuáticos y en los microorganismos del suelo.
En México, el porcentaje de agua recolectado en los sistemas de alcantarillado que recibe algún tipo de tratamiento es de 57% (Conagua, 2016), esta agua se utiliza en el riego de cultivos agrícolas en Valle del Mezquital, Hidalgo. En este estado se siembra una superficie aproximada de 456 855.69 ha, de las cuales 80% son de temporal y 20% son de riego. Los cultivos con mayor superficie sembrada son: maíz grano, frijol y avena forrajera (Servicio de Información Agroalimentaria y Pesquera [SIAP], 2017). Cabe mencionar que el agua residual de la Ciudad de México no es la única fuente de agua en esta zona agrícola, pues otras fuentes de agua subterránea y superficial, de calidad variable, se utilizan en la irrigación.
El uso de agua residual en la irrigación puede generar problemas de salinidad, sodicidad y toxicidad en el suelo y en los cultivos. En este sentido, es importante considerar el riesgo de salinidad sódica, debido a que influye de manera negativa disminuyendo la permeabilidad del suelo (Richards et al., 1982) y, como consecuencia, afecta la disponibilidad de agua para el cultivo; además, debido a que se reduce la infiltración del agua en el suelo, este se inunda y disminuye la aireación que provoca diversos problemas en los cultivos. Estos problemas pueden relacionarse con la RAS elevada en el agua de riego (Ayers & Westcot, 1987); sin embargo, el tipo de suelo y el clima también influyen en los problemas relacionados con la salinidad y sodicidad, de manera que el riesgo de salinización y sodificación es mayor en un suelo arcilloso, comparado con un suelo arenoso.
Con respecto del clima, Kovda, Egorov & Hills (1973) indicaron que las regiones con escasa precipitación pluvial (las zonas áridas y semiáridas) estarán mayormente afectadas por la concentración de sales en la superficie del suelo.
La RAS es una variable que indica la proporción de sodio sobre el calcio (
Esta investigación tuvo un enfoque cuantitativo, su alcance fue descriptivo y correlacional. La hipótesis central planteó que los valores conjuntos de CE-RAS mayores de 0.250 dS m-1 y 3 mmol L-1 afectan negativamente la calidad del agua para uso agrícola; los altos valores de RAS en el agua de riego están relacionados con el incremento en el PSI del suelo. El objetivo de esta investigación fue evaluar la calidad agronómica del agua residual a partir de su composición iónica, así como estimar el riesgo de salinización y sodificación del suelo por la aplicación del agua al riego agrícola.
Materiales y Métodos
Para realizar esta investigación se utilizaron los siguientes materiales: Sistema de Posicionamiento Global (GPS Garmin ® Etrex Venture HC); potenciómetro (Hanna instruments® pH 210); puente de conductividad eléctrica (Hanna instruments® HI 255); espectrofotómetro (Jenway® 7305); espectrofotómetro de flama (Instrumentation laboratory ® AutoCal flame photometer 643). El software que se utilizó fue SAS 9.0, sigmaplot 10.0 y Quantum Gis 2.18.
Muestreo
Durante los meses comprendidos entre septiembre del año 2015 y abril del año 2016 se recolectaron y analizaron 188 muestras de agua de origen residual doméstica e industrial, ríos, presas, canales de riego y drenaje agrícola, en 135 estaciones de muestreo distribuidas en la red de drenaje Ciudad de México-Valle del Mezquital (Figura 1). El muestreo se realizó de acuerdo con la NMX-AA-003-SCFI-1980 y considerando la accesibilidad a los sitios (Diario Oficial de la Federación [DOF], 1980). Todas las estaciones de muestreo se registraron con un sistema de posicionamiento global (Tabla 1).
Tabla 1 Estaciones de muestreo en la red de drenaje Ciudad de México-Valle del Mezquital.
| ID | Coordenadas | Altitud | Estación de muestreo | Referencia | Estado | |
|---|---|---|---|---|---|---|
| N | O | m | ||||
| 1 | 19.8313333 | -99.1186944 | 2293 | Canal de riego | Zumpango-Tequisquiac | Estado de México |
| 2 | 19.7851667 | -99.09475 | 2278 | Canal la laminadora | Nextlalpan-Zumpango | Estado de México |
| 3 | 19.6843611 | -99.0446389 | 2246 | Canal Tonanitla I | Sta. María Tonanitla | Estado de México |
| 4 | 19.7343056 | -99.0678611 | 2245 | Canal Nextlalpan | Nextlalpan | Estado de México |
| 5 | 19.7271944 | -99.0835556 | 2244 | Canal Sn. Francisco | Nextlalpan | Estado de México |
| 6 | 19.6715333 | -99.0404833 | 2240 | Canal Tonanitla II | Sta. María Tonanitla | Estado de México |
| 7 | 19.6256167 | -99.04575 | 2239 | Canal puente Pemex | Los Héroes de Tecámac | Estado de México |
| 8 | 19.7855556 | -99.1666389 | 2239 | Gran canal | Zumpango | Estado de México |
| 9 | 19.7855556 | -99.1666389 | 2239 | Canal de riego | Zumpango | Estado de México |
| 10 | 19.8029167 | -99.1136111 | 2238 | Laguna de Zumpango | Zumpango | Estado de México |
| 11 | 19.7009444 | -99.0829167 | 2235 | Túnel emisor oriente lumbrera 11 | Tultepec | Estado de México |
| 12 | 19.808 | -99.1106944 | 2233 | Dren Ávila Camacho | Zumpango | Estado de México |
| 13 | 19.9021111 | -99.1226389 | 2228 | Túnel Tequixquiac | Tequixquiac | Estado de México |
| 14 | 19.4670883 | -99.0100833 | 2225 | Canal Peñón-Texcoco | Texcoco | Estado de México |
| 15 | 19.9135 | -99.1437778 | 2213 | Arrollo Tequixquiac | Tequixquiac | Estado de México |
| 16 | 19.9039722 | -99.1460556 | 2204 | Túnel Tequixquiac | Tequixquiac | Estado de México |
| 17 | 19.9649167 | -99.1756944 | 2180 | Río Tula | Apaxco de Ocampo | Estado de México |
| 18 | 19.9649167 | -99.1756944 | 2180 | Drenaje Apaxco | Apaxco de Ocampo | Estado de México |
| 19 | 20.0285556 | -99.2033056 | 2145 | Canal de riego Texas | Atotonilco de Tula | Estado de Hidalgo |
| 20 | 20.2482222 | -99.4245 | 2118 | Río Chapatongo | José María Pino Suarez | Estado de Hidalgo |
| 21 | 20.1166667 | -99.2042778 | 2111 | Canal de riego Teltipan | Teltipan de Juárez | Estado de Hidalgo |
| 22 | 20.1220833 | -99.2525278 | 2105 | Canal Tlahuelilpan | Tlahuelilpan | Estado de Hidalgo |
| 23 | 20.0582778 | -99.26875 | 2103 | Canal Pemex II | Atitalaquia-Cardonal-Tula | Estado de Hidalgo |
| 24 | 20.0565833 | -99.2196944 | 2098 | Canal de riego Atitalaquia | Atitalaquia | Estado de Hidalgo |
| 25 | 20.0536944 | -99.3130278 | 2094 | Canal Pemex IV | El llano-Tula de Allende | Estado de Hidalgo |
| 26 | 20.02075 | -99.2135556 | 2093 | Río Tula | Atotonilco de Tula | Estado de Hidalgo |
| 27 | 20.2139444 | -99.1340833 | 2091 | Canal de riego Morelos III | Mixquiahuala | Estado de Hidalgo |
| 28 | 20.1449167 | -99.2347222 | 2091 | Canal de riego Tlahuelilpan | Tlahuelilpan | Estado de Hidalgo |
| 29 | 20.0591389 | -99.2270833 | 2089 | Canal de riego la Quina | Atitalaquia | Estado de Hidalgo |
| 30 | 20.0591389 | -99.2270833 | 2089 | Cascada la Quina | Atitalaquia | Estado de Hidalgo |
| 31 | 20.0593889 | -99.2392222 | 2087 | Canal Pemex I | Atitalaquia-Cardonal | Estado de Hidalgo |
| 32 | 20.0742778 | -99.3162778 | 2085 | Canal Endhó | El llano-Tula de Allende | Estado de Hidalgo |
| 33 | 20.2214167 | -99.1373333 | 2079 | Canal de riego Morelos II | Mixquiahuala | Estado de Hidalgo |
| 34 | 20.05525 | -99.3046389 | 2077 | Canal Pemex III | Atitalaquia-El llano | Estado de Hidalgo |
| 35 | 20.0984167 | -99.3417778 | 2076 | Canal Villagrán I | Tula-Sta. Ana Ahuehuepan | Estado de Hidalgo |
| 36 | 20.0745833 | -99.3337222 | 2064 | Canal Canadiense | Tula -Sta. Ana Ahuehuepan | Estado de Hidalgo |
| 37 | 20.1279722 | -99.2423611 | 2050 | Canal Tlahuelilpan | Tlahuelilpan | Estado de Hidalgo |
| 38 | 20.1557222 | -99.2303333 | 2049 | Canal Requena | Tlahuelilpan | Estado de Hidalgo |
| 39 | 20.1588056 | -99.2304444 | 2047 | Canal de riego el Tinaco | Tlahuelilpan | Estado de Hidalgo |
| 40 | 20.1286667 | -99.3500556 | 2047 | Canal Villagrán II | Sta. Ana Ahuehuepan | Estado de Hidalgo |
| 41 | 20.0662222 | -99.3295556 | 2040 | Canal puente verde | Tula de Allende | Estado de Hidalgo |
| 42 | 20.1971389 | -99.2241944 | 2024 | Canal de riego Tezontepec II | Tezontepec-Mixquiahuala | Estado de Hidalgo |
| 43 | 20.1451667 | -99.3579722 | 2022 | Presa Endhó | Endhó | Estado de Hidalgo |
| 44 | 20.1451667 | -99.3579722 | 2022 | Presa Endhó (dren) | Endhó | Estado de Hidalgo |
| 45 | 20.1638611 | -99.3673611 | 2017 | Canal de riego | Endhó | Estado de Hidalgo |
| 46 | 20.2298056 | -99.1363056 | 2016 | Canal de riego Morelos I | Mixquiahuala | Estado de Hidalgo |
| 47 | 20.1971389 | -99.2241944 | 2014 | Canal de riego Tezontepec I | Tezontepec-Mixquiahuala | Estado de Hidalgo |
| 48 | 20.0531111 | -99.3357222 | 2002 | Río Tula | Tula de Allende | Estado de Hidalgo |
| 49 | 20.2453333 | -99.17875 | 2000 | Canal de riego el Progreso | Progreso | Estado de Hidalgo |
| 50 | 20.3163611 | -99.1985278 | 1994 | Canal de riego la Mora | Xochitlán | Estado de Hidalgo |
| 51 | 20.2908333 | -99.1878611 | 1994 | Canal de riego Xoxitlan | Xochitlán | Estado de Hidalgo |
| 52 | 20.3436389 | -99.3477222 | 1989 | Presa Dolores | Cerro Azul-Oxtotipán | Estado de Hidalgo |
| 53 | 20.1908611 | -99.2547778 | 1984 | Canal de riego Tezontepec IV | Tezontepec | Estado de Hidalgo |
| 54 | 20.3606667 | -99.3273056 | 1984 | Canal Rojo Gómez | Cerro Azul-Xamajé | Estado de Hidalgo |
| 55 | 20.4243889 | -99.3511944 | 1978 | Canal de riego Vicente Aguirre | Alfajayucan | Estado de Hidalgo |
| 56 | 20.2664167 | -98.9554444 | 1977 | Canal de agua residual | Actopan | Estado de Hidalgo |
| 57 | 20.2641944 | -98.9601667 | 1975 | Canal de riego Actopan | Actopan | Estado de Hidalgo |
| 58 | 20.2681111 | -99.0028333 | 1973 | Canal de riego Sn. Salvador | Poxindejé | Estado de Hidalgo |
| 59 | 20.1910278 | -99.2791667 | 1973 | Manantial Tezontepec | Tezontepec | Estado de Hidalgo |
| 60 | 20.1881389 | -99.2420278 | 1972 | Canal de riego Tezontepec III | Tezontepec | Estado de Hidalgo |
| 61 | 20.2595 | -98.9707778 | 1970 | Dren Boxtha | Actopan | Estado de Hidalgo |
| 62 | 20.3584722 | -99.3228056 | 1970 | Presa Rojo Gómez | Cerro Azul | Estado de Hidalgo |
| 63 | 20.1943889 | -99.2796111 | 1964 | Río Tula | Tezontepec | Estado de Hidalgo |
| 64 | 20.2808056 | -99.0116111 | 1949 | Pozo Sn. Salvador | Sn. Salvador | Estado de Hidalgo |
| 65 | 20.3753056 | -99.33225 | 1946 | Canal de riego Xamajé | Xamajé | Estado de Hidalgo |
| 66 | 20.3139722 | -99.0073333 | 1936 | Canal de riego caxuxi | Bominthza | Estado de Hidalgo |
| 67 | 20.3431667 | -99.2069167 | 1928 | Canal de riego Tlacotlapilco | Tlacotlapilco | Estado de Hidalgo |
| 68 | 20.3984167 | -99.1915278 | 1927 | Canal de riego Ecoalberto | Tlacotlapilco | Estado de Hidalgo |
| 69 | 20.3448056 | -99.0295833 | 1926 | Canal de riego boxani | Lagunilla | Estado de Hidalgo |
| ID | Coordenadas | Altitud | Estación de muestreo | Referencia | Estado | |
| N | W | m | ||||
| 70 | 20.3526667 | -99.03675 | 1924 | Canal de riego Lagunillas II | Lagunilla | Estado de Hidalgo |
| 71 | 20.2860278 | -99.0091944 | 1921 | Drenaje agrícola | Sn. Salvador-El Bondhó | Estado de Hidalgo |
| 72 | 20.3869167 | -99.0679444 | 1920 | Canal de riego Yolotepec II | Yolotepec | Estado de Hidalgo |
| 73 | 20.36125 | -99.0375 | 1920 | Canal de riego Lagunillas II | Lagunilla-Patria Nueva | Estado de Hidalgo |
| 74 | 20.3921944 | -99.0794167 | 1917 | Canal de riego Yolotepec I | Yolotepec | Estado de Hidalgo |
| 75 | 20.3767778 | -99.0536667 | 1917 | Canal de riego Yolotepec III | Yolotepec-Patria Nueva | Estado de Hidalgo |
| 76 | 20.3928056 | -99.0868333 | 1913 | Canal de riego | Yolotepec-Julián Villagrán | Estado de Hidalgo |
| 77 | 20.4871111 | -99.0813611 | 1887 | Canal de riego debodhé-florida | Pozuelos | Estado de Hidalgo |
| 78 | 20.2513017 | -99.19595 | 1887 | Río Tula | Progreso | Estado de Hidalgo |
| 79 | 20.2513017 | -99.19595 | 1887 | Agua de infiltración | Progreso | Estado de Hidalgo |
| 80 | 20.4347222 | -99.3625556 | 1872 | Presa Vicente Aguirre | Antonio Corrales | Estado de Hidalgo |
| 81 | 20.4838889 | -99.1206389 | 1862 | Presa Debodhé | Debodhé | Estado de Hidalgo |
| 82 | 20.4590556 | -99.3411667 | 1850 | Canal de riego Xigüi | Vía Huichapan-Ixmiquilpan | Estado de Hidalgo |
| 83 | 20.4559167 | -99.3693056 | 1846 | Canal de riego Sn. Francisco | Alfajayucan-Yonthé Grande | Estado de Hidalgo |
| 84 | 20.4142778 | -99.3487778 | 1845 | Río Alfajayucan | Alfajayucan | Estado de Hidalgo |
| 85 | 20.326 | -99.2226389 | 1837 | Río Tula | Chilcuautla | Estado de Hidalgo |
| 86 | 20.326 | -99.2226389 | 1837 | Agua de infiltración para riego de nopal | Chilcuautla | Estado de Hidalgo |
| 87 | 20.326 | -99.2226389 | 1837 | Agua de infiltración para riego de nopal | Chilcuautla | Estado de Hidalgo |
| 88 | 20.4733611 | -99.3290833 | 1837 | Canal de riego el Portezuelo | Portezuelo | Estado de Hidalgo |
| 89 | 20.5050278 | -99.3119167 | 1803 | Canal de riego Portezuelo 2 | Portezuelo | Estado de Hidalgo |
| 90 | 20.4785 | -99.3635278 | 1803 | Canal de riego el Bermejo | Yonthé Grande | Estado de Hidalgo |
| 91 | 20.4092222 | -99.2058333 | 1800 | Canal de riego El Alberto | Tlacotlapilco-Ixmiquilpan | Estado de Hidalgo |
| 92 | 20.43525 | -99.1568333 | 1793 | Canal principal alto Ixmiquilpan | Taxadhó | Estado de Hidalgo |
| 93 | 20.4851667 | -99.3663056 | 1791 | Embalse el Bermejo | Yonthé Grande | Estado de Hidalgo |
| 94 | 20.5001389 | -99.1571389 | 1790 | Canal de riego Arenalito | El Nith-Debodhé | Estado de Hidalgo |
| 95 | 20.4748333 | -99.3655 | 1790 | Canal de riego Yonthé Grande | Yonthé Grande | Estado de Hidalgo |
| 96 | 20.4950278 | -99.1635556 | 1789 | Canal de riego la estación | El Nith-Debodhé | Estado de Hidalgo |
| 97 | 20.4961667 | -99.1568889 | 1789 | Canal de riego el bangandhó | El Nith-Debodhé | Estado de Hidalgo |
| 98 | 20.4234167 | -99.1696389 | 1789 | Canal de riego Maguey Blanco | Parque acuático Maguey Blanco | Estado de Hidalgo |
| 99 | 20.5055556 | -99.1357222 | 1788 | Canal de riego EST-57 | Debodhé | Estado de Hidalgo |
| 100 | 20.4905833 | -99.1123333 | 1787 | Presa Debodhé (dren) | Debodhé | Estado de Hidalgo |
| 101 | 20.4829444 | -99.2718611 | 1784 | Canal de riego dexthó | Ixmiquilpan-Portezuelo | Estado de Hidalgo |
| 102 | 20.3741944 | -99.2236389 | 1784 | Río Tula | Tlacotlapilco | Estado de Hidalgo |
| 103 | 20.4924722 | -99.1148056 | 1775 | Canal de riego Debodhé | Debodhé | Estado de Hidalgo |
| 104 | 20.5072778 | -99.1392222 | 1772 | Canal de riego Capula | Debodhé | Estado de Hidalgo |
| 105 | 20.4268889 | -99.2270556 | 1769 | Río Tula en Ecoalberto | Tlacotlapilco-Ixmiquilpan | Estado de Hidalgo |
| 106 | 20.4268889 | -99.2270556 | 1769 | Canal de riego | Tlacotlapilco-Ixmiquilpan | Estado de Hidalgo |
| 107 | 20.5047222 | -99.1435278 | 1766 | Drenaje agrícola bangandhó | El Nith-Debodhé | Estado de Hidalgo |
| 108 | 20.4902222 | -99.1944167 | 1761 | Canal de riego | El Nith-Debodhé | Estado de Hidalgo |
| 109 | 20.4426389 | -99.1741111 | 1759 | Canal de agua residual | El Tephé | Estado de Hidalgo |
| 110 | 20.4819167 | -99.38775 | 1758 | Agua de infiltración | Sn. Fco. Sacachichilco | Estado de Hidalgo |
| 111 | 20.4756944 | -99.3901389 | 1758 | Río Sn. Francisco | Sn. Fco. Sacachichilco | Estado de Hidalgo |
| 112 | 20.4432222 | -99.1718333 | 1755 | Canal de agua residual el Tephé | El Tephé | Estado de Hidalgo |
| 113 | 20.4933056 | -99.1760833 | 1754 | Drenaje agrícola | El Nith-Debodhé | Estado de Hidalgo |
| 114 | 20.5170278 | -99.15475 | 1752 | Río Chicabasco | Capula-El Rosario | Estado de Hidalgo |
| 115 | 20.5170278 | -99.15475 | 1752 | Canal de riego Chicabasco | Capula-El Rosario | Estado de Hidalgo |
| 116 | 20.48825 | -99.2731667 | 1752 | Drenaje agrícola Dexthó | Ixmiquilpan-Portezuelo | Estado de Hidalgo |
| 117 | 20.4493611 | -99.1791111 | 1750 | Canal de riego Siqueiros | El Tepe | Estado de Hidalgo |
| 118 | 20.4841667 | -99.3843333 | 1747 | Canal Xigatza | Sn. Fco. Sacachichilco | Estado de Hidalgo |
| 119 | 20.4923333 | -99.1822778 | 1746 | Canal de riego La joya | El Nith-Debodhé | Estado de Hidalgo |
| 120 | 20.4969722 | -99.2736667 | 1746 | Canal de riego Dexthó 2 | Ixmiquilpan-Portezuelo | Estado de Hidalgo |
| 121 | 20.5029167 | -99.38725 | 1746 | Presa Madho Corrales | Sn. Fco. Sacachichilco | Estado de Hidalgo |
| 122 | 20.4795278 | -99.2492222 | 1745 | Canal de riego el mexicano | Ixmiquilpan-Portezuelo | Estado de Hidalgo |
| 123 | 20.4810278 | -99.2553333 | 1742 | Canal de riego el mexicano 2 | Ixmiquilpan-Portezuelo | Estado de Hidalgo |
| 124 | 20.5248889 | -99.3238056 | 1720 | Canal de riego Tasquillo | Tasquillo | Estado de Hidalgo |
| 125 | 20.5270833 | -99.321 | 1709 | Canal de riego Tasquillo | Tasquillo | Estado de Hidalgo |
| 126 | 20.4863056 | -99.2108056 | 1706 | Canal de riego | Ixmiquilpan | Estado de Hidalgo |
| 127 | 20.0605 | -99.2221111 | 1694 | Río salado Atitalaquia | Atitalaquia | Estado de Hidalgo |
| 128 | 20.4806667 | -99.2210833 | 1693 | Río Tula | Ixmiquilpan | Estado de Hidalgo |
| 129 | 20.4821389 | -99.2151944 | 1693 | Canal de agua residual | Ixmiquilpan | Estado de Hidalgo |
| 130 | 20.5499722 | -99.2916389 | 1645 | Río Tula | Juchitlán | Estado de Hidalgo |
| 131 | 20.5499722 | -99.2916389 | 1645 | Manantial | Juchitlán | Estado de Hidalgo |
| 132 | 20.5499722 | -99.2916389 | 1645 | Balneario Tzindejéh | Juchitlán | Estado de Hidalgo |
| 133 | 20.66125 | -99.48775 | 1596 | Presa Zimapán | Saucillo | Estado de Hidalgo |
| 134 | 20.576 | -99.3463611 | 1590 | Río Tula | Tasquillo | Estado de Hidalgo |
| 135 | 20.8645 | -99.4455 | 935 | Río Moctezuma | La Mora | Estado de Querétaro |
Fuente: Elaboración propia.
Análisis fisicoquímico del agua
La concentración de Ca2+, Mg2+, CO3 2-, HCO3 - y Cl- se determinó mediante titulación volumétrica (Eaton, Greenberg & Clescerl, 1998). La concentración de Na+ y K+ fue determinada por flamometría y el SO4 2- por espectrofotometría (Richards et al., 1982). La medición del pH se realizó con un potenciómetro (DOF, 2016). La CE, expresada en unidades dS m-1 a 25 °C, se midió con un puente de conductividad eléctrica (Eaton et al., 1998). Estos análisis fisicoquímicos se realizaron en el laboratorio de Ciencias Ambientales, perteneciente al Postgrado de Hidrociencias del Colegio de Postgraduados, México.
Análisis estadístico
Una vez que se obtuvieron todos los resultados del análisis físico-químico del agua, se realizó el análisis estadístico a cada una de las variables, este consistió en determinar: prueba de normalidad con el método de Kolmogorov-Smirnov, asimetría, curtosis, mínimo, máximo, promedio, mediana, desviación estándar, amplitud, coeficiente de variación (CV), cuartiles y valores extremos, así como la relación entre algunas variables mediante el coeficiente de correlación y la regresión lineal simple (Montgomery & Runger, 2015).
Calidad del agua, riesgo de salinización y sodificación del suelo
La calidad del agua para riego agrícola se determinó de acuerdo con los criterios propuestos por Richards et al. (1982) y Ayers & Westcot (1987). El riesgo de sodificación se estimó mediante las ecuaciones 4 y 5 utilizando el enfoque original de Gapón (Richards et al., 1982), y relacionando la CE con la RAS se estimó el riesgo de reducción de la infiltración del agua en el suelo (Ayers & Westcot, 1987).
En el cálculo de la RAS no se consideró el ión Mg2+, debido a que las
propiedades del Ca2+ y Mg2+ son diferentes (Velázquez-Machuca et al., 2002). Con
respecto de su carga, ambos iones son divalentes, pero tienen distinto tamaño;
el radio iónico del Ca2+ es de 0.99 Å y el del Mg2+ es de
0.65 Å, por ello su energía de adsorción es diferente; además, el carbonato de
magnesio es de mayor solubilidad, comparado con el carbonato de calcio, por lo
cual el Mg2+ se mantiene mayor tiempo en solución mientras que el
Ca2+ precipita como carbonato (Kovda et al., 1973). La ecuación de la RAS tiene su fundamento en la
ley de acción de masas, esta ley establece que la magnitud de una reacción
química es proporcional a la concentración molar de las sustancias reaccionantes (
donde XNa+ y X1/2Ca2+ representan la fase adsorbida de sodio y calcio; Na+ y Ca2+ es la concentración de sodio y calcio en la fase soluble. Para suelos salinos, la ecuación de RAS es una estimación indirecta del contenido de Ca2+ y Na+ intercambiable, de manera que K representa la constante de intercambio iónico:
Conociendo el valor de la RAS del agua de riego (RASar), mediante la ecuación 5, se estimó el porciento de sodio intercambiable del suelo (PSI):
donde KG es la constante de intercambio iónico, el valor propuesto por el USDA es de 0.01475 (Richards et al., 1982), pero depende de cada tipo de suelo, así que se consideró: para un suelo arenoso KG1 = 0.007244, para un suelo franco KG2 = 0.0118614 y para un suelo arcilloso KG3 = 0.016899 (Velázquez-Machuca et al., 2002).
Mediante la ecuación propuesta por Bower, Ogata & Tucker (1968) se estimó la RAS en el agua de drenaje (RASaj), esta fórmula considera únicamente la precipitación de Ca2+; es decir, esta ecuación no tiene en cuenta la disolución de cationes de los minerales del suelo:
donde FL es la fracción de lixiviación (FL = 1.0); 8.4 es el pH de un suelo no sódico en equilibrio con la calcita, este pH es el límite a partir del cual el Ca2+ precipita como CaCO3; pHs es el pH del agua en donde el contenido de Ca2+, CO3 2- y HCO3 - están en equilibrio, es decir, no hay saturación o subsaturación de calcita, el pHs se estimó mediante el enfoque conceptual de Langelier (1936):
Donde
Donde I es la fuerza iónica de la solución, C es la concentración de iones expresada en unidades mol L-1; y Z es la valencia de cada ión. La I es una medida del campo eléctrico de una solución y está relacionada con la CE (Solomon, 2001). La estimación de I es necesaria para ajustar el valor de RASaj.
Se utilizó la ecuación de RAS propuesta por Suarez (1981) (RAS°), la cual ajusta la concentración de Ca2+ en el agua al valor de equilibrio esperado después del riego en los primeros milímetros del suelo con una presión parcial de dióxido de carbono de 0.0007 atm:
donde K1 y K2 corresponden a la primera y segunda constante
de disociación del ácido carbónico, Kps es el producto de solubilidad de la
calcita ([K1=6.3429, K2=10.2510 y Kps=8.3187] MacIness & Belcher, 1933);
KCO2 es el producto de solubilidad del dióxido de carbono en agua
([KCO2=6.3514] Harned &
Davis, 1943); ( es el coeficiente de actividad del Ca2+ y
HCO3
- estimado con la ecuación siguiente:
En este estudio se estimó la RAS de la solución del suelo (RASAS) a partir de la composición iónica del agua de riego (RASar), considerando la tendencia hacia la precipitación (ISL+) o disolución (ISL-) de Ca2+ con el enfoque conceptual de Langelier (1936), y sustituyendo el término 8.4-pHs por pH-pHs en la ecuación de Bower; de esta manera, se tuvo en cuenta la posible disolución y precipitación de Ca2+, y se obtuvo la ecuación 11:
donde pH es el pH medido en el agua de riego, y pH-pHs estima el índice de saturación de carbonato de calcio (ISL) (Langelier, 1936).
Resultados y Discusión
Composición iónica y calidad del agua de riego
En este estudio se encontró variación en la CE y STD (CV = 33%), por lo cual se consideró que esta agua residual presentó una concentración muy heterogénea (tabla 2) a lo largo de la red de drenaje Ciudad de México-Valle del Mezquital, pero mantuvo su composición bicarbonatada-sódica. En la siguiente secuencia se ordenaron los iones de mayor a menor concentración: Na+ > Mg2+ > Ca2+ > K+, y HCO3 - > Cl- > SO4 2- > CO3 2-. De acuerdo con Ontiveros-Capurata et al. (2013), esta es una de las características principales que presenta el agua de origen residual.
Tabla 2 Estadísticos descriptivos de la composición iónica del agua en la red de drenaje Ciudad de México-Valle del Mezquital.
| Asimetría | Curtosis | K-S | Min. | Max. | Media | Mediana | Desv. Est. | Amplitud | CV | Q1 | Q3 | 95% | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| pH | 0.98 | 1.26 | 0.01 | 6.95 | 9.86 | 7.75 | 7.60 | 0.46 | 2.91 | 6.02 | 7.40 | 8.11 | 8.54 | |
| CE | dS m-1 | 0.47 | 1.22 | 0.01 | 0.278 | 3.684 | 1.562 | 1.609 | 0.53 | 3.40 | 33.93 | 1.094 | 1.890 | 2.330 |
| Ca2+ | | | 0.07 | 0.13 | 0.15 | 0.48 | 3.80 | 2.11 | 2.14 | 0.63 | 3.32 | 29.90 | 1.74 | 2.50 | 3.20 |
| Mg2+ | | | 0.38 | 0.17 | 0.10 | 0.68 | 7.31 | 3.35 | 3.25 | 1.13 | 6.63 | 33.80 | 2.39 | 4.12 | 5.20 |
| Na+ | | | 1.06 | 3.47 | 0.01 | 1.39 | 27.23 | 9.01 | 9.09 | 3.68 | 25.84 | 40.85 | 5.96 | 11.26 | 14.54 |
| K+ | meq L- | 1.39 | 2.55 | 0.01 | 0.16 | 1.70 | 0.74 | 0.69 | 0.26 | 1.54 | 35.91 | 0.61 | 0.81 | 1.31 |
| CO3 2- | 1 | 4.89 | 23.26 | 0.01 | 0.00 | 1.12 | 0.03 | 0.00 | 0.16 | 1.12 | 485.85 | 0.00 | 0.00 | 0.00 |
| HCO3 - | | | 0.58 | 1.92 | 0.15 | 1.34 | 19.62 | 7.77 | 7.70 | 2.57 | 18.28 | 33.14 | 5.66 | 9.44 | 11.72 |
| Cl- | | | 0.67 | 1.30 | 0.02 | 0.83 | 12.98 | 5.07 | 4.93 | 1.86 | 12.15 | 36.83 | 3.61 | 6.21 | 7.96 |
| SO4 2- | | | 0.24 | 0.57 | 0.12 | 0.41 | 5.28 | 1.91 | 1.98 | 0.81 | 4.87 | 42.43 | 1.33 | 2.52 | 3.02 |
| STD | mg L-1 | 0.48 | 1.35 | 0.05 | 190.72 | 2563.33 | 1066.60 | 1092.28 | 359.34 | 2373 | 33.69 | 774.53 | 1289.73 | 1579.17 |
| I | mol L-1 | 0.29 | 0.64 | 0.01 | 0.0070 | 0.0808 | 0.0374 | 0.0384 | 0.012 | 0.073 | 32.70 | 0.0260 | 0.0455 | 0.0543 |
| K-S: Prueba de normalidad de Kolmogorov-Smirnov (p-Valor), con α=0.05; n=188; CV: coeficiente de variación; Q1: primer cuartil; Q3: tercer cuartil | ||||||||||||||
Fuente: Elaboración propia
Las variables estudiadas, de acuerdo con los valores de asimetría y curtosis, presentaron una distribución asimétrica, lo cual se corroboró con la prueba de Kolmogorov-Smirnov (p-valor < () en la mayoría de las variables. El pH tuvo valores entre 6.95 y 9.86, con un coeficiente de variación (CV) muy bajo (6.02%). El tercer cuartil (Q3 = 8.11) indicó la prevalencia de condiciones ligeramente alcalinas en el agua residual, mismas que pueden atribuirse a la descomposición de materia orgánica contenida en esta agua. Los valores extremos de pH (Figura 2), mayores que el límite superior y que presentaron mayor alcalinidad, se encontraron en el canal Rojo Gómez (pH = 9.86), laguna de Zumpango (pH = 9.20), río Alfajayucan (pH = 8.61), presa Madhó Corrales (pH = 8.60) y canal de riego el mexicano (pH = 8.59). Los valores de pH en el límite inferior con tendencia hacia la neutralidad se encontraron en el canal Pemex por la vía Atitalaquia-Tula (pH = 6.95), río Tula por la vía Actopan-Ixmiquilpan (pH = 6.98), canal de riego en Atitalaquia (pH = 7.02), gran canal en Zumpango (pH = 7.04) y canal de riego en Xamajé (pH = 7.17).

Fuente: Elaboración propia.
Figura 2 Diagramas de la distribución del pH y la CE en la red de drenaje Ciudad de México-Valle del Mezquital.
Con respecto de la CE, esta se encontró entre 0.278 dS m-1 y 3.684 dS m-1, el Q1 = 1.094 dS m-1 y el Q3 = 1.890 dS m-1, los valores extremos en el límite superior corresponden al agua de drenaje agrícola en Nextlalpan (3.684 dS m-1), el Nith-Debodhé (3.398 dS m-1), Bangandhó (3.212 dS m-1), el Tephé (2.469 dS m-1 y el drenaje en la estación mercado-Ixmiquilpan (2.442 dS m-1). Las concentraciones más bajas, en el límite inferior, se encontraron en la presa Dolores (0.278 dS m-1), canal Pemex III en Atitalaquia (0.439 dS m-1), canal Tlahuelilpan (0.454 dS m-1 laguna de Zumpango (0.592 dS m-1) y río Chapatongo (0.618 dS m-1).
Con base en los datos de CE, el agua representa riesgo de salinidad alto (Richards et al., 1982) y uso restringido (Ayers & Westcot, 1987), es recomendable su aplicación en suelos con buen drenaje y cultivos tolerantes a la salinidad. En este sentido, Can-Chulim et al. (2014) y Sánchez-Bernal, Camacho-Escobar, Rodríguez-León & Ortega-Escobar (2013) indicaron que la tolerancia de un determinado cultivo a niveles extremos de salinidad está relacionada con el tipo de cultivo, etapa fenológica y tipo de iones.
En Valle del Mezquital, la mayor superficie sembrada corresponde a los cultivos de maíz grano, frijol y avena forrajera (SIAP, 2017), por lo que se espera que el efecto de la salinidad sea diferente para cada cultivo en relación con la germinación, desarrollo y rendimiento. El maíz y la avena se consideran moderadamente tolerantes; el frijol se considera sensible pero su respuesta a la salinidad es diferente entre las variedades de este cultivo, y se desarrolla de manera distinta en soluciones con diverso tipo de sales. Con el incremento en la concentración iónica disminuye el porcentaje de germinación de variedades de frijol; en relación con este aspecto, Can-Chulim et al. (2017) establecieron la siguiente secuencia de sales que causaron mayor daño en la etapa de germinación y plántula: NaHCO3>NaCl>Na2SO4; asimismo, encontraron que el frijol azufrado fue la variedad más tolerante, el NaHCO3 fue la sal que causó el menor porcentaje de germinación.
Los datos de CE-RAS (Figura 3) indicaron que la clasificación del agua para riego presentó alta variación entre C2, C3 y C4 con respecto del riesgo de salinización y S1, S2, S3 en relación con el riesgo de sodificación, ambos problemas están relacionados con la calidad del agua de riego. Lo anterior se interpretó como la heterogeneidad en la calidad del agua; es decir, el agua residual que se conduce de la Ciudad de México hacia el Valle del Mezquital tuvo variación en su concentración iónica, y por lo tanto su calidad química no es homogénea. La distribución de los datos de CE-RAS indicó que esta agua no es de calidad apropiada para la irrigación de la mayoría de los cultivos.

Fuente: Elaboración propia.
Figura 3 Riesgo de salinidad y sodicidad por los valores de conductividad eléctrica (CE) y relación de adsorción de sodio del agua de riego (RASar) en la red de drenaje Ciudad de México-Valle del Mezquital.
La influencia de cada uno de los iones en la CE, en la concentración de STD y en la I se determinó mediante el análisis de correlación de Spearman (tabla 3), al igual que la relación entre la I, CE y STD. Los iones que influyeron en la CE se establecieron en la siguiente secuencia, ordenados de mayor a menor influencia: cationes: Na+>Mg2+>Ca2+>K+, aniones HCO3 ->Cl->SO4 2-. En este mismo orden se encontró la influencia de los iones en la concentración de STD y en la I.
Tabla 3 Matriz de correlación de Spearman en la red de drenaje Ciudad de México-Valle del Mezquital.
| CE | Ca2+ | Mg2+ | Na+ | K+ | HCO3- | Cl- | SO4 2- | STD | I | |
|---|---|---|---|---|---|---|---|---|---|---|
| dS m-1 | ------------------------------- meq L-1 ------------------------------- | mg L-1 | mol L-1 | |||||||
| CE | 1 | |||||||||
| Ca2+ | 0.679 | 1 | ||||||||
| Mg2+ | 0.874 | 0.624 | 1 | |||||||
| Na+ | 0.975 | 0.603 | 0.795 | 1 | ||||||
| K+ | 0.625 | 0.392 | 0.509 | 0.577 | 1 | |||||
| HCO3- | 0.972 | 0.684 | 0.824 | 0.962 | 0.604 | 1 | ||||
| Cl- | 0.963 | 0.661 | 0.841 | 0.950 | 0.627 | 0.920 | 1 | |||
| SO4 2- | 0.784 | 0.551 | 0.827 | 0.744 | 0.409 | 0.694 | 0.721 | 1 | ||
| STD | 0.998 | 0.675 | 0.861 | 0.980 | 0.628 | 0.979 | 0.960 | 0.773 | 1 | |
| I | 0.993 | 0.697 | 0.907 | 0.956 | 0.608 | 0.958 | 0.953 | 0.819 | 0.889 | 1 |
| P-valor < 0.0001 en todos los casos. α=0.05. | ||||||||||
Fuente: Elaboración propia.
Se encontró la misma secuencia de concentración iónica, de manera que, de acuerdo con la teoría de disociación iónica, la CE, la concentración de STD y la I dependen de la concentración total de iones en solución. Los iones que tuvieron mayor influencia en la CE y en la I fueron Na+, HCO3 -, Cl- y Mg2+; de igual manera, estos iones fueron los de mayor concentración en el agua residual. La relación entre la I, CE y STD fue muy alta (Rho = 0.98), en todos los casos el p-valor fue de 0.0001, y dado que este estadístico de prueba fue menor que el estadístico de comparación (( = 0.05), se aceptó que estas variables están correlacionadas (Ha: rx,y > 0), excepto la variable CO3 2-.
El análisis de varianza de la regresión para estimar la concentración de STD (mg L-1) a partir de la CE (dS m-1) se muestra en la tabla 4. En este caso, el estadístico de prueba fue menor que el estadístico de comparación; por lo tanto, la regresión es significativa para explicar los valores de STD a partir de la CE. La concentración de STD puede estimarse con la siguiente ecuación: STD = (676.8398 × CE) + 9.1959. Richards et al. (1982) recomendaron estimar la concentración de STD utilizando la ecuación: STD = (640 × CE). López-García et al. (2016) encontraron la siguiente ecuación: STD = (698 × CE). Sin embargo, con la finalidad de evaluar la calidad del agua de riego, no es conveniente generalizar estas estimaciones, pues como se observó, cada ecuación de regresión corresponde a un conjunto de datos en particular. La ecuación de regresión encontrada en esta investigación es válida únicamente para la amplitud de datos medidos de CE en este estudio (figura 4); es decir, la CE y la concentración de STD dependen de la concentración total de iones en la solución; por lo tanto, es necesario medir la concentración de cada uno de los iones para conocer el origen de la CE y de la concentración de STD para luego establecer la recta de regresión.
Tabla 4 Análisis de varianza para establecer el nivel de significancia de la regresión STD-CE en la red de drenaje Ciudad de México-Valle del Mezquital.
| Variable dependiente Y (STD, mg L-1) | Variable independiente X (CE, dS m-1) | ||||
|---|---|---|---|---|---|
| Fuente de variación | Grados de libertad | Suma de cuadrados | Cuadrado de la media | F-valor | Pr>F |
| Regresión | 1 | 24076934.75 | 24076934.75 | 64119.4 | <0.0001 |
| Error | 186 | 69843.24 | 375.50 | ||
| Total | 187 | 24146777.99 | |||
| R2=0.9971 | CV=1.8167 | ||||
| Predictor | Coeficiente | Error estándar | t-valor | Pr>t | |
| Constante | β0=9.1959 | 4.4085 | 2.09 | 0.0383 | |
| CE (dS m-1) | β1=676.8398 | 2.6729 | 253.22 | <0.0001 | |
Fuente: Elaboración propia.

Fuente: Elaboración propia.
Figura 4 Regresión lineal simple de las variables CE y STD en la red de drenaje Ciudad de México-Valle del Mezquital.
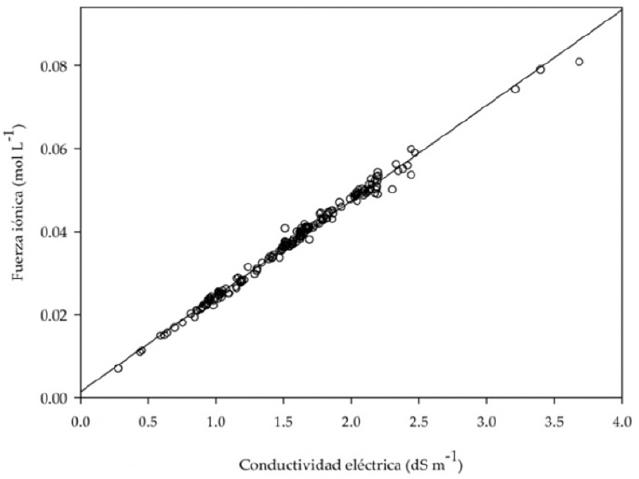
El análisis de varianza de la regresión para estimar la fuerza iónica (mol L-1) a partir de la CE (dS m-1) se muestra en la tabla 5. En este caso, el estadístico de prueba fue menor que el estadístico de comparación; por consiguiente, la regresión es significativa para explicar los valores de I a partir de la CE (Figura 5), mediante la siguiente ecuación: I = (0.02299 × CE) + 0.00150. En su investigación, López-García et al. (2016) encontraron la siguiente ecuación: I = (0.0116 × CE). La diferencia entre estas ecuaciones de regresión se atribuyó a la concentración iónica, pues, aunque ambos estudios coincidieron en la misma zona (Valle del Mezquital), el tamaño de muestra fue diferente, así como el periodo de muestreo. Asimismo, se encontró variabilidad en la concentración iónica, pero con dominancia de sodio y bicarbonato.
Tabla 5 Análisis de varianza para establecer el nivel de significancia de la regresión I-CE en la red de drenaje Ciudad de México-Valle del Mezquital.
| Variable dependiente Y (I, mol L-1) | Variable independiente X (CE, dS m-1) | ||||
|---|---|---|---|---|---|
| Fuente de variación | Grados de libertad | Suma de cuadrados | Cuadrado de la media | F-valor | Pr>F |
| Regresión | 1 | 0.02778912 | 0.02778912 | 21850.6 | <0.0001 |
| Error | 186 | 0.00023655 | 0.00000127 | ||
| Total | 187 | 0.02802567 | |||
| R2=0.9915 | CV=3.013 | ||||
| Predictor | Coeficiente | Error estándar | t-valor | Pr>t | |
| Constante | β0=0.00150 | 0.00025656 | 5.86 | <0.0001 | |
| CE (dS m-1) | β1=0.02299 | 0.00015556 | 147.82 | <0.0001 | |
Fuente: Elaboración propia.
Estimación del riesgo de sodificación del suelo
La estimación de la RAS fue realizada con diferentes ecuaciones (tabla 6). El máximo valor de esta variable, en todos los casos, fue el estimado con la ecuación de RASaj, debido a que únicamente considera la precipitación de Ca2+, lo cual ocasiona el incremento de la relación Na+/ Ca2+, y ello indica valores de RAS altos en la solución del suelo, mismos que pueden atribuirse al proceso de precipitación de Ca2+.
Tabla 6 Estadísticos descriptivos de la relación de adsorción de sodio y del pHs en la red de drenaje Ciudad de México-Valle del Mezquital.
| Mínimo | Máximo | Media | Mediana | Desv. Est. | Amplitud | CV | Q1 | Q3 | 95% | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| pHs | 6.65 | 8.52 | 7.20 | 7.14 | 0.28 | 1.87 | 3.89 | 7.02 | 7.39 | 7.66 | |
| RASar | | | 2.83 | 32.76 | 8.81 | 8.53 | 3.64 | 29.92 | 41.30 | 6.60 | 10.00 | 14.08 |
| RASaj | | | 2.47 | 71.90 | 19.85 | 19.76 | 9.35 | 69.43 | 47.09 | 13.06 | 23.52 | 32.25 |
| RAS° | mmol L-1 | 2.08 | 17.28 | 6.65 | 6.72 | 2.02 | 15.20 | 30.46 | 5.32 | 7.57 | 9.78 |
| RASAS | | | |
0.12 | 77.48 | 14.43 | 13.81 | 9.16 | 77.35 | 63.45 | 7.92 | 19.64 | 24.86 |
| CV: coeficiente de variación; Q1: primer cuartil; Q3: tercer cuartil | |||||||||||
Fuente: Elaboración propia.
Debe considerarse que la disolución de los minerales del suelo, principalmente el Ca2+, disminuye la RAS en la solución del suelo. En este estudio se encontró que el agua residual tiene la capacidad de disolver y precipitar calcio, la precipitación de Ca2+ favorece el efecto coagulante en los coloides del suelo e incrementa la RAS del agua del suelo, de manera que el Na+, si no es lixiviado, puede ser absorbido por las plantas, ocasionando problemas de toxicidad en cultivos sensibles (Ayers & Westcot, 1987).
La RAS corregida (RAS°) (Suarez, 1981) tuvo un promedio de 6.65 mmol L-1; 95% de las muestras de agua tuvieron una RAS° menor de 9.78 mmol L-1. Esta ecuación proporciona una buena estimación de la RAS de la solución del suelo, ya que considera el ajuste de Ca2+ al valor de equilibrio esperado después del riego, y tiene en cuenta que el coeficiente de actividad del Ca2+ y del HCO3 - disminuye con el aumento en la salinidad (I); además, considera el efecto del dióxido de carbono y del bicarbonato sobre el Ca2+ (Can-Chulim, Ramírez-Ayala, Ortega-Escobar, Trejo-López & Cruz-Díaz, 2008).
La RAS del agua de riego (RASar) tuvo un coeficiente de variación de 41.30%, este indica la heterogeneidad de valores que se encontraron entre 2.83 mmol L-1 y 32.76 mmol L-1. El promedio fue 8.81 mmol L-1 y la mediana fue 8.53 mmol L-1, los cuartiles tuvieron los valores siguientes: Q1 = 6.62 mmol L-1, Q3 = 10.01 mmol L-1. En 95% de los casos la RAS fue menor de 14.12 mmol L-1, estos datos indicaron la dominancia de Na+ sobre el Ca2+ en el agua residual; por lo tanto, existe el riesgo de acumulación de sodio en el suelo debido a la aplicación de esta agua en el riego agrícola. En el suelo, el Na+ desplaza al Ca2+, y el Na+ ocupa los sitios de intercambio en la micela coloidal, provocando la sodificación de los suelos (Richards et al., 1982); este proceso de sodificación será más intenso en suelos arcillosos y de menor intensidad en suelos arenosos. En Valle del Mezquital predominan los leptosoles, feozems, vertisoles, litosoles, suelos calcáreos, con diversa textura (francos, arcillosos, arenosos) (Hernández-Silva, Flores-Delgadillo, Maples-Vermeersch, Solorio-Munguía & Alcalá-Martínez, 1994); así que incrementando el contenido de Ca2+, de manera controlada, directamente en el agua residual, podrá disminuir el valor de la RAS y, con ello, el riesgo de sodificación del suelo (López-García et al., 2016); no obstante, se encontró que el agua residual en esta área de estudio tiene la capacidad de precipitar Ca2+; por lo tanto, el riesgo de sodio se encontrará en el agua del suelo ((RASAS) y puede ocasionar problemas de toxicidad por sodio en los cultivos sensibles como el frijol.
Por otra parte, el agua residual con ISL- tiene la capacidad de disolver Ca2+, así que en los suelos que son irrigados con esta agua, se puede disolver el Ca2+ existente, y este puede lixiviarse en el agua de drenaje fuera de la zona de raíz del suelo. En estas condiciones el Na+ puede ocupar los sitios de intercambio en la micela coloidal, manifestándose el proceso de sodificación gradual del suelo, 18% de las muestras de agua mostraron la tendencia hacia la solubilización de Ca2+ con valores negativos en el ISL (tabla 7).
Tabla 7 Distribución de frecuencias del índice de saturación de carbonato de calcio en la red de drenaje Ciudad de México-Valle del Mezquital.
| Índice de saturación | Frecuencia absoluta | Frecuencia relativa | Frecuencia relativa acumulada |
|---|---|---|---|
| ISL (+) tendencia hacia la precipitación de Ca2+ | 154 | 81.91 | 81.91 |
| ISL (-) tendencia hacia la solubilización de Ca2+ | 34 | 18.08 | 100 |
| Total | 188 | 100 |
Fuente: Elaboración propia.
El agua residual saturada (ISL+) tiene la capacidad de precipitar Ca2+, así que en los suelos irrigados con esta agua la precipitación de Ca2+ puede reemplazar al Na+ adsorbido en la micela coloidal; de esta manera, el Na+ pasa a la solución del suelo e incrementará su concentración, el Na+ en solución podrá lixiviarse en el agua de drenaje fuera de la zona de raíz del suelo. La tendencia hacia la precipitación de Ca2+ con valores positivos en el ISL se observó en 82% de las muestras de agua analizadas; por lo cual, su aplicación en la irrigación de cultivos representa riesgo de sodicidad.
La RAS de la solución del suelo (RASAS) fue estimada teniendo en
cuenta los valores del índice de saturación. El 18% de las muestras de agua
tuvieron valores negativos del IS y estos se relacionaron con la disminución de
la RASAS; es decir, la RAS del agua de riego (RASar) fue
1.21 veces mayor que la RAS de la solución del suelo estimada (RASAS)
(mediana de la proporción RASar/RASAS = 1.21), lo cual se
interpretó como indicador de la posible solubilización de Ca2+, y en
estas condiciones se estimó mayor riesgo de sodificación del suelo por la
solubilización y lixiviación de Ca2+. El 82% de las muestras de agua
presentaron tendencia hacia la precipitación de Ca2+ (IS+) y esta se
relacionó con el aumento en la RASAS (Rho = 0.868). La RAS del agua
de riego (RASar = 8.81 mmol L-1) fue 0.60 veces menor que
la RAS de la solución del suelo estimada (RASAS = 14.43 mmol
L-1), la mediana de la proporción
RASar/RASAS fue 0.60, lo que supone un riesgo de
sodificación del suelo menos intenso y lento. Asimismo, este valor estimado de
RASAS (RASAS [
Los valores altos de CE y RAS en el agua de drenaje, mayores que los del agua de riego, son indicadores de la lixiviación de sales sódicas y de las de mayor solubilidad presentes en el suelo, ya que las sales de menor solubilidad (como CaCO3) se precipitan en el suelo, esto incrementa la proporción Na+/Ca2+ en el agua de drenaje y, con ello, aumenta la CE y la RAS en estos efluentes (Sánchez-Bernal, Ortega-Escobar, Sandoval-Orozco, Hernández-Viruel & Estrada-Vázquez, 2012). De esta forma la aplicación excesiva de láminas de agua residual (> 1 m) en la irrigación de cultivos en Valle del Mezquital puede generar una fracción de lixiviación de 0.45, lo cual ayuda a mantener bajos los niveles de salinidad por efecto de lavado del suelo (Hoffman, 1990). Los conceptos aquí expuestos deberán corroborarse experimentalmente en esta zona agrícola.
En este trabajo de investigación se estimó el PSI del suelo (tabla 8) a partir de la RAS del agua de riego (RASar) y tres valores de la constante de intercambio iónico (Velázquez-Machuca et al., 2002). Se observó que el PSI estimado siguió la tendencia hacia la sodicidad. En todos los casos, el PSI estimado para un suelo arenoso fue menor que para un suelo arcilloso, esto indica que los suelos arcillosos tienen mayor riesgo para desarrollar problemas de sodicidad debido a su mayor superficie de intercambio y gran número de cargas negativas expuestas. La superficie de todos los minerales tiene cargas eléctricas, pero las arcillas, como la montmorillonita, tienen la mayor capacidad de intercambio catiónico. Los cationes son adsorbidos con diferente fuerza, los iones con mayor fuerza de adsorción tienen la capacidad de desplazar más fácilmente a los de adsorción débil; este proceso se conoce como intercambio catiónico (Werner, 1996).
Tabla 8 Valores estimados del PSI a partir de la RASar del agua de la red de drenaje Cd. de México-Valle del Mezquital con diferentes valores de K para tres tipos de suelo.
|
|
Mínimo | Máximo | Media | Mediana | Desv. Est. | Amplitud | CV | Q1 | Q3 | 95% |
|---|---|---|---|---|---|---|---|---|---|---|
| PSI-K1 | 2.01 | 19.18 | 5.95 | 5.82 | 2.19 | 17.16 | 36.90 | 4.57 | 6.76 | 9.27 |
| PSI-K2 | 3.25 | 27.98 | 9.34 | 9.19 | 3.24 | 24.73 | 34.74 | 7.28 | 10.62 | 14.34 |
| PSI-K3 | 4.57 | 35.63 | 12.74 | 12.60 | 4.17 | 31.06 | 32.76 | 10.06 | 14.47 | 19.26 |
| CV: coeficiente de variación; Q1: primer cuartil; Q3: tercer cuartil | ||||||||||
Fuente: Elaboración propia.
El cambio en el PSI estimado depende de la RAS y del valor de K, así que para un valor fijo de RAS se tiene diferente PSI; el PSI más bajo se encontró en la línea de puntos inferior y corresponde al valor de K = 0.007244 para un suelo arenoso, el PSI más alto está en la línea de puntos superior y corresponde al valor de K = 0.016899 para un suelo arcilloso (figura 6). El USDA considera que un suelo es sódico cuando su valor de PSI es mayor de 15 y la CE menor de 4 dS m-1, salino-sódico cuando el PSI sea mayor de 15 y la CE mayor de 4 dS m-1, y un suelo salino cuando el PSI sea menor de 15 y la CE mayor de 4 dS m-1 (Richards et al., 1982); no obstante, los problemas relacionados con la salinidad y la sodicidad del suelo y los cultivos pueden encontrarse en diversos valores de PSI y CE del suelo.

Fuente: Elaboración propia.
Figura 6 Porciento de sodio intercambiable (PSI) estimado a partir de la RAS (RASar) del agua de la red de drenaje Ciudad de México-Valle del Mezquital, y diferentes valores de la constante de intercambio iónico (K).
Para evaluar los posibles problemas de infiltración debido a la CE y RAS del agua de riego, se realizó el diagrama de la figura 7. Los valores de CE-RAS que se encuentren a la izquierda de la línea superior dentro del diagrama indican riesgo severo de infiltración debido a la baja concentración y RAS elevada; en este caso, se trata de agua sódica con baja concentración iónica, la cual tiene alta capacidad para disolver los minerales del suelo, incluyendo al calcio. Esto disminuye la estabilidad y degrada la estructura del suelo, las partículas del suelo se dispersan y obstruyen el espacio poroso, disminuyendo la capacidad de infiltración del agua en el suelo. Los valores de CE-RAS que se encuentren a la derecha de la línea inferior dentro del diagrama no representan problemas de infiltración, pues debido a la mayor concentración de sales tienen un efecto coagulante por una mayor cantidad de cationes divalentes (Sánchez-Bernal et al., 2012); sin embargo, el problema de sodicidad puede presentarse en el suelo cuando la proporción de sodio con respecto del calcio sea mayor de 3:1 (Ayers & Westcot, 1987).

Fuente: Elaboración propia.
Figura 7 Reducción relativa de la infiltración provocada por la salinidad y la relación de adsorción de sodio (RASar) del agua de la red de drenaje Ciudad de México-Valle del Mezquital.
Con respecto del riesgo de la disminución de la infiltración del agua en el suelo, se estimó que, del total de muestras de agua, en aproximadamente 75% no se presentaron problemas de infiltración y en el 25% restante el riesgo de reducción de la infiltración del agua en el suelo fue ligero.
A medida que se incrementa la cantidad de agua de riego, se mantiene bajo el nivel de salinidad en la capa arable del suelo (Hoffman, 1990). No obstante, la radiación solar ocasiona la evaporación del agua del suelo, la transpiración del cultivo y el incremento de la temperatura, estos fenómenos causan la precipitación de las sales de menor solubilidad y el ascenso capilar de las sales de mayor solubilidad hacia la superficie del suelo (Kovda et al., 1973). En este sentido, se estimó que los suelos agrícolas en Valle del Mezquital tienen diferente grado de afectación por salinidad y sodicidad debido a la aplicación del agua residual en la irrigación de cultivos.
Cuellar-Carrasco, Ortega-Escobar, Ramírez-Ayala & Sánchez-Bernal (2015) y López-García et al. (2016) encontraron resultados similares a los reportados en este estudio y, al igual que Sánchez-Bernal et al. (2012), estos autores coincidieron en que el uso del agua residual de salinidad sódica ocasiona efectos negativos en el suelo y en los cultivos irrigados con esta agua, y su uso puede incrementar el PSI del suelo debido a una RAS elevada, e incrementar la salinidad de la solución del suelo, lo cual puede afectar el desarrollo normal de los cultivos.
Conclusiones
De acuerdo con los resultados obtenidos bajo las condiciones en que se realizó esta investigación, se concluyó que el agua residual de la red de drenaje Ciudad de México-Valle del Mezquital presentó una alta variación en su concentración iónica, pero prevaleció su composición bicarbonatada-sódica, manifestándose en una amplitud de valores de CE, RAS y PSI.
La RAS es un buen indicador para estimar el riesgo de sodificación del suelo por el uso del agua en el riego agrícola, lo cual depende de la calidad del agua y del tipo de suelo, y es de mayor magnitud para suelos arcillosos que para los arenosos.
Se cumplieron los objetivos y no se rechazó la hipótesis planteada. La amplitud de valores de la RAS se atribuyó a la variabilidad en la relación iónica de sodio con respecto al calcio, y se debe a las diversas descargas y mezcla de agua de origen residual urbano e industrial.
La estimación de la RAS del agua del suelo (RASAS) indicó que la tendencia hacia la precipitación de Ca2+ en el suelo puede mantener bajos los niveles de sodio en el suelo. Esto mismo se estimó con la ecuación de la RAS del suelo propuesta por Suarez (RAS°), así que, incrementando el contenido de Ca2+ de manera controlada directamente en el agua residual, puede disminuir la RAS y consecuentemente el riesgo de sodificación del suelo, expresado como PSI.
Finalmente, no se recomienda el uso de esta agua en la irrigación debido al riesgo de salinización que representa su valor elevado de CE y su dominancia de iones de sodio y bicarbonato que pueden acumularse en la capa arable y dañar la estructura del suelo.











 nueva página del texto (beta)
nueva página del texto (beta)