Introducción
Actualmente se realizan estudios para incrementar la eficiencia de hornos de fundición de escoria de aluminio, lo que permite la disminución en el consumo de energía y de emisiones al medio ambiente. Debido a que el proceso de fundición de escoria es muy complejo, los hornos utilizados requieren de combustibles que generen altas temperaturas. La experimentación en este tipo de equipos industriales es muy complicada dada la alta temperatura a la que se trabaja; por esta razón, se requiere el uso de técnicas numéricas de las cuales se puedan obtener datos confiables para diseñar, mejorar o modificar los hornos existentes (Cadavid, Herrera & Amell, 2010; Nieckele, Naccache & Gomes, 2004). En la Universidad Politécnica de Juventino Rosas (UPJR) se pretende hacer uso de las herramientas de simulación numérica y, con eso, sustituir en gran parte las pruebas experimentales.
Se han reportado muchos estudios que utilizan las técnicas numéricas para analizar el fenómeno de combustión en hornos, además de determinar la influencia de diferentes factores que afectan en la eficiencia del proceso. Zhou, Yang, Reuter & Boin (2006) estudiaron un horno rotatorio para reciclado de chatarra y analizaron mediante la dinámica computacional de fluidos (CFD, por sus siglas en inglés) los fenómenos térmicos, determinando así la influencia del tamaño, la forma y la calidad de la chatarra. Por su parte, Cadavid et al. (2010) estudiaron un horno de crisol auto-regenerativo en tres dimensiones, comparando sus resultados con datos experimentales. Para modelar la turbulencia utilizaron el modelo k-e RNG, el cual acoplaron con la ecuación de radiación y la reacción química generada por la combustión de gas natural, encontrando que la radiación es el principal mecanismo de transferencia de calor hacia el crisol en el seno de la flama.
La combustión es una reacción exotérmica en la cual la energía es liberada cuando la reacción ocurre. Es el fenómeno principal para transferir calor hacia el material a fundir, ya sea de manera directa o indirecta. Lamentablemente, una mala combustión provoca que se generen gases contaminantes no deseados y que las temperaturas en las cámaras de combustión disminuyan. El diseño de un quemador y la determinación de los parámetros que pueden afectar la efectividad de la flama generada por la combustión de gas natural en el horno son estudiados por Tu et al. (2015).
Se han realizado estudios a diferentes tipos de combustibles en hornos rotatorios, variando las corrientes de entrada y enriqueciendo la corriente de aire con oxígeno. Por ejemplo, Shen, Guo, Yu, Austin & Zulli (2011) y Wang et al. (2016) encuentran que el gradiente de temperatura se incrementa con las corrientes enriquecidas, se mejora la eficiencia de la combustión, pero se sacrifica la uniformidad en los campos de temperatura generados.
En el presente trabajo se realizó un análisis del fenómeno de combustión dentro de un horno de crisol para materiales no ferrosos, el cual tiene forma cilíndrica, con el crisol de forma ovalada y trunca en la parte superior. El horno usa gas metano como combustible, de tal forma que se requiere conocer el flujo de alimentación tanto del gas como del aire para alcanzar su temperatura de operación para fundición de escoria de aluminio, la cual es superior a 1200 K. Para ello se realizaron varias simulaciones por CFD, usando el software ANSYS FLUENT V16 En ellas se variaron los flujos de gases, con lo cual se encontró la proporción metano-aire que maximiza la temperatura en el horno, lo cual permite incrementar la eficiencia y, por lo tanto, tener mayores ahorros de costos y facilidad operativa.
Metodología
Los hornos de crisol utilizan combustibles fósiles para realizar la combustión. En la cámara de combustión, el calor es transferido por convección y radiación hacia el crisol y este, a su vez, transfiere el calor por conducción al metal para que alcance la temperatura de fusión. En el estudio realizado en el horno, se usó gas natural como combustible y se consideró que la reacción de combustión se llevó a cabo en oxidación completa, por lo que los productos que se forman son únicamente el dióxido de carbono y el agua. Cabe mencionar que el nitrógeno es un inerte que no reacciona y, por lo tanto, se mantiene invariable en los productos. La reacción química para la combustión del gas natural con aire se presenta en la ecuación 1.
En la Figura 1 se muestra una fotografía del horno y del crisol en los cuales se basa este trabajo para realizar el estudio.
Preparación de la malla
Las dimensiones del horno de crisol se presentan en la Tabla 1. El modelo diseñado por medio de diseño asistido por computadora (CAD, por sus siglas en inglés) se discretizó en el software MESHING; se generó una malla tetraédrica híbrida, obteniendo 95 205 volúmenes de control.
Tabla 1 Dimensiones del modelo de horno de crisol.
| Variable | Medida [m] |
| Diámetro del horno | 0.70 |
| Diámetro superior del crisol | 0.53 |
| Diámetro inferior del crisol | 0.25 |
| Altura del horno | 0.73 |
| Altura del crisol | 0.6 |
| Altura de la base | 0.13 |
| Diámetro de la base | 0.25 |
| Diámetro del quemador | 0.08 |
| Orificios de entrada de gases (15) | 0.004 |
| Orificio central de la entrada de gas | 0.01 |
| Diámetro de entrada de aire | 0.10 |
Fuente: Elaboración propia.
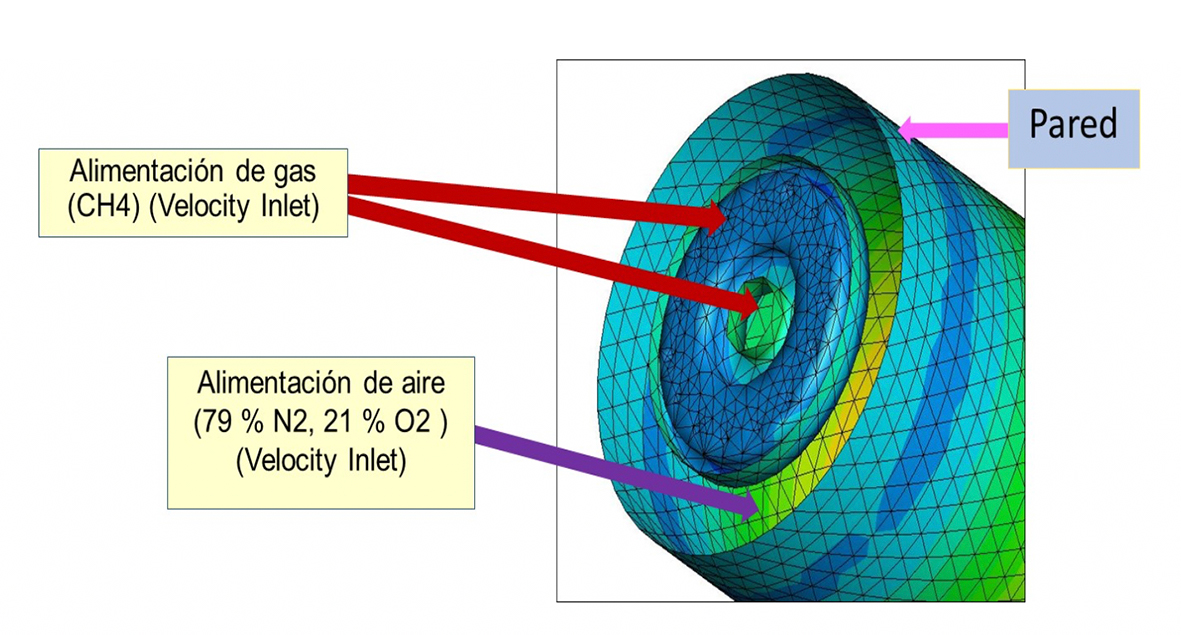
El análisis de sensibilidad de malla fue omitido para este trabajo, debido a que existe evidencia de que resulta impráctico, según varios estudios. Movahedi & Rahimi (2015) encontraron que el uso de un análisis de sensibilidad mejora los resultados, pero incrementa el coste computacional. Yuan & Tao (2007) estudiaron mallas con diferentes tamaños y determinaron que en mallas muy finas se generan inestabilidades de combustión, mientras que Zamora (2015) determina que el uso de mallas finas no garantiza la precisión en los resultados de los análisis frente a una malla gruesa. Por otro lado, al trabajar en una sola fase, se eliminan los errores presentes cuando se calcula la interfase y, más aún, si se trabaja en un estado transitorio. Así, el mallado del horno se realizó de manera que se puedan evitar inestabilidades numéricas y errores de cálculo en las celdas por medio del ajuste de factores como la agudeza y la relación de aspecto de las celdas. La malla representativa para el horno de crisol se puede apreciar en la Figura 2 para diferentes ángulos de vista, así como un acercamiento a la entrada de los gases para su observación a detalle.

Fuente: Elaboración propia.
Figura 2 Malla del dominio de control. a) Vista lateral, b) Alzado y c) Acercamiento a la entrada del quemador.
La solución numérica de las ecuaciones generadas por el modelo fue calculada mediante el uso del software ANSYS FLUENT V16.2 en su versión estudiantil, lo cual limita a un máximo de 100 000 nodos en las mallas generadas en cualquier modelo.
Modelos matemáticos
Dado que las alimentaciones del aire y del combustible al horno se realizan en forma gaseosa, se trabajó la simulación en una sola fase, adecuando las concentraciones de cada uno de los componentes a los sistemas estudiados. Además, debido a que los gases son sometidos a temperaturas muy altas y a presión atmosférica, se considera que se comportan idealmente.
Para un sistema de combustión de gases, el mezclado del combustible con el oxígeno juega un papel muy importante, debido a que la presencia de este en gran cantidad favorece la combustión completa. La flama producida durante la combustión genera una gran cantidad de turbulencia, la cual favorece el mezclado de los gases de combustión con el aire remanente y, consecuentemente, se aumenta la transferencia de calor por convección en el sistema. Para la simulación de estos fenómenos se utilizó el modelo k-épsilon estándar, debido a que cuenta con ecuaciones de cálculo para la disipación de la energía cinética, pero, al ser un modelo de dos ecuaciones, no incrementa en demasía el esfuerzo computacional; además, para una mejor simulación de la transferencia de calor, se utilizó el modelo Finite Rate/Eddy Dissipation para la combustión, el cual contribuye en el cálculo de la disipación de la energía en los pequeños remolinos formados dentro de todo el dominio.
Para el cálculo de la energía desprendida por la reacción se utilizó la ecuación:
donde:
La entalpía sensible h, para gases ideales está dada por:
y el término fuente de energía debido a la reacción puede ser expresado de la siguiente manera:
Todas las ecuaciones de conservación se resolvieron de manera segregada y secuencial en estado cuasiestacionario.
Condiciones de frontera
Para realizar la solución de los modelos matemáticos utilizados, se requiere la especificación de las condiciones de frontera, estas se declaran en cada una de las partes de la geometría que representen, ya sean entradas o salidas de flujo o, bien, paredes. Las condiciones de frontera para las entradas de los gases al horno se muestran en la Figura 3.
Las condiciones para la reacción química fueron idealizadas, ya que, en la realidad, las condiciones ambientales, la calidad de los combustibles y las condiciones de la cámara de combustión crean múltiples variables como la generación de productos secundarios y reacciones competitivas. Los nuevos productos generados provocan interferencias para llevar a cabo el objetivo de este trabajo, que es el cambio de los perfiles de temperatura asociado al cambio en la proporción metano/oxígeno. De esta forma, este trabajo se basó en la combustión del componente principal del gas natural (CH4) y, como oxidante principal, el aire seco, considerando 79% de nitrógeno y 21% de oxígeno en mol. Se desprecian los otros componentes en el aire, como el argón. Se simularon tres casos variando los flujos de entrada del metano/oxígeno, utilizando proporciones molares de 1:5.5, 1:11.08 y 1:36.86, manteniendo el mismo flujo molar total en la entrada de los gases de combustión, como lo sugieren Amelio & Morrone (2007). Las velocidades correspondientes a estos flujos se presentan en la Tabla 2. La temperatura de inyección de los gases fue de 300 K.
Tabla 2 Velocidades de entrada de aire teórico y gas natural.
| Caso | Aire m/s | Gas m/s |
| 1 | 60 | 40 |
| 2 | 30 | 10 |
| 3 | 50 | 5 |
Fuente: Elaboración propia.
Las paredes del horno fueron consideradas como adiabáticas y se consideró únicamente la transferencia de calor asociada a la convección.
Resultados
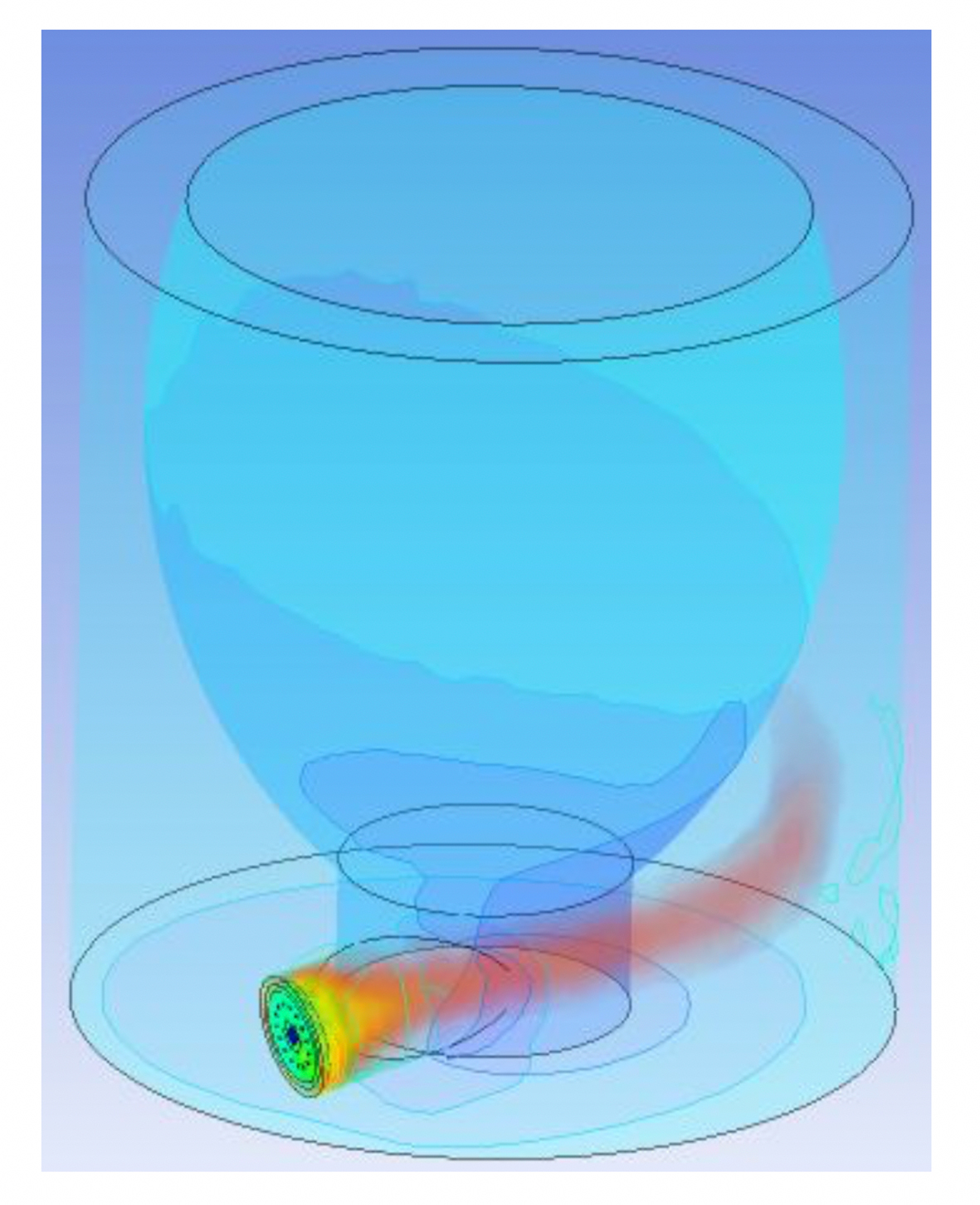
El modelado en 3D de la combustión en un horno de crisol mediante el uso de CFD proporciona información sobre los fenómenos físicos que suceden en la cámara de combustión. Los resultados hidrodinámicos se obtuvieron para la malla generada y se muestran en la Figura 4, en la cual se puede apreciar el movimiento interno de las líneas de corriente. Al salir del quemador, los gases de combustión adquieren una dirección horizontal, pero chocan con la pared del refractario, generando turbulencia en el interior. El movimiento de las partículas de los gases de combustión es en forma de espiral ascendente, el cual tiene la salida en la parte superior del horno. Las velocidades promediadas de los gases son 21.65 m/s, 7.65 m/s y 8.029 m/s, para los Casos 1, 2 y 3, respectivamente.
La Figura 5 presenta el cono formado por la flama, el cual, al chocar con las paredes, adquiere la forma curva, siguiendo la estructura circular de la pared exterior del horno. La longitud de flama alcanzada es de aproximadamente 1 m, calculado por los métodos propuestos por Beerer (2013) y Deng, Wu & Su (2017).
Comportamiento de la temperatura
La máxima temperatura que se puede alcanzar en la combustión del metano con oxígeno es la temperatura adiabática de llama. Se forma el cono de la llama a la salida del quemador, sitio en donde se presentan los mayores registros de temperatura, aproximadamente 2100 K.
La temperatura promediada alcanzada en el Caso 1 es de 1700 K, tal como se aprecia en el código de colores presentado en la Figura 6, por lo que se considera que es adecuada para realizar fundiciones de metales no ferrosos.
Para el Caso 2 (Figura 7a), la temperatura media alcanzada es de los 1240 K, lo que también la hace factible para fundir metales no ferrosos. La Figura 7b muestra los contornos de temperatura del Caso 3, encontrando que se tiene un máximo de 800 K.

Fuente: Elaboración propia.
Figura 7 Contornos de temperatura en la cámara de combustión, a) Caso 2 y b) caso 3.
En los tres casos, el comportamiento de la flama es similar; es decir, se forma el cono de la flama y allí es donde se presentan los mayores registros de temperatura (2210 K). Al ascender en la cámara de combustión, se puede apreciar que la distribución de temperatura se unifica, esto debido a la turbulencia generada, lo que hace que se mezclen todos los gases presentes en la cámara de combustión, los cuales se encuentran a diferentes temperaturas. Es importante señalar que en el Caso 2 se logra alcanzar una temperatura adecuada para la fundición con los flujos más bajos de aire y gas, esto representa un ahorro en combustibles, traduciéndose en ahorro monetario y disminuyendo la emisión de gases que generan contaminación.
En el Caso 1, los gases en la salida tienen una temperatura muy elevada, esto como un indicativo de que no se está extrayendo toda la energía útil a los humos y, por lo tanto, queda un remanente importante y susceptible de aprovechamiento. Si se considera constante el flujo de calor en los humos, se nota la clara influencia negativa de la falta de reactivos (Figura 7b), puesto que el calor disponible disminuye debido a que el aire que adicionalmente ingresa a la combustión consume parte de la energía química transformada.
Comportamiento de la Fracción Másica de los Gases
Las mediciones de CO2 y O2 son sumamente relevantes en los análisis de los productos de combustión, ya que se relacionan directamente con la eficiencia del fenómeno de combustión. En el Caso 1, el oxígeno disminuye en su concentración másica desde 0.23 hasta 0.13, mientras que el CO2 se genera desde cero hasta una concentración másica de 0.064. Estos valores son altos en comparación con los obtenidos por el Caso 2 y 3, los cuales se muestran en la Tabla 3.
Tabla 3 Mediciones de parámetros en la salida del horno.
| Mediciones en la Salida | CASO 1 | CASO2 | CASO 3 |
| Velocidad promedio [m/s] | 21.65 | 7.65 | 8.029 |
| Temperatura promedio [K] | 1716.20 | 1185.31 | 753.04 |
| Fracción Másica CH4 | 7.70e-14 | 3.17e-15 | 1.98e-15 |
| Fracción Másica de O2 | 0.13 | 0.18 | 0.21 |
| Fracción Másica de CO2 | 0.064 | 0.029 | 0.008 |
| Fracción Másica de H2O | 0.052 | 0.024 | 0.007 |
| Transferencia de calor total [W] | 31887.98 | 7952.04 | 4378.89 |
Fuente: Elaboración propia.
La Figura 8a muestra la fracción másica del bióxido de carbono, en ella se aprecia que en el Caso 1 se genera una gran cantidad, esto debido a que no se oxida totalmente el metano, ya que la relación de alimentación es 1:5.5; por esta razón, la concentración de oxígeno disminuye considerablemente en la cámara de combustión (Figura 8b), provocando de forma inmediata una baja eficiencia térmica.
En el Caso 2 se trabaja en una relación 1:11.08, en ella se puede analizar que se tiene una combustión total del metano. Controlando estas velocidades de entrada, se tendría un ahorro económico y energético, y se evitarían al máximo los gases dañinos para el medio ambiente. Aunado a esto se tiene un buen nivel de temperatura, lo cual es suficiente para que se realice de forma correcta la fundición de aluminio.
En el Caso 3 se alimenta un alto exceso de aire, relación 1:36.86 (Figura 8a y 8b), por lo que al analizar la fracción másica del metano se puede apreciar que se quemó totalmente (lo muestra el color azul). El análisis de la fracción másica del aire resalta el exceso con que fue inyectado a la cámara de combustión.
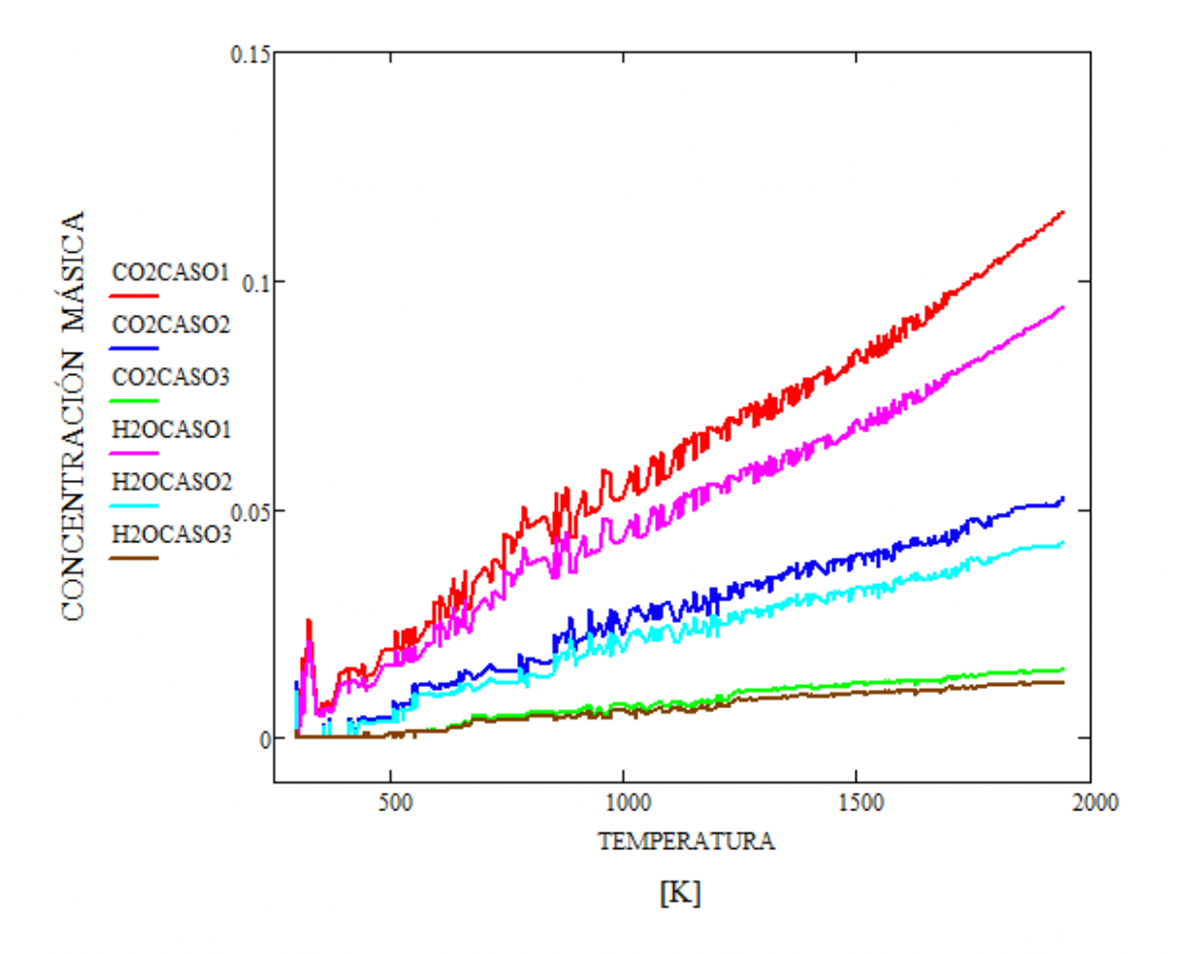
En la Figura 8 se realiza una comparación del consumo de oxígeno y la generación de dióxido de carbono respecto a la temperatura, representándose los tres casos analizados. La línea morada y la línea roja representan datos obtenidos de la simulación del Caso 1, en estas se puede apreciar una alta formación de CO2, esto en comparación con los casos 2 y 3.
La producción de CO2 y H2O están relacionados directamente con la eficacia de la oxidación del metano con oxígeno. Debido a que se alimenta aire seco compuesto únicamente de oxígeno y nitrógeno, la concentración de los productos (agua/dióxido de carbono) inicia de cero (Figura 9). En el Caso 1, donde los flujos son mayores, se obtiene una mayor cantidad de dióxido de carbono y agua, llegando hasta 0.13 y 0.9, respectivamente. Para el Caso 3, donde los flujos son los más bajos, se tiene la producción de dióxido de carbono y agua con los niveles más bajos, aproximadamente 0.01. En el Caso 2, donde la temperatura promediada máxima alcanzada es de 1240 K, las concentraciones máximas de dióxido de carbono y agua son de 0.055 y 0.045, respectivamente, lo que indica que este caso es el adecuado para realizar la fundición de aluminio.
Análisis Térmico
La eficiencia de un quemador está asociada a la energía química que se transforma en calor; es decir, entre más calientes estén los gases de combustión, más eficiente es el quemador. Con esto se tienen menos pérdidas caloríficas debido a la formación de vapor de agua, disociación de especies y pérdidas de calor en la llama radiante.
En el Caso 1 se presenta un exceso según la relación 1:5.5, con lo que se obtiene altas temperaturas, a diferencia de las temperaturas logradas en la relación 1:36.86 del Caso 3. Es decir, utilizar excesos grandes de aire sería desfavorable energéticamente, y emplear excesos muy bajos conllevaría a tener mezclas poco íntimas de aire y combustible con la consecuente emisión de reactivos sin reaccionar y la generación de gases tóxicos que se producen a altas temperaturas.
El calor de combustión es la suma de todos los términos de entalpía, donde se restan los términos de aire y del metano de los términos de los productos de la reacción de oxidación. La gráfica de la Figura 10 muestra el comportamiento del poder calorífico superior e inferior contra el inverso del número de Reynolds del flujo de gas, calculados para los tres casos analizados. Debido a los cambios de presión originados en los remolinos que se forman dentro de la cámara de combustión y a la temperatura de entrada de los reactivos (aire-metano), las moléculas de agua se pueden condensar, desprendiendo calor en este proceso y aportándolo a la cantidad de calor total, de esta manera se obtiene el llamado poder calorífico superior (línea roja, Figura 10). La línea azul de la Figura 10 muestra la gráfica del poder calorífico inferior, en el cual el agua formada en la reacción se considera que se mantiene en estado gaseoso, por lo que se desaprovecha la energía liberada en la condensación. De la gráfica se puede determinar que el poder calorífico total es proporcional al gasto de los gases de los reactivos.
En el Caso 2 se logra alcanzar una temperatura adecuada para la fundición de aluminio, utilizando flujos más bajos de aire y gas que en el Caso 1, lo que se traduce en ahorro de combustibles, por lo tanto, se disminuirán las emisiones de los gases que generan contaminación.
Conclusiones
Las líneas de corriente mostradas en los resultados demuestran que el modelo k-( RNG predice de manera adecuada la hidrodinámica, ya que se observa que los gases ascienden en forma de espiral hasta la salida de la cámara de combustión, con una pequeña retención en la zona de la flama, tal como se esperaría en este tipo de hornos. Se observa también la generación de remolinos a la salida del quemador, provocados por la mezcla de los gases y la reacción de combustión.
Los hornos de crisol para la fundición de metales no ferrosos operan a altas temperaturas (600 °C < T < 1700 °C), y la calidad de la combustión tendrá implicaciones en la calidad del producto, la productividad y la emisión de contaminantes; por esta razón, se analizó el efecto que producen la alimentación de gases a diferentes proporciones molares. En el Caso 1 se inyectaron corrientes muy grandes de los reactivos, por lo que la producción de CO2 y H2O fue muy elevada. Aunque la temperatura alcanzó los 1800 K, la producción de CO2 alcanzó la fracción de 0.13, lo que perjudica la eficiencia de la reacción de combustión. Como la molécula de dióxido de carbono es más pesada que la del oxígeno, tiende a desplazarlo de la zona de entrada de los gases y esto hace que se genere una reacción incompleta, traduciéndose en una disminución en la eficiencia de la reacción.
Aunque se entiende que el exceso de aire en una combustión favorece la oxidación completa del metano hasta CO2, el Caso 3 indica que demasiado aire puede provocar un enfriamiento en la flama, lo cual baja el rendimiento del horno, como en este caso donde no se alcanza la temperatura adecuada. Un punto importante ambiental es que, si la velocidad y la cantidad del aire en comparación con el metano es suficientemente grande, una parte del metano puede ser arrastrada fuera del horno sin haber reaccionado, lo cual, además de presentar un aumento de costo en el proceso, es contaminante y peligroso.
El análisis de los perfiles de velocidad, temperatura, turbulencia y fracción másica permiten una mayor comprensión del efecto de las variables en el fenómeno de combustión. Se pueden variar los flujos y los parámetros geométricos del modelo para obtener datos confiables para diseños futuros. La simulación se realizó suponiendo que el horno de crisol es aislado con un material de propiedades térmicas acordes al proceso y con una geometría tal que minimiza las pérdidas de calor. Por esta razón, la disposición geométrica de la base del crisol está elevada, ya que, de no estarlo, se calentaría la parte superior del crisol, provocando que no exista una óptima convección en el metal fundido. En el caso contrario, si la base es muy alta, provoca que el calor de la flama no llegue al crisol de forma directa, sino que solo se caliente la misma base. Con este diseño se garantizan: óptimas condiciones aerodinámicas en la corriente de gases de combustión, teniendo una combustión estable y un régimen de calentamiento uniforme en las paredes del crisol.











 nueva página del texto (beta)
nueva página del texto (beta)