Introduction

The cochlea is the primary receptor organ for hearing, its principal role is to transform incoming sound pressure into vibrations of the basilar membrane which give rise to electrical signals ¹, it has been an object of research for several decades. The human cochlea has a spiral form with two and a half turns and consists of three fluid filled compartments: scala vestibuli, scala media, and scala tympani from the basal turn to apex (show Figure 1). The scala vestibuli and scala tympani are separated by the cochlear partition which consists of the Basilar Membrane (BM) and the organ of Corti ^2,3.

Figure 1 The structure of the cochlea. 

Mammalian auditory systems have the capability of detecting and analyzing sounds over a wide range of frequency and intensity, for example, humans can hear sounds with frequencies from 20Hz to 20kHz and over an intensity range up to 120 decibels⁴.

Generally, cochlear hearing loss involves damage in the structure inside the cochlea, and can be observed in the response of the BM. Abnormalities in the BM's function can result in many diseases that can be lead to the hearing loss. An example of such a diseases is the Alport Syndrome (AS) ⁵ and Meniere’s disease. As it is already known that the cochlea is inaccessible during life, which means that the pathologic basis of hearing loss can only be obtained by post-mortem studies of the cochlea or by developing credible animal models. Mathematical modeling is therefore, particularly attractive tool in cochlea’s research and its pathology ⁶. The majority of human cochlea modeling focuses on efforts to accurately simulate BM vibratory characteristics ⁷ by using system of forced harmonic oscillators equation that has been previously proposed by Lesser and Berkeley ⁸ and developed by Jimenez-Hernandez ⁹ with the objective to obtain a relation for determining the effect of physical parameters of BM on its maximum amplitude displacement in response to an input stimulus in the auditory system.

To contribute to the knowledge of alterations associated to cochlear disorders in BM, this paper aims to explore and understand the decrease of the maximum amplitude displacement along the BM perturbation by using the computational passive cochlear model ⁹. Based on the Jimenez-Hernandez model, we introduce new physicals parameters that we called ε_s and ε_d as a perturbation of stiffness and damping in the modeling equation of the BM displacement, with the objective to simulate the normal and abnormal function of the BM and predict the effect of increasing of the physicals parameters on the BM motion, so this model can be as an example of the utility of mathematical models to better understand the behavior of the inner ear.

Model of the passive cochlea

In the modeling of the cochlea, there are two types: passive and active models. In passive cochlea, the vibration of oneradial section of the CP is often simplified to BM movement only. However, in active cochlea, the vibrations of the different parts of the CP in relation to each other are modeled, as well as the detailed motions of the cellular structures within the OC, in our work, we used the passsive model.

The cochlea is modeled as having two rectangular compartments filled with fluid and separated by the BM, as adopted from the model of Lesser and Berkley ⁸. The upper compartment corresponds to the scalavestibuli, and the lower compartment to the scala tympani. For simplicity, the scalamedia is omitted from the model ¹⁰ as shown in Figure 2.

Figure 2 Shematic diagram of the cochlea, adapted from the model of Lesser and Berkley (1972) 

The whole BM can be modeled as a harmonic oscillator having varying properties along the membrane such as m(x) mass per unit area, C(x) damping coefficient, and k(x) stiffness per unit area ⁹. The deflection of the membrane is then represented by a one-dimensional wave equation which is the solution to the forced harmonic oscillator equation;

(1)

We consider each section of the Membrane as a forced harmonic oscillator, which is excited by an external force Fejωt     that represents the driving force on each section of the BM. This force is produced by vibration transmitted into the cochlea by the oval window, where F is the magnitude of the driving force and ω is its angular frequency. This implies that the driving force Fejωt     is periodic and complex. Therefore, we can consider that the displacement is also complex, and conclude that the solution of the differential equation is defined by displacement η= A_mejωt    , where A_m is the complex amplitude.

Our goal is toincrease the stiffness k(x) and the damping C(x)in order to show the effect of this perturbation on the amplitude A_m of the displacement𝜂, if we put k(x)←k(x)+ε_s and C(x)←C(x)+ε_d, the differential equation describing the resulting motion of the system is as follows

(2)

(3)

Where

and

The solution of the Equation (3) is defined as follows

where

Using the complex form of η

where

Then η is the solution of the following equation

(4)

Thus,

(5)

(6)

Then the amplitude A_m is defined by,

(7)

Thus,

(8)

Numerical results

Consider that the angular frequency is ω=2πf, the amplitude A_m in Equation (12) can be expressed by,

Now, we can obtain the expression of the amplitude A_m of displacement of the BM to a specific excitation frequency of the system occurs. For the values of m(x), C(x) and k(x), we use the parameters of Neely^{11, 12}.

In this section, we simulate our results to determine the effect of increasing the physical parameters on the amplitude A_m of the displacement of basilar membrane.

Table 1 represents the values of m(x), C(x) and k(x) proposed by Neely ¹¹.

Table 1 Neely parameters of passive cochlea model¹¹  

First, we studied the effect of an increase in the stiffness on amplitude A_m .

In the Figure 3, we show the results obtained by increasing the stiffness of BM. At the position of BM x=1.05560 cm, increasing the stiffness up to 10² normal, we observe that no slightly change in the amplitude of BM, and when we increase the stiffness up to 10⁴ normal caused larger decrease in the amplitude of BM.

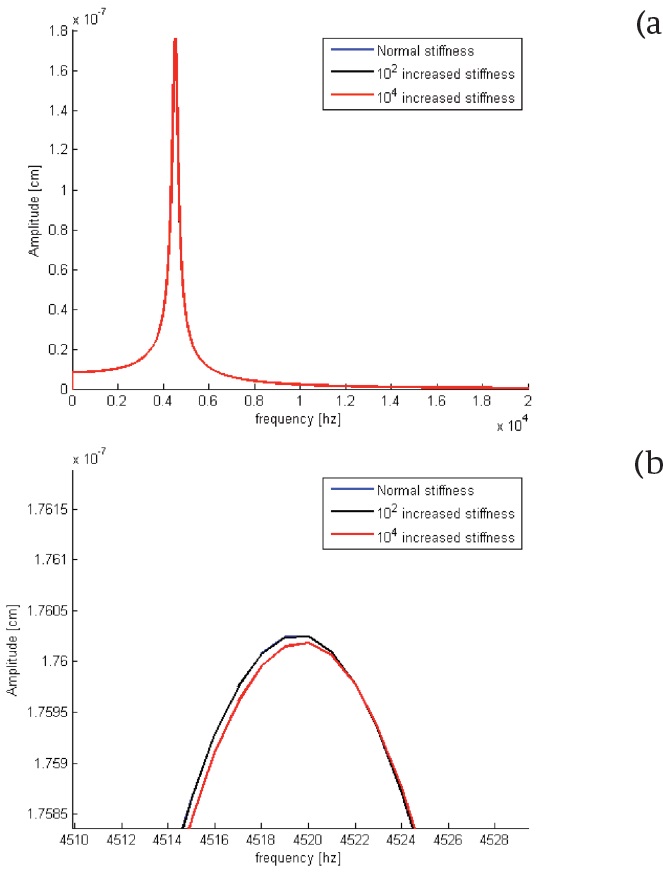
Figure 3. (a) The changes observed in basilar membrane amplitude after an increase in the value of stiffness, (b) Zooming of (a). 

To understand well, we plot the variation of the amplitude in function of the stiffness, this is illustrated in Figure 4.

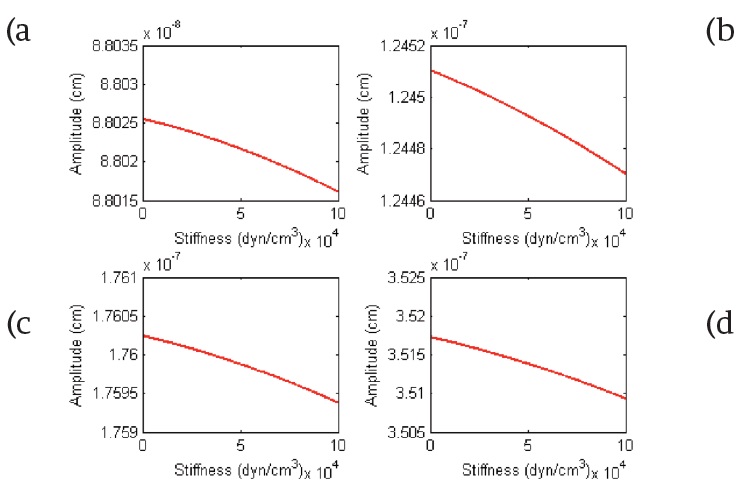
Figure 4 The amplitude of the BM displacement according to the perturbation stiffness. (a) x=0.36281 cm and f= 9 040 Hz , (b) x= 0.7095 cm and f= 6 390 Hz, (c) x= 1.05560 cm and f= 4 520 Hz, (d) x= 1.74700 cm and f= 2 260 Hz. 

In Figure 4, the amplitude decreases when the stiffness ε_s increases, for example we take 0 <  εs≤104. That means the BM becomes stiffer, which implies the hearing loss.

Next, we studied the effect of an increase in the damping of BM on the Amplitude A_m. At the same position of BM x=1.05560, increasing the damping up to 10² normal substantially decreased the amplitude of BM.

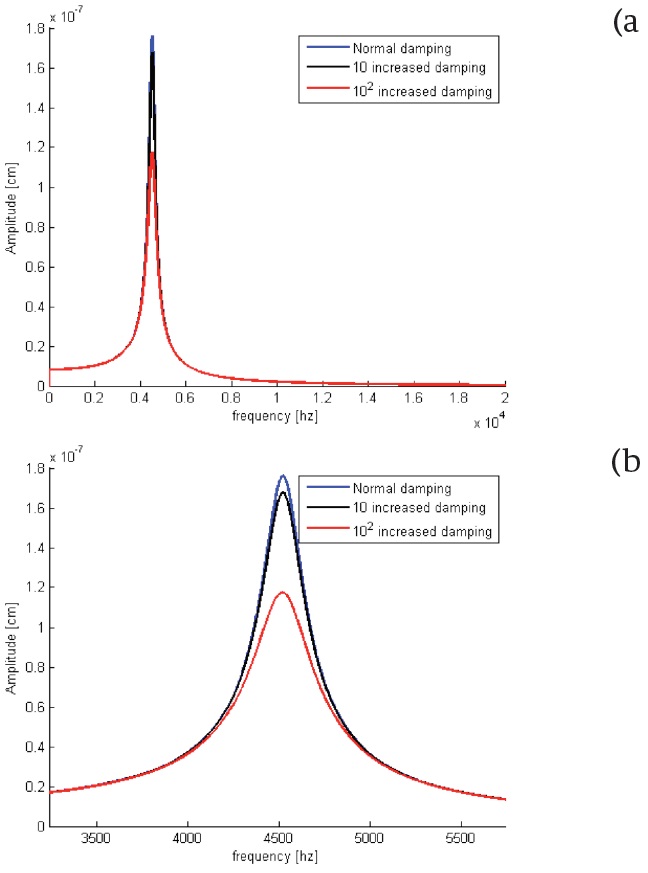
Figure 5 (a) The changes observed in basilar membrane amplitude after an increase in the value of stiffness, (b) Zooming of (a). 

Then, we plot the variation of the amplitude in function of the damping; this is illustrated in Figure 6.

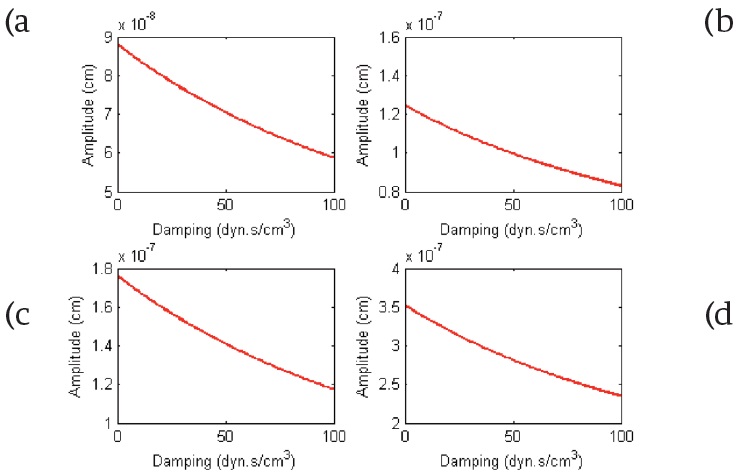
Figure 6 The amplitude of the BM displacement according to the perturbation damping .(a) x=0.36281 cm and f= 9 040 Hz , (b) x= 0.7095 cm and f= 6 390 Hz, (c) x= 1.05560 cm and f= 4 520 Hz, (d) x= 1.74700 cm and f= 2 260 Hz. 

The Figure 6 confirms that the amplitude decreases, when we increase the perturbation damping ε_d along the length of the BM and various excitation frequencies. The maximum displacement of each distance decreases when the perturbation ε_d is above than 0.1 dyn/cm³.

Finally, in the Figure 7 we analyze the case when we increase the both parameters stiffness and damping, we observe that the increasing of stiffness and damping reduced the amplitude of BM, which gives the perturbation of functioning of the cochlea that load to hearing loss.

Figure 7 The changes observed in the basilar membrane amplitude after an increase in the value of stiffness and damping. 

Conclusions

The cochlea is a very small and delicate organ and is very difficult to study experimentally. Many important questions of cochlea mechanics are mathematically solved by using numerical simulations.

The present study investigated the predicting effect of physical parameters on the amplitude of BM. A passive cochlea model was developed using the solution of one dimensional equation.

Typical, an increase in stiffness or in damping system will change the forced response of a vibrating system, which is presented and verified in our studies by increasing the stiffness, damping and both parameters.

By analysis of the model, we have proved that the increasing of stiffness and damping reduced the amplitude of BM, which gives the perturbation of functioning of the cochlea that can load to hearing loss.