INTRODUCCIÓN
La secuenciación de ADN es un proceso que permite obtener el orden de cada uno de los nucleótidos que conforman la molécula de ADN. Tiene una larga lista de aplicaciones y es tecnología clave para la investigación de algunos tipos de cáncer, así como el desarrollo de la medicina genómica, la biología y la agricultura. Las máquinas de secuenciación paralela masiva son tecnologías capaces de secuenciar millones de cadenas de ADN al día [1-3], sin embargo, procesan fragmentos con un número muy pequeño de nucleótidos (entre 35 y 1100), por lo que el resultado de la secuenciación no es un genoma completo, sino pequeñas lecturas cortas que representan fragmentos del mismo. Una manera de reconstruir el genoma a partir de los millones de lecturas cortas es mediante el proceso de alineación [3], el cual consiste en ubicar cada lectura corta tomando como referencia un genoma secuenciado previamente. No obstante, los billones de lecturas cortas, así como la gran longitud del genoma de referencia (3000 millones de nucleótidos para el genoma humano) complican el proceso, además de que deben tomarse en cuenta las diferencias biológicas entre ambas cadenas (inserciones, supresiones o mutaciones de nucleótidos), así como los posibles errores de las máquinas de secuenciación. Para realizar el proceso de alineación se utilizan diferentes algoritmos de elevada complejidad temporal y espacial, algunos basados en programación dinámica [4,5], siendo muy precisos pero requiriendo gran cantidad de recursos computacionales, y otros basados en heurísticas [6,7], los cuales son menos exactos pero más rápidos. Alternativamente los métodos pueden utilizar estimaciones estadísticas [8], basadas principalmente en métodos bayesianos o de máxima verosimilitud o incluso aplicar herramientas de procesamiento digital de señales [9], entre otras técnicas.
La estrategia siembra y extiende
Recientemente se ha optado por combinar las técnicas heurísticas con aquellas basadas en programación dinámica para acelerar la alineación de lecturas, realizando un balance entre velocidad y precisión. La más importante de tales estrategias se denomina siembra y extiende (Figura 1).
Durante la etapa de siembra se intenta encontrar una subcadena de la lectura corta (semilla) que se alinee exactamente en uno o más lugares del genoma de referencia. Esta aproximación se basa en la premisa de que si existe un alto grado de similitud de una subcadena de la lectura en una región de la referencia, entonces es más probable que exista un buen alineamiento de toda la lectura corta en esta zona. Para la etapa de extensión se intenta extender la semilla en ambas direcciones, en esta etapa toda la lectura corta es alineada respecto a la cadena de referencia en las zonas encontradas durante la siembra. La extensión permite determinar de forma precisa la existencia de mutaciones, inserciones o supresiones en la lectura respecto a la referencia. Muchos alineadores modernos implementan la técnica siembra y extiende, tal es el caso de BWA-SW [10], BWA-MEM [11], Bowtie2 [12] y Cushaw2 [13]. Para la etapa de siembra, dichos programas realizan un pre-procesamiento del genoma, obteniendo índices de búsqueda eficientes mediante los algoritmos basados en Tablas Hash [14], o en la Transformada de Burrows-Wheeler [15]. Posteriormente, para la extensión implementan algoritmos basados en programación dinámica, tales como el Smith-Waterman [16], o el Needleman-Wunsch [17].
En este artículo se presenta el desarrollo de ABPSE, un alineador eficiente en tiempo y espacio, que realiza la alineación de lecturas cortas mediante la estrategia siembra y extiende. La siembra utiliza los índices de FM [18] para realizar las búsquedas exactas de semillas, y la extensión el algoritmo de programación dinámica basado en paralelismo a nivel de bit propuesto por Myers [19]. En particular, el algoritmo de Myers está basado en la distancia de Levenshtein para calcular la similitud entre cadenas, tal algoritmo toma las ventajas del paralelismo a nivel de bit del tamaño de palabra del procesador de una computadora, esto es eficiente debido a que los procesadores realizan cálculos con un tamaño entero de palabra en un ciclo de memoria. Básicamente, los cálculos de las puntuaciones y las comparaciones de cadenas son obtenidos simultáneamente mediante una serie de operaciones binarias que comprenden AND, OR, XOR, complementos, desplazamientos y sumas. Después de una profunda revisión de la literatura, se encontró que el algoritmo de Myers no ha sido usado antes en estas aplicaciones.
El resto del artículo se organiza de la siguiente manera, en la siguiente sección se presenta el diseño del software de alineación, iniciando con la descripción del esquema a bloques general propuesto, y culminando con la descripción detallada de los algoritmos y estrategias en cada módulo dentro del mismo. En una sección posterior, se presentan, analizan y comparan los resultados de ejecución obtenidos. Finalmente, se establecen las conclusiones principales.
METODOLOGÍA
El modelo a bloques del programa de alineación desarrollado se muestra en la Figura 2. La implementación del mismo fue realizada utilizando el modelo secuencial de desarrollo de software. Los datos de entrada del alineador son: los archivos con los índices de FM del genoma de referencia, el archivo con las lecturas cortas en formato FASTQ, la cadena de referencia comprimida y un valor de error opcional n proporcionado por el usuario, que limita el número de errores permitidos en la alineación. La salida es un archivo con la posición y la trayectoria de alineación en el formato SAM [20].
El proceso inicia en el módulo de siembra, obteniendo las semillas a partir de la lectura corta. Para determinar las semillas, primero se intenta alinear la lectura entera respecto a la cadena de referencia, mediante el algoritmo de búsqueda hacia atrás de Ferragina y Manzini [18]. Si la lectura se alinea de forma exacta entonces se excluye todo el proceso de extensión y se procede de inmediato a generar los resultados de la alineación en formato SAM. En caso contrario, se obtienen las subcadenas de la lectura que se alineen de manera exacta a la referencia, siendo consideradas semillas si tienen una longitud no menor a cierta longitud mínima precalculada. Una vez obtenida una semilla, el segundo paso es calcular la región real donde ésta se ha alineado en la cadena de referencia. El resultado de este paso es una subcadena de la referencia que será usada como entrada en la fase de extensión.
Una vez finalizada la etapa de siembra se inicia la etapa de extensión, la cual tiene como objetivo alinear de forma inexacta la lectura corta y el segmento de la referencia encontrado en la etapa de siembra. El proceso inicia con el cálculo de la distancia de edición entre ambas cadenas utilizando el algoritmo de Myers [19], obteniendo los vectores de bits que representan la matriz de programación dinámica. Posteriormente, se procede a calcular la ruta de alineación utilizando los vectores de bits en un recorrido de la matriz hacia atrás. Finalmente, a partir de los resultados de la alineación se construye el archivo en formato SAM, que representa la salida del alineador y contiene toda la información de la alineación de la lectura corta.
El módulo de siembra
El módulo de siembra obtiene las semillas a partir de cada lectura corta y posteriormente los segmentos de la referencia en las regiones de siembra donde las semillas se han alineado. ABPSE utiliza semillas con máxima coincidencia exacta (SMEM, del inglés Super Maximal Exact Match), pues proveen mayor exactitud en la alineación y utilizan menos tiempo de cómputo que otras semillas, como las de longitud fija [21]. En particular, la longitud de una semilla SMEM puede ser tan grande como la lectura corta, de tal manera que se puede determinar inmediatamente cuándo una lectura corta se alinea exactamente a la cadena de referencia sin necesidad de realizar la etapa de extensión.
Para asegurar hallar al menos una semilla que se alinee en forma exacta a la cadena de referencia, la lectura, al inicio, se divide en (n+1) regiones de longitud fija como en la Figura 3, basado en el principio del palomar [22]. También se estableció la longitud mínima de la semilla igual al tamaño de estas regiones, como lo indica la Ecuación 1.
La búsqueda de semillas inicia en uno de los extremos de la lectura, intentando encontrar intervalos de alineación exacta mayores a la longitud de semilla mínima. Por ejemplo, si la búsqueda termina dentro de la primera región, la semilla se descarta al no cumplir con el tamaño mínimo (Figura 3a), reanudando una nueva búsqueda en el carácter inmediato a su izquierda. Si la búsqueda, por el contrario, termina en la región dos, se ha encontrado una semilla candidata, y ésta se almacena y se procede a reiniciar una nueva búsqueda a partir del inicio de la región 2 (Figura 3b).
Por otra parte, tomando en cuenta que mientras el valor de n aumenta, el tamaño de la semilla disminuye y en consecuencia se provocan alineaciones falsas en múltiples regiones de la referencia, ABPSE permite valores de n entre 0 y 3, y lecturas cortas con longitud mínima de 60 nucleótidos.
Para implementar la etapa de siembra se utiliza el algoritmo de búsqueda hacia atrás basado en los índices de FM. Estos índices son una estructura de datos conformada por la Transformada de Burrows-Wheeler (TBW) de la cadena de referencia, el Arreglo de Sufijos (AS) que contiene todas las posiciones de inicio de los sufijos en la referencia, una Matriz de Ocurrencias (Occ) de los cuatro caracteres del alfabeto Σ = {A, C, G, T} en la TBW y un vector de frecuencia (C). Dichos índices proporcionan una estructura eficiente en espacio para realizar búsquedas exactas de cadenas.
El Algoritmo 1 adaptada de la referencia [18], realiza la búsqueda exacta de cadenas. Las variables k y l representan el intervalo donde aparece el sufijo buscado, P representa la cadena patrón a buscar, i es un apuntador y σ el carácter del patrón que se está procesando actualmente. Las líneas del 5 al 10 representan el núcleo del proceso de búsqueda, básicamente, el ciclo toma cada carácter del patrón una por una y va encontrando los intervalos donde aparece el sufijo que se va formando. Finalmente, el algoritmo retorna el intervalo [k, l] si k ≤ l o un intervalo vacío en caso contrario (líneas 11 al 15).
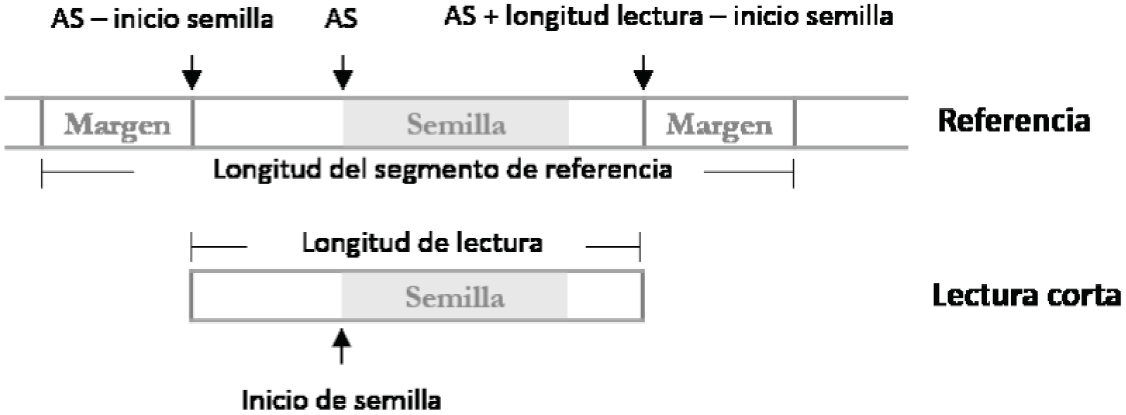
Por cada semilla obtenida mediante el algoritmo 1 se almacenan 3 datos importantes: la posición de inicio de la semilla en la lectura corta, el tamaño de la semilla y los valores del intervalo (k y l). La posición de inicio y el tamaño de la semilla, permiten saber con exactitud a partir de dónde debe extenderse la semilla hacia ambos lados, mientras que el intervalo determina las (l-k+1) regiones donde la semilla se ha alineado, utilizándose como índices del arreglo de sufijos (AS). En específico, el valor del arreglo de sufijos es utilizado para calcular la posición de inicio y fin del segmento de la referencia que será utilizado en la etapa de extensión, tal como se muestra en la Figura 4.
Es posible que durante la alineación se realicen operaciones de eliminación de nucleótidos en la lectura corta, lo cual significa que hay inserciones de caracteres en la cadena de referencia y por consiguiente la región requiere un espacio mayor al tamaño de la lectura corta. Es por esta razón que se agregan márgenes en cada extremo de la región previamente encontrada usando un valor de margen igual al número de errores permitidos para la alineación.
El módulo de extensión
La etapa de extensión se implementa utilizando el algoritmo de Myers, el cual se basa en el cálculo de la distancia de edición de Levenshtein, definida como el número mínimo de operaciones de inserción, eliminación o sustitución, necesarias para transformar una cadena a otra. La manera formal de calcular la distancia de edición de Levenshtein es mediante el algoritmo de Programación Dinámica (PD) que utiliza las fórmulas recursivas de la Ecuación (2).
Donde C[i,j] contiene la mínima distancia de edición entre el segmento del patrón P1,P2…Pi y todos los posibles sufijos del texto T1, T2,…Tj. Por ejemplo, dadas dos cadenas similares T=“ATCATGAA” y P= “TCAGT”, entonces, la matriz de distancia de edición que representa el cálculo de la similitud entre las dos cadenas es la que se muestra en la Figura 5.
En tal caso, examinando la última fila de la matriz puede notarse que las subcadenas de T que terminan en la posiciones 4, 6 y 7 están a solo dos transformaciones del patrón P.
Puede notarse que cada celda de la matriz difiere de las celdas vecinas únicamente por 3 valores (1, 0, -1). Mediante esta observación, Myers recodificó la matriz de PD representando solo las diferencias entre las celdas vecinas en cada fila y columna sucesiva, utilizando las fórmulas en las Ecuaciones (3) y (4). Así se obtienen las matrices de deltas mostradas en la Figura 6.

Figura 6. Representación de la matriz de programación dinámica en deltas. a) Delta vertical ∆v. b) Delta horizontal ∆h.
Posteriormente, cada columna se almacena mediante dos vectores de bits, VP y VN para la matriz de deltas verticales y, HP y HN para la matriz de deltas horizontales como se muestra en la Figura 7. Cada posición de estos vectores almacenan un 1 cuando se cumplen sus igualdades de acuerdo a las Ecuaciones (5), (6), (7), y (8), en caso contrario almacenan un 0, donde la notación Wi,j indica el bit de la i-ésima posición en el entero W de la j-ésima columna. De esta manera, una columna de la matriz original se ha representado en 4 vectores de bits, lo cual reduce el espacio utilizado para calcular la distancia de edición.

Figura 7. Representación en vectores de bits de la matriz de programación dinámica. a) VP, b) VN, c) HP y d) HN.
Myers demostró que estos vectores pueden obtenerse recursivamente mediante las Ecuaciones (9-14), donde Xv y Xh son vectores auxiliares, y Eq es un vector que codifica la igualdad de caracteres. El análisis se basa en que una columna de la matriz de edición solo puede calcularse a partir de los valores de la columna previa.
El Algoritmo 2 representa el algoritmo de Myers al estilo de programación en C adaptado de [19]. Donde la variable score contiene el último valor de cada columna de la matriz de distancia de edición original, calculada a partir del previo valor de score y el vector HP.
Cálculo de la trayectoria de alineación
El algoritmo previo obtiene únicamente la distancia de edición entre las cadenas, sin embargo, en esta aplicación se requiere de la trayectoria de alineación completa, por lo que fueron necesarias algunas modificaciones. En la Figura 8 se muestran todas las rutas posibles de alineación entre las cadenas P y T, donde las flechas de dirección indican la celda de la cual puede preceder la celda C[i,j] durante el cálculo de la matriz.
En el ejemplo, la mejor distancia de edición es 1, entonces, a partir de la casilla con este valor puede recorrerse la matriz hacia atrás y determinar la ruta de alineación; el proceso se realiza de derecha a izquierda y se apoya en flechas verticales, horizontales y diagonales. Finaliza cuando llega a una casilla de la primera fila de la matriz o se hayan recorrido todas las columnas. Una flecha en diagonal significa una coincidencia o sustitución de caracteres entre las dos cadenas; una vertical, una inserción respecto al patrón; y una horizontal la eliminación de un carácter en el patrón.
Como puede verse, las flechas horizontales y verticales coinciden perfectamente con los unos dentro de los vectores HP y VP de la Figura 7, por lo que pueden utilizarse en el recorrido hacia atrás. Sin embargo, no hay información sobre las diagonales, solo la del vector Eq, lo cual no es suficiente si los caracteres comparados no coinciden entre ellos. Para remediarlo, fue extendida la tabla presentada en el artículo original del algoritmo [19] con las posibles combinaciones de entrada, tal como se muestra en la Tabla 1, donde para clarificar el concepto se han incluido a la derecha ejemplos de combinaciones de entrada que justifican los valores de la salida D. A partir de ahí, pueden derivarse de forma inmediata el vector de la Ecuación 15, el cual representa los movimientos diagonales.
Tabla 1. Tabla de verdad para obtener el vector D.
| No. | Δhin | Δvin | D | Δhout | Δvout | Vista de las 4 casillas | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | -1 | -1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 2 | 1 | ||
| 2 | 0 | -1 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | ||
| 3 | 1 | -1 | 1 | 1 | -1 | |||||||||
| 4 | -1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | ||
| 5 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | ||
| 6 | 1 | 0 | 1 | 0 | -1 | |||||||||
| 7 | -1 | 1 | 1 | -1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | ||
| 8 | 0 | 1 | 1 | -1 | 0 | 2 | 1 | 1 | 0 | 1 | 0 | 2 | ||
| 9 | 1 | 1 | 1 | -1 | -1 | |||||||||
| 10 | -1 | -1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 2 | 1 | ||
| 11 | 0 | -1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | ||
| 12 | 1 | -1 | 0 | 1 | -1 | |||||||||
| 13 | -1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | ||
| 14 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | ||
| 15 | 1 | 0 | 1 | 1 | 0 | |||||||||
| 16 | -1 | 1 | 0 | -1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | ||
| 17 | 0 | 1 | 1 | 0 | 1 | 2 | 1 | 1 | 1 | 1 | 1 | 2 | ||
| 18 | 1 | 1 | 1 | 0 | 0 | |||||||||
El vector D, para el caso que se ha tratado como ejemplo en este artículo, se muestra en la Figura 9.
A partir de los vectores VP, HP y D, pueden obtenerse con facilidad todas las rutas de alineación. Por ejemplo, el Algoritmo 3 realiza el recorrido hacia atrás para obtener una posible ruta de alineación. Las entradas del algoritmo son los vectores D y VP que representan las direcciones en diagonal y vertical, m es la longitud de la lectura corta, dmin es la distancia mínima de edición y col la columna donde se encontró dicha distancia. La definición de las variables se realiza en las líneas 2 a 4, donde la variable CIGAR almacena todas las operaciones de la alineación, la variable bit_actual es una máscara auxiliar que permite identificar en que bit se encuentra el recorrido dentro de cada vector de bits e i es un apuntador de índice de la variable CIGAR.
El núcleo del programa se encuentra entre las líneas 5 y 17, donde se realiza el recorrido de la matriz hacia atrás, revisando los vectores D y VP hasta que ya no pueda desplazarse más el bit de la máscara auxiliar o cuando el contador de columna col sea igual a cero. La ruta de alineación o CIGAR, almacena la serie de operaciones que transforman la lectura al texto de referencia, una coincidencia o sustitución de nucleótidos se representa con la letra M, una inserción con la letra I y una eliminación con la letra D. En el proceso, es probable que la lectura corta deba alinearse más a la izquierda del segmento de referencia, lo cual sucede cuando la columna llega a cero antes que la máscara auxiliar, por lo que es necesario agregar operaciones de inserción en el CIGAR, lo anterior se realiza en las líneas 19 a 22. Finalmente, en la línea 24 se invierte la cadena resultante antes de ser retornada por la función. El CIGAR para el ejemplo que se ha tratado en este artículo se muestra en la Figura 10, donde puede verse claramente la alineación y las operaciones realizadas. Luego, el CIGAR se compacta según las especificaciones del formato SAM, obteniendo una versión corta del resultado; en este caso es “3M1I1M”. Evidentemente, ambas operaciones pueden ser realizadas por la misma función, lo cual ocurre en el código real del alineador.
Extendiendo el algoritmo para lecturas con longitud mayor a w
La descripción anterior es válida cuando el tamaño de la lectura m es mayor al tamaño de la palabra w del procesador, la cual está limitada a 64 en los procesadores modernos. Para eliminar dicha limitante fue necesario el procesamiento a bloques como se muestra en la Figura 11.
Por cada vector de bits en el algoritmo original, ahora se requieren b= m/w vectores. El cálculo se realiza columna a columna, comenzando con el vector de bits del primer bloque y continuando en forma descendente, tomando en cuenta que, a diferencia de los vectores de bits en los bloques superiores de la matriz, las cuales contienen valores de 0 en el bit menos significativo, el resto de los bloques pueden contener valores de 0 o 1 debido al desplazamiento de bits de los bloques que los anteceden en la columna. Además, los vectores de bits en los bloques del último nivel pueden extenderse más allá del bit que corresponde a la longitud m de la cadena patrón, es decir bitmax = w - m (mod w). Por lo que para calcular el valor de la distancia de edición es necesario un seguimiento preciso de dicho bit, lo cual se realiza mediante una máscara binaria apropiada.
RESULTADOS Y DISCUSIÓN
Para probar la funcionalidad y eficiencia del programa desarrollado se alinearon varios conjuntos de prueba, con un millón de lecturas cortas cada uno, y longitudes de 64, 100 y 128 nucleótidos, a los cromosomas 19, 20, 21 y 22 del genoma humano. Las lecturas cortas fueron generadas de forma artificial utilizando el programa wgsim con una razón de mutaciones de 0.4%, la cual representa el límite de variaciones en el caso del genoma humano [23], donde el 25% de esas mutaciones son indels (inserciones y eliminaciones) y el 70% de los indels son extendidos. El error de secuenciación fue configurado a 0.1%, valor típico en las máquinas de secuenciación actuales [1]. Todas las pruebas fueron realizadas en una computadora con procesador Intel Core i7 de Sexta generación, 16 GB en RAM y 1 TB en disco duro, con sistema operativo Ubuntu 14.04.
En la Tabla 2 se muestran los tiempos de alineación obtenidos, donde puede observarse que incluso los conjuntos de lecturas cortas de 128 nucleótidos, requieren menos de 150 segundos de procesamiento. Lo cual se debe principalmente al paralelismo a nivel de bit del algoritmo utilizado en la etapa de extensión. También puede observarse una dependencia directa del tiempo de alineación con respecto a la longitud de la lectura, y que los tiempos de alineación permanecen prácticamente constantes aun cuando se incrementa la longitud de las cadenas de referencia.
Tabla 2. Tiempos de ejecución de ABPSE.
| Referencia | Longitud de lectura (nts) | ||
|---|---|---|---|
| 64 | 100 | 128 | |
| Chr21 | 97,61 s. | 111,16 s. | 140,35 s. |
| Chr22 | 106,11 s. | 113,87 s. | 137,21 s. |
| Chr19 | 101,20 s. | 131,41 s. | 145,19 s. |
| Chr20 | 107,33 s. | 120,88 s. | 143,42 s. |
Esto último es muy apropiado, ya que permite la alineación de lecturas a cadenas de referencia muy grandes sin tiempos extras de cómputo, y se debe a la complejidad temporal del algoritmo usado en la etapa de siembra (búsqueda basada en índices de FM), la cual es una función de la longitud de las lecturas cortas y no de la longitud de la cadena de referencia.
Adicionalmente, se determinó la cantidad de lecturas que se alinearon correcta e incorrectamente a su origen. Esto fue posible debido a que el generador de lecturas artificiales, wgsim, proporciona la ubicación exacta de donde es extraída cada una de sus lecturas. De esta manera, mediante una función de comparación se validan los resultados de ABPSE. En esta prueba, se consideran correctas aquellas alineaciones en un intervalo de ±3 nucleótidos de su posición original, considerando la posibilidad de inserciones o eliminaciones en relación al genoma de referencia. Los resultados se muestran en la Tabla 3, donde puede notarse un porcentaje promedio de 96.2% de alineaciones correctas, 1.39% de alineaciones incorrectas y 2.41% de lecturas no alineadas. Las alineaciones incorrectas son provocadas principalmente por regiones repetidas, lo cual puede mejorarse posteriormente al utilizar lecturas apareadas.
Tabla 3. Exactitud de alineación con ABPSE.
| Referencia | Tipo de resultado | Longitud de lectura (nts) | ||
|---|---|---|---|---|
| 64 | 100 | 128 | ||
| Chr21 | Alineadas | 986558 | 976349 | 967040 |
| No alineadas | 13442 | 23651 | 32960 | |
| Correctas | 976101 | 970002 | 961044 | |
| Incorrectas | 10457 | 6347 | 5996 | |
| Chr22 | Alineadas | 985954 | 976409 | 967229 |
| No alineadas | 14046 | 23591 | 32771 | |
| Correctas | 956513 | 955025 | 947981 | |
| Incorrectas | 29441 | 21384 | 19248 | |
| Chr19 | Alineadas | 985117 | 975625 | 967397 |
| No alineadas | 14883 | 24375 | 32603 | |
| Correctas | 962164 | 963039 | 956562 | |
| Incorrectas | 22953 | 12586 | 10835 | |
| Chr20 | Alineadas | 986079 | 976309 | 967061 |
| No alineadas | 13921 | 23691 | 32939 | |
| Correctas | 972866 | 968010 | 959421 | |
| Incorrectas | 13213 | 8299 | 7640 | |
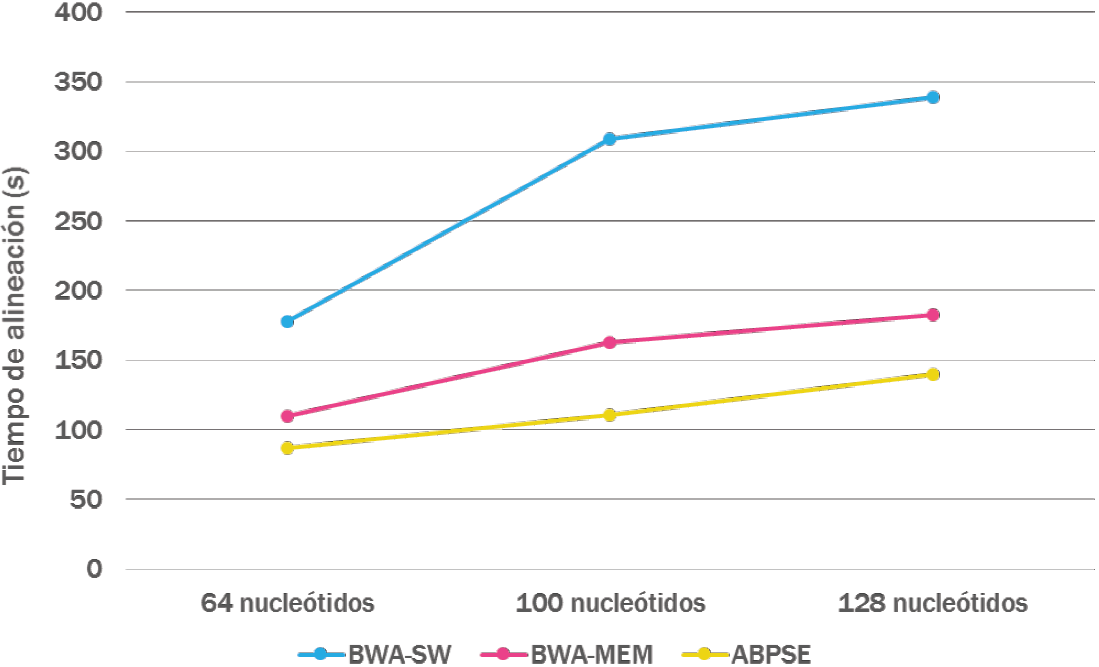
Finalmente, se compararon los tiempos de ejecución del alineador propuesto y el de los populares programas de alineación BWA-SW y BWA-MEM. Ambos programas utilizan la estrategia siembra y extiende, y los índices de FM para la etapa de siembra. En la extensión BWA-SW utiliza el algoritmo de Smith-Waterman mientras que BWA-MEM utiliza una combinación de alineación local y global. La comparación fue realizada utilizando un solo núcleo del procesador en cada uno de los programas. La Figura 12 muestra los resultados al alinear conjuntos de 1 millón de lecturas al genoma humano completo.
Puede observarse como el alineador propuesto proporciona un factor de aceleración superior a 2.45x respecto al programa BWA-SW y 1.36x respecto al alineador BWA-MEM, ambos programas han sido catalogados entre los más rápidos y exactos alineadores de ADN en la actualidad [24,25]. Estas mejoras en la velocidad son muy significantes, puesto que en un proceso normal de alineación, los billones de lecturas que deben alinearse implican días completos de procesamiento, lo cual con ABPSE podría realizarse en solo unas horas. Factores de alineación superiores solo se han reportado mediante aceleradores Hardware basados en unidades de procesamiento gráfico GPUs [26], o en FPGAs [27], aunque estas son excelentes opciones, su elevado costo suele ser una limitante. En esta prueba ABPSE utilizó en promedio solo 7.6 GB de memoria RAM, lo cual permite su ejecución en cualquier computadora convencional.
El número promedio de lecturas mapeadas correcta e incorrectamente, también fue contrastado en esta prueba, obteniendo los resultados de la Figura 13.
Puede observarse una eficiencia comparable entre los tres programas. En particular, al calcular el error de alineación definida mediante la Ecuación 16, se obtienen valores de 0.0401, 0.0181 y 0.0178 para BWA-SW, ABPSE Y BWA-MEN respectivamente.
Lo anterior refleja una eficiencia muy cercana entre BWA-MEM y ABPSE, siendo mayor a la de BWA-SW. La ligera desventaja en relación a BWA-MEN puede superarse en versiones posteriores al refinar la técnica de sembrado.
CONCLUSIONES
En este artículo se presentó el desarrollo de un programa de alineación de lecturas cortas de ADN que implementa la estrategia siembra y extiende, utilizando la combinación de dos algoritmos muy eficientes. En la etapa de siembra se utilizó el algoritmo de búsqueda hacia atrás basado en los índices de FM que permite realizar búsquedas exactas de cadenas de forma muy rápida independientemente de la longitud de la cadena de referencia. Para la etapa de extensión se implementó el algoritmo de programación dinámica de Myers que calcula la distancia de edición entre dos cadenas. Este último algoritmo fue extendido para obtener la trayectoria de alineación de las cadenas utilizando vectores de bits. Mediante las pruebas realizadas se demuestra que la combinación de dichos algoritmos permite el desarrollo de alineadores de alta velocidad, gracias al paralelismo a nivel de bit en la etapa de extensión. A pesar de que la exactitud del alineador es muy bueno, ésta podría mejorarse si se exploran otros tipos de semillas en la etapa de siembra. Por otra parte, la etapa de extensión podría ser implementada directamente en hardware, donde el tamaño del entero no es un factor limitante, evitando de esta manera la programación a bloques y en consecuencia permitiendo la aceleración al máximo del programa, así como la alineación de lecturas mucho más largas.











 nueva página del texto (beta)
nueva página del texto (beta)