Introducción

El problema inverso electroencefalográfico (PIE) consiste en determinar, a partir de mediciones electroencefalográficas sobre el cuero cabelludo, las fuentes bioeléctricas que generan dichas mediciones. Las fuentes representan grandes conglomerados de neuronas que trabajan de forma sincronizada para generar potenciales que puedan ser registrados en el cuero cabelludo a través de un electroencefalógrafo ^[1]. El PIE es un problema mal planteado en el sentido de Hadamard^[2], esto es: Un problema es mal planteado si no tiene solución, o tal solución no es única ya que existen diferentes fuentes que pueden producir la misma medición, o presenta una inestabilidad numérica, que se refleja en el hecho de que pequeños cambios en la medición pueden producir grandes variaciones en la localización de la fuente. Para tratar esta inestabilidad se utilizan los llamados métodos de regularización ^[2], que permiten encontrar soluciones estables aproximadas a partir de la medición con error. Para el estudio del PIE, se requiere considerar el llamado problema directo, el cual consiste en determinar la medición cuando se conoce la fuente. A diferencia del problema inverso, el problema directo tiene buenas propiedades numéricas, es decir, si dos fuentes están cercanas, las respectivas mediciones también lo estarán. Esto se demuestra abajo cuando se llegue al planteamiento operacional del problema.

Las fuentes bioeléctricas pueden dividirse en corticales y subcorticales y su estudio puede hacerse por separado sin pérdida de generalidad. En este trabajo, sólo se considera el caso en el que la fuente se localiza sobre la corteza cerebral. En este caso, el problema de identificación de la fuente tiene solución única ^[3], por lo que el mal planteamiento del PIE está asociado con la inestabilidad numérica. Para manejar esta inestabilidad, se utiliza el método de regularización de Tikhonov ^[2], eligiendo el parámetro de regularización por medio del método de la curva L^[4]. En este trabajo, se propone un algoritmo para identificar fuentes de corriente dipolar que modelan focos epilépticos. Las fuentes de corriente dipolar se definen por medio de la función delta de Dirac y el momento dipolar ^[5]. Para aproximar a la función delta de Dirac, se utilizan funciones campana. En el primer paso, el algoritmo identifica al centro de la función campana, con lo que se halla el centro de la función delta de Dirac. En el segundo paso, se determina el momento dipolar, con lo que se determinan los parámetros de la fuente de corriente dipolar. En ambos casos se utiliza el funcional de Tikhonov y se encontró que puede considerarse el mismo parámetro de regularización. El algoritmo propuesto es implementado en una geometría formada por dos círculos concéntricos, procediendo por dos caminos: 1) usando series de Fourier (armónicos circulares); 2) usando el método del elemento finito (MEF) y el Método de Gradiente Conjugado (MGC) ^[6]. En ambos casos se obtienen tanto el centro como el momento dipolar de la fuente y con ello se mostró que el algoritmo propuesto muestra buenos resultados. Los resultados son ilustrados a través de ejemplos sintéticos que muestran la factibilidad del algoritmo propuesto para determinar los parámetros de la fuente de corriente dipolar. Los dos métodos pueden extenderse al caso tridimensional y con ello, el algoritmo propuesto. Además, que el segundo camino puede utilizarse para geometrías irregulares.

Cabe destacar que el problema de identificar los parámetros de la fuente dipolar es no lineal y que se propone un algoritmo que encuentra dichos parámetros a través de dos problemas inversos lineales que utilizan el método de regularización de Tikhonov, y el parámetro de regularización se obtiene mediante el método de la curva L. Los resultados numéricos mostraron que puede elegirse el mismo parámetro de regularización para ambos problemas. Además, el primer paso del algoritmo puede aplicarse para fuentes más generales que las funciones campana, lo que podría permitir considerar otro tipo de actividad diferente a la epiléptica o aproximar a las fuentes de corriente dipolar por medio de otra clase de funciones.

Problema de Contorno Electroencefalográfico Cortical

Se considera a la cabeza Ω-1 ∪ Ω2 como un medio conductor compuesto por dos medios homogéneos donde Ω₁ representa al cerebro, Ω₂ al resto de las capas que componen la cabeza (líquido intracraneal, cráneo, cuero cabelludo), σ₁ y σ₂ son las conductividades de Ω₁ y Ω₂ las cuales se suponen constantes, S₁ representa la superficie de la corteza cerebral, S₂ a la superficie del cuero cabelludo y Ω-1 =Ω1∪ S1 (ver Figura 1).

Figura 1 Representación esquemática de la cabeza. 

El estudio del problema de identificación de fuentes se realiza a través del siguiente problema de contorno ^[3]:

-σ1∆u1 =0, en Ω1, (1)

-σ2∆u2 =0, en Ω2, (2)

u1  =u2 , en S1, (3)

σ1∂u1∂n1=σ2∂u2∂n1+g, sobre S1, (4)

σ2∂u2∂n2=0, sobre S2, (5)

donde g es la fuente que representa a un foco epiléptico, ui=uΩi, i = 1, 2 y u representa el potencial eléctrico en Ω, el símbolo Δ representa el operador Laplaciano. La condición de frontera (3) corresponde a la continuidad del potencial u y la condición de frontera (4) está asociada con el salto en los flujos de corriente debido a la presencia de la fuente g. La condición de frontera (5), se obtiene al considerar que la conductividad de Ω^c es cero (la conductividad del aire). De las fórmulas de Green se deduce la siguiente condición de compatibilidad:

∫S1gxdx=0 (6)

Llamaremos al problema (1)-(5), Problema de Contorno Electroencefalográfico Cortical (PCEC). Asociados al PCEC se tienen las siguientes definiciones.

Definición 1: Dada g definida sobre S₁, el problema directo consiste en hallar la medición V=uS2, donde u es la solución del PCEC.

Definición 2: Dada una función V definida sobre S₂, el problema inverso consiste en determinar una fuente g definida sobre S₁, tal que la solución u del problema directo correspondiente a g, satisfaga que uS2=V.

Método de Elemento Finito y el Método de Gradiente Conjugado

El MEF puede emplearse para resolver el PCEC tanto en geometría simple como irregular. En ambos casos se considera la expresión para la solución débil (7). A fin de ilustrar el algoritmo propuesto, sólo se desarrolla el caso de geometría simple, a saber, el caso en que la región Ω se representa por medio de círculos concéntricos. Para aproximar el espacio U , se considera una triangulación de elemento finito τh de Ω donde h es la longitud de más largo de ejes de τh, es decir, la región Ω-   se aproxima por una región poliédrica Ω-h=∪Τ∈τhΤ (ver Figura 1). El espacio L₂ (Ω) se aproxima por el espacio discreto L2Ω=vh ∈CΩh:vhΤ ∈P1, ∀ Τ∈τh donde C(Ωh) denota el espacio de las funciones continuas definidas sobre Ωh; P1 es el conjunto de los polinomios de grado uno sobre Ω_h. Así, las integrales que definen a la solución débil (7) se convierten en integrales sobre la región poliédrica. El cálculo de las integrales puede realizarse por medio de diferentes métodos de integración. Se utiliza la regla del trapecio. El sistema de ecuaciones lineales algebraicas que se obtiene al aplicar el MEF, puede ser resuelto por el método de Cholesky ^[7], ^[8].

Para hallar la solución del problema inverso, se debe minimizar el funcional de Tikhonov. Esto se realiza por medio del Método del Gradiente Conjugado (MGC) ^[8, ⁹, ^10]. Para aplicar el MGC se utiliza el siguiente problema de valores en la frontera:

El cual es conocido como problema de contorno electroencefalográfico cortical adjunto, denotado como PCECA. Con este problema se define el operador adjunto A* : L₂ (S₂) → L₂ (S₁) con regla de correspondencia A*v=wS1. Ya que el MGC es un método iterativo, en cada paso de la iteración se deben resolver tanto el PCEC como el PCECA ^[3].

Se propone una expresión para una fuente de corriente dipolar concentrada en la corteza cerebral, explicada en la siguiente Sección.

Resultados numéricos y discusión

En esta Sección, se presentan ejemplos numéricos para ilustrar el algoritmo propuesto. Se considera que la región Ω está determinada por dos círculos concéntricos centrados en el origen, es decir, Ω₁ es un dominio circular de radio R₁ y Ω₂ es un dominio anular con radio interior R₁ y radio exterior R₂, como se muestra en la Figura 1. Por simplicidad se consideran los siguientes valores σ₁ =3 y σ₂=1. Los ejemplos sintéticos son generados tomando una fuente superficial g_β definida por (12); posteriormente se resuelve el problema directo, es decir, se calcula V=uS2, donde u es la solución del PCEC. Entonces el potencial V es dado como dato de entrada para minimizar el funcional de Tikhonov(10) y determinar los parámetros de la fuente dipolar siguiendo los pasos del método descrito previamente:

Primer paso: Determinar de manera estable el centro ɑ_𝛼𝛿 de la función campana que define a g_𝛼(𝛿),N (y con ello al centro aproximado de la función delta de Dirac) recuperada usando los métodos desarrollados en ^[3].

Segundo paso: Determinar el momento dipolar a partir de P→α1δ a aα(δ), α1(δ) y de (13) o (15), los cuales usan el desarrollo en series de Fourier tomando como base los armónicos circulares así como el MEF, respectivamente.

Para determinar los parámetros de regularización α(δ) y α1(δ) se utiliza el método de la curva L, donde δ es el error que se comete cuando se mide V, es decir, en vez de V se conoce V_𝛿 con Vδ -VL2(S2)≤δ. Los datos con error V_𝛿 son obtenidos agregando un error aleatorio usando la función rand de MATLAB, definiendo

donde Error=δmáxV2rand1,s-1 es un vector de números aleatorios de longitud s (s es un número de nodos de la frontera exterior S₂). Para el caso de coeficiente de Fourier se agrega un error aleatorio a los coeficientes exactos usando también a la función rand.

En los ejemplos siguientes se consideran los errores absolutos EA(.,.) y relativos ER(.,.) en las normas de los espacios correspondientes.

Ejemplo 1 (Identificación de los parámetros de la fuente usando series en armónicos circulares): Se considera que en la fuente de corriente dipolar jpx=P→δ(x-a) se toma ɑ = (𝛼₁, 𝛼₂) = (0,1), P→=p1,p2=(1,1). Para calcular la medición producida por la fuente, se utiliza una aproximación de la fuente en la forma (12) y la expresión (8) con N=30, β=0.1, σ₁ =3, σ₂=1, R₁=1, R₂=1.2. Los coeficientes gk1 y gk2 de gβ∈L2(S1) son obtenidos usando la función quadl de MATLAB. En la Figura 2(a), se muestra dicha fuente g_β (línea punteada) y su aproximación g_β,N (línea continua) con series cuyo error absoluto es de 0.0103 (para N=30). Los datos perturbados V_𝛿 son generados como en (16) agregando un error aleatorio a los coeficientes de Fourier de V, es decir,

donde

para i = 1, 2 y para k = 1,2, …, N. Después de aplicar el algoritmo para identificar una fuente aproximada g_𝛼(𝛿),N por el método propuesto en ^[3], con 𝛼(𝛿) = 10^-4 se obtiene el centro aproximado ɑ_𝛼(𝛿) de la función campana g_𝛼(𝛿),N. En coordenadas polares el centro exacto de la fuente exacta g_β está dado para θ0=π2, es decir, cos⁡π2, sen⁡π2=(0,1).

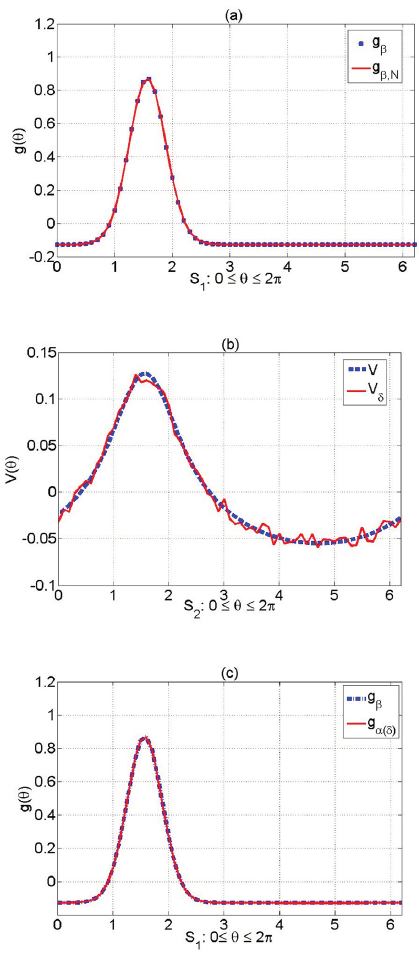
Figura 2: (a) Fuente exacta g_β (línea punteada) y su aproximación por su serie de Fourier truncada g_β,N (línea continua). (b) Medición exacta V (línea punteada) y perturbada V_𝛿 (línea continua). (c) Fuentes exacta g_β (línea continua) y recuperada g_𝛼(𝛿) (línea punteada). 

Para determinar el momento dipolar P→α1 se aplica (13). En la Tabla 1 se muestran los resultados obtenidos del centro y momento dipolar para diferentes valores de 𝛿. Además, se expresan los errores absoluto y relativo entre el centro exacto y aproximado y entre el momento dipolar exacto y el momento dipolar aproximado. Se observa que el mayor error relativo ocurre en la solución aproximada de P→α1δ, que es del mismo orden que la perturbación ER (V_𝛿, V) de los datos de entrada V_𝛿 para 𝛿 = 0.1, 0.01. Los resultados numéricos muestran que las soluciones numéricas ɑ_𝛼(𝛼) y P→α1(δ) convergen a las soluciones exactas cuando 𝛿 tiende a cero. En este caso, la fuente dipolar superficial recuperada correspondiente a los parámetros ɑ_𝛼(𝛿) y P→α1(δ) es denotada por g_𝛼(δ). En la Figura 2(c), se muestra la fuente g_β y la fuente recuperada g_𝛼(δ) determinada a partir de los datos perturbados mostrados en la Figura 2(b) para δ = 0.1.

En este caso, el valor del parámetro de regularización de α(𝛿) y 𝛼₁(𝛿) es de 10-4. Los errores absolutos correspondientes de las soluciones numéricas son EA (ɑ, ɑ_𝛼(𝛿)) = 8.5279×10^-4 y EAP,P→α1(δ)=0.0068. Los errores calculados indican que los datos recuperados ɑ_𝛼(𝛿) y P→α1(δ) por el método propuesto son una buena aproximación a los datos exactos de ɑ y P→ .

En la Tabla 2, se muestran los resultados de la recuperación de los parámetros ɑ_𝛼(𝛿) y P→α1(δ) para diferentes valores del centro ɑ y del momento dipolar P→, así como los errores absoluto y relativo entre el centro exacto y aproximado y entre el momento dipolar exacto y aproximado. Nótese que las Tablas 1 y 2, muestran que con 𝛼(𝛿) = 𝛼₁(𝛿) se obtienen buenos resultados, es decir, los dos parámetros de regularización pueden ser iguales.

Ejemplo 2 (Identificación de los parámetros de la fuente usando el MGC y el MEF): Se considera la misma región circular del ejemplo anterior con los mismos valores para σ1, σ2, R1, R2 y para los parámetros ɑ, P→,  β para la fuente dipolar. Como antes, la función g_β es aproximada por medio de los primeros N = 30 términos de su serie de Fourier truncada que se denota por g_β,N . Para calcular la solución del problema directo y generar los datos perturbados, se procede como en Ejemplo 1. Para resolver el PCEC por el MEF se emplea una malla denotada por M ₁ (nn, ne), donde nn es el número de nodos y elementos (triángulos), respectivamente. El tamaño de malla M₁ es denotado por h. En este ejemplo se toma h = 0.1, de donde nn=774 y ne=1470. La malla M₁ fue generada usando el pdetool de MATLAB.

La Tabla 3 muestra los resultados numéricos para el caso de datos perturbados V_𝛿, para diferentes valores de 𝛿, donde 𝛼(𝛿) es el parámetro de regularización, ε es el criterio de paro (o tolerancia) del MGC, n es el número de iteraciones del MGC para determinar la fuente superficial aproximada gαδ,hn y ɑ_𝛼(𝛿) es el centro aproximado determinado a partir de gαδ,hn. Por último, α1δ es el parámetro de regularización que se utiliza para determinar, a partir de los datos V_𝛿 y por medio de (15), el momento dipolar aproximado P→α1(δ). Asimismo, se muestran los errores absoluto y relativo entre el centro exacto y aproximado y entre el momento dipolar exacto y aproximado. Se puede observar que el comportamiento cualitativo es muy similar al obtenido en el Ejemplo 1. Numéricamente, el mayor error relativo de la solución aproximada ocurre en P→α1(δ), el cual es del mismo orden que la perturbación ER (V, V_𝛿) de los datos de entrada V_𝛿, para 𝛿 =0.1, 0.01. Además, las soluciones numéricas ɑ_𝛼(𝛿) y P→α1(δ) convergen a soluciones exactas cuando 𝛿 tiende a cero.

La fuente dipolar superficial recuperada corresponde a ɑ _𝛼(𝛿) y P→α1(δ) es denotada por g_α(𝛿),h . En la Figura 3(b) se muestra la fuente exacta g_β y a fuente recuperada g_α(𝛿),h determinada a partir de los datos perturbados, mostrados en la Figura 3(a) para 𝛿 = 0.1 en la malla M₁ (774,1470) cuyo tamaño de malla es h = 0.1.. En este caso, los valores del parámetro de regularización α(𝛿)=10^-4 y n = 6 eligiendo un criterio de paro (tolerancia) del MGC ε = 10^-3 (el cual sirve para los diferentes valores de 𝛿), y el parámetro de regularización α₁(𝛿) = 10^-4 para determinar P→α1(δ) de (14) a partir de los datos V_𝛿. En este caso EA(ɑ, ɑ_𝛼) = 6.3075×10^-4 y EAP,P→α1(δ). = 1.2239×10^-1 Estos errores indican que los datos recuperados ɑ_𝛼 y P→α1(δ) por el método propuesto dan una buena aproximación a los datos exactos de a y P→.

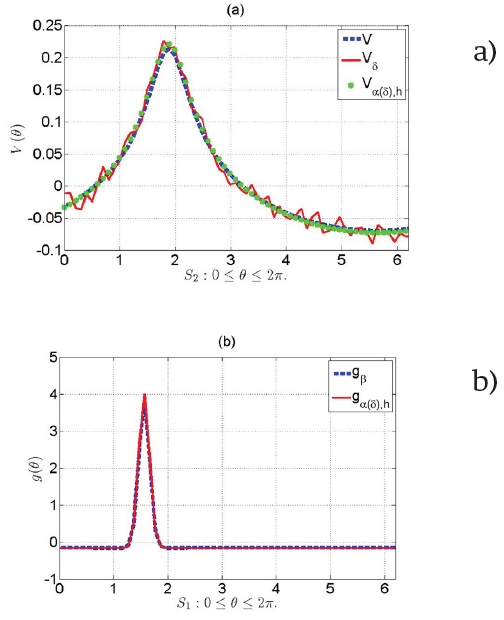
Figura 3  (a) Medición exacta (V, línea punteada), perturbada (Vδ, línea continua) y medición a partir de la fuente g_α(𝛿),h (V_α(𝛿),h, asteriscos). (b) Fuentes exacta (g_β, línea punteada) y recuperada a partir del algoritmo (g_α(𝛿),h, línea continua). 

Se muestran resultados similares en la Tabla 4 para 𝛿 = 0.1 y diferentes valores del centro y del momento dipolar P→ para la fuente dipolar g_β con β = 0.1, usando la malla M₁ (774,1470) cuyo tamaño de malla es h = 0.1. Además, se muestran los errores absoluto y relativo como en las Tablas anteriores. En la Tabla 4 se observa que los datos ɑ_𝛼(𝛿) y P→α1(δ) se recuperan de manera estable por el método propuesto.

Por lo tanto, se ha mostrado que el método propuesto recupera soluciones numéricas estables en el caso de datos con error V_δ, tal como se ilustra en la Figura 3.

En las ecuaciones (13) y (15), puede emplearse en vez de la medición V_δ , el potencial que corresponde a la solución encontrada en la primera parte del algoritmo. Ya que el método es estable se obtendrán resultados similares.

Conclusiones

Los resultados numéricos mostraron que el algoritmo propuesto es convergente, estable y que el parámetro de regularización de cada uno de los problemas en que se divide el algoritmo, puede elegirse igual (usando el método de la curva L) y el nivel de error es del orden del error de medición y con ello, la factibilidad del algoritmo propuesto. Entre las ventajas de este método para identificar de manera estable fuentes de tipo dipolar, se hallan que el problema no lineal se dividió en dos problemas lineales (para los cuales se pudieron aplicar algunos resultados conocidos) y que puede extenderse a geometrías complejas y tridimensionales. Sin embargo, debe analizarse su posible aplicación a fuentes más generales.

En un trabajo futuro, se explorará la posibilidad de aplicar el algoritmo a otro tipo de fuentes que se expresen por medio de un conjunto finito de parámetros, las cuales pueden representar diferentes tipos de actividad eléctrica; otra posibilidad es el de usar otro tipo de expresión para aproximar a la función delta de Dirac la cual pueda dar ventajas numéricas.