Artículos

 

Análisis de transición dinámica: un enfoque no paramétrico aplicado a la región centro de México (1988-2003)

 

Analysis of dynamic transition: a non-parametric focus applied to Mexico's central region (1988-2003)

 

Analyse de transition dynamique: un abord non paramétrique appliqué à la région centrale du Mexique (1988-2003)

 

Análise de transição dinâmica: um enfoque não-paramétrico aplicado à região centro do México (1988-2003)

 

動態分析過渡：一種非參數方法適用於墨西哥地區的中心（1988-2003）

 

Rafael Borrayo López * y Juan Manuel Castañeda Arriaga**

 

* Investigador titular de tiempo completo del Instituto de Investigaciones Económicas-UNAM. Correo electrónico: mara@unam.mx.

** Consultor independiente. Correo electrónico: jmanuelca@gmail.com.

 

Fecha de recepción: 4 de mayo de 2011.
Fecha de aceptación: 7 de agosto de 2011.

 

Resumen

La teoría del crecimiento (neoclásica, endógena y de la nueva geografía económica) y el desarrollo de nuevas técnicas computacionales han fertilizado el campo de conocimiento del análisis económico-espacial y, más recientemente, el uso de métodos paramétricos se ha complementado con el desarrollo de métodos semi y no paramétricos que han potenciado el análisis de procesos de crecimiento. Desde esta perspectiva, en este estudio se realiza un análisis de dinámica de la distribución (ADD) de una medida del ingreso regional aplicado a la región centro de México, a escala municipal. Este análisis exploratorio de datos encuentra evidencia sobre la importancia de efectos espaciales y, en particular, los relativos a la existencia de una estructura económica estratificada, como una manifestación del nivel de polarización global.

Palabras clave: convergencia, autocorrelación, heterogeneidad, movilidad, polarización.

 

Abstract

The theory of growth (neoclassical, endogenous and that of the new economic geography) and the development of new computerized techniques have fertilized the field of knowledge in spatial economic analysis and, more recently, the use of parametric methods has been complemented by the development of semi- and non- parametric methods which have fortified the analysis of growth processes. From this perspective, this study makes use of a dynamic distribution analysis (DDA) to measure regional income applied to Mexico's central region, on a municipal scale. This exploratory analysis of data finds evidence of the importance of spatial effects and, in particular, of those relative to the existence of a stratified economic structure, as a manifestation of the level of global polarization.

Key words: convergence, autocorrelation, heterogeneity, mobility, polarization.

 

Résumé

La théorie de la croissance (néoclassique, endogène et de la nouvelle géographie économique) et le développement de techniques informatiques ont fertilisé le champ de connaissance de l'analyse économico-spatiale et, plus récemment, l'usage de méthodes paramétriques a été complémenté par le développement de méthodes semi et non paramétriques qui ont rendu possible l'analyse des processus de croissance. En adoptant cette perspective, il est effectué dans cette étude une analyse de dynamique de la distribution (ADD) d'une mesure du revenu régional appliqué à la région centrale du Mexique, à l'échelle municipale. Cette analyse exploratoire de données avère l'importance d'effets spatiaux, notamment ceux relatifs à l'existence d'une structure économique stratifiée, ce qui met en évidence le degré de polarisation global.

Mots clés : convergence, auto-corrélation, hétérogénéité, mobilité, polarisation.

 

Resumo

A teoria do crescimento econômico (neoclássica, endógena e da nova geografia econômica) e o desenvolvimento de novas técnicas computacionais fertilizaram o campo de conhecimento da análise econômico-espacial e, mais recentemente, a utilização de métodos paramétricos se complementou com o desenvolvimento de métodos semi e nãoparamétricos que potencializaram a análise dos processos de crescimento. Desde essa perspectiva, no presente estudo se realiza uma análise de dinâmica da distribuição (ADD) de uma medida da renda regional aplicada à região centro do México, à escala municipal. Esta análise exploratória de dados encontra evidencia sobre a importância de efeitos espaciais e, em particular, os relativos à existência de uma estrutura econômica estratificada, como uma manifestação do nível de polarização global.

Palavras-chave: convergência, auto-correlação, heterogeneidade, mobilidade, polarização.

 

摘要

增長理論（新古典主義，源性和新經濟地理學）和新的計算技術的發展已受精的空間經濟分析，以及最近的知識領域，參數方法的使用已被補充與發展方法和半參數分析增強了生長過程。從這個角度來看，這項研究是一種分佈動態分析（ADD）是適用於墨西哥中部地區在市級，地區收入的措施。這種探索性數據分析發現對空間效果的重要證據，特別是有關一個分層作為全球兩極分化水平的體現經濟結構的存在

關鍵詞：收斂，自相關，異質性，流動性，兩極分化

 

Introducción

La existencia, extensamente documentada, de disparidades entre países y regiones dentro de una nación es un problema que concentra crecientemente la atención en la investigación y en el debate de política pública. El objeto de interés particular consiste en saber si tales diferencias se amplían, estabilizan o disminuyen en el tiempo y comprender los procesos reales que las explican. Conocer la dirección y el monto del cambio necesita de métodos de cuantificación más robustos y rigurosamente construidos, porque las acciones sociales e individuales para superar las desigualdades, en todas sus escalas, pasa necesariamente por la asignación de recursos limitados en un contexto de conflictos institucionales y de intereses diversos.

En general, la forma dominante de tratar analíticamente fenómenos estructurales de esta naturaleza se sustenta en la teoría del crecimiento económico¹ y, el análisis empírico, en el desarrollo de nuevas técnicas de cuantificación, en particular no paramétrica y semiparamétrica, que se han vuelto viables de operar por la disponibilidad de recursos computacionales más potentes (computadoras veloces y software especializado). Los desarrollos teóricos y empíricos considerados para este trabajo se apoyan en la crítica iniciada por Quah (1993, 1997)² a la tradición que surge de los trabajos de Barro (1992) y Barro y Sala-i-Martin (1995) sobre convergencia entre países y regiones. Una breve síntesis sobre este amplio e intenso debate la ofrece Islam (2003) en términos de las distintas nociones e interpretaciones del concepto de convergencia y sus desarrollos metodológicos asociados (Cuadro 1). En las revisiones recientes de Durlauf y Quah (1999), Temple (1999) y Durlauf et al (2005), se identifican dos grandes grupos de métodos: i) análisis econométrico y el ii) análisis de la dinámica de una distribución (ADD), con base en técnicas no paramétricas.

Los estudios empíricos que usan este segundo grupo con frecuencia revelan patrones complejos de crecimiento regional que involucran la coexistencia de procesos de persistencia, divergencia-convergencia y movilidad entre regiones, en asociación a distribuciones de ingreso con múltiples formas de agrupación, lo que sugiere que la atención exclusiva sobre la existencia (o no) de convergencia puede conducir a simplificar el análisis de los procesos de dinámica regional. En consecuencia, se ha seleccionado un enfoque no paramétrico para el análisis de una muestra de datos sobre una medida de "ingreso" de cada uno de los municipios de la región centro de México (RCM), el cual tiene como ventajas: i) usar la información de la distribución completa de los datos,³ ii) permite identificar movimientos relativos de cada región o procesos de dinámica intradistributiva (movilidad, persistencia, polarización y estratificación) y iii) al menos, se le reconoce también la ventaja de no imponer forma funcional alguna a esa dinámica.

Para el caso de México dominan los estudios sobre análisis convergencia de tipo paramétrico,⁴ pero los estudios que usan técnicas no paramétricas son menos frecuentes y, aunque sin ser exhaustivos, se mencionan los trabajos de Aroca et al (2005), García-Verdú (2005) —con desagregación estatal—, y Valdivia (2008) que trabaja la RCM para la escala municipal, como en este trabajo, pero con una estrategia metodológica diferente. Este análisis exploratorio se compone esencialmente de dos partes: Sección 2) un ADD básico y Sección 3) un ADD con efectos espaciales y filtro espacial. En la primera parte se formula el ADD y sus tres componentes: forma, movilidad y proyección de largo plazo y, en la segunda parte se incorporan al análisis los efectos espaciales de autocorrelación y heterogeneidad.

 

Análisis de la dinámica de una distribución (ADD) básico

Este trabajo recupera para su aplicación los desarrollos metodológicos que surgen a partir del trabajo de Quah (1993, 1997) como análisis de la dinámica de una distribución (distribution dynamics) y los trabajos de análisis empírico sobre el crecimiento económico que se revisan con detalle en Durlauf y Quah (1999) y Durlauf, Johnson y Temple (2005). Estos autores documentan las críticas sobre las insuficiencias del enfoque econométrico en la identificación de las características evolutivas de la distribución transversal de una variable en el tiempo, que son: i) el análisis de la forma general (externa), ii) la dinámica dentro de la distribución (movilidad) y iii) el comportamiento de largo plazo (o ergódico).⁵ Propiamente, este es un análisis de dinámica de una distribución (ADD) o transición dinámica, y tiene como soporte un modelo estadístico o probabilístico. Para construir el modelo se postula algún mecanismo que gobierne la evolución de una distribución en el tiempo (secuencia de distribuciones transversales) con apoyo del concepto de kernel estocástico, como un operador matemático que sintetiza la información completa sobre la dinámica de la distribución.⁶

Dada una estructura de datos con n observaciones, que son realizaciones (x_i) de una variable aleatoria, {X¡}ⁿ_i=1, i.i.d. ~ F, donde F denota una función de distribución desconocida cuya estimación representa el objetivo principal; aunque en particular el interés se enfoca a la estimación de la densidad asociada (ƒ= F) suponiendo que ésta existe.⁷ La forma más simple de modelar la evolución de esta distribución transversal es un proceso auto-regresivo de primer orden, cuya dinámica {F_t : t ≥ O} o equivalentemente {ƒ_t : t ≥ 0} se especifica así.⁸

Donde u_t+1 es una secuencia de perturbaciones, Τ* es un operador que mapea las medidas de probabilidad (densidades) desde el tiempo t al t+1, y es un operador derivado que en su definición quedan absorbidas o "encriptadas" las perturbaciones; esto es, la relación entre densidades del periodo t al periodo t+1 (Ec. 1) contiene la información completa sobre la dinámica intra-distributiva o movilidad de la unidades observadas.

Cuando la variable de interés es continua (como el ingreso) cualquier discretización será siempre arbitraria e importa porque los postulados sobre la conducta dinámica inferida de la distribución y las implicaciones de esa conducta en el largo plazo son sensibles a tal partición (Bulli, 2001), la misma propiedad de Markov puede resultar alterada.⁹ La técnica de kernel estocástico es una manera de superar este problema de discretización del espacio-ingreso.¹⁰

En consecuencia, si X_t toma valores en un espacio-ingreso continuo, el operador Τ* debe interpretarse como una función de transición o kernel estocástico: ƒ(x,t,y,s), que es la función de densidad de X_t+s = y condicional a X_t = x. De tal manera que:

Si el mecanismo de transición es invariante en el tiempo, la matriz de densidad de probabilidad de transición sólo depende del intervalo de tiempo s y puede escribirse como la densidad condicional ƒ_s(y|x). Igualmente, bajo los dos supuestos del caso discreto, la expresión que describe la evolución de la distribución en el tiempo quedará como:

Esta ecuación (3) se resuelve para la probabilidad ƒ_s(y|x) :

La densidad condicional describe la probabilidad de que una región dada se mueva a un cierto estado de ingreso relativo (más rico o más pobre) conocido su nivel de ingreso inicial.¹¹ Hasta aquí tenemos todos los elementos del modelo probabilístico de transiciones con el cual realizar un análisis de movilidad o dinámica intra-distributiva. Una vez que se ha estimado la densidad condicional ƒ_s(y|x) será posible proyectar la distribución del ingreso regional hacia el futuro.¹² Es importante porque la observación de la forma de la distribución ergódica complementa un análisis de convergencia. Mientas una densidad real en un tiempo dado puede reflejar un desequilibrio (histórico) ocasionado por shocks estructurales del pasado, la densidad ergódica muestra un equilibrio futuro en ausencia de cambios estructurales. El cálculo de ƒ_∞(y) es importante porque si esta distribución estacionaria muestra una tendencia hacia un "punto-masa", sugiere un proceso de convergencia hacia una estructura más igualitaria. Si por el contrario, la tendencia es hacia la formación de dos puntos (bimodal) o más, puede interpretarse como una manifestación de polarización del ingreso. El propósito de un ADD consiste en destacar la dinámica implícita en el periodo cubierto por los datos, de ninguna manera derivar un pronóstico (Quah, 1993).

En síntesis, hemos expuesto los fundamentos necesarios para elaborar un análisis de dinámica de una distribución (ADD) o transición dinámica con sus tres componentes básicos: i) la forma general (externa), ii) la dinámica dentro de la distribución (movilidad) y iii) su comportamiento de largo plazo (o ergódico).

 

Datos y análisis exploratorio de datos

Una recomendación metodológica para un estudio empírico consiste en empezar con un análisis exploratorio de datos, seguido de un análisis confirmatorio (Tukey, 1980). La fuente de información utilizada para esta aplicación proviene de los censos económicos (1988, 1993, 1998 y 2003) del Instituto Nacional de Estadística, Geografía e Informática de México (INEGI). Las unidades de observación son los municipios y, en particular, se extraen de los censos los 535 correspondientes a la región centro de México (RCM), "depurados" preliminarmente para conformar una muestra de 499 municipios.¹³

La variable de interés para esta aplicación es una medida aproximada del "ingreso regional" per cápita y se propone para tal aproximación el cociente del valor agregado censal bruto (VACB) entre la población ocupada (PO) a escala municipal. No utilizamos a la población debido a la presencia del fenómeno de commuting sobretodo en las zonas metropolitanas de la RCM. Este cociente tiene además la ventaja de ser medido sobre la misma base, el VACB y la PO son medidas estrechamente asociadas al lugar de trabajo, cuestión diferente si empleamos población total para relativizar el VACB. Aunque propiamente es también una medida gruesa de productividad regional, el uso que se hará a lo largo del capítulo será simplemente como ingreso regional en el contexto del análisis empírico del crecimiento.¹⁴

En México es muy escasa la generación de estadísticas regionales de producción y empleo, lo poco y parcialmente existente remite al nivel de entidad federativa y, salvo casos especiales, los censos concentran la información disponible con el detalle requerido. En Valdivia (2008) puede encontrar el lector precisiones sobre el acotamiento del universo de representación¹⁵ y sobre los problemas asociados a la medición del empleo regional, el papel de la "informalidad" y otros aspectos de la sub-representación.

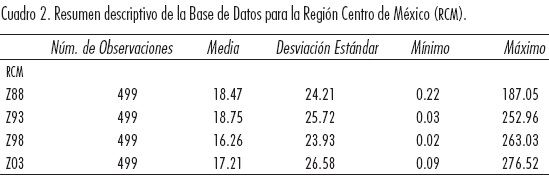
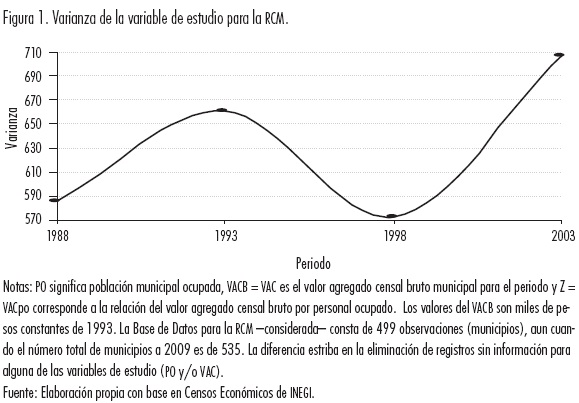
Las características generales que destacan de los datos originales de la muestra de la RCM son: i) el rango de variación entre valores máximos y mínimos es muy amplio, el coeficiente de ambos oscila entre 2 y 4 órdenes de magnitud (8.39E+02, 7.52E+03, 1.36E+04, 3.24E+03) para cada uno de los años de los censos;¹⁶ ii) una varianza que oscila contrastantemente de creciente a decreciente y luego a creciente para los periodos secuenciados de la muestra (Cuadro 2 y Figura 1); y iii) la distribución empírica (estimador de densidad kernel) es marcadamente asimétrica, con fuertes sesgos en ambas colas, aunque concentra muchos valores hacia los niveles bajos de ingreso regional y una cola muy prolongada y dispersa hacia los ingresos altos (Figuras 2.a y 2.b).¹⁷ En suma, se trata de una distribución empírica difícil de manejar analíticamente.

Debido a la característica asimétrica y sesgada que exhibe la distribución se impone realizar un diagnóstico de normalidad. Las gráficas 'Q-N', en la Figura 5.a, muestran un comportamiento muy desviado respecto de una densidad normal, particularmente en las colas, que sugiere una fuerte presencia de valores extremos con alto riesgo de los efectos nocivos de los llamados datos outliers. Esto sugiere un tratamiento preeliminar de los datos que reduzca este problema, pero sin alterar significativamente la estructura de los datos. Es usual en la literatura empírica explorar con diferentes operadores matemáticos de transformación para "alinear" mejor los datos de la distribución empírica a una curva "bien comportada" (ver Figura 5.b).

 

Análisis empírico de transición dinámica para la RCM

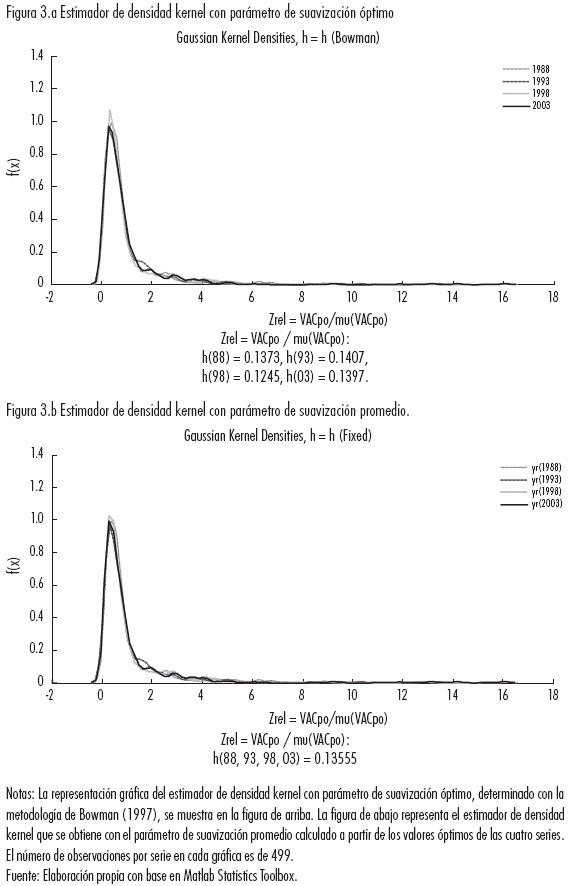
Empezamos ahora con un análisis de la evolución de la forma de la distribución de los datos para la RCM cuyos fundamentos fueron expuestos en la sección anterior. En la Figura 3.a se muestran las distribuciones empíricas para los datos originales (relativizados) que son estimadores de densidad kernel con parámetro de suavización "óptimo", calculado mediante la metodología de Bowman (1997), y en la Figura 3.b los estimadores de densidad kernel calculados con el promedio de los valores óptimos para cada una de las cuatro series.

En las figuras el valor de 1.0 sobre el eje horizontal indica el ingreso regional promedio de la RCM y la altura de la curva en un punto registra la probabilidad de que una región particular tenga cierto ingreso relativo. Para todas las fechas, aunque hay cambios de forma, la evidencia gráfica sobre diferencias en las formas externas es muy débil y las fluctuaciones hacia la cola derecha de la densidad no terminan por conformar modas sugerentes de una estructura de datos globalmente estable.

Ante las características que muestran las distribuciones empíricas se opta por realizar una transformación logarítmica de los datos para la que en las Figuras 4.a y 4.b se muestra el efecto correspondiente: se reducen las observaciones que se desvían fuertemente del resto de unidades de la muestra y se presentan repartidos a ambos lados de la distribución de la variable transformada.

Muchas pueden ser las fuentes que explican la existencia de estos datos outliers, desde la recolección y tratamiento inicial hasta que, en realidad, se trata de observaciones que están mostrando comportamientos de las regiones extraordinariamente buenos o malos. Los resultados de las gráficas 'Q-N' en Figuras 5.a y 5.b, justifican entonces la transformación en el sentido de que se ajustan mejor los datos a una densidad normal.

Como la densidad condicional ha de evaluarse en el tiempo inicial y el final, la precisión de la estimación disminuye fuertemente si el tamaño de la muestra es pequeño. Una desventaja del enfoque kernel continuo es que el investigador necesita muchas observaciones con el fin de obtener estimados confiables de la dinámica intra-distributiva, por lo que, la eficiencia de la estimación requiere de un tamaño de muestra lo más grande posible. En nuestro caso de aplicación se ilustra para el año de 1988 y 2003, la muestra agrupa transiciones quinquenales por un total de 998 observaciones (2 series, cada una con 499 datos) y se considera adecuado para los objetivos buscados.

Los resultados de las estimaciones del kernel estocástico se presentan en las Figuras 6.a y 6.b para el periodo de 15 años.

Una forma natural de empezar a interpretar los resultados consiste en aprovechar el poder de las técnicas gráficas para el análisis de dinámica de una intradistribución. La Figura 6.a muestra una gráfica 3D de la densidad condicional estimada, el eje vertical mide la probabilidad asociada a cada par de puntos del plano x(1988) vs. y(2003). Esta gráfica es una colección de densidades condicionales, una al lado de la otra, que resultan del plano de corte en t paralelo al eje t+15; en su conjunto muestra cómo la distribución evoluciona de t a t+15. Las líneas paralelas al eje y(2003) tienen asociada la probabilidad de transitar desde el punto correspondiente en el eje x(1988) a cualquier otro punto 15 años después.

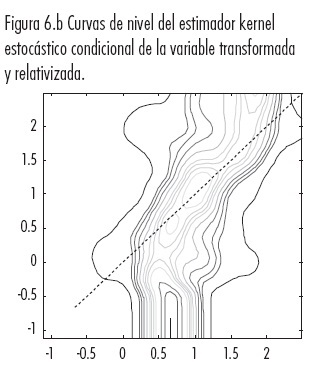
Sin embargo, la dinámica de intra-distribución regional puede visualizarse con mayor claridad en una gráfica de curvas de nivel (contour-plot), que resulta de la proyección de la densidad condicional sobre planos de X-Y que parten del correspondiente al de densidad máxima. Las líneas de la Figura 6.b conectan puntos con el mismo nivel de densidad de probabilidad del gráfico 3D.¹⁸ Es directo interpretar los puntos sobre la diagonal (45-grados) como una situación de persistencia, una región localizada sobre esos puntos se mantienen en el mismo estado en t y en t+15- Entonces si toda la masa de probabilidades se concentra alrededor de la diagonal de 45 grados, indica un fenómeno global de persistencia o ausencia de movilidad. Aún cuando la concentración no sea tan estrecha a la diagonal, la alineación de los aglomerados y los picos (islas) alrededor de ella sugieren un bajo grado de movilidad y ligeros cambios en la forma de la distribución del ingreso regional.

En consecuencia, a partir del máximo global los planos de corte definidos como un porcentaje de éste generan las curvas visualizadas correspondientes a diferentes niveles son: (96, 86, 82, 76, 66, 54, 46, 34, 22, 10, 6 y 1 -niveles que se leen desde el exterior hacia el interior—), son regiones del espacio muestra que tienen asociada una probabilidad constante. Una línea horizontal en 1.0 localiza regiones con ingreso igual al promedio de la RCM al tiempo t y una línea vertical en 1.0 localiza regiones con ingreso igual al promedio en t+15. Así, imagine el lector cualquier línea (o barra) horizontal con centro en las modas y a ambos lados se pueden identificar cotas al 99% y al 50%, si la diagonal principal cruza dentro del rango del 50% se considera como evidencia de fuerte persistencia, pero si cruza dentro del rango del 99% habrá mucha más movilidad intradistributiva y baja persistencia.¹⁹

Las Figuras 6.a y 6.b revelan tres características estructurales importantes, la coexistencia de procesos de persistencia, movilidad y polarización. En el rango de ingreso entre 0.7-1.5 veces el promedio de la RCM para t+15, se observa una fuerte persistencia (parte central), pero también una alta movilidad en los rangos de ingresos bajos y menor en los ingresos altos. Las regiones con ingresos debajo de 0.5 en t tienden a mejorar significativamente su posición relativa en el horizonte de transición de 15 años evidenciando un claro proceso de catchingup de las regiones más pobres. En contraste, regiones con ingresos arriba de 1.5 en t pierden sus posiciones relativas, ahora son más pobres. En suma se trata de un proceso de convergencia global que se expresa por el corrimiento de la masa de probabilidad en dirección contraria al movimiento del reloj. Dado que implícitamente se ha establecido un corte aproximadamente al 50% del máximo global, que se corresponden con las seis curvas de nivel aglomeradas partiendo desde los núcleos o centros, y aislando las curvas de nivel restantes, es posible identificar fragmentación o formación de "ínsulas" que sugieren la presencia de polarización o existencia de regímenes espaciales o clubes de convergencia.

El análisis de la densidad ergódica complementa el ADD y como se afirma líneas arriba, el valor de este tipo de análisis radica en que mientas una densidad real en un tiempo dado puede reflejar un desequilibrio (histórico) ocasionado por shocks estructurales del pasado, la densidad ergódica muestra un equilibrio futuro en "ausencia" de cambios estructurales, es decir, proyecta hacia delante una densidad que ha absorbido (integrado en su estructura) tales shocks. En la Figura 7 el comparativo entre la distribución empírica inicial (1988) y la distribución estacionaria sugiere presencia de unimodalidad, los resultados aparentemente son consistentes con el análisis de la forma global de la distribución empírica de los datos y el proceso de convergencia global identificado; sólo ocurren desplazamientos de la masa de probabilidades que la achatan en el centro y se corren ligeramente hacia niveles de ingresos altos y bajos.

Con el fin de realizar las interpretaciones económicas es importante notar que, por construcción, ƒ_∞(y) es independiente de las condiciones iniciales, ya que se asume que la distribución transversal de las regiones evoluciona a lo largo del tiempo de acuerdo con una ley de movimiento ƒ_s(y|x) que se mantiene inalterada, la influencia de las posiciones iniciales de las regiones se habrá desvanecido con el tiempo.²⁰

 

ADD con efectos espaciales

Estos desarrollos incorporan al análisis la variable espacio en la medida en que se empiezan a identificar patrones de conectividad entre regiones económicas para elaborar después, conjeturas con fundamento empírico que se transformen en explicaciones sobre las formas globales y locales de interacción económica. En otras palabras: la forma mediante la cual la acumulación de capital (privado y público) influye o determina específicamente la conformación de agrupamientos regionales (clusters) funciona u opera de manera diferenciada, ya sea que en algunos grupos de regiones los canales dominantes se expresan por vínculos interindustriales, flujos de comercio interregional y de población, flujos de tipo commuting, de intercambio de capital humano o cualquier combinación de éstos.

Tales procesos generan efectos espaciales decisivos para la identificación y cuantificación de los determinantes de procesos de crecimiento regional. En el enfoque tradicional de regresión que incorpora estos efectos se abordan como procesos de dependencia y de heterogeneidad espaciales empleando técnicas de localización relativa y absoluta. Es abundante la literatura que reconoce la importancia de los efectos espaciales para entender la dinámica de crecimiento regional. La estadística y la econometría espacial ofrecen instrumentos rigurosos para identificar y cuantificar formas bien definidas de dependencia y heterogeneidad y, por tanto, es un referente básico y necesario para entender por efectos espaciales a las combinaciones o mezclas posibles de efectos de dependencia y/o heterogeneidad que deben ser incorporados en la construcción de modelos.²¹ Es probable que la heterogeneidad espacial caracterice patrones de desarrollo económico bajo la forma de regímenes espaciales y/o heterogeneidad de grupos: un cluster de regiones ricas (centro) que se distingue de un cluster de regiones pobres (periferia, ver Ertur et al, 2006).

Los vínculos entre autocorrelación y heterogeneidad espacial son muy complejos,²² en estudios econométricos aplicados es usual encontrar ambos simultáneamente.²³ Pero también están presentes cuando está mal especificado el modelo. Un enfoque paramétrico tiene una ventaja sobre un enfoque no paramétrico: puede abordar procesos de dependencia y de heterogeneidad espacial simultáneamente, mientras que las técnicas no paramétricas tienen que trabajar con distribuciones condicionales (condicionamiento). Sin embargo, ambos son enfoques que con mayor frecuencia se complementan en la investigación. El primero refiere al núcleo de instrumentos "duros" del llamado análisis confirmatorio de datos y el segundo enfoque con instrumentos propios de un análisis exploratorio de datos espaciales (Tukey, 1980; Anselin, 1996). La recomendación metodológica de "consenso" consiste simplemente en: 1) empezar con un análisis exploratorio de datos espaciales para describir distribuciones espaciales, detectar patrones espaciales de asociación global y local, sugerir la presencia de regímenes espaciales (clubes) y otras formas de heterogeneidad espacial necesarias para elaborar conjeturas o hipótesis preliminares, y después 2) usar métodos paramétricos para estimar modelos que incorporan efectos de dependencia y heterogeneidad espaciales, más robustos en las pruebas de hipótesis y propios de un análisis confirmatorio de datos (Anselin, 1988). En esta sección se realiza, fundamentalmente, un análisis exploratorio de datos espaciales que consiste de:

1) un análisis clásico de autocorrelación espacial (global y local), usando el estadístico de Moran y su gráfico de dispersión para visualizar patrones de asociación espacial e inestabilidad o heterogeneidad espacial (Anselin, 1996); y

2) un análisis de condicionamiento particular mediante un filtrado espacial, que "separa" o condiciona mediante una medida de correlación espacial local (Fischer y Stumpner, 2008).

Este condicionamiento es específico en tanto que busca remover la autocorrelación espacial (esencialmente local) aunque sea insuficiente para eliminar a plenitud los efectos perturbadores debido a la dependencia espacial.²⁴

 

Autocorrelación y heterogeneidad espaciales

Como en un tratamiento paramétrico, el enfoque metodológico para el análisis empírico sigue la recomendación de Anselin (1990) de siempre realizar primero una prueba de detección de autocorrelación espacial y después proceder a la identificación de los diferentes regímenes o clubes (heterogeneidad) mediante la instrumentación del Indice de Moran.²⁵

Para nuestra aplicación la evidencia de autocorrelación espacial es positiva y significativa,²⁶ pues los estadísticos para las cuatro distintas fechas (valores p) son numéricamente despreciables. Esto sugiere que la distribución del ingreso regional es aglomerada, es decir, regiones con alto ingreso se localizan cerca de sus regiones similares con más frecuencia que si las localizaciones fueran estrictamente aleatorias.

Más aún los resultados son robustos en el sentido de la selección de la matriz de pesos espaciales, para todos los arreglos el índice local es creciente hasta 1998 y decreciente en el último quinquenio (Cuadro 3 y Figura 8).

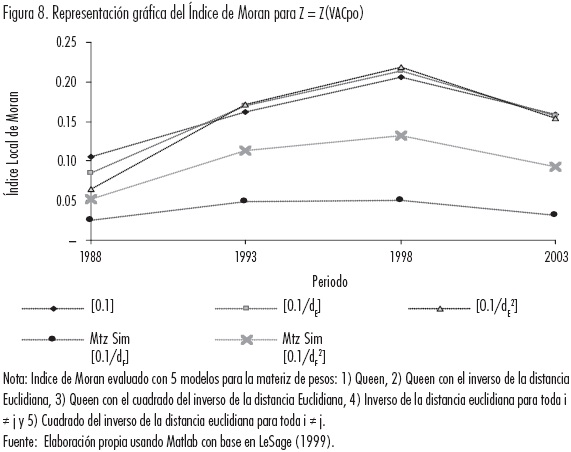
Posteriormente mediante una gráfica de Moran se examina la inestabilidad espacial en la forma de regímenes (Anselin, 1996).

La serie de Figuras 9.a-d muestra las gráficas de Moran con una W seleccionada, para la variable transformada logarítmicamente, revelando lo siguiente: no son dominantes los aglomerados ubicados en AA y BB pero es significativa la autocorrelación positiva entre ellos. Esto parece ser así porque los grupos de regiones pobres con regiones vecinas ricas y los grupos de regiones ricas con regiones vecinas pobres (BA y AB) en número no son despreciables y sugiere también la presencia de fuerte heterogeneidad espacial en los municipios de la RCM, de tal manera que, si existen procesos de convergencia, éstos pueden ser diferentes a través de los clubes identificados. Entonces, están presentes la autocorrelación y la heterogeneidad espaciales y es posible cuantificar la primera pero de la segunda, mediante este enfoque, sólo puede ser sugerida. Más aún, la polarización parece ser persistente en el periodo completo ya que la composición de los clubes parece que permanece globalmente inalterada. La gráfica de Moran es siempre un buen inicio, muy ilustrativo de las interrelaciones complejas entre dependencia y heterogeneidad en la forma de regímenes espaciales; no obstante, la detección de los diferentes regímenes o clubes debería ser endógena y esta discusión está más allá del alcance de este ensayo.

Una manera útil de valorar si la regresión lineal es una aproximación adecuada al patrón de dependencia espacial en los datos, se puede realizar mediante una regresión local robusta, tal como un lowess (locally weighted scatterplot smoother). Un patrón no lineal diferente, que alterna patrones de asociación positiva y negativa, o que muestra claramente las pendientes diferentes en todos los smoother, que evidencian lo inadecuado de una medida global única para la asociación espacial. Cuando las pendientes distintas pueden asociarse con observaciones aglomeradas espacialmente, sugieren la presencia de regímenes espaciales diferentes o heterogeneidad espacial (ver gráficas superior-derecha en Figuras 10.a y 10.b).

Las Figuras 10.a y 10.b muestran las gráficas del índice de Moran global y el ajuste local a lo largo de y y las vecindades Wy para 1988 y 2003, respectivamente. Es clara la relación entre aumento de autocorrelación local conforme aumenta el nivel de ingresos regionales en 1988 y 2003, y una mucho más baja capacidad de aglomerar de las regiones con bajos ingresos; este comportamiento se acentúa con el aumento del índice de Moran local en 2003. Con el tratamiento desagregado (municipal) es muy posible que sean dominantes las tres zonas metropolitanas (Ciudad de México, Toluca y Puebla-Tlaxcala) en la determinación de las distancias críticas, las cuales oscilan entre 25 y 32 km.²⁷

El índice Moran local puede interpretarse como un indicador de aglomeración espacial y los clusters locales pueden identificarse mediante un estadístico que sea significativamente diferente de cero. Debido a que la distribución de tal estadístico es usualmente desconocida, Anselin (1995) sugiere el método de Montecarlo para generarla, el cual consiste de una "aleatorización" condicional del vector z, es condicional en el sentido de que z_i es fija.²⁸

Con el análisis que se construye para la variable transformada [XLrel=ln(Z)/µ(ln(Z)] se ha detectado la presencia de autocorrelación espacial (global) e interesa ahora tener alguna idea de su efecto sobre los patrones mostrados en la distribución. Para utilizar la información completa de la muestra, incluyendo las regiones localizadas en los cuadrantes BA y AB, y cuantificar el nivel de autocorrelación local, se procede a instrumentar un filtro espacial y generar una variable filtrada (Z^F, asociada o "sintética"). Puede ser que para algunas series calcular la variable transformada [XLrel=ln(Z)/µ(ln(Z)] primero y después la variable filtrada [XLrel^F] presente algunas diferencias con el procesamiento como se hace aquí (Z^F → X^FLrel); sin embargo, no hay regla en la literatura que resuelva entre ambos.²⁹

 

ADD con condicionamiento por filtrado espacial

La estimación del kernel estocástico descansa en el supuesto de que cada región representa una observación independiente que proporciona información única y útil para estimar la dinámica de transición del ingreso. Esencialmente, las observaciones transversales para cada punto en el tiempo son vistas como una muestra proveniente de una distribución X que se asume aleatoria y univariada. Si las X_i (i = 1, ... ,n) son independientes se dice que no hay estructura espacial. La independencia implica la ausencia de autocorrelación espacial, mientras que presencia de autocorrelación refleja una escasez de independencia entre las regiones. Esta dependencia puede surgir desde problemas de medición, fronteras entre regiones, pero también, de externalidades o interacciones entre ellas tales como difusión del conocimiento, comercio interregional o flujos migratorios o de tipo commuting, todas son fuentes importantes de violación de este supuesto. Por lo que resulta siempre una buena práctica evaluar este aspecto para evitar falsas inferencias e interpretaciones equivocadas.

Una manera de tratar este problema consiste en un filtro para la variable X que permita separar los efectos espaciales de los efectos totales de una variable (Fischer y Stumpner, 2008). Garantizar independencia espacial permite usar un kernel estocástico para estimar adecuadamente la distribución del ingreso regional subyacente y analizar su evolución en el tiempo. El filtro espacial consiste en una transformación de la variable autocorrelacionada espacialmente en una variable independiente por remoción de la dependencia espacial incorporada en ella.³⁰ La variable original X se descompone en una variable no espacial filtrada y una variable espacial residual (L_X). Así, la diferencia entre las observaciones (sin y con filtro), , representa el componente espacial asociado, pero no correlacionado con la variable X, por lo tanto: . En consecuencia, la variable filtrada debe ser interpretada como aquella parte del ingreso por trabajador de una región que no es explicada por los efectos spillover (Maza y Villaverde, 2008) o cierto tipo de interacciones espaciales entre regiones vecinas que no son las propias a la heterogeneidad espacial (diferencias de estructuras económicas) dentro del sistema de regiones.

El procedimiento de transformación depende de identificar una distancia apropiada (δ) dentro de la cual regiones vecinas son dependientes espacialmente, y examinar cada observación individual por su contribución a la dependencia espacial incorporada en la variable original (Getis y Griffith, 2002). Hay varias posibilidades para identificar δ, pero usaremos el filtro de Getis el cual se basa en el estadístico G_i (Fischer y Getis, 2010) que se evalúa para una serie creciente de distancias hasta que ya no sea evidente la presencia de autocorrelación espacial. Conforme aumenta la distancia desde una observación (región-i) si hay dependencia espacial el valor de G aumenta hasta un punto a partir del cual empieza a descender, cuando se alcanza el límite asumido para la autocorrelación, se identifica un δ-crítico asociado. La observación filtrada se define entonces por:

donde la x_i es la observación del ingreso original para la región-i con como el valor esperado; además conocido el valor δ, se define

con .³¹ Ahora se define el estadístico de autocorrelación espacial local de Getis y Ord como:

donde el numerador es la suma de todas las x_j dentro de δ, pero sin incluir x_i; el denominador es la suma de todas las x_j sin incluir x_i Este estadístico propiamente está midiendo el efecto de la vecindad ('aglomeración'), cuando el cálculo incluye a i (G* (δ)).

La ecuación (5) compara el valor observado de G_i(δ) con su valor esperado, que es E[G_i(δ)]=(n-1)^-1W_i. El valor esperado representa la realización de la variable X en la región-i cuando no hay autocorrelación; si éste es el caso, para la distancia δ entonces los valores observado x_i y esperado de serán iguales. Cuando G_i(δ) es relativamente alto respecto a su valor esperado, la diferencia será positiva indicando autocorrelación espacial entre las observaciones con valores altos. Cuando G¡(δ) es relativamente bajo respecto a su valor esperado, la diferencia será negativa indicando autocorrelación espacial entre las observaciones con valores bajos. Tal diferencia representa el componente espacial de la variable X en i, L_X, una variable espacial asociada no correlacionada con la variable X de tal manera que (Getis y Griffith, 2002).

El factor de filtrado E[G_i(d)]/G_i(d) disminuye el valor de x_i si la mayoría de las observaciones x_j, dentro de la vecindad d_ij ≤ dde x_i, se localizan arriba del promedio, y aumenta x_i si las observaciones están abajo del promedio. Esta transformación es un "contrapeso" a la aglomeración de datos abajo y arriba del promedio, por ende corrige por autocorrelación espacial positiva.

Combinando el procedimiento de filtrado anterior con la estimación del kernel estocástico antes descrito se puede generar una densidad de largo plazo (ergódica, 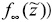implicada por la función ) estimada: . Donde y denotan las observaciones de Y y Z filtradas espacialmente. Para evaluar la influencia del espacio sobre el crecimiento del ingreso y la dinámica de la convergencia a través de las regiones, se considera un kernel estocástico específico que mapea la distribución Y a la distribución filtrada espacialmente mediante: . Donde el kernel estocástico no describe transiciones en el tiempo, sino transiciones desde una distribución del ingreso regional no-filtrada a una filtrada espacialmente y, así cuantificar los efectos de la dependencia espacial. Si tales efectos de interacción entre regiones no importan, entonces el kernel estocástico sería un mapeo identidad. Otro enfoque de filtrado emplea la descomposición de una eigen-función basada en la matriz de distancia usada para calcular el estadístico I-Moran. Sin embargo, ambos enfoques son efectivos y llegan aproximadamente a conclusiones similares (Getis y Griffith, 2002). Un enfoque completamente diferente de filtrado es el empleado por Quah (1997) y Basile (2007).

 

Interpretación de los resultados del filtrado espacial

El cálculo de las distancias críticas (en km) requeridas para el filtro espacial de la variable sin y con transformación (ver Cuadro 4) arroja resultados congruentes con lo antes expuesto: aumenta el valor del índice Moran con la transformación y disminuye la distancia crítica (cálculos que se llevaron a cabo con las rutinas de Ferstl, 2007).³²

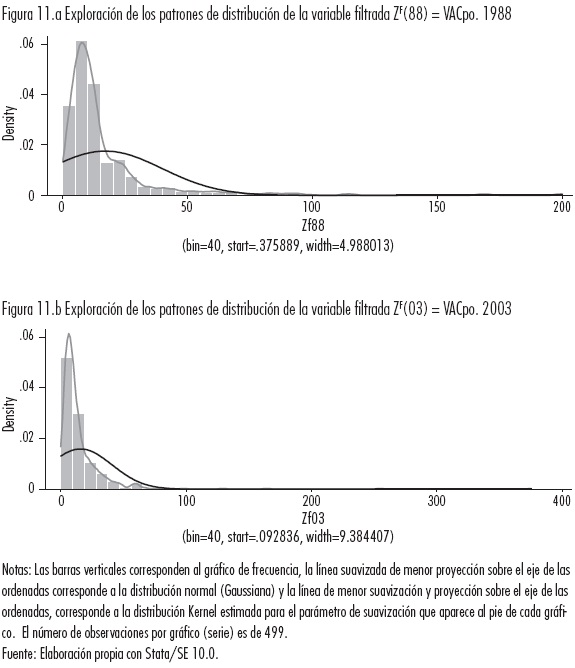
Para visualizar el efecto del filtro espacial, en las Figuras 11.a y 11.b se muestran los patrones de distribución de la variable filtrada, que comparan con los mostrados en las Figuras 1.a y 1.b para la variable sin filtrar: podrá observarse cambios en las formas de las distribuciones empíricas que, por ligeros que parezcan —visualmente— sugieren procesos de movilidad intra-distributiva.

El efecto de la transformación y el filtrado de la variable original (o "cruda") se visualiza claramente en los gráficos de caja (ver Figuras 12.a y 12.b); aunque no resulte evidente visualmente el cambio entre la variable transformada sin y con filtro espacial para la RCM (comparar Figuras 4.b y 12.b).

Por otra parte, en las Figuras 13.a y 13.b se muestra —para la variable filtrada y transformada—, las distribuciones estimadas con parámetros de suavización óptimos (para cada serie) y para el promedio de éstos, donde el efecto conjunto de la transformación y el filtro es perceptible, aunque el debido al filtro sugiera ser muy débil.

Esto se confirma con la serie de Figuras 14.a, 14.b, 14.c, 14.d, en particular con las curvas de nivel, en tanto que no se observan cambios sustantivos del patrón en la distribución estocástica de los datos.

Si la variable filtrada debe ser interpretada como aquella parte del ingreso por trabajador de una región, toda vez aislados los efectos spillover o de interacción espacial de las regiones vecinas (Maza y Villaverde, 2008), se considera entonces que el filtro tiene el efecto de mostrar de manera más transparente la información relativa a la estructura de los datos o de heterogeneidad espacial. En suma, se sostiene que de un patrón con evidencia de convergencia y alta movilidad en los valores bajos y altos, este se transforma (invierte) a un patrón con alta persistencia en toda la distribución y presencia de clubes a lo largo de la diagonal, que sustentan la existencia de una estructura regional estratificada, pero no de polarización extrema.

 

Conclusiones

El estudio se inserta en el llamado análisis empírico del crecimiento económico, muy bien documentado en Durlauf y Quah (1999), Temple (1999) y Durlauf et al (2005). Aunque las técnicas de medición de procesos de dinámica regional y los desarrollos en la teoría económica (espacial) no avanzan en paralelo, indudable es que las nuevas técnicas computacionales de cuantificación han impactado significativamente la manera de construir modelos empíricos con fundamento en la teoría. Precisamente es la teoría en sus múltiples expresiones, dominante y heterodoxa, la que más se ha beneficiado al disponer ahora de instrumentos analíticos más potentes para describir y elaborar pruebas de hipótesis derivadas de ella.

Una comprensión aceptable de los procesos de dinámica regional requiere entonces, tanto de la revisión de la teoría del crecimiento como del empleo de las nuevas formas de cuantificar estos procesos de cambio espacio-temporales, para fundamentar mejor decisiones de política pública. Un ADD como el ofrecido, en este artículo, aporta en esta dirección. Sobre todo cuando el ámbito de las políticas públicas son las de corte regional, porque tienen como foco principal el incidir sobre fenómenos económico-sociales complejos y difíciles de medir como los asociados a las disparidades regionales.

Es indudable que los métodos más robustos de investigación están aún asociados a la construcción de modelos de especificación paramétrica y conforman el llamado análisis confirmatorio de datos. Sin embargo, es cada vez más frecuente encontrar en la literatura una recomendación metodológica importante, que consiste en complementar siempre toda investigación regional con un buen análisis exploratorio de datos espaciales, mediante técnicas no paramétricas, que ayude a la especificación inicial de una propuesta paramétrica. Aunque como se ha mostrado, un ADD es más que un ejercicio necesario que ofrece información sustantiva para evitar errores en la especificación de modelos "definitivos".

Si como los resultados sugieren, existe un patrón que estadísticamente muestra heterogeneidad espacial persistente como soporte para elaborar el correlato económico de polarización regional, entonces una recomendación factible sería la elaboración de un modelo en cuya especificación esté presente un tratamiento adecuado para los subgrupos de regiones: sobre alguna de las perspectivas de investigación empírica futura, Durlauf (2003) sostiene que el análisis econométrico estándar no trata adecuadamente la heterogeneidad, por lo que se debería prestar menos atención al establecimiento de ajustes ad hoc en los modelos lineales de crecimiento y dirigir los esfuerzos principalmente a la identificación de subgrupos de economías que puedan ser descritas de manera aceptable por un modelo lineal común. Una vez obtenidas estas agrupaciones, un segundo paso natural sería el análisis de los factores que explican por qué una unidad de observación en concreto forma parte de una agrupación determinada.³³

 

Agradecimientos

Los autores agradecen los valiosos comentarios de los evaluadores anónimos, con los cuales fue posible mejorar de manera importante la estructura del proyecto de investigación en el que se inserta este ensayo. Asimismo, agradecen a Robert Ferstl (Vienna University of Economics and Business Administration) el incondicional apoyo para el uso de las rutinas instrumentadas en Matlab, dirigidas a lograr el filtro espacial de la variable de estudio.

 

Bibliografía

Anselin, L., "Spatial Dependence and Spatial Structural Instability in Applied Regression Analysis", en Journal of Regional Science 30, 1990, pp. 185-207.         [ Links ]

----------, "The Moran Scatterplot as an ESDA Tool to Assess Local Instability in Spatial Association" en Fisher, M., H. J. Scholten, and D. Unwin (coords.), Spatial Analytical Perspectives on GIS, London UK, Taylor & Francis, Cap 8, 1996, pp. 121-138.         [ Links ]

----------, "Spatial Econometrics", en Baltagi, B. H. (coord.), A Companion to Theoretical Econometrics , Oxford UK, Blackwell Publishing Ltd., Cap. 14, 2001, pp. 310-330.         [ Links ]

----------, Spatial Econometrics: Methods and Models, Dordrecht, the Netherlands: Kluwer Academic Publishers, 1988.         [ Links ]

----------, "Local Indicators of Spatial Association (LISA)", en Geographical Analysis 27, 1995, pp. 93-115.         [ Links ]

Arbia, G., R. Basile, y G. Piras, "Analyzing Intra-distribution Dynamics: a Reappraisal", Discussion Paper REAL 05-T-11, The Regional Economics Applications Laboratory, University of Illinois, December 2005.         [ Links ]

Aroca, P., M. Bosch y W Maloney, "Spatial Dimensions of Trade Liberalization and Economic Convergence: Mexico 1985-2002", en The World Bank Economic Review, vol 19, num. 3, 2005, pp. 345-378.         [ Links ]

Barro, R. J. y X. Sala-i-Martin, Economic Growth, The MIT Press, Cambridge, Massachusetts (2^nd Ed.), 1995.         [ Links ]

----------, "Convergence", en Journal of Political Economy, 100 (2), 1992, pp. 223-251.         [ Links ]

Basile, R., "Intra-distribution Dynamics of Regional per-capita Income in Europe: Evidence from Alternative Conditional Density Estimators", Working Paper num. 75, Istituto di Studi e Analisi Economica, Rome, January 2007.         [ Links ]

Bianchi, M., "Testing for Convergence: Evidence from Non-Parametric Multimodality Tests", en Journal of Applied Econometrics, Vol. 12, 1997, pp. 393-409.         [ Links ]

Borrayo, R. y J. M., Castañeda, "Análisis de dinámica distributiva (ADD): una aplicación a la región centro de México (RCM, 1988-2003)", en Quintana, L., A. Roldán y R. Vela (coords.), Técnicas modernas de análisis económico espacio-regional, México, Cap. 5, 2010, pp. 1-132, (en dictamen).         [ Links ]

Bowman, A. W., and A. Azzalini, Applied Smoothing Techniques for Data Analysis, Oxford University Press, New York, 1997.         [ Links ]

Bulli, S., "Distribution Dynamics and Cross-Country Convergence: A New Aprroach", en Scottish Journal of Political Economy, Vol. 48, num. 2, May 2001, pp. 226-243.         [ Links ]

Cermeño, R., "Decrecimiento y convergencia de los estados mexicanos. Un análisis de panel", en El Trimestre Económico, vol. LXVIII, núm. 272, 2001, pp. 603-629.         [ Links ]

Chiquiar D., "Why Mexico's Regional Income Convergence Broke Down", en Journal of Development Economics , 77, 2005, pp. 257-275.         [ Links ]

Durlauf, S. N., "La hipótesis de convergencia 10 años después", en C L M. Economía, núm. 2 , Primer Semestre de 2003, pp. 55-74.         [ Links ]

Durlauf, S. N. y D. Quah., "The New Empirics of Economic Growth", en Taylor, J. y M. Woodford (coords), Handbook of Macroeconomics, Amsterdam, North-Holland, Elsevier, Vol. 1A, Parte 1, Cap. 4, 1999, pp. 235-308.         [ Links ]

Durlauf, S., P. Johnson, y J- Temple, "Growth Econometrics", en Aghion, P. y S. N. Durlauf, (coords), Handbook of Economic Growth, Amsterdam, North-Holland, Elsevier, Vol. 1A, Cap 8, 2005, pp. 555-677.         [ Links ]

Ertur, C, J. Le Gallo y C. Baumont, "The European Regional Convergence Process, 1980-1995: Do Spatial Regimen and Spatial Dependence Matter?", en International Regional Science Review, 29, 1, 2006, pp. 3-34.         [ Links ]

Esquivel, G., "Convergencia regional en México, 1940-1995", en El Trimestre Económico, vol. LXVI, núm.264, 1999, pp. 725-761.         [ Links ]

Ferstl, R., "Spatial Filtering with EViews and MATLAB", en Austrian Journal of Statistics, Vol. 36, num. 1, 2007, pp. 17-26.         [ Links ]

Fischer, M. y A. Getis (cords.), Handbook of Applied Spatial Analysis: Software Tools, Methods and Applications, Springer-Verlag Berlin Heidelberg, 2010.         [ Links ]

Fischer, M. M. y P. Stumpner, "Income Distribution Dynamics and Crossregion Convergence in Europe. Spatial Filtering and Novel Stochastic Kernel Representations", en J Geograph Syst 10, 2008, pp. 109-139.         [ Links ]

García-Verdú, R., "Income, Mortality, and Literacy Distribution Dynamics Across States in México: 1940-2000", en Cuadernos de Economía, vol. 42, mayo 2005, pp. 165-192.         [ Links ]

Getis, A. y D.A.Griffith, "Comparative Spatial Filtering in Regression Analysis", en Geographical Analysis, 34(2), 2002, pp. 130-140.         [ Links ]

Hyndman, R. J., "Computing and Graphing Highest Density Regions", en The American Statistician, Vol. 50, num. 2, 1996, pp. 120-126.         [ Links ]

Islam, N., "What Have we Learnt from the Convergence Debate?" en Journal of Economic Surveys, Vol. 17, num. 3, 2003, pp. 310-362.         [ Links ]

Johnson, P. A., "A Continuous State Space Approach to Convergence by Parts", en Economics Letters, 86(3), March 2005, pp. 317-321.         [ Links ]

LeSage, J. P., "Applied Econometrics Using MATLAB", en Econometrics Toolbox, 1999, http://www.econ.utoledo.edu.         [ Links ]

Magrini, S., "The Evolution of Income Disparities Among the Regions of the European Union", en Regional Science and Urban Economics, 29(2), 1999, pp. 257-281.         [ Links ]

----------, "Analysing Convergence Through the Distribution Dynamics Approach: Why and How?", en Working Paper Department of Economics (2007) num. 13 /WP/2007, Ca' Foscari University of Venice, Italy.         [ Links ]

Maza, A. y J. Villaverde, "Spatial Effects on Provincial Convergence and Income Distribution in Spain: 1985-2003", en Tijdschrift voor Economische en Sociale Geografie, Vol. 100, num. 3, Royal Dutch Geographical Society KNAG; 2009, pp. 316-331.         [ Links ]

McKelvey, R.D., W. Zavoina, "A Statistical Model for the Analysis of Ordinal Level Dependent Variables", en Journal of Mathematical Sociology 4, 1975, pp. 103-120.         [ Links ]

Mendoza, M. A., "La dinámica económica regional en México: 1940-2002", en Territorio y Economía, núm. 7, otoño, 2004.         [ Links ]

Pedroza, J., A. Sánchez y M. A. Mendoza, "Convergencia hacia la economía regional líder en México: un análisis de cointegración en panel", en El Trimestre Económico, Vol. LXXVI (2), núm. 302, abril-junio de 2009, pp. 407-431.         [ Links ]

Phillips, P.C., D. Sul, "Transition Modeling and Econometric Convergence Tests", en Econometrica, 75 (6), 2007, pp. 1771-1855.         [ Links ]

Quah D., "Empirical Cross-section Dynamics in Economic Growth", en European Economic Review 37 (2-3), 1993, pp. 426-434.         [ Links ]

----------, "Regional Convergence Clusters Across Europe", en European Economic Review, 40(3-5), 1996a, pp. 951-958.         [ Links ]

----------, "Empirics for Economic Growth and Convergence", en European Economic Review, 40(6), 1996b, pp. 1353-1375.         [ Links ]

----------, "Empirics for Growth and Distribution: Stratification, Polarization, and Convergence Clubs", en JEcon Growth 2(1), 1997, pp, 27-59.         [ Links ]

Rey, S. J., "Spatial Empirics for Economic Growth and Convergence", en Geographical Analysis, 33(3), 2001, pp. 195-214.         [ Links ]

Rey, S. J. y M. V. Janikas, "Regional Convergence, Inequality and Space", en Journal of Economic Geography, 5(2), 2005, pp. 155-176.         [ Links ]

Stokey, N. y Robert E. Lucas Jr., Recursive Methods in Economic Dynamics, Harvard University Press, Cambridge, MA,1989.         [ Links ]

Temple, J., "The New Growth Evidence", en Journal of Economic Literature, 37, 1999, pp. 112-156.         [ Links ]

Tukey, J. W., "We Need Both Exploratory and Confirmatory", en The American Statistician, Vol. 34, num. 1, Feb., 1980, pp. 23-25.         [ Links ]

Valdivia, L. M., "Desigualdad regional en el centro de México. Una exploración espacial de la productividad en el nivel municipal durante el periodo 1988-2003", en Investigaciones Regionales, 13, 2008, pp. 5-34.         [ Links ]

 

Notas

¹ En sus tres vertientes: neoclásica, endógena y más recientemente, nueva geografía económica.

² Un enfoque alternativo y complementario que permite abordar procesos dinámicos insuficientemente tratados por las técnicas econométricas, tales como: aglomeración, estratificación y polarización regional.

³ La unidad de observación es el municipio, pero a lo largo del texto se denominará "región".

⁴ Trabajos representativos de este tipo son: Esquivel, 1999; Cermeño, 2001; Mendoza, 2004; Chiquiar, 2005. En una breve síntesis de resultados, para una desagregación de datos a nivel estatal, la mayoría de los estudios documentados y analizados en estos trabajos han encontrado que en el periodo 1970-2004 no existe la suficiente evidencia sobre un proceso de convergencia; sin embargo, hay consenso que para el subperiodo 1970-1985 existe un proceso de convergencia sigma y beta absoluta, mientras que para el periodo 1985-2004 todo indica que existe un proceso de divergencia absoluta (Pedroza et al, 2009).

⁵ En general, en un ADD las entidades de estudio (unidades observadas) pueden ser agentes individuales tales como: consumidores, empresas u hogares (microdatos) o corresponder a espacios económicos de escala global, nacional o regional (macrodatos).

⁶ En la base de este enfoque está una ecuación en diferencias estocástica cuyo desarrollo teórico proviene de Stokey y Lucas (1989); para mayores detalles y exposición formal véase Quah (1996a, 1997) y Durlauf y Quah (1999).

⁷ En lugar de suponer un modelo paramétrico para la distribución (v. gr. una distribución normal con esperanza y varianza desconocidas), sólo se asume que la densidad existe y es posible "alisarla" de forma adecuada (diferenciable).

⁸ Si representamos por {X(t):t≥0} un proceso estocástico con realizaciones {x_i(t)}ⁿ_i=1 o datos del ingreso de las n regiones en el tiempo t, podemos denotar por Fx(t) la distribución de x(t) y mediante ƒ_x(t) una medida de probabilidad asociada a la F_x(t) para simplificar la notación se emplea ƒ_t y F_t respectivamente.

⁹ Si X_t es una variable discreta en el espacio-ingreso, el operador Τ* puede interpretarse en una matriz de probabilidades de transición (markoviana), M, y la Ec. (1) se convierte en: ƒ_t+l = M '_t(ƒ_t). Si además se asume que el mecanismo de transición subyacente es invariante en el tiempo, las matrices M_t pueden promediarse para obtener una matriz M única que describe la dinámica de la distribución discretizada. En general, bajo los dos supuestos expuestos, para s periodos después la Ec. (2) toma la forma siguiente: ƒ_t+1 = (M^s)(ƒ_t). Debido a que el valor propio más grande de la matriz de probabilidad de transición (M) es único, M_s converge a una matriz de transición de rango 1 (Quah, 1996 y 1997). Por lo tanto, todas sus filas deben ser iguales y, más aún, iguales a un vector de probabilidad que cumple con: ƒ_∞ = M ' ƒ_∞. El vector ƒ_∞ es el vector fila ergódico, corresponde al límite de (10) conforme s→∞ y representa el límite de largo plazo de la distribución del ingreso entre las regiones.

¹⁰ Entre las posibilidades metodológicas disponibles están Magrini (1999) adopta un procedimiento que se considera reduce el grado de arbitrariedad en la discretización mediante la selección que minimice el error (cuadrado medio o absoluto integrado) de la aproximación; Bulli (2001) recomienda adoptar un método que denomina de discretización regenerativa, originalmente usado en la literatura de cadenas de Markov Monte Carlo; y Hyndman et al (1996), empleado por Basile (2007), el enfoque de densidades condicionales "apiladas".

¹¹ El estimador de la densidad condicional 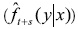se calcula de la siguiente manera: 1) se usa una función kernel que para la distribución conjunta se especifica como un producto de dos kernel univariados (gaussianos):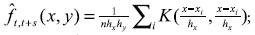donde z_i = (x_i,y_i) es la i-ésima observación de la muestra y z=(x, y) es un punto fijo, las h son los bandwith respectivos; 2) la distribución marginal de x se obtiene por integración numérica con respecto a y de la distribución conjunta: ; y finalmente, 3) la distribución condicional se obtiene dividiendo los estimadores de densidad anteriores, según la ecuación (4). Se emplearon los algoritmos programados por Magrini (2007).

¹² Siempre que exista una ƒ_s(y|x), la densidad de largo plazo (ƒ_∞(y)) puede obtenerse como una solución de:(Johnson, 2004).

¹³ La RCM está delimitada por seis estados: Distrito Federal, Hidalgo, México, Morelos, Puebla y Tlaxcala. Se conforman cuatro series de datos transversales (desagregación municipal) para los años 1988, 1993, 1999 y 2003. Es de señalar también que la selección de la RCM para ilustrar el ADD fue porque los programas utilizados demandan un gran tiempo de procesamiento numérico para el caso nacional en plataforma Windows.

¹⁴ Es sabido que en la investigación empírica sobre crecimiento económico las variables de interés se relativizan por la población para aislar del análisis su tratamiento explícito. Sin embargo, para efectos de un ADD es alta la pertinencia del uso de la población ocupada, es más 'natural' esta forma relativizada, respecto de la absoluta, cuando el interés está en los cambios en la distribución del ingreso

¹⁵ Los censos reportan unidades establecidas (con local fijo), excluyendo las actividades del sector agropecuario y de pesca, aunque contienen una buena representatividad en términos de incluir a las unidades más dinámicas de cada uno de los sectores.

¹⁶ Esta disparidad se acentúa para la muestra nacional a escala municipal, dicho coeficiente es de 3 a 4 órdenes de magnitud (2.45E+03, 7.58E+04, 8.04E+04, 3.28E+03).

¹⁷ Las pruebas de multimodalidad realizadas empleando la técnica descrita en Bianchi (1997), con distribuciones independientes entre los años, documentan la existencia de una moda para las series 1988 y 1993, así como tres modas para los años de 1998 y 2003, ver Borrayo y Castañeda (2010).

¹⁸ Un concepto equivalente a estas curvas, pero más riguroso, es el propuesto por Hyndman (1996) llamado de la región de más alta densidad (o HDR, highest conditional region).

¹⁹ Para identificar patrones son necesarias algunas convenciones, se emplean las sugeridas por Fischer y Stumpner (2008).

²⁰ Sin embargo, es difícil que en la realidad se satisfagan estas restricciones, las regiones tienden a localizarse a diferentes rangos en el espacio-ingreso, los datos más bien presentan agrupamientos que pueden inducir a fallar en la identificación de patrones reales de crecimiento. Por lo que hay razones para buscar técnicas alternativas más robustas.

²¹ Siguiendo a Anselin (2001) la autocorrelación espacial puede definirse como la coincidencia de valores con similitud de localización; esto es, hay autocorrelación positiva cuando valores similares de una variable aleatoria, medida para las diferentes localidades, tiende a aglomerarse en el espacio, por ejemplo, regiones ricas y pobres tienden a agruparse en vecindades geográficas aunque obedecen a causas estructurales distintas. Por heterogeneidad espacial refiere a que las conductas económicas no son estables a través del espacio. En modelos de regresión la heterogeneidad puede reflejarse en la variación de los coeficientes, es decir, la inestabilidad estructural a través del espacio, o mediante cambios en las varianzas de los errores a través de las observaciones, es decir, heterocedasticidad.

²² Sin embargo, la distinción entre la heterogeneidad y la dependencia no es siempre evidente. Hay necesidad de mejorar los procedimientos de búsqueda de especificación entre estos dos efectos espaciales básicos (Rey y Janikas, 2005).

²³ Más aún, en series transversales pueden ser observadas equivalentemente, por ejemplo, en fenómenos de polarización, un cluster espacial de residuales extremos en un centro puede ser interpretado como heterogeneidad entre un centro y una periferia, o como autocorrelación espacial implicada por un proceso estocástico espacial que produce aglomeración de valores en el centro.

²⁴ Otra posibilidad es el condicionamiento general, involucra a variables exógenas (en la jerga del enfoque econométrico) que se asocian usualmente a los llamados determinantes estructurales del crecimiento (Quah 1996b, 1997). El análisis por condicionamiento se entiende como un proceso que normaliza las observaciones de cada uno de los municipios con respecto a un ingreso promedio pesado de los vecinos o de una vecindad definida por un criterio de similitud o equivalente. Este enfoque remite a los esquemas de condicionamiento a la Quah, que es una forma alternativa para evaluar el papel de las interacciones espaciales entre regiones vecinas, requerido para elaborar explicaciones sobre la dinámica de crecimiento regional. En Borrayo y Castañeda (2010) se documenta la aplicación de esta clase de condicionamiento.

²⁵ Definido por la expresión:

donde wij es elemento genérico de la matriz de pesos espaciales para el par de regiones (i, j); es el valor promedio o esperado de la variable x; n el número de observaciones o tamaño de la muestra y definido , Wz es el retardo espacial asociado a la variable x en desviaciones del promedio, en cuya expresión el estadístico I es funcionalmente equivalente a la pendiente de una ecuación de regresión lineal simple de Wz sobre z. Un valor de I grande respecto del valor esperado, E(I) = —1/(n—1) , significa autocorrelación positiva y viceversa.

²⁶ La hipótesis nula que se evalúa es la no existencia de autocorrelación espacial. Para evaluar la significancia estadística, se estandariza el índice y se compara con la distribución normal estandarizada: 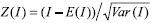donde Z(I) es el 'p-value' con una probabilidad ('prob') reportados en la tabla de la izquierda; esto es, para un nivel de confianza ∞ = 0.05, la hipótesis nula se rechaza para toda 'prob' < ∞/2.

²⁷ Este es un ejercicio que requiere de una evaluación adicional no considerada en este estudio.

²⁸ El razonamiento implícito en este procedimiento está en la necesidad de evaluar la significancia estadística del vínculo entre una región y sus vecindades. Es decir, el estadístico de Moran es calculado entre un estado-i y un gran número de "vecindades" hipotéticas construidas como permutaciones aleatorias de regiones extraídas desde la muestra completa. Entonces, el índice de Moran de la vecindad verdadera es comparada contra su distribución.

²⁹ Para efectos comparativos, se procedió a correr los dos casos y todo indica que, para nuestras series, es prácticamente equivalente transformar y luego filtrar que al contrario —ver Cuadro 4. Sin embargo, debido a que la variable de análisis es la variable cruda Z = VACpo, el proceso se lleva a cabo sobre el ejercicio: Z^F → X^FLrel. Ver detalles en Borrayo y Castañeda (2010).

³⁰ Este procedimiento de filtrado-Getis está diseñado para convertir variables dependientes (x) en variables independientes (filtrada, x^F), de tal manera que la diferencia entre ellas sea una nueva variable que representa los efectos espaciales incorporados en x.

³¹ En la instrumentación del algoritmo, Ferstl (2007) considera para el cálculo de d_ij, la distancia euclidiana a partir de las coordenadas cartesianas de los centroides para los polígonos de cada municipio:

donde (θ,ω) son las coordenadas cartesianas.

³² Esta es la parte de los algoritmos computacionales que más demanda velocidad de procesamiento, por eso el ejercicio originalmente planeado para la escala nacional se redujo a la RCM.

³³ Justo en esta dirección y derivado de este análisis exploratorio de datos, los autores han trabajado en un análisis confirmatorio construido metodológicamente con un procedimiento de dos pasos: i) identificación endógena de clubes de convergencia mediante un algoritmo de agrupamiento con base en una prueba estadística denominada log t (Phillips y Sul, 2007) y ii) una vez realizado el paso (i), se procede con un modelo de regresión logit ordenado (McKelvey y Zavoina, 1975) para analizar el papel que juegan las condiciones iniciales y las características estructurales en la formación de clubes de convergencia para la RCM. Los resultados preliminares confirman la presencia de tres clubes de convergencia para esta región (el borrador del documento, está disponible a solicitud expresa y debidamente justificada).