1. Introducción
La investigación sobre innovación y crecimiento económico ha despertado gran interés en los círculos académicos en las últimas décadas. El vínculo que los une no es fortuito, depende de factores y decisiones que se combinan en el largo plazo para moldear el desarrollo económico. La importancia de la innovación en las sociedades contemporáneas radica en que constituye una estrategia global para aumentar la productividad, la cual, a su vez, eleva el nivel de bienestar. Algunas teorías ven esta asociación como un proceso evolutivo por el que, de alguna manera, transitan las economías (teorías evolutivas); otras subrayan fuerzas exógenas y endógenas al sistema económico sobre las que se puede incidir mediante políticas públicas (teorías clásicas y neoclásicas del crecimiento). También están los argumentos de fuerzas de aglomeración espacial (nueva geografía económica) que modifican esta relación, sobre todo, en ámbitos subnacionales.
La consolidación de un sistema de sociedad creativa trascendió aspectos adicionales vinculados a la economía -institucionales, políticos, marco jurídico y fuerzas de aglomeración (Aghion et al., 2015)-, mientras que la acumulación de factores productivos -efectos spillover, capital humano, gasto en infraestructura, inversión en investigación y desarrollo (I+D) y, finalmente, innovación y cambio tecnológico (Romer, 1986; Lucas, 1988; Barro, 1990; Sala-i-Martin, 2000)- se conjugan para propiciar crecimiento sostenido de largo plazo, ante las necesidades de una población en constante aumento. Es en esta dinámica que resulta crucial que los procesos de innovación compensen los rendimientos decrecientes de los factores productivos, amplíen la frontera de producción y eviten la interrupción del crecimiento.
Una economía innovadora es fundamental en la actualidad (Lucas, 1988; Romer, 1990; Grossman y Helpman, 1991; Aghion y Howitt, 1992), ya que permite desplazar la frontera de producción, a la vez que genera incentivos para la acumulación de capital físico (Romer, 1990). En décadas recientes los países que observaron mayores niveles de innovación y tasas de crecimiento también fueron los que invirtieron más recursos en I+D (Organización para la Cooperación y el Desarrollo Económicos [OCDE], 2015; Ulku, 2004; Hasan y Tucci, 2010; Agénor y Neanidis, 2015), lo que llevó a ampliar las diferencias en producto per cápita, tecnología, capacidad de innovación y niveles de bienestar (Fagerberg et al., 2010; Yanhui et al., 2015).
Los análisis en innovación y crecimiento de la economía mexicana destacan una relación positiva. A nivel de entidades federativas, la evidencia de Mendoza et al. (2008) y Beltrán-Morales et al. (2018) se apoya en un panel de datos; mientras que Guzmán y Gómez (2010) y Guzmán et al. (2012) estudian la relación a largo plazo entre patentes y producción, y concluyen que existe cointegración. Por su parte, Mungaray et al. (2015) y Ríos-Flores y Ocegueda (2018) abordan un índice de capacidad innovadora en un panel dinámico.
En México, el crecimiento económico de los últimos 30 años fue desalentador. En la década de los noventa del siglo pasado, el crecimiento fue por debajo del 1.6%, en promedio anual; en los 2000 fue de sólo 0.12%; mientras que de 2010 a 2017 se ubicó en 1.5%. En 2019 se retrocedió en -0.3% y los pronósticos para 2020 anunciaban una caída todavía mayor.1
En todo esto, ¿qué papel tuvieron la innovación y el gasto en investigación? Los datos señalan que los rendimientos de la innovación (0.67 solicitudes por cada 100 mil habitantes) son muy bajos en relación, por ejemplo, con el promedio de los países miembros de la OCDE (45 solicitudes por cada 100 mil habitantes). Además, el país concentra asimetrías regionales en casi cualquier variable económica y social. Tan sólo en innovación la Ciudad de México promedia poco más de tres patentes por cada 100 mil habitantes, mientras que el estado de Guerrero tiene 0.04.2
El propósito de este análisis es abordar la relación innovación-crecimiento desde un modelo de datos de panel dinámico interregional estimado con la metodología GMM-Sistema propuesta por Arellano y Bond (1991 y 1998) y Blundell y Bond (1998). El panel se integra por 32 observaciones de corte transversal (entidades del país) y 24 temporales, correspondientes a los datos anuales del periodo 1994-2017. El método Arellano-Bond permite seleccionar variables instrumentales que mejoran la precisión de los estimadores, reduce el problema de endogeneidad y controla la correlación serial.
El contexto regional mexicano evoca algunas preguntas de interés como: ¿qué tan importante es la innovación para el crecimiento regional? ¿Tendrá alguna influencia la política pública de apoyo a la innovación (Programa de Estímulos a la Innovación [PEI])? ¿Inciden las diferencias sectoriales en la relación innovación-crecimiento? ¿Habrá diferencias sustantivas entre sectores y regiones del país? La hipótesis que se plantea es que la innovación, vista a través de la acumulación de patentes, incide positivamente en el nivel de ingreso per cápita de las entidades federativas, además, esta asociación se refuerza con los programas públicos de estímulos.
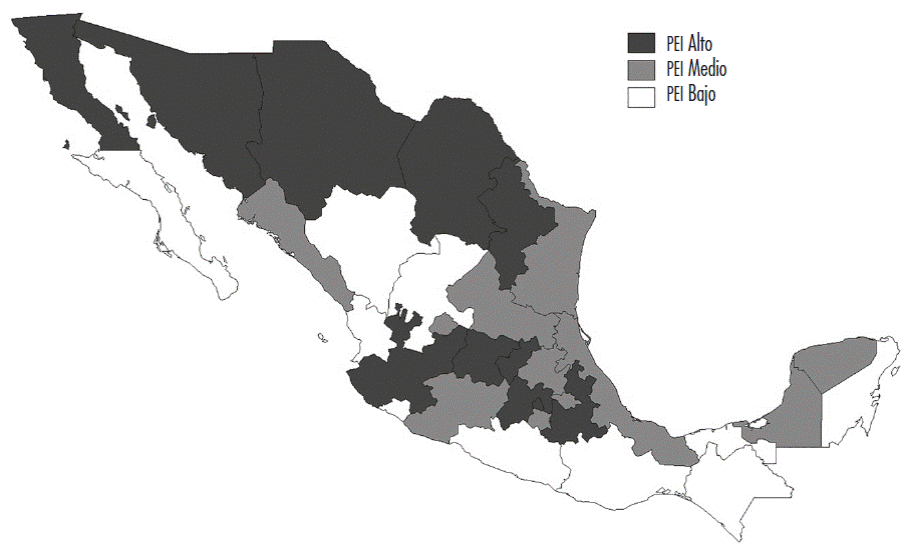
La presente investigación contribuye a la discusión del tema innovación-crecimiento en varias formas. Primero, al usar criterios de regionalización basados en el ejercicio del pei es posible evaluar la eficacia de esta política pública.3 Segundo, el tamaño relativo de los sectores económicos, como criterio de regionalización, permite entender la influencia del peso sectorial en la relación. Tercero, la evidencia descansa en un enfoque de rezagos distribuidos que captan procesos acumulativos de los efectos de las variables. Finalmente, se presenta un modelo teórico cuya ecuación de estimación combina ideas de las teorías del crecimiento evolucionista, clásica y geografía económica.
Los hallazgos subrayan efectos positivos, como predice la teoría, sin embargo, muestran una tendencia gradual a disminuir a partir de la crisis internacional de 2008, lo que es reflejo del componente multinacional del patentamiento mexicano, ya que esta gran depresión se sintió con mayor intensidad en las áreas más globalizadas de las economías. También se encuentra que la política de estímulos a la innovación llevó a reducir las desigualdades regionales, ya que las regiones clasificadas como Sur y PEI-Bajo (por lo general conformadas por entidades federativas económicamente más atrasadas) estiman una elasticidad crecimiento-innovación más elevada en comparación al Centro, Norte, PEI-Medio y PEI-Alto, regiones económicamente más avanzadas.
Con la introducción como primera sección, el documento cuenta con seis secciones más. En la segunda sección se revisa la literatura del tema; en la tercera se expone el marco teórico y metodológico; mientras que en la cuarta se describen los datos y las variables. La quinta sección estima y analiza los resultados y, finalmente, en la sexta sección se concluye.
2. Revisión de literatura
Dos pilares teóricos de la relación innovación-crecimiento son la economía evolucionista y la nueva teoría del crecimiento económico (Acs y Varga, 2002; Antonelli, 2017). La primera sostiene que el crecimiento económico es impulsado por innovaciones, producto de inversiones empresariales incentivadas por la búsqueda de ganancias. Esta teoría también enfatiza aspectos institucionales y político-regionales, así como elementos microeconómicos que impactan el crecimiento económico, incluyendo comportamiento y tamaño de las empresas (Aghion et al., 2015).
Para la teoría evolucionista, la relación tiene implicaciones dinámicas. Se explica a partir de mecanismos sistémicos presentes en el proceso, pero también por la presencia de comportamientos aleatorios que generan o renuevan alguna variación de los factores que inciden en la innovación y el cambio tecnológico (Nelson y Winter, 1982; Dosi y Nelson, 1994, entre otros).
El aspecto evolutivo en el modelo de Aghion y Howitt (1992) descansa en el concepto de "destrucción creativa" sugerido por Schumpeter (1942). El crecimiento económico es resultado del progreso tecnológico y éste, a su vez, es producto de la competencia entre empresas dedicadas a la investigación en innovación. Para Aghion y Howitt (1992), la innovación es un proceso vertical que desplaza tecnología previa y privilegia tecnologías nuevas y mejoradas.
La nueva teoría del crecimiento económico, en cambio, valora los factores productivos de mayor importancia (Sala-i-Martin, 2000). Algunos elementos clave son los efectos spillover del conocimiento que derivan de la inversión física (Romer, 1986), el capital humano (Lucas, 1988), el capital público de infraestructura (Barro, 1990) y el gasto en I+D (Romer, 1990).
Particularmente, en Romer (1990) el crecimiento económico es impulsado por el cambio tecnológico que genera incentivos para la acumulación continua de capital, motivado por las decisiones de maximizar ganancias. De ahí se explica gran parte del incremento de la productividad que conduce al crecimiento. Romer (1990) se basa en una visión horizontal de la innovación, la tecnología existente no desaparece, sino que se suma a los inventos que paulatinamente se van introduciendo al mercado. Al considerar la no rivalidad de las ideas, el modelo se adentra en el terreno de los rendimientos crecientes a escala, priorizando la competencia monopolística.
Tanto Romer (1990) como Aghion y Howitt (1992) sitúan la inversión en I+D como el factor determinante de la innovación y, consecuentemente, del crecimiento económico sostenido. El gasto acumulado y las mejoras tecnológicas amplían el stock disponible para realizar otras innovaciones (Romer, 1990; Stokey, 1995), lo que genera spillovers que benefician no sólo a quienes generan innovación, sino también al resto de agentes productivos, al igual que en Griliches (1990).
Aún lejos de la frontera tecnológica, la innovación puede impulsar el crecimiento en regiones y países en desarrollo (Fagerberg et al., 2010), además, comprender ampliamente las opciones innovadoras que ayudan al crecimiento de las economías emergentes (Ahlstrom, 2015).
La evidencia empírica reciente que confirma estas ideas es abundante, tanto internacional como regionalmente. Bilbao-Osorio y Rodríguez-Pose (2004) analizan dicha conexión en una muestra de países de la Unión Europea. La innovación, medida como el número de solicitudes de patentes por cada millón de habitantes, genera efectos positivos que varían en función del nivel de desarrollo de los países. Igual resultado demostró Ulku (2004) en dos ejercicios sobre países miembros y no miembros de la OCDE. A partir de un modelo de panel dinámico estimado por el método general de momentos (GMM) de Arellano-Bond, para el periodo 1981-1997, la autora encuentra que las innovaciones (solicitudes de patentes) tienen impactos positivos en el PIB per cápita de ambas muestras. Entre los resultados destaca que el tamaño del mercado y el nivel de ingreso se asocian positivamente con la innovación. Al centrar la hipótesis en cuatro sectores de la manufactura, en 17 países de la OCDE (México incluido), Ulku (2007) llega a resultados similares.
Por su parte, Rodríguez-Pose y Crescenzi (2008) encuentran elasticidades positivas entre la tasa de crecimiento y el gasto en I+D de 15 países de la Unión Europea y concluyen que el PIB per cápita, como indicador del nivel de productividad regional, es más bajo cuanto mayor es la distancia con la frontera tecnológica. Hasan y Tucci (2010) destacan que los países que poseen empresas de mayor calidad de patentes, así como aquellos que las han aumentado, experimentan mayor crecimiento. En Polonia, Hungría y República Checa los efectos son también positivos, aunque de magnitud moderada (Pece et al., 2015), lo mismo que en una muestra de 38 países durante 1981-2008 (Agénor y Neanidis, 2015). Sin embargo, Feki y Mnif (2016) reportan un efecto negativo en el corto plazo que se compensa y se vuelve positivo a largo plazo en un conjunto de 35 naciones en desarrollo.
Los autores Kacprzyk y Doryn (2017), no encuentran impactos significativos entre antiguos y nuevos miembros de la Unión Europea, pero sí un vínculo positivo cuando sólo se considera el grupo de países nuevos, lo que significa que, al estar más alejado del estado estacionario, más fuerte es la relación. El progreso tecnológico es el detonante principal del crecimiento de la productividad en provincias de China, como lo señalan Wu et al. (2017) y Zhou y Luo (2018). La inversión en innovación puede crear mercados nuevos que no sólo son la base para el crecimiento económico sostenido, sino también una forma de lograr prosperidad en los países pobres (Christensen et al., 2019).
Las instituciones también pueden fomentar o reprimir las actividades empresariales productivas y de innovación (Acemoglu y Robinson, 2012; Rodrik et al., 2004, entre otros), impulsar la creación de mercados (Tomizawa et al., 2019) y mejorar las reglas de propiedad intelectual para proteger a los agentes innovadores (Peng et al., 2017). Para Hu (2015), el cambio de imitación tecnológica a innovación de Corea del Sur no fue lineal, se requirieron políticas e instituciones en función de la etapa de desarrollo económico y tecnológico.
La causalidad también ha sido objeto de análisis, ya que puede existir bidi-reccionalidad entre innovación y crecimiento. Maradana et al. (2017 y 2019) utilizan técnicas de cointegración y modelos autorregresivos para sugerir causalidad unidireccional en algunos casos y bidireccional en otros. Avila-Lopez et al. (2019) detectan causalidad bidireccional en varios países de Latinoamérica. No sólo se debe fomentar la innovación, sino también las inversiones que incrementan el nivel de ingreso per cápita.
En México, la hipótesis innovación-crecimiento ha rendido relaciones positivas cuya causalidad va de la primera a la segunda. Gould y Gruben (1995) enfatizan relaciones positivas y sensibles a la estructura de mercado, ya que el vínculo tiende a ser más fuerte en regiones más abiertas y con esquemas robustos de propiedad intelectual. La importancia de la integración comercial también es apoyada en Ríos-Flores y Ocegueda (2018). Mendoza et al. (2008) muestran evidencia positiva, pero moderada desde indicadores regionales. La conexión también es favorable en Torres-Preciado et al. (2014) y se refuerza con la presencia de externalidades positivas de la innovación (medida desde patentes). Mungaray et al. (2015) encuentran impactos positivos desde la capacidad innovadora a ingresos y productividad de las exportaciones de bienes de alta tecnología. Beltrán-Morales et al. (2018) ubican una relación positiva entre la serie nacional de patentes (por ocupado) y el producto per cápita durante 1988-1998.
3. Modelo teórico y ecuación de estimación
Modelo teórico
En la función de producción tradicional, el producto final (Y) se representa como una combinación de insumos que crece a medida que la contribución marginal del capital (F K ) es positiva (Solow, 1956):
con s como la tasa de ahorro, K el capital y L el trabajo. Dado que se asumen rendimientos constantes, la acumulación continua de capital es necesaria para que no decline el nivel de producto. Para ello, es esencial la tecnología (con su actividad de innovación y patentamiento). Las mejoras en la tecnología (A) incentivan la acumulación de capital y producto (Romer, 1990), por lo que ésta debe ser endógena, es decir:
Sin embargo, entender el papel de la tecnología no ha sido sencillo. En algunos casos se ha tratado como dependiente del stock de capital, a través del aprendizaje y la experiencia, al igual que en Arrow (1962); otros la representaron como capital humano, en línea con Lucas (1988); mientras que para Romer (1986) y seguidores se constituye a partir de los esfuerzos de investigación de las empresas por desarrollar conocimiento (tecnología), que luego se vuelve público. Para Romer (1990), el problema radica en considerar la tecnología como un bien público, cuando en realidad se comporta como un bien parcialmente excluible, ya que primero se explota como sistema de patentes para después erigirse en un bien común.
Sin embargo, existen otros factores que deben tomarse en cuenta. Para la nueva geografía económica, la actividad económica se concentra en ciertas regiones, pero no en otras (Krugman, 1993 y 1995); aunque también hay un marco institucional influyendo en el proceso de innovación (eficiencia productiva) (Nelson y Winter, 1982). Aquí, la innovación resulta de la producción o transformación de conocimiento para crear otros productos y procesos, de tal forma que se crean entornos evolutivos; así, la innovación futura depende de la innovación del pasado y de la destrucción creativa (economía schumpeteriana).
Si se asumen efectos aditivos separados sobre el producto para relajar el supuesto de sustitutos perfectos (Romer, 1990), se agregan elementos institucionales y espaciales como la concentración regional y, finalmente, se expresa (2) en forma per cápita:
En la ecuación (3), E captura la eficiencia productiva (marco institucional), la cual cambia de manera lenta, por lo que se asume que es constante; C t representa la concentración económica (procesos de aglomeración), la cual varía en el tiempo; A t es un stock disponible de tecnología (conocimiento tecnológico) con 𝜙 > 0, k t es el stock de capital per capita con γ > 1. La parte entre paréntesis puede pensarse como la productividad que está en función del marco institucional, la aglomeración y las diferencias en tecnología. Si se linealiza la ecuación (3), se agrega el término de error aleatorio (ε) y se define In E= α, entonces:
El producto per cápita es una combinación del nivel de progreso tecnológico, el stock de capital per cápita y los procesos de aglomeración. Debido a los rendimientos decrecientes al capital, las conductas dinámicas de A t y C t son clave en las fluctuaciones del producto per cápita.
Finalmente, para analizar conjuntos de economías el modelo en la ecuación (4) se representa como una estructura de panel y se agregan variables control sobre características específicas:
donde Χ i,t es una matriz de variables control, β j y un vector de coeficientes a ser estimados y 𝜂 i y 𝜑 t son los efectos fijos individuales.
Metodología
Se define un modelo de rezagos distribuidos para probar el planteamiento previo donde, además, se busca tomar en cuenta que los efectos de la innovación podrían acumularse indefinidamente, aunque progresivamente decrecientes, y captar variaciones entre regiones y sectores. La ecuación estándar con una cantidad desconocida de rezagos de las variables explicativas se define como:
donde L es el operador de rezago polinomial. Para superar la condición de una cantidad ilimitada de rezagos, se asume el criterio de Koyck, es decir, los efectos de los rezagos caen de forma geométrica (Greene, 2008). Así, considerando un factor fijo, λ, de reducciones sucesivas en periodos previos:
Restando la ecuación (7) de la (6) y reordenando términos:
Donde
Así, el modelo se puede extender al caso de regresión múltiple de
Dos medidas de interés son el valor medio y la mediana de los rezagos, ya que dan una idea de la velocidad a la cual y responde a un cambio en x (Greene, 2008):
Rezago medio:
Finalmente, expresando la ecuación (9) como una estructura de panel dinámico:
Para resolver problemas de endogeneidad e inconsistencia de las estimaciones, se usa el método GMM-Sistema que contempla rezagos de la variable endógena como instrumentos, ya sea en niveles y/o en diferencias (Arellano y Bond, 1991 y 1998; Blundell y Bond, 1998). La validez de los instrumentos se revisa mediante la prueba de sobreidentificación de Sargan, mientras que la no correlación serial se verifica con las pruebas de orden 1 y 2 sugeridas en Arellano y Bond (1998).
Modelo empírico, variables y fuente de datos
Se mide la innovación con el número de solicitudes de patentes reportado por el IMPI y se estandariza por cada 100 mil habitantes (coeficiente de inventiva). La variable dependiente es el PIB por entidad federativa del Instituto Nacional de Estadística y Geografía (INEGI) y se considera por persona. Los datos de población estatal se obtienen de las proyecciones realizadas por el Consejo Nacional de Población (CONAPO).
El modelo empírico incluye variables como acumulación de capital físico, aglomeración y tamaño relativo de las economías estatales, así como dummies de región y sector de la actividad económica. Como capital acumulado se utiliza el stock de capital industrial estimado en Germán-Soto (2008). A falta de cifras de inversión real por entidad federativa, este indicador es atractivo, ya que es una acumulación de inversiones a precios constantes de los sectores más intensivos en el uso de capital productivo (minería, electricidad, gas y agua, construcción y manufacturas). Como medida de aglomeración se utiliza la densidad de población por kilómetro cuadrado (el área estatal se obtiene del INEGI). Economías más densamente pobladas tienden a elevar los ingresos. Romer (1990), entre otros autores, señala que el modelo se puede ampliar incluyendo alguna medida de capital humano, pero en este caso el uso de indicadores de capital humano resulta insatisfactorio, debido a la colinealidad presente con aglomeración.
Durante el periodo de análisis, la densidad poblacional mantuvo una correlación del 98% con educación, medida como años de escolaridad promedio. Algunos autores encuentran que cuando aumenta el tamaño del mercado (densidad de población), también lo hace la inversión en capital humano (Duranton y Puga, 2004), o que capital humano se correlaciona fuertemente con población (Sedgley y Elmslie, 2001 y 2004). Por lo tanto, la aglomeración, aparte de ser útil en captar características intrínsecas de las economías regionales, también resulta atractiva para inferir sobre el potencial papel del capital humano.4 El tamaño relativo de las economías estatales se mide por el cociente producto estatal a nacional.
Una vez definido el conjunto de indicadores, el modelo empírico final es:
donde PIBpc es el ingreso per cápita, INN es la medida de innovación, AGLO es el índice de aglomeración, SC es el stock de capital y TAM es el tamaño relativo de las economías.
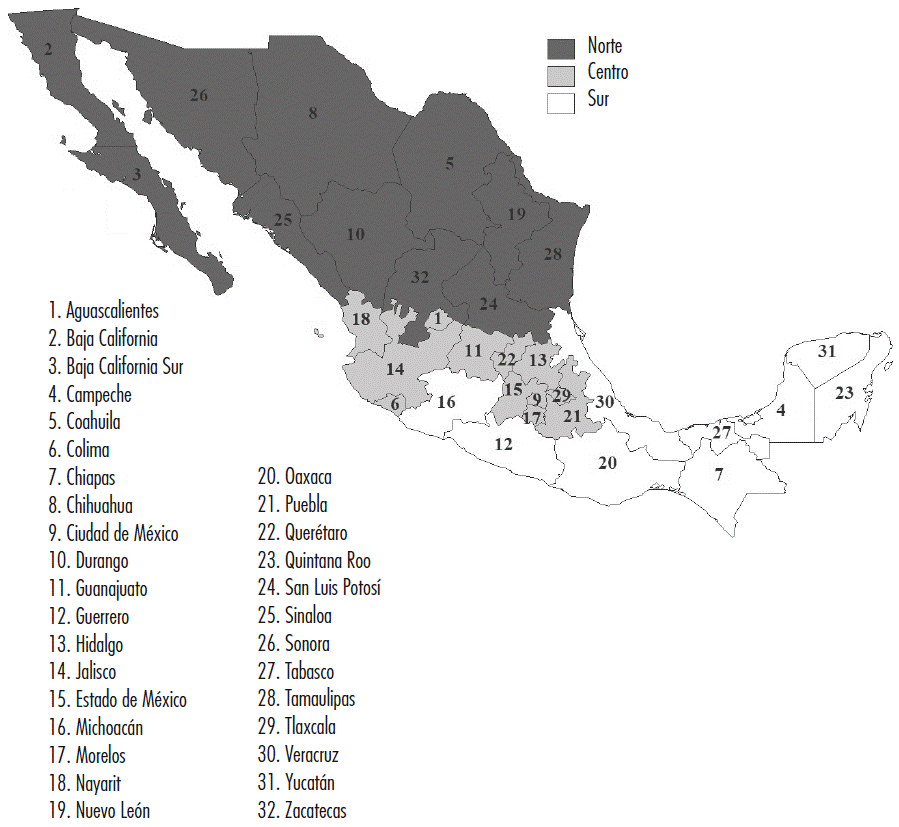
Para captar la evidencia empírica se definen tres criterios de regionalización: nivel de ingreso per cápita (regiones de ingresos altos, medios y bajos), grado de participación en el programa de estímulos a la innovación (regiones con PEI-Alto, PEI-Medio y PEI-Bajo) y ubicación geográfica (tres macro regiones: Norte, Centro y Sur). El criterio de ingresos per cápita se definió a partir del promedio de esta variable entre 2009 y 2017, mientras que para el PEI se midió la intensidad con la que cada entidad federativa participó en el programa de estímulos a la innovación en el mismo periodo. En ambos casos, la idea es tener una clasificación sin el sesgo ocasionado por el desempeño de algún año en particular. En el caso de la regionalización geográfica se siguió, en lo posible, la conformación Norte-Centro-Sur. Las tres clases de regiones se pueden representar en la misma ecuación de regresión, de manera simultánea, para formar un modelo interregional:
donde DUM r es la dummy de la r-ésima región. La ecuación (12) se estima en forma restringida y no restringida, al asumir esta última efectos diferenciales por sector económico (primario, secundario y terciario). La definición de la ecuación (12) permite realizar análisis comparativo interregional, un aspecto crucial cuando se conducen estudios regionales.
4. Análisis estadístico-descriptivo
La generación de patentes por entidad federativa observa un comportamiento asimétrico y concentrado en intervalos inferiores de la distribución (véase Figura 1). En el rango de 1 a 20 solicitudes se ubica 65% de los casos, mientras el nivel superior, mayor a 100, sólo se observa 4.9% de los registros totales.
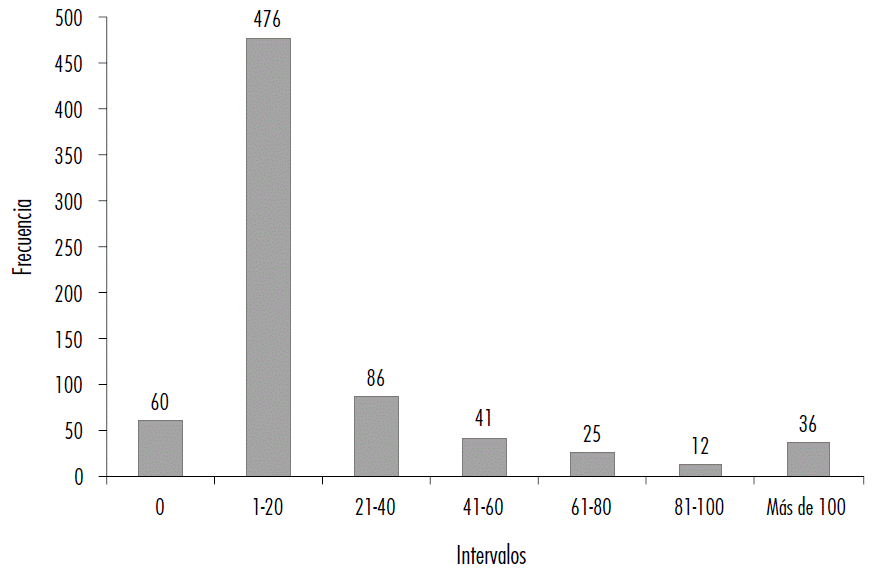
Fuente: elaboración propia con base en información del IMPI (2018).
Figura 1 Distribución de la solicitud de patentes
Mientras tanto, la relación entre patentes por cada 100 mil habitantes y PIB per cápita de 2017, último del periodo de análisis, es positiva, aunque la pendiente no es muy fuerte (véase Figura 2). El acentuado rasgo asimétrico se vuelve más visible con el análisis de las estadísticas básicas (véase Tabla 1). Se destaca la gran distancia entre valores máximos y mínimos. El PIB per cápita estatal promedia la cifra más elevada en el estado de Campeche, de 2003 (MXN$1 413 millones),5 un ingreso similar al de países como Noruega y Finlandia y superior al de Estados Unidos de América.
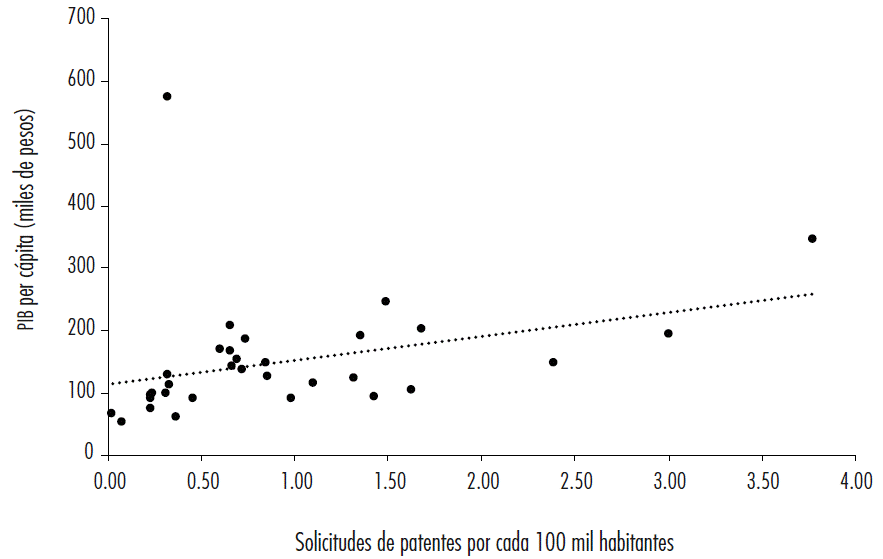
Fuente: elaboración propia con base en información del INEGI (2018) y del IMPI (2018).
Figura 2 Relación entre coeficiente de inventiva y PIB per cápita, 2017
Tabla 1 Estadística descriptiva de las variables básicas, 1994-2017
| Observaciones | Media | Desviación estándar | Valor mínimo | Valor máximo | |
| PIB per cápita (Y) | 736 | 147897 | 180 007 | 49 185 | 1 413 430 |
| Coeficiente de inventiva (INN) | 736 | 5.25 | 7.81 | 0.05 | 66.09 |
| Tamaño de economía (TAM) | 736 | 3.13 | 3.22 | 0.51 | 17.89 |
| Stock capital per cápita (SC) | 736 | 70 278 | 86 985 | 87 094 | 734 545 |
| Densidad de población (AGLO) | 736 | 286 | 1 027 | 5 | 5 993 |
Fuente: elaboración propia.
No obstante, el ingreso de Campeche obedece en gran medida a las actividades de extracción de petróleo, cuyos recursos monetarios no permanecen en la entidad, por lo que un mejor parámetro de comparación es el ingreso per cápita de la Ciudad de México, cuyo valor máximo asciende a MXN$345 558 (millones anuales), monto parecido al de países como Barbados, Lituania y República Eslovaca.
La cifra más baja del panel se observa en el estado de Oaxaca, en 1995 (MXN$49 185 millones), semejante a la de países como Nicaragua o Ghana.6 La densidad poblacional también presenta una varianza grande. La Ciudad de México tiene el valor más alto en 2004, con 5 993 habitantes por km2; mientras el estado con menor densidad es Baja California Sur, con cinco habitantes por km2 en 1994.
En cuanto al tamaño relativo de las economías estatales, el valor más alto lo posee la Ciudad de México, en 1995, al participar con 17.89% de la economía nacional, mientras que el más bajo se atribuye a Colima, en 2005, con 0.51%. En cuanto al stock de capital industrial per cápita se observa que las dos principales entidades petroleras, Campeche y Tabasco, también presentan niveles más altos de todo el periodo. El valor mínimo del stock de capital industrial pertenece a Quintana Roo, en 2017, una entidad con poca industria, pero con clara vocación turística.
En las Figuras 3, 4 y 5 se clasifican los estados del país con base en los criterios de regionalización macro definidos previamente. La concentración de los niveles más elevados de ingreso y recursos ejecutados dentro del PEI se da en el norte del país, la Ciudad de México, Jalisco y Querétaro, principalmente.
5. Resultados
En las estimaciones con GMM-Sistema se aplica la opción de dos etapas.7 Los resultados se presentan en las Tablas 2, 3 y 4. La Tabla 2 constituye un análisis sin regionalizar. Por cada 1% de incremento en el coeficiente de inventiva se genera un aumento de 0.063% de los ingresos. La estimación es estadísticamente significativa y superior a la relación estimada para países de ingreso medio que utilizan una variable de innovación y crecimiento comparables.
Tabla 2 Crecimiento-innovación, resultados desde la muestra absoluta
| Variable | Muestra absoluta | |
| ln(Yt-1) | 0.432 *** | (41.40) |
| ln(INN) | 0.063 *** | (17.20) |
| ln(SC) | 0.030 *** | (12.00) |
| ln(AGLO) | -0.189 *** | (7.15) |
| ln(TAM) | 0.667 *** | (27.60) |
| Dummy de crisis de 2008 | -0.016*** | (17.50) |
| Constante | 6.530 *** | (62.50) |
| Diagnósticos de regresión | ||
| Prueba Sargan | 31.84 | [0.97] |
| Correlación serial (orden 1) | -4.56 *** | [0.00] |
| Correlación serial (orden 2) | 0.18 | [0.86] |
| Efectos de largo plazo | ||
| Mediana de los rezagos | 0.826 | |
| Rezago medio | 0.761 | |
| Elasticidad de la innovación | 0.111 | |
Notas: valores t entre paréntesis y p-values entre corchetes. El superíndice *** indica significancia al 1%.
Fuente: elaboración propia.
Tabla 3 Crecimiento-innovación, resultados del modelo interregional restringido
| Variable/Región | Ingreso | PEI | Geografía | |||
| ln(Yt-1) | 0.441*** | (14.60) | 0.404*** | (20.70) | 0.510*** | (23.10) |
| ln(INN)*D1 | 0.079*** | (3.53) | 0.022 | (0.87) | 0.048 | (1.37) |
| ln(INN)*D2 | 0.049*** | (2.79) | 0.051** | (2.27) | 0.042** | (2.06) |
| ln(INN)*D3 | 0.038*** | (3.98) | 0.053*** | (3.65) | 0.06** | (2.34) |
| ln(TAM)*D1 | 0.590*** | (4.45) | 1.130*** | (5.14) | 0.577*** | (2.93) |
| ln(TAM)*D2 | 0.707*** | (4.13) | 0.806*** | (6.58) | 0.473** | (2.25) |
| ln(TAM)*D3 | 0.615*** | (9.77) | 0.427*** | (6.13) | 0.532*** | (6.72) |
| ln(SC)*D1 | 0.034 | (1.47) | 0.017 | (0.83) | -0.025 | (-0.83) |
| ln(SC)*D2 | -0.023 | (-0.62) | 0.011 | (0.38) | 0.055 | (1.49) |
| ln(SC)*D3 | 0.039** | (2.09) | 0.053*** | (3.68) | 0.029 | (1.32) |
| ln(AGLO)*D1 | -0.371* | (-1.66) | -0.115 | (-0.41) | -0.197 | (-0.36) |
| ln(AGLO)*D2 | -0.080 | (-0.34) | 0.096 | (-0.25) | 0.004 | (0.01) |
| ln(AGLO)*D3 | 0.017 | (0.06) | -0.193 | (-0.72) | -0.396 | (-0.87) |
| Constante | 6.330*** | (15.60) | 6.120*** | (15.40) | 5.770*** | (11.30) |
| Diagnósticos de regresión | ||||||
| Prueba Sargan | 31.64 | [0.97] | 31.32 | [0.95] | 31.29 | [0.94] |
| Correlación serial (orden 1) | -4.66*** | [0.00] | -4.53*** | [0.00] | -4.032*** | [0.00] |
| Correlación serial (orden 2) | -0.108 | [0.91] | 0.193 | [0.85] | 0.534 | [0.59] |
| Efectos de largo plazo | ||||||
| Mediana de los rezagos | 0.847 | 0.765 | 1.029 | |||
| Rezago medio | 0.789 | 0.678 | 1.041 | |||
| Elasticidad de innovación en D1 | 0.141 | n.s. | n.s. | |||
| Elasticidad de innovación en D2 | 0.088 | 0.086 | 0.086 | |||
| Elasticidad de innovación en D3 | 0.068 | 0.089 | 0.122 | |||
Notas: valores t entre paréntesis y p-values entre corchetes. n.s. = "no significativo". Los superíndices ***, ** y * indican significancia al 1, 5 y 10°%, respectivamente. D, para j = 1, 2 y 3 son dummies para las categorías de cada criterio de región usado en el modelo interregional y toman valores de la siguiente manera: D1 = 1para ingreso alto, PEI-Alto, Norte; 0 en otro caso. D2 = 1 para ingreso medio, PEI-Medio, Centro; 0 en otro caso. D3 = 1 para ingreso bajo, PEI-Bajo, Sur; 0 en otro caso. Fuente: elaboración propia.
Tabla 4 Crecimiento-innovación, resultados del modelo interregional no restringido por sector
| Variable/Sector | Primario | Secundario | Terciario | |||
| ln(Yt-1) | 0.430*** | (20.50) | 0.397*** | (11.00) | 0.404*** | (18.80) |
| ln(INN)*D1 | 0.065 | (1.46) | 0.082*** | (4.02) | 0.080** | (2.45) |
| ln(INN)*D2 | 0.064** | (2.40) | 0.069* | (1.77) | 0.085** | (2.15) |
| ln(INN)*D3 | 0.065** | (2.33) | 0.054*** | (2.62) | 0.037*** | (3.47) |
| ln(TAM)*D1 | 0.031 | (1.02) | 0.683*** | (7.98) | -0.002 | (-0.07) |
| ln(TAM)*D2 | -0.086 | (-0.25) | 0.847*** | (2.94) | 0.015 | (0.71) |
| ln(TAM)*D3 | 0.069 | (1.49) | 0.303* | (1.92) | 0.063* | (1.65) |
| ln(SC)*D1 | 0.651*** | (2.70) | 0.070* | (1.72) | 0.875*** | (5.18) |
| ln(SC)*D2 | 0.675*** | (7.48) | -0.007 | (-0.21) | 0.667*** | (7.71) |
| ln(SC)*D3 | 0.654*** | (12.10) | 0.044* | (1.69) | 0.623*** | (9.72) |
| ln(AGLO)*D1 | -0.165 | (-0.28) | -0.393* | (-1.72) | -0.282 | (-0.68) |
| ln(AGLO)*D2 | -0.375 | (-0.63) | -0.386 | (-0.54) | -0.562 | (-1.15) |
| ln(AGLO)*D3 | -0.224 | (-0.58) | 0.007 | (0.02) | -0.022 | (-0.09) |
| Constante | 6.800*** | (13.70) | 7.130*** | (8.53) | 7.210*** | (14.00) |
| Diagnósticos de regresión | ||||||
| Prueba Sargan | 31.30 | [0.97] | 31.10 | [0.96] | 31.60 | [0.95] |
| Correlación serial (orden 1) | -4.42*** | [0.00] | -4.53*** | [0.00] | -4.60*** | [0.00] |
| Correlación serial (orden 2) | 0.36 | [0.72] | 0.19 | [0.85] | 0.21 | [0.83] |
| Efectos de largo plazo | ||||||
| Mediana de los rezagos | 0.821 | 0.750 | 0.765 | |||
| Rezago medio | 0.754 | 0.658 | 0.678 | |||
| Elasticidad de innovación en D1 | n.s. | 0.136 | 0.134 | |||
| Elasticidad de innovación en D2 | 0.112 | 0.114 | 0.143 | |||
| Elasticidad de innovación en D3 | 0.114 | 0.090 | 0.062 | |||
Notas: valores t entre paréntesis y p-values entre corchetes. n.s. = "no significativo". Los superíndices ***, ** y * indican significancia al 1, 5 y 10°%, respectivamente. Definición de regiones, véanse notas de la tabla 3. Fuente: elaboración propia.
Pece et al. (2015) destacan valores de 0.1% (Polonia), 0.5% (República Checa) y 0.6% (Hungría). Para una muestra de 58 países, Hasan y Tucci (2010) estiman una elasticidad de PIB per cápita a patentes cercana a 0.04% en economías de alto y bajo ingreso, mientras que Feki y Mnif (2016) estiman un efecto de 0.02% en 35 países en desarrollo.
Ulku (2004) encuentra que la elasticidad entre solicitudes de patentes y PIB per cápita de varias submuestras de países de la OCDE oscila entre 0.04 y 0.06%; en tanto que estimaciones de Kacprzyk y Doryn (2017), para la zona europea, van de 0.02 a 0.08%, usando definiciones de patentes del sistema EPO, y de 0.003 a 0.12% para las establecidas desde la USPTO.8 Ríos y Castillo (2015) estiman variaciones que van de 0.02% (con patentes) a 0.04% (coeficiente de inventiva) en una muestra conjunta de países desarrollados y en desarrollo. Esta primera aproximación es consistente, tanto con la teoría, como con varios de los estudios de corte nacional e internacional que usan metodologías y variables similares.
En México, Ríos-Flores y Ocegueda (2018) no encuentran significancia desde patentes, pero cuando ensayan con el coeficiente de inventiva obtienen una elasticidad estadísticamente significativa de 0.03%. Al considerar la relación en un modelo interregional, las elasticidades innovación-crecimiento fluctúan entre 0.03 y 0.06%, entre regiones de alto, medio y bajo ingreso, valores muy cercanos a los de este trabajo y que pueden ser comparables al usar técnicas de estimación y regionalización similares. Mungaray et al. (2015) estiman efectos que elevan el PIB per cápita en 0.15% por cada aumento porcentual de la capacidad innovadora de México, valor superior al de países de la OCDE y la Unión Europea. Finalmente, Beltrán-Morales et al. (2018) estiman elasticidades entre 0.03 y 0.05% durante 1998-2008, al usar número de patentes o patentes relativizadas por sueldos y salarios.
El tamaño de la economía y el stock de capital físico también ejercen efectos positivos y significativos sobre los ingresos. Además, la variable dummy sobre la crisis internacional de 2008 resultó negativa y significativa, por lo que este evento ha contribuido en debilitar el crecimiento. Hay que recordar que la innovación que se realiza en México, al igual que en otros países en desarrollo, presenta un fuerte componente multinacional, en la medida que esta actividad es dominada por empresas extranjeras que buscan explotar los rendimientos crecientes que genera una nueva invención. En México, una proporción importante de las patentes (cerca de 90%) es de origen extranjero, por lo tanto, ante una crisis global como la de 2008, se reduce significativamente la actividad multinacional que se ve reflejada en patentamiento y, en consecuencia, las derramas regionales se ven afectadas negativamente.
El modelo no presenta problemas de sobreidentificación (prueba Sargan), es decir, hay una correcta selección de las condiciones de momentos. La prueba Arellano-Bond sostiene que en el segundo orden deja de existir autocorrelación serial, como debe ser. La mediana de los rezagos en la Tabla 2 es 0.87, es decir, 50% del cambio total en el ingreso per cápita se logra en poco menos de un periodo. El valor de rezago medio es de 0.76 y representa un promedio ponderado de los rezagos. Finalmente, el multiplicador de largo plazo de la innovación indica que ante un incremento sostenido del 1% en el coeficiente de inventiva se produce un aumento de 0.11% en el ingreso per cápita estatal.
Las Tablas 3 y 4 reportan la evidencia regional y sectorial. La primera columna de la Tabla 3 corresponde al criterio de regionalización basado en ingresos. La elasticidad innovación-crecimiento más elevada se observa en la región de ingresos altos (0.079%), mientras que el efecto más pequeño se encuentra en la de menor ingreso (0.038%). Esto sugiere efectos jerarquizados por nivel de ingresos.
Los resultados no son muy diferentes a los obtenidos por Hasan y Tucci (2010) a nivel de países, como ya se comentó, pero son más cercanos a los de Ulku (2004) y se encuentran dentro del rango estimado por Kacprzyk y Doryn (2017) para países de la zona europea. Además, al igual que en Ulku (2004), las economías de mayor ingreso mostraron también mayor elasticidad.
La mediana de los rezagos del modelo regionalizado por ingresos es 0.85, muy similar a la estimada para la muestra absoluta (véase Tabla 2). El efecto multiplicador de largo plazo es mayor en la región de ingresos elevados, de 0.14%, un valor ligeramente superior al encontrado para la muestra global.
Los resultados basados en regiones con pei muestran que el efecto de corto plazo de la innovación sobre el ingreso per cápita es muy similar en las regiones PEI-Medio y PEI-Bajo, ligeramente superior al 0.05%. En consecuencia, el multiplicador de largo plazo de estas regiones también es semejante: un incremento sostenido de 1% en el coeficiente de inventiva aumentará en 0.09% el ingreso per cápita de las entidades de estas dos regiones. Los resultados de esta regionalización sugieren que el PEI jugó un papel decisivo en el efecto que tiene la innovación sobre el ingreso estatal, aunque fue no significativo para el grupo de entidades que ejercen más recursos dentro del programa, esto puede suceder porque posiblemente muestran una mayor cercanía a la relación de equilibrio.
En los resultados por región geográfica, la elasticidad entre innovación e ingreso per cápita es mayor en la región Sur (0.06%) que en el Centro (0.042%), mientras en el Norte, aunque más elevada, fue no significativa. Estas diferencias de corto plazo explican que el efecto de largo plazo también es mayor en el Sur (de 0.12%) que en el Centro (0.09%). En sí, las intensidades de elasticidad parecen reflejar la condición de rendimientos decrecientes, cuanto más lejanos del crecimiento potencial, como sería el caso del Sur, existe un efecto mayor.
La hipótesis no restringida sobre diferencias sectoriales (véase Tabla 4) señala efectos no significativos del coeficiente de inventiva sobre el ingreso per cápita de las entidades de mayor tamaño relativo del sector primario, un resultado relacionado al nivel bajo de tecnología que caracteriza a este sector.
Las entidades de tamaño medio y pequeño del sector primario presentan efectos de corto plazo muy similares (0.064 y 0.065, respectivamente), lo que sugiere que el crecimiento económico es menos dependiente de este grupo de actividades productivas. Sin embargo, las entidades con mayor tamaño de los sectores secundario y terciario estiman efectos de innovación más elevados (alrededor del 0.08%) en comparación a las de menor proporción (entre 0.04 y 0.05%). Este mismo resultado comparativo interregional se mantiene en relación con el multiplicador de largo plazo, que se ubica entre 0.06 y 0.14%.
En general, los resultados confirman la mayor importancia que reviste el sector más relacionado con el uso de capital productivo para innovar, además de que son consistentes con la hipótesis de efectos diferenciados no sólo entre regiones, sino también entre sectores de la actividad económica, un aspecto que, en el caso mexicano, es importante distinguir para enfocar una adecuada política de innovación (Unger, 2011).
6. Conclusiones
Los ejercicios empíricos coinciden con la teoría y reafirman la idea según la cual la innovación es un factor que estimula el crecimiento económico. El efecto de la innovación sobre el nivel de ingreso per cápita de las entidades es muy cercano al estimado en países de la OCDE y en los de ingreso medio.
El efecto de la innovación en el crecimiento económico varió con la presencia de políticas públicas como el pei. Fue mayor en regiones económi camente en desventaja, por lo que se deduce que también podría ser usado para reducir las desigualdades regionales. El crecimiento se podría potenciar fortaleciendo programas que buscan impulsar la innovación.
El impulso a la innovación no sólo impacta con mayor fuerza la productividad de regiones alejadas de la frontera tecnológica, sino también contri buye a mejorar la capacidad de asimilar y, eventualmente, producir nuevas tecnologías. En este sentido, es importante tomar en consideración lo que se conoce como la trampa de "algo mejor" (Ahlstrom, 2015), es decir, invertir demasiados recursos en tratar de superar las innovaciones de los países tecnológicamente más avanzados, cuando bien se pueden generar productos y procesos que mejoren endógenamente la productividad de los mercados locales, o incluso fomentar su creación, un área de oportunidad que presentan las actividades económicas del país.
El camino hacia una economía innovadora puede ser complejo. Los resultados indican la utilidad de diseñar instrumentos de políticas públicas que apoyen y den continuidad a programas que ya están en marcha con una visión de largo plazo. Los efectos de la innovación tienden a ser más importantes en las regiones con mayor tamaño de los sectores secundario y terciario. Se podría investigar la contribución de la innovación dentro de actividades económicas más específicas, por ejemplo, para dirigir políticas públicas de apoyo a la innovación con mayor efecto en el crecimiento económico. También parece deseable concentrar los esfuerzos de innovación en industrias tecnológicamente más intensivas, de acuerdo con la categorización que ha venido construyendo y actualizando la OECD (2003).
A pesar de las ventajas que presenta el número de patentes como indicador de innovación, entre las que se cuentan su sencillez y facilidad de aplicación, así como la cualidad de permitir comparaciones homogéneas en espacio y tiempo, no hay que olvidar que el concepto de innovación es mucho más amplio, al cubrir procesos y diseños organizacionales novedosos que se encuentran directamente ligados a la producción de bienes y servicios y que, muchas de las veces, son difíciles de concentrar en un solo indicador. Por lo tanto, el parámetro de patentamiento usado es únicamente una aproximación al comportamiento real que intenta medir.
Aún con estas limitantes, es posible concluir que la relación crecimiento-innovación es positiva y, además, puede ser potenciada mediante políticas públicas que consideren la diversidad regional del país.











 texto en
texto en