Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Problemas del desarrollo
versión impresa ISSN 0301-7036
Prob. Des vol.53 no.210 Ciudad de México jul./sep. 2022 Epub 05-Dic-2022
https://doi.org/10.22201/iiec.20078951e.2022.210.69800
Articles
Financial sector and export-led growth: Mexico, 1995-2020
aAutonomous Metropolitan University (UAM), Azcapotzalco Campus, Economics Department, Mexico. Email address:montenegro@azc.uam.mx.
bUniversidad Veracruzana (University of Veracruz), Economics Faculty, Mexico. Email address: edvaldes@uv.mx.
This article seeks to analyze the role of Foreign Direct Investment (FDI) and bank credit to the industrial sector as expansion factors for the productive sector in Mexico from 1995 to 2020. During this period, Mexico was transitioning from an economy with high tariff protection to an open economy, under the generally accepted theoretical postulate that financial repression impeded the free flow of investment. This scenario was unfavorable for an industry that was beginning to reconfigure itself within the framework of a secondary export model. Analysis was conducted using a Markov regime switching model and an Error Correction Vector Model (ECVM). The selected models do not reveal any causal relationship from the financial sector to the real sector or vice versa.
Key Words: Bank Credit to the Industrial Sector (BCIS); financial constraint; Foreign Direct Investment (FDI); Markov-Switching
El objetivo de este trabajo es analizar el papel de la Inversión Extranjera Directa (IED) y el Crédito Bancario al Sector Industrial (CBSI) como factores de expansión del sector productivo en México durante el periodo 1995-2020, en la transición de una economía con alta protección arancelaria a una economía abierta, bajo el postulado teórico generalmente aceptado de que la represión financiera impedía el libre flujo de la inversión; escenario desfavorable para una industria que empezaba a reconfigurarse en el marco de un modelo secundario exportador. Se empleó un modelo de cambio de régimen de Markov y un modelo de Vectores de Corrección de Error (VECM). Los modelos seleccionados no reflejan relación alguna de causalidad del sector financiero al sector real o viceversa.
Palabras clave: Crédito Bancario al Sector Industrial (CBSI); restricción financiera; Inversión Extranjera Directa (IED); Markov-Switching
Clasificación JEL: B50; G0; E01; N1
1. INTRODUCTION
Export-led growth represents the application of a new consensus in developing countries. The argument focuses on the economic benefits of an open market using technological innovation, which promotes the creation of new products and competition in international markets. The success of the Southeast Asian export-oriented economies, known in the 1970s as New Industrialized Economies,12 was the typical reference for this statement; this strategy aimed at increasing productive capacity by focusing on external markets appeared to be viable in other economies. However, with the Great Recession, contradictions started to emerge in export-led growth due to the contraction of demand in developed countries. This had a negative impact on the health of emerging markets due to their high dependence on this growth engine (Palley, 2012, p. 142).
Meeting external demand can be seen as a way to produce new goods in sectors with strong productivity and growth (productive efficiency gains). This growth is not only a result of the traditional convergence hypothesis (Barro and Sala-I Martin, 1991 and 1992; Quah, 1993 and 1996; Aghion and Howitt, 2009) as it is closely related to trade and trade openness. This gives way to the need to define strategies for transferring capital and human resources to sectors geared toward external markets, resulting in structural imbalances (Gaffard and Saraceno, 2008, pp. 1062-1063). As such, investment redistribution among sectors is dual in nature, with the destruction of productive capacity in certain spaces and its creation in others.
Resolving these imbalances necessitates the feasibility of mobilizing financial resources to meet the demand for credit that such a redirection of productive capacity entails. The key point is that once the neo-export industrial policy has been defined, the viability of resource displacement it implies must be based on an ad hoc monetary and credit policy. In this case, this creates the problem of restricting financing of an export-led growth model. In the end, if the strategy is successful, the economy will have been led to a new equilibrium, after the rupturing and restructuring of the previous status quo, which means the reallocation of investment and an efficient credit system that supports the new growth model’s financing needs.
The neo-export strategy’s achieving a soft landing depends largely on the balances available for investment in conjunction with an efficient credit system to mobilize them towards new sectors of financing demand. Here is where the specific conditions of the analyzed space become relevant, i.e., those of an economy with a medium level of industrialization. This means the analysis of internal financing. The response to this, for five decades, has been the suggested ineffectiveness of the proposal of perfect markets from conventional theories on monetary and financial processes with a single interest rate or markets structured by term rates, when what was in effect was actually a fragmented market of real interest rates. Or they even worked off of a perfect substitution between real money balances and physical capital and, where convenient, used a complementarity approach to take on these variables (McKinnon, 1973, p. 3).
The underlying issue is the importance of theorizing with basic assumptions which are “better suited to explaining the relationship between monetary processes and capital accumulation in the underdeveloped world” (McKinnon, 1973, p. 3). Another aspect of the period’s strong tariff protectionism framework was proposing the convenience of opening the economy pari passu with the capital market’s liberalization to absorb imports’ external financing, which would lead to the dismantling of the protectionist scheme.
This was all within the framework of a financial repression understood as the weak depth of the banking system and great segmentation of access to credit, with its majority in a small number of large companies. This strongly limits the resources to the rest of an economy fragmented into a multitude of micro units with inefficient self-financing practices. As a result, one expects Foreign Direct Investment (FDI) and Bank Credit to the Industrial Sector (BCIS)13 to be factors in the productive sector’s expansion.
This article is structured in five sections, including the introduction: the second analyzes the link between trade openness and financial restrictions by compiling the seminal ideas on the subject of McKinnon (1973) and Gurley and Shaw (1960); the third takes on the characterization and measurement of financial constraints and their impact on the Mexican economy; the fourth section presents the methodology used to study the dynamics between the financial sector and the real sector; the fifth sets forth the results obtained for the Mexican economy in the period of 1995-2020. Finally, the conclusions are presented. These suggest that external financing and BCIS did not contribute to production’s growth level, as they do not show any relationship which would allow one to infer any causality from the financial sector to the real sector in the period studied.
2. TRADE OPENNESS AND FINANCIAL CONSTRAINTS
Trade openness is a type of structural change and can therefore integrate itself with technical progress as it entails the destruction of productive capacity and the construction of something new to replace it (Gaffard and Saraceno, 2008, p. 1063). In other words, the coordination between the phases of building productive capacity and its utilization and between investment and consumption which characterizes the equilibrium are altered during the process of structural change. If the product that an economy is capable of generating depends on labor and the size of the capital stock, given the state of production techniques, if labor is omitted, the net production capacity increases in step with the increase in capital stock destined for investment. However, in order to make an efficient allocation of investment, the ad hoc financial systems which make this possible are necessary (Gurley and Shaw, 1960, p. 47).
The result is that the restructuring of productive sectors for neo-export specialization will depend largely on trade openness and the free flow of capital. Restructuring can take on different forms and “is likely to have distributional impacts-both in the short term as a consequence of adjustment costs and in the long term as a result of permanent changes in relative [productive] factor demands,” as Rodrik (1998, p. 6) points out. In other words, the imbalances of the new strategy are the flip side of productive efficiency gains, which the author dramatically emphasizes with “No pain, no gain!”
An old mentality: financing and development
The construction of a unified monetary and financial theory, just like the renown of Gurley and Shaw (1960) and McKinnon (1973) as pioneers in the subject, have been around for a long time (Lucas, 1984; Williamson and Mahar, 1998; Lipsky, 2009; Aghion and Howitt, 2009). Nowadays we recognize that its approach has two sides: the economy was generally dealt with a “real sector” analysis (income, product, work, wealth) leaving by the wayside financial aspects. This is because “a basic theoretical paradigm focuses on the fundamental mechanisms of the growth process, whereas finance is like the lubrication that reduces frictions and thereby enables the machinery to function” (Aghion and Howitt, 2009, p. 129). The financial system was therefore relegated to second place until Gurley and Shaw (1960, p.515) established that development included both finance and goods.14
The resulting underlying problem was to combine the microeconomic analysis of financing with that of investment volume which the financial system could provide. Specifically, the intermittent nature of investment opportunities available to each firm suggests that to keep the returns of holding money high, the average return on physical capital in the economy should not drop when the financial system becomes more efficient and investment volume increases. However, a financial system based on self-financing is limiting even if ideally managed. Thus, a maximum is defined for the optimal profitability of money (McKinnon, 1973, p. 64).
Monetary authorities are therefore forced to set, in an underdeveloped economy, a real rate of return on holding money lower than that which could be earned from intramarginal investments in physical capital in some firm-households. This is because the effect produced by competing assets of high cash balances reduces the flow of lower-return investments that are within the margin of other firms. Therefore, financial institutions eliminate the limitation of self-financing by granting credit, this makes it possible to more effectively pool the savings of the agents (McKinnon, 1973, p. 65).
Gurley and Shaw (1960, p. 47) point out that the financial system can stimulate savings and investment in efficient uses or they can retard savings and divert them to inefficient uses; consumer savings, along with any business savings, are directed to increases in real money balances and necessarily flow to the financial sector, through banks and are thus available for use as an investment.
Because of the existence of complementarity between physical capital, real money balances and fiat money, the issuance of which bears no relation to the expansion of bank credit for investments, self-financing expresses that capital markets in underdeveloped economies do not operate efficiently (McKinnon, 1973, pp. 83-84). This is a problem that would be remedied by the liberalization of the financial sector in order to channel external financing funds with high prospective return rates into investment opportunities of varying magnitude which result from the inefficiency of self-financing.
Consequently, the local monetary system becomes more costly by relying on bank credit in order to promote and attract external savings in the international capital market at competitive interest rates (McKinnon, 1973, p. 83). The implied assumption is a scarcity of internal savings in what we now call emerging economies and an abundance in developed ones.
However, in developing economies, bank credit is not very dynamic in terms of expanding its field of influence due to the fact that the bulk of access to financing is limited to activities specializing in import and export,15 large-scale mining, large manufacturing and service companies, international companies and government agencies. Meanwhile, a large number of micro, small and medium-sized businesses find it hard to qualify for bank credit.16 McKinnon (1973, pp. 83-84) calls this phenomenon “financial repression.” It is the banks’ inability to obtain profitable rates of return, and in real terms is reflected in a low, and sometimes even negative, yield for their depositors. That is why an increase in the efficiency of bank credit is a necessary condition in alleviating the real magnitude of the monetary sector and thus mitigates financial repression.
Strictly speaking, capital is one more commodity in the economy and figures into the plans of agents in the system to buy and sell, and is therefore considered one of the most efficient markets for allocating resources. Some authors use this as the basis to propose a need to deregulate the financial system, given that it encourages production level growth, thus contributing to improved social well-being.
McKinnon (1973) and Shaw (1973) believe economies with legal reserves, regulated interest rates, inefficient credit channeling and zero growth of financial intermediaries cannot provide access to loans, nor offer incentives to save and accumulate capital. Therefore, any allocation of resources made would be inefficient. They conclude that based on financial liberalization, the determination of savings and investment levels would result in greater efficiency in the allocation of investments which then fosters economic growth.
Williamson and Mahar (1998, pp. 2-3) meanwhile indicate that government involvement plays an important part in full liberalization. This should allow any enterprise that satisfies specific criteria based on prudential considerations relating to capital, skills and reputation to enter the field of financial services. Nevertheless, banks must have the autonomy to decide how to manage their resources, and the government in turn must withdraw from the ownership of financial institutions and eliminate controls placed on international capital flows. The elimination of credit controls and the deregulation of interest rates are then added to full liberalization. However, it is important to note that these authors believe that banking autonomy and regulation are not separate as the former is understood as prudential supervision exercised by the central bank.17
Finally, the main question that McKinnon (1973), Gurley and Shaw (1960) originally debated is the incorporation of financial matters in the topic of economic growth. The current debate is of a different nature: it seeks to determine whether the financial aspect causes growth in the same dimension as the real sector, and does not to deny the importance of both factors in growth. Ultimately, the role of an efficient financial system is no longer conceived only as a mechanism that streamlines the allocation of resources as a kind of lubricant for the frictions of the real sector.
For this reason, Levine (2005, p. 870) believes that if finance explains growth, an explanation is needed as to how financial development operates in resource allocation decisions in a way that drives productivity growth without limiting it to the analysis of savings. A strong connection between the financial system and long-term economic growth was found in a wide array of empirical studies (Levine, 2005, p. 921), specifically that the theory and empirical evidence do not show the financial system responding only to economic activity or that financial development is only an aggregate of economic growth.
3. SOME STYLIZED FACTS ON THE REAL AND FINANCIAL SECTORS IN MEXICO
As Venegas et al.explain (2009, p. 256), the financial reforms in Mexico took place in the late 1970s, which coincided with the creation of the Mexican IPC Stock Index,18 in parallel with the country’s entry into the market of negotiable government bonds, liberalization of banks, a reduction in the requirements placed on banks’ reserves, the non-intervention on certain interest rates, the opening of the capital account, as well as the devaluation of the peso. All of the above made it possible to replace national intermediation in deposits with international operations between the late 1970s and early 1980s.
The aims were to bring about less friction in the workings of the capital and money markets, achieve greater efficiency and competitiveness and favor greater integration with international financial markets. The deregulation process therefore focused on the gradual elimination of credit controls and restrictions imposed on the financial sector, thus promoting the entry of foreign portfolio investment. This decision sought to develop the public and private sectors by promoting new means of financing (Cabello, 1999, p. 216).
A consultation of references in historical order after this moment will yield different results. Bandiera et al. (2000), for example, upon finding a long-term negative relationship between savings and financial liberalization in Mexico, point out that financial repression had a positive but small effect on the financial system’s development by driving savings’ interest rates. Along the same lines, Venegas et al. (2009, p. 280) found empirical evidence a decade later suggesting that financial development had a positive, albeit small, influence on economic growth in Mexico in the period of 1961-2007 and that financial repression tends to slow down growth. This is due to this effect being inversely proportionate to financial development. However, they found no short-term effects between repression, financial development and the level of economic activity.
According to Kindelberger (2012, pp. 233-295), this supports an important factor with regards to most economies worldwide. In the last hundred years the increase in the credit supply was generated by the banks and resulted in a multitude of new financial instruments favoring a systematic development for reducing transaction costs, such as maintaining liquidity and monetary balances.
Along the same lines, De la Cruz and Alcántara (2011, pp. 32-33) showed that the total credit granted by commercial banks tends to increase the level of production; however, by disaggregating the destination of credit by sector, only that destined for services and consumption has a positive effect on Mexico’s economic activity. They also find a bidirectional causal relationship between consumer credit and production levels as a close interaction of banking processes encouraging aggregate demand prevails, in spite of the financial sphere having a weak relationship with the country’s generation of added value. Meanwhile, Clavellina (2013, pp. 31-32) offers up empirical evidence that suggests a negative causality of total credit in the determination of product. This could be explained by the low quality of financial intermediation which in turn triggers non-optimal results. These then affect the Mexican economy’s performance by directing a large part of its resources to unproductive activities such as consumption and the public sector.
By estimating equations for cointegration and for Mexico’s common cycle, Portal and Feitó (2014, p. 92) were able to determine the presence of a positive long-term relationship between commercial banking’s sectoral loans and activity levels in the secondary and tertiary sector. This suggests that commercial banks’ credit allocation to sectors of economic activity positively influence these sectors’ growth for the period of 1995-2012.
Furthermore, Landa (2019, p. 50) identified in the Mexican economy an inverse relationship regarding the scope commercial banking, an issue arising from highly targeted credit and an insufficient savings rate; Landa also identified earnings which are driven by the stock market. This suggests that the satisfactory levels of liquidity provided by the stock market’s segment is related to financial stability and production’s growth rate.
In spite of the financial market’s liberalization policies in the late 1980s, such as the elimination of legal reserves, non-selectivity in credit policies, liberalization of active and passive interest rates, international banking’s operating in the country, authorization of financial groups and the privatization of commercial banking, among others, in 1994 Venegas et al. (2009, pp. 256-258) verified that new financial-business groups in larger segments controlled 50% of the assets. Today, the seven largest banks control 78.34% of the assets in the system. Of these, five are foreign and account for 62.85% of the sector.19
In terms of the banking system’s depth,20 Mexico is known as a country lagging behind other Latin American countries: 27% of its population has a bank account and approximately 90% of daily transactions in the country are made in cash (Herrera, 2019, March 12); credit to the non-financial private sector is around 42% of the GDP, well below the average of the five largest countries in Latin America (72% of GDP), and even further from the 143% average of emerging countries (Savedra, 2019, August 12). Specifically, in 2019 in Mexico’s non-financial private sector, the ratio of total financing to GDP was close to 40%, while in Chile it was over 170% (Bank of Mexico [BdeM]21 , 2019).
Téllez and Venegas (2019) have likewise found, based on different panel data specifications, that the determinants of Mexico’s financial system’s intraregional depth are as follows: the current state of the law or institutions; banking competition and regulation; formal employment, as well as the propensity to save and financial education. Therefore, the low degree of financial intermediation is conditioned, as Herman and Klemm (2017) point out, on the sector’s structural aspects. While there has been credit growth in the last decade, driven by increased supply, there appears to be some lag in credit cycles relative to business cycles.
Fukuda (2019), with the use of Vector Error Correction Models (VECM), similarly finds empirical evidence that suggests globalization and financial deepening in Mexico, understood as the proportion of internal credit granted by banks to the private sector, have a negative influence on economic growth. According to López and Basilio (2016, pp. 227-228), the deregulation of the financial system caused a contraction in credit destined for productive activities and revealed commercial banking’s speculative and rentier nature. The latter in turn obstructs intermediation between productive activities and financing.
In summary, in theoretical terms it is assumed that the dynamic of economic activity levels is that BCIS and FDI should not behave differently in the economy’s periods of recession or recovery, given that allocation in the financial sector is efficient and the resources channeled from abroad encourage production level growth. However, in the case of economies such as Mexico, the dynamics of bank credit have a structural restriction as they are mainly aimed at import- and export-related activities. In addition, the aforementioned data reflects a situation of financial repression and fragmentation which liberalization policies should have done away with after operating for four decades.
With the aim of answering these questions, we will first study the dynamics between the financial sector and the real sector, using the Markov methodology for regime change to analyze the short- and long-term relationships exhibited by BCIS, FDI and the production level in terms of which phase of the business cycle they find themselves in and the probability of remaining there. Second, a VECM will be used to study how these variables react to long-term equilibrium.
4. METHODOLOGY
Two models were used to capture the dynamics of the activity level of the economy, FDI and BCIS: the first is a Markov-Switching model, with which the average duration of recessions and recoveries is obtained to determine if the aforementioned variables can be synchronized within the period studied.
Along these lines, Hamilton (1994, pp. 677-684) points out that if a process changed in the past, it could clearly change again in the future, and that this should be taken into account when drawing up a forecast. Moreover, regime change should not be considered the result of a perfectly foreseeable deterministic event. Quite the contrary, regime change is itself a random variable. Therefore, a complete time series model would include a description of the law of probability which governs the nature of change μ1, μ2.
These observations suggest that the process could be considered to be influenced by an unobserved random variable
Where
According to Mejía (2000, pp. 392-395), the state s t is not directly observed, therefore the probability that the process is in state 1 on date t is conditional on the data observed up to date t. This algorithm can be considered a formalization of the statistical identification of inflection points in a time series with the filter and, specifically, the softest probabilities used to identify periods of contraction and expansion.
The second model is a VECM and, according to Pesaran (2015), it allows one to determine the variables’ trajectory based on their long-term equilibrium if there are different dynamic specifications to represent these equilibria, as is the case of the autoregressive distributed lag model (ARDL). This model will be effective, regardless of whether the regressors are integrated to the order of I(0) or I(1), or are co-integrated with each other, meaning that the appropriate lag for each variable can be included (Pesaran et al. , 2001). As the ARDL model is a single equation dependent on its own lags and those of the explanatory variables, which need to at least be weakly exogenous (Enders, 2014), we opted for the VECM as the latter allows one to study the dynamics between the three variables as it is a multiple equation system.
Now, if the variables are co-integrated (that is, they have a long-term relationship), they will share the same stochastic trends and therefore cannot deviate too much. This is how the error correction representation reacts to long-term deviation from the equilibrium (Enders, 2014). We followed the proposal of Kilian and Lütkepohl (2017) in incorporating the concept of cointegration, represented in its simplified form in the VECM equation as:
Where y t-1 is the vector of the variables in levels (not stationary) and Π is an r rank non-singular matrix. The range of Π is therefore referred to as the cointegration range of process y t . If this matrix r rank K × K can be broken down as a product of two matrices, then the VECM equation (Kilian and Lütkepohl, 2017) can be rewritten as follows:
Where ß' is the cointegration matrix and α is the adjustment rate matrix, which makes the error correction term explicit (aß'y t _ 1 ). In other words, if it is possible to decompose the Πγ t - 1 matrix, the use of VECM as explained by Loría (2007, p. 275) allows one to combine “economic theory [by finding stable long-term relationships established by the theory] and the statistical adjustment of the imbalance that can exist in the short-term.”
5. RESULTS
This section analyzes the main empirical regularities which characterize the Mexican economic cycle, BCIS and FDI with quarterly data in the period of 1995-202022 which were seasonally adjusted and then adjusted to 2013 prices; in the case of FDI, the series was seasonally adjusted and an index based on 2013 was constructed. The cyclical patterns of GDP and BCIS were evaluated using Hamilton’s (2018) proposed methodology; meanwhile, in order to ascertain whether the variables described above can be synchronized within recessions and recoveries, a Markov-switching probability model was elaborated with the methodology Hamilton set forth (1994) and used to obtain each phase’s average duration. Furthermore, a VECM was used to determine whether BCIS, FDI and GDP have any long-term relationship.
After determining the recovery and recession phases of GDP and BCIS, they were used to study the amplitude and duration of each (see Table 1). When GDP was in a recessionary period, it presented an average duration of 8.99 quarters, with a cyclical component average of -.05523 and a standard deviation of 0.04020; BCIS showed an average duration of 24.90 with an average of -0.1355 and a standard deviation of 0.12721; FDI had an average duration of 1.899 with an average of -0.6276 and a standard deviation of 0.2597. In recovery phases, GDP presented an average duration of 25.93 quarters and an average of 0.01921; FDI had an average duration of 28.28 with an average of 0.07562 and BCIS showed an average duration of 22.52 and an average component of 0.1384.
Table 1 Descriptive statistics of recessions and recoveries for GDP, BCIS and FDI.
| Recessions | Recoveries | |||||
| Statistics | GDP | BCIS | FDI | GDP | BCIS | FDI |
| Average duration (quarter) | 8.99 | 24.90 | 1.899 | 25.93 | 22.52 | 28.28 |
| Average of the cyclical component | -0.05523 | -0.1355 | -0.6276 | 0.01921 | 0.1384 | 0.07562 |
| Standard deviation | 0.04020 | 0.12721 | 0.25970 | 0.01866 | 0.1484 | 0.30008 |
| Asymmetry | -2.05883 | -1.2006 | 0.3706 | -0.23375 | 1.2078 | 1.95172 |
| Kurtosis | 8.72079 | 4.9460 | 2.2316 | 2.43964 | 4.6315 | 9.78157 |
Source: created by the authors.
Based on the empirical regularities found, asymmetry can be inferred in the two phases that characterized the business cycle as none of three series presented any symmetry in duration or amplitude during contractionary phases. In absolute terms, GDP showed an average for the cyclical component lower than the BCIS and FDI averages, a situation which repeated itself during the recovery periods. Empirical evidence implies a different dynamic and, to verify this, Markov-chains were used to model phases in order to identify the probability of each of the three-time series staying in a state of recession or recovery.
Figure 1 shows the GDP’s and BCIS’s probability of transitioning from the economic cycle; FDI is excluded as it is in recovery for most of the study period. BCIS had three phases of recession: the first, of a prolonged magnitude, in periods of recession it could be assumed to have been contemporaneous to the economic cycle and was countercyclical during episodes of recovery; in the second and third phases it was contemporaneous to the Mexican economic cycle; however, these results do not allow any conjecture to be made since so much of the period analyzed is in recession.
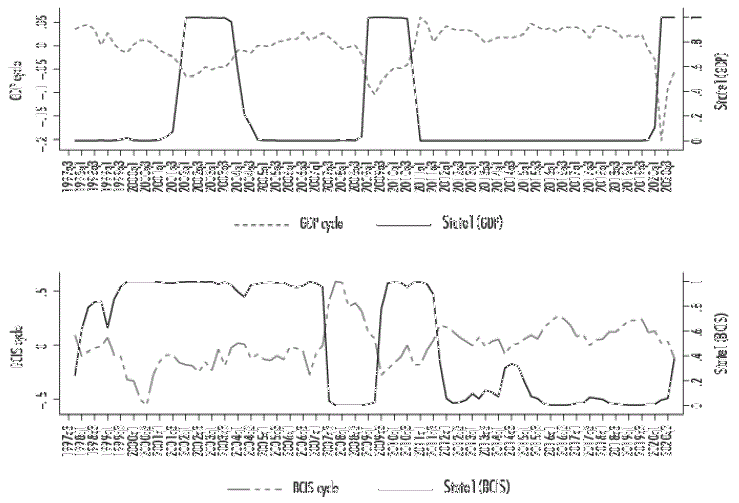
Source: Created by the authors.
Figure 1 Cyclical component of GDP and probability to transition 1997-2020.
The evidence for BCIS and FDI reports the presence of asymmetric behaviors in each of the phases of the economic cycle for BCIS and FDI with respect to their magnitude and duration. This was corroborated with the values obtained from the final matrices. The probability of remaining in the recovery phase or transitioning to it in the next period is, in the case of GDP 88.52%, 82.04% for BCIS and 84.666% for FDI, thereby demonstrating a different dynamic between GDP, BCIS and FDI in the recovery phases of the economic cycle. In phases of recession, the probability of remaining in it in the following period was 67.42% for GDP, while FDI has a much lower probability at 7.35% and 83.83% for BCIS. Empirical evidence demonstrates synchronization between the national economy, BCIS and FDI in phases of recovery or recession to be non-existent.
As no empirical evidence was found to suggest the existence of any synchronization between the variables analyzed, we proceeded to estimate a VECM to try to capture the effects of BCIS and FDI on the economic activity level, which would imply a positive relationship between the two. Thus, the Augmented Dickey-Fuller (ADF), Phillips-Perron (PP) and Kwiatkowski, Phillips, Schmidt and Shin (KPSS) tests were used to corroborate the series’ order of integration.
As the three series are stationary23 in their first difference, we proceed to choose the optimal number of lags so we may present the VECM model to be estimated. According to the information criteria of Akaike, Hannan-Quinn and the final error prediction, we concluded that two lags should be included in the model.24
We then verified the existence of at least one cointegration equation using the Johansen test. The eigenvalues and the graphs themselves confirm the existence of at least one cointegrating equation. The results of this test are presented in Table 2.
Table 2 Johansen cointegration test.
| Number of low HQ cointegration equations | Eigenvalue | Line | ||||||
| Test | 0.10 | 0.05 | 0.01 | Test | 0.10 | 0.05 | 0.01 | |
| r = 0 | 56.34 | 18.9 | 21.07 | 25.75 | 65.99 | 28.71 | 31.52 | 37.22 |
| r <= 1 | 9.31 | 12.91 | 14.9 | 19.19 | 9.65 | 15.66 | 17.95 | 23.52 |
| r <= 2 | 0.34 | 6.5 | 8.18 | 11.65 | 0.34 | 6.5 | 8.18 | 11.65 |
Source: created by the authors.
The model estimated using the information obtained from the optimal number of lags, the order of integration of the time series and the Johansen test are as follows:
Where Y i is the GDP logarithm, Cr i is the BCIS logarithm and IE i is the FDI index logarithm. The results of the VECM estimation (1) are presented in Tables 3, 4 and 5. In the case of the GDP equation, the coefficient of the first FDI and BCIS lag are negative without being statistically significant; only the lag itself is statistically significant. In the case of the FDI equation, only the FDI lag turned out to be significant; as for the BCIS equation, the GDP lag is significant as is the bank credit lag.
Table 3 Results of the VECM estimation (1) for the GDP equation.
| Variable | Coefficient | Standard error | Statistic t | P-value |
| Constant | -0.0065399 | 0.3357471 | -0.019 | 0.9845 |
| IE_t-1 | -0.0038629 | 0.007425 | -0.52 | 0.6041 |
| Cr_t-1 | -0.0879212 | 0.0500208 | -1.758 | 0.082 |
| Y_t-1 | -0.2111485 | 0.1028195 | -2.054 | 0.0427 |
| EC1 | 0.0010140 | 0.0108663 | -0.04 | 0.9683 |
Source: created by the authors.
Table 4 Results of the FDI equation estimation.
| Variable | Coefficient | Standard error | Statistic t | P-value |
| Constant | -38.0168 | 4.5329 | -8.387 | 0.000 |
| IE_t-1 | -1.0173 | 0.1021 | -9.966 | 0.000 |
| Cr_t-1 | -0.891 | 0.6739 | -1.322 | 0.189 |
| Y_t-1 | 1.5037 | 1.3192 | 1.14 | 0.257 |
| EC1 | 1.2301 | 0.1467 | -8.385 | 0.000 |
Source: created by the authors.
Table 5 Results of the BCIS equation estimation.
| Variable | Coefficient | Standard error | Statistic t | P-value |
| Constant | -0.95606 | 0.50849 | -1.88 | 0.0631 |
| IE_t-1 | -0.01292 | 0.01145 | -1.128 | 0.2621 |
| Cr_t-1 | 0.60538 | 0.0756 | 8.008 | 0.000 |
| Y_t-1 | 0.29299 | 0.14799 | 1.98 | 0.0506 |
| EC1 | 0.07292 | 0.03851 | 1.879 | 0.0633 |
Source: created by the authors.
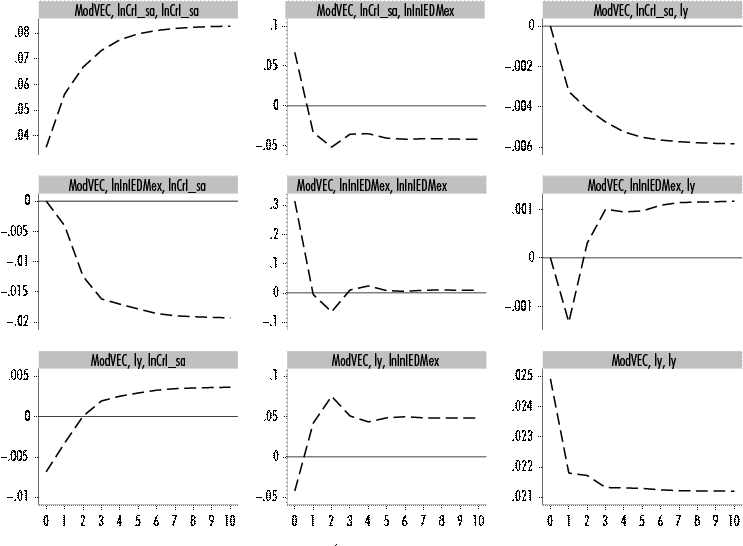
The model is stable, and furthermore, the serial correlation and heteroscedasticity tests show that the model does not present any problems. The stationarity of the errors in each equation was also checked and the residuals of the three equations were found to be stationary with trend and constant (see Tables A3 and A4 of the Statistical Appendix). The impulse response functions of the estimated model are presented in Figure 2.
Empirical evidence obtained through impulse response functions suggests the BCIS’s two standard deviation shock’s depressive effect on production level growth, as well as its contractionary effect on FDI. On the other hand, the short-term recessionary effect of FDI on GDP and BCIS is evident. Meanwhile, GDP shocks have a contractionary effect on FDI and BCIS in the short-term. In turn, Table 6 presents the GDP variance decomposition, from which we can conclude that in period 10 GDP variability explains itself at 85.53%, meanwhile FDI is at 7.91% and BCIS at 6.54%.
Table 6 Decomposition of GDP variance.
| P | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Y_t | 0.9908 | 0.94937 | 0.9353 | 0.9062 | 0.8879 | 0.8789 | 0.8709 | 0.8639 | 0.8592 | 0.8553 |
| IE_t | 0.0091 | 0.02644 | 0.0280 | 0.0500 | 0.0623 | 0.0660 | 0.07059 | 0.0749 | 0.0772 | 0.0791 |
| Cr_t | 0.0000 | 0.0241 | 0.0366 | 0.0437 | 0.0496 | 0.0550 | 0.0584 | 0.0610 | 0.0635 | 0.0654 |
Source: created by the authors.
In addition to the above, the Granger causality test was performed to determine whether the events in past periods could provide information on the events that are currently transpiring (see Table 7). This is how the results obtained allow us to reject the null hypothesis, which itself establishes that the GDP growth rate does cause, in the Granger test, the BCIS growth rate. At the same time, the BCIS growth rate causes the FDI growth rate. However, no causal relationship of FDI to GDP or BCIS to GDP was found as the test statistic obtained is not significant.
6. CONCLUSIONS
Financial liberalization and trade openness were implemented, in accordance with the Washington Consensus, as part of a structural adjustment meant to overcome the 1980s’ Latin American Debt Crisis (Williamson, 1991).
With this framework, an estimate was made for the relationship between the BCIS, FDI and Mexico’s economic activity during the period of 1995-2020 using two proposals. The first was a spatial representation of state using a Markov-Switching model which showed that FDI in Mexico was in recovery for most of the period studied. In the case of BCIS, it showed three phases of recession: the first has a prolonged amplitude which could be assumed as contemporaneous to the economic cycle in periods of recession and countercyclical in periods of recovery, while in the second and third phases it would be considered as contemporaneous with Mexico’s economic cycle. However, these results did not allow us to make any conjecture on the series’ behavior since so much of the period analyzed was in recession.
The second proposal used a VECM to determine the dynamics between GDP, BCIS and FDI. From the Johansen test it was concluded that there is a long-term relationship between the variables. The estimates made suggest, through impulse response functions, that shocks in FDI and BCIS can cause a contractionary dynamic in economic activity levels; however, the variance decomposition showed that BCIS and FDI explain about 14.50% of GDP variability in the tenth period.
Furthermore, the Granger causality test suggests a unidirectional behavior going from GDP to BCIS or FDI as there is no causality from BCIS or FDI towards GDP. These results suggest that BCIS or FDI do not encourage the productive sector’s growth after the transition which the Mexican economy underwent in the early 1990s. This highlights the lack of credit depth as it is linked to large companies’ export activities, when in the country the overwhelming majority of economic units are micro, small and medium enterprises that find it hard to meet bank credit requirements.
The paradox is that, although the liberalization process that took place in the early 1980s met most of the established theoretical guidelines, its implementation did not fully permeate the economic system as the financial fragmentation and repression to be overcome keenly survived. Since we saw no relationship which allows us to infer any causality from the financial to the real sector in the period studied, this means that the empirical evidence found does not suggest external financing and BCIS contributed to the growth of production levels.
REFERENCES
Aghion, P. y Howitt, P. (2009). The economics of growth. The MIT Press. [ Links ]
Banco de México (BdeM) (2019). Banco de México. Reporte de estabilidad financiera. https://www.banxico.org.mx/publicaciones-y-prensa/reportes-sobre-el-sistema-financiero/%7B04E197EE-B6FC-7BA1-72A0-32D3E6C9BF28%7D.pdf. [ Links ]
______(2021). Sistema de Información Económica. https://www.banxico.org.mx. [ Links ]
Bandiera, O., Caprio, G., Honohan, P. y Schiantarelli, F. (2000). Does financial reform rise or reduce saving? The Review of Economics and Statistics, 82(2).https://www.jstor.org/stable/2646818. [ Links ]
Barro, R. y Sala-I-Martin, X. (1991). Convergence across states and regions. Brooking Papers on Economic Activity, 22(1). https://doi.org/10.2307/2534639. [ Links ]
______y Sala-I-Martin, X. (1992). Convergence. Journal of Political Economy, 100(2). https://doi.org/10.1086/261816. [ Links ]
Cabello, A. (1999). Globalización y liberalización financieras y la Bolsa Mexicana de Valores: del auge a la crisis. Plaza y Valdés. [ Links ]
Clavellina, J. (2013). Crédito bancario y crecimiento económico en México. Economía Informa, 2013(378 ).https://www.elsevier.es/es-revista-economia-informa-114-articulo-credito-bancario-crecimiento-economico-mexico-S0185084913713069. [ Links ]
Comisión Económica para América Latina y el Caribe (CEPAL) (2019). El desempeño de empresas exportadoras según su tamaño. Un guía de indicadores y resultados. https://repositorio.cepal.org/bitstream/handle/11362/44664/S1900418_es.pdf?sequence=1&isAllowed=y. [ Links ]
De la Cruz, J. y Alcántara, J. (2011). Crecimiento económico y el crédito bancario: un análisis de causalidad para México. Revista de Economía, 28(77 ). https://doi.org/10.33937/reveco.2011.25. [ Links ]
Enders, W. (2014). Applied Econometric Time Series. John Wiley (Original publicado en 1994). [ Links ]
Fukuda, T. (2019). Mexico's finance-growth nexus with trade openness, FDI and portfolio investment: evidence from cointegration analysis. Ecos de Economía, 23(49 ). https://doi.org/10.17230/ecos.2019.49.2. [ Links ]
Gaffard, J. y Saraceno, F. (2008). Croissance Par Les Exportations, Fragilité Financière Et Gradualisme: Quels Défis Pour La Chine? Revue économique, 59(6).https://www.jstor.org/stable/25483978. [ Links ]
Gurley, J. y Shaw, E. (1960). Money in a theory of finance. Booking Institution. [ Links ]
Hamilton, J. (1994). Time Series Analysis. Princeton University Press. [ Links ]
______(2018). Why you should never use the Hodrick-Prescott Filter. The Review of Economics and Statistics, 100(5). https://doi.org/10.1162/rest_a_00706. [ Links ]
Herman, A. y Klemm, A. (2017). Financial deepening in Mexico. IMF Working Paper, no. 17/19. International Monetary Fund. [ Links ]
Herrera, A. (2019, 12 de marzo). México iniciará programas piloto para reducir uso de dinero en efectivo. Agencia EFE. https://www.efe.com/efe/america/mexico/mexico-iniciara-programas-piloto-para-reducir-uso-de-dinero-en-efectivo/50000545-3935719. [ Links ]
Instituto Nacional de Estadística y Geografía (INEGI) (2019). Censos económicos 2019. https://www.inegi.org.mx/contenidos/saladeprensa/boletines/2020/OtrTemEcon/CenEconResDef2019_Nal.pdf. [ Links ]
Kilian, L. y Lütkepohl, H. (2017). Structural vector autoregressive analysis (Themes in modern econometrics). Cambridge University Press. [ Links ]
Kindelberger, C. (2012). Manías, pánicos y cracs: historia de las crisis financieras. Ariel. [ Links ]
Landa, H. (2019). Restricción financiera y crecimiento económico en México. Investigación económica, 78(309 ). http://dx.doi.org/10.22201/fe.01851667p.2019.309.70118. [ Links ]
Levine, R. (2005). Finance and growth: theory and evidence. En P. Aghion y S. Durlauf (ed.). Handbook of Economic Growth, vol. 1A (pp. 865-934). North Holland Publishing. [ Links ]
Lipsky, J. (2009). Finance and economic growth, Remarks by First Deputy Managing Director John Lipsky. IMF. https://www.imf.org/en/News/Articles/2015/09/28/04/53/sp101909. [ Links ]
López, T. y Basilio, E. (2016). Economic growth and financial development in Mexico: from a virtuous circle of a bidirectional causality to a financial subordination. En N. Levy y E. Ortiz (ed.). The financialization response to economic disequilibria (pp. 213 -230). Edward Elgar Publishing. [ Links ]
Loría, E. (2007). Econometría con aplicaciones. Pearson Prentice Hall. [ Links ]
Lucas, R. (1984). Money in theory of finance, Carnegie-Rochester Conference Series on Public Policy, 21. https://doi.org/10.1016/0167-2231(84)90003-4. [ Links ]
McKinnon, R. (1973). Money and capital in economic development. The Broo-kings Institution. [ Links ]
Mejía, P. (2000). Asymmetries and common cycles in Latin America: evidence from Markov-Switching models. Economía Mexicana Nueva Época, 9(2).http://www.economiamexicana.cide.edu/num_anteriores/IX-2/04_PABLO_MEJIA_189-225.pdf. [ Links ]
Palley, T. (2012). The rise and fall of export-led growth. Investigación Económica, 71(280 ).http://www.scielo.org.mx/scielo.php?script=sci_abstract&pid=S0185-16672012000200006&lng=es&nrm=iso&tlng=en. [ Links ]
Pesaran, M. (2015). Time series and panel data econometrics. Oxford University Press. [ Links ]
Pesaran, M., Shin, Y. y Smith, R. (2001). Bounds testing approaches to the analysis of level relationships. Journal of Applied Econometrics, 16(3). https://doi.org/10.1002/jae.616. [ Links ]
Portal, M. y Feitó, D. (2014). Crédito y crecimiento económico en México: un análisis para los sectores de actividad económica. Equilibrio Económico. Revista de Economía, Política y Sociedad, 10(1).http://www.equilibrioeconomico.uadec.mx/descargas/Rev2014/Rev14Sem1Art3.pdf. [ Links ]
Quah, D. (1993). Galton's fallacy and tests of the convergence hypothesis. The Scandinavian Journal of Economics, 95(4).https://www.jstor.org/stable/3440905. [ Links ]
______(1996). Twin peaks: growth and convergence in models of distribution dynamics. The Economic Journal, 106(43).https://www.jstor.org/stable/2235377. [ Links ]
Rodrik, D. (1998). Symposium on globalization in perspective: an introduction. Journal of Economic Perspectives, 12(4).https://www.jstor.org/stable/2646891. [ Links ]
Savedra, P. (2019, 12 de agosto). Inclusión financiera-. Prioritaria para el crecimiento más acelerado e inclusivo. El Universal. https://www.eluniversal.com.mx/opinion/pablo-saavedra/inclusion-financiera-prioritaria-para-crecimiento-acelerado. [ Links ]
Shaw, E. (1973). Financial deepening in economic development. Oxford University Press. [ Links ]
Téllez, I. y Venegas, F. (2019). Determinants of financial deepening in Mexico: a dynamic panel data approach. Revista de Métodos Cuantitativos para la Economía y la Empresa, 27. https://www.upo.es/revistas/index.php/Rev-MetCuant/article/view/2761. [ Links ]
Venegas, F., Tinoco, M. y Torres, V. (2009). Desregulación financiera, desarrollo del sistema financiero y crecimiento económico en México: efectos de largo plazo y causalidad. Estudios Económicos, 24(2).https://www.redalyc.org/articulo.oa?id=59713143003. [ Links ]
Williamson, J. (1991). El cambio en las políticas económicas de América Latina. Gernika. [ Links ]
Williamson, J. y Mahar, M. (1998). A survey of financial liberalization. Princeton Essays in International Finance, 211(1).https://ies.princeton.edu/pdf/E211.pdf. [ Links ]
3Along these lines, Landa’s current reflections on the subject (2019, p.36) are telling in the sense that “common conjecture in empirical literature is that the financial system’s best performance - based on banks and/or capital markets - leads to healthier economic growth rates as the financial frictions which the productive apparatus faces are reduced and, with this, industrial innovation and competition increase.”
4In Mexico, the case study taken on here, 1% of export companies account for 68% of all exports (CEPAL, 2019) and are naturally eligible for reliable credit.
5With regards to credit fragmentation, 94.9% of businesses in Mexico are micro in size, 4.9% small or medium-sized and 0.2% are large (National Institute of Statistics and Geography [INEGI], 2019).
6Autonomy consists in banks being able to appoint executives, hire personnel and structure payments, choose where to open or close branches and the type of activities to take part in.
8Comisión Nacional Bancaria y de Valores, Panorama Anual de Inclusión Financiera 2020 (National Banking and Securities Comission, Annual Panorama of Financial Inclusion 2020).
9The number of access points per 10,000 adults; impact and intensity which the banking network has on the economy. In other words, the degree of financial inclusion for a country’s population.
11We used data published by the BdeM (2021).
12The test results are found in Table A1 of the statistical appendix.
13The full information criteria is presented in Table A2 of the Statistical appendix.
STATISTICAL APPENDIX
a) Unit root tests of the time series and information criteria for the estimation of the VECM model
Table A1 Unit root and stationarity tests
| Variable | Specification | ADF | PPP | KPSS | order |
| GDP Log | constant | -7.77 | -12.21 | 0.189 | l(1) |
| trend | -8.191 | -12.49 | 0.0451 | l(1) | |
| BCIS log | constant | -4.867 | -5.475 | 0.041 | l(1) |
| trend | -5.077 | -5.643 | 0.137 | l(1) | |
| FDI log | constant | -13.71 | -16.229 | 0.143 | l(1) |
| trend | -13.78 | -16.239 | 0.0359 | l(1) |
Source: created by the authors.
Table A2 Information criteria.
| Criterion | 1 | 2 | 3 | 4 | 5 | 6 |
| AIC | -1 5.77681 | -15.98261* | -15.860271 | -15.748885 | -1 5.694724 | -15.610127 |
| HQ | -15.64323 | -15.748853* | -15.526323 | -15.3147 | -1 5.160407 | -14.975626 |
| SC | -15.44570* | -15.403188 | -15.032515 | -14.672802 | -14.370315 | -14.037391 |
| FPE | 1.40699E-07 | 0.0000001* | 1.2976E-07 | 1.4552E-07 | 1.5441E-07 | 1.6933E-07 |
Note: * optimal number of lags for each information criterion.
Source: created by the authors.
b) Diagnostic test (inverse roots, serial correlation, homoscedasticity and stationarity of equation errors)
Table A3 Diagnostic tests for VECM´s residuals (1).
| Test | Chi ˄ 2 | DF | P-value |
| ARCH (multivariate) | 522 | 540 | 0.7032 |
| Portmanteau Test (asymptotic) | 58.745 | 75 | 0.9165 |
| LM test for autocorrelation (order 1) in the residuals VECM | 5.9963 | 9 | 0.74029 |
| LM test for autocorrelation (order 2) in the residuals VECM | 9.3308 | 9 | 0.40732 |
| Eigenvalue [0 .586283; 0 .300466; 0 .300466; 0.185387 ] |
Source: created by the authors.
Table A4 Stationarity tests for the VECM equation errors (1).
| Errors | ADF | PP | KPSS | |
| GDP Eq. | Constant | -7.274 | -9.900 | 0.127 |
| trend | -7.411 | -9.978 | 0.062 | |
| Cr Eq. | Constant | -7.079 | -9.614 | 0.0398 |
| trend | -7.578 | -9.831 | 0.033 | |
| IE Eq. | Constant | -6.758 | -9.527 | 0.0417 |
| trend | -6.713 | -9.477 | 0.0439 |
Source: created by the authors.
Received: July 19, 2021; Accepted: February 02, 2022











 texto en
texto en