Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Madera y bosques
versión On-line ISSN 2448-7597versión impresa ISSN 1405-0471
Madera bosques vol.18 no.1 Xalapa mar. 2012
Artículo de investigación
Modelos de biomasa aérea y foliar en una plantación de pino de rápido crecimiento en Oaxaca
Above-ground and needle biomass models on a fast-growing pine plantation in Oaxaca
Gerardo Rodríguez-Ortiz1,2, Héctor M. De Los Santos-Posadas1*, Víctor A. González-Hernández1, Arnulfo Aldrete1, Armando Gómez-Guerrero1 y Aurelio M. Fierros-González1
1 Colegio de Postgraduados, Carretera México-Texcoco, km. 36.5, CP 56230, Montecillo, Texcoco, Edo. México. * Autor para correspondencia, c.e.: hmsantos@colpos.mx
2 Dirección actual. División de Estudios de Posgrado e Investigación, Instituto Tecnológico del Valle de Oaxaca, Ex-Hacienda de Nazareno, Oaxaca, CP 71230.
Manuscrito recibido el 17 de abril de 2010.
Aceptado el 13 de marzo de 2012.
RESUMEN
El vigor de un árbol se puede evaluar a partir del follaje, que si bien representa de 4% a 6% de la biomasa total del árbol, es el componente principal para los procesos fisiológicos. El objetivo de este estudio fue estimar la biomasa de acículas en ramas individuales y árbol completo, y ajustar modelos de partición de biomasa aérea en árboles plantados de Pinus patula Schl. et Cham. La biomasa de acículas por rama se estimó con un modelo lineal, que empleó área basal de rama viva, altura de rama y el seccionamiento de copa como variables independientes. La biomasa de los componentes aéreos se estimó con coeficientes de determinación de 0,86; 0,92 y 0,88; para madera con corteza, ramas y acículas, respectivamente. Para madera con corteza se utilizó el diámetro normal (DN) y altura de árbol (AT) en un modelo lineal; la biomasa de ramas y follaje con ecuaciones no lineales que se basaron en el diámetro de copa viva (DCV) y área de copa para ramas; y DCV y AT para la biomasa de follaje. La biomasa total aérea por árbol se estimó con un R2 = 0,87; utilizando DN y AT. La biomasa a una edad de 14 años se distribuyó en 92,9%; 4,7% y 2,4% para madera, ramas y follaje, respectivamente.
Palabras clave: Diámetro basal de rama viva, diámetro de copa viva, Pinus patula, sección de copa.
ABSTRACT
A forest tree health can be accurately assessed by evaluating foliage biomass; even when it represents only 4% to 6% of the total tree biomass, it is the main driver of every major physiological processes. This research was mainly focused on estimating accurately needle biomass at branch and tree level on fast growing trees of Pinus patula Schl. et Cham. Needle biomass per branch was estimated with a linear model, which used live branch basal area, live branch height, and crown section like independent variables. Above ground components were estimated with determination coefficients of 0,86, 0,92 and 0,88 for wood with bark, branches and needles. For the wood with bark model, diameter at breast height (DBH) and total tree height (HT) were used in a linear structure; total branch biomass was fitted with a non-linear model, using live crown diameter (LCD) and crown area (CA) while total needle biomass used LCD and HT on a non-linear model. The aboveground total biomass per tree was estimated with R2 = 0.87, using DBH and HT. At 14 years old, biomass partition was estimated to be 92,9%, 4,7% and 2,4% for wood with bark, branches and needles, respectively.
Key words: Basal live branch diameter, live crown diameter, Pinus patula, crown section.
INTRODUCCIÓN
Ante el cambio climático global las plantaciones forestales de rápido crecimiento adquieren mayor importancia como reservorios de carbono. Por ello, el estimar confiablemente la biomasa (cantidad total de materia orgánica presente) es vital para una determinación adecuada del potencial de secuestro de carbono (Garzuglia y Saket, 2003; Návar et al., 2002). Con frecuencia, tales estimaciones involucran una importante fuente de incertidumbre en los modelos de flujo de carbono (Houghton et al., 2000), sobre todo cuando se utilizan relaciones alométricas poco apropiadas. La distribución de biomasa aérea de los árboles en sus diferentes órganos está influenciada por las condiciones ambientales y de manejo silvícola. Por ejemplo, en Pinus patula se han encontrado incrementos en el crecimiento diametral y en la biomasa global cuando el árbol crece asociado con especies fijadoras de nitrógeno (Gutiérrez-Guzmán et al., 2004).
A pesar que la biomasa foliar sólo representa de 4% a 6% de la biomasa total del árbol, es uno de los componentes más importantes en la productividad de un rodal, porque es donde ocurren muchos procesos fisiológicos fundamentales para el crecimiento, como intercepción de luz, fotosíntesis neta, transpiración, respiración, eliminación de CO2 (Gower y Norman, 1991; Margolis et al., 1995), y es donde se genera la productividad primaria neta (Gholz y Cropper, 1991). Puesto que el follaje presenta estacionalidad con los patrones climáticos y es muy sensible al manejo silvícola, la biomasa foliar debe ser estimada con precisión para explicar la productividad de un rodal. Ello indica que los modelos futuros de crecimiento y rendimiento del rodal deben incluir a este componente, porque involucrarían ecuaciones más específicas para un determinado sitio. En consecuencia, los modelos generados para estimar el follaje deberán ser también sensibles a los factores del ambiente y de manejo, así como superar la inherente dificultad para medir este componente con precisión, pues a medida que el tamaño de los árboles se incrementa, su evaluación consume más tiempo y recursos.
Pinus patula Schl. et Cham. es una pinácea endémica de México y de las más explotadas en el país (Sánchez-González, 2008). Proporciona un alto potencial productivo mediante manejo silvícola simple y posee una amplia variedad fenotípica y genética en la calidad de la madera (Barnes et al., 1994; Dvorak et al., 2000). Sus productos se aprovechan en una amplia gama de usos, por ello fue una de las primeras especies de pinos mexicanos en ser plantadas y mejoradas genéticamente en Sudáfrica (Perry, 1991), y sus áreas de plantación se extendieron a otros países (Dvorak et al., 2000; Valencia y Vargas, 2001). Ixtlán de Juárez es una comunidad pionera del estado de Oaxaca en trabajos serios de plantaciones forestales de rápido crecimiento con P. patula y otras especies. En las plantaciones se ha utilizado germo-plasma de árboles selectos de sus rodales naturales. El establecimiento de diversos ensayos inició en 1995 en una superficie de 5 ha en donde se utilizaron áreas fraccionadas de terrenos que anteriormente estaban ocupados con cultivos agrícolas. Desde 2004, se establecieron parcelas con aclareos aplicados bianualmente en P. patula, en las que se ha reportado un incremento corriente anual, antes y después de las intervenciones de 14,9 m3ha-1año-1 y 36,3 m3ha-1año-1, respectivamente. Con esta tasa de crecimiento la comunidad de Ixtlán se encuentra motivada para extender la superficie plantada con árboles de rápido crecimiento (Servicios Técnicos Forestales Ixtlán de Juárez, 2008).
OBJETIVO
Encontrar modelos matemáticos que permitan estimar con suficiente precisión la biomasa de acículas en ramas individuales y en el árbol completo, así como modelos que estimen la partición de biomasa aérea en árboles plantados de Pinus patula Schl. et Cham. en Ixtlán, Oaxaca, de manera que los modelos puedan ser aplicados a datos de inventario en la plantación.
METODOLOGÍA
El área de estudio
La plantación de 5 ha de P. patula se estableció en 1995 en la comunidad de Ixtlán de Juárez, Oaxaca. Se localiza en terrenos planos y con pendientes de 20% a 40%, a una altitud promedio de 2550 m, a 17° 22' 38,69" LN y 096° 28' 44,8" LO. Las plántulas se obtuvieron de semilla de árboles selectos de la misma comunidad y se establecieron en suelos preparados con maquinaria pesada. El estudio se efectuó en seis parcelas de 20 m x 20 m, delimitadas en 2004; en cinco de ellas se aplicaron aclareos y en la otra no se hicieron (testigo). Los aclareos se aplicaron en intervalos de dos años. En 2008 se hicieron mediciones de diámetro normal (DN, cm), diámetro al pie (DP, cm), diámetro de copa en dos ejes (N-S, E-O, m) y altura total (AT, m) y se calculó área de copa (AC, m2), área basal (AB, m2ha-1), volumen total (VT, m3) y volumen extraído en cada corta (Tabla 1). El VT se determinó mediante el modelo que se utiliza para esta especie:
VT = 0,076528 x DN1,672251 x AT1,333502 (TIASA, 1993), con DN y AT en metros.

Muestreo de madera con corteza
Con los datos de DN y AT se obtuvieron las estructuras diamétricas de cada parcela y la caracterización del tipo de dominancia de la copa. Se seleccionaron, en forma aleatoria, 30 árboles para derribo (cinco por parcela), todos ellos sanos y no bifurcados, distribuidos en las categorías diamétricas, constituidos por tres árboles suprimidos, siete intermedios, 15 codominantes y cinco dominantes. Cada árbol se identificó con su número de parcela, etiqueta de campo y número de derribo. El derribo se realizó en 2009 con motosierra a una altura de 30 cm. En cada árbol derribado se midió diámetro (cm) en el tocón (DT), DN y en la altura del inicio de copa viva (DCV); altura de tocón (HT), AT, longitud de fuste limpio (LFL) y longitud de copa viva (LCV), todas en metros. Después de la separación de ramas del fuste principal, se cortaron trozas de 1 m de longitud, del tocón a la punta; cada troza se pesó en verde (PV en kg) con una báscula electrónica Tororey®, serie EQB/EQM, con capacidad de 100 kg, y se midió el diámetro inferior y superior de las mismas. En la primera troza se obtuvieron dos rodajas (inferior y superior) de 5 cm de espesor; en el resto de las trozas sólo la superior. Todas las trozas fueron identificadas por números progresivos y embolsadas, por cada árbol. En el punto de medición de DT, DN y DCV, así como en la parte media del fuste limpio, se obtuvieron rodajas de 5 cm de espesor. En cada rodaja se determinó el PV (g) en campo y el volumen verde por desplazamiento de agua (VV, cm3) en laboratorio; luego de ser secada en estufa a 102 °C hasta peso constante, se pesó en seco (PS, g) en balanza analítica Sartorius® con capacidad de 1620 g. Con estos datos se determinó el peso específico o densidad relativa básica (PE = PS/VV) de cada rodaja. A cada rodaja se le midió diámetro con corteza (Dcc, cm) y grosor de corteza (GC, cm), y por diferencia se calculó el diámetro sin corteza (Dsc, cm). Con esta información más la longitud de troza y la altura de la sección a la cual fue extraída la rodaja, se cubicaron las trozas y el árbol completo, mediante la metodología de trozas sobrepuestas (Bailey, 1995). Debido a que la densidad de la madera disminuye del centro a la periferia y de la base hacia el ápice y aumenta con la edad de los árboles juveniles, la parte media del fuste es una representación confiable de su densidad promedio (Deene y Hale, 1999). Así, con el producto del PE promedio por árbol (kg m-3) y el VV de cada troza se obtuvo el PS de cada sección y los acumulados para todo el árbol (kg). Se construyeron gráficos entre la altura de la sección y el volumen acumulado con corteza (Vcc m3) y el PS acumulado de todos los árboles, con la intención de detectar anomalías en los datos obtenidos.
Muestreo de ramas y acículas
A los 30 árboles derribados se les separaron las ramas del fuste. En cada rama se identificó o midió: número de verticilo foliar (de la base de copa a punta), número consecutivo de rama, longitud del pie del árbol al punto de inserción de la rama (AR, m), longitud de rama (LR, m) y diámetro basal de rama (DBR, cm) a 1 cm de separación del fuste. El volumen de rama (Vr, cm3) se calculó con la fórmula del cono. En la parte media de la copa, del lado norte, se eligieron aleatoriamente tres ramas de crecimiento medio. De ellas se obtuvieron tres secciones de 5 cm de longitud, que se identificaron y metieron en bolsas de papel. En laboratorio se obtuvo el VV de cada sección con ayuda de una probeta de 250 ml, así como el PV y PS en balanza analítica (este último después del secado en estufa a 102 °C). Con estos datos se pudo estimar el PE de cada muestra. Se obtuvo el PE promedio de rama por árbol (kg m-3). Para la biomasa de ramas individuales y de árbol completo, se utilizó el mismo procedimiento empleado en el componente madera.
Para el muestreo de acículas se seleccionó aleatoriamente una sub-muestra de 20 árboles. En cada árbol se seleccionó al azar una rama por verticilo en la que las acículas se separaron, y luego se obtuvo el PV de las acículas y de la rama. Debidamente identificadas en bolsas de papel, las acículas se llevaron a laboratorio y se secaron a 75 °C por tres días en una estufa. Finalmente, se determinó el PS del follaje en balanza analítica Sartorius®. Con la biomasa de acículas de 314 ramas, se aplicaron modelos de regresión lineal y no lineal para apreciar su cinética en función de las variables obtenidas en las ramas. El modelo de mejor R2 se utilizó para estimar la biomasa de acículas de 1328 ramas más. La suma de la biomasa estimada de acículas y la biomasa de la muestra proporcionaron la biomasa por árbol de este componente.
Análisis estadístico de la información y estrategias de ajuste
La base de datos con la biomasa de cada árbol y de cada uno de sus componentes (madera con corteza, ramas y acículas), y demás variables medidas, se integró. Los análisis se realizaron con el paquete estadístico SAS (SAS, 1996). En cada variable se comprobaron los supuestos de normalidad y homogeneidad de varianzas. Los análisis de regresión lineal se realizaron con PROC GLM, los no lineales con PROC MODEL y los análisis de varianza con PROC ANOVA, todos ellos procedimientos de SAS. Se probaron modelos de regresión lineal y no lineal para estimar la biomasa de cada componente y la biomasa total por árbol, así como la partición de biomasa aérea.
RESULTADOS
Estimación de biomasa foliar por rama y por árbol
Todos los modelos se estimaron mediante una muestra de 314 ramas, correspondientes a 20 árboles. Las variables independientes que se utilizaron en las ecuaciones no lineales para estimar la biomasa de acículas por rama fueron (las ecuaciones 1 y 2 se probaron sobre la base que el producto de las variables mejora sustancialmente la predicción de biomasa):

(función geométrica de Edwards y Penney, 1997).

(función beta modificada- De Los Santos-Posadas, 1998).
donde
BAR: biomasa de acículas por rama (g).
DBR: diámetro basal de rama (cm).
ABR: área basal de rama (= DBR2, cm2).
AR: altura de rama (desde el suelo, m).
LR: longitud de rama (de la base a la punta de yema apical, m).
ARR: altura relativa de rama con respecto a la longitud de copa [(AR-LFL)/LCV].
SEC: altura de rama con respecto a la altura total del árbol (AR/AT).
β0,1,2,3,4: parámetros de los modelos de regresión.
En el análisis preliminar de los datos se encontraron mejores alternativas mediante el producto de área x altura x largo de rama. Estos modelos evitan la predicción negativa de valores de biomasa para ramas pequeñas de la parte inferior de la copa. Los modelos lineales empleados para explicar el comportamiento de BAR estuvieron basados en el área de la sección de la base y altura de rama, más una variable dicotómica de posición en el fuste (Xi) que permite definir la sección inferior, media o superior de la copa donde la rama estaba localizada. Tales modelos fueron tomados de De Los Santos-Posadas (1998):
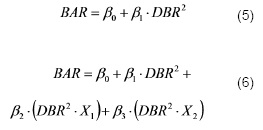

donde las variables son las mismas definidas anteriormente y
X1: 1 si la rama está en la sección inferior 1 (AR/AT < 0,6 = 1), 0 de otra manera.
X2: 1 si la rama está en la sección media 2 (AR/AT > 0,6 y < 0,8 = 2), 0 de otra manera.
El modelo no lineal de la ecuación 1 presentó el mejor ajuste, con un coeficiente de determinación de 0,82 y menor error estándar, que incluye las tres variables medidas en ramas. En contraparte, el modelo lineal (Ec. 5) dio el mayor error en la estimación de biomasa (BAR), con un R2 = 0,70 y únicamente está en función del área basal de rama (Tabla 2).

Los valores de los parámetros de los modelos no lineales se muestran en la tabla 3. Todos los parámetros presentan significancia (p < 0,05) en el valor de t, con excepción del parámetro β3 de la ecuación 3.

En todos los modelos lineales, la ordenada al origen no fue significativa y tampoco lo fue el parámetro β2 de la ecuación 6, lo que sugiere que la cantidad de acículas por rama viva de la parte inferior y la parte superior de la copa no son estadísticamente diferentes. Es de destacar que en la ecuación 7 los valores de t se incrementan y los errores estándar para los parámetros de estimación se reducen (Tabla 4), lo que genera la mejor estimación lineal.

Al realizar las estimaciones con estos modelos a nivel árbol, se optó por aquellas basadas en la ecuación 7, porque producen estimaciones totales por árbol intermedias entre el modelo más optimista (Ec. 3) y el más conservador (Ec. 6), y además incluye en su estructura variables de área basal de rama, altura y la sección de copa de la rama.
Modelos por componente y de partición de biomasa aérea en el árbol
Para la madera con corteza en el fuste, los modelos de mejor estimación de biomasa están en función del diámetro normal y altura del árbol (Tabla 5). Debido al menor error estándar que genera, a la simpleza de su expresión y al coeficiente de determinación de 0,87, la ecuación 10 es la más conveniente para estimar la cantidad de madera con corteza en el fuste, Bmad = 144,08 - 0,82DN2 - 8,09AT + 0,07(DN2 x AT).

El modelo mostró un C.V. de 21% y una significancia estadística para β1 y β3 de p < 0,02 (Tabla 6).
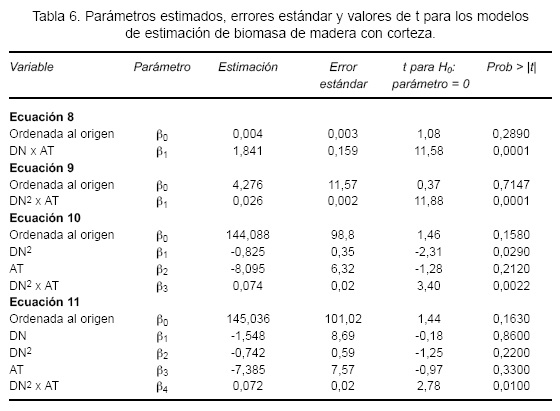
En el componente biomasa en ramas se encontraron mejores ajustes al utilizar las variables referidas a la copa del árbol: diámetro (DCV), longitud (LCV) y área (AC). Los modelos de mejor ajuste se encontraron por el método SUR del procedimiento MODEL del SAS y fueron:

donde
Brama: biomasa de ramas (sin acículas) por árbol (kg).
DCV: diámetro medido al inicio de la copa viva (cm).
LCV: longitud de copa viva (m).
AC: área de copa (cuadrado del diámetro de copa, m).
En la ecuación 12 se tiene un nivel de ajuste con R2 = 0,90 y un error estándar de 0,27. Para la ecuación 13 el nivel de ajuste mejora a R2 = 0,92, y el error se reduce a 0,24. La inclusión de variables referidas a la copa mejora la estimación de biomasa en ramas, en comparación con el uso de variables clásicas de fácil medición, como diámetro y altura del árbol.
En biomasa de follaje (Bfollaje), la ecuación 14 fue la de mejor ajuste:
Bfollaje = 0,00019 x DCV2,138 x AT1,559 con R2 = 0,88 y error estándar de 0,14.
Para la biomasa aérea total por árbol (Btotal) se utilizó la ecuación 15 Btotal = β1(DN x AT)b1 y un sistema de partición de variables de la forma kj Btotal, donde kj representan la fracción del componente con respecto a la biomasa total. Este sistema de ecuaciones fue ajustado mediante el método SUR del procedimiento MODEL. La biomasa total por árbol presentó un coeficiente de determinación de 0,87 y un error estándar de 5,0, modelo en el que se utilizan diámetro normal y altura total en forma no lineal (Fig. 1).
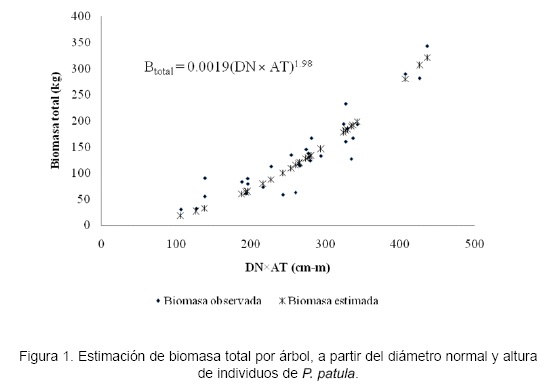
El valor de kj obtenido para madera con corteza, ramas y follaje fue de 0,929; 0,047 y 0,024; respectivamente. Todos los parámetros del sistema de ecuaciones presentaron significancia estadística (p = 0,0001), excepto la ordenada al origen. La biomasa total del árbol se distribuye de la siguiente manera: 92,9% (R2 = 0,99) en madera con corteza en el fuste, 4,7 % (R2 = 0,70) en ramas sin acículas y 2,4 % (R2 = 0,75) en follaje.
DISCUSIÓN
Estimación de biomasa foliar por rama y por árbol
La variable independiente más importante para estimar la biomasa foliar en ramas individuales es el área basal de la rama viva (función del cuadrado del diámetro de base), que proporciona una bondad de ajuste de 70% en el modelo lineal simple (Ec. 5) y una relación lineal significativa, al igual que el parámetro de estimación de la pendiente (p < 0,0001) (tablas 2 y 4). Según KüBner y Mosandl (2000), la cantidad de biomasa y área foliar en la rama está en función de la proporción de tejido vivo conductivo (albura) del área basal de rama, lo cual podría estar sucediendo con la biomasa foliar soportada por las ramas de P. patula. Esto fue determinado por Rodríguez-Ortiz et al. (2011b) para la misma especie y lugar del presente estudio, donde cada unidad de área de albura (cm2) del tallo abastece 0,082 m2; 0,090 m2 y 0,149 m2 de área foliar en el área de sección transversal a la altura del tocón, diámetro normal e inicio de copa viva, respectivamente. Al adicionar al modelo la variable 'altura de la posición de la rama' (AR), la ecuación 2 mejora su bondad de ajuste en 6,8%, con respecto a la ecuación 5; y al incluir 'longitud de rama' (Ec. 1), el coeficiente de determinación se incrementa en 11,7%, con respecto a la ecuación 5 (tablas 3 y 4). Esta es la mejor estimación no lineal para la biomasa del follaje en ramas individuales de P. patula. Este resultado coincide con el encontrado para Pinus sylvestris donde se obtuvo una bondad de ajuste de 83% en una relación no lineal (Jonckheere et al., 2005). Las ecuaciones 3 y 4 tienen estimaciones de biomasa en ramas con R2 semejante (0,81), ya que incluyen, además del diámetro basal, la altura relativa de rama con respecto a la longitud de copa viva del árbol (ARR) y la altura de rama con respecto a la altura del árbol (SEC). Los mayores valores de t en la estimación de los parámetros de regresión son indicativos del incremento en la precisión de los mismos, con la consiguiente reducción en su error estándar (Monroy y Návar, 2004). Estos requisitos deseables se cumplen en los coeficientes de regresión de la ecuación 7 (Tabla 4), con excepción de la ordenada al origen, que resultó no significativa (p = 0,3371) pero que es necesaria para producir estimaciones de mínimos cuadrados corregidos. De esta manera, la ecuación 7 es el modelo lineal de mejor estimación para BAR, ya que mejora el coeficiente de determinación en 10,2% con respecto a usar sólo ABR y proporciona resultados semejantes al encontrado en biomasa de follaje por rama en Abies balsamea (L.) (Gilmore y Zenner, 2005). Esto podría ser el resultado de incluir variables dicotómicas que denotan la posición de la rama (Xi), que permiten definir la sección de copa a la cual la rama pertenece y que son convenientes de incluir, como fue demostrado para otras especies de coníferas (Bartelink, 1996; Temesgen, 2003). Además, la biomasa y área foliar presentan variación entre las secciones inferior, media y superior de la copa (Kershaw y Maguirre, 1995).
Modelos por componente y de partición de biomasa aérea a nivel árbol
En la estimación del componente madera con corteza en el fuste, los modelos lineales (ecuaciones 10 y 11) presentaron mejores coeficientes de determinación (R2) que la ecuación lineal (Ec. 9) y que la ecuación no lineal (Ec. 8) (Tabla 5). El modelo lineal (Ec. 10) con bondad de ajuste 0,87 (R2) y un bajo error estándar (4,9), utiliza variables independientes similares a la variable combinada para volumen total de la forma DN2, AT. Esto permite inferir que la biomasa de este componente en P. patula guarda una relación lineal estrecha con el diámetro, y que la inclusión de la variable AT en el modelo permite mejorar el coeficiente de determinación. Esto fue demostrado por Acosta-Mireles et al. (2002) y Brown (2001) en otras coníferas y coincide con los resultados encontrados por Návar et al. (2004) en plantaciones jóvenes de pinos en Durango, México.
La estimación de biomasa en ramas sin acículas tuvo un coeficiente de determinación de 0,92 (Ec. 13), al utilizar el diámetro al inicio de copa viva (DCV) y el área de copa proyectada (AC) en una ecuación no lineal. En P. patula la variable más importante fue DCV, ya que por tratarse de árboles jóvenes, el área de la sección en ese punto es casi totalmente conductiva y puede reflejar la biomasa de ramas que es capaz de soportar, como fue demostrado por Pinazo et al. (2007) para Pinus taeda. El AC es una variable que ayuda a explicar la biomasa de ramas en la copa y además guarda una estrecha relación con el diámetro normal de P. patula.
Esto coincide con lo encontrado para P. sylvestris (R2 = 0,9) por Jonckheere et al. (2005). Debido a que la biomasa de un individuo se identifica con su índice de productividad, el AC puede ser un indicador del vigor del árbol. Acosta et al. (2003) encontraron en diversas especies forestales que el vigor puede ser explicado por el área de la silueta de la copa (AC), misma que guarda una relación directa con la biomasa foliar y ramas. Por ello, mediante la evaluación de la biomasa en árboles jóvenes de P. patula se podrían conocer indirectamente los individuos que se van incorporando a nuevas categorías diamétricas con el fin de asegurar el éxito de las plantaciones. La biomasa foliar presentó una relación no lineal con el diámetro de copa viva y la altura del árbol, con una bondad de ajuste de 0,88.
Esto se contrapone con otros investigadores (Jonckheere et al., 2005; Mencuccini y Grace, 1995), quienes con un modelo polinómico basado en DN encontraron ajustes con R2 = 0,95 para este componente en P. sylvestris. Sin embargo, la inclusión del DCV en el modelo se justifica por la relación existente entre la biomasa aérea y el tejido conductivo que la sustenta, lo cual podría utilizarse para caracterizar la arquitectura de copas y la acumulación de biomasa en el árbol. Según diversos estudios (Fassola et al., 2008; Laclau, 2003; Pinazo et al., 2007), la tasa de transpiración del follaje es proporcional al área foliar y la tasa de provisión de agua hacia la copa es proporcional al área de tejido conductivo, que en el DCV es de 90% en P. taeda. Para otras especies, sobre todo de plantaciones jóvenes como la del presente estudio, se puede asumir que la sección del DCV es casi totalmente conductiva y puede ser utilizada como una expresión indirecta de la biomasa foliar o directa del área de albura resultante de distintos tratamientos silvícolas, como fue desarrollado en P. taeda por Fassola et al. (2005) quienes encontraron que la sección del diámetro de copa viva presentó mejores ajustes que la sección del DN, ya que a esta altura muchos tejidos han dejado de ser conductivos. El modelo propuesto para estimar biomasa foliar tiene la inherente dificultad de la medición del DCV; pero de acuerdo con Fassola et al. (2008) así se tienen mayores criterios con fundamentos biológicos (que no determinísticos), para que dichos modelos permitan predecir la acumulación de tejidos en árboles, como fue desarrollado por Rodríguez-Ortiz et al. (2011a) en el mismo lugar y especie del presente estudio, la arquitectura de la copa y consecuentemente la estructura de las ramas. Los componentes de biomasa aérea varían con la edad de rodal; cuando éste es joven, la biomasa se concentra de mayor a menor proporción en madera, ramas y follaje.
La biomasa aérea total (Btotal) y su partición se ajustó mediante un sistema de ecuaciones que utilizan el DN y altura de árboles mediante una estructura no lineal, con R2 de 0,87 para Btotal. Este resultado es similar al encontrado por Schroeder et al. (1997) y Ter-Mikaelian y Korzukhin (1997), pues en otras especies las mejores relaciones de la biomasa aérea total se desarrollaron con modelos de regresión no lineal. A medida que un rodal envejece, la proporción del componente rama y follaje se incrementa, con la consecuente reducción en el componente madera, tal y como fue observado en una plantación de Hevea brasiliensis (Monroy y Návar, 2004) de 14 años, donde se reportaron valores de 79,63% y 20,36% para madera y ramas, respectivamente; a una mayor edad, la biomasa en madera se redujo a 73,9%. Este comportamiento inicial se encontró en la plantación de P. patula de 14 años de edad, donde la biomasa en madera con corteza, ramas y follaje fue de 92,9%; 4,7% y 2,4%, respectivamente.
El haber encontrado un modelo preciso de biomasa para cada componente aéreo permitió obtener el ajuste de biomasa total aérea como función de variables de fácil medición (DN, AT) determinadas en inventarios forestales. Para poder aplicarlos a otras condiciones basta conocer la función de volumen para determinar factores de expansión de biomasa (FEB) variables, con los que es posible conocer la biomasa aérea total de Pinus patula sólo con medir su DN y AT. Así, se evitaría repetir el experimento realizado en este estudio para otras condiciones de crecimiento de la especie, pero no evitaría realizar el experimento para otras especies.
Este FEB fue determinado a partir del modelo de estimación de biomasa total (Btotal) y del modelo de volumen total utilizado por la comunidad (VT):
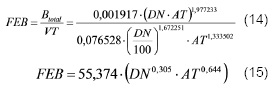
donde
FEB: factor de expansión de biomasa variable.
Btotal: biomasa total aérea (kg).
VT: volumen de fuste total (m3).
DN: diámetro normal (cm).
AT: altura total (m).
El producto del FEB por el volumen total de madera en el fuste (obtenido en un inventario forestal) proporciona la estimación de biomasa total aérea del individuo; en esto radica la importancia de los modelos determinados en este estudio.
CONCLUSIONES
A diferencia de otros estudios, donde la biomasa de acículas por rama y para árbol completo se estima con base en el diámetro normal como variable independiente, en el estudio que aquí se presenta el mejor modelo de tipo lineal (Ec. 7) utiliza variables relacionadas con ramas individuales, como área de la sección, altura de rama y sección específica de la copa a la cual la rama pertenece. Estas variables son más susceptibles a las variaciones del medio ambiente, sitio y manejo del rodal.
De esta manera, las ecuaciones generadas en este trabajo serán específicas para estimar la biomasa foliar del sitio de plantación o de otros con condiciones similares con los niveles de densidad encontrados, pero que si se aplicaran a condiciones diferentes a las aquí evaluadas, podrían dar estimaciones inciertas de biomasa foliar. Sin embargo, la utilidad de los modelos de biomasa aérea encontrados es su compatibilidad con las ecuaciones de estimación del volumen maderable, situación que permite utilizarlos en otras condiciones, mediante el empleo de factores de expansión de biomasa variables.
Aunque la heterocedasticidad (heterogeneidad de varianzas asociadas con el tamaño de las ramas) es una característica implícita de las variables dasométricas, que otros métodos de biomasa foliar poseen, los modelos aquí propuestos para P. patula reducen estos problemas porque la copa se clasificó en secciones, y producen una estimación media de follaje de 3,2282 kg árbol-1 e incluyen una variable de posición (Xi) que determina la sección específica de la copa donde la rama pertenece. Esto puede permitir detectar diferencias en la distribución del follaje en la copa, así como obtener funciones de distribución de biomasa foliar y ser ventajosas en las comparaciones de las predicciones totales.
La biomasa total del componente aéreo para Pinus patula se estimó mediante el diámetro normal y la altura del árbol en un modelo no lineal con bondad de ajuste de (R2) 0,87. A una edad de 14 años, la biomasa se distribuye en 92,9%; 4,7% y 2,4% para madera, ramas y follaje, respectivamente. Estos coeficientes de partición son muy similares a los estimados por Figueroa-Navarro et al. (2010) para P. patula cultivado en rodales naturales en Zacualtipán, Hidalgo (89,2%; 9,5% y 1,3% para madera, ramas y follaje, respectivamente) donde, sin embargo, existe una mayor concentración de biomasa total en ramas, sin duda debida a la heterogeneidad del espaciamiento que impide una poda natural uniforme. No obstante, la proporción de follaje está en general muy por debajo del 4%-6% encontrado en otras especies de coníferas, lo que sugiere que como especie, P. patula tiene una eficiencia fotosintética notable.
REFERENCIAS
Acosta M., M., F. Carrillo A. y O.S. Magaña T. 2003. Técnica de la silueta para estimar área foliar y biomasa aérea en especies forestales. Revista Mexicana de Ciencias Forestales 28:45-56. [ Links ]
Acosta-Mireles, M., J. Vargas-Hernández, A. Velázquez-Martínez y J. D. Etchevers-Barra. 2002. Estimación de la biomasa aérea mediante el uso de relaciones alométricas en seis especies arbóreas en Oaxaca, México. Agrociencia 36:725-736. [ Links ]
Bailey, R.L. 1995. Upper-stem volumes from stem-analysis data: an overlapping bolt method. Canadian Journal of Forest Research 25:170-173. [ Links ]
Barnes, R.D., J.S. Birks, G. Battle y L.J. Mullin. 1994. The genetic control of ring width, wood density and tracheid length in the juvenile core of Pinus patula. Southern African Forestry Journal 169:15-20. [ Links ]
Bartelink, H.H. 1996. Allometric relationships on biomass and needle area of Douglas-fir. Forest Ecology and Management 86:193-203. [ Links ]
Brown, S. 2001. Measuring carbon in forests: current status and future challenges. Environmental Pollution 116:363-372. [ Links ]
De Los Santos-Posadas, H.M. 1998. Estimation of individual branch and whole tree leaf biomass from loblolly pine. Master of Science, University of Georgia. Athens, Georgia. 86 p. [ Links ]
Deene, M. y M. Hale. 1999. Cell wall and lumen percentages in relation to wood density of Nothofagus nervosa. IAWA Journal 20:23-36. [ Links ]
Dvorak, W.S., G.R. Hodge, J.E. Kietzka, F. Malan, L.F. Osorio y T.K. Stanger. 2000. Pinus patula. In: Conservation and Testing of Tropical and Subtropical Forest Tree Species by the CAMCORE Cooperative, College of Natural Resources, NCSU. Raleigh, NC. EUA. p: 148-173. [ Links ]
Edwards, Jr. C.H. y D. Penney. 1997. Calculus with analytic geometry. 4th Edition. Prentice Hall. 960 p. [ Links ]
Fassola, H., E. Crechi, S. Barth, A. Keller, M. Pinazo, R. Martiarena, A. Von Wallis e I. Figueredo. 2008. Relación entre la biomasa aérea y la sección transversal en la base de copa viva de Pinus taeda L. en el norte de la provincia de Misiones, Argentina. In: XIII Jornadas Técnicas Forestales y Ambientales. Facultad de Ciencias Forestales, UNAM-EEA Montecarlo, INTA. El Dorado, Misiones, Argentina. [ Links ]
Fassola, H.E., S.M. Lacorte, A.N.I. Pachas y R. Pezzuti. 2005. Factores que influencian la producción de biomasa forrajera de Axonopus jesuiticus Valls, bajo dosel de Pinus taeda L. en el nordeste de Corrientes. Revista de Investigaciones Agropecuarias 34:21-38. [ Links ]
Figueroa-Navarro, C.M., G. Ángeles-Pérez, A. Velázquez-Martínez y H.M. de los Santos-Posadas. 2010. Evaluación de la biomasa en un bosque bajo manejo de Pinus patula Schltdl. et Cham. en Zacualtipán, Hidalgo. Rev. Mex. Cien. For. 1(1): 105-112. [ Links ]
Garzuglia, M. y M. Saket. 2003. Wood volume and woody biomass. Food and Agricultural Organization of the United Nations. Roma, Italy. 30 p. [ Links ]
Gholz, H.L. y W.P. Cropper. 1991. Carbohydrate dynamics in mature Pinus elliottii var. elliottii trees. Canadian Journal of Forest Research 21:1742-1747. [ Links ]
Gilmore, D.W. y E.K. Zenner. 2005. Foliage-sapwood area relationships for balsam fir in North-Central Minnesota. NJAF 22:203-210. [ Links ]
Gower, S.T. y J.M. Norman. 1991. Rapid estimation of leaf-area index in conifer and broad-leaf plantations. Ecology 72:1896-1900. [ Links ]
Gutiérrez-Guzmán, B., J.D. Etchevers-Barra, A. Velázquez-Martínez y J. Almaraz-Suárez. 2004. Influencia del aile (Alnus firmifolia) en el crecimiento de plantas de Pinus patula. Terra Latinoamericana 23:89-96. [ Links ]
Houghton, R.A., D.L. Skole y C.A. Nobre. 2000. Annual fluxes of carbon from deforestation and regrowth in the Brazilian Amazon. Nature 403: 301-304. [ Links ]
Jonckheere, I., B. Muys y P. Copping. 2005. Allometry and evaluation of in situ optical LAI determination in Scots pine: a case study in Belgium. Tree Physiology 25:723-732. [ Links ]
Kershaw, Jr. J.A. y D.A. Maguirre. 1995. Crown structure in western hemlock, Douglas-fir, and grand fir in western Washington: trends in branch-level mass and leaf area. Canadian Journal of Forest Research 25:1897-1912. [ Links ]
KüBner, R. y R. Mosandl. 2000. Comparison of direct and indirect estimation of leaf area index in mature Norway spruce stands of eastern Germany. Canadian Journal of Forest Research 30: 440-447. [ Links ]
Laclau, P. 2003. Biomass and carbon sequestration of ponderosa pine plantations and native cypress forests in northwest Patagonia. Forest Ecology and Management 180:17-333. [ Links ]
Margolis, H., R. Oren, D. Whitehead y M.R. Kaufmann. 1995. Leaf area dynamics of conifer forests. In: Smith W.K. y T.M. Hinckley (Eds.). Ecophysiology of coniferous forests. Academic Press. p: 181-223. [ Links ]
Mencuccini, M. y J. Grace. 1995. Climate influences the leaf area/sapwood area ratio in Scots pine. Tree Physiology 15:1-10. [ Links ]
Monroy, R.C. y J.J. Návar. 2004. Ecuaciones de aditividad para estimar componentes de biomasa de Hevea brasiliensis Muell. Arg., en Veracruz, México. Madera y Bosques 10:29-43. [ Links ]
Návar C., J.J., J. Nájera y E. Jurado. 2002. Biomass estimation equations in the Tamaulipas thornscrub of northeastern Mexico. Journal of Arid Environments 52:167-179. [ Links ]
Návar C., J.J., N. González B., J.J. Graciano L., V. Dale y B. Parresol. 2004. Additive biomass equations for pine species of forest plantations of Durango, Mexico. Madera y Bosques 10:17-28. [ Links ]
Perry, P.J. 1991. The pines of Mexico and Central America. Timber Press Inc. Portland, Oregon. EUA. 231 p. [ Links ]
Pinazo, M.A., R.A. Martiarena, A. Von Wallis, E. Crechi, N.M. Pahr y O. Knebel. 2007. Efectos de la intensidad de raleo sobre la compartimentalización y stock de carbono en plantaciones de Pinus taeda L. establecido sobre ultisoles de Misiones. Revista de Investigaciones Agropecuarias 36:5-20. [ Links ]
Rodríguez-Ortiz, G., A. Aldrete, V.A. González-Hernández, H.M. De Los Santos-Posadas A. Gómez-Guerrero y A. M. Fierros-González. 2011a. ¿Afectan los aclareos la acumulación de biomasa aérea en una plantación de Pinus patula? Agrociencia 45(6):719-732. [ Links ]
Rodríguez-Ortiz, G., V.A. González-Hernández, A. Aldrete, H.M. De Los Santos-Posadas A. Gómez-Guerrero y A. M. Fierros-González. 2011b. Modelos para estimar crecimiento y eficiencia de crecimiento en plantaciones de Pinus patula en respuesta al aclareo. Revista Fitotecnia Mexicana 34(3):205-212. [ Links ]
Sánchez-González, A. 2008. Una visión actual de la diversidad y distribución de los pinos de México. Madera y Bosques 14(1):107-120. [ Links ]
SAS Institute. 1996. SAS/STAT User's guide. SAS Institute, Inc., Raleigh, NC. [ Links ]
Schroeder, P., S. Brown, J. Mo, R. Birdsey y C. Cieszewsky. 1997. Biomass estimation for temperate broadleaf forest of the United States using inventory data. Forest Science 43:424-434. [ Links ]
Servicios Técnicos Forestales Ixtlán de Juárez. 2008. Informe de actividades de los servicios técnicos forestales de Ixtlán de Juárez, Oaxaca. s/p. [ Links ]
Temesgen, H. 2003. Evaluation of sampling alternatives to quantify tree leaf area. Canadian Journal of Forest Research 33:82-95. [ Links ]
Ter-Mikaelian, M.T. y M.D. Korzukhin. 1997. Biomass equations for sixty five North American tree species. Forest Ecology and Management 97:1-24. [ Links ]
TIASA (Técnica Informática Aplicada. S. A.). 1993. Programa de manejo integral forestal de Ixtlán de Juárez 1993-2002. Oaxaca, México. 290 p. [ Links ]
Valencia M., S. y J.J. Vargas H. 2001. Correlaciones genéticas y selección simultánea del crecimiento y densidad de la madera de Pinus patula. Agrociencia 35:109-119. [ Links ]
Woods, K.D., A.H. Feiveson y D.B. Botkin. 1991. Statistical analysis for biomass density and leaf-area index estimation. Canadian Journal of Forest Research 21:974-989. [ Links ]
Nota
Este documento se debe citar como: Rodríguez-Ortiz, G., H.M. De los Santos-Posadas, V.A. González-Hernández, A. Aldrete, A. Gómez-Guerrero y A.M. Fierros-González. Modelos de biomasa aérea y foliar en una plantación de pino de rápido crecimiento en Oaxaca. Madera y Bosques 18(1):25-41.














