Introducción
La alometría, se define como el análisis de la relación de proporción entre las distintas medidas o los aumentos relativos de un organismo (Goukd, 1966; Gayon, 2000) y permite predecir la dimensión de una variable a través de cualquier otra en un mismo individuo (Dietze, Wolosin y Clark, 2008). En el área forestal, se ha modelado la relación alométrica entre variables de diámetro normal (d), diámetro de tocón (dt) (Benítez-Naranjo, Rivero-Vega, Vidal-Corona, Rodríguez-Rodríguez y Álvarez-Rivera, 2004; Pompa-García, De los Santos-Posadas, Zepeda-Bautista y Corral-Rivas, 2011; Hernández-Ramos et al., 2016), altura total (A) (Martínez-López y Acosta-Ramos, 2014; García et al., 2017), volumen (V) (Quiñonez, Cruz, Vargas y Hernández, 2012; García-Cuevas et al., 2017); biomasa aérea (B) y carbono acumulado (C) (Avendaño, Acosta, Carrillo y Etchevers, 2009; Razo-Zárate, Gordillo-Martínez, Rodríguez-Laguna, Maycotte-Morales y Acevedo-Sandoval, 2013). En particular, la A y el d son cruciales para la planeación de los programas de manejo en los bosques, debido a que son las variables más registradas en los inventarios forestales y están correlacionadas entre sí (Prodan, Peters, Cox y Real, 1997).
En México, la relación alométrica entre A-d ha sido analizada para Pinus teocote Schiede ex Schltdl. en el occidente del estado de Hidalgo y Nanacamilpa, Tlaxcala (Hernández et al., 2015; Guerra-De la Cruz et al., 2019), P. pseudostrobus Lindl. en la Comunidad Indígena de San Juan Nuevo Parangaricutiro, Michoacán (Hernández-Ramos et al., 2018a; Hernández-Ramos et al., 2018b) y P. montezumae Lamb. en Nanacamilpa, Tlaxcala (Guerra-De la Cruz et al., 2019), por mencionar algunos; sin embargo, la información es escasa para especies tropicales, ya que solo se reportan para P. chiapensis Martínez-Andresen, Cinnamomum sp. y Melia azedarach L. establecidas en plantaciones forestales de Tlapacoyan, Veracruz (Castillo-Gallegos, Jarillo-Rodríguez y Escobar-Hernández, 2018), ya sea mediante modelos locales generalizados, o bajo el enfoque de modelos de efectos mixtos (MEM) (Corral-Rivas, Álvarez-González, Crecente-Campo y Corral-Rivas, 2014).
Los MEM, a diferencia de los ajustes tradicionales por mínimos cuadrados ordinarios (MCO), tienen la particularidad de agrupar la variabilidad de la información por variable de clasificación dentro del ajuste estadístico, al emplear covariables adicionales al modelo empleado (García y Rapelli, 2011; Seoane, 2014). Esta variabilidad particular, que se incluye dentro de la formulación del modelo al considerar tanto parámetros fijos que son comunes a la muestra como aleatorios que son particulares para cada nivel de agrupación y en donde los niveles múltiples de clasificación compensan las diferencias en los grados de libertad en la estructura de los modelos ajustados (De los Santos-Posadas, Montero-Mata y Kannien, 2006) y mejoran significativamente la modelación de la relación alométrica A-d (Corral-Rivas et al., 2014; Corral, Silva y Quiñonez, 2019).
La mejora estadística de la aplicación de los MEM se ha documentado al incluir covariables adicionales a los ajustes; por ejemplo, los trabajos de Stankova y Duéguez-Aranda (2013) en Pinus sylvestris L., cubriendo distintas regiones de Bulgaria; Corral-Rivas et al. (2014), al ajustar esta relación a 25 especies en un bosque mixto en Durango, México; Petrás, Bosela, Mecko, Oszlányi y Popa (2014), quienes ajustan a Picea abies Karst., Abies alba L. y Fagus sylvatica L. ecuaciones altura-diámetro en bosques de Eslovaquia; Ercanli (2015), al modelar la altura a través del diámetro en Fagus orientalis Lipsky en el noroeste de Turquía; y Sharma, Vacek y Vacek (2016), quienes ajustaron la relación en bosques mixtos de Quercus petraea (Matt.) Liebl y Alerce europeo Miller en la Republica Checa.
Lysiloma latisiliquum (L) Benth. (‘tzalám’) es una especie que crece en los bosques tropicales sub-caducifolios secos próximos a las costas y sobre suelo calizo, preferentemente calcáreos de textura franca con buen drenaje (Pennington y Sarukhán, 2016). La especie se distribuye de manera natural en Cuba, Haití, Puerto Rico, República Dominicana, Las Bahamas, sur de Florida, EE. UU., México, Belice y Guatemala entre los 0 m y 400 m de altitud (Betancourt, 1987; Organización Internacional de las Maderas Tropicales [OIMT], 2012).
Los árboles alcanzan hasta 20 m de altura total (A) y 120 cm de diámetro normal (d) (Betancourt, 1987; Pennington y Sarukhán, 2016), pero comúnmente suelen tener 30 cm de d en promedio (Negreros-Castillo y Martínez, 2011); la especie es de importancia para los aprovechamientos forestales en la Península de Yucatán (Synnott, 2009) y la industria del aserrío en Quintana Roo (Instituto Nacional de Estadística y Geografía [Inegi], 2017), por su madera preciosa y de densidad alta (0.70 g/cm3 a 0.88 g/cm3) (Comisión Nacional Forestal [Conafor], 2008; OIMT, 2012). Además, es una planta ornamental que suele utilizarse como alimento para el ganado en temporada de estiaje (Betancourt, 1987; Baldizán et al., 2008).
La información silvícola documentada para L. latisiliquum va desde la estimación de volúmenes totales y de fuste limpio en Quintana Roo y Campeche (De los Santos, 1976; Patiño, López y Gómez, 1994), tasas de crecimiento e incremento en diámetro para bosques secundarios de Escárcega, Campeche (López-Torres y Tamarit-Urias, 2005), crecimiento y repoblación en bosques de Quintana Roo (Negreros-Castillo y Martínez, 2011), un sistema biométrico en Quintana Roo (Vargas-Larreta et al., 2017) y la representación cuantitativa de la relación entre el dt con el d, así como de A y volumen (v) (García et al., 2017); sin embargo, no se cuenta con información sobre la relación entre la A y el d, aun cuando éstas variables son fundamentales para la elaboración de planes de manejo forestal (Prodan et al., 1997). Así como por la importancia que tiene la especie en Quintana Roo (Synnott, 2009) y la relación alométrica A-d en los aprovechamientos forestales (Prodan et al., 1997).
Objetivos
Determinar el modelo alométrico con efectos mixtos que mejor describe la relación altura total-diámetro normal (A-d) para árboles de Lysiloma latisiliquum en Quintana Roo, México; planteando la hipótesis que el modelo con inclusión de efectos mixtos tiene un ajuste superior en comparación con la forma tradicional.
Materiales y métodos
Área de estudio. Quintana Roo se ubica en el sureste mexicano con características topográficas de lomeríos bajos y llanuras rocosas, con clima cálido sub-húmedo (Aw), temperatura media anual de 26 °C y precipitación media de 1300 mm (Inegi, 2016). Estas condiciones propician el desarrollo de selvas; baja caducifolia y mediana sub-perennifolia (Secretaría de Medio Ambiente y Recursos Naturales-Conafor [Semarnat-Conafor], 2014), donde se focalizó el estudio.
Datos. La información utilizada incluye datos de altura total (A), diámetro normal (d), diámetro de copa (dc) y altura de fuste limpio (Af) de 2214 árboles y obtenida de 175 conglomerados del Inventario Nacional Forestal y de Suelos (2004-2009) para el estado de Quintana Roo, además del municipio (M), tipo de vegetación primaria (Vp): selva baja caducifolia o selva mediana sub-perennifolia; y altitud del conglomerado (Conafor, 2016). En la muestra se tienen diámetros normales de entre 7.5 cm y 80 cm, con alturas totales que van de 7 m a 22 m (Tabla 1).
Tabla 1 Estadísticas básicas de la muestra utilizada de Lysiloma latisiliquum en Quintana Roo, México.
| Estadístico | Variable | |||
| Diámetro normal (cm) | Altura total (m) | Diámetro de copa (m) | Altura de fuste limpio (m | |
| Número de observaciones | 2214 | 2214 | 2214 | 2214 |
| Media | 18.1 | 11.4 | 3.5 | 3.6 |
| Máximo | 80.0 | 22.0 | 10.8 | 10.0 |
| Mínimo | 7.50 | 7.0 | 0.5 | 1.0 |
| Varianza | 78.28 | 8.12 | 2.54 | 2.63 |
| Desviación estándar | 8.85 | 2.85 | 1.59 | 1.62 |
| Índice de curtosis | 5.60 | 0.36 | 1.08 | 0.87 |
Los registros tanto del diámetro de copa (dc), como de la altura de fuste limpio se agruparon en categorías de un metro, con el fin de reducir su variabilidad dentro de los análisis estadísticos como covariables (e.g. un árbol de 1.48 m de diámetro de copa pertenece a la categoría de 1 m y un árbol de 2.54 m de altura, pertenece a la categoría de 3 m).
Para comprender con mayor detalle la relación entre la altura total-diámetro normal (A-d) y conocer la estabilidad mecánica de la especie, se determinó el índice de esbeltez (IE) definido como la relación de proporcionalidad entre la altura total y el diámetro normal de los árboles (A/d) (Nájera-Luna y Hernández-Hernández, 2018; Hernández et al. 2018c). Para representar la tendencia de este índice, se agruparon los 2214 registros de árboles por categoría diamétrica a cada 5 cm (Cd: e.g. 5, 10, 15, 20,…) para reducir la variabilidad (16 pares de datos en total) y ajustar un modelo de tipo alometríco [1].
Donde:
IE: índice de esbeltez (A/d)
Cd: categoría diamétrica
a n : parámetros a estimar
Modelos locales A-d. Se ajustaron seis modelos de tipo local A-d reportados en la literatura (Hossfeld, 1822; Weibull, 1951; Burkhart y Strub, 1974; Bates y Watts, 1980; Kiviste, Álvarez, Rojo y Ruiz, 2002; Da Cunha y Guimarães, 2009; Uzoh, 2017) en el programa R® por medio del paquete para modelos no lineales (nl) y el método de máxima verosimilitud (ML) (R core Team, 2015) (Tabla 2).
Tabla 2 Modelos locales altura total-diámetro normal (A-d) ajustados para Lysiloma latisiliquum en Quintana Roo, México.
| Número | Modelo | Forma |
| 2 | Chapman-Richards (Uzoh, 2017) |
|
| 3 | Hossfeld (1822) |
|
| 4 | Weibull (1951) |
|
| 5 | Bates y Watts (1980) |
|
| 6 | Burkhart y Strub (1974) |
|
| 7 | Vestjordet-1 - Naslund (Da Cunha y Guimarães, 2009) |
|
El ajuste estadístico y selección del modelo de mejor ajuste se realizó a través de la significancia de los parámetros (p < 0.05), el mayor valor del coeficiente de determinación (R 2) y los menores valores en los errores estándar aproximados (Eea) de los parámetros, así como en los criterios de información de Akaike (AIC) y Bayesiano (BIC), por sus siglas en inglés (Corral-Rivas et al., 2014; Guerra-De la Cruz et al., 2019). Además, se verificaron los supuestos de normalidad de los errores mediante la tendencia lineal de los cuantiles con respecto a los residuales estandarizados, así como la homocedasticidad de los residuales (SAS Institute Inc., 2014).
Modelos de efectos mixtos A-d. Para verificar la existencia de diferencias significativas en cada covariable por incluir al mejor modelo local bajo el enfoque de efectos mixtos: entre conglomerados, municipios (M) y altitudes, tipos de vegetación primaria (Vp) y categorías diamétricas (CD), así como entre clases de copa (Cc) y alturas de fuste limpio (Af), se utilizó un modelo lineal generalizado (GLM, por sus siglas en inglés) (Gil, 2001) a un nivel de confiabilidad de 95% (p = 0.05) mediante la prueba de hipótesis del error tipo I (Minitab, 2019).
Con el fin de explicar la aportación de las covariables en la relación A-d, dentro del mejor modelo de tipo local fueron incluidos los efectos, para después ser ajustados como efectos mixtos en R® con el procedimiento nlme y la técnica ML. En el ajuste se incluyó una estructura de correlación de orden de media móvil de autocorrelación (corARMA(p,q)) para eliminar y/o disminuir la correlación entre las variables, donde p son los enteros no negativos de orden autorregresivo y q el orden de promedio móvil de la estructura ARMA, lo cual en ambos casos son predeterminados a cero (Pinheiro y Bates, 2000; R core Team, 2015). De esta forma, se incluirá individualmente el efecto en cada uno de los parámetros del modelo y se realizarán modificaciones para verificar cuál explica mejor la variabilidad de la muestra (Calama y Montero, 2004; Castedo, Diéguez-Aranda, Barrio, Sánchez y Von Gadow, 2006).
La selección del mejor modelo con efectos mixtos se realizó de igual forma que en los modelos anteriores, al considerar la significancia de sus parámetros (p < 0.05), valores altos del R 2 , así como valores bajos de AIC y BIC (Corral-Rivas et al., 2014; Guerra-De la Cruz et al., 2019). Aun cuando la modelación bajo el enfoque de efectos mixtos asume una distribución normal con media igual a cero y una matriz de varianzas-covarianzas representada con la expresión 8 y que engloba toda la variabilidad de la muestra utilizada (Littell, Milliken, Stroup, Wolfinger y Schabenberger, 2006), se verificaron en el mejor modelo los supuestos de normalidad de los errores donde la tendencia hacia una línea recta es lo deseable y la homocedasticidad de los residuales para verificar que no se tenga un aumento en los residuales a medida que a variable estimada incrementa (SAS Institute Inc., 2014).
Donde
Capacidad de predicción de los modelos y validación de sus ajustes. La precisión de los ajustes se verificó a través del sesgo promedio de los residuales (E, m) y la diferencia agregada expresada en porcentaje (DA, %), que buscan menores valores en las desviaciones de las predicciones obtenidas con el mejor modelo respecto de los datos reales (Prodan et al., 1997; Lencinas y Mohr-Bell, 2007).
Con el propósito de realizar una validación estadística del modelo de efectos mixtos seleccionado como el mejor, se utilizaron 4682 pares de datos A-d obtenidos de diversos estudios en nueve ejidos del estado de Quintana Roo (Calakmul, Chan Santa Cruz, Dzula, Nuevo Becal, Nuevo Tabasco, Petcacab, Pimienta, San Felipe Bacalar e Xyatil); con estos datos, los cuales fueron independientes al ajuste, se efectuó una comparación de medias a 99% de confiabilidad (prueba de t) asumiendo medias iguales (R core Team, 2015; Martínez, Sánchez y Faulin, 2006).
Resultados
El índice de esbeltez (IE) disminuye con el aumento en las dimensiones del arbolado, lo cual ocasiona que el individuo sea más estable a daños mecánicos causados por vientos o huracanes, y de forma implícita disminuye el crecimiento y la relación alometríca; i.e. un árbol con diámetro normal de 35 cm tiene un IE de 0.43, mientras que para otro con diámetro de 60 cm se tiene un IE de 0.32 m (Fig. 1).

Fig. 1 Relación entre índice de esbeltez (IE: Altura total/diámetro normal) y categoría diamétrica (CD) para árboles de Lysiloma latisiliquum en Quintana Roo, México.
El ajuste de los modelos locales A-d, revela parámetros significativos en todos los modelos (p < 0.001), valores de R 2 que explican más de 44% en la variabilidad de la muestra; sin embargo, el modelo 3 (Hossfeld, 1822) es el que tiene los mejores ajustes estadísticos, el mayor valor de R 2 y los menores valores de AIC y BIC, así como los más bajos errores estándar aproximados (Eea) para los parámetros estimados (Tabla 3).
Tabla 3 Parámetros estimados y estadísticos de ajuste de los modelos locales altura total-diámetro normal (A-d) para Lysiloma latisiliquum en Quintana Roo, México.
| Modelo | Parámetro | Estimador | Eea | Valor t | Pr > |t| | R 2 | AIC | BIC |
| 2 |
|
18.463539 | 1.23416 | 14.96 | < 0.001 | 0.4631 | 9549.724 | 9572.534 |
|
|
0.025538 | 0.00621 | 4.11 | < 0.001 | ||||
|
|
0.567570 | 0.04238 | 13.39 | < 0.001 | ||||
| 3 |
|
-2.256239 | 0.56868 | -3.97 | < 0.001 | 0.4634 | 9548.554 | 9571.364 |
|
|
1.031533 | 0.06962 | 14.82 | < 0.001 | ||||
|
|
0.045283 | 0.00189 | 23.92 | < 0.001 | ||||
| 4 |
|
20.114992 | 2.06945 | 9.72 | < 0.001 | 0.4629 | 9550.624 | 9573.434 |
|
|
0.110408 | 0.00542 | 20.36 | < 0.001 | ||||
|
|
0.656520 | 0.04999 | 13.13 | < 0.001 | ||||
| 5 |
|
19.321100 | 0.36210 | 53.36 | < 0.001 | 0.4598 | 9561.403 | 9578.510 |
|
|
14.820100 | 0.61960 | 23.92 | < 0.001 | ||||
| 6 |
|
16.427300 | 0.18740 | 87.66 | < 0.001 | 0.4448 | 9621.923 | 9639.03 |
|
|
-7.595000 | 0.18590 | -40.85 | < 0.001 | ||||
| 7 |
|
-1.218723 | 0.02952 | -41.29 | < 0.001 | 0.4537 | 9586.158 | 9603.266 |
|
|
-0.238162 | 0.00168 | -141.72 | < 0.001 |
Eea: error estándar asintótico; R 2: coeficiente de determinación; AIC y BIC; criterios de información Akaike (AIC) y Bayesiano (BIC).
Además de lo anterior, el modelo Hossfeld (1822) de tres parámetros se ajusta mejor a los registros de A-d que los modelos de dos parámetros, los cuales tienden a subestimar la A (Burkhart y Strub, Vestjordet-1-Neslund, Bates y Watts), mientras que las expresiones de tres parámetros se apegan de mejor forma a la tendencia de la información (Fig. 2).

Fig. 2 Modelos locales altura total-diámetro normal (A-d) ajustados para Lysiloma latisiliquum en Quintana Roo, México.
El modelo Hossfeld (1822), cumple satisfactoriamente con los supuestos de regresión: normalidad de los datos (tendencia lineal entre los cuantiles y los residuales estandarizados, Fig. 3a) y homocedasticidad de los residuales (distribución homogénea, Fig. 3b).
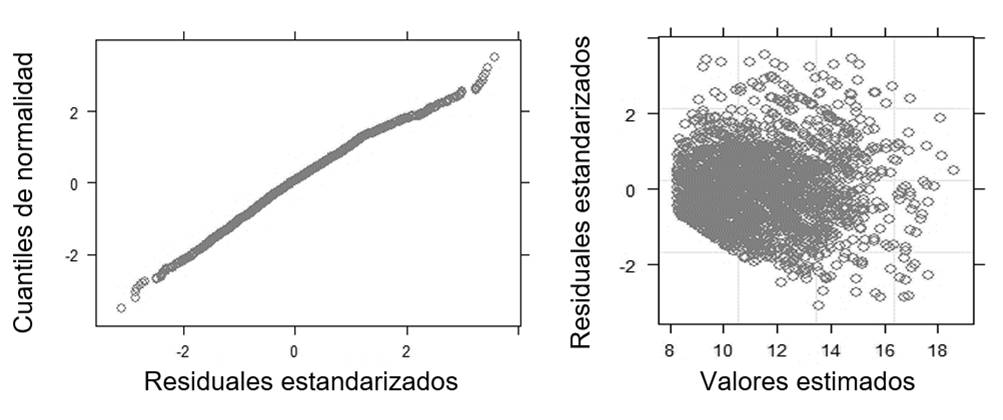
Fig. 3 Pruebas gráficas de normalidad (a) y homocedasticidad (b) del modelo Hossfeld (1822) altura total-diámetro normal (A-d) para Lysiloma latisiliquum en Quintana Roo, México.
Debido a que no existieron diferencias significativas entre los dos tipos de vegetación (p > 0.05), la covariable Vp es la única que no se incluyó en el ajuste de modelos mixtos (Tabla 4).
Tabla 4 Prueba de comparación de medias para las covariables analizadas.
| Covariable | gl | Error Tipo I | Cuadrado de la media | Valor de F | Pr > F |
| Conglomerado | 175 | 10611.201 | 60.635 | 16.80 | <0.0001 |
| Municipio (M) | 5 | 690.574 | 138.115 | 17.65 | <0.0001 |
| Altitud | 10 | 1425.420 | 142.542 | 18.98 | <0.0001 |
| Vegetación primaria (Vp) | 1 | 8.134 | 8.134 | 1.04 | 0.3080 |
| Categoría diamétrica (CD) | 13 | 1798.294 | 138.330 | 46.15 | <0.0001 |
| Clase de copa (Cc) | 9 | 7408.887 | 823.210 | 274.67 | <0.0001 |
| Altura de fuste limpio (Af) | 11 | 2095.882 | 190.535 | 63.57 | <0.0001 |
Al ajustar por MEM el modelo Hossfeld (1822) en sus tres variantes
los resultados señalan que el parámetro
Tabla 5 Valor y significancia de los parámetros estimados con el modelo Hossfeld (1822) altura total-diámetro normal (A-d) ajustado bajo el enfoque de efectos mixtos para Lysiloma latisiliquum en Quintana Roo, México.
| Covariable | Número | Parámetro de inclusión del efecto | Parámetro | Estimador | Eea | Valor t | Pr > t | Phi | Se | Su | ||
| Conglomerado | 3 | . | 1 |
|
|
-0.96193 | 0.663 | -1.451 | 0.1469 | 0.215 | 3.161 | 1.766 |
|
|
0.90680 | 0.070 | 12.895 | < 0.001 | ||||||||
|
|
0.04926 | 0.002 | 26.196 | < 0.001 | ||||||||
| 3 | . | 2 |
|
|
-1.75752 | 0.479 | -3.670 | < 0.001 | 0.060 | 0.254 | 1.601 | |
|
|
0.92328 | 0.065 | 14.139 | < 0.001 | ||||||||
|
|
0.05242 | 0.002 | 30.605 | < 0.001 | ||||||||
| 3 | . | 3 |
|
|
0.02560 | 0.500 | 0.051 | 0.9592 | 0.027 | 0.015 | 1.562 | |
|
|
0.54588 | 0.066 | 8.212 | < 0.001 | ||||||||
|
|
0.06765 | 0.002 | 29.913 | < 0.001 | ||||||||
| Municipio (M) | 3 | . | 4 |
|
|
-0.76689 | 0.960 | -0.799 | 0.4243 | 0.279 | 1.564 | 2.030 |
|
|
0.96632 | 0.082 | 11.837 | < 0.001 | ||||||||
|
|
0.04710 | 0.002 | 21.334 | < 0.001 | ||||||||
| 3 | . | 5 |
|
|
-2.01182 | 0.659 | -3.051 | 0.0023 | 0.275 | 0.135 | 2.018 | |
|
|
1.07957 | 0.098 | 10.996 | < 0.001 | ||||||||
|
|
0.04657 | 0.002 | 21.317 | < 0.001 | ||||||||
| 3 | . | 6 |
|
|
-2.05210 | 0.666 | -3.083 | 0.0021 | 0.279 | 0.008 | 2.023 | |
|
|
0.98361 | 0.081 | 12.069 | < 0.001 | ||||||||
|
|
0.05233 | 0.004 | 13.162 | < 0.001 | ||||||||
| Altitud | 3 | . | 7 |
|
|
-2.68400 | 0.811 | -3.311 | < 0.001 | 0.248 | 1.189 | 2.031 |
|
|
1.03879 | 0.082 | 12.630 | < 0.001 | ||||||||
|
|
0.04542 | 0.002 | 20.409 | < 0.001 | ||||||||
| 3 | . | 8 |
|
|
-2.68848 | 0.663 | -4.055 | < 0.001 | 0.239 | 0.093 | 2.017 | |
|
|
1.05603 | 0.087 | 12.080 | < 0.001 | ||||||||
|
|
0.04503 | 0.002 | 20.459 | < 0.001 | ||||||||
| 3 | . | 9 |
|
|
-2.62005 | 0.672 | -3.896 | < 0.001 | 0.245 | 0.005 | 2.024 | |
|
|
1.05328 | 0.083 | 12.753 | < 0.001 | ||||||||
|
|
0.04536 | 0.003 | 16.696 | < 0.001 | ||||||||
| Categoría diamétrica (CD) | 3 | . | 10 |
|
|
-2.22206 | 0.706 | -3.149 | 0.0017 | 0.261 | 0.000 | 2.087 |
|
|
1.02573 | 0.086 | 11.895 | < 0.001 | ||||||||
|
|
0.04550 | 0.002 | 19.405 | < 0.001 | ||||||||
| 3 | . | 11 |
|
|
-2.22206 | 0.706 | -3.149 | 0.0017 | 0.261 | 0.000 | 2.087 | |
|
|
1.02573 | 0.086 | 11.895 | < 0.001 | ||||||||
|
|
0.04550 | 0.002 | 19.405 | < 0.001 | ||||||||
| 3 | . | 12 |
|
|
-2.22206 | 0.706 | -3.149 | 0.0017 | 0.261 | 0.000 | 2.087 | |
|
|
1.02573 | 0.086 | 11.895 | < 0.001 | ||||||||
|
|
0.04550 | 0.002 | 19.405 | < 0.001 | ||||||||
| Clase de copa (Cc) | 3 | . | 13 |
|
|
-5.68216 | 1.001 | -5.674 | < 0.001 | 0.295 | 2.049 | 2.019 |
|
|
1.13459 | 0.078 | 14.497 | < 0.001 | ||||||||
|
|
0.04737 | 0.002 | 22.310 | < 0.001 | ||||||||
| 3 | . | 14 |
|
|
-3.82082 | 0.636 | -6.008 | < 0.001 | 0.281 | 0.169 | 1.989 | |
|
|
0.91488 | 0.097 | 9.440 | < 0.001 | ||||||||
|
|
0.05281 | 0.002 | 24.886 | < 0.001 | ||||||||
| 3 | . | 15 |
|
|
-0.53888 | 0.638 | -0.844 | 0.3985 | 0.276 | 0.010 | 1.971 | |
|
|
0.54852 | 0.081 | 6.745 | < 0.001 | ||||||||
|
|
0.06268 | 0.004 | 15.797 | < 0.001 | ||||||||
| Altura de fuste limpio (Af) | 3 | . | 16 |
|
|
-3.72035 | 1.148 | -3.239 | 0.0012 | 0.216 | 3.454 | 1.869 |
|
|
0.98089 | 0.066 | 14.781 | < 0.001 | ||||||||
|
|
0.04684 | 0.002 | 25.927 | < 0.001 | ||||||||
| 3 | . | 17 |
|
|
-2.59269 | 0.528 | -4.913 | < 0.001 | 0.208 | 0.236 | 1.840 | |
|
|
0.91592 | 0.094 | 9.751 | < 0.001 | ||||||||
|
|
0.04593 | 0.002 | 25.943 | < 0.001 | ||||||||
| 3 | . | 18 |
|
|
-1.93356 | 0.554 | -3.489 | < 0.001 | 0.243 | 0.010 | 1.902 | |
|
|
0.93536 | 0.068 | 13.707 | < 0.001 | ||||||||
|
|
0.04414 | 0.003 | 13.055 | < 0.001 | ||||||||
Eea: error estándar aproximado; Phi: desviación estándar de los residuos en el sistema; Se y Su: desviación estándar de efectos aleatorios.
Los ajustes con efectos mixtos indican mayores valores del coeficiente de determinación, con respecto al modelo general Hossfeld (1822) (ver Tabla 3), al incluir las covariables tales como municipio y altitud (R 2 = 0.49 - 0.50; modelos 3.4 al 3.9), clase de copa y altura de fuste limpio (R 2 = 0.50 - 0.58; modelos 3.13 al 3.18), así como conglomerado (R 2 = 0.64 - 0.72; modelos 3.1 al 3.3) (Tablas 5 y 6). Por lo anterior, y debido a que el modelo 3.3 tiene un parámetro no significativo (p > 0.05; Tabla 5), el modelo 3.2 con un sesgo promedio de los residuales (E) menor a la milésima y una diferencia agregada (DA %) inferior a 1% (Tabla 6) se destaca como el mejor bajo el enfoque de efectos mixtos.
Tabla 6 Valores estadísticos y capacidad de ajuste del modelo Hossfeld (1822) altura total/diámetro normal (A-d) al incluir covariables para Lysiloma latisiliquum en Quintana Roo, México.
| Modelo | R 2 | AIC | BIC | E (m) | DA % | ||
| 3 | . | 1 | 0.6428 | 8951.60 | 8985.82 | 0.0000865 | -0.8958014 |
| 3 | . | 2 | 0.7051 | 8705.10 | 8739.31 | 0.0001344 | -0.8865417 |
| 3 | . | 3 | 0.7193 | 8650.58 | 8684.79 | 0.0001504 | -0.8834272 |
| 3 | . | 4 | 0.4944 | 9266.74 | 9300.95 | 0.0001734 | -0.8789920 |
| 3 | . | 5 | 0.5000 | 9248.85 | 9283.06 | 0.0002258 | -0.8688400 |
| 3 | . | 6 | 0.4976 | 9254.80 | 9289.02 | 0.0002321 | -0.8676177 |
| 3 | . | 7 | 0.4942 | 9308.72 | 9342.94 | 0.0006913 | -0.7787227 |
| 3 | . | 8 | 0.5017 | 9288.31 | 9322.52 | 0.0007277 | -0.7716698 |
| 3 | . | 9 | 0.4982 | 9297.26 | 9331.48 | 0.0007495 | -0.7674444 |
| 3 | . | 10 | 0.4634 | 9397.45 | 9431.66 | 0.0007812 | -0.7613004 |
| 3 | . | 11 | 0.4634 | 9397.45 | 9431.66 | 0.0007812 | -0.7613004 |
| 3 | . | 12 | 0.4634 | 9397.45 | 9431.66 | 0.0007812 | -0.7613005 |
| 3 | . | 13 | 0.5004 | 9229.54 | 9263.75 | 0.0001006 | -0.8930704 |
| 3 | . | 14 | 0.5156 | 9188.94 | 9223.15 | 0.0003882 | -0.8772176 |
| 3 | . | 15 | 0.5245 | 9160.10 | 9194.32 | 0.0003882 | -0.8373936 |
| 3 | . | 16 | 0.5727 | 9010.34 | 9044.55 | 0.0002198 | -0.8699954 |
| 3 | . | 17 | 0.5859 | 8949.25 | 8983.46 | 0.0003370 | -0.8473028 |
| 3 | . | 18 | 0.5580 | 9050.85 | 9085.07 | 0.0005430 | -0.8074247 |
R 2: coeficiente de determinación; criterios de información Akaike (AIC) y Bayesiano (BIC); DA %: diferencia agregada expresada en porciento; E: sesgo promedio de los residuales.
El modelo 3.2 Hossfeld seleccionado como el mejor bajo el enfoque de efectos mixtos y las estimaciones con una muestra independiente (4682 pares de datos A-d), obtenida de nueve ejidos en el estado de Quintana Roo, fueron estadísticamente iguales (t = 4.475; p = 0.01) (Fig. 4).
Discusión
El aprovechamiento de especies tropicales de madera dura en Quintana Roo toma en cuenta un diámetro mínimo de corta (DMC) de 35 cm (Vester y Navarro, 2007; Gallegos et al., 2012), en el cual se tiene un índice de esbeltez de 0.43, valor que fue inferior al reportado para Swietenia macrophylla King (IE = 0.51) en Quintana Roo (Hernández et al., 2018), especie guía en el aprovechamiento forestal y en la que se basan las actividades silvícolas dentro del bosque tropical (Synnott, 2009), lo que sugiere una forma geométrica del fuste tipo ‘paraboloide’ en árboles de Lysiloma latisiliquum (Arias, 2004).
Este índice de esbeltez es debido a su relación con la tensión del crecimiento donde las fibras son cortas (Vignote, Molinero, Gerard y Diez, 1996), lo que ocasiona que la especie o especies puedan ser más estable a daños mecánicos por vientos, lluvias y/o huracanes, así como a intervenciones silvícolas en donde la apertura de claros sea intensiva; sin embargo, con un incremento en diámetro promedio (0.2 y 0.5 cm año-1) (López-Torres y Tamarit-Urias, 2005; Negreros-Castillo y Martínez, 2011; Pineda-Herrera, Carreón-Santos, Valdez-Hernández y Interián-Ku, 2019) inferior al de especies tendientes a una forma tipo ‘cilindro’ y de rápido crecimiento como S. macrophylla (0.69 cm año-1) (Hernández-Ramos, Valdez-Hernández, García-Cuevas, Tadeo-Noble y Reyes-Hernández, 2020).
El modelo 3.2 Hossfeld explicó mejor la relación A-d para árboles de Lysiloma latisiliquum en Quintana Roo, México, debido a que su ajuste bajo el enfoque de efectos mixtos fue estadísticamente superior en comparación con la forma tradicional. Esto es debido a que al agrupar la información e incluirla como una covariable bajo dicho enfoque de efectos mixtos, la varianza se reduce y se hace más homogénea (García y Rapelli, 2011), por asumir que la varianza es específica para cada agrupación y nivel de clasificación (Quevedo, Jerez, Moret y Noguera, 2010; Seoane, 2014); además, se compensan las diferencias en los grados de libertad del modelo a distintos niveles (De los Santos-Posadas et al., 2006), situación que se refleja directamente en el aumento de los valores del coeficiente de determinación (R 2 ) y la reducción en los criterios de información AIC y BIC con respecto al modelo general. La mejora estadística que se tuvo en este trabajo al agrupar la información por covariable concuerda con las mejoras reportadas por Arias (2004) en seis especies tropicales de Costa Rica, al incluir en el modelo Wenk, Antanaitis y Smelko (1990) la densidad del rodal como una covariable (R 2 de 0.82 a >0.90).
De acuerdo con las evidencias estadísticas, el modelo 3.2 Hossfeld es confiable para realizar estimaciones de altura total a través del diámetro normal en los bosques naturales de Lysiloma latisiliquum en el estado de Quintana Roo, tal y como lo demuestran Arias (2004) al obtener un máximo en el valor de R 2 de 0.64 en seis especies maderables en Costa Rica; Ercanli, (2015) de 0.85 en Fagus orientalis Lipsky en Tukey; Castillo-Gallegos et al. (2018) con valores de 0.78, 0.49 y 0.35 para las especies de Cinnamomum sp, Melia azedarach L. y Pinus chiapensis (Martínez) Andresen, respectivamente. Además, con ello se pueden reducir tiempos y esfuerzos en el levantamiento de la información de campo en los inventarios forestales, así como realizar estimaciones de altura acordes con las condiciones de la vegetación para la elaboración de planes de manejo forestal.
Conclusiones
La variabilidad de las condiciones ambientales y de crecimiento modifican la relación entre la altura total y el diámetro normal en Lysiloma latisiliquum en los bosques tropicales de Quintana Roo, México, por lo que utilizar un modelo ajustado de forma tradicional que no incluya los efectos mencionados deja de ser una alternativa confiable para modelar dicha relación.
El ajuste de modelos de altura total y diámetro normal bajo el enfoque de efectos mixtos en L. latisiliquum, demostró que es una opción de mejora estadística y precisión en la estimación de la altura total a través del diámetro normal en árboles de esta especie que crecen en bosques tropicales de Quintana Roo, México.
El modelo propuesto (Hossfeld 3.2) es una alternativa de ahorro en tiempo y recursos para el registro de la altura total en los inventarios forestales de L. latisiliquum en Quintana Roo; además, el índice de esbeltez puede ser incluido como parámetro de estabilidad mecánica para justificar tratamientos a rodales de esta especie y planear las actividades silvícolas dentro de los programas de manejo forestal propuestos.











 nueva página del texto (beta)
nueva página del texto (beta)



