Recursos naturales renovables

 

Sistema compatible de ahusamiento–volumen para Pinus cooperi Blanco en Durango, México

 

Compatible taper–volume system for Pinus cooperi Blanco in Durango, México

 

Francisco Cruz–Cobos¹, Héctor M. De los Santos–Posadas²* y J. René Valdez–Lazalde²

 

¹ Instituto Tecnológico Forestal de El Salto, Durango. (fcruzb@colpos.mx).

² Forestal. Campus Montecillo. Colegio de Postgraduados. 56230, Montecillo, Estado de México. *Autor responsable: (hmsantos@colpos.mx), (valdez@colpos.mx)

 

Recibido: Junio, 2007.
Aprobado: Marzo, 2008.

 

Resumen

Se presenta el desarrollo de un sistema compatible de volumen comercial y ahusamiento para estimar volumen sin corteza de Pinus cooperi Blanco. El sistema se basó en un modelo lineal polinómico previamente usado en Durango, México, y modificado en función de los datos para añadir flexibilidad. El modelo de volumen total obtenido a partir del sistema aproxima en su estructura al modelo de volumen total de Schumacher y Hall. Las ecuaciones se ajustaron como un sistema completamente simultáneo para compensar la variación entre ahusamiento y volumen comercial acumulado que se da en cualquier punto del fuste. La estructura incluye efectos mixtos (EM) para controlar la variabilidad debida al árbol, corregir heterocedasticidad y lograr predicciones precisas en árboles de alto valor comercial. La información adicional que provee la estructura de EM mejora notablemente la capacidad predictiva en la parte baja del fuste. Adicionalmente, el ajuste simultáneo del sistema de ahusamiento–volumen mediante EM reduce los errores estándares de los estimadores de los parámetros.

Palabras clave: Análisis troncales, efectos aleatorios, sistema de ecuaciones.

 

Abstract

The development of a compatible taper–volume system is presented for estimating volume without bark of Pinus cooperi Blanco. The system was based on a polynomial linear model previously used in Durango, México, and modified as a function of the data to add flexibility. The model of total volume obtained from the system approximates in its structure the total volume model of Schumacher and Hall. The equations were adjusted as a completely simultaneous system to compensate for the variation between taper and accumulated marketing volume, which occurs at any point of the bole. The structure includes mixed effects (ME) to control the variability due to the tree, correct heterocedasticity and to obtain precise predictions in trees of high commercial value. The additional information provided by the structure of ME noticeably improves the predictive capacity in the lower part of the bole. In addition, the simultaneous fit of the taper–volume system by means of ME reduces the standard errors of the estimators of the parameters.

Key words: Stem analysises, random effects, equations system.

 

Introducción

El volumen maderable de un árbol se estima usualmente a través de dos tipos de ecuaciones: de volumen o de ahusamiento; si el ahusamiento es el coeficiente de estrechamiento del diámetro a lo largo del fuste, es posible estimar directamente mediante una ecuación el diámetro a cualquier altura y la altura a cualquier diámetro (Clutter et al., 1983; Torres et al., 1993). Una vez definida la ecuación de ahusamiento es posible, mediante su integración matemática, obtener estimaciones del volumen total o parcial del fuste a cualquier límite de longitud o diámetro mínimo deseado (Lynch et al., 1992). Alternativamente, si se desea evitar la integración se pueden ajustar modelos de volumen comercial y usarse directamente para la cubicación del arbolado en pie, donde existe una ecuación de ahusamiento implícita (Demaerschalck, 1973; Clutter, 1980). Cuando se tiene un par de ecuaciones de volumen y ahusamiento definidas por los mismos parámetros y una estructura geométrica común es posible definir un sistema compatible de ahusamiento–volumen.

El ajuste de un sistema compatible volumen–ahusamiento puede darse mediante mínimos cuadrados ordinarios (MCO) o como un sistema de ecuaciones simultáneas. Al ajustar el sistema ahusamiento–volumen con métodos como ecuaciones aparentemente no relacionadas y máxima verosimilitud con información completa (SUR y FIML por sus siglas en inglés) los estimadores de los parámetros son consistentes, ya que se ajusta simultáneamente el ahusamiento y el volumen acumulado, lo cual representa una ventaja. Contrariamente, bajo MCO el modelador debe decidir si se minimiza el error en la ecuación de ahusamiento o en la de volumen comercial, pero no en ambas (Borders, 1989; Fang et al., 2000).

El ajuste como un sistema de ecuaciones simultáneas puede complementarse con la adición de efectos aleatorios bajo el enfoque de modelos de efectos mixtos (MEM). En los modelos de volumen–ahusamiento el análisis mediante MEM permite un uso más eficiente de los datos al controlar la variación aleatoria individual y desplazar los problemas de heterocedasticidad y autocorrelación; además, es posible usar estimaciones de los efectos aleatorios para tener predicciones más precisas (Fang y Bailey, 2001).

El objetivo del presente trabajo fue generar un sistema compatible de ahusamiento y volumen comercial para Pinus cooperi, especie que aporta el mayor volumen y valor a la producción maderable en el Estado de Durango debido a buenas características tecnológicas y largos fustes limpios. El ajuste se hizo con modelos de efectos mixtos.

 

MATERIALES Y MÉTODOS

Datos de volumen y ahusamiento

La investigación se efectuó en los predios La Vaca, El Embudo y El Hueco también conocido como Navíos, cubriendo una superficie forestal de 2264 ha en el municipio de Durango, Durango, México. Los predios se localizan entre 104° 59' 44" y 105° 05' 42" O y 23° 55' 10" y 24° 01' 00" N, con una altitud promedio de 2500 m y una temperatura promedio anual de 15° C. Las especies de árboles son del genero Pinus y Quercus, entre las que destacan por su valor económico y volumen de aprovechamiento, P. cooperi Blanco, P. leiophylla Sch. et Cham, P. teocote Sch. et Cham y P. engelmannii Carr.

Se obtuvieron datos de 29 análisis troncales de P. cooperi Blanco siguiendo la técnica reportada por Manzanilla (1981); para ello se seleccionaron árboles sin daño físico o mecánico de todas las categorías de diámetro y alturas presentes. Para los cálculos de cubicación se usó el método de trozas traslapadas que permite obtener volúmenes totales y parciales más precisos (Bailey, 1995). Los datos de ahusamiento y volumen acumulado se presentan en la Figura 1. Además se tuvo datos de 10 árboles de la misma especie recolectados del predio Ejido La Victoria cercano al área en estudio; eran árboles derribados, de los cuales se obtuvo el diámetro a la altura del tocón y a 2 m. Los datos se usaron para validar y probar las metodologías propuestas.

Desarrollo del modelo compatible ahusamiento–volumen

Para generar el sistema compatible de ahusamiento–volumen se tomó como base el modelo de ahusamiento Cielito 1 (Rentería, 1995), con el que se han obtenido buenos ajustes en P. cooperi Blanco en Durango, y en otras especies del Estado de Chihuahua (Corral et al., 1999). Para Durango este modelo se ajustó a partir de la altura del tocón y del diámetro normal, dando mejores resultados en el segundo caso; sin embargo, dos de sus parámetros no fueron estadísticamente significativos. En Chihuahua se ajustó el modelo sólo a partir del diámetro normal. El modelo Cielito 1 es lineal:

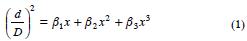
donde, d=diámetro sin corteza (cm) a una altura dada (h), así d=0 cuando h=H; D=diámetro normal (cm) a h=1.3 m; x = (H–h)/H; h=altura del fuste al diámetro (d); H=altura total a la punta (m); β_i=parámetros del modelo.

Para calcular el volumen de una troza (V_troza) a cierta altura del fuste se integra el diámetro d a lo largo de la sección deseada como un sólido en revolución mediante una expresión de la forma:

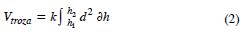
donde, 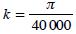es la constante volumétrica cuando d está expresado en centímetros y la longitud de la troza en metros, y 3d es el diferencial sobre la altura del fuste.

Despejando d² de la Ecuación (1) y sustituyendo en la Ecuación (2) se tiene:

Así, el volumen de una troza (V_troza) definida entre dos alturas del fuste h₂ y h₁ es:

Siguiendo este desarrollo, el volumen total del fuste (V), del tocón a la punta, se define como:

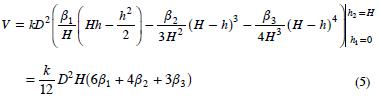
La Ecuación (5) se puede reducir a la forma V=αD²H, expresión que representa el modelo de factor de forma constante.

Sin embargo, la ecuación de ahusamiento Cielito 1 (1), y en consecuencia su correspondiente ecuación compatible de volumen (5), presentan dos aspectos poco deseables:

1) La normalidad de la variable a ajustar. El modelo Cielito 1 utiliza como variable dependiente a variable no normal que restringe sus valores entre cero y uno; por tanto, la estructura no lineal propuesta bajo MCO debe ser más eficiente tanto en ajuste como para caracterizar sus parámetros sin tener que recurrir a un ajuste bajo modelos lineales generalizados.

2) Restricciones del ajuste. Aunque el modelo no restringe el ahusamiento a d=D, el ajuste se hace de forma tal que cuando h=1.3 m entonces haciendo que 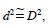, donde, 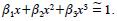= 1. Sin embargo, restringir en dos puntos una ecuación de ahusamiento puede resultar en comportamientos ilógicos; por ejemplo, para predicciones donde h> 1.3 m es posible que d²>D².

Dado que la ecuación busca estimar diámetros decrecientes a partir de D, el cual es el único diámetro conocido, esta condición debe cambiarse por una que garantice que para todo h>1.3 m, d²>D². Esto se logra con la incorporación del nuevo parámetro (ó) que asociado a la variable diámetro normal flexibiliza las condiciones de ajuste del modelo:

Así, el modelo de ahusamiento propuesto (Cielito 1 Modificado) es:

Es posible verificar que tanto V_troza como V son extensiones directas del desarrollo previo; así, la ecuación compatible de volumen para Cielito 1 Modificado es:

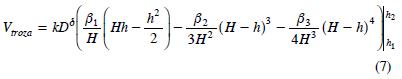
La Ecuación (8) es reducible a la forma V=αD^δH, donde La ecuación (8) es una aproximación la estructura de Schumacher y Hall (1933) de la forma V=αD^δH^γ, donde en este caso γ=1.

De manera similar, la estructura de V_troza es modificable a una expresión de volumen comercial acumulado (V_comercial) definiendo los límites de integración de la siguiente forma:

donde, h_c es la altura sobre el tocón a la que se da el V_comercial y h_t es la altura del tocón. Así la forma desarrollada de esta expresión es:

Con esta expresión se completa el sistema de ahusamiento –volumen comercial que al ajustar el ahusamiento implica el modelo de volumen comercial y viceversa.

Toda función de ahusamiento debe permitir el cálculo de la altura a la cual se da el diámetro mínimo comercial deseado, lo cual es particularmente útil para nuestra ecuación de V_comercial. Sin embargo, para el sistema propuesto la solución de h en la Ecuación (6) presenta el inconveniente de manejar raíces imaginarias que se pueden reducir hasta desaparecer durante la simplificación algebraica, una vez que se sustituyen los valores del ajuste. Dado el trabajo teórico implicado y el hecho de que no todos los paquetes convencionales pueden resolver una raíz imaginaria, se decidió que es más práctico el cálculo numérico de la solución de x_i iterando la expresión:

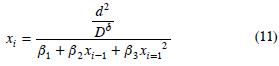
que con una tolerancia definida (ξ), dada por 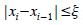permite calcular el valor de x para d y D dados. Es posible verificar que cualquier valor inicial positivo para x_x–1 produce valores que convergen en un valor positivo menor de uno donde obviamente h=H(1–x).

Estrategia de ajuste

Para facilitar la discusión sobre el ajuste del sistema compatible propuesto se abrevia la Ecuación (6) como d_ij=f(D_i, H_i, h_ij,; p) y la Ecuación 10 como V_ij,=g(k, D_i, H_i, h_ij; p), donde f(.) define la estructura del modelo de ahusamiento y g(.) al modelo de volumen comercial, p es el vector de parámetros p = (β₁, β₂, β₃, δ) estimables del sistema y d_ij es el diámetro del i–ésimo árbol observado a la h_ij altura sobre el fuste. De igual manera para el volumen acumulado V_ij .

El sistema de ecuaciones propuesto puede ajustarse más eficientemente si se permite la inclusión de efectos aleatorios. Así, es posible mejorar las características de los parámetros al compensar por el efecto de variables tomadas en una misma unidad experimental y simultáneamente ajustar los datos de ahusamiento–volumen. Esto es posible usando una estructura bivariada con efectos aleatorios. Tomando como base la formulación de Hall y Clutter (2004), el sistema compatible ahusamiento–volumen, se puede expresar como:

donde, d_i es el vector de observaciones de ahusamiento en el i–ésimo árbol; V_i es el vector de observaciones de volumen comercial en el i–ésimo árbol y:

quedando definidos los efectos aleatorios del modelo por:

Así se tiene un solo parámetro con efectos mixtos de la forma β₂+b_2i y la estructura de e_i hasta este punto se asume como homocedástica (σ²I), pero puede flexibilizarse a nivel de componente (ahusamiento o volumen) para modelar tanto heterocedasticidad como autocorrelación por componente.

Para observar el efecto de las modificaciones realizadas al modelo original de ahusamiento Cielito 1, inicialmente se ajustaron las ecuaciones de ahusamiento (1) y (6) y las de volumen (4) y (10) por separado a través de MCO. Luego se ajustó el sistema propuesto de manera simultánea y con efectos mixtos bajo el método de Máxima Verosimilitud Restringida (RMV).

Los modelos de volumen ajustados considerando efectos mixtos ofrecen ventajas sobre la regresión tradicional (MCO) cuando se requieren predicciones altamente precisas para árboles de gran valor comercial. Lo anterior se logra sin tener que modificar la estructura del modelo para incluir observaciones adicionales; esto es posible ya que los datos pueden usarse para estimar los efectos aleatorios específicos del individuo e incorporarlos directamente en nuestra predicción.

Para ejemplificar el uso del modelo de efectos mixtos cuando se dispone de información a priori de un árbol se parte de la información básica para nuestro sistema ahusamiento–volumen, es decir del diámetro normal ( D) y la altura total (H). Si adicionalmente se conoce la altura del tocón (h_t) y el diámetro a esta altura (d_t), un diámetro adicional medido a una altura por encima de 1.3 m (d) y la altura a tal diámetro (h_d), se tiene información suficiente para estimar el valor b_2i especifico de ese árbol y usarlo en las estimaciones. Simplificando la notación de Fang y Bailey (2001) para el caso particular del sistema de ahusamiento–volumen propuesto, es posible entonces estimar el efecto aleatorio específico con el vector de información adicional:

donde, d₀ es el vector de tres diámetros conocidos y V₀ es el vector de los volúmenes a esos diámetros.

Así el efecto específico por árbol puede estimarse como:

donde,

Las derivadas parciales del sistema β₂ respecto a corresponden a:

Estas ecuaciones han sido simplificadas para el caso específico. La notación completa puede verse en Vonesh y Chinchilli (1997).

 

RESULTADOS Y DISCUSIÓN

Estructura original vs estructura propuesta

Aunque los resultados de los ajustes de los modelos de ahusamiento no son comparables dadas las diferentes escalas de la variable dependiente, es posible comparar valores como R² y el coeficiente de variación (CV). El modelo de ahusamiento modificado (6) tuvo un mayor valor de R² y un CV menor (Cuadro 1). El cambio en la estructura no sólo permite flexibilizar el ajuste por la adición de un parámetro sino que tiene consecuencias en la capacidad predictiva del mismo. Además, todos los parámetros son altamente significativos, en contraste con el modelo original (1) donde β₂ fue significativo a un valor de rechazo de 0.057. Para comparar los cuadrados medios de los errores (CME), se obtuvo un estimador del CME para el diámetro comercial (d) de la ecuación de ahusamiento (1), a partir de los resultados del ajuste de dicha ecuación, bajo la siguiente manipulación algebraica:

Si entonces De esta manera el estimador del CME resulta de la expresión y el CME=6.25, superior al del modelo modificado (3.5337).

Si se observan los residuales de ambos modelos (Figura 2) se aprecia que en el modelo (1) existe un desajuste que tiende a sobreestimar sistemáticamente los diámetros en la punta y cercano a la base de los fustes, mientras que la estructura de los residuales del modelo (6) es mucho más deseable.

En cuanto a la ecuación compatible de volumen (10), también se observa que existen ganancias en la R², CME y niveles de significancia de los parámetros, comparados con la ecuación (4) de volumen original (Cuadro 2). Los residuales de ambos modelos presentan tendencias muy similares y problemas de heterocedasticidad (Figura 3).

Ajustes bajo MEM

Los parámetros estimados bajo RMV (Cuadro 3) para ahusamiento (6) y V_comercial (10) muestran que al considerar la correlación contemporánea se puede reducir de manera considerable el error estándar de los parámetros del modelo, además de unificar los valores por componente. En estos estadísticos se puede apreciar que los estimadores de los parámetros β_i de la ecuación de volumen y de ahusamiento obtenidos simultáneamente con RMV presentan desviaciones estándar menores que los obtenidos con MCO (Cuadro 2 y 3), lo cual hace estos parámetros más eficientes.

Torres y Magaña ( 2001) mencionan que es común que la mayoría parte de los modelos de volumen sufran problemas de heterocedasticidad dado que a mayores valores de diámetro y altura la variación en los volúmenes de los árboles se hace más grande. Este problema se puede observar en los residuales de las ecuaciones de volumen (4) y (10), ajustadas por MCO (Figura 3), por lo que recomienda corregir esta deficiencia. Sin embargo, al observar los residuales del sistema de ahusamiento–volumen propuesto ajustados simultáneamente (Figura 4) se nota que no existe tendencia de heterocedasticidad en ambos modelos, por lo que se confirma que el ajuste con efectos mixtos ayuda a reducir este problema (Fang y Bailey, 2001).

Estimación de efectos específicos con información adicional del inventario

Para validar la pertinencia de la estructura propuesta se usaron datos de diez árboles del Ejido La Victoria, los cuales fueron cubicados con la misma metodología que los usados para el ajuste. En estos árboles se midieron cuatro diámetros a alturas fáciles de medir en campo (altura del tocón, 0.6, 1.3 y 2.0 m ); los diámetros normales de estos árboles oscilaban entre 24 y 40 cm con alturas totales entre 12 y 28 m. Se decidió comparar las predicciones a cuatro alturas comerciales medidas en pies 12 (3.67 m), 20 (6.11 m), 30 (9.17 m) y altura total con y sin el uso de la estructura de efectos aleatorios. Se usó como una medida de comparación de la eficiencia de ambos ajustes el sesgo, definido cómo 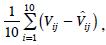donde V_ij es el volumen acumulado observado del i–ésimo árbol a la j–ésima altura y 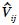el volumen estimado con y sin efectos aleatorios del i–ésimo árbol a la j–ésima altura.

Cuando se considera la variabilidad especifica del árbol los volúmenes predichos son más precisos que los obtenidos con el modelo de efectos fijos hasta la altura comercial de 30 pies (Cuadro 4). Desde este punto el modelo con efectos fijos es más adecuado ya que la información adicional proporcionada corresponde a las partes bajas del tronco. Considerando que las primeras trozas o trocería primaria tienen un valor comercial de hasta cinco veces más que la punta o producto secundario, y que las diferencias entre ambos volúmenes a esta altura es hasta 3%, se recomienda medir al menos esta información adicional en árboles de fuste recto y buena conformación para obtener mejores valores estimados para los productos de alto valor, sobre todo cuando se inventarían predios cuya posibilidad estimada es de varios miles de metros cúbicos. Esto se reflejaría en una estimación más adecuada de los dividendos económicos potenciales en ejidos / comunidades o conjuntos prediales que además del aprovechamiento procesan sus productos maderables. Cuando se estima el volumen total, el modelo con sólo efectos fijos es más preciso que el de efectos mixtos.

 

CONCLUSIONES

Las modificaciones realizadas al modelo de ahusamiento Cielito 1 permitieron mejorar el ajuste del ahusamiento y del volumen comercial teniéndose una estructura más flexible. El ajuste del sistema de cubicación compatible como un sistema con efectos mixtos no sólo es robusto, sino que permite usar información adicional para la cubicación en pie, que puede ser programada para lograr cálculos más precisos sobre todo para trocería de alto valor.

Además, con un ajuste MEM es estadísticamente más correcto el supuesto de eficiencia de los parámetros estimados al desplazar la heterocedasticidad en el volumen comercial sin complicar demasiado su estructura.

Para una valoración más precisa de las ganancias netas del uso de los modelos de efectos mixtos en la estimación del volumen comercial, se necesitarían pruebas de distribución de productos con datos de inventario, así como el costo adicional por tomar información de dos diámetros más de cada árbol que presuma características de alto valor comercial.

 

LITERATURA CITADA

Bailey, R. L. 1995. Upper–stem volumes from stem–analysis data: an overlapping bolt method. Can. J. For. Res. 25: 170–173.        [ Links ]

Borders, B. E. 1989. Systems of equations in forest stand modelling. For. Sci. 35(2): 548–556.        [ Links ]

Clutter, J. L. 1980. Development of taper functions from variable–top merchantable volume equations. For. Sci. 26: 117–120.        [ Links ]

Clutter, J. L., J. C. Forston, L.V. Pienaar, G. H. Brister, and R. L. Bailey. 1983. Timber Management a Quantitative Approach. John Wiley & Sons Inc. USA. 333 p.        [ Links ]

Corral R., S., J. J. Návar CH. y F. Fernández S. 1999. Ajuste de funciones de ahusamiento a los perfiles fustales de cinco Pináceas de la región de El Salto, Durango. Madera y Bosques 5(2): 53–65.        [ Links ]

Demaerschalk, J. P. 1973. Integrated systems for the estimation of tree taper and volume. Can. J. For. Res. 3: 90–94.        [ Links ]

Fang, Z., and R.L. Bailey. 2001. Nonlinear mixed effects modeling for slash pine dominat height growth following intensive sivicultural treatments. For. Sci. 47(3): 287–300.        [ Links ]

Fang, Z., B. E. Borders, and R. L. Bailey. 2000. Compatible volume–taper models for loblolly and slash pine based on a system with segmented–stem form factors. For. Sci. 46(1): 1–12.        [ Links ]

Hall, D. B., and J. L. Clutter. 2004. Multivariate multilevel nonlinear mixed effects models for timber yield predictions. Biometrics 60: 16–24.        [ Links ]

Manzanilla B., H. 1981. Los sitios permanentes de investigación silvícola un sistema integrado para iniciarse en el cultivo de los ecosistemas forestales, Secretaría de Agricultura y Recursos Hidráulicos, Instituto Nacional de Investigaciones Forestales y Agropecuarias, Boletín Técnico Núm. 116. 68 p.        [ Links ]

Lynch, T. B., S. T. Chang, and J. P. Chandler. 1992. Estimation of individual tree volume by importance sampling and antithetic variates from the cylindrical shells integral. Can. J. For. Res. 22: 326–335.        [ Links ]

Pinheiro, C. J. and D. M. Bates. 2000. Mixed–effects models in S and S–PLUS. Springer–Verlag, New York, Inc. 527 p.        [ Links ]

Rentería A., J. B. 1995. Estimación del volumen comercial de Pinus cooperi Blanco mediante modelos de ahusamiento en Durango. II Congreso Mexicano de Recursos Forestales, Resumen de Ponencias. Montecillo, México. 91 p.        [ Links ]

Schumacher, F. X. and F. S. Hall. 1933. Logarithmic expression of the timber volume. J. Agric. Res. 47(9): 719–734.        [ Links ]

Torres R., J. M., O. S. Magaña T. y G. A. Valles G. 1993. Funciones de ahusamiento para 8 especies forestales del Estado de México. I Congreso Mexicano de Recursos Forestales, Resumen de Ponencias. Saltillo, Coahuila. 109 p.        [ Links ]

Torres R., J. M. y O. S. Magaña T. 2001. Evaluación de Plantaciones Forestales. Ed. LIMUSA, México. 472 p.        [ Links ]

Vonesh, E. F., and V. M. Chinchilli. 1997. Linear and Nonlinear Models for the Analysis of Repeated Measurements. Marcel Dekker, New York. 560 p.        [ Links ]