Servicios Personalizados
Revista
Articulo
Indicadores
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Agrociencia
versión On-line ISSN 2521-9766versión impresa ISSN 1405-3195
Agrociencia vol.43 no.5 Texcoco jul./ago. 2009
Recursos naturales renovables
Mitos y falacias del método hidrológico del número de curva del SCS/NRCS
Myths and fallacies about the curve number hydrological method of the SCS/NRCS
Fernando Paz–Pellat*
Campus Córdoba y Montecillo, Colegio de Postgraduados. Km. 36.5 Carretera México–Texcoco. 56230. Montecillo, Estado de México. *Autor responsable: (pellat@colpos.mx)
Recibido: Abril, 2008.
Aprobado: Abril, 2009.
Resumen
La modelación de la relación precipitación–escurrimiento directo es un requerimiento básico en la gestión de cuencas hidrográficas, particularmente bajo condiciones de información escasa. Un modelo simple de esta relación es muy atractivo para las aplicaciones hidrológicas. En este trabajo se analizan las hipótesis intrínsecas en el método simple del número de curva (NC) del Soil Conservation Service / Natural Resources Conservation Service del USDA. La formulación básica entre la precipitación y el escurrimiento directo del método del NC es revisada en cuanto a sus implicaciones, concluyéndose que no tiene bases hidrológicas.
Palabras clave: Hipótesis intrínsecas, método del número de curva, relación precipitación–escurrimiento
Abstract
The modeling of the rainfall–direct runoff relationship is a basic requirement in the dynamics of watersheds, especially when information is scarce. A simple model of this relationship is very attractive in hydrological applications. In this paper an analysis is made of the hypotheses intrinsic to the simple method of the curve number (NC) of the USDA Soil Conservation Service / Natural Resources Conservation Service. The basic formulation of the rainfall–direct runoff relationship of the NC method is revised with a focus on its implications, coming to the conclusion that it has no hydrological support.
Key words: Intrinsic hypotheses, curve number method, rainfall–runoff relationship.
INTRODUCCIÓN
La búsqueda de una relación simple entre la precipitación (P) y el escurrimiento (Q) directo ha sido una de las tareas básicas de los modeladores de los procesos hidrológicos en cuencas o en parcelas experimentales. Este trabajo es particularmente crítico cuando la información de precipitación disponible en la mayoría de las cuencas hidrográficas sólo existe a nivel diario. Así, el SCS (Soil Conservation Service del U. S. Department of Agriculture; actualmente llamado NRCS o Natural Resources Conservation Service) planteó en la década de los cuarenta (Mockus, 1949) una aproximación práctica a la relación entre la precipitación y el escurrimiento directo. De estos desarrollos emergió el denominado método del número de curva (NC) del SCS (1972), que actualmente es usado por el NRCS (2004) y muchas otras instituciones nacionales e internacionales. Las bases históricas del método del NC se pueden revisar en la página del NRCS (2007)1.
El modelo del NC establece una relación empírica entre el escurrimiento directo Q (mm) y la precipitación P (mm), a escala diaria, como:

donde, Ia (mm) es la abstracción inicial antes del escurrimiento (almacenamientos superficiales, intercepción por la vegetación, evapotranspiración, infiltración antes de la saturación del suelo y otros factores) y S (mm) es un parámetro de retención, el cual varía espacialmente por cambios en el tipo y uso del suelo, manejo y pendiente; así como por cambios temporales en la humedad del suelo.
El parámetro Ia generalmente se expresa en función de S:

donde, el valor de k es puesto generalmente como 0.2 (SCS, 1972; NRCS, 2004) y S es estimado como:

donde, NC (0 a 100), adimensional, es función de la humedad antecedente del suelo, la pendiente del terreno, el uso del suelo y sus prácticas de manejo, principalmente.
La Ecuación 1 permite establecer una relación funcional entre P y Q que se utilizan en forma práctica, ya que depende sólo de NC que se puede estimar a partir de información disponible (mapas temáticos del Instituto Nacional de Estadística, Geografía e Informática, por ejemplo), aunque no actualizada, en las cuencas hidrográficas; con excepción del uso de la tecnología de los sensores remotos. Esta ecuación da una falsa apariencia de funcionalidad, particularmente cuando se tiene el soporte institucional del SCS/NRCS. En el apartado siguiente se revisan sus hipótesis intrínsecas, esto bajo una argumentación estrictamente matemática, para evitar caer en discusiones estériles relacionadas con los ajustes de datos experimentales a una ecuación matemática. La línea de discusión es muy simple y pragmática, si la ecuación usada para realizar ajustes experimentales no tiene sustento hidrológico, entonces no tiene sentido seguir usándola y hay que buscar otra ecuación que sí lo tenga.
HIPÓTESIS INTRÍNSECAS DEL MÉTODO DEL NÚMERO DE CURVA
Para aclarar las implicaciones de la Ecuación 1, en la Figura 1 se presentan dos escenarios de la relación P–Q.

La hipótesis básica planteada en el método del NC es que a medida que la intensidad de la precipitación es mayor, entonces el suelo se saturará rápidamente y todo lo que se precipita escurrirá (Q = P), representado por la línea punteada que pasa por el origen en la Figura 1. En la misma figura se presenta una curva, con línea sólida, que tiene una fase no lineal y después una lineal que intersecta el eje P en S y es paralela a la línea Q = P (pendiente unitaria). Así, sin pérdida de generalidad, se puede suponer que la relación P–Q está compuesta de dos fases: una no–lineal inicial y después una lineal, cuya transición está dada por el punto (PT, QT). La fase lineal se presenta en forma completa, más allá de la transición suavizada, a partir del punto (PL, QL). De la Figura 1, resulta aparentemente claro que el método del NC aproxima el patrón mostrado de alguna forma la relación no lineal (en sus dos fases).
En esencia, el método del NC parte de la idea de que la relación no–lineal deberá tender a una línea que cumpla la condición Q = P cuando P sea grande (saturación del suelo). Esto puede formularse arbitrariamente como:

donde, la segunda relación se obtuvo de la ecuación de la línea recta (fase lineal) mostrada en la Figura 1. El planteamiento de las relaciones (4) se puede generalizar para cualquier pendiente λ, donde λ = 1 es un caso cualquiera. La argumentación siguiente es válida para cualquier valor de λ, usando P = λP.
La obtención de la Ecuación 1, caso de Ia = 0, es simplemente producto de igualar las dos relaciones en (4):

El caso general dado por Ia > 0, implica sólo un desplazamiento sobre el eje P del origen de la Figura 1 al nuevo definido por (Ia, 0). En este caso, la precipitación se interpreta como una precipitación efectiva Pe = P–Ia. La relación (1) se obtiene del cambio de P por Pe en la relación (5).
En el aspecto de las aplicaciones empíricas del método del NC, es interesante señalar que su autor principal Mockus, en una entrevista con Victor Ponce2 señalo que la relación implicada en el método del NC, (P–Q)/S = Q/P, fue utilizada después de probar muchas relaciones empíricas y los resultados obtenidos en el ajuste a los datos experimentales fueron satisfactorios. Este argumento puramente empírico es circular, ya que la relación utilizada tiene ambas variables de los dos lados de la ecuación, por lo que se obtienen resultados estadísticos mejores en forma artificial que las relaciones en formato normal.
Implicaciones del método del número de curva
El desarrollo mostrado anteriormente para obtener el método del NC implica:
a) La relación (1) no busca aproximar el comportamiento no–lineal de P–Q y sólo es consecuencia de la hipótesis de suponer una pendiente unitaria cuando P es grande. De hecho, el método del NC no supone nada sobre la fase no lineal de la relación entre P y Q, Figura 1.
b) La hipótesis definida por la relación (5) sólo se satisface cuando P tiende a infinito (es decir, nunca, ya que ésta es indeterminada y el límite supuesto sólo es un artefacto matemático) y aproxima algo la relación entre P y Q cuando P es muy grande (Mishra et al., 2005). La forma simple de decir lo mismo es que S y Ia tienden a cero en la Ecuación 1.
c) El método del NC no permite obtener PT o PL, ya que estos puntos no están definidos (PT y PL tienden a infinito).
HACIA UNA MEJOR APROXIMACIÓN MATEMÁTICA
El uso de funciones matemáticas para relacionar P con Q es sin duda un problema abierto cuando no se utiliza conocimiento hidrológico. Como primera aproximación, en lo siguiente se presenta un esquema de modelación que puede justificarse en términos teóricos, además de que se obtienen excelentes ajustes empíricos a los datos experimentales (no mostrados).
Tal como se muestra en forma esquemática en la línea continua de la Figura 1, el patrón entre la precipitación y el escurrimiento puede aproximarse como compuesta de dos fases: una exponencial y una lineal.
• Crecimiento exponencial:

• Crecimiento lineal:
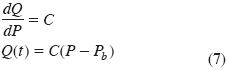
donde, r es una tasa relativa de cambio, C es la tasa máxima de cambio y Pb (= S en la Figura 1) es el tiempo cuando P = 0 (proyectado) en la fase lineal de la relación P–Q.
La relación (6) muestra que los cambios instantáneos de escurrimiento por cambios instantáneos en la precipitación son función del escurrimiento previo.
La relación (7) muestra una fase posterior a la exponencial de tipo lineal y representa la situación donde se ha alcanzado la tasa de cambio máxima y la relación P–Q mantiene una pendiente constante (que puede ser menor a 1.0). El modelo expo–lineal propuesto tiene como solución el patrón exponencial y el lineal como únicos, por lo que puede reproducir comportamientos exponenciales, lineales y expo–lineales. Eso le da una gran versatilidad en los ajustes a datos experimentales.
Las dos fases planteadas pueden ser analizadas en forma independiente haciéndolas compatibles en los puntos de transición (Figura 2) o se puede generar un modelo con una transición gradual entre ambos tipos de patrones. En el último caso, en el momento de la transición del patrón exponencial al lineal las tasas de cambio deben ser iguales:


El modelo expo–lineal es simplemente la solución de los dos tipos de patrones representados por las ecuaciones diferenciales anteriores sujeta a la condición dada por la relación de igualdad de las tasas de cambio (adaptado de Goudriaan y van Lar, 1994):

Con las siguientes características:

donde, PT es la precipitación donde la condición (8) se cumple. La relación Q – (dQ/dP) es un sigmoideo simétrico para el modelo expo–lineal:

Una justificación simple del modelo expo–lineal propuesto puede realizarse usando consideración de respuestas hidrológicas fraccionales en una cuenca, en relación a la respuesta máxima (Q = λP). Steenhuis et al. (1995) plantearon que la hipótesis de la hidrología de área variable, donde la precipitación que cae sobre un suelo no saturado se infiltra incrementando el contenido de humedad del suelo hasta que el perfil del suelo se satura y la precipitación adicional se convierte en escurrimiento (Hewlett y Hibbert, 1967; Dunne y Black, 1970; Boughton, 1987), puede plantearse como:

donde, Af (C en la ecuación 7) es la fracción de área de la cuenca o parcela experimental que contribuye al escurrimiento (fracción de área saturada de suelo del área total). Esta fracción tiene un comportamiento temporal gradual de saturación, hasta alcanzar su máximo para un evento de precipitación dado e implica una relación no–lineal y lineal (compuesta) como la mostrada con línea continua en la Figura 1.
CONCLUSIONES
De la discusión anterior se puede concluir con toda certeza que el método del NC, relación (1), es consecuencia de la hipótesis absurda de igualar dos líneas rectas (Q = P y Q = P–S, Figura 1; donde P puede ser la precipitación efectiva), que por definición no convergen entre sí. Esta hipótesis sólo es válida cuando S tiende a cero y P tiende a infinito (reductio ad absurdum); esto es un límite matemático que puede interpretarse como que dos líneas rectas nunca serán iguales, a menos que tengan un origen común. Más allá de este intento sin sustento hidrológico, el método del NC no tiene ninguna base teórica o de otro tipo, más allá de su facilidad de aplicación y el argumento de hacerlo operacional a través del uso de la relación entre S y el NC.
La argumentación del uso del método del NC para valores intermedios de P está sesgada por las hipótesis usadas. El caso extremo, base del método, de que Q = P nunca se cumple por la sencilla razón de que dos líneas rectas paralelas con orígenes distintos jamás se juntan. Los otros casos no extremos están definidos en forma arbitraria y pueden o no pueden generar buenos ajustes experimentales.
Después de 35 años de uso del método del NC de forma indiscriminada (validada muy pocas veces; y, cuando esto es así, sólo se comporta bien cuando P es muy grande), es imperativa una formulación hidrológicamente sólida entre P y Q, en un esquema simple similar al formato del NC. El seguir buscando darle solidez al método a través de relaciones empíricas o adecuaciones ad hoc (Mishra et al., 2005), parte de hacer viable un absurdo sin bases teóricas.
En el sentido propositivo de esta contribución, se ha planteado un modelo alterno al método del número de curva que tiene un sustento hidrológico sólido, dentro del contexto de modelos simples y operacionales. El modelo expo–lineal propuesto requiere tres parámetros para su caracterización. En trabajos posteriores, usando un esquema de simplificación similar al desarrollado para el número de curva (tipo de suelo y condición de la cobertura de vegetación), se plantea la reducción de los parámetros del modelo expo–lineal a solo uno, volviéndose atractivo como un sustituto operacional del método del NC.
AGRADECIMIENTO
El autor agradece al Profesor Jorge Etchevers del Colegio de Postgraduados la revisión crítica del borrador inicial de este trabajo.
LITERATURA CITADA
Boughton, W. C. 1987. Evaluating partial areas of watershed runoff. J. Irrigation and Drainage Eng. ASCE 113: 356–366. [ Links ]
Dunne, T., and R. D. Black. 1970. Partial area contributing to storm runoff in a small New England watershed. Water Resources Res. 6: 1296–1311. [ Links ]
Goudriann, J., and H. M. van Laar. 1994. Modelling potential crop growth processes. Textbook with exercises. Current Issues in Production Ecology. Kluwer Academic Publishers, Dordrecht 238 p. [ Links ]
Hewlett, J. D., and A. R. Hibbert. 1967. Factors affecting the response of small watersheds to precipitation in humid are. In: Sopper, W. E., and H. W. Loll (eds). Proceedings of the International Symposium on Forest Hydrology. Pergamon, Oxford, England pp: 275–290. [ Links ]
Mishra, S. K., M. K. Jain, P. K. Bhunya, and V. P. Singh. 2005. Field applicability of the SCS–CN–based Mishra–Singh general model and its variants. Water Resources Manage. 19: 37–62. [ Links ]
Mockus, V. 1949. Estimation of total (and peak rates of) surface runoff for individual storms. Exhibit A of appendix B. Interim Survey Report. Grand (Neosho) River Watershed. Soil Conservation Service. United States Department of Agriculture. [ Links ]
NRCS. 2004. Part 630 Hydrology. National Engineering Handbook. Chapter 10 Estimation of direct runoff from storm rainfall. Natural Resources Conservation Service. United States Department of Agriculture. (210–VI–NEH, July 2004). [ Links ]
SCS. 1972. Section 4: Hidrology. National Engineering Handbook. Soil Conservation Service. United States Department of Agriculture. [ Links ]
Steenhuis, T. M., M. Wincell, J. Rossing, J. A. Zollweg, and M. F. Walter. 1995. SCS runoff equation revisited for variable–source runoff areas. J. Irrigation and Drainage Eng. 121: 234–238. [ Links ]
1 http://www.wsi.nrcs.usda.gov/products/W2Q/, consultada el 8 de diciembre de 2007.
2 http://www.wsi.nrcs.usda.gov/products/W2Q/. Consultada en Octubre 13 del 2007.














