1 Introduction
The growing demand and the lack of fossil fuels [1], along with their effects such as air pollution and global warming, have forced to consider alternative energy sources. Solar energy is one of the most promising renewable energy due to its unlimited source of power. Nowadays, the solar photovoltaic energy has attracted the attention in many areas of engineering, increasing its use through the years [2] as a result of its free-emission electrical power generation [3], easy maintenance and availability in isolated areas.
The modeling of solar cells is a complex task attributable to their nonlinear (I - V) behavior and their high dimensionality. Moreover, there exist several factors that adversely affect the modeling of solar cells such as the temperature, the partially shaded conditions [4], just for mention a few. The most efficient method for generating solar cell models is the use of an equivalent electrical system. In the literature, there are two main models reported: the single and the double diode model. The most common configuration is the single diode model which considers five design parameters [5]. On the other hand, the double diode model involves seven design parameters [6] that must be defined. Recent advances in solar cell systems have conducted to the development of more accurate models than those produced by the electronic circuits of one or two diodes. One example of these new models is the configuration of three diodes proposed in [7].
Under this approach, other important factors of the solar cell can be characterized to improve its operative precision by considering ten different design parameters. Different to other studies, in this paper, the three-diode model is considered for the experimental comparisons.
Several methods have been reported in the literature for the estimation of parameters in solar cells. Some examples involve those based on Newton methods [7], the Lambert functions [8] and least squares [10,11]. Such techniques can determinate solar cells parameters with a relative good precision; however, they frequently deliver sub-optimal solutions because of their inability to overcome local optima [11].
Evolutionary Computation (EC) techniques are optimization approaches that solve difficult engineering problems due to their efficient search strategies which allow finding optimal solutions. Several EC methods and their variations have been proposed as an alternative to classical techniques for estimating the parameters of solar cells. Essentially, these methods have produced better results than those obtained by classical methods regarding accuracy and robustness. Some examples of such proposals involve Genetic Algorithms (GA) [13,14], Particle Swarm Optimization (PSO) [15,16], Artificial Bee Colony (ABC) [17,18], Differential Evolution (DE) [19,20], Harmony Search (HS) [21,22], Cuckoo Search (CS) [23,24], just for mention a few. However, most of these studies report only a single EC technique considering a minimal number of solar cell models [25-27].
Each EC algorithm has been designed to fulfill the conditions of specific problems since no one approach can optimize all problems effectively. Under such circumstances, the performance of each EC approach must be correctly assessed considering the application context. This paper presents a comparative study of the most popular EC algorithms currently in use for the parameter estimation of single, double and three diode models in solar cells. The techniques considered in the study involve Artificial Bee Colony (ABC) [27], Differential Evolution (DE) [28], Harmony Search (HS) [29], Gravitational Search Algorithm (GSA) [30], Cuckoo Search (CS) [31], Differential Search Algorithm (DSA) [32], the Crow Search Algorithm (CSA) [33], and Covariant Matrix Adaptation with Evolution Strategy (CMA-ES) [35,36]. The experimental results of this study present the relative performance of each EC technique validated under statistical tests.
This paper is organized as follows; Section 2 presents a brief description of evolutionary computation techniques used in this work. Section 3 details the three equivalent circuit models for the solar cell parameter estimation. In Section 4, the experimental results are reported. In Section 5, the non-parametric statistical tests used for the experimental validation is presented. Finally, in Section 6 the conclusions are discussed.
2 Evolutionary Computation (EC) Techniques
EC techniques are useful tools that allow solving complex problems with a good performance. These algorithms are designed to optimize a set of the task with specific characteristics. Under such circumstances, no one method can solve all problems efficiently. The performance of an EC method is directly determined by the balance between the exploration and exploitation of its optimization process. Therefore, different EC approaches have been developed, where both concepts are specifically combined to produce a particular search strategy. In this section, a brief description of the EC methods used in the comparisons is presented.
2.1 Artificial Bee Colony (ABC)
Artificial Bee Colony was proposed by Karaboga [27] inspired by the behavior of honeybee
swarm. The ABC employs a population
where
where f(•) is the fitness function to be minimized. When a new
food source is computed, a greedy selection handle, if the new food source
v
i
is better than the actual
2.2 Differential Evolution (DE)
Storn and Price developed Differential evolution algorithm [28], which is a stochastic vector-based evolutionary technique, which utilizes m-dimensional vectors defined as follow:
where
where F is a constant that controls the magnitude of differential variation within the interval [0, 2]. On the other hand, to increment the diversity of the mutated vector, a crossover is incorporated. It is represented as follows:
Finally, the vector selection produces the final value comparing the fitness values between the can didate vector against the original as follows:
2.3 Harmony Search (HS)
Harmony search algorithm was introduced by Geem [29]. This optimization method is
particularity based on the improvisation process taking place in jazz music. HS
defines a harmony memory with a population of N individuals
represented as
When a new harmony is produced, a uniform random number between [0,1] is generated r 1 , if this number is less than the harmony-memory consideration rate (HMCR), the new harmony is generated with memory considerations, otherwise, the new harmony is re-initialized with random values between bound limits. The generation process of a new harmony is described below:
To determinate which element should be adjusted by the pitch process, further examinations must be considered. For this operation two parameters are defined: The pitch-adjusting rated (PAR) and bandwidth factor (BW). PAR considers the frequency of adjustment while BW controls the magnitude of the local search process. This complete operation can be described as follows:
2.4 Gravitational Search Algorithm (GSA)
Rashedi proposed Gravitational Search Algorithm [30] which is based on the laws of gravity.
This technique emulates the candidate solutions as masses, which are attacked
one each other by the gravitational forces. Under this approach, the quality
(mass) of an individual is determined by its fitness value. The GSA uses a
population of N individuals that represent an
m-dimensional vector
where Ma j is the active gravitational mass related to individual j, Mp i . is the passive gravitational mass of individual i, G(t) is the gravitational constant, ε is a constant, and R ij is the Euclidian distant between i and j individuals. In GSA, the balance between exploration and exploitation is made by modifying G(t) through the iterations. The sum of all forces acting on individual i is expressed bellow:
the acceleration of each individual at time t is given bellow:
where Mn i is the inertia mass of individual i, with this, the velocity and position for each individual are computed as follows:
After evaluating the fitness of each individual, their inertia, and gravitational masses are updated, where a heavier individual means a better solution, fort this, GSA uses the follows equations:
where are the fitness function and best (t) and worst (t) represent the best and worst solution of the complete population at time t.
2.5 Particle Swarm Optimization (PSO)
Particle Swarm Optimization, introduced by Kennedy [36], is based on the behavior of birds
flocking. The PSO uses a group of N particles
where ω is the inertia weighs used to control the velocity (i = 1,2,..,N), (j = 1,2,...,p). c 1 and c 2 are the acceleration coefficients that adjust the movement of each individual in the positions g and p * respectively. r 1 and r 2 are two random numbers between [0,1]. Therefore, to calculate the new position of the individuals used the following equation is employed:
Once the new position is computed, it is evaluated by a cost function. If the new solution is better that the last one, then it is replaced, otherwise it remains.
2.6 Cuckoo Search (CS)
The cuckoo search was proposed in 2009 by Deb and Yang [31]. This technique emulates the parasite
behavior of cuckoo birds through the use of the Lévy flights [37]. CS uses a population of
where
where Γ(•) is the Gamma distribution. Once s i is calculated, c i is computed as follows:
where ⊕ is the element-wise multiplications. Ones are obtained, the new candidate solution is estimated as bellow:
2.7 Differential Search Algorithm (DSA)
Differential search algorithm [32] imitates the Brownian-like random-walk movement
used by an organism to migrate. In the DSA a population
where ri ∈ [1, NP] is a random integer within the population range and ri ≠ i. A is a scale factor that regulate the position changes of the individuals. For the search process, the stopover position is determined as below:
where j = [1,…, d] and r i,j can take the value of 0 or 1. After the selection of the candidate solution, each individual is evaluated by a cost function f(•) to determinate their quality, then a criterion of selection is used which is described as follows:
2.8 Crow Search Algorithm (CSA)
The crow search algorithm was originally proposed by Askarzadeh [33], based on the
intelligent behavior of crows. CSA uses a population of
where r
i
and r
j
are random numbers between [0,1], fl is a parameter that
controls the flight length.
2.9 Covariant Matrix Adaptation with Evolution Strategy (CMA-ES)
CMA-ES [35,36] is an evolutionary
algorithm proposed by Hansen based on the estimation of the covariant matrix on
the search data. The CMA-ES uses a population of
where N(μ, C) is a normally
distributed random vector with a mean μ and a covariance matrix
C. The next weighted mean
where
where
where B k is an orthogonal matrix and D k is a diagonal matrix. The adaptation of global step size for the next generation is given by the following equation:
where
3 Modeling of Solar Cells
Solar cells are one of the most essential and increasingly clean energy sources. For this reason, their correct modeling has become an important task nowadays. Several alternatives for the solar cell modeling have been proposed in the literature [38-40]. However, the most common models are the equivalent circuits models [5, 6, 41], known as Single diode model (SDM), Double diode model (DDM) and Three diode model (TDM).
3.1 Single Diode Model (SDM)
The single diode model is the basic and most used model for the representation of the solar cell behavior. This model uses a diode connected in parallel with the source of current. Fig. 1 presents a representation of this model. Considering the circuit theory, the total current of single diode model is calculated as follows:
where k is the Boltzmann constant, q is the electron charge, I SD is the diffusion current, V cell is the terminal voltage, R p and R S are the parallel and serial resistances. For the single diode model, the parameters that determinate its performance is given by five parameters; R S , R p , I L , I SD and n.
3.2 Double Diode Model (DDM)
The double diode model is another alternative to characterize the solar cell behavior. Under this circuit, instead of using only one diode, it involves two diodes in a parallel array as is shown in Fig. 2. Therefore, the total current of this model is calculated as follows:
where the diodes and leakage currents are calculated as follows:
In the double diode model, the elements that must be determined are R s , R p , I L , I SD1 , I SD2 , n 1 and n 2 .
3.3 Three Diode Model (TDM)
Recent advances in solar cell systems have conducted to the development of more accurate models than those produced by the electronic circuits of one or two diodes. One example of these new models is the configuration of three diodes proposed in [7]. The three diode model is a representation of the solar cell models which include a third diode in parallel with the original two diodes. The model considers the effects of a new current ID 3 and factor n 3 that allow improving the modeling accuracy. Similarly to the two diode model, the total current is calculated as:
In the case of three diode model, the parameter R S is replaced by R SO (1+KI) to find the variation of R S with I cell . Where I cell is the load current and K is a parameter that must be determined as the other parameters, for this, the parameters to be tuned are R SO , R p , I L , I D1 , I D2 , I D3 , n 1, n 2, n 3 and K.
The solar cells can be configured as modules [42,43], which are an array of individual solar cells connected in serial and parallel. When the cells are connected to serial the voltages increases N S times, in the case of cells connected in parallel only the current components increases in N P times. So that, the output of a module of N s × N p cells is computed as follows:
3.4 Solar Cells Parameter Identification as an Optimization Problem
The identification of solar cells can be faced as an optimization problem. Under this approach, the objective is the correct approximation of the I - V output between the true model and the equivalent circuit model. With this results, each optimization technique is evaluated by a cost function to determinate the quality of the approximation. For the identification process, the equations (23, 24) and (28) are rewritten to reflex the difference of the experimental data as follows:
For the three models x represents the parameters to be estimated, for the single diode model (SDM) x = [R s , R p , I L , I SD , n], in the double diode model (DDM) x = [R s , R p , I L , I SD1 , I SD2 , n 1, n 2] and for the three diode model (TDM) x = [R so , R p , I L , I SD1 , I SD2 , I SD3 , n 1, n 2, n 3. K]. In order to evaluate the quality of each candidate solution, the root means square error (RMSE) is considered:
During the optimization process, the parameters are adjusted to minimize the cost function until a stop criterion is reached. Since the data acquisition is in variant environmental conditions, the objective function presents noisy characteristics and multimodal properties [44]. Under such circumstances, the estimation process is considered as a complex task [45].
4 Experimental Results
For the experiments, an illustrative set of three different solar cell devices have been considered to examine the performance of our approach: the C60 mono-crystalline solar cell (SUNPOWER), the D6P Multi-crystalline Photovoltaic Cell (DelSolar) and KC200GT Photovoltaic Solar Module (Shell Solar). The experimental section consists of three experiments.
In the first experiment, The SUNPOWER solar cell has been used for parameter estimation considering the single and double diode models over different operative conditions. In the second experiment, the DelSolar cell is identified considered the single, double and three diode models. Finally, in the third experiment, the Shell Solar system is identified by using the single and double diode models.
For the Single Diode Model, the number of parameters to be determined is five, in the Double Diode Model 7 and for the Three Diode Model 10. It is important to remark that the three Diode Model involves three fixed parameters [46]. In the three diode model, I SC is the short circuit current and R S is also replaced with R SO (1+KI) to find the variation of R S respect to the current I. The lower and upper solar cells parameters ranges for each model are shown in Table 1.
Table 1 Solar cells parameters ranges for Single, Double, and Three Diode Model
| Single Diode Model | Double Diode Model | Three Diode Model | ||||||
|---|---|---|---|---|---|---|---|---|
| Parameter | Lower | Upper | Parameter | Lower | Upper | Parameter | Lower | Upper |
| R S (Ω) | 0 | 0.5 | R S (Ω) | 0 | 0.5 | R SD (Ω) | 0 | 1 |
| R P (Ω) | 0 | 200 | R P (Ω) | 0 | 100 | R P (Ω) | 0 | 100 |
| I L (A) | I SC | I L (A) | I SC | I L (A) | I SC | |||
| I SD (μA) | 0 | 1 | I SD1 (μA) | 0 | 1 | I SD1 (μA) | 0 | 1 |
| n 1 | 1 | 2 | I SD1 (μA) | 0 | 1 | I SD2 (μA) | 0 | 1 |
| - | - | - | n 1 | 0 | 2/3 | I SD3 (μA) | 0 | 1 |
| - | - | - | n 2 | 0 | 2/3 | n 1 | 1 | |
| - | - | - | - | - | - | n 2 | 2 | |
| - | - | - | - | - | - | n 3 | 0 | 3 |
| - | - | - | - | - | - | k | 0 | 1 |
In the experiments, each algorithm is compared regarding its estimation accuracy. The methods considered in the comparison are the Artificial Bee Colony (ABC), Crow Search Algorithm (CSA), Cuckoo Search (CS), Differential Evolution (DE), Differential Search Algorithm (DSA), Gravitational Search Algorithm (GSA), Harmony Search (HS), Particle Swarm Optimization (PSO) method [12], and the Co-variance Matrix Adaptation Evolution Strategies (CMA-ES).
These methods are considered as the most popular EC algorithms currently in use. The parameter setting of each EC method for the experimental analysis is defined according to its own references which have demonstrated through experimentation produce the best optimization results. Such configurations are summarized below:
ABC: limit = 100 , by using [16].
CSA: AP = 0.1 and fl = 2.
CS: p a = 0.25 in concordance with [23].
DE: F = 0.4 and C r = 0.4 [47].
DSA: p 1 = 0.3 and p 2 = 0.3 according to [32].
GSA: G 0 = 100 and α= 20 [30].
HS: HMRC = 0.95 and PAR = 0.3 [22].
PSO: c 1 = 0.5, c 2 = 2.5 , the weight factor w decreases from 0.9 to 0.4 according to [48].
CMA-ES: The parameters are configured according to [34, 35].
In the study, two performance indexes are compared: the root means square error (RMSE) and standard deviation after 40 individual executions. The first index evaluates the accuracy of the algorithm whereas the latter measures its robustness.
In the comparisons, each algorithm is set with 50 individuals.
To eliminate the random effect, each experiment is tested for 40 independent runs. In the comparison, a fixed number of iterations (2000) has been considered as a stop criterion. This stop criterion has been decided to keep compatibility with similar works published in the literature.
4.1 Identification of C60 Mono-Crystalline Solar Cell
The first experiment involves the parameter estimation of a solar cell C60 Mono-crystalline, considering four different sun irradiations: (1000 W/m2), (800 W/m2 ), (500 W/m2) and (300 W/m2) at T = 25°C. In the estimation process, the SDM, as well the DDM models, are used. Table 2, 3, 4 and 5 present the results for the cases of (1000 W/m2), (800 W/m2), (500 W/m2) and (300 W/m2), respectively.
Table 2 Solar cells (Mono-crystalline C60) parameters estimation, Mean and Standard deviation for the Single Diode Model (SDM) and Double Diode Model (DDM) at 1000 W/m 2
| SDM | |||||||||
| Parameters | ABC | CSA | CS | DE | DSA | GSA | HS | PSO | CMA-ES |
| RS (Ω) | 0.005065 | 0.006535176 | 0.00168 | 0.00466 | 0.0051363 | 0.00542089 | 0.00920948 | 0.0034763 | 0.00662421 |
| Rp (Ω) | 183.463 | 114.252273 | 199.3241 | 199.4603 | 152.35831 | 79.83066 | 164.621448 | 39.481739 | 200 |
| IL (A) | 6.240779 | 6.21459738 | 6.546991 | 6.23187 | 6.2295673 | 3.53701901 | 6.41504223 | 6.2343094 | 6.21432845 |
| ID (A) | 2.08E-06 | 2.79016E-07 | 6.27E-08 | 3.3E-06 | 2.197E-06 | 2.4077E-06 | 5.3421E-06 | 3.595E-06 | 2.41E-07 |
| n | 1.697168 | 1.496370914 | 1.345742 | 1.7507 | 1.7033435 | 1.87810036 | 1.82172571 | 1.7523015 | 1.48357172 |
| Min RMSE | 0.010921 | 0.009935587 | 0.267794 | 0.010551 | 0.0099479 | 0.03315632 | 0.01324157 | 0.0113077 | 0.00992256 |
| Max RMSE | 0.014243 | 0.01156138 | 0.268449 | 0.012094 | 0.0115475 | 0.20423651 | 0.07939054 | 0.0369322 | 0.0104022 |
| Average RMSE | 0.011869 | 0.010522777 | 0.268275 | 0.011191 | 0.0106624 | 0.1058941 | 0.02830248 | 0.0169241 | 0.00995462 |
| std | 0.00066 | 0.000461744 | 0.000122 | 0.000316 | 0.0004252 | 0.04410207 | 0.01343111 | 0.0047521 | 0.00010586 |
| DDM | |||||||||
| Parameters | ABC | CSA | S | DE | DSA | GSA | HS | PSO | CMA-ES |
| RS (Ω) | 0.005678 | 0.006503674 | 0.002098 | 0.006623 | 0.006368 | 4.6383E-05 | 0.00585544 | 0.0058646 | 6.62E-03 |
| Rp (Ω) | 104.5934 | 191.2923658 | 188.4067 | 135.4169 | 161.64551 | 89.7438772 | 23.2336847 | 70.063423 | 2.00E+02 |
| IL (A) | 6.226711 | 6.214465293 | 6.54696 | 6.216998 | 6.2162283 | 3.29376151 | 6.09719654 | 6.2251079 | 6.21432845 |
| ID1 (A) | 2.52E-06 | 2.98848E-09 | 6.48E-07 | 1.29E-06 | 2.551E-07 | 3.5163E-06 | 8.3191E-07 | 8.32E-07 | 2.41E-07 |
| ID2 (A) | 1.01E-06 | 2.86929E-07 | 2.73E-08 | 1.91E-07 | 1.984E-07 | 9.9952E-07 | 9.2192E-07 | 5.353E-07 | 4.16E-16 |
| n1 | 2.996087 | 1.548379914 | 1.936987 | 2.1322 | 21.4991135 | 1.96725788 | 1.7084817 | 1.8053035 | 1.48357169 |
| n2 | 1.619807 | 1.499321137 | 1.290596 | 1.466079 | 1.6776963 | 1.90130136 | 1.66715067 | 1.5634685 | 1.48324541 |
| Min RMSE | 0.010186 | 0.009922907 | 0.267669 | 0.009963 | 0.0099278 | 0.01742442 | 0.01243733 | 0.0104161 | 0.00992256 |
| Max RMSE | 0.011947 | 0.021592727 | 0.26857 | 0.03142 | 0.0309824 | 0.05321138 | 0.04337821 | 0.0137103 | 0.01167399 |
| Average RMSE | 0.010878 | 0.018137755 | 0.268162 | 0.014355 | 0.0128385 | 0.03266309 | 0.01869163 | 0.0115566 | 0.00994816 |
| std | 0.000528 | 0.000230786 | 0.000189 | 0.000341 | 0.0002764 | 0.00833028 | 0.00624268 | 0.0008043 | 0.00124354 |
Table 3 Solar cells (Mono-crystalline C60) parameters estimation, Mean and Standard deviation for the Single Diode Model (SDM) and Double Diode Model (DDM) at 800 W/m 2
| SDM | |||||||||
| Parameters | ABC | CSA | CS | DE | DSA | GSA | HS | PSO | CMA-ES |
| RS (Ω) | 0.000488 | 0.000804375 | 2E-05 | 0.000608 | 0.0009882 | 0.00513349 | 0.00031329 | 0.0206406 | 0.00163057 |
| Rp (Ω) | 120.7382 | 98.41301429 | 192.0449 | 199.9999 | 131.57376 | 105.754974 | 77.0013758 | 66.393912 | 24.8933861 |
| IL (A) | 4.882213 | 4.881234281 | 5.130919 | 4.878856 | 4.8774982 | 3.76620098 | 4.70079256 | 4.8472653 | 4.88245696 |
| ID (A) | 2.15E-06 | 1.80815E-06 | 2.96E-09 | 2.12E-06 | 1.464E-06 | 2.9701E-06 | 3.8413E-06 | 6.636E-06 | 6.87E-07 |
| n | 1.728899 | 1.709113752 | 1.170159 | 1.727269 | 1.684991 | 1.85447388 | 1.80017479 | 1.8717672 | 1.60471698 |
| Min RMSE | 0.004947 | 0.004868946 | 0.490195 | 0.004944 | 0.004869 | 0.01796734 | 0.00803614 | 0.0059932 | 0.00486895 |
| Max RMSE | 0.006511 | 0.00633468 | 0.490546 | 0.005489 | 0.0051846 | 0.16861586 | 0.0824437 | 0.0320081 | 0.0050412 |
| Average RMSE | 0.005311 | 0.005094385 | 0.490393 | 0.005165 | 0.0049925 | 0.08699095 | 0.02791164 | 0.0169787 | 0.00487734 |
| std | 0.000262 | 0.000331104 | 7.47E-05 | 0.000131 | 7.706E-05 | 0.03347491 | 0.01654392 | 0.0070283 | 3.0309E-05 |
| DDM | |||||||||
| Parameters | ABC | CSA | CS | DE | DSA | GSA | HS | PSO | CMA-ES |
| RS (Ω) | 0.001232 | 0.001737993 | 4.04E-05 | 0.001437 | 0.0012232 | 0.00013346 | 0.00077359 | 0.0005271 | 0.00163057 |
| Rp (Ω) | 119.4226 | 74.60410516 | 192.1913 | 31.65655 | 92.170396 | 94.7860962 | 38.135595 | 54.42826 | 24.8933897 |
| IL (A) | 4.87627 | 4.876536455 | 5.130963 | 4.880101 | 4.8766252 | 2.94761087 | 4.87654863 | 4.8827055 | 4.88245696 |
| ID1 (A) | 1.33E-06 | 1.72118E-06 | 6.3E-10 | 1.25E-06 | 7.495E-07 | 1.1397E-06 | 5.4769E-06 | 1.97E-06 | 4.12E-20 |
| ID2 (A) | 0.004192 | 2.67912E-07 | 1.94E-08 | 6.06E-07 | 4.097E-07 | 9.9984E-07 | 2.4922E-07 | 3.501E-07 | 6.87E-07 |
| n1 | 1.674555 | 1.920364455 | 1.090282 | 2.045905 | 1.6671119 | 1.9393706 | 1.89673872 | 1.7292267 | 1.96919786 |
| n2 | 51.2116 | 1.533094915 | 1.999292 | 1.598242 | 1.6469724 | 1.81085015 | 1.65114007 | 1.812426 | 1.60471696 |
| Min RMSE | 0.004884 | 0.004870705 | 0.489958 | 0.004879 | 0.00487 | 0.01021258 | 0.00666149 | 0.0049378 | 0.00486895 |
| Max RMSE | 0.005309 | 0.005923922 | 0.490594 | 0.005059 | 0.0053881 | 0.03878291 | 0.02295133 | 0.0077401 | 0.00505602 |
| Average RMSE | 0.005044 | 0.004957579 | 0.490274 | 0.004934 | 0.0050934 | 0.02353969 | 0.01157486 | 0.0057249 | 0.00491157 |
| std | 0.000144 | 0.000171857 | 0.000156 | 3.71E-05 | 0.0001448 | 0.00730923 | 0.00383631 | 0.0008088 | 3.6698E-05 |
Table 4 Solar cells (Mono-crystalline C60) parameters estimation, Mean and Standard deviation for the Single Diode Model (SDM) and Double Diode Model (DDM) at 500 W/m 2
| SDM | |||||||||
| Parameters | ABC | CSA | CS | DE | DSA | GSA | HS | PSO | CMA-ES |
| RS (Ω) | 0.0016 | 0.003883448 | 1.17E-05 | 0.003187 | 0.0039048 | 0.00821181 | 0.00642602 | 0.4181931 | 0.00441815 |
| Rp (Ω) | 163.4687 | 199.973256 | 198.2291 | 200 | 130 | 115.937296 | 109.512364 | 168.0123 | 48.9235971 |
| IL (A) | 3.038953 | 3.037506852 | 3.364666 | 3.039108 | 3.0385235 | 1.59703402 | 3.09297001 | 3.0363817 | 3.04073716 |
| ID (A) | 2.33E-06 | 7.66902E-07 | 4.89E-11 | 1.16E-06 | 7.455E-07 | 8.4011E-07 | 7.4442E-06 | 1.78E-06 | 4.93E-07 |
| n | 1.769269 | 1.640749248 | 1.006255 | 1.685994 | 1.6376616 | 1.94585248 | 1.93745184 | 1.7383762 | 1.59453154 |
| Min RMSE | 0.004097 | 0.003977713 | 0.775675 | 0.004006 | 0.0039789 | 0.00621321 | 0.00573558 | 0.0043468 | 0.00397771 |
| Max RMSE | 0.004518 | 0.00485107 | 0.775887 | 0.004348 | 0.0043833 | 0.05531805 | 0.03164257 | 0.0079782 | 0.00404263 |
| Average RMSE | 0.004288 | 0.00408547 | 0.775706 | 0.004139 | 0.0040739 | 0.03202631 | 0.01165965 | 0.0055138 | 0.00398091 |
| std | 9.52E-05 | 0.000195093 | 3.73E-05 | 8.61E-05 | 9.076E-05 | 0.01185082 | 0.00541076 | 0.0009191 | 1.2258E-05 |
| DDM | |||||||||
| Parameters | ABC | CSA | CS | DE | DSA | GSA | HS | PSO | CMA-ES |
| RS (Ω) | 0.004034 | 0.004177475 | 7.24E-05 | 0.003613 | 0.0041682 | 0.00056852 | 6.1811E-05 | 0.0009983 | 0.00441815 |
| Rp (Ω) | 77.26164 | 53.46679376 | 199.3801 | 190.1412 | 76.437153 | 83.6005286 | 105.243007 | 193.65696 | 48.9235809 |
| IL (A) | 3.045323 | 3.03984558 | 3.364619 | 3.03873 | 3.0393953 | 1.84818457 | 3.0452358 | 3.0414082 | 3.04073717 |
| ID1 (A) | 6.91E-07 | 3.52681E-06 | 6.22E-11 | 8.18E-07 | 7.987E-10 | 1.8939E-06 | 5.2676E-06 | 3.468E-06 | 4.93E-07 |
| ID2 (A) | 0.000382 | 6.38146E-08 | 1.01E-10 | 5.59E-07 | 5.927E-07 | 9.9958E-07 | 6.8983E-07 | 9.414E-07 | 2.05E-20 |
| n1 | 1.630061 | 1.995274001 | 1.63944 | 1.950576 | 1.7433395 | 1.98517022 | 1.88922847 | 1.9159403 | 1.59453153 |
| n2 | 30.69521 | 1.439759222 | 1.03605 | 1.617409 | 1.6134584 | 1.91104148 | 1.99442602 | 1.7420063 | 1.9973227 |
| Min RMSE | 0.003986 | 0.003977746 | 0.775707 | 0.003984 | 0.003978 | 0.00519559 | 0.00485494 | 0.0040001 | 0.00397771 |
| Max RMSE | 0.004303 | 0.00445058 | 0.776099 | 0.004639 | 0.0041926 | 0.01890252 | 0.01283665 | 0.0046005 | 0.00407281 |
| Average RMSE | 0.004106 | 0.004025824 | 0.775866 | 0.004214 | 0.0040236 | 0.01149578 | 0.00692778 | 0.00416 | 0.00402082 |
| std | 0.000113 | 9.35314E-05 | 9.82E-05 | 2.21E-05 | 5.435E-05 | 0.0032242 | 0.00151241 | 0.0001555 | 0.00016829 |
Table 5 Solar cells (Mono-crystalline C60) parameters estimation, Mean and Standard deviation for the Single Diode Model (SDM) and Double Diode Model (DDM) at 300 W/m 2
| SDM | |||||||||
| Parameters | ABC | CSA | CS | DE | DSA | GSA | HS | PSO | CMA-ES |
| RS (Ω) | 0.022856 | 0.024935901 | 1.28E-07 | 0.021591 | 0.019553 | 0.0057405 | 0.01079812 | 0.0157213 | 0.03784345 |
| Rp (Ω) | 89.60072 | 96.99719894 | 199.9309 | 200 | 196.57055 | 95.1381775 | 117.815101 | 198.31323 | 20.3660429 |
| IL (A) | 1.815495 | 1.799703082 | 2.16471 | 1.804586 | 1.8048883 | 0.647616 | 1.81085624 | 1.8076504 | 1.8066546 |
| ID (A) | 6.67E-07 | 1.66103E-07 | 1.75E-11 | 6.07E-07 | 1.356E-06 | 2.2364E-08 | 4.8415E-06 | 4.25E-06 | 4.88E-11 |
| n | 1.680349 | 1.537152887 | 1.000012 | 1.669162 | 1.7645843 | 1.97885237 | 1.93524352 | 1.9192075 | 1.02519908 |
| Min RMSE | 0.005007 | 0.004163427 | 0.972854 | 0.004777 | 0.0041294 | 0.00669648 | 0.00603242 | 0.0050737 | 0.00324028 |
| Max RMSE | 0.00604 | 0.005120555 | 0.972854 | 0.005612 | 0.0055624 | 0.02650582 | 0.0148986 | 0.0069059 | 0.00484652 |
| Average RMSE | 0.005533 | 0.004597845 | 0.972854 | 0.005207 | 0.0049094 | 0.01435318 | 0.00831713 | 0.0059562 | 0.00364383 |
| std | 0.000167 | 0.000266064 | 7.89E-08 | 0.000162 | 0.0003 | 0.00500556 | 0.00195439 | 0.0003223 | 0.00060098 |
| DDM | |||||||||
| Parameters | ABC | CSA | CS | DE | DSA | GSA | HS | PSO | CMA-ES |
| RS (Ω) | 0.019759 | 0.009998557 | 1.11E-06 | 0.019881 | 0.0099999 | 0.00294815 | 0.00572879 | 0.0049867 | 0.03453452 |
| Rp (Ω) | 108.4338 | 190.951882 | 198.7353 | 199.9866 | 199.49798 | 89.6325187 | 29.6722844 | 60.11981 | 1.28E+02 |
| IL (A) | 1.808202 | 1.801598482 | 2.164701 | 1.806197 | 1.8026873 | 1.64108059 | 1.79601671 | 1.7960872 | 1.80E+00 |
| ID1 (A) | 1.4E-06 | 5.36334E-06 | 1.3E-09 | 1.12E-06 | 6.436E-06 | 2.6725E-06 | 2.3832E-06 | 5.283E-06 | 2.87E-08 |
| ID2 (A) | 9.51E-07 | 9.9852E-07 | 1.77E-11 | 6.06E-07 | 9.032E-07 | 9.8344E-07 | 7.7925E-07 | 5.803E-07 | 1.12E-09 |
| n1 | 1.767764 | 1.999925106 | 1.941844 | 1.744111 | 1.9999988 | 1.97590137 | 1.8494644 | 1.968805 | 1.85070386 |
| n2 | 4.789302 | 1.892108949 | 1.0004 | 2.260392 | 1.999976 | 1.81370144 | 1.96612708 | 1.9296981 | 1.18E+00 |
| Min RMSE | 0.004836 | 0.00683517 | 0.972855 | 0.004646 | 0.0068351 | 0.0076357 | 0.00749499 | 0.0069709 | 0.00349494 |
| Max RMSE | 0.00596 | 0.007264676 | 0.972864 | 0.005748 | 0.0068425 | 0.01570402 | 0.01230902 | 0.0075616 | 0.00573986 |
| Average RMSE | 0.005606 | 0.006895311 | 0.972859 | 0.005281 | 0.0068354 | 0.01074707 | 0.00871806 | 0.0071482 | 0.00489288 |
| std | 0.000299 | 8.98654E-05 | 2.38E-06 | 0.000227 | 1.212E-06 | 0.00152859 | 0.00095817 | 0.0001411 | 0.0005975 |
Experimental results from Tables 2, 3, 4 and 5 show that the CMA-ES presents the best possible performance; however, CSA and DSA maintain also very good index values. The rest of the algorithms produce results with different performance levels.
One exception, in the results, was the standard deviation in which the lower values have been reached by the CS in the single diode at (1000 W/m2), the DE in the double diode at (800 W/m2), the CS and DSA at (300 W/m2) for the single and double diode, respectively.
4.2 Identification of multi-crystalline solar cell D6P
The second experiment considers the parameter estimation of a multi-crystalline solar cell D6P. The identification examines two different solar irradiations (1000 W/m2) and (500 W/m2) at T = 25°C, for the Single Diode Module (SDM), double Diode Model (DDM) and the Three Diode Model (TDM). Table 6 and 7 present the results for the cases of (1000 W/m2) and (500 W/m2), respectively.
Table 6 Solar cells (Mono-crystalline D6P) parameters estimation, Mean and Standard deviation for the Single Diode Model (SDM), Double Diode Model (DDM) and Three Diode Model (TDM) at 1000 W/m 2
| SDM | |||||||||
| Parameters | ABC | CSA | CS | DE | DSA | GSA | HS | PSO | CMA-ES |
| RS (Ω) | 4.93E-03 | 0.00550083 | 0.006453 | 0.005662 | 0.005988 | 0.005038 | 0.001861 | 0.4709873 | 0.47098731 |
| Rp (Ω) | 7.50E+01 | 100 | 99.45801 | 100 | 99.99615 | 66.07779 | 80.98159 | 57.768198 | 57.7681979 |
| IL (A) | 8.31E+00 | 8.30252074 | 8.299179 | 8.300678 | 8.294515 | 6.897731 | 8.23392 | 8.2149683 | 8.21496834 |
| ID (A) | 1.57E-06 | 5.34E-07 | 6.53E-08 | 3.51E-07 | 1.64E-07 | 1E-05 | 7.31E-06 | 8.249E-06 | 8.2489E-06 |
| n | 1.606934 | 1.50376702 | 1.335087 | 1.466456 | 1.404038 | 1.90333 | 1.776386 | 1.7966804 | 1.79668045 |
| Min RMSE | 0.023204 | 0.02320388 | 0.015645 | 0.019481 | 0.019044 | 0.034982 | 0.034982 | 0.0260146 | 0.01552954 |
| Max RMSE | 0.025538 | 0.02553847 | 0.023851 | 0.023045 | 0.024382 | 0.216904 | 0.216904 | 0.0447331 | 0.02003157 |
| Average RMSE | 0.024574 | 0.02457448 | 0.019163 | 0.020916 | 0.021132 | 0.108073 | 0.108073 | 0.0311407 | 0.01892337 |
| std | 0.00069 | 0.00068966 | 0.002722 | 0.000794 | 0.001218 | 0.047229 | 0.047229 | 0.0036418 | 0.00082729 |
| DDM | |||||||||
| Parameters | ABC | CSA | CS | DE | DSA | GSA | HSz | PSO | CMA-ES |
| RS (Ω) | 5.70E-03 | 0.00555699 | 0.006699 | 0.006064 | 0.006557 | 0.002284 | 0.003773 | 0.0041813 | 0.00418127 |
| Rp (Ω) | 6.71E+01 | 100 | 89.09031 | 100 | 99.96804 | 35.31513 | 55.90306 | 79.052877 | 79.0528766 |
| IL (A) | 8.29E+00 | 8.30146867 | 8.281023 | 8.296526 | 8.288297 | 7.172523 | 8.287227 | 8.3190704 | 8.31907043 |
| ID1 (A) | 3.82E-06 | 3.92E-07 | 3.55E-08 | 1.57E-07 | 1.71E-10 | 3.94E-06 | 4.96E-06 | 4.837E-06 | 4.8375E-06 |
| ID2 (A) | 2.48E-07 | 4.30E-07 | 2.22E-11 | 1.8E-07 | 4.63E-08 | 1E-06 | 9.89E-07 | 1.198E-08 | 1.198E-08 |
| n1 | 5.71E+00 | 1.88991907 | 1.293362 | 23.35675 | 1.176865 | 1.86705 | 1.770647 | 1.7332564 | 1.73325637 |
| n2 | 1.438037 | 1.48667571 | 1.389624 | 1.412048 | 1.313473 | 1.62115 | 1.712209 | 1.8487766 | 1.84877659 |
| Min RMSE | 0.02146 | 0.02146031 | 0.017369 | 0.019226 | 0.017316 | 0.029422 | 0.029422 | 0.0215297 | 0.01707178 |
| Max RMSE | 0.025601 | 0.02560146 | 0.027343 | 0.023371 | 0.02305 | 0.06036 | 0.06036 | 0.0281581 | 0.02145989 |
| Average RMSE | 0.023643 | 0.02364294 | 0.024494 | 0.021652 | 0.020183 | 0.039861 | 0.039861 | 0.0252211 | 0.01940024 |
| std | 0.001206 | 0.0012056 | 0.002065 | 0.001091 | 0.001305 | 0.00789 | 0.00789 | 0.0016887 | 0.00098192 |
| TDM | |||||||||
| Parameters | ABC | CSA | CS | DE | DSA | GSA | HS | PSO | CMA-ES |
| ID1 (A) | 1.21E-10 | 1.177E-10 | 1.21E-10 | 8.59E-26 | 1.21E-10 | 1.23E-10 | 1.24E-10 | 1.249E-08 | 1.2486E-08 |
| ID2 (A) | 8.23E-11 | 2.1463E-07 | 2.13E-13 | 3.31E-05 | 3.82E-21 | 9.20E-13 | 7.97E-07 | 2.312E-07 | 2.3123E-07 |
| ID3 (A) | 4.92E-04 | 9.9377E-06 | 1.2E-15 | 2.52E-19 | 3.14E-14 | 2.33E-10 | 8.69E-06 | 7.016E-06 | 7.0156E-06 |
| n3 | 8.80E+01 | 2.41406574 | 0.863338 | 2.993156 | 98.52522 | 2.996657 | 2.97427 | 2.6504631 | 2.65046313 |
| Rso (Ω) | 8.02E-03 | 0.00738269 | 0.008045 | 0.002745| | 0.008045 | 0.008008 | 0.005064 | 0.0063443 | 0.00634432 |
| K | 6.74E-04 | 0.01435204 | 9.35E-09 | 1.74E-16 | 1.91E-15 | 0.004806 | 0.016666 | 0.0474956 | 0.04749557 |
| Rsh (Ω) | 1.84E+00 | 2.12835817 | 1.819064 | 4.077476 | 1.818718 | 99.99369 | 36.85799 | 69.683667 | 69.6836673 |
| Min RMSE | 0.020393 | 0.02039341 | 0.020388 | 0.020393 | 0.019618 | 0.023934 | 0.062702 | 0.0262095 | 0.01949509 |
| Max RMSE | 0.020471 | 0.02047111 | 0.020393 | 0.020393 | 0.03713 | 0.0333 | 39.09412 | 0.0550369 | 0.02038819 |
| Average RMSE | 0.020404 | 0.02040431 | 0.020393 | 0.020393 | 0.025195 | 0.0535 | 9.684074 | 0.0400163 | 0.02010918 |
| std | 1.62E-05 | 1.6213E-05 | 9.3E-07 | 5.66E-09 | 0.00665 | 0.000455 | 8.682488 | 0.0052987 | 0.00028239 |
Table 7 Solar cells (Mono-crystalline D6P) parameters estimation, Mean and Standard deviation for the Single Diode Model (SDM), Double Diode Model (DDM) and Three Diode Model (TDM) at 500 W/m 2
| SDM | |||||||||
| Parameters | ABC | CSA | CS | DE | DSA | GSA | HS | PSO | CMA-ES |
| RS (Ω) | 0.004157 | 0.01159328 | 2E-09 | 0.005909 | 0.00681 | 0.001227 | 0.000849 | 0.0029151 | 0.00749966 |
| Rp (Ω) | 69.17906 | 100 | 99.99913 | 100 | 99.99975 | 35.77021 | 94.14903 | 43.577466 | 100 |
| IL (A) | 4.156335 | 4.13161166 | 4.6471 | 4.142898 | 4.141783 | 2.647298 | 4.202613 | 4.1544498 | 4.140932 |
| ID (A) | 1.49E-06 | 2.27E-10 | 7.22E-11 | 3.12E-07 | 1.51E-07 | 7.05E-06 | 9.55E-06 | 3.263E-06 | 7.25E-08 |
| n | 1.586101 | 1 | 1.000001 | 1.435838 | 1.376114 | 1.933243 | 1.807051 | 1.6732462 | 1.31973729 |
| Min RMSE | 0.017136 | 0.01713641 | 0.567476 | 0.016359 | 0.015404 | 0.018751 | 0.018751 | 0.017759 | 0.01416909 |
| Max RMSE | 0.018008 | 0.01800797 | 0.567477 | 0.017199 | 0.017287 | 0.076983 | 0.076983 | 0.0188433 | 0.01740387 |
| Average RMSE | 0.017607 | 0.01760732 | 0.567476 | 0.016775 | 0.016542 | 0.043495 | 0.043495 | 0.0183816 | 0.01611262 |
| STD | 0.000187 | 0.00018661 | 8.51E-08 | 0.00021 | 0.000376 | 0.013287 | 0.013287 | 0.0002893 | 0.00111236 |
| DDM | |||||||||
| Parameters | ABC | CSA | CS | DE | DSA | GSA | HS | PSO | CMA-ES |
| RS (Ω) | 6.51E-03 | 0.00711864 | 7.29E-05 | 0.005624 | 0.006064 | 0.00253 | 0.004874 | 0.0055739 | 0.00557385 |
| Rp (Ω) | 7.98E+01 | 100 | 99.91123 | 100 | 61.38597 | 49.47878 | 82.65916 | 82.816173 | 82.816173 |
| IL (A) | 4.16E+00 | 4.14223473 | 4.646989 | 4.144588 | 4.144383 | 4.158399 | 4.146255 | 4.1468956 | 4.14689559 |
| ID1 (A) | 8.07E-07 | 1.19E-07 | 8.61E-11 | 1.59E-06 | 2.08E-07 | 4.32E-06 | 9.28E-07 | 7.139E-06 | 7.1389E-06 |
| ID2 (A) | 1.87E-07 | 9.57E-08 | 9.06E-10 | 1.32E-07 | 9.99E-07 | 9.94E-07 | 8.06E-07 | 3.587E-07 | 3.5869E-07 |
| n1 | 3.66E+01 | 1.35906364 | 1.007153 | 1.800635 | 1.404134 | 1.81406 | 1.980265 | 1.5796227 | 1.5796227 |
| n2 | 1.392767 | 1.77294891 | 1.950849 | 1.380061 | 1.999837 | 1.603871 | 1.528525 | 1.4499956 | 1.44999562 |
| Min RMSE | 0.015887 | 0.01588696 | 0.567477 | 0.016084 | 0.01645 | 0.017171 | 0.017171 | 0.0165929 | 0.01519835 |
| Max RMSE | 0.017786 | 0.01778611 | 0.567613 | 0.017333 | 0.018129 | 0.019554 | 0.019554 | 0.0174407 | 0.01735582 |
| Average RMSE | 0.017235 | 0.01723534 | 0.567503 | 0.016818 | 0.017597 | 0.018417 | 0.018417 | 0.017041 | 0.01624427 |
| std | 0.000408 | 0.000408 | 2.78E-05 | 0.000279 | 0.000373 | 0.000565 | 0.000565 | 0.0002042 | 0.00048383 |
| TDM | |||||||||
| Parameters | ABC | CSA | CS | DE | DSA | GSA | HS | PSO | CMA-ES |
| ID1 (A) | 2.10E-10 | 2.1006E-10 | 1.58E-13 | 1.55E-10 | 6.72E-11 | 1.21E-10 | 1.65E-10 | 4.144E-08 | 4.1445E-08 |
| ID2 (A) | 3.24E-15 | 2.1954E-07 | 2.93E-10 | 6.89E-21 | 6.02E-19 | 5.47E-07 | 6.31E-07 | 4.874E-07 | 4.8742E-07 |
| ID3 (A) | 4.83E-10 | 3.4658E-11 | 7.69E-14 | 1.02E-15 | 3.12E-13 | 1.19E-14 | 9.28E-06 | 4.896E-06 | 4.8958E-06 |
| n3 | 9.32E+01 | 1.78535981 | 0.784333 | 0.684267 | 0.792991 | 0.99053 | 1.945619 | 2.1120764 | 2.11207644 |
| Rso (Ω) | 1.03E-02 | 0.00999985 | 0.001608 | 0.011271 | 0.01 | 0.007961 | 0.002745 | 0.0071011 | 0.00710112 |
| K | 4.35E-11 | 2.4762E-06 | 0.002556 | 4.17E-15 | 0.039095 | 0.003907 | 0.098125 | 0.0547249 | 0.05472488 |
| Rsh (Ω) | 7.10E-01 | 0.70491482 | 99.97324 | 0.707655 | 0.69295 | 67.37059 | 0.632458 | 70.815981 | 70.8159813 |
| Min RMSE | 0.042226 | 0.04222615 | 0.567153 | 0.042226 | 0.041832 | 0.043415 | 0.089162 | 0.0439661 | 0.04059946 |
| Max RMSE | 0.042227 | 0.04222669 | 0.567277 | 0.042226 | 0.042156 | 1.6245 | 5.652148 | 0.0800799 | 0.04197422 |
| Average RMSE | 0.042226 | 0.04222618 | 0.5672 | 0.042226 | 0.04195 | 0.2893 | 1.757516 | 0.0592006 | 0.04142937 |
| Std | 1.03E-07 | 1.0326E-07 | 3.12E-05 | 9.81E-18 | 0.000115 | 0.000455 | 1.565291 | 0.0102721 | 0.00034344 |
According to the Tables, the CMA-ES obtains the best results in comparison with the others techniques for the SDM, DDM and TDM models. In case of the standard deviation, the best results were obtained by the ABC in the single diode at (1000 W/m2), DE in the three-diode model at (1000 W/m2) and CS in the single and double diode at (500 W/m2).
4.3 Identification of Multi-Crystalline Module KC200GT
Finally, the third experiment analyzes the parameter estimation of a Multi-crystalline module KC200GT. The identification examines the Single Diode Model (SDM) and the Double Diode Model (DDM) for the conditions of (1000 W/m2), (800 W/m2), (600 W/m2), (400 W/m2 ) and (200W/m2). Table 8, 9, 10, 11 and 12 present the results of each algorithm for the cases of (1000 W/m2), (800 W/m2), (600 W/m2 ), (400 W/m2) and (200W/m2), respectively. Tables 8 and 9 demonstrate that CMA-ES shows competitive results finding the minimum RMSE value in the most of the cases; however, the CS and DE are also able to find a good solution with considerable precision. In the experiments, the CMA-ES obtains the best result for almost all cases, except the standard deviation in several cases such as CS in the single diode model at (800 W/m2) and (600 W/m2). On the other hand, the DSA obtain the lower standard deviation for the single and double diode model at (400 W/m2 and (200 W/m2).
Table 8 Solar cells Module (Multi-crystalline KC200GT) parameters estimation, Mean and Standard deviation for the Single Diode Model (SDM) and Double Diode Model (DDM) at 1000 W/m 2
| SDM | |||||||||
| Parameters | ABC | CSA | CS | DE | DSA | GSA | HS | PSO | CMA-ES |
| RS (Ω) | 0.00819725 | 0.008598412 | 0.009702 | 0.008254 | 0.0085027 | 0.00532522 | 0.006372 | 0.0086455 | 0.00838946 |
| Rp (Ω) | 14.2746543 | 287.7649217 | 278.3281 | 300 | 274.24082 | 162.599163 | 145.730272 | 70.236383 | 500 |
| IL (A) | 8.45231967 | 8.401473158 | 8.395708 | 8.405986 | 8.4081122 | 5.51397782 | 8.1667034 | 8.4517976 | 8.40253114 |
| ID (A) | 2.1304E-06 | 8.80807E-07 | 1.02E-07 | 1.24E-06 | 1.218E-06 | 4.8699E-06 | 9.1479E-06 | 5.298E-06 | 1.23E-06 |
| n | 1.63367968 | 1.542895531 | 1.361663 | 1.575057 | 1.5744236 | 1.83695064 | 1.81751613 | 1.7462203 | 1.57520904 |
| Min RMSE | 0.00619726 | 0.005158409 | 0.006143741 | 0.006055 | 0.0051727 | 0.01676816 | 0.0077667 | 0.0071031 | 0.00506031 |
| Max RMSE | 0.00819386 | 0.006852389 | 0.006919949 | 0.006854 | 0.0066646 | 0.08468712 | 0.03851485 | 0.0182919 | 0.00594658 |
| Average RMSE | 0.00697368 | 0.006031249 | 0.006439478 | 0.00623 | 0.0059189 | 0.05137936 | 0.01626893 | 0.0110058 | 0.00536039 |
| Std | 0.00051988 | 0.000375625 | 0.000262026 | 0.000192 | 0.0003831 | 0.0164289 | 0.00766401 | 0.0026008 | 0.00013732 |
| DDM | |||||||||
| Parameters | ABC | CSA | CS | DE | DSA | GSA | HS | PSO | CMA-ES |
| RS (Ω) | 0.01018216 | 0.010537688 | 0.010568 | 0.010349 | 0.0105334 | 0.00579965 | 0.0125366 | 0.4753595 | 0.01040301 |
| Rp (Ω) | 136.897439 | 133.9638333 | 264.3318 | 299.9873 | 299.97365 | 169.410993 | 245.068672 | 141.23624 | 197.337864 |
| IL (A) | 8.37444967 | 8.371571382 | 8.371119 | 8.371028 | 8.3703729 | 4.12627659 | 8.01575802 | 8.074969 | 8.37548908 |
| ID1 (A) | 6.439E-08 | 2.32597E-15 | 7.8E-09 | 1.36E-08 | 3.258E-13 | 9.9792E-09 | 4.8326E-09 | 2.546E-09 | 1.15E-10 |
| ID2 (A) | 2.2274E-08 | 8.47844E-09 | 2.55E-09 | 2.69E-08 | 8.692E-09 | 9.9249E-09 | 5.1778E-09 | 1.771E-09 | 1.25E-08 |
| n1 | 8.73132142 | 1.351574739 | 1.194356 | 1.227365 | 1.1265378 | 1.6933772 | 1.17566595 | 1.5137775 | 1.24036008 |
| n2 | 1.25726919 | 1.199160692 | 1.875205 | 1.747515 | 1.2006042 | 1.89036558 | 1.51451236 | 1.1106203 | 1.22215402 |
| Min RMSE | 0.00473273 | 0.004717362 | 0.004821636 | 0.004718 | 0.0047173 | 0.01310982 | 0.00566407 | 0.0061483 | 0.00471767 |
| Max RMSE | 0.00518495 | 0.004856829 | 0.004741333 | 0.004753 | 0.004756 | 0.09772879 | 0.06769827 | 0.0190041 | 0.00472145 |
| Average RMSE | 0.00487024 | 0.004737393 | 0.00482412 | 0.004728 | 0.0047213 | 0.05200618 | 0.0274881 | 0.0114809 | 0.004719 |
| Std | 0.00011032 | 2.80154E-05 | 8.61837E-07 | 8.93E-06 | 6.524E-06 | 0.01691836 | 0.01305747 | 0.0041682 | 7.0567E-06 |
Table 9 Solar cells Module (Multi-crystalline KC200GT) parameters estimation, Mean and Standard deviation for the Single Diode Model (SDM) and Double Diode Model (DDM) at 800 W/m 2
| SDM | |||||||||
| Parameters | ABC | CSA | CS | DE | DSA | GSA | HS | PSO | CMA-ES |
| RS (Ω) | 0.00560748 | 7.82E-05 | 2.84E-05 | 5.75E-03 | 1.08E-03 | 0.00473677 | 1.76E-03 | 0.5313321 | 0.00392955 |
| Rp (Ω) | 156.472585 | 499.9948083 | 472.2883 | 500 | 499.99812 | 2.86E+02 | 115.897865 | 98.146888 | 500 |
| IL (A) | 6.74823457 | 5.13E+00 | 5.130815 | 6.745251 | 5.131 | 1.35389938 | 5.13099889 | 2.9315738 | 5.131 |
| ID (A) | 3.56E-06 | 5.16E-09 | 3.67E-07 | 2.53E-06 | 1.80E-08 | 7.58E-08 | 4.55E-06 | 3.48E-06 | 2.60E-10 |
| n | 1.6482632 | 1.187243554 | 1.441785 | 1.610137 | 1.2151826 | 1.84E+00 | 1.71599654 | 1.7138988 | 1.00003708 |
| Min RMSE | 0.00607673 | 0.153164765 | 0.153071491 | 0.006144 | 0.1530621 | 0.15859113 | 0.15484765 | 0.1549824 | 0.00596914 |
| Max RMSE | 0.00770129 | 0.154739618 | 0.153109032 | 0.006847 | 0.1532002 | 0.21342771 | 0.1611923 | 0.1601034 | 0.00681995 |
| Average RMSE | 0.0069878 | 0.153856882 | 0.153088145 | 0.006439 | 0.1531086 | 0.16944026 | 0.15669185 | 0.15735 | 0.00637779 |
| Std | 0.00037055 | 0.000400204 | 8.81371E-06 | 0.00023 | 3.457E-05 | 0.01004141 | 0.00143392 | 0.0013584 | 0.00015752 |
| DDM | |||||||||
| Parameters | ABC | CSA | CS | DE | DSA | GSA | HS | PSO | CMA-ES |
| RS (Ω) | 0.00652112 | 0.002510291 | 0.004005 | 0.007576 | 0.0039691 | 0.00323222 | 8.39E-04 | 2.61E-01 | 0.00400321 |
| Rp (Ω) | 290.306499 | 471.3428232 | 499.4977 | 5.564204 | 5.00E+02 | 2.75E+02 | 2.55E+02 | 365.18762 | 500 |
| IL (A) | 6.72995842 | 5.130923625 | 5.131 | 6.775167 | 5.1309999 | 2.85E+00 | 5.13E+00 | 3.89E+00 | 5.131 |
| ID1 (A) | 7.78E-07 | 1.48E-10 | 4.82E-10 | 4.07E-08 | 2.58E-10 | 1.96E-10 | 9.69E-09 | 6.76E-09 | 2.57E-10 |
| ID2 (A) | 7.30E-07 | 1.71E-10 | 2.56E-10 | 6.39E-08 | 3.03E-11 | 9.92E-09 | 4.43E-09 | 5.24E-09 | 8.86E-21 |
| n1 | 1.49260116 | 1.014655345 | 1.787907 | 1.347456 | 1.0001267 | 1.73017437 | 1.17802325 | 1.808445 | 1 |
| n2 | 50.4069533 | 1.764172097 | 1.00E+00 | 1.317329 | 1.9897464 | 1.61841891 | 1.66892515 | 1.1611895 | 1.99938964 |
| Min RMSE | 0.00474219 | 0.153022239 | 0.152992432 | 0.004718 | 0.1529846 | 0.1550537 | 0.15346329 | 0.1534739 | 0.00471636 |
| Max RMSE | 0.00535054 | 0.153360344 | 0.153025772 | 0.004818 | 0.1530329 | 0.1682246 | 0.16383126 | 0.1604568 | 0.00475133 |
| Average RMSE | 0.00495841 | 0.153098018 | 0.15301046 | 0.00473 | 0.1530076 | 0.1619196 | 0.15583403 | 0.1556357 | 0.00472412 |
| STD | 0.00016899 | 6.08071E-05 | 9.66935E-06 | 1.58E-05 | 1.29E-05 | 0.00284984 | 0.00231309 | 0.0015596 | 7.5167E-06 |
Table 10 Solar cells Module (Multi-crystalline KC200GT) parameters estimation, Mean and Standard deviation for the Single Diode Model (SDM) and Double Diode Model (DDM) at 600 W/m 2
| SDM | |||||||||
| Parameters | ABC | CSA | CS | DE | DSA | GSA | HS | PSO | CMA-ES |
| RS (Ω) | 0.00579404 | 4.69E-06 | 0.000354 | 0.00471 | 1.99E-09 | 0.02399241 | 3.23E-04 | 0.4360552 | 9.29E-19 |
| Rp (Ω) | 103.380418 | 494.4540364 | 4.19E+02 | 11.75391 | 499.99974 | 2.75E+02 | 297.465108 | 2.40E+02 | 500 |
| IL (A) | 5.03219147 | 3.364709848 | 3.36464 | 5.064251 | 3.36471 | 1.52204555 | 3.36E+00 | 2.97E+00 | 3.36471 |
| ID (A) | 4.38E-07 | 5.72E-11 | 6.08E-08 | 1.25E-06 | 4.86E-10 | 1.76E-09 | 2.17E-06 | 2.79E-06 | 2.61E-10 |
| n | 1.43825761 | 1.00107902 | 1.320566 | 1.535283 | 1.029505 | 1.926606 | 1.68277169 | 1.76E+00 | 1 |
| Min RMSE | 0.00656172 | 0.240433034 | 0.240272335 | 0.006144 | 0.2402715 | 0.24175207 | 0.24147391 | 0.2415572 | 0.00589603 |
| Max RMSE | 0.00937572 | 0.241981687 | 0.240302873 | 0.007021 | 0.2404957 | 0.26679805 | 0.24479858 | 0.2442355 | 0.00681995 |
| Average RMSE | 0.00737129 | 0.241182992 | 0.240281109 | 0.006459 | 0.2403316 | 0.24944009 | 0.24224258 | 0.2426385 | 0.00623948 |
| Std | 0.00064136 | 0.000392438 | 8.22765E-06 | 0.000235 | 5.655E-05 | 0.00521166 | 0.00076707 | 0.0006874 | 0.00013652 |
| DDM | |||||||||
| Parameters | ABC | CSA | CS | DE | DSA | GSA | HS | PSO | CMA-ES |
| RS (Ω) | 0.00663807 | 1.81E-06 | 7.46E-06 | 7.65E-03 | 5.30E-12 | 3.95E-03 | 1.67E-03 | 0.0156249 | 6.69E-18 |
| Rp (Ω) | 6.47586816 | 493.0062779 | 4.80E+02 | 3.829101 | 499.99997 | 2.51E+02 | 3.67E+02 | 2.41E+02 | 500 |
| IL (A) | 5.06785663 | 3.364709691 | 3.364706 | 5.10E+00 | 3.36471 | 2.08921992 | 3.36404429 | 8.69E-01 | 3.36471 |
| ID1 (A) | 1.11E-07 | 5.25E-11 | 3.02E-10 | 2.82E-10 | 2.61E-10 | 4.09E-10 | 6.27E-09 | 5.54E-09 | 2.61E-10 |
| ID2 (A) | 1.28E-08 | 5.64E-11 | 9.76E-09 | 1.59E-08 | 5.06E-15 | 4.18E-10 | 4.48E-09 | 4.12E-09 | 1.69E-20 |
| n1 | 1.32627965 | 1.813680317 | 1.007273 | 1.287049 | 1 | 1.67217836 | 1.16332975 | 1.4373337 | 1 |
| n2 | 16.9103492 | 1.000368025 | 1.772075 | 1.195659 | 1.9984145 | 1.58346052 | 1.61249948 | 1.1380601 | 1.98601177 |
| Min RMSE | 0.00474395 | 0.240326451 | 0.2402723 | 0.004719 | 0.2402715 | 0.24114319 | 0.24074788 | 0.2410345 | 0.00471636 |
| Max RMSE | 0.00527847 | 0.241718986 | 0.240276037 | 0.004751 | 0.2402715 | 0.24875306 | 0.24933665 | 0.2423547 | 0.00474795 |
| Average RMSE | 0.00494073 | 0.240753244 | 0.240274015 | 0.004727 | 0.2402715 | 0.24357299 | 0.24184863 | 0.2417584 | 0.00472412 |
| Std | 0.00013252 | 0.000424668 | 9.58666E-07 | 6.2E-06 | 2.082E-09 | 0.00155382 | 0.00139945 | 0.000263 | 7.8217E-06 |
Table 11 Solar cells Module (Multi-crystalline KC200GT) parameters estimation, Mean and Standard deviation for the Single Diode Model (SDM) and Double Diode Model (DDM) at 400 W/m 2
| SDM | |||||||||
| Parameters | ABC | CSA | CS | DE | DSA | GSA | HS | PSO | CMA-ES |
| RS (Ω) | 0.00828988.73E-09 | 0.00013 | 0.008543 | 1.01E-09 | 8.84E-03 | 0.00262176 | 0.4076231 | 2.47E-16 | |
| Rp (Ω) | 244.788126 | 499.9985195 | 5.00E+02 | 15.25072 | 499.99657 | 226.435541 | 364.481124 | 341.52765 | 5.00E+02 |
| IL (A) | 3.37145929 | 2.164709998 | 2.164709 | 3.388371 | 2.16E+00 | 1.47930568 | 2.16E+00 | 1.1096869 | 2.16E+00 |
| ID (A) | 2.24E-06 | 1.64E-11 | 1.04E-08 | 2.03E-06 | 4.69E-10 | 8.90E-09 | 9.91E-07 | 1.72E-06 | 2.43E-10 |
| n | 1.61640042 | 1.000000439 | 1.20E+00 | 1.606847 | 1.029216 | 1.69801672 | 1.63653468 | 1.6495691 | 1 |
| Min RMSE | 0.00645975 | 0.300912307 | 0.300845399 | 0.006144 | 0.3008454 | 0.30158912 | 0.30100127 | 0.3010593 | 0.00543773 |
| Max RMSE | 0.01174902 | 0.302867207 | 0.300845464 | 0.007065 | 0.3008454 | 0.32471022 | 0.3035138 | 0.3040074 | 0.00681995 |
| Average RMSE | 0.00764025 | 0.301076997 | 0.300845412 | 0.006528 | 0.3008454 | 0.3082867 | 0.30152288 | 0.3023678 | 0.00643948 |
| Std | 0.00094938 | 0.000375184 | 1.30416E-08 | 0.000307 | 1.585E-15 | 0.0050065 | 0.00053007 | 0.0007353 | 0.00025252 |
| DDM | |||||||||
| Parameters | ABC | CSA | CS | DE | DSA | GSA | HS | PSO | CMA-ES |
| RS (Ω) | 0.01188791 | 2.04E-07 | 6.97E-05 | 0.012755 | 1.98E-12 | 2.24E-02 | 1.25E-03 | 2.70E-01 | 8.77E-18 |
| Rp (Ω) | 16.8146454 | 5.00E+02 | 448.477 | 5.031745 | 5.00E+02 | 2.45E+02 | 3.64E+02 | 4.35E+02 | 500 |
| IL (A) | .37079874 | 2.16E+00 | 2.164703 | 3.41E+00 | 2.16E+00 | 2.16E+00 | 2.16E+00 | 9.38E-01 | 2.16471 |
| ID1 (A) | 1.67E-07 | 1.66E-11 | 2.50E-10 | 4.89E-09 | 1.74E-15 | 1.00E-08 | 9.39E-09 | 6.64E-09 | 1.71E-21 |
| ID2 (A) | 1.33E-09 | 3.20E-11 | 7.17E-09 | 4.18E-08 | 2.43E-10 | 9.98E-09 | 7.20E-09 | 1.86E-09 | 2.43E-10 |
| n1 | 1.36986811 | 1.000009475 | 1.000271 | 2.454186 | 1.9889716 | 1.78140319 | 1.26138542 | 1.5581188 | 1.98855852 |
| n2 | 310.20159 | 1.95998006 | 1.857724 | 1.266697 | 1 | 1.80164641 | 1.22777934 | 1.1065305 | 1 |
| Min RMSE | 0.00476202 | 0.300849656 | 0.300845428 | 0.004718 | 0.3008454 | 0.30106051 | 0.30097447 | 0.3009636 | 0.00378198 |
| Max RMSE | 0.00633534 | 0.301050402 | 0.300845888 | 0.004845 | 0.3008454 | 0.30564935 | 0.30159409 | 0.3014975 | 0.00476034 |
| Average RMSE | 0.00501231 | 0.300961924 | 0.30084558 | 0.004725 | 0.3008454 | 0.3023613 | 0.30114073 | 0.301172 | 0.0045456 |
| Std | 0.00026864 | 3.31744E-05 | 9.054E-08 | 8.71E-06 | 7.976E-14 | 0.00092921 | 0.0001444 | 0.0001434 | 8.7065E-06 |
Table 12 Solar cells Module (Multi-crystalline KC200GT) parameters estimation, Mean and Standard deviation for the Single Diode Model (SDM) and Double Diode Model (DDM) at 200 W/m 2.
| SDM | |||||||||
| Parameters | ABC | CSA | CS | DE | DSA | GSA | HS | PSO | CMA-ES |
| RS (Ω) | 0.01141702 | 5.44E-08 | 1.61E-02 | 1.05E-02 | 0.0145769 | 0.01762537 | 0.0018854 | 1.79E-01 | 0.02447924 |
| Rp (Ω) | 147.191212 | 499.9912692 | 167.8188 | 201.0279 | 339.93184 | 2.21E+02 | 1.70E+02 | 429.52154 | 24.3117548 |
| IL (A) | 1.68087497 | 2.164709998 | 1.675382 | 1.676926 | 1.6757034 | 1.41175765 | 1.68040673 | 1.6786414 | 1.68007665 |
| ID (A) | 3.78E-07 | 1.65E-11 | 7.55E-08 | 6.07E-07 | 1.66E-07 | 9.70E-06 | 6.38E-06 | 2.40E-06 | 4.50E-10 |
| n | 1.43443606 | 1.000000995 | 1.300344 | 1.481847 | 1.3638056 | 1.91865929 | 1.75798573 | 1.6323506 | 1 |
| Min RMSE | 0.00640138 | 0.300942015 | 0.3008454 | 0.006144 | 0.3008454 | 0.30114476 | 0.30098639 | 0.3011497 | 0.00606314 |
| Max RMSE | 0.00965965 | 0.302323073 | 0.300845451 | 0.007015 | 0.3008454 | 0.32671827 | 0.30270375 | 0.3048593 | 0.00681995 |
| Average RMSE | 0.00744433 | 0.301011783 | 0.30084541 | 0.00653 | 0.3008454 | 0.30861766 | 0.30154735 | 0.3025211 | 0.00643948 |
| Std | 0.00077881 | 0.000243937 | 1.10173E-08 | 0.000198 | 5.385E-16 | 0.00578398 | 0.00043297 | 0.0008678 | 0.00043752 |
| DDM | |||||||||
| Parameters | ABC | CSA | CS | DE | DSA | GSA | HS | PSO | CMA-ES |
| RS (Ω) | 0.02301243 | 6.55E-08 | 0.024463 | 0.022756 | 0.0240381 | 1.65E-02 | 0.02084871 | 2.29E-02 | 2.45E-02 |
| Rp (Ω) | 257.694441 | 499.1710598 | 23.34492 | 51.2072 | 3.62E+01 | 255.333055 | 402.097715 | 4.02E+02 | 24.3117565 |
| IL (A) | 1.67617312 | 2.164709912 | 1.680472 | 1.68E+00 | 1.68E+00 | 1.60E+00 | 1.66829732 | 1.6706903 | 1.68E+00 |
| ID1 (A) | 3.47E-09 | 1.00E-11 | 4.50E-10 | 1.66E-09 | 6.67E-10 | 4.74E-11 | 6.83E-09 | 1.84E-09 | 1.47E-21 |
| ID2 (A) | 1.08E-09 | 1.65E-11 | 2.71E-09 | 8.54E-10 | 2.93E-10 | 7.87E-09 | 7.08E-09 | 2.45E-09 | 4.50E-10 |
| n1 | 6.73073562 | 1.92E+00 | 1.000026 | 1.062261 | 1.018037 | 1.64570227 | 1.19967205 | 1.0677641 | 1.86977567 |
| n2 | 1.04000367 | 1.000039816 | 1.777667 | 2.290439 | 1.9428294 | 1.14876342 | 1.17225141 | 1.670724 | 1 |
| Min RMSE | 0.00472589 | 0.300855771 | 0.300845424 | 0.004718 | 0.3008454 | 0.30118528 | 0.30096118 | 0.3009839 | 0.00471636 |
| Max RMSE | 0.00535393 | 0.301022601 | 0.300845711 | 0.004851 | 0.3008454 | 0.30648166 | 0.30158047 | 0.3015689 | 0.00474499 |
| Average RMSE | 0.00494432 | 0.30095187 | 0.300845559 | 0.004725 | 0.3008454 | 0.30264489 | 0.30111403 | 0.3011762 | 0.00472412 |
| Std | 0.00016301 | 3.00989E-05 | 7.51683E-08 | 6.7E-06 | 6.492E-14 | 0.00130048 | 0.00014352 | 0.0001382 | 6.1847E-06 |
4.4 Statistical Analysis
For the validation of the obtained results, we proceed to statistically analyze the data acquired for each EC technique during the estimation process. The study combines the Wilcoxon test and the Bonferroni correction. The Wilcoxon analysis [49, 50] measure the difference between two related methods. This test considers the 5% of significance level over the Average RSME values (p-value, 0.05). Since the results reveal that the alleged best algorithm is the CMA-ES, the comparison considers seven groups for the test: CMA-ES vs ABC, CMA-ES vs CSA, CMA-ES vs CS, CMA-ES vs DE, CMA-ES vs DSA, CMA-ES vs HS and CMA-ES vs PSO. In the Wilcoxon test, the null hypothesis is considered as there is not difference enough between approaches, and as an alternative hypothesis if exists significance difference between both approaches.
On the other hand, as the number of elements in the comparison is high, the possibility to produce an error type 1 increases. In order to avoid this problem, the significance value (p-value) must be readjusted using the Bonferroni correction [51,52].
Therefore, once we have the p-values obtained by Wilcoxon method, they are compared with the new n-value calculated by the Bonferroni test, if is n>p the null hypothesis is rejected, avoiding the error type 1. With the intention to simplify the analysis of the results, in table 13, the symbols ▲, ► and ▼ are used.
Table 13 Wilcoxon test for the SDM and DDM for the Mono-crystalline cell and the Multi-crystalline Module and SDM, DDM and TDM for the Multi-crystalline cell at different irradiation conditions after the Bonferroni correction
| C60 Mono-crystalline | |||||||||
| IR | CMA-ES vs | ||||||||
| ABC | CROW | CS | DE | DS | GSA | HS | PSO | ||
| 1000 | SDM | 1.43E-14 ▲ | 1.43E-14 ▲ | 1.28E-14 ▲ | 1.28E-14 ▲ | 1.51E-13 ▲ | 1.33E-14 ▲ | 1.39E-14 ▲ | 1.43E-14 ▲ |
| DDM | 1.01E-05 ▲ | 0.100873 ▲ | 1.53E-14 ▲ | 1.64E-14 ▲ | 5.2E-05 ▲ | 1.45E-14 ▲ | 1.14E-13 ▲ | 6.90E-08 ▲ | |
| 800 | SDM | 1.66E-14 ▲ | 1.66E-14 ▲ | 1.30E-14 ▲ | 1.28E-14 ▲ | 1.03E-12 ▲ | 1.34E-14 ▲ | 1.58E-14 ▲ | 1.43E-14 ▲ |
| DDM | 1.76E-05 ▲ | 0.176388 ▲ | 1.35E-14 ▲ | 1.51E-14 ▲ | 1.12E-07 ▲ | 1.48E-14 ▲ | 1.46E-14 ▲ | 7.21E-08 ▲ | |
| 500 | SDM | 1.43E-14 ▲ | 1.43E-14 ▲ | 1.29E-14 ▲ | 1.29E-14 ▲ | 3.58E-13 ▲ | 1.42E-14 ▲ | 1.63E-14 ▲ | 1.43E-14 ▲ |
| DDM | 1.29E-06 ▲ | 0.012867 ▲ | 1.24E-14 ▲ | 1.39E-14 ▲ | 1.74E-05 ▲ | 1.50E-14 ▲ | 1.45E-14 ▲ | 1.56E-08 ▲ | |
| 300 | SDM | 1.44E-14 ▲ | 1.57E-08 ▲ | 1.44E-14 ▲ | 1.67E-12 ▲ | 2.22E-12 ▲ | 1.35E-13 ▲ | 1.54E-14 ▲ | 1.31E-14 ▲ |
| DDM | 4E-09 ▲ | 1.44E-14 ▲ | 1.38E-14 ▲ | 1.39E-14 ▲ | 1.44E-14 ▲ | 1.28E-14 ▲ | 1.53E-14 ▲ | 1.36E-14 ▲ | |
| D6P100 Multi-crystalline | |||||||||
| IR | CMA-ES vs | ||||||||
| ABC | CROW | CS | DE | DS | GSA | HS | PSO | ||
| 1000 | SDM | 2.81E-14 ▲ | 9.96E-06 ▲ | 1.99E-06 ▲ | 5.84E-04 ▲ | 1.74E-04 ▲ | 1.44E-14 ▲ | 1.44E-14 ▲ | 1.44E-14 ▲ |
| DDM | 5.04E-04 ▲ | 1.28E-12 ▲ | 2.08E-12 ▲ | 1.56E-09 ▲ | 1.38E-11 ▲ | 1.44E-14 ▲ | 2.22E-12 ▲ | 2.22E-12 ▲ | |
| TDD | 8.66E-04 ▲ | 3.47E-04 ▲ | 6.91E-08 ▲ | 5.10E-05 ▲ | 7.98E-09 ▲ | 1.43E-14 ▲ | 2.92E-12 ▲ | 2.92E-12 ▲ | |
| 500 | SDM | 4.08E-14 ▲ | 6.56E-04 ▲ | 1.24E-14 ▲ | 1.23E-04 ▲ | 1.59E-04 ▲ | 1.44E-14 ▲ | 1.44E-14 ▲ | 1.44E-14 ▲ |
| DDM | 3.44E-05 ▲ | 7.91E-14 ▲ | 1.44E-14 ▲ | 1.69E-11 ▲ | 1.64E-13 ▲ | 6.73E-09 ▲ | 1.11E-12 ▲ | 1.11E-12 ▲ | |
| TDDD | 1.06E-14 ▲ | 1.06E-14 ▲ | 1.06E-14 ▲ | 1.06E-14 ▲ | 1.06E-14 ▲ | 1.06E-14 ▲ | 1.06E-14 ▲ | 1.06E-14 ▲ | |
| Mod. kc200gt Mono-crystalline | |||||||||
| IR | CMA-ES vs | ||||||||
| ABC | CROW | CS | DE | DS | GSA | HS | PSO | ||
| 1000 | SDM | 2.08E-11 ▲ | 1.36E-14 ▲ | 2.36E-11 ▲ | 7.18E-04 ▲ | 6.55E-08 ▲ | 2.85E-14 ▲ | 1.28E-14 ▲ | 2.44E-14 ▲ |
| DDM | 1.94E-14 ▲ | 1.63E-14 ▲ | 1.63E-14 ▲ | 2.79E-05 ▲ | 1.55E-06 ▲ | 1.51E-14 ▲ | 1.24E-14 ▲ | 2.44E-14 ▲ | |
| 800 | SDM | 1.58E-11 ▲ | 1.35E-14 ▲ | 2.44E-11 ▲ | 4.05E-04 ▲ | 7.44E-08 ▲ | 2.75E-14 ▲ | 1.25E-14 ▲ | 2.54E-14 ▲ |
| DDM | 2.81E-14 ▲ | 1.45E-14 ▲ | 1.44E-14 ▲ | 9.31E-05 ▲ | 2.14E-06 ▲ | 1.61E-14 ▲ | 1.22E-14 ▲ | 2.50E-14 ▲ | |
| 600 | SDM | 6.35E-14 ▲ | 1.36E-14 ▲ | 2.44E-11 ▲ | 4.73E-04 ▲ | 5.44E-08 ▲ | 3.14E-14 ▲ | 1.30E-14 ▲ | 2.49E-14 ▲ |
| DDM | 1.55E-14 ▲ | 1.44E-14 ▲ | 1.44E-14 ▲ | 1.13E-05 ▲ | 1.35E-06 ▲ | 1.71E-14 ▲ | 1.24E-14 ▲ | 2.44E-14 ▲ | |
| 400 | SDM | 1.94E-12 ▲ | 1.40E-14 ▲ | 2.44E-11 ▲ | 2.71E-04 ▲ | 7.84E-08 ▲ | 2.94E-14 ▲ | 1.25E-14 ▲ | 2.44E-14 ▲ |
| DDM | 1.44E-14 ▲ | 1.49E-14 ▲ | 1.44E-14 ▲ | 7.47E-05 ▲ | 1.51E-06 ▲ | 1.55E-14 ▲ | 1.23E-14 ▲ | 2.42E-14 ▲ | |
| 200 | SDM | 8.1E-12 ▲ | 1.33E-14 ▲ | 2.44E-11 ▲ | 2.72E-04 ▲ | 6.74E-08 ▲ | 3.12E-14 ▲ | 1.21E-14 ▲ | 2.41E-14 ▲ |
| DDM | 3.27E-14 ▲ | 1.41E-14 ▲ | 1.44E-14 ▲ | 2.13E-05 ▲ | 1.46E-06 ▲ | 1.89E-14 ▲ | 1.27E-14 ▲ | 2.49E-14 ▲ | |
Here ▲ indicates that CMA-ES performs better than its respective counterpart, ▼ means that CMA-ES performs worse than the compared technique, and ► symbolizes that there is no significant difference between the compared techniques.
The n-value determined by Bonferroni correction considering the value of 0.00139. Table 13 presents the result of the statistical study. It analyzes the indexes of all estimation process for the solar cells.
According to Table 13, the CMA-ES outperforms (▲) the rest of the techniques used in this study for the three equivalent models regarding the statistical analysis.
4.5 Response Graphics
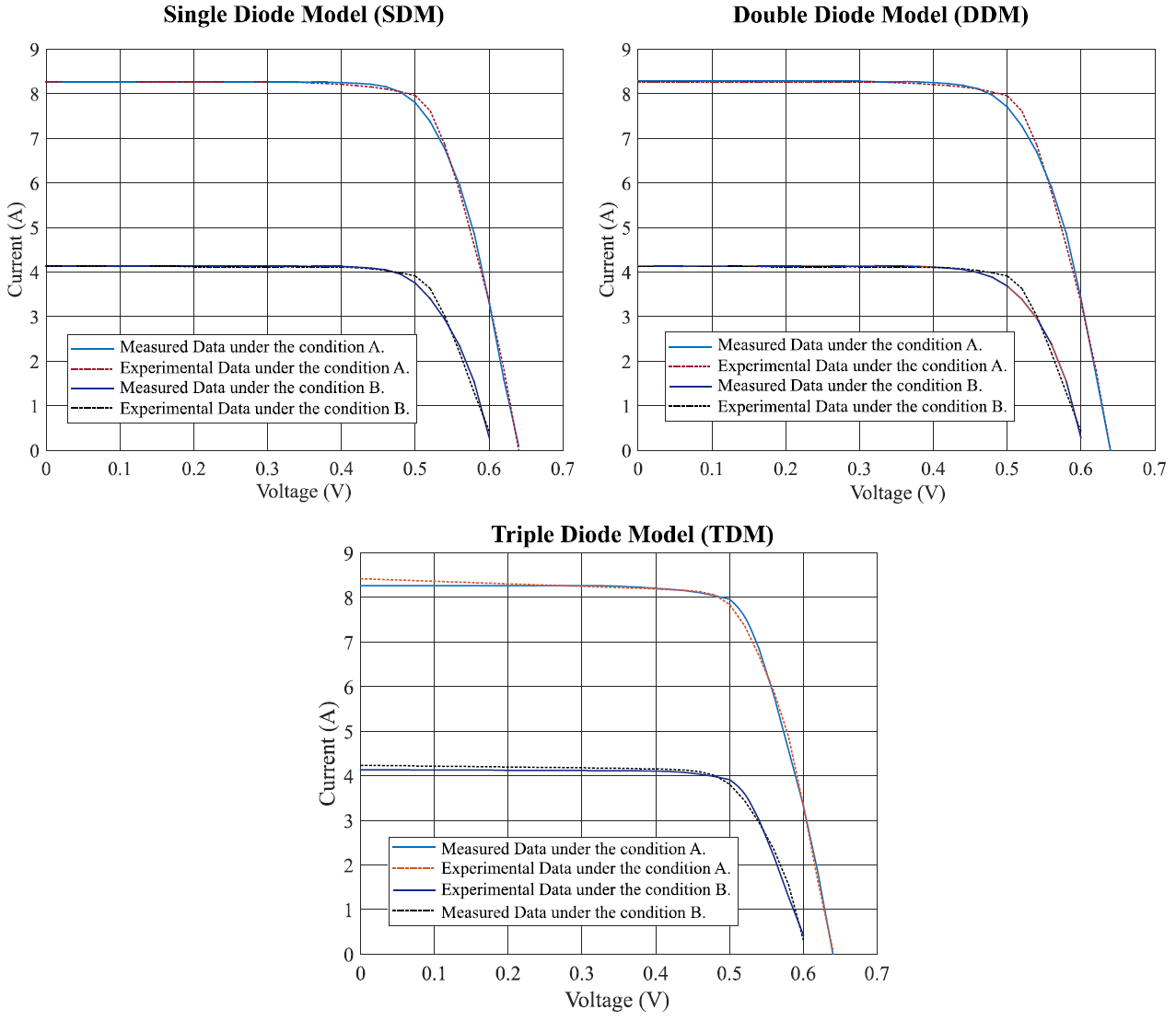
Figure 4 shows the absolute error curves between the measured data and the values determined by the CMA-ES model under 1000 W/m 2 and 500 W/m 2 for the SDM, DDM and TDM. In figure 5, the I-V characteristics between the measured data and the approximate model found by the CMA-ES are shown. This figure considers two different conditions. In the condition A, the irradiation is set in 1000 W/m 2 while for the condition B, the irradiation is 500 W/m 2. The D6P100 Multi-crystalline solar cell is used to represent the responses for the SDM, DDM and TDM.
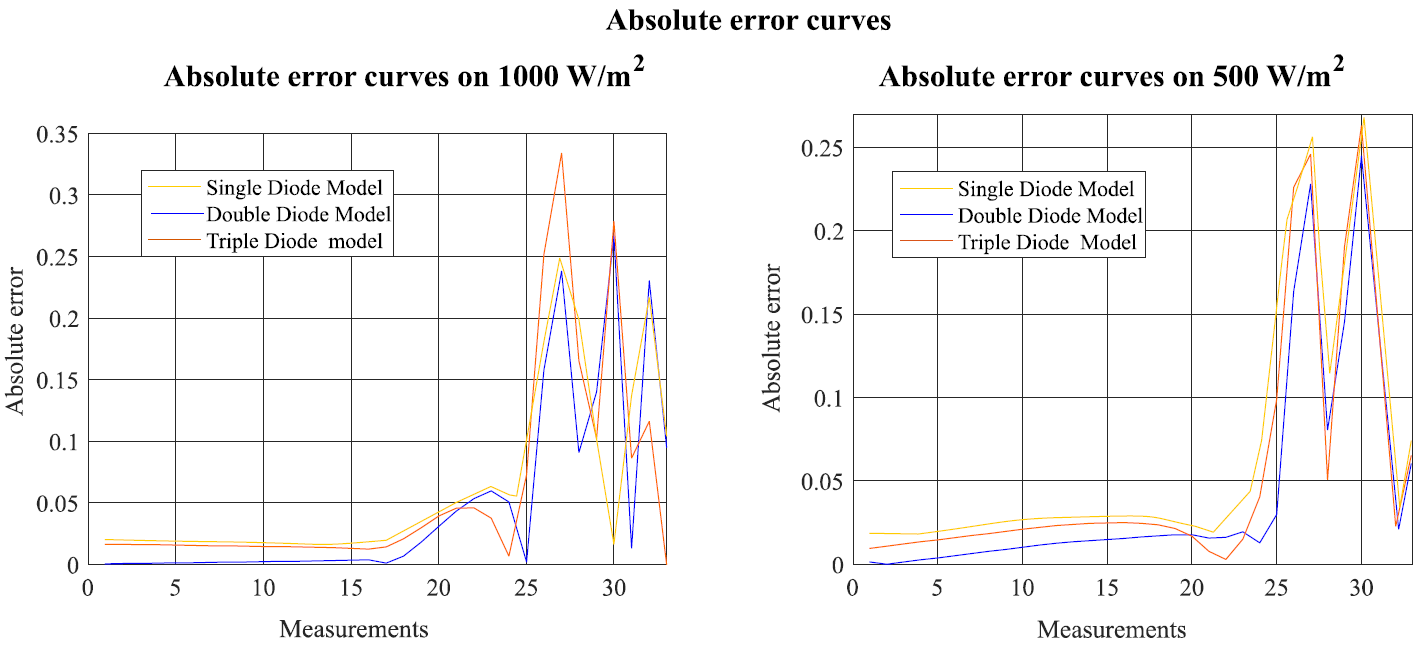
Fig. 4 Absolute error curves generated by the CMA-ES for the D6P100 Multi-crystalline solar cell under two irradiation conditions: 1000 W/m 2 (Condition A) and 500 W/m 2 (Condition B) for the SDM, DDM and, TDM
5 Conclusions
Several proposals of evolutionary computation (EC) methods to estimate the parameters of solar cells have been reported in the literature. However, most of them report only a single EC technique considering a minimal number of solar cell models. In this work, a comparative study of solar cells parameter estimation is discussed. In the comparison different EC Techniques are used, such as Artificial Bee Colony (ABC), Crow Search Algorithm (CSA), Cuckoo Search (CS), Differential Evolution (DE), Differential Search (DSA), Gravitational Search Algorithm (GSA), Harmony Search (HS), Particle Swarm Optimization (PSO) and Covariant Matrix Adaptation with Evolution Strategy (CMA-ES). The comparison was developed over three equivalent solar cell models, the Single Diode (SDM), Double Diode Model (DDM) and Three Diode Model (TDM) using a Mono-crystalline solar cell for the SDM and DDM, a Multi-crystalline solar cell for the SDM, DDM and TDM and a solar cell module for the SDM and DDM.
The estimation of parameters in solar cells represents a complex task due to their dimensionality and non-linearity of the generated error surface. After comparing the capabilities of each EC technique, it has found that the CMA-ES outperformed the rest of the techniques regarding minimum and average root mean square error (RMSE). In the case of the standard deviation, the best results were distributed among CMA-ES, CS, DE, and DSA. The results have been validated through a statistical study that combines the Wilcoxon test and the Bonferroni correction.











 nueva página del texto (beta)
nueva página del texto (beta)