1 Introduction
Mobile Ad Hoc Networks (MANETs) can be defined as a collection of mobile nodes that dynamically form a temporary network without using any centralized network infrastructure to ensure communication [1]. In MANETs, the mobile nodes are connected through wireless links. Each mobile node can act both as an end node and as an intermediate node relaying packets for the benefit of other nodes [2].
Since MANETs comprise of mobile nodes, the nodes participating in the network usually need to be untethered, and thus powered by batteries, which provide limited energy. As mobile nodes are constantly communicating with each other, the energy dissipation rate is higher. Due to the limited capacity of mobile node batteries, energy conservation is a fundamental criterion when designing routing algorithms. Routing is one of the main factors affecting the energy dissipation rate in MANETs. Therefore, energy efficiency has drawn the attention of the researcher community. Most of the research work focuses on developing an accurate energy-efficient routing protocol.
Energy-efficient routing protocols amend the shortest path by including energy as the criteria to select the best path. The current energy-efficient routing protocols perform two tasks:
It tends to reduce the energy required for performing active communication when mobile nodes are receiving or transmitting the data packets.
It tends to reduce the passive energy that the mobile nodes consume in its idle mode when they just communicate control messages and not data packets.
It has been demonstrated that the energy-efficient routing problem in Manets is an NP-hard problem [3], and therefore difficult to solve. Metaheuristic algorithms have been devised to find the proper solutions for the NP-hard problems in a reasonable time [4].
The population-based metaheuristic algorithms play a very important role in finding the best optimal paths in routing. Genetic Algorithm (GA) is a population-based metaheuristic algorithm, which is considered as a powerful tool to solve the NP-hard problems [5].
In this paper, we propose a new optimization approach for energy-efficient routing based on a Genetic Algorithm to find a path(s) with the lowest energy cost while routing data in MANETs. In the proposed approach, a new fitness function is designed. This function is based on three multiple-layer energy metrics: (1) Transmission and Reception Power, (2) Node connectivity index, and (3) Remaining energy capacity.
Due to the mobility of nodes in MANETs, new energy-efficient path need to be constantly recalculated. Genetic Algorithm makes possible maintaining a backup of paths that consume minimum power. Therefore, our approach also aims to find alternative paths, which can substitute the original path found when it is no longer operational. Our proposed approach solves two problems:
Finding an optimal energy-efficient path to transfer data between mobile nodes.
Providing alternate paths when one path gets failed.
Experiments have proved that our approach is effective and efficient. The remainder of this paper is structured as follows: In section 2, we provide a short discussion of related work. In section 3, we detailed and present the proposed approach. Section 4, the experimental results are discussed and compared with existing approaches. Section 5, conclusion and some perspectives are drawn.
2 Related Work
Minimizing energy consumption is a very important issue in MANETs. During the last decade, the researcher community has made considerable efforts to develop energy-efficient routing protocols based on genetic algorithms. Therefore, we propose some of the work carried out in this field.
In the study of Ibukunola et al. [6], the objective is to describe the Geographical Adaptive Fidelity (GAF) energy model, which is one of the best-known topology management models used to improve energy efficiency in MANETs by grouping network nodes into virtual grids. In order to minimize the energy consumption, the authors used the genetic algorithms and the simulated annealing metaheuristics in MANETs modeled by rectangular GAF and compare them.
Sonia Ahuja et al. [7], present an energy-efficient hybrid routing algorithm in MANETs using genetic algorithms and ACO Ant colony optimization. To select the optimized path between the mobile nodes, the proposed genetic algorithm depends on the minimum cost of the multicast tree and bounded end-to-end delay.
Brindha et al. [8], proposed an energy-efficient unicast routing protocol using genetic algorithms in MANETs. The proposed work considers multiple QoS metrics such as end-to-end delay, bandwidth, hop count and energy as important metrics for effective and reliable path selection.
Antipathy et al. [9], presented an energy and mobility aware route optimization technique based on genetic algorithms. For selecting the optimal path, the proposed route optimization technique applied a fitness function based on three metrics, namely: the estimated geometrical distance (EGD), min-max battery capacity (MMBC) and node connectivity index (NCI).
Pawan et al. [10], proposed a new routing protocol in MANETs using genetic algorithms to select a path that consumes less energy to ensure the communication between the source and the destination node. The authors assume that every node has all the information about their neighbors. The fitness of a path is based on the transmission power of a path, which depends mainly upon the distance between two mobile nodes.
Farden Far et al. [11], used genetic algorithms to increase the efficiency of the OLSR routing protocol and it aims at better energy conservation in MANET. The most optimal path was selected based on the remained energy of each node and the distance between the nodes. The authors used the weight factor which has been determined based on energy consumption combined with shortest paths.
Renu Choudhary et al. [12], proposed a new power-aware routing protocol for MANETs using genetic algorithms to find a path that consumes minimum power while routing data in MANETs. The proposed algorithm is based on table-driven protocols.
Each node in the network manages a table that allows it to store the information concerning the paths to route data to all the other neighboring nodes.
Two metrics are used to calculate the fitness of a path: (1) Average Remaining Battery Power of all the nodes in the path (2) Number of nodes selected in that path.
We report in Table 1 the main common and different points between our work and some of those mentioned above.
Table 1 Summary of Works using Genetic Algorithms
| Authors | Resolution methods | Description | Routing Metrics Considered |
| Sonia Ahuja et al. (2014) | ‒ Genetic algorithms ‒ ACO Ant colony optimization |
Present an energy-efficient hybrid algorithm for routing in MANETs by using genetic algorithm and ACO Ant colony optimization to select the optimized path between the mobile nodes | ‒ Bounded end-to-end delay ‒ The minimum cost of the multicast tree |
| Ganapathy et al. (2017) | ‒ Genetic algorithms | Present an energy and mobility aware route optimization technique based on genetic algorithms for selecting the optimal path | ‒ Estimated geometrical distance ‒ Min-max battery capacity ‒ Node connectivity index |
| Pawan et al. (2018) | ‒ Genetic algorithms | Propose a new routing protocol in MANETs using genetic algorithms to select a path that consumes minimum energy to route data between two nodes in the networks. | ‒ The transmission power of a path |
| Renu Choudhary et al. (2019) | ‒ Genetic algorithms | Propose a new power-aware routing protocol for MANETs, which use routing tables to get information about different nodes and apply genetic algorithms to find a path with less energy cost while routing data | ‒ Average Remaining Battery Power of all the
nodes in the path ‒ Number of nodes selected in the path |
| Our study | ‒ Genetic algorithms | We present a new energy-efficient routing approach based on genetic algorithms to find a path with the lowest energy cost to the destination | ‒ Transmission and Reception power ‒ Node Connectivity Index ‒ Remaining Energy Capacity |
The feature of the proposed work comparing to those referred to in Table 1 is that we introduce in this article a combination of energy routing metrics from multiple layers. In this work, we propose a new function to calculate the fitness of the path based on this combined metric. The proposed work aims also to provide alternate paths when one path gets failed.
3 Proposed Approach
The energy efficiency problem we are concerned about is cast as an optimization problem. During the last decade, various optimization metaheuristic methods have been proposed to solve NP-hard problems in MANETs. Genetic algorithms have found a special place among those optimization methods. Genetic algorithms are described as one of the most effective metaheuristics widely used in MANETs for solving convoluted optimization problems, such as the dynamic multicast problem, routing optimization problem, QoS route selection problem, Energy-efficient based multicast routing problem [13], etc.
Our proposed approach provides energy efficiency for MANETs by using Genetic Algorithms to select the path(s) with the lowest energy cost to transfer data between two mobile nodes. The aim of using the Genetic Algorithms based routing is that complexity in finding the least costly energy path does not increase rapidly with the number of nodes of the network, which in contrast to other optimization algorithms has also been considered as an advantage [11]. New hardware implementations of genetic algorithms [14] have shown their ability to fast computation. In this regard, the Genetic algorithms are quite promising for energy-efficient routing in MANETs.
3.1 Overview of Genetic Algorithm
Genetic Algorithms are evolutionary algorithms that use techniques inspired from the Darwinian theory of evolutionary [15], The mode of operation of a GAs is modeled on biological principles of natural selection and survival of the best adapted to the environment individuals. GAs were proposed and investigated by John Holland [16], leading to his book “Adaptation in Natural and Artificial Systems”, 1975.
GA is an evolutionary optimization technique, which uses special operators such as selection, crossover, and mutation to solve problems, which are difficult to solve by using conventional approaches. GAs maintain a population of candidate solutions, where each candidate solution is usually coded and it corresponds to a chromosome. A set of chromosomes forms a population, where characteristics of one population are forwarded into the next population.
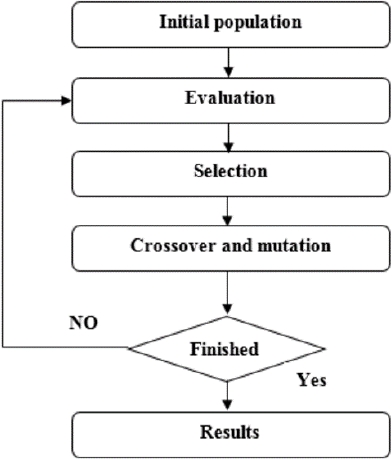
GAs calculate the fitness of all individuals in the population using a fitness function. The fitness evaluation function is defined in terms of metrics to optimize; it plays an important role in GAs because it provides information about how good is each solution. To improve results, GAs select the best solutions using a selection operator. The major operation of GAs (Figure. 1) is as follows [17]:
The beginning of GAs is a set of solutions generate randomly called the initial population.
-
The evolution from one generation to the next one involves mainly three steps
Fitness evaluation: compute the fitness of each solution.
Selection: GAs select "parents" (fittest solutions) proportional to their fitness values from the current population to participate in crossover for creating the next generation.
Crossover and/or mutation: GA reproduces "children" from selected parents using crossover and/or mutation operators.
The different genetic operators can be applied to the population repeatedly. GAs stops when an acceptable solution is found, when convergence criterions met, or when a predetermined limit number of iteration is reached.
3.2 Energy Efficiency Metrics Considered in our Approach
Before selecting an appropriate metric for energy-efficient routing, we must first focus on the causes of energy depletion. In MANETs, a mobile node consumes its battery energy based on the operations it performs. There are four energy consumption modes, which consumes different levels of energy [18]:
Transmission Mode: when a node is transmitting a packet to another node.
Reception Mode: when a node is receiving a packet from another node. The receiving node may be the destination node or just an intermediate node.
Idle /Overhearing Mode: even when no messages are being transmitted over the medium, the nodes keep listening to the medium with listening energy. 4. Sleep Mode: when the radio is temporary switched off (no communication is possible). The node spends sleep energy.
Energy-efficient routing protocols use energy metrics to select the most efficient path. According to Waheb A. Jabbar et al. [19], the energy-efficient routing algorithms use different energy metrics to select a path, those metrics can be classified into four categories: (1) transmission power, (2) Remaining Energy capacity, (3) Estimated node lifetime and (4) Combined energy metrics.
It is no longer appropriate to use only one metric to determine the path cost. The different approaches based on a single metric, are nearsighted and do not take into account all the possible causes of energy depletion in the network. In order to avoid this, it is best to use a combination of multiple energy metrics to find the path with the lowest energy cost to the destination.
Therefore, we consider three multiple-layer energy metrics in our energy model to calculate the path cost:
Transmission and Reception Power: These parameters aim to choose paths that have low transmission and reception power. In MANETs, the transmission and reception power of a path depends mainly upon the distance between the nodes.
Node connectivity index: The connectivity index of a node is the number of direct neighboring nodes with one-hop. By avoiding nodes with several direct neighbors, the node gains in listening energy.
Remaining energy capacity: This parameter is important to select the next-hop node because we want to select paths, which include less depleted nodes.
This energy model minimizes the energy consumed during an active communication when mobile nodes are transmitting or receiving packets in the network, as well as during an inactive communication when mobile nodes stay idle, but they are in a listening state.
3.3 Fitness Function
In this paper, our insight is to determine a set of multiple layer energy metrics. We focus on designing a novel combined energy metric based on the described metrics and integrate it into our fitness function.
Here, for each metric used in our approach, we always consider a k-hop Path P= N0, N1, · · ·, Nk from the source node N0 to the destination node Nk. The following notations listed in Table 2 are used in the rest of this paper.
Table 2 Explanation of the notations
| Notations | Meaning |
| Cp (Pi) | Cost of path Pi |
| Cn(i) | Energy Cost of node Ni |
| PT (i) | Transmission power of node Ni |
| PTmax | Maximum transmission power |
| PR (i) | Receiving power by node Ni |
| PRmax | Maximum receiving power |
| Er (i) | Remaining energy capacity of node Ni |
| E0 | initial energy capacity of node Ni |
| Econs (i) | Consumed energy by node Ni |
| N | Node Connectivity Index of node Ni |
| Nmax | Number of nodes in the network minus one |
In order to calculate the energy cost of a node, we use the above metrics, where every metric is assigned with a weight value to adjust the impact of each routing metric as shown in the equation (1).
The energy cost function of a node is a single function that is formed by combining the weighted metrics and it aims at minimizing the weighted sum:
The basic idea of this approach is to optimize the energy efficiency by selecting the (1) minimum of Transmission and Reception Power, (2) minimum of Node connectivity index and (3) minimum of consumed energy, which is nothing more than the maximum of Remaining energy capacity:
The metric of optimization is the path cost between the source node and the destination node. The objective is to find the path with the minimum total cost. The new node’s energy cost function computed in equation (1) is used to calculate the paths costs between every source and destination nodes. Our proposed Fitness function is shown in Equation (4):
where n indicates the number of nodes in the path.
3.4 Genetic Algorithm for Energy Efficient Routing
In this paper, a new algorithm using GAs has been proposed to find the best solution by identifying the energy-efficient path(s) between the source node and the destination node. The proposed algorithm also finds alternate paths, which can be used when the original path found is no longer operational. The adaptation of the genetic algorithm in our approach is as follow:
Generate a random initial population of feasible routing paths.
Calculate the fitness function of all paths belonging to the population.
Repeat steps 4 to 8 until an optimal solution is reached.
Select random parent’s paths, which will participate in crossover to generate new paths.
Perform cross over to generate new children paths and calculate the fitness of every newly generated path.
Sort population by fitness after adding the newly generated children paths in population.
Remove the worst paths from the population.
Perform mutation and a new population is generated for the next iteration.
Step1: Encoding Population
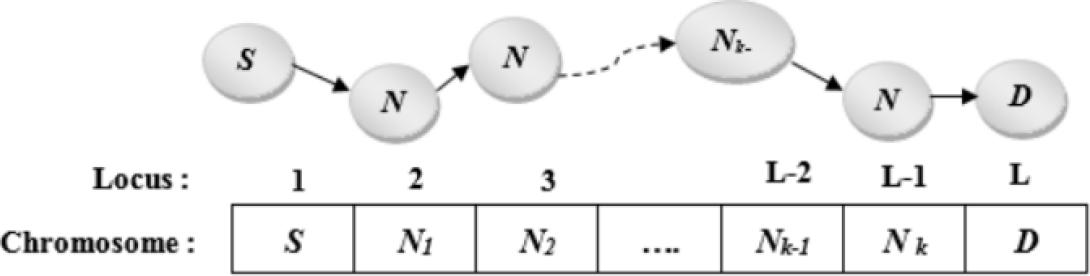
In our proposed approach, a feasible solution corresponds to a path, which is represented by a succession of nodes. We adopt a decimal-coded. Very intuitively, each chromosome represents a path. Any existing feasible path is encoded by a sequence of positive integers representing the identifiers of nodes through which a routing path passes. The first locus gene is always reserved for the source node and the last locus for the destination node. Though the length of each chromosome is a variable, it should not exceed the total number of nodes present in the network. To avoid creating loops, the same node must appear only once in a chromosome. An example of path encoding is shown in Fig.2.
Step2: Initial Population
A small population size leads to rapid convergence before reaching an acceptable solution. Contrarily, if the population size is too large, this leads to unnecessary computations. In this study, the appropriate population size is obtained such that the optimum reached cannot be improved easily. After several trials and experiments, we use a set of 100 feasible routing paths generated randomly as an initial population.
Step3: Fitness Evaluation
The fitness function takes a single solution as a parameter and returns a value indicating how good the solution is. After generating the initial population, we will select the best individuals, who will participate in the improvement of our population. The selection of individuals depends on fitness function values. In this work, we consider Equation (4) as the fitness function.
Step 4: The Selection of Individuals
This step is about selecting the best parents from the population and forming a mating pool. Whether a parent is selected from the population is a matter of probability. There are different methods of selection in GAs literature [20]. The well-known is the "roulette wheel" method, the "elitist" method and the "tournament" method. In our approach, we used the elitist method to select the best individuals according to their fitness values.
Step 5: The Crossing of Individuals
The crossing consists of combining two individuals (called parents) of the mating pool to bring out two new individuals (called children), with characteristics from both parents but not necessarily better than the parents.
Many crossover operators exist in GAs literature [20]. The main ones are "single-point crossover", "double-point crossover", "Multi-point crossover", "Uniform crossover". The single-point crossover is the most common.
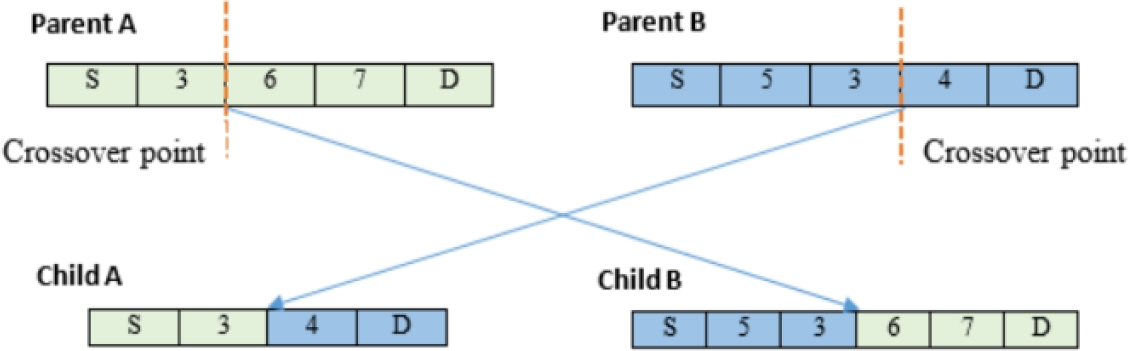
In our approach, we apply a single-point crossover. We can assume that any two parents are chosen for the crossover process. These two parents should contain at least one common intermediate node, which is considered as a meeting point to perform crossover. To generate child1, we copy all the nodes from parent A into child A up to the meeting point, and then copy remaining nodes from parent B into child A. Same process is done for generating child B, we copy all the nodes from parent B to child B up to the meeting point and then copy remaining nodes from parent A into child B. An example of Single-Point Crossover is shown in Fig.3.
Step 6: Mutation
The mutation is usually applied after the process of crossover. This operator is applied to children to improve their fitness value by randomly modifying, with a small mutation probability, the value of a component of the individual. The mutation is traditionally considered a marginal operator although it somehow confers on genetic algorithms the property of ergodicity (i.e. all points in the search space can be reached). This operator is therefore of great importance. It has a dual role in performing a local search and/or exit a trap (remote search).
In our approach, to perform the mutation over an individual, instead of randomly selecting a gene, as in standard GA, we select the node in the chromosome, which dissipates the maximum energy. The purpose of selecting this node for mutation is to reduce the total energy dissipation by the node and hence, to increase the network lifetime. This can be done by decreasing the node connectivity index of the selected node.
Step 7: Convergence
The Genetic Algorithm starts with a random initial population. The steps of GAs are repeated until reaching an end criterion. Once the maximum number of generations reached, we get a population of best solutions.
This can be overcome by setting an appropriate number of iterations for the genetic algorithm. In our approach, the number of iterations is set to 30 after carrying out some preliminary runs on each data set.
4 Results
MATLAB R2010a software has been used to implement the proposed Genetic Algorithm approach. Our studies involve a random network of 10 nodes. In this study, node 1 is set as the source node and node 6 is the destination node.
The performance of the Genetic Algorithm is greatly affected by several parameters, such as the population size, the selection rate, the crossover and mutation rates. Several experiments are conducted to study the impact of those parameters on the performance of our approach.
In our experiments, we have observed that the performance of our proposed Genetic Algorithm can be improved when the selection rate is increased up to 0.6–0.9, the mutation rate is increased up to 0.4–0.6, and the crossover rate is increased up to 0.7–0.9.
The genetic parameters used in our approach are as follows:
| Selection Rate: | 0.8, |
| Crossover Operator sed: One-point crossover, | |
| Crossover Rate: | 0.7, |
| Mutation Rate: | 0.05, |
| Individual Number: | 100, |
| Iterations Number: | 30. |
Step1: Initial Population
The initial population of 100 individuals is shown in Table 3.
Table 3 The Initial Population
| Individuals | Routing Path | |||||||||
|
Node 1st |
Node 2nd |
Node 3rd |
Node 4th |
Node 5th |
Node 6th |
Node 7th |
Node 8th |
Node 9th |
Node 10th |
|
| Indv01 | 1 | 2 | 10 | 9 | 5 | 4 | 3 | 6 | 0 | 0 |
| Indv02 | 1 | 2 | 4 | 5 | 9 | 3 | 6 | 0 | 0 | 0 |
| Indv03 | 1 | 7 | 2 | 10 | 3 | 5 | 6 | 0 | 0 | 0 |
| Indv04 | 1 | 7 | 2 | 4 | 3 | 9 | 10 | 8 | 6 | 0 |
| Indv05 | 1 | 2 | 4 | 3 | 9 | 10 | 7 | 6 | 0 | 0 |
| Indv30 | 1 | 2 | 7 | 10 | 8 | 5 | 9 | 3 | 6 | 0 |
| Indv31 | 1 | 5 | 8 | 10 | 2 | 7 | 9 | 4 | 6 | 0 |
| Indv32 | 1 | 5 | 4 | 7 | 2 | 10 | 8 | 6 | 0 | 0 |
| Indv98 | 1 | 3 | 4 | 5 | 9 | 7 | 2 | 10 | 8 | 6 |
| Indv99 | 1 | 3 | 4 | 9 | 5 | 8 | 10 | 2 | 7 | 6 |
| Indv100 | 1 | 3 | 4 | 2 | 7 | 9 | 10 | 8 | 5 | 6 |
Table 3 illustrates:
‒ Horizontally: Individuals forming the initial population and representing the feasible routing paths.
‒ Vertically: positive integers that represent the IDs of nodes through which a routing path passes.
‒ A '0' will appear in a row as an element to signify a blank space.
Step2: Fitness Evaluation
This step is to evaluate each individual in the population according to equation (4) as shown in Table 4.
‒ The initial population cost is 41.235 and the cost of the best path is 25,936.
‒ Best Path of the population: Path No 2.
‒ Path cost = 25,936.
‒ Route = [1, 2, 4,5, 9, 3, 6].
‒ The number of active nodes = 7.
Table 4 Population evaluation
| Individuals | Routing Path | Fitness | |||||||||
|
Node 1st |
Node 2nd |
Node 3rd |
Node 4th |
Node 5th |
Node 6th |
Node 7th |
Node 8th |
Node 9th |
Node 10th |
||
| Indv01 | 1 | 2 | 10 | 9 | 5 | 4 | 3 | 6 | 0 | 0 | 40,49833 |
| Indv02 | 1 | 2 | 4 | 5 | 9 | 3 | 6 | 0 | 0 | 0 | 25,936 |
| Indv03 | 1 | 7 | 2 | 10 | 3 | 5 | 6 | 0 | 0 | 0 | 30,266 |
| Indv04 | 1 | 7 | 2 | 4 | 3 | 9 | 10 | 8 | 6 | 0 | 42,72033 |
| Indv05 | 1 | 2 | 4 | 3 | 9 | 10 | 7 | 6 | 0 | 0 | 48,3203333 |
| Indv30 | 1 | 2 | 7 | 10 | 8 | 5 | 9 | 3 | 6 | 0 | 51,7266667 |
| Indv31 | 1 | 5 | 8 | 10 | 2 | 7 | 9 | 4 | 6 | 0 | 33,4463333 |
| Indv32 | 1 | 5 | 4 | 7 | 2 | 10 | 8 | 6 | 0 | 0 | 38,214 |
| Indv98 | 1 | 3 | 4 | 5 | 9 | 7 | 2 | 10 | 8 | 6 | 59,7383333 |
| Indv99 | 1 | 3 | 4 | 9 | 5 | 8 | 10 | 2 | 7 | 6 | 44,506 |
| Indv100 | 1 | 3 | 4 | 2 | 7 | 9 | 10 | 8 | 5 | 6 | 43,6196667 |
Step 3: Since Nbr = 0 < Nbrmax = 30, we proceed to step 4.
Step 4: Selected Population
In this step, we select 80 percent of the individuals forming the initial population as shown in Table 5. In our study, individuals are sorted in descending order according to their fitness value.
Table 5 The Selected Population
| Individuals | Routing Path | Fitness | |||||||||
|
Node 1st |
Node 2nd |
Node 3rd |
Node 4th |
Node 5th |
Node 6th |
Node 7th |
Node 8th |
Node 9th |
Node 10th |
||
| Indv02 | 1 | 2 | 4 | 5 | 9 | 3 | 6 | 0 | 0 | 0 | 25,936 |
| Indv13 | 1 | 2 | 4 | 7 | 5 | 3 | 6 | 0 | 0 | 0 | 28,98666 |
| Indv03 | 1 | 7 | 2 | 10 | 3 | 5 | 6 | 0 | 0 | 0 | 30,266 |
| Indv31 | 1 | 5 | 8 | 10 | 2 | 7 | 9 | 4 | 6 | 0 | 33,4463333 |
| Indv32 | 1 | 5 | 4 | 7 | 2 | 10 | 8 | 6 | 0 | 0 | 38,214 |
| Indv01 | 1 | 2 | 10 | 9 | 5 | 4 | 3 | 6 | 0 | 0 | 40,49833 |
| Indv04 | 1 | 7 | 2 | 4 | 3 | 9 | 10 | 8 | 6 | 0 | 42,72033 |
| Indv99 | 1 | 3 | 4 | 9 | 5 | 8 | 10 | 2 | 7 | 6 | 44,506 |
| Indv30 | 1 | 2 | 7 | 10 | 8 | 5 | 9 | 3 | 6 | 0 | 51,7266667 |
Step 5: Cross Population
70 percent of the selected individuals are used to do cross over. Take the following example From Table 6:
‒ Parent1 = Path No 1= [1, 2, 10, 9, 5, 4, 3, 6].
‒ Path cost = 40, 49833.
‒ Parent2 = Path No 3 = [1, 7, 2, 10, 3, 5, 6]
‒ Path cost = 30,266.
‒ Node Selected for Cross Over = 10.
‒ Child1 = Path No 101 = [1, 2, 10, 3, 5, 6].
‒ Path cost = 28, 94366.
‒ Child2 = Path No 102 = [1,7,2,10,9,5, 4, 3, 6].
‒ Path cost= 42,506.
Table 6 The Cross Population
| Individuals | Routing Path | Fitness | |||||||||
|
Node 1st |
Node 2nd |
Node 3rd |
Node 4th |
Node 5th |
Node 6th |
Node 7th |
Node 8th |
Node 9th |
Node 10th |
||
| Indv02 | 1 | 2 | 4 | 5 | 9 | 3 | 6 | 0 | 0 | 0 | 25,936 |
| Indv101 | 1 | 2 | 10 | 3 | 5 | 6 | 0 | 0 | 0 | 0 | 28,94366 |
| Indv13 | 1 | 2 | 4 | 7 | 5 | 3 | 6 | 0 | 0 | 0 | 28,98666 |
| Indv03 | 1 | 7 | 2 | 10 | 3 | 5 | 6 | 0 | 0 | 0 | 30,266 |
| Indv31 | 1 | 5 | 8 | 10 | 2 | 7 | 9 | 4 | 6 | 0 | 33,4463333 |
| Indv32 | 1 | 5 | 4 | 7 | 2 | 10 | 8 | 6 | 0 | 0 | 38,214 |
| Indv01 | 1 | 2 | 10 | 9 | 5 | 4 | 3 | 6 | 0 | 0 | 40,49833 |
| Indv102 | 1 | 7 | 2 | 10 | 9 | 5 | 4 | 3 | 6 | 0 | 42,506 |
| Indv04 | 1 | 7 | 2 | 4 | 3 | 9 | 10 | 8 | 6 | 0 | 42,72033 |
| Indv99 | 1 | 3 | 4 | 9 | 5 | 8 | 10 | 2 | 7 | 6 | 44,506 |
| Indv30 | 1 | 2 | 7 | 10 | 8 | 5 | 9 | 3 | 6 | 0 | 51,7266667 |
It can be observed that the crossover operation generates a new path (child 1), which have less path cost as compared to both of the parents.
Step 6: Mutated Population
As shown in Table 7, this step is for performing mutation. In this example, a mutation with probability 0.05 for all individuals is performed.
Table 7 The Mutated Population
| Individuals | Routing Path | Fitness | |||||||||
|
Node 1st |
Node 2nd |
Node 3rd |
Node 4th |
Node 5th |
Node 6th |
Node 7th |
Node 8th |
Node 9th |
Node 10th |
||
| Indv02 | 1 | 2 | 4 | 5 | 9 | 3 | 6 | 0 | 0 | 0 | 25,936 |
| Indv101 | 1 | 2 | 10 | 3 | 5 | 6 | 0 | 0 | 0 | 0 | 28,94366 |
| Indv13 | 1 | 2 | 4 | 7 | 5 | 3 | 6 | 0 | 0 | 0 | 28,98666 |
| Indv03 | 1 | 7 | 2 | 10 | 3 | 5 | 6 | 0 | 0 | 0 | 30,266 |
| Indv31 | 1 | 5 | 8 | 10 | 2 | 7 | 9 | 4 | 6 | 0 | 33,4463333 |
| Indv32 | 1 | 5 | 4 | 7 | 2 | 10 | 8 | 6 | 0 | 0 | 38,214 |
| Indv01 | 1 | 2 | 10 | 9 | 5 | 4 | 3 | 6 | 0 | 0 | 40,49833 |
| Indv102 | 1 | 7 | 2 | 10 | 9 | 5 | 4 | 3 | 6 | 0 | 42,506 |
| Indv04 | 1 | 7 | 2 | 4 | 3 | 9 | 10 | 8 | 6 | 0 | 42,72033 |
| Indv99 | 1 | 3 | 4 | 9 | 5 | 8 | 10 | 2 | 7 | 6 | 44,506 |
| Indv30 | 1 | 2 | 7 | 10 | 8 | 5 | 9 | 3 | 6 | 0 | 51,7266667 |
The fitness of the population is improving after each iteration. The resulting population becomes a new population. We increment the generation Nbr by 1 and we proceed to step 3.
Step 7-a: Best Individuals
The average path cost in this population after 30 iterations is minimized to 23.0427 and the cost of the optimal path is 21,807.
Step 7-b: Optimal Solution
In this stage, we get the optimal path with the lowest energy cost.
Many energy-efficient routing approaches based on genetic algorithms have been developed, which are usually based on different energy routing metrics applied for selecting the optimized path. For effective benchmarking, we conducted a series of experiments varying the energy routing metrics. For that, we choose to consider the study performed by Pawan et al. [10], and the study performed by Choudhary et al. [12]. The reason for selecting these studies is because of the similar aim in finding the least costly energy path. Further, the selected studies used different energy routing metrics.
In the study of Pawan et al. [10], The fitness of a path is based on transmission power as an energy metric. While, in the study of Choudhary et al. [12] the fitness of a path is based on two metrics: the average remaining battery power of all the nodes in the path, and the number of nodes selected in that path. However, the experimental environment, as well as the design parameters of Pawan et al. [10] and Choudhary et al. [12], differs from our approach, and for performing comparative analysis we required the similar testbed. Therefore, in order to compare the overall performance of our Genetic Algorithm, we implement the principle of the Genetic Algorithm introduced by Pawan et al. [10] and Choudhary et al. [12] using the same parameters as in our approach.
When implementing the study of Pawan et al. [10], we get an optimal path with a number of nodes equal to 6 and path cost equal to 51.74633. We note that our proposed algorithm selects a path having 20% less number of active nodes with less path cost. However, when implementing the study of Choudhary et al. [12], we get an optimal path having a number of nodes equal to 5 and path cost equal to 36.23633. We note that our proposed algorithm selects a path having a 10% less number of active nodes with less path cost.
Table 10 summarizes the results comparison of our approach with the other two implemented approaches.
Table 8 Best Individuals
| Routing Path | Fitness | |||||||||
|
Node 1st |
Node 2nd |
Node 3rd |
Node 4th |
Node 5th |
Node 6th |
Node 7th |
Node 8th |
Node 9th |
Node 10th |
|
| 1 | 5 | 4 | 6 | 0 | 0 | 0 | 0 | 0 | 0 | 21,985 |
| 1 | 7 | 2 | 4 | 6 | 0 | 0 | 0 | 0 | 0 | 23,18366 |
| 1 | 7 | 4 | 6 | 0 | 0 | 0 | 0 | 0 | 0 | 21,807 |
| 1 | 7 | 10 | 8 | 6 | 0 | 0 | 0 | 0 | 0 | 23,7576667 |
| 1 | 5 | 9 | 7 | 6 | 0 | 0 | 0 | 0 | 0 | 22,456667 |
Table 9 Optimal Solution
| Routing Path | Fitness | |||||||||
|
Node 1st |
Node 2nd |
Node 3rd |
Node 4th |
Node 5th |
Node 6th |
Node 7th |
Node 8th |
Node 9th |
Node 10th |
|
| 1 | 7 | 4 | 6 | 0 | 0 | 0 | 0 | 0 | 0 | 21,807 |
Our proposed approach offers better results than the other approaches studied. The results obtained confirm the potential of the proposed Genetic Algorithm.
5 Conclusion and Future Work
Energy consumption is a very challenging issue in MANETs. In this paper, in the context of optimizing the energy consumption while routing data in MANETs, a new energy efficiency approach based on genetic algorithms is proposed and implemented.
The proposed approach can comprehensively assess three proposed multiple-layer energy routing metrics (Transmission and Reception Power, Node connectivity index, and Remaining energy capacity). These metrics are combined according to Equation (1) and used for calculating the energy quality of mobile nodes. Then, genetic operators such as selection/ crossover and mutation are applied for selecting an optimal path that consumes less energy to ensure the communication between the mobile nodes according to the minimum value of the fitness function. After several trials and experiments, the appropriate population size was determined and used with the selected GA operators rate to get the best fitness function value.
Our proposed approach provides us a set of optimal paths with less energy cost to transfer data from the source node to the destination node. Since MANET are dynamic and links between nodes forming a path are likely to have a break at any time, our approach uses an alternate path for data transfer.
Our approach is compared to other recent studies that solve the same instance. The proposed approach achieves a better performance than the study performed by Pawan et al. [10], and the study performed by Choudhary et al. [12]. The fitness value of the Optimal path generated by our approach is 21,80700 while Pawan et al. [10] and Choudhary et al. [12] studies generated a path cost of 51.74633 and 36.23633 respectively. The outcomes show the effectiveness of the proposed approach to solve the problem of energy consumption.
Future studies will be conducted to implement our GA approach on a mobile ad hoc network having thousands of mobile nodes, and its performance can be checked. Also, future work may focus on comparing our approach to other metaheuristic algorithms like the firefly algorithm and Tabu search to check If they can equally minimize energy consumption effectively as GA achieved in this study.











 nueva página del texto (beta)
nueva página del texto (beta)