1 Introducción
El impacto social de las enfermedades crónicas en la población es uno de los temas de actualidad en la investigación científica a nivel mundial [1]. Son notables los esfuerzos realizados por los grupos de investigación, con evidente interés en minimizar los efectos negativos de este tipo de enfermedades. Como ejemplo prominente del tipo de esfuerzos que se realizan a nivel internacional, se puede mencionar el diagnóstico médico por medio de algoritmos inteligentes, cuyo auge es reconocido hoy en día. Para los profesionales que tratan temas de salud pública, es evidente que el diagnóstico temprano de una enfermedad crónica en un paciente aumenta sus posibilidades de supervivencia [2].
El diagnosticar una enfermedad en etapas tempranas, implica reducir el impacto negativo que tienen sobre la población, aumentando la calidad de vida de los pacientes al brindar el tratamiento adecuado, además de proporcionar información útil para el posible desarrollo de una cura [3]. En este sentido, son relevantes para el ser humano las enfermedades crónicas, las cuales se caracterizan por ser de progresión lenta y de larga duración. Según la Organización Mundial de la Salud, este tipo de enfermedades aparecen debido a factores ambientales; o bien, son de carácter hereditario. El cáncer, la diabetes y la hipertensión son ejemplos de algunas enfermedades crónicas comunes [4-7].
A fin de ejemplificar la gravedad de las afectaciones que produce la primera enfermedad mencionada, es preciso mencionar que, a nivel mundial, el cáncer de mama es el tipo de cáncer más común en las mujeres, y es un problema de salud grave en todo el mundo. En México, el cáncer de mama es la segunda causa de muerte en mujeres de 20 años en adelante. Además, cada nueve minutos se detecta un nuevo caso y existen más de 60,000 mujeres de 14 años y más con este padecimiento [8].
Respecto de la disciplina llamada cómputo inteligente (en inglés: computational intelligence), es conocido que fue introducida en 1994 por James Bezdek en un importante artículo, donde el autor enunció los fundamentos del cómputo inteligente, así como las diferencias de la nueva disciplina respecto de la inteligencia artificial [9].
Las técnicas de cómputo inteligente aplicadas a la medicina se han convertido en un área de investigación cada vez mayor en todo el mundo, y la aplicación y el desarrollo de nuevos modelos y algoritmos para el diagnóstico o la predicción de enfermedades es un tema de investigación activo. No obstante que, por lo regular, los algoritmos de cómputo inteligente son eficaces en el área médica, tienen puntos débiles que vale la pena enfrentar, entre los que sobresale el hecho de que algunos algoritmos se comportan como “cajas negras”, lo que hace imposible determinar qué instancias se clasificaron incorrectamente y por qué [11].
Los modelos enmarcados dentro del cómputo inteligente tienen diversas ideas conceptuales que forman la base de los algoritmos, en ambas fases: aprendizaje y clasificación. Entre los más famosos e importantes del estado del arte se pueden mencionar algunos notables: existen, entre otros, los clasificadores bayesianos, cuyo funcionamiento está basado, principalmente, en el Teorema de Bayes [12]; también son muy conocidos y eficaces los clasificadores kNN (k vecinos más cercanos, por sus siglas en inglés) [13]; por otro lado, los árboles de decisión (el algoritmo C4.5, por ejemplo) son modelos de clasificación muy utilizados por su sencillez y efectividad [14].
Adicionalmente, se han generado modelos que imitan a la naturaleza para clasificar patrones, entre los que destacan los basados en modelos matemáticos de las neuronas del cerebro humano, que son los clasificadores neuronales [15-17]; a este enfoque pertenecen los algoritmos de aprendizaje profundo (deep learning), cuyas aplicaciones exitosas son tan populares hoy en día [18]. Asimismo, la optimización de funciones analíticas sirve de base teórica en el diseño y funcionamiento de eficaces algoritmos de clasificación inteligente de patrones, llamados máquinas de soporte vectorial (SVM, por sus siglas en inglés) [19].
Una base conceptual del cómputo inteligente que es relevante para el presente trabajo de investigación es la que da soporte a un conjunto de modelos conocidos como asociativos. El primer modelo asociativo registrado en los anales de la literatura es la Lernmatrix, creada en 1961 por Karl Steinbuch [20]; y a partir de ahí se ha generado un número considerable de modelos asociativos que han dado lugar a aplicaciones relevantes en diversos ámbitos [21-34].
En el presente artículo se aplican al ámbito médico los algoritmos más importantes y eficaces de cómputo inteligente que ofrece la plataforma WEKA [35]; además, en la tarea del pre-diagnóstico de enfermedades se aplica por primera vez un algoritmo de reciente creación, denominado Lernamtrix tau[9], que es un algoritmo mejorado de la Lernmatrix original [20].
El resto del artículo está estructurado como sigue: en la sección 2 se presentan algunos trabajos del estado del arte relacionados con el diagnóstico médico, donde los autores proponen soluciones algorítmicas para este propósito. Por su parte, en las secciones 3 y 4 se describen, respectivamente, los bancos de datos de enfermedades y los algoritmos de cómputo inteligente que se utilizarán en la sección 5, donde se exponen los resultados experimentales de la presente investigación. Finalmente, en la sección 6 se incluyen las conclusiones y se bosquejan algunas ideas para trabajo futuro.
2 Trabajos relacionados
En la comunidad médica internacional se acepta que un diagnóstico temprano es necesario para atender la creciente carga de las enfermedades crónicas, dado que la mayoría se desarrollan rápidamente causando muertes y mermando la calidad de vida de las personas que las padecen. Para el pre-diagnóstico médico, se han propuesto varias soluciones algorítmicas en los últimos años, y en esta sección se mencionan de manera breve algunas de las más destacadas.
En [1], Fazekas abordó la periodicidad de la leucemia infantil en Hungría utilizando series de tiempo estacionales. El análisis de la estacionalidad de la leucemia linfoide infantil en Hungría se realizó tanto en el número total de pacientes como en las series de datos divididas. Los autores encontraron una cierta periodicidad en las fechas del diagnóstico en pacientes con leucemia. Aunque hubo alguna diferencia en los patrones de los picos de componentes estacionales de las tres series de tiempo, la mayoría de los picos cayeron dentro de los meses de invierno en las tres series de tiempo evaluadas. Esto fue más significativo en el grupo de todos los pacientes y en el grupo de edad más joven.
Dada la importancia de las enfermedades crónicas y el número de personas que las padecen, Abdar estudió la enfermedad hepática mediante el uso de métodos propios del área de la minería de datos [3]. El autor utilizó un nuevo árbol de decisión que permite identificar con mayor precisión enfermedades del hígado.
Chang y colaboradores desarrollaron un sistema web de apoyo de decisiones que considera principalmente el análisis de sensibilidad, así como las decisiones previas y posteriores óptimas y necesarias para el diagnóstico de algunas enfermedades crónicas, como la enfermedad granulomatosa crónica. Este sistema toma como base varios factores, entre ellos el Teorema de Bayes, para integrar las opiniones de los expertos y la información obtenida por el sistema, lo cual sirve como base al personal experto para tomar de decisiones de calidad en cuanto al diagnóstico médico [36].
En la investigación realizada por Vyas y sus colaboradores, los autores establecen que para entender una enfermedad es necesario comprender los mecanismos moleculares, tales como el número de interacciones proteína-proteína. Ellos enfocaron sus trabajos a una enfermedad crónica muy relevante: la diabetes mellitus; propusieron un modelo basado en SVM que permite clasificar las huellas estructurales y genómicas de esta enfermedad [37].
Para el cáncer de mama, Mungle propone un algoritmo de agrupamiento híbrido k-means para cuantificar el índice proliferativo de células de cáncer de mama basado en el conteo de núcleos Ki-67, por medio de imágenes RGB de cáncer de mama teñido con K-67, obteniendo un buen desempeño en el modelo propuesto [38].
En un estudio realizado por Golub, se propone el uso de expresiones genéticas de microarreglos de DNA, para llevar a cabo la clasificación de cáncer en leucemias agudas. Utilizando un clasificador automático de reconocimiento de patrones, se lograron identificar nuevos tipos de cáncer de leucemia [39].
Para las enfermedades crónicas del riñon, Polat menciona que la precisión de los algoritmos de clasificación depende del uso de algoritmos de selección de características correctos para reducir la dimensión de los conjuntos de datos. por lo que en su propuesta utilizó un algoritmo de SVM para el diagnóstico, además de métodos de reducción de la dimensionalidad [40].
En su investigación para la detección de cáncer de mama por medio de imágenes, Padmavathy propone un sistema de inferencia adaptativo neurodifuso (ANFIS) para clasificar imágenes, y logró una exactitud cercana al 98% en la clasificación [41].
En el mismo tenor, Guidi propone realizar la detección de cáncer de próstata por medio de imágenes; para ello, identifica automáticamente a los pacientes que pueden beneficiarse de un tratamiento adaptativo, comparando los tratamientos de radioterapia administrada contra la planificada. La herramienta desarrollada pudo clasificar a los pacientes con diferentes niveles generales de variaciones morfológicas y predecir posibles problemas causados por diferencias relevantes entre la dosis planificada y la administrada [42].
En un artículo publicado recientemente, Gózalez-Patiño propone aplicar metaheurísticas a la segmentación de imágenes mamográficas, para la detección oportuna de cáncer de mama. Los resultados mostraron una menor tasa de error al utilizar estas metaheurísticas para la segmentación, en comparación con métodos clásicos como el de Otsu [43].
3 Bancos de datos de enfermedades
En esta sección se presentan breves resúmenes de los bancos de datos de enfermedades, los cuales fueron seleccionados para realizar los experimentos de esta investigación.
Los bancos de datos que aquí se presentan se tomaron del repositorio de datos KEEL [44] y del Repositorio de la Universidad de California en Irvine (UCI) [45]. Son bancos de datos de las enfermedades crónicas más comunes, como cáncer de mama, enfermedades de la tiroides y enfermedades cardíacas.
Wisconsin: este banco de datos fue donado al repositorio UCI por el Dr. WIlliam H. Wolberg del Hospital de la Universidad de Wisconsin. Este banco de datos contiene información de casos clínicos de pacientes con cáncer de mama que se sometieron a cirugía; consta de 9 atributos numéricos, y un total de 683 patrones distribuidos en dos clases: tumores benignos y tumores malignos.
El banco de datos New Thyroid fue donado al repositorio UCI por Stefan Aberhard de la Universidad James Cook, en Australia. Este banco de datos contiene información de pacientes que padecen de la tiroides; consta de 5 atributos numéricos y un total de 215 patrones. Las tres clases de la función tiroidea son: normal, hipertiroidismo e hipotiroidismo. Tomando como base el banco de datos New Thyroid, KEEL generó 2 bancos de datos de dos clases:
New-thyroid1: las dos clases son hipertiroidismo y el resto de los 215 patrones.
New-thyroid2: las dos clases son hipotiroidismo y el resto de los 215 patrones.
Haberman: este banco de datos contiene casos de un estudio realizado entre 1958 y 1970 en el Hospital Billings de la Universidad de Chicago sobre la supervivencia de pacientes que se habían sometido a cirugía por cáncer de mama; consta de 3 atributos numéricos, y un total de 306 patrones distribuidos en dos clases: el paciente sobrevivió 5 años o más (clase 1), o el paciente murió dentro de 5 años (clase 2).
Spectfheart: este banco de datos describe el diagnóstico de imágenes de tomografía computarizada SPECT, con el propósito de detectar anomalías cardiacas; consta de 44 atributos numéricos, y un total de 267 patrones distribuidos en dos clases: normal o anormal.
En la Tabla 1 se resumen las características de los cinco bancos de datos descritos previamente. En cada caso, se especifica el nombre del banco de datos, el número de atributos de que está formado cada patrón, el número de patrones que contiene el banco de datos y, finalmente, el número de clases en que se distribuyen todos los patrones de ese banco de datos.
4 Algoritmos de cómputo inteligente
En esta sección se dará una explicación breve de los algoritmos que fueron utilizados en la fase experimental para la clasificación de patrones, en cada uno de los bancos de datos descritos previamente en la sección 3.
En total se han seleccionado diez algoritmos de cómputo inteligente, entre los que se consideran los mejores en el estado del arte para realizar la tarea de clasificación de patrones.
En la subsección 4.1 se describen brevemente nueve algoritmos, los mejores de los diferentes enfoques, que se han seleccionado de entre todos los que ofrece la plataforma WEKA [35].
Se ha seleccionado un décimo algoritmo, el cual se describe en la subsección 4.2 y es de reciente aparición en la literatura científica. Se trata del clasificador denominado Lernmatrix tau[9], el cual y pertenece al enfoque asociativo de clasificación de patrones [21, 46] y es un caso particular del nuevo paradigma minimalist machine learning [47].
4.1 Algoritmos de la plataforma WEKA
A continuación, se describen brevemente los nueve algoritmos clasificadores de patrones que se han seleccionado en la plataforma WEKA [35]:
NaiveBayes: este clasificador pertenece al enfoque probabilístico. Para su operación, utiliza el Teorema de Bayes de una forma ingenua (Naïve), porque considera a todos los atributos independientes desde el punto de vista probabilístico, contrario a lo que ocurre normalmente en el mundo real [12].
SMO: este algoritmo pertenece a las máquinas de soporte vectorial (SVM), las cuales son un conjunto de métodos para clasificación de patrones, para cuyo funcionamiento utilizan la optimización de funciones y los llamados vectores de soporte. Este tipo de algoritmos tratan de encontrar un hiperplano que separe de la mejor manera a las clases; y si no se logra, se utiliza el truco del kernel para transformar los patrones a un espacio de dimensión mayor a la original. Un kernel puede ser una función lineal, polinomial, de base radial o sigmoide [19].
Logistic: este algoritmo es la regresión logística, la cual es una técnica estadística de aprendizaje automático. Toma como entradas valores reales y hace una predicción sobre la probabilidad de que la entrada pertenezca a una clase determinada. Esta probabilidad es calculada con base en una función sigmoidea, cuya expresión involucra a la función exponencial [48].
MultilayerPerceptron: el MLP es una red neuronal artificial formada por múltiples capas (layers), con cuyo diseño se intenta resolver problemas de clasificación con clases que no son linealmente separables. El MLP es considerado por la comunidad científica como un excelente clasificador de patrones; junto con las SVM es el “enemigo a vencer” en todos los estudios comparativos. El MLP está formado principalmente por tres capas: la capa de entrada, la capa oculta y la capa de salida: En esta última capa se encuentran las neuronas cuyos valores de salida corresponden a la etiqueta de clase [15-17].
J48: este tipo de algoritmos de clasificación (los árboles de decisión) son de los más usados en tareas de clasificación de patrones. J48 es el nombre que se da en WEKA a un tipo de árbol de decisión derivado del antiguo ID3. Los árboles de decisión son apreciados porque son explicables, están basados en la teoría de grafos y permiten ver de forma estructurada cómo se clasifican las instancias de un conjunto de datos. La estructura contiene un nodo raíz en la parte superior del árbol, y los nodos intermedios llamados hojas que corresponden a los atributos. En la parte inferior del árbol se visualizan las clases [14].
RandomTree: es un algoritmo de clasificación de patrones que consiste en la construcción de un árbol de decisión de manera aleatoria [49].
RandomForest: este clasificador consiste en un bosque aleatorio; es una combinación de árboles de decisión. Se generan múltiples árboles de manera aleatoria, y cada árbol de decisión emite un voto unitario para la clase más popular, y de esa manera es posible clasificar un patrón de entrada [50].
IB1: este algoritmo es la versión que ofrece WEKA del clasificador 1-NN, el cual asigna a un patrón de prueba la clase a la que pertenece su vecino más cercano (nearest neighbor). El acrónimo IB proviene del inglés “Instance Based” [51].
IB3: este algoritmo es la versión que ofrece WEKA del clasificador 3-NN, el cual asigna a un patrón de prueba la clase que resulta por votación en los tres vecinos más cercanos.
4.2 El nuevo algoritmo Lernmatrix tau, [9]
El clasificador de patrones Lernmatrix tau [9] es un algoritmo de cómputo inteligente que pertenece al enfoque asociativo de clasificación de patrones [21].
El algoritmo Lernmatrix tau[ 9] fue publicado recientemente [46]. Se deriva directamente del primer modelo asociativo, la Lernmatrix [20], y es un caso particular del nuevo paradigma minimalist machine learning [47].
De acuerdo con [20], en la fase de
aprendizaje de la Lernmatrix original, a cada patrón de entrada binario
Sin en problema hay p clases, para iniciar la fase de aprendizaje se crea una matriz M llena de valores cero con p filas y n columnas, y para cada pareja del conjunto de aprendizaje la matriz M actualiza sus valores de entrada de acuerdo con la siguiente regla de Steinbuch:
Si
Para ello, se opera la matriz M con el patrón
Este proceso se expresa así:
Se esperaría que el algoritmo descrito arrojara la clase correcta para cada patrón de prueba. Sin embargo, este es el caso ideal, porque en la realidad la Lernmatrix sufre de un problema llamado saturación, que evita la recuperación correcta de los patrones one-hot de salida en porcentajes que hacen que la Lernmatrix sea un clasificador no competitivo con los clasificadores del estado del arte.
El nuevo algoritmo Lernmatrix tau [9] mejora de manera notable los resultados de la Lernmatrix original, en la tarea de clasificación de patrones. Además de las expresiones originales (1) y (2), la Lernmatrix tau [9] usa el código Johnson-Möbius y una nueva transformada original, a la que los autores llamaron tau[9].
El código Johnson-Möbius convierte un arreglo de números reales en un conjunto de cadenas binarias con una estructura muy simple. Primeramente, se fija un número de decimales y, si se requiere, se truncan los números reales para que queden representados con ese número fijo de decimales; luego, mediante restas y escalamientos adecuados, se convierten todos los números del arreglo en enteros no negativos.
Como ejemplo ilustrativo, apliquemos el código Johnson-Möbius a este arreglo de 5 números reales: 1.7, -0.1, 1.9, 0.2 y 0.6. Al restar -0.1 y escalar por 10, el arreglo se transforma en 5 enteros no negativos: 18, 0, 20, 3 y 7. Finalmente, para formar la cadena binaria se considera el número máximo del arreglo (en este ejemplo ese máximo es 20) y se representa con unos (en este caso, 20 unos).
En este ejemplo el cero se representa con 18 ceros, y los demás se representan con tantos unos como indique su valor, antecedidos de una cadena de ceros hasta completar 20 dígitos binarios. El arreglo convertido se presenta en la Tabla 2.
Tabla 2 Johnson-Möbius
| 1.7 | 00111111111111111111 |
| -0.1 | 00000000000000000000 |
| 1.9 | 11111111111111111111 |
| 0.2 | 00000000000000000111 |
| 0.6 | 00000000000001111111 |
La piedra angular del nuevo algoritmo Lernmatrix tau [9] es la transformada tau[9], la cual convierte un dígito binario en una dupla de dígitos binarios, de acuerdo con lo siguiente:
La aparente simplicidad de la transformada tau [9] es lo que permite mejorar de manera notable el rendimiento de la Lernmatrix, hasta convertir el nuevo algoritmo en un clasificador competitivo en el estado del arte.
Fase de aprendizaje de la Lernmatrix tau, [9]:
Aplicar el código Johnson-Möbius a todos los patrones de entrada.
Aplicar la transformada tau [9] a todas las componentes de los patrones de entrada transformados en el paso 1.
Asociar con cada patrón de entrada transformado en el paso 2 un patrón de salida one-hot.
Realizar la fase de aprendizaje de la Lernmatrix de acuerdo con (1) para obtener la matriz M.
Fase de recuperación de la Lernmatrix tau, [9]:
5 Resultados experimentales
Es esta sección se describen los experimentos realizados, los resultados obtenidos, así como los métodos de validación y las medidas empleadas para la comparación del desempeño de los algoritmos en la clasificación de los bancos de datos de enfermedades, los cuales fueron seleccionados previamente.
Los experimentos con los nueve algoritmos descritos en la subsección 4.1, se realizaron en la plataforma WEKA, mientras que el nuevo algoritmo Lernmatrix tau [9], descrito en la subsección 4.2, se programó en lenguaje Python.
Todos los experimentos se realizaron en una computadora personal con sistema operativo Windows 10, con un procesador Intel (R) Core (TM) i5-7300HQ CPU a 2.4 GHz y RAM de 8 GB.
5.1 Método de validación
Por la naturaleza de los experimentos, la presente investigación está inmersa en el paradigma supervisado del cómputo inteligente. Esto significa que en cada experimento es preciso definir un conjunto de aprendizaje y un conjunto de prueba, a partir de los bancos de datos; y ambos conjuntos deben formar una partición.
En la literatura especializada existen varias maneras de crear estas particiones. Son los métodos de validación, entre los que sobresalen boostrap, hold-out, leave-one-out y el método más utilizado: k-cross-fold-validation [44].
Cuando se aplica k-cross-fold-validation, el valor más popular de k es 10. Sin embargo, dado que algunos de los bancos de datos que se usan en los experimentos son desbalanceados, se recomienda 5 para el valor de k; es decir, se recomienda el uso de 5-cross-fold-validation como método de validación [52].
5.2 Medida de desempeño
En los bancos de datos de enfermedades, es común que los patrones se agrupen en dos clases. Por ejemplo, en el banco de datos Wisconsin que se describió en la sección 3, los 683 patrones se distribuyen en dos clases: tumores benignos y tumores malignos.
En la jerga médica, cuando alguien padece una enfermedad, se dice que esa persona dio positivo a esa enfermedad; y una persona que no sufre esa enfermedad es un caso negativo. Bajo esta nomenclatura, en el caso del banco de datos Wisconsin, los tumores malignos corresponden a los patrones de la clase de los positivos, mientras que los tumores benignos corresponden a los patrones de la clase de los negativos.
En general, en un banco de datos de enfermedades, a una clase se le llama POSITIVO, y a la otra, NEGATIVO.
Al aplicar un clasificador a un banco de enfermedades con dos clases, el resultado de presentar al clasificador un patrón de prueba tiene cuatro posibilidades:
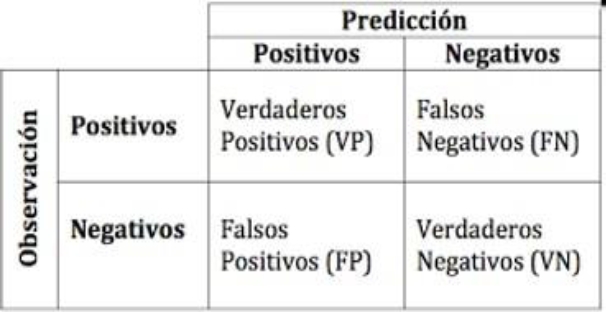
El patrón de prueba es positivo y el resultado que da el clasificador es positivo. Se trata de un VERDADERO POSITIVO (VP).
El patrón de prueba es positivo y el resultado que da el clasificador es negativo. Se trata de un FALSO NEGATIVO (FN).
El patrón de prueba es negativo y el resultado que da el clasificador es positivo. Se trata de un FALSO POSITIVO (FP).
El patrón de prueba es negativo y el resultado que da el clasificador es negativo. Se trata de un VERDADERO NEGATIVO (VN).
Después de aplicar el clasificador a todos patrones de prueba en un experimento dado, los resultados finales se pueden representar en un arreglo llamado matriz de confusión, como se muestra en la Figura 1.
Obsérvese que VP y VN corresponden a los casos donde el clasificador acertó.
Por otro lado, FP y FN corresponden a los casos donde el clasificador cometió errores. Lo ideal, evidentemente, es que estos dos valores estén muy cercanos a cero (o que sean cero).
De la matriz de confusión se derivan dos medidas de desempeño que, a su vez, permiten definir la medida de desempeño que usamos en los experimentos de esta investigación, porque es apropiada para bancos de datos desbalanceados.
La primera medida se llama SENSIBILIDAD, y se define como la fracción de la cantidad de patrones que el algoritmo clasificó como positivos, entre el total de los positivos en el banco de datos; es decir:
La segunda medida es la ESPECIFICIDAD, y se define como la fracción de la cantidad de patrones que el algoritmo clasificó como negativos, entre el total de los negativos en el banco de datos; es decir:
A partir de las (4) y (5) se define una medida de desempeño llamada Exactitud Balanceada (BA por las siglas en inglés de Balanced Accuracy), la cual es apropiada para bancos de datos desbalanceados, porque no tiene la desventaja de la exactitud simple, cuyo valor tiende a sesgarse hacia la clase mayoritaria:
El mayor valor posible es 1, cuando no hay errores de clasificación; es decir cuando FP y FN tienen ambos valor cero (lo cual es muy raro).
Un valor de 0.50 para BA equivale a tirar un volado. Se espera que en un experimento normal, el resultado que arroje BA esté por encima de 0.50, cercano a 1 de preferencia.
Dependiendo del banco de datos, valores de BA arriba de 0.90 son excelentes, mientras que valores entre 0.80 y 0.90 son buenos. Los valores entre 0.60 y 0.80 son regulares, y los valores de BA debajo de 0.60, cercanos a 0.50 son realmente malos.
5.3 Resultados y discusión
En esta sección se presentan los resultados de los experimentos, usando el método de validación 5-fold-cross-validation y BA como medida del desempeño de los 10 clasificadores.
En la Tabla 3 se presentan los resultados encontrados al aplicar los 10 algoritmos de clasificación descritos en la sección 4, a los 5 bancos de datos descritos en la sección 3.
Todos los resultados representan el valor de BA con dos decimales.
Tabla 3 Resultados
| Algoritmos | Bancos de datos | ||||
| wsc | nwt1 | nwt2 | hbrm | spec | |
| NB | 0.96 | 0.98 | 0.98 | 0.57 | 0.77 |
| SVM | 0.97 | 0.77 | 0.75 | 0.50 | 0.50 |
| LR | 0.96 | 0.96 | 0.96 | 0.54 | 0.62 |
| MLP | 0.95 | 0.95 | 0.95 | 0.58 | 0.66 |
| J48 | 0.94 | 0.94 | 0.94 | 0.57 | 0.60 |
| RT | 0.92 | 0.98 | 0.91 | 0.58 | 0.65 |
| RF | 0.96 | 0.95 | 0.92 | 0.55 | 0.60 |
| IB1 | 0.94 | 0.97 | 0.98 | 0.64 | 0.59 |
| IB3 | 0.96 | 0.96 | 0.92 | 0.55 | 0.58 |
| LM-τ[9] | 0.96 | 0.99 | 0.99 | 0.52 | 0.62 |
En la Tabla 3 se han marcado con negrilla los mejores valores para cada uno de los bancos de datos. Se puede observar que sólo 4 de los 10 algoritmos de clasificación de patrones quedaron al menos una vez en primer lugar: NB en el banco de datos spec, SVM en el banco de datos wsc, IB1 en el banco de datos hbrm; y con el algoritmo LM-τ[9] ocurre algo interesante, porque este algoritmo queda en primer lugar, no en uno, sino en dos bancos de datos: nwt1 y nwt2.
Pero hay más: en el banco de datos wsc, a pesar de que LM-τ[9] no quedó en primero, pero sí quedó en segundo lugar; es decir, sigue siendo muy competitivo. Y en el banco de datos spec, LM-τ[9] no quedó entre los últimos, sino en cuarto lugar.
En el banco de datos hbrm LM-τ[9] queda en penúltimo lugar, quedando por arriba sólo de SVM (uno de los “enemigos a vencer” en general). Esto ocurre con la medida de desempeño BA; sin embargo, veamos qué ocurre cuando sólo tomamos en cuenta los enfermos, es decir los casos positivos.
Normalmente, a los médicos les interesa saber qué tan bien se detectan los casos positivos, y para ello se usa la SENSIBILIDAD. Sorpresivamente, si tomamos en cuenta esta medida de desempeño, en el banco de datos hbrm LM-τ [9] queda en tercer lugar (no en penúltimo) con un valor de 0.31, quedando por encima solamente IB1 (0.43) y RF (0.40).
6 Conclusiones y trabajo futuro
En el presente artículo se han presentado los resultados de aplicar 9 algoritmos de cómputo inteligente en la clasificación de bancos de datos de enfermedades.
Aprovechando la plataforma WEKA y el contenido de los repositorios KEEL y UCI, se realiza un estudio experimental para estudiar el desempeño que exhiben esos clasificadores de patrones al ser aplicados en el pre-diagnóstico de algunas enfermedades crónicas de importancia en el contexto de la salud de los seres humanos.
Además de los 9 clasificados elegidos entre los mejores del estado del arte, se aplica por primera vez un algoritmo de reciente aparición en la literatura científica: se trata del clasificador de patrones Lernmatrix tau [9], que es un algoritmo de cómputo inteligente perteneciente al enfoque asociativo de clasificación de patrones.
En la parte experimental del presente artículo se aplicaron estos algoritmos de cómputo inteligente en bancos de datos de cáncer de mama, hipertiroidismo e hipotiroidismo. Los resultados que se derivaron de los experimentos muestran la superioridad del desempeño de las máquinas de soporte vectorial, del algoritmo IB1 y, de manera notable, del nuevo algoritmo Lernmatrix tau [9].
Los desempeños alcanzados permiten confirmar, con un alto grado de certeza, la utilidad de los modelos de cómputo inteligente en el pre-diagnóstico de enfermedades crónicas.
Como trabajo futuro, se plantea aplicar los 10 algoritmos clasificadores de patrones del presente artículo en otros bancos de datos de enfermedades de diferente naturaleza, así como en bancos de datos de otros ámbitos de la actividad humana.
SE plantea también, en trabajo futuro, comparar los desempeños aquí descritos contra los desempeños de modelos que han alcanzado renombre recientemente, como los algoritmos de deep learning.











 nueva página del texto (beta)
nueva página del texto (beta)