1 Introduction
Plant are one of the important living forms exist on earth, the number of plants estimated to be around is 350,000 - 400,000 species [1]. Plants play a major role in various areas, such as food, medical science, industry, and the environment. However, many species of plants are endangered because of environmental pollution, plus the consumption of the plants in our daily life. Therefore, it is very important to study plant identification for plant protection and determine the useful and dangerous plants [2, 3].
Plant identification is studying and classifying an unknown plant into one of the groups of pre-known classes and species. Plant identification is currently one of the most actively researched areas of computer vision, image processing and analysis [4]. Plants can be identified according to the shapes, colors, textures and structures of their leaf, bark, flower, seedling, and morph.
Nevertheless, if the plant classification is based on only two-dimensional images, it is very difficult to study the shapes of flowers, seedling, and morph of plants because of their complex three-dimensional structures. Plant leaves are two dimensional in nature and hold important features that can be useful for identification of various plant species [5]. Since leaves are the organ of plants and their shapes vary between different species, the leaf shape provides valuable information for plant identification [3].
To implement the identification system, several features were extracted that combined shape, color, texture, and vein features. Then, all those features were processed by using Principal Component Analysis (PCA) to obtain orthogonal features. Several approaches have been introduced to classify a leaf [6], such as K-Nearest Neighbor Classifier (K-NN), Probabilistic Neural Network (PNNs), Genetic Algorithm (GA), Support Vector Machine (SVM) [7, 8, 9]. A PNNs is an implementation of a statistical algorithm called kernel discriminated analysis in which the operations are organized into a multilayered feed forward network with four layers [10].
The main contribution of this work is to find a quick and reliable method that will help in identifying the species of plants, using image of leaves and for this project PNNs has been used because this technique can be considered fast when executing the program, also the training time for the network is very short. Finally, when using a given smooth factor; the same results are always guaranteed for training the network when used the same data, the last reason mentioned above makes this technique suitable for studying effect feature in the system and comparing it with another features.
The rest of the paper is organized as follows. Section 2 presents related work of the study. Section 3 describes the proposed method. In Section 4, experimental results are discussed in detail. Section 5 concludes the study.
2 Related Work
In 2011 in [18], the authors identified plants depending on the shape, color, veins and texture of leaf as major parameters, these parameters used in PNNs gave high accuracy, up to 93.75%, especially when applied on Flavia dataset. The dataset included 32 kinds of leaves to be identified.
According to the results, the accuracy has been improved from the original work [9], i.e., from 90.31% to 93.75%. In 2011, Muhammad et al. [11] described a method applied on the oil palm trees to identify the disease on the leaves and other parts of the plants using the fuzzy classifier approach. In this method a digital image of the oil palm leaf was taken, analyzed and produced an algorithm depending on the shape, texture and color of the leaf that infected by a disease or pest outbreak. In 2011, Jyotismita and Ranjan [12] proposed an automatic systems or intelligent systems used for recognizing plant types and species, depending on the image of leaf, this study showed two methods; The first one was based on Moment-Invariant (M-I) model and the second one was the Centroid-Radii (C-R) model. The Neural Network (NN) was used as a main classifier for database of 180 images divided into three groups of 60 images each, resulted in accuracy, ranges from 90%-100%.
In 2012, Kadir et al. [13] presented method that deals with ZM & other morphological and geometrical features, color moments and Grey-Level Co-occurrence Matrix (GLCM). In order to implement the identification system, two principals have been used; first approach used a distances measure (Euclidean distance the accuracy was 94.69% and City block distance, in which accuracy reaches 93.75%) and the second is using the PNNs of 93.44% accuracy when used Flavia dataset. Results showed that the ZM has a positive influence as an effective feature in identification process when combined with other features.
In 2012, Kadir et al. [7] demonstrated that plants can be recognized depending on their leaf shape, vein, color and texture, using PCA, technique for various multi features of leaf. The PCA was used to convert the features above into orthogonal feature that can be handled within PNNs, in order to identify them by the last one. This system tested on two datasets, Foliage (contain various color leaves), and Flavia (contain green leaves). The results were improved by using the PCA rather than PNNs alone. The quality of the result raised up from 93.43% without PCA to 95.75% with PCA, and by using 25 features instead of 54 features.
In 2013, Kue-Bum and Kwang-Seok [1] illustrated that leaf vein and shape can be utilized for plant classification, the principle used in this research relied on the major veins and frequent domain data, using Fast Fourier Transform (FFT) method in addition to the distance between the contours and the central axis of the leaf. From 32 plants, 1,907 leaves were collected and 21 features of a leaf have been used in this method. Results of the proposed leaf recognition system showed that the average recognition rate was 97.19%.
In 2013, Bin et al. [3] introduced a mobile plant leaf identification system using smart phone. The main idea of this study relied on three characteristics of shape contour, the convexity and the concavity features for leaf plant identification.
A new application has been implemented to create multi-scale shape descriptor. The speed of the recognition process has been improved up to 170 times faster than any other proposed approaches. This online application is to identify plant leaves using smart phones and server platform.
3 Proposed Method
The main contribution of this work is building model leaf plant identification system integrates a number of processes: specimen collection and image preparation, feature extraction, creating dataset of victor feature for all samples, normalization data, transformed feature using PCA, classifier system PNN and leaf identification results.
The flow diagram of the work is illustrated in Figure 1.
3.1 Image Acquisition
A corpus of 2839 leaves were collected from 24 different plant species. The range number of leaves for each species were between 75 and 163, which have been collected from different trees and shrubs from the mountains of Kurdistan region of Iraq. The process of choosing the samples collection of leaves was performed under certain limitations.
In addition, the selected leaves have to be cleaned and undamaged, green in color and to be terminal (in case of compound leaves). Finally, all leaves were collected from the middle region of the bough of trees or shrubs.
Canon scanner LIDE 110 has been used for image acquisition. In image acquisition, the following is required: placing the upper surface of the leaf on the scanning surface in a longitude orientation and the leafstalk at the bottom, as shown in Figure 2, set the scanner to resolution (400 dpi), document type color photo, and set a white paper as the background of the leaf.
This simple background enables to see the leaf easily, scan and save it in (.jpg) format. The saved sample will be used later in the approach system. In naming the samples, by use five digits (00000) method where the first two digits refer to a species name and last digits refer to a sample numbers, e.g. (01050) means the leaf type is one and sample number fifty.
3.2 Image Pre-processing
After leaf image acquisition is obtained, feature extraction is needed as a preprocessing, to improve image data and preparing the image for the next step.
This pre-processing contains some operations on the image samples; gray scale conversion, image segmentation binary conversion and image smoothing.
3.2.1 Grey-Scale Image Segmentation
The first and more important step in identification and recognition system is the object segment from the background. This work was performed in several steps; first converted the image from RGB image to gray-scale image by keeping only the luminance values from the red, green, or blue Using Formula 1. Monochrome color is also known as grayscale, which have only a range of colors between white and black.
Therefore, a grayscale image contains only shades of gray and no true color. Grayscale images can be saved digitally and been expressed as luminance. The luminance can also be described as brightness or intensity, which can be measured on a scale from black (zero intensity) to white (full intensity). Most image file formats support a minimum of 8-bit grayscale, which provides 28 or 256 levels of luminance per pixel. Some formats support 16-bit grayscale, which provides 216 or 65,536 levels of luminance:
Spatial filtering applied to reduce the noise, which may happen in the leaf samples by external factors. e.g., environmental effect, sample collection or scanning operation. Mean filtering is also refers to Average Filtering, where the output pixel value is the mean of its neighborhood, the filtering mask is as follows (3x3 as an example). In practical, the size of the mask controls the degree of smoothing and loss of the details, Figure 3 shows filtering example.
Selecting threshold is very important manner as is used in the segmentation method. If the selected threshold was bigger than usual; then a lot of pixels from background will be set as object set and vice versa. Otsu selection method been used to handle global threshold by implying Matlab function (level = graythresh (gray-scale image)), since this function depends on Otsu selection method. The results are between [0,1] then multiplying this value with maximum gray level in the gray-scale image.
The results of the global threshold will be used to separate pixels of the object from the pixels of the background. Selected threshold and converted gray-scale image to binary image. In this logical image, each pixel has value of one or zero, the first one appears white color which represents the object and second appear black color which represents the image background or vice versa.
3.2.2 Filling Regions and Set Background to White
After segmentation, it is very common to have some small regions, which do not belong to the object of interest due to noise. Matlab function depends on the filling regions based on set dilations, complementation, and intersection.
Using (B1 = bwareaopen(B, P)) function removes from a binary image all connected components (objects) that have fewer than P pixels and producing another binary image B1. This operation is known as an area opening. This function is repeated twice, first on the result of segmentation and second on the invert result from the first one.
The background of the scanned leaves images is not similar, so to reduce the effect of variety color background; all pixels of background have to be set to white pixels. The final result B1 will be used as an index for selecting the pixels from gray-scale image or RGB. Figure 4 shows the results for region fill and set background gray-scale image or RGB to white.

Fig. 4 Region Fill and Set Background Gray-scale Image to White: (a) binary images after segmentation named B, (b) binary image after fill region named B1, (c) binary image after fill region ~B1named B2, (d) original RGB image of leaf, (e) gray-scale image, and (f) gray scale image after set all background pixel white
3.2.3 Cropping the Image
There are three main reasons for cropping or cutting the image; first to reduce the size of the image without changing the size of the leaf in the image, second to find the maximum length and width for the leaf in the image, third reason to make the leaf object in the middle. Figure 5 presents examples of cropping an image.
3.3 Feature Extraction
Feature extraction method extracting new features from original dataset, and it is very beneficial when we want to decrease the number of resources required for processing without missing relevant feature dataset [14, 15]. Feature extraction is another important phase in this work. It has been declared in detail in the following sub-sections such as extracting some features from shapes (28 features), color (12 features) and texture (5 features).
More so, 3 features have been added from vein of the leaf. All the features created a feature vector for each sample and all these feature vectors were stored in an array of features; where, each row represented the feature vector for one sample while, number of columns represented the number of feature extraction of the sample, which will be used in the classification system for training and testing.
3.3.1 Shape Feature
The shape features used to describe the global feature of leaf. Some of shape feature in this work were calculated including area, perimeter, convex area and convex perimeter, which is considered to be as global shape features. This can be done by using mathematical morphology, logic operation between binary images and morphological operation.
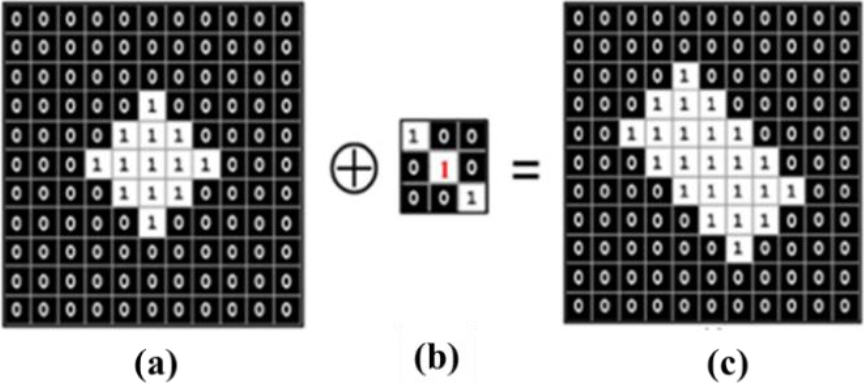
Dilation is the increase in the thickness or the growing of an object in the binary image. The shape referred by Structure Element (SE) is controlling the increasing in thickness of the object. The dilation of A by B, denoted 𝐴 ⊕ 𝐵, is defined as:
Considering the SE as a mask. The reference point of the structure element is placed on all those pixels in the image that have value 1.
All of the image pixels that correspond to black pixels in the structure element are given the value 1 in A ⊕ B. Then placing the elements of B into the output image. Figure 6 illustrates how dilation works: (a) refers to original binary image with a diamond object, (b) indicates SE with three pixels arranged in a diagonal line at angle of 135ᵒ, the origin of the SE is clearly identified by a red1 and (c) contains dilated image, 1 at each location of the origin such that the SE overlaps at least 1-valued pixel in the input image (a).
However, erosion means decreasing the thickness of objects in a binary image. The of A by B, denoted 𝐴 ⊖ 𝐵, is defined as:
In other words, erosion of A by B is the set of all SE origin location where the translated B has no overlap with the background of A. the output image 𝐴 ⊖ 𝐵 is set to zero. B is place at every black point in A. If A contains B (that is, if A AND B is nor equal zero) then B is placed in the output image. The output image is the set of all elements for which B translated to every pint in A is contained in A. Figure 7 illustrates how erosion works: (a) Original binary image with a diamond object, (b) SE with three pixels arranged in a diagonal line at angle of 135ᵒ, the origin of the SE is clearly identified by the red 1 and (c) Eroded image, a value of 1 at each location of the origin of the SE, such that the element overlaps only 1-valued pixel of the input image.
Using the two main operations in combine, dilation and erosion, can produce more complex sequences. Figure 8 shows an example of the effect of opening and closing processes by use (Disk SE with the radius 3), on the leaf sample. Using both operations together is more useful for morphological filtering. An opening operation is defined as erosion followed by a dilation using the same SE for both operations. The basic two inputs for opening operator are an image to be opened, and a structuring element. Using the structure elements B to do the open operation on the set A, expressed as 𝐴 ∘ 𝐵, definite as:

Fig. 8 calculate area, parameter for both leaf binary image convex hull leaf image: (a) Binary image, (b) Extract boundary of leaf from binary used morphological operation, (c) Convex hull leaf image from binary leaf image, and (d) Extract boundary of convex hull leaf from (c) used morphological operation
Closing is opening performed in reverse. The main inputs of the closing operator are an image to be closed and a structuring element. Use B to erode A plainly first, then on the results obtained, use B to dilate operation. In addition, using B to do closing on A, expressed as 𝐴 ∙ 𝐵, definite as:
After that area, perimeter, convex area and convex perimeter features were extracted.
The 24 features were extracted from C-R where each feature is the radii length between the point in boundary and centered. Calculating area from binary image of leaf, perimeter from boundary image, convex area from convex hull image of leaf, convex perimeter from convex boundary image, as it is shown in Figure 9.
The C-R method is used in this work to extract 24 features. As its illustrated in Figure 10, the boundary leaf image and its centroid are used. The centroid was computed from the average boundary pixels. After that, the degree of angle for each point in the leaf boundary is computed using the Matlab function (th = atand (x-xc/y-yc)), where x and y are any axis boundary points and xc and yc are axis points for centroid leaf. After that the radii for specific angle was computed. In this work, the radii for angles (zero,15, 30, ..., 345) in the anticlockwise was computed where the enter value between angles is 15ᵒ.
3.3.2 Color Features (Color Moments)
Color moments represent color features, to characterize a color image; features can be extracted from color information on the leaf by using statistical calculation such as mean (µ), standard deviation (σ), kurtosis (γ) and skewness (θ), which are called color moments. In this work, those moments were applied to each component in RGB color space, where four features are calculated from each channel.
Moment 1. It is called Mean. It provides average color value in the image:
where MN represents the total number of pixels in the image.
Moment 2. It is called Standard Deviation. The stander deviation is the square root of the variance of the distribution:
Moment 3. It is called Skewness. It gives measure of the degree of asymmetry in the distribution:
Moment 4. It is called Kurtosis. It gives the measure of peakedness or flatness in the distribution:
3.3.3 Texture Features
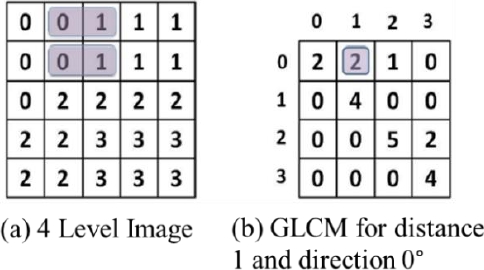
Texture is one of the most used characteristics of the leaf plant image. The gray-scale image is often used in texture image analysis. A gray image can be used to describe the spatial distribution of light intensity. The total intensity has limited value; it is spread over the image so that bright areas have high energy density, and the dark areas have low energy density. GLCM is usually used to capture texture features. Figure 11 below represents the formation of the GLCM of the grey-level (4 levels) images at the distance d = 1 and the direction of 0°.
In this work, GLCM is used to capture texture information in the leaf. Five features were derived from GLCM (Energy, Contrast, Inverse Difference Moments IDM, Entropy and Correlation). Since the distance value between two pixels is one and the direction (angle) is: 0, 45, 90, 135 degrees, for four GLCMs, then five features were obtained by averaging them.
3.3.4 Vein Features Extraction
Vein Features consider a kind of problem in image segmentation process. As leaf vein is so thin that many noises will be introduced into the segmentation result when the region-based method is applied. The region-based method can be used to achieve a good segmentation result.
The key point of the region-based method is how to select the right threshold. In this case, the region-based method is not applicable only if a morphological operation been held for the image, because the color difference is local between the leaf vein and its background in the image. Vein features will be extracted by means of morphological operations done on the gray scale image of the leaf. To do that first extract vein area from leaf and extract leaf area from the same leaf. In this work, three features were extracted from veins.
The first two features extracted by using Equation 10. The third feature computed by the summation of vein area used in feature one and vein area used in feature two. Figure 12 shows an example to extract the three features from leaf veins:
3.4 Data Normalization
Transforming a clean raw of data into specific range using many techniques is called Data Normalization. Its highly used in order to reduce noise and redundancy of objects, so that to standardizing all features of the dataset into predefined criterion. Data normalizations techniques include min-max normalization, Z-Score normalization are used in this work. The Min-Max normalization technique involves the linear transformation on raw data. MinA and MaxA are minimum and maximum value for the attribute A, as shown in Equation 11. This technique maps the value of attribute A into range of [0,1]:
Z-Score normalization technique is useful when the actual minimum and maximum value of attribute A are unknown the value of an attribute using standard deviation and mean of the attribute A, which is calculated by Equation 12:
where
3.5 Principal Component Analysis (PCA)
The algorithm of PCA applied on the features vector before using classification method. After founding eigenvectors and eigenvalues from matrix by using algorithm of PCA. It was noticed that the eigenvalues are not similar. In fact, it turns out that the eigenvector with the highest eigenvalue is the principle component of the matrix.
The eigenvector with the largest eigenvalue was the one that pointed down the last of the data. It is the most significant relationship between the data dimension.
It is possible to ignore the components of lesser significance although some information may lose, but if the eigenvalues are small, the loose of information will not be much. The final features vector will have less dimensions than the original if some components are leave out.
3.6 Leaf Identification by PNNs
The other important part of the identification system is PNNs as a classifier. PNNs is a well-known neural network that consists of 4 units: first, input units, second, pattern units, third, summation units, and forth, output units.
In this work, PNNs was used to classify all types of leaves, created the network using Matlab function (net=newpnn(P1, T, smoothing factor); where net is the created PNNs, P1 dataset for training it content row is features and columns are number of sample a, T vector target for dataset of training and smoothing factor.
The parameter that needs to be determined for optimal PNNs performance is the smoothing parameter. One way of determining this parameter is to select an arbitrary set of σ, train the network and test it on a validation set. The procedure was repeated to find the set of σ that gives the minimum misclassification.
The testing part using Matlab function (y = sim(net, P2)), where net is PNNs, P2 is a dataset for testing and y is the matrix for the vector, produced by output layer.
It is a classification decision, in which a class with maximum probabilities will be assigned by 1 and other classes will be assigned by 0. For both datasets, (I=vec2ind(y)) Matlab function has been used to convert the result from vector to index to identify the leaf plant.
4 Experimental Results
This section presents and discusses the experimental results for leaf identification system performance, the tests are arranged to explore the effects of each data normalization type, such effects method of converting RGB to gray-scale image, setting all pixels of background image sample to white, also the effects of choosing types of feature and mixture between different features, then the effects of PCA. Finally, the proposed work compared with previous works.
4.1 Dataset
There are two kinds of dataset used in experiments. First dataset come from specimen collection, which contains 24 kinds of plat leaves. Second dataset (Flavia) has been used which contains 32 kinds of plant leaves. Based on those datasets, 50 plants per species from first dataset and 40 from the second were employed to train the network and 25 per species from first dataset and 10 from the second were used to test the performance of the proposed work.
Before using the second dataset, the correction of the rotation for all the leaf images, to the same rotation in first dataset, have been done. To compute the overall accuracy of the proposed work using Equation 13:
where NR is the number of images correctly recognized and NT is the total number of query input images
In this part, two types of data normalization on feature vectors have been tested. First one Min-Max data normalization and Z-Score data normalization using both datasets sample; first dataset (A) and second dataset (B). It's worth mentioning, all these steps before applying the PNNs.
Table 1 illustrates the results of PNNs, when selecting different value of spread (smoothing) factor (σ), for both Min-Max & Z-Score data normalization on the features of dataset (A&B).
Table 1 PNNs classification accuracy for all leaf types and using all feature after normalization for both datasets (A and B)
| Dataset A | Dataset B | ||||||
| Min-Max | Z-Score | Min-Max | Z-Score | ||||
| σ | Accuracy % | σ | Accuracy % | σ | Accuracy % | σ | Accuracy % |
| 0.14 | 97 | 1 | 97.83 | 0.2 | 97.5 | 1.3 | 97.1875 |
| 0.13 | 98.1666 | 0.9 | 98.1666 | 0.19 | 97.8125 | 1.2 | 97.5 |
| 0.12 | 98.1666 | 0.8 | 98.1666 | 0.18 | 97.8125 | 1.1 | 97.5 |
| 0.11 | 98.1666 | 0.75 | 98.1666 | 0.16 | 97.8125 | 1.05 | 97.5 |
| 0.1 | 98.3333 | 0.72 | 98.1666 | 0.14 | 97.8125 | 1 | 97.5 |
| 0.09 | 98.3333 | 0.71 | 98.3333 | 0.12 | 97.8125 | 0.95 | 97.5 |
| 0.08 | 98.3333 | 0.7 | 98.3333 | 0.1 | 97.8125 | 0.9 | 97.5 |
| 0.075 | 98.3333 | 0.65 | 98.3333 | 0.08 | 97.8125 | 0.85 | 97.5 |
| 0.07 | 98.3333 | 0.6 | 98.3333 | 0.07 | 97.8125 | 0.8 | 97.5 |
| 0.06 | 98.3333 | 0.59 | 98.3333 | 0.06 | 97.8125 | 0.75 | 97.5 |
| 0.05 | 98.3333 | 0.58 | 98.1666 | 0.05 | 97.8125 | 0.7 | 97.5 |
| 0.04 | 98.1666 | 0.5 | 98.1666 | 0.04 | 97.8125 | 0.65 | 97.5 |
| 0.03 | 98 | 0.4 | 98 | 0.03 | 97.8125 | 0.6 | 97.5 |
| 0.02 | 97.66 | 0.2 | 97.83 | 0.02 | 95 | 0.5 | 97.1875 |
From Table 1, it was observed that the average accuracy of the system when using both methods of normalization on the dataset (A), the maximum accuracy that can be reached is (98.3333%) in the different range of smooth factors values for (Max-Min) where the range values between (0.03-0.11) and for (Z-Score) the range values where between (0.58-0.72).
It is also observed that the average accuracy of the system when using the (Min-Max) on the dataset (B) was better than of using (Z-Score).
The average accuracy in the first one reach the maximum accuracy (97.8125%) in the range of smooth factors values which is between (0.02-0.2) and the second one reach the maximum accuracy (97.5%) in the range of smooth factors values which is between (0.5-1.3).
4.2 Experimental Results for Feature Types
To know the performance of each group of features (shape, textures, color and vein) in the proposed work, the dataset (A) are used. Min-Max and Z-Score are applied for data normalization to make the comparison between both methods and the performance of the system by PNN were calculated.
Figure 13 shown the histogram of average accuracy for system by feature type on the dataset (A).
From Figure 13, the shape feature has the higher performance when using the Centroid-Radii and some other morphological feature, which is considered to be as global shape features, comparing with color, texture and vein features. A number of performances for the system have been performed for evaluation of the results.
The first main effect come from the shape features, the second main effect coming from texture feature. In addition, secondary effect comes from the color and final effect of vein can be considered weak.
Finally, the results of (Z-Score) method normalization is little bid better than (Min-Max) method in shape, color and vein. More so, various features have been tested to highlight all the effects on system performance for each type and hybrid between all of them. Table 2 illustrated the various feature and their performance.
Table 2 Various feature and their performance for the dataset (A)
| No. | Features | Performance | |
| Min-Max normalization | Z-Score normalization | ||
| 1 | C_R | 78.16 % | 77.50 % |
| 2 | C_R+ Aspect ratio | 77.83 % | 78.50% |
| 3 | C_R+ Aspect ratio + Roundness | 90.50 % | 91.33% |
| 4 | C_R+ Aspect ratio + Roundness + Solidity | 91.33 % | 92.00% |
| 5 | Shape (C_R+ Aspect ratio + Roundness + Solidity + Convexity) | 92.66 % | 92.50% |
| 6 | Color | 76.66 % | 75.66 % |
| 7 | Texture | 78.33 % | 78.33 % |
| 8 | Vein | 30.00 % | 29.83 % |
| 9 | Shape + Color | 97.16 % | 97.00 % |
| 10 | Shape + Texture | 98.33 % | 98.16 % |
| 11 | Shape + Vein | 94.00 % | 94.00% |
| 12 | Shape + Color + Texture | 98.50 % | 98.33 % |
| 13 | Shape + Color + Vein | 97.66 % | 97.50 % |
| 14 | Shape + Texture + Vein | 97.16 % | 97.16 % |
| 15 | Color + Texture | 92.66 % | 92.66 % |
| 16 | Color + Vein | 80.83 % | 81.16 % |
| 17 | Color + Texture + Vein | 93.16 % | 93.16 % |
| 18 | Texture + Vein | 82.83 % | 81.66 % |
| 19 | Shape + Color + Texture + Vein | 98.33 % | 98.33% |
From the above table, significant information appears when using the mixture from feature types.
The maximum average accuracy of classification system was reached (98.5%) when using shape, color and texture features, this result is better than average accuracy (98.3333%) when using all features. In addition, it was found that the average accuracy of the system reaches to (98.3333%) when using shape and texture features, which is equivalent to the average accuracy of system when using all the features.
Table 3 shows the accuracy for all 24 kinds of leaf plant from dataset (A).
4.6 Experimental Results for PCA
Applying the PCA on both dataset (A and B), for reducing the dimensions of feature before using PNN. Table 4 shows the results when PCA was used in the system using dataset (A). Table 5 shows the results when PCA was used in the system using dataset (B).
Table 4 Results when PCA was used in the system for the dataset A
| Min-Max & PCA | Z-Croc & PCA | ||||
|
Dimension of Feature |
Range (σ) |
Total Accuracy for all classes |
Dimension of Feature |
Range σ |
Total Accuracy for all classes |
| 48 | 0.05 - 0.1 | 98.33% | 48 | 0.59 - 0.71 | 98.33% |
| 35 | 0.08 - 0.13 | 98.33% | 35 | 0.5 - 0.71 | 98.33% |
| 30 | 0.09 - 0.16 | 98.33% | 30 | 0.54 - 0.71 | 98.33% |
| 25 | 0.09 - 0.15 | 98.33% | 25 | 0.63 - 0.71 | 98.33% |
| 20 | 0.09 - 0.16 | 98.33% | 20 | 0.62 - 0.75 | 98.33% |
| 15 | 0.16 | 98.50% | 15 | 0.62 - 0.76 | 98.33% |
| 10 | 0.05 - 0.12 | 98.00% | 10 | 0.3 - 0.5 | 98.00% |
Table 5 Results when PCA was used in the system for the dataset B
| Min-Max & PCA | Z-Croc & PCA | ||||
|
Dimension of Feature |
Range (σ) |
Total Accuracy for all classes |
Dimension of Feature | Range σ |
Total Accuracy for all classes |
| 48 | 0.03 - 0.19 | 97.81% | 48 | 0.6 - 1.2 | 97.5% |
| 35 | 0.08 - 0.24 | 97.81% | 35 | 0.6 - 1.19 | 97.5% |
| 30 | 0.08 - 0.15 | 97.81% | 30 | 0.59 - 1.19 | 97.5% |
| 25 | 0.09 - 0.14 | 97.81% | 25 | 0.5 - 1.03 | 97.5% |
| 20 | 0.1 - 0.13 | 98.12% | 20 | 0.7 - 0.9 | 97.81% |
| 15 | 0.11 - 0.19 | 97.81% | 15 | 0.66 - 0.76 | 97.81% |
| 10 | 0.14 - 0.16 | 97.5% | 10 | 0.6 - 1 | 96.85% |
Based on Table 4, the optimum accuracy on the dataset (A) was reached (98.5%) network using smoothing factor (0.16) when the dimension was reduced to 15 feature for using Min-Max data normalization on features vector and transfer the data vector by PCA. Table 6 show the accuracy of it is PNN, average of execution time for all operations on the leaf sample image for dataset A.
Table 6 Results for PNN with PCA, dimension was reduced to 15 and 20 features, for all samples (A and B)
| Dataset | Total test sample |
Total correct sample |
Total incorrect sample |
Average time Sec. |
Accuracy % |
| A | 2839 | 2806 | 33 | 2.126577 | 98.83 |
| B | 1901 | 1875 | 19 | 2.893612 | 98.63 |
Also based on Table 5, the optimum accuracy on the dataset (B) was reached 98.12% network using smoothing factor between (0.1-0.13) when the dimension was reduced to 20 feature for using Min-Max data normalization on features vector and transfer the data vector by PCA. Table 6 show the accuracy of it is PNN.
4.7 Comparison with Other Systems
Using the dataset B (Flavia) and comparing it with several researches who have used Flavia dataset, Table 7 list the accuracy of this work and other methods proposed by other researchers. It is shown that the proposed system gave better accuracy than the others.
Table 7 Comparison of accuracy
| Researcher | Features | Number of Feature | Method | Accuracy |
| Kadir [7] | All Feature | 54 | PNN | 93.75% |
| With PCA | 25 | PNN | 95.00% | |
| Stephen [16] | All Feature | 12 | ------ | ------ |
| With PCA | 5 | PNN | 90.3120% | |
| Krishna [17] | All Feature | 12 | SVM-BDT | 96% |
| PNN | 91% | |||
| Kadir [18] | All Feature | 12+ Zernike moments 2-8 | Fourier-Moment | 62% |
| Euclidean distance | 94.69% | |||
| 12+ Zernike moments 2-4 | Cite block distance | 93.75% | ||
| 12+ Zernike moments 2-10 | PNN | 93.44% | ||
| Kumar [19] | morphological | ---- | AdaBoost_MLP | 95.42% |
| Ahmed [20] | Shape+vien | ---- | SVM | 87.40% |
| Jeon [21] | HOG+FIFT | ---- | CNN | 90% |
| Quoc Bao [22] | HOG | ---- | SVM | 92% |
| ---- | ---- | CNN | 95.5% | |
| Proposed work | All Feature | 48 | PNN | 97.81% |
| With PCA | 20 | PNN | 98.13% |
5 Conclusion
In this work, the idea of using visual feature (i.e., color, texture, shape, and vein) have been investigated, to extract the content features from various types of leaf images of plant. PNNs was used to classify the sample images, for identifying plants. In this work, system was tested on two dataset; the first one, included 2,839 image of leaves for 24 different plant species, and Flavia was the second dataset of included 1,901 image of leaves for 32 different plant species. Choice of normalization data will affect the performance of the whole system by depending on data type of feature vectors.
Shape as one of the features, have the higher performance when using the Centroid-Radii and some other morphological feature. The shape was better from texture, color, and vein feature extraction from all the samples because the shape of leaf is usually various in different species of plant.
Results of Table 2 show that positive and negative effects can be found although not in all cases gives good results after blending between features. The positive effect increases the performance, e.g., if combining shape with color and texture, the system reaches accuracy 98.5% on dataset (A), while there is no negative effect on classification (e.g., if combining shape with all other feature, the system reaches accuracy 98.33% on dataset (A)).
The PCA improves the accuracy of the system, when the effect ignore some dimension, the ignored dimensions depend on the components of lesser significance, that have small eigenvalue in order to improve the accuracy of system, (e.g., from 98.33% to 98.5% when dataset (A) was used and from 97.81% to 98.12% when dataset Flavia was used).











 nueva página del texto (beta)
nueva página del texto (beta)