1 Introduction
Soccer is the most popular sport in the world, which was temporarily suspended due to the pandemic from March 2020. Traditional prediction approaches based on domain experts forecasting and statistical methods are challenged by the increasing amount of diverse football-related information that can be processed [1].
A subset of Artificial Intelligence is Machine Learning, which is the discipline that deals with the study of methods for pattern recognition in datasets undergoing data analysis. In particular, it deals with the development of algorithms that learn from data and make predictions or regressions. Each methodology is based on building a specific model [11].
The data to be subjected to a pattern in the learning phase can be arrays composed by a single value per element, or multivariate values. These values are often referred to as characteristics or attributes [11].
Machine learning is divided into three main areas: supervised, unsupervised, and reinforcement learning. Since machine learning generally focuses on prediction based on known properties learned from training data, our approach is based on supervised learning. In supervised learning, the dataset contains both inputs (or the feature set) and desired outputs (or objectives). That’s how; we know the properties of the data. The goal is to make predictions [5].
This ability to monitor algorithm training is a big part of why machine learning has become so popular. In this paper we propose to create a supervised learning model using different machine learning algorithms like Logistic Regression, Support Vector Machines, Decision Trees and Naive Bayes, that can predict as winner or loser a football team, from the number of goals scored in a match, obviously without consulting the goals scored by the opponent team, for which a data set is prepared from the information provided by a betting support page1, which concentrates the results of the first division of the Mexican football league from the 2012 season to March 2020.
2 Related Work
In [2], Deep neural networks (DNNs) and artificial neural networks (ANNs) have been used to predict the results of football matches, using a data set that collects the results and performances of international football teams in previous matches, where they divide the data sets into sections for training, validation and testing, they used their model to predict the results in the 2018 World Cup, obtaining an accuracy of 63.3 %.
In [3], the authors use the APSO automatic clustering method to divide the data set, in this case professional soccer players, into their position: goalkeepers, midfielders, defenders and strikers, in addition to applying a combination of machine learning techniques of particle swarm optimization (PSO) and support vector regression (SVR), to estimate the value of football team players in the transfer market, where they achieve an accuracy of 74 %.
In [4], the authors propose a Softmax regression model, which is a generalization of the logistic regression model, to predict the outcome of football matches based on the publicly available information of results of previous matches, of the Portuguese first division league.
The prediction is formulated as a problem of classification with three classes: victory of the home team, draw or victory of the visiting team (Away Team).
3 Methodology
Based in [5], we proposed a Model, considering first dividing the data into two: Training set and testing set, instead of using all the data as in [5], in addition to Logistic Regression apply other supervised learning algorithms such as: Naive Bayes, Decision Trees and Support Vector Machines in order to contrast the results and get a better accuracy. For this analysis, we first consider the draws and then another omitting these, in order to improve efficiency.
3.1 Getting the Dataset
The database to carry out this work was taken from page mentioned above and contains the results of the matches held by the teams of the Mexican soccer league from 2012 to March 2020 seasons.
The data set consists of the results of 2,612 games held by the teams of the first division of the Mexican soccer league and has 17 characteristics of each match, such as season, date, time of the match, the home team, the visiting team, goals scored by the home team and by the visitor, the winner and percentage data of the matches. (Table 1).
Table 1 Initial dataset
| Season | Date | Time | Home | Away | HG | AG | Res | PH | PD | PA | MaxH | MaxD | MaxA | AvgH | AvgD | AvgA | |
| 0 | 2012/2013 | 21/07/2012 | 01:30 | Chiapas | U.A.N.L.-Tigres | 0 | 4 | A | 2.93 | 3.34 | 2.60 | 2.95 | 3.50 | 2.64 | 2.74 | 3.10 | 2.51 |
| 1 | 2012/2013 | 21/07/2012 | 03:30 | Club Tijuana | Puebla | 2 | 0 | H | 1.91 | 3.58 | 4.49 | 2.24 | 3.58 | 4.49 | 1.93 | 3.26 | 3.83 |
| 2 | 2012/2013 | 21/07/2012 | 23:00 | Cruz Azul | Monarcas | 0 | 0 | D | 2.02 | 3.53 | 4.13 | 2.10 | 3.70 | 4.13 | 2.00 | 3.26 | 3.56 |
| 3 | 2012/2013 | 21/07/2012 | 23:00 | Queretaro | Club Leon | 0 | 2 | A | 3.82 | 3.25 | 2.22 | 3.82 | 3.35 | 2.29 | 3.26 | 3.18 | 2.16 |
| 4 | 2012/2013 | 22/07/2012 | 01:00 | Monterrey | Club America | 0 | 0 | D | 1.85 | 3.87 | 4.50 | 2.10 | 3.87 | 4.50 | 1.92 | 3.37 | 3.79 |
| … | … | … | … | … | … | ... | … | … | … | … | … | … | … | … | … | … | … |
| 2607 | 2019/2020 | 15/03/2020 | 01:00 | U.A.N.L.- Tigres | Juarez | 3 | 2 | H | 1.59 | 3.92 | 6.36 | 1.65 | 4.06 | 6.50 | 1.57 | 3.85 | 5.82 |
| 2608 | 2019/2020 | 15/03/2020 | 03:00 | Guadalajara Chivas | Monterrey | 1 | 1 | D | 2.82 | 3.21 | 2.67 | 2.90 | 3.28 | 2.78 | 2.74 | 3.14 | 2.58 |
| 2609 | 2019/2020 | 15/03/2020 | 18:00 | Toluca | Atlas | 2 | 3 | A | 1.99 | 3.41 | 4.12 | 2.05 | 3.55 | 4.20 | 1.96 | 3.34 | 3.85 |
| 2610 | 2019/2020 | 16/03/2020 | 00:00 | Santos Laguna | Necaxa | 2 | 1 | H | 1.70 | 4.09 | 4.80 | 1.77 | 4.13 | 5.50 | 1.68 | 3.90 | 4.60 |
| 2611 | 2019/2020 | 16/03/2020 | 02:15 | Club America | Cruz Azul | 0 | 1 | A | 2.75 | 3.57 | 2.52 | 3.00 | 3.57 | 2.70 | 2.68 | 3.37 | 2.49 |
| 2612 rows x 17 columns | |||||||||||||||||
3.2 Exploring and Viewing Data
Examining the data set, we find that from the 2,612 matches played, the result in 726 of them were draws, so the data set omitting the draws is now reduced to 1,886 markers in which one team won and consequently the other lost.
From table 2, it follows that the percentage of draw matches are 27.7% of the total matches played.
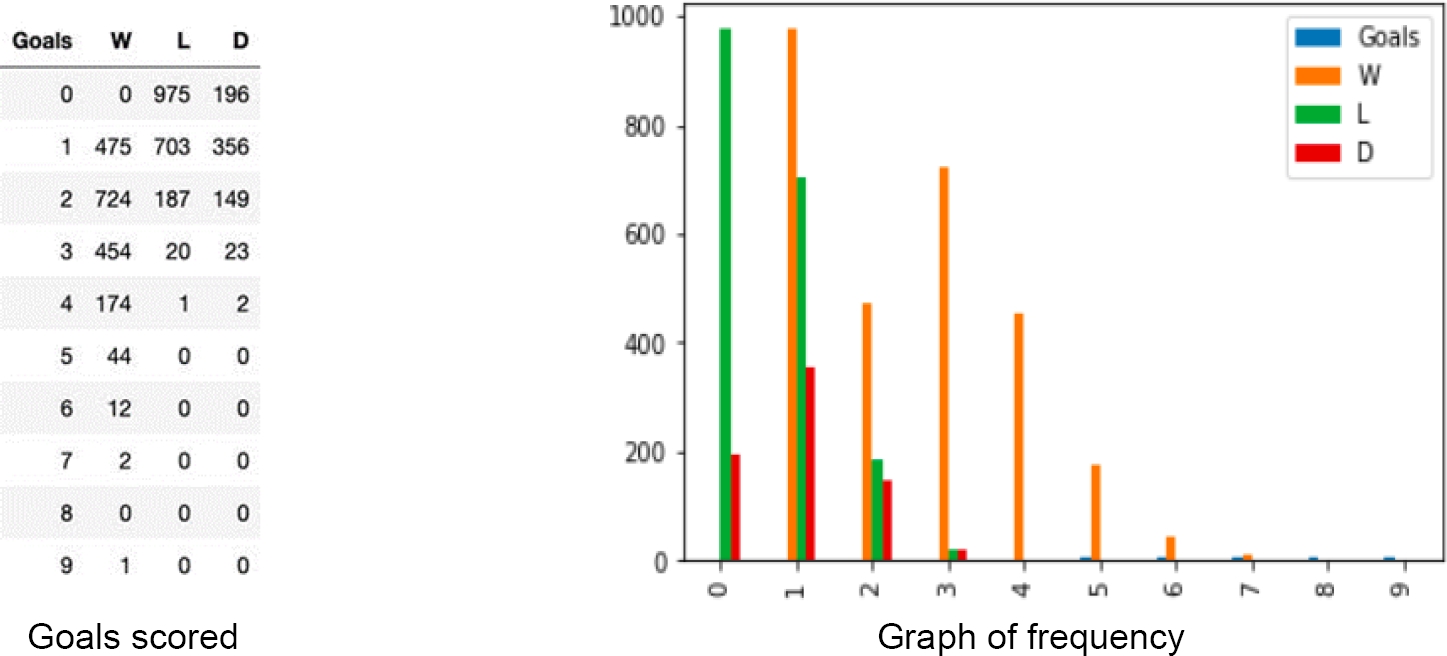
This study is centered in the number of goals that make a soccer team win or lose a match, as we can see in figure 1, with zero and one goals losing is more probable and with two or more goals the probability of winning a match is increased.
3.3 Preprocessing the data
For the purpose of this work, which is to predict from the number of goals scored by team, whether it is a loser or winner, the information reported in the following columns is sufficient:
– HG number of goals scored by the home team,
– AG number of goals scored by the visiting team,
-
– Res result of the game:
Table 3 shows the data set with the columns of interest.
Table 3 Data set with the columns selected
| Home | Away | HG | AG | Res | Home | Away | HG | AG | Res | ||
| 0 | Chiapas | U.A.N.L.-Tigres | 0 | 4 | A | 0 | Chiapas | U.A.N.L.-Tigres | 0 | 4 | A |
| 1 | Club Tijuana | Puebla | 2 | 0 | H | 1 | Club Tijuana | Puebla | 2 | 0 | H |
| 2 | Cruz Azul | Monarcas | 0 | 0 | D | 3 | Queretaro | Club Leon | 0 | 2 | A |
| 3 | Queretaro | Club Leon | 0 | 2 | A | 5 | Santos Laguna | Atl. San Luis | 2 | 1 | H |
| 4 | Monterrey | Club America | 0 | 0 | D | 7 | Toluca | Guadalajara Chivas | 2 | 1 | H |
| 2607 | U.A.N.L.- Tigres | Juarez | 3 | 2 | H | 2606 | Club Leon | U.N.A.M. Pumas | 3 | 1 | H |
| 2608 | Guadalajara Chivas | Monterrey | 1 | 1 | D | 2607 | U.A.N.L.- Tigres | Juarez | 3 | 2 | H |
| 2609 | Toluca | Atlas | 2 | 3 | A | 2609 | Toluca | Atlas | 2 | 3 | A |
| 2610 | Santos Laguna | Necaxa | 2 | 1 | H | 2610 | Santos Laguna | Necaxa | 2 | 1 | H |
| 2611 | Club America | Cruz Azul | 0 | 1 | A | 2611 | Club America | Cruz Azul | 0 | 1 | A |
| With draws | Without draws | ||||||||||
3.4 Features extraction
For the choice of characteristics, two more columns are added to the table: W is a winner, L is a loser.
Columns W and L contain the number of goals that made the team win or lose the match respectively. In the case of a draw (D), we will have that the values of W and L are equal, as happens in rows 2, 4 and 2608 of table 4.
Table 4 Data set with the columns W and L added
| Home | Away | HG | AG | Res | W | L | Home | Away | HG | AG | Res | W | L | ||
| 0 | Chiapas | U.A.N.L.-Tigres | 0 | 4 | A | 4 | 0 | 0 | Chiapas | U.A.N.L.-Tigres | 0 | 4 | A | 4 | 0 |
| 1 | Club Tijuana | Puebla | 2 | 0 | H | 2 | 0 | 1 | Club Tijuana | Puebla | 2 | 0 | H | 2 | 0 |
| 2 | Cruz Azul | Monarcas | 0 | 0 | D | 0 | 0 | 3 | Queretaro | Club Leon | 0 | 2 | A | 2 | 0 |
| 3 | Queretaro | Club Leon | 0 | 2 | A | 2 | 0 | 5 | Santos Laguna | Atl. San Luis | 2 | 1 | H | 2 | 1 |
| 4 | Monterrey | Club America | 0 | 0 | D | 0 | 0 | 7 | Toluca | Guadalajara Chivas | 2 | 1 | H | 2 | 1 |
| 2607 | U.A.N.L.-Tigres | Juarez | 3 | 2 | H | 3 | 2 | 2606 | Club Leon | U.N.A.M. Pumas | 3 | 1 | H | 3 | 1 |
| 2608 | Guadalajara Chivas | Monterrey | 1 | 1 | D | 1 | 1 | 2607 | U.A.N.L.-Tigres | Juarez | 3 | 2 | H | 3 | |
| 2609 | Toluca | Atlas | 2 | 3 | A | 3 | 2 | 2609 | Toluca | Atlas | 2 | 3 | A | 3 | 2 |
| 2610 | Santos Laguna | Necaxa | 2 | 1 | H | 2 | 1 | 2610 | Santos Laguna | Necaxa | 2 | 1 | H | 2 | 1 |
| 2611 | Club America | Cruz Azul | 0 | 1 | A | 1 | 0 | 2611 | Club America | Cruz Azul | 0 | 1 | A | 1 | 0 |
| 2612 rows x 7 columns | 1886 rows x 7 columns | ||||||||||||||
| With draws | Without draws | ||||||||||||||
To create the feature vector X, column W is concatenated with column L to form a single vector, as shown in Figure 2.
The vector X of features is formed by the 5224 markers obtained by the teams in the 2612 matches played, in the case of considering draws. The size of vector X is reduced to 3772 without draws. Let us observe that it can be won with two goals, as in the case of the second match that had a score 2-0, but it can also lose with two goals, as happened in the antepenultimate match shown, which was a score of 3-2, we must also take into account that there are draws, as in the case of the third match that had a score of 0-0, note that in ties, the score appears in both W and L.
Given that a team won or lost with a certain number of goals, the vector of labels Y is created from the vector of features X. In the vector of labels Y, the marker of the winning team is replaced by a 1 and that of the loser by a 0, this vector is shown in figure 3.
3.5 Classification model
A common machine learning practice is to evaluate an algorithm. This evaluation consists of dividing the data into two parts, one called the training set, with which the algorithm learns the properties of the data, and the other called the test set, in which those properties were tested [5].
To obtain the training and test vectors, the X and Y vectors were divided in such a way that the training vector retains 75% of its size and the remaining 25% constitutes the test vector, it is important to reserve a percentage of the markers to verify the operation of the model.
After the selection of the training and test sets, we apply four Machine Learning algorithms for the construction of the prediction model, including Logistic Regression, Naive Bayes, Support Vector Machine and Decision Trees.
3.5.1 Logistic Regression
Logistic regression is a type of statistical and probabilistic classification model. It is used to predict a binary response, the result of a categorical dependent variable (that is, a label of class Y), based on one or more variables that make up the vector of characteristics X. [5]
One expression of the logistic function is:
This function is useful because it restricts the output to values between 0 and 1, which can be interpreted as a probability.
3.5.2 Naïve Bayes
The n-dimension vector X=(x1, x2, x3,..., xn). The Bayesian classifier assigns each X to one of the target classes in the set {C1, C2,..., Cm,}. This assignment is made on the basis of the probability that X belongs to the target class Ci. That is, X is assigned to class Ci if and only I important to reserve a percentage of the markers to verify the operation of the model.
After the selection of the training and test sets, we apply four Machine Learning algorithms for the construction of the prediction model, including Logistic Regression, Naive Bayes, Support Vector Machine and Decision Trees.
P(Ci | X)> P (Cj | X) for every j such that 1 ≤ j ≤ m where:
To simplify the calculation, the assumption of conditional class independence is made, which means that for each class, the attributes are independent. The classifier that develops from this assumption is known as the Naive Bayes classifier.
3.5.3 Support Vector Machine
It is a supervised learning technique initially designed to fit a linear limit between the samples of a binary problem.
It is a classification algorithm that transforms a set of training data into a higher dimension. Optimize a hyper plane that separates the two classes in minimal classification errors. The hyper plane is represented as follows:
Dividing the data points into classes separated by a gap as wide as possible. The data points closest to the classification limit are known as support vectors.
3.5.4 Decision trees
A decision tree is one of the simplest and most intuitive techniques of automatic learning, based on the divide and conquer paradigm.
In a decision tree, an internal node represents a characteristic or attribute, a branch a decision rule and each leaf node represents a result. The tree splits in a recursive way.
Decision tree impelling chooses significant features. Choice tree actuation is the learning of choice tree classifier, so building tree structure where every inside hub (no leaf hub) signifies quality test:
Here pi is the probability that arbitrary vector in D belongs to label i [12].
Once the algorithms are applied, then the evaluation metrics are applied.
3.6 Evaluation Metrics
The basic measure of a classifier's performance is its accuracy. It is defined as the number of correctly predicted examples divided by the total number of examples.
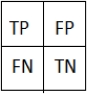
Although accuracy is the most common metric for evaluating classifiers, there are cases where the value of correctly predicted elements of one class is different from the prediction value of elements of another class. In those cases, accuracy is not a good performance metric and a more detailed analysis is need. The confusion matrix helps us define different metrics considering those scenarios. In a binary problem, there are four possible cases:
– True positives (TP): When the classifier predicts a sample as positive and it really is positive
– False positives (FP): When the classifier predicts a sample as positive and it really is negative.
– True negatives (TN): When the classifier predicts a sample as negative and it really is negative.
– False negative (FN): When the classifier predicts a sample as negative and it really is positive [1].
This information can be summarized in a matrix, called the confusion matrix, as illustrated in figure 4.
To evaluate the effectiveness of the proposed methods, the following metrics were used.
Accuracy: It is the number of correct predictions among the total number of examples
Precision: It is the number of correct positive results between the amount of positive results predicted by the classifier
Recall: It is the number of correct positive results divided by the number of positive results.
F1-score: it is the harmonic mean between precision and recall:
4 Results and discussion
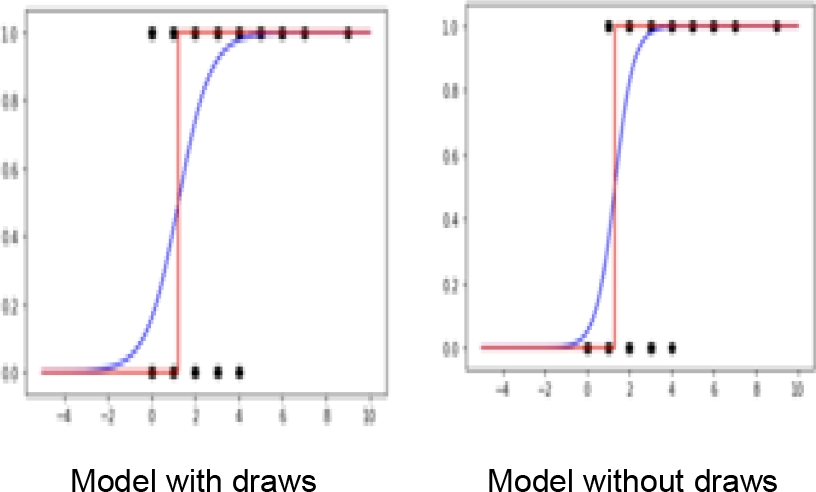
Figure 5 shows a scatter plot, the fitting of the regression model (blue) and prediction of the logistic regression model (red). We noted that:
In the prediction model, it can be seen that with zero goals, the team lost, but with one goal the team can win a match, but also can lost and with two or more, the team wins.
We saw that there was a change in the logistic regression curve without ties, where a more abrupt change from 0 to 1 is appreciated than the one of the logistic regression curve where ties were taken into account, its happen because the likelihood for the regression logistic model for the cases of zero and one goals scored are more closed to zero and the case of two or more goals are more closed to one.
According to those confusion matrixes showed in figure 6 the accuracy performances without draws is 84% and 74 % with draws in the best of the cases. Table 5 shows a comparison of the accuracy obtained with the different algorithms with and without ties.
Table 5 Accuracy of prediction algorithms
| Algorithm | Accuracy With draws | Accuracy Without draws |
| Logistic Regression | 0.753 | 0.845 |
| Naive Bayes | 0.753 | 0.845 |
| Support Vector Machine | 0.753 | 0.845 |
| Decision Trees | 0.753 | 0.845 |
Comparison of the four classifier algorithms is presented in table 6 and the classification performance indicators: precision, recall and F1 score.
Table 6 Sensitivity, Accuracy and F1
| Algorithm | Precision | Recall | F1-score | Precision | Recall | F1-score |
| With draws | Without draws | |||||
| Logistic Regression | 0.63 | 0.803 | 0.709 | 0.775 | 0.904 | 0.83 |
| Naive Bayes | 0.63 | 0.803 | 0.709 | 0.775 | 0.904 | 0.83 |
| Decision Tree | 0.63 | 0.803 | 0.709 | 0.775 | 0.904 | 0.83 |
| Support Vector Machine | 0.63 | 0.803 | 0.709 | 0.775 | 0.904 | 0.83 |
5 Conclusions and Future Work
An analysis was done of soccer results from 2012 to march 2020 seasons of sporting activity in the Mexican league, prior to the pandemic where 2612 matches were played, applying the four classifier algorithms mentioned above to predict winning or losing results, according to the number goals scored by a team, agreed with the same accuracy in the best of the cases.
A justification for the coincidence of the results is explained by the probability, if we look at the number of goals scored in Figure 1, without considering the draws the accumulated error is 18.1% in the worst case that is, predicting defeat when it is victory and vice versa, so the accuracy is 81.9%. Now considering the ties the error increases to 26.9% and the accuracy decreases to 73.1%. So, for this very particular case, the result of accuracy is the same, regardless of the machine learning algorithm used here. Also as a curious fact, we observe in the same table that there is no score of 8 goals.
Accuracy is increased by omitting ties because it is then considered a separable problem, which improves the result reported in [5].
When predicting only win and lose the problem is binary so the Softmax Regression model algorithm was not used.
As future work, more characteristics can be considered to be able to predict the outcome of a soccer match.











 nueva página del texto (beta)
nueva página del texto (beta)