1 Introduction

Feature reduction is important in data mining, since its benefits are: simpler and cheaper data collection; less space in memory and disk; smaller processing times, both in training and classification; better visualization and understanding of the results [⁶].

The reduced set of features should not appreciably decrease the accuracy (percentage of correct answers) of a classifier that uses it.

Moreover, when an object has hundreds of thousands of features, classification becomes complicated, due to ’the course of dimensionality’: as the number of features (dimensions) increase, the data set is very sparsely distributed in the huge spanned dimension space, and many regions of this space are empty [¹⁷].

This provokes a curious fact: the distance (for any reasonable metric) between any two points is about the same. Any point is more or less equidistant to all the others [¹].

Any three points lie in an almost equilateral triangle. Classifiers that use ’distance’ no longer work well. Such space challenges our intuition about ’closeness’ and ’clustering’, for instance.

Another difficulty arises when data sets are imbalanced, because objects of a certain class are much more abundant than those of other classes.

For instance, sampling the population of a city, the number of people having cancer is quite small compared to the number of people do not having cancer, say, 5% versus 95%.

Many classifiers are tempted to assign to the ’healthy’ class any person, since its error (percentage of incorrect results) will be at most 5%. The main contributions in this paper are:

The paper is organized as follows. Section 1 introduces the reader to the feature selection area. Section 2, Related works, describes relevant previous work. Section 3 describes the FSOC algorithm and its foundation.

Section 4 compares FSOC with other state-of-the-art selection algorithms, using a statistical analysis. Finally, the last Section contains our conclusions and future work.

The algorithms for feature reduction fall in two groups: feature extraction and feature selection. The first group generates new features by combining the original features.

The number of new features is smaller than the number of the original features. Each object in the dataset is now described by the new features.

The new features are a linear or non-linear combination of the original features, and they are used to span a lower dimensional subspace for the original space, or, in recent subspace techniques, for each pattern class.

Unfortunately, these feature extraction or combination algorithms work mainly with only numeric features or categorical, but not both [¹⁴], and they present limitations when the classes are highly imbalanced. That is, when the apriori probabilities of the classes are very different. Therefore, they are not suitable for data sets having a mixture of numerical and categorical features. In addition, the resulting features are difficult to explain to a user that seeks to understand why a particular instance was classified in a certain way.

These techniques reformat, transform and combine the features of each object. For this reason, these algorithms were not considered in this paper.

The second group selects a subset of features from the complete set, called ’relevant features’ because they provide information to correctly discriminate the instances with respect to the class; in other words, the features have a correlation with the class [¹⁰, ⁷].

The goal in both groups is to obtain a good set of features, defined by [⁹] as those that are correlated with the target class but have little or no correlation with each other. The most important methods for feature selection are filter and wrapper methods.

2 Related Work

Most classifiers in data mining have some weakness when the data set has redundant features or features that are not very relevant. In several publications, metrics have been designed to evaluate the relevance of features [⁴].

Some metrics only work in numeric, nominal or mixed spaces; for example, the Pearson and Spearman correlation work only with numerical data, while the information gain, the symmetric uncertainty coefficient, V Cramer and confusion measure work with nominal features.

CMCD, based on the theory of class separation, relates numerical and mixed features [¹³]. However, these metrics only allow measuring the correlation between two features, and do not provide information about whether these features have high correlation with the target class.

Different methods for feature extraction and feature selection has been proposed and used in different areas of knowledge, such as the energy sector, the education sector, recommendation systems, among others.

In article [⁸], a strategy is presented to increase the efficiency of classifying the stress (low, medium and high) of a driver, through the obtaining and analyzing biological changes such as blood pressure, heartbeat, muscle activity, among others.

The process is carried out through two stages; the first consists of obtaining the new features obtained through feature extraction with the intention of reducing ’altered’ measures and characterizing them.

Subsequently, discriminative common vectors are used to generate an identifying vector for drivers and thus classify them. Moreover, for the discriminative vectors, it is necessary to obtain eigenvectors and eigenvalues to transform the space and it could be limited if the matrices are large.

In addition, the explanation of the final result is confusing, because the vectors generated comes from a series of transformations and combinations between features. In [¹⁸] some linear and non-linear techniques for the generation of subspaces are explained, which use Cholesky decomposition to create a matrix that approximates the original data.

The uniqueness of these techniques is that they involve Kernel functions to approximate more complex (non-linear) data. Once this matrix is obtained, the training values can be transformed by its orthogonal representation.

Furthermore, these transformations and new representations of the data cause a lesser understanding of the generated model, and do not always help in decision making. In [²], the use of latent factor models in recommendation systems is proposed because of their ease in dealing with scattered matrices (with missing values).

The main idea is to use the high correlations between columns and rows in order to rotate the axes system and eliminate the redundancy in pair wise correlations. These models map the values of the features into a smaller dimensional space and thereby infer recommendation items based on information from other users.

In [³], Principal Components Analysis (PCA) is used to evaluate and obtain an energy sustainability index for rural communities.

Features such as population density, per capita energy consumption, per capita production, proportion of local residents and tourists, among others, were considered. The result shows that a certain region of France has a better energy index than the rest.

A set of new features is obtained by a linear combination of the original features. Two possible drawbacks are: only numerical features can be combined; and the semantics or meaning of this new set is difficult to understand, and the contribution of the original features is not clear.

Instead, the methods of selecting features maintain the meaning of the original features, since they only exclude less relevant features. In [⁹], the heuristic called merit is proposed to know how ’good’ a subset of features is.

This heuristic takes into account the usefulness of the features individually, while at the same time it measures the level of correlation between them.

In other words, the merit is the ratio of the correlation between the features with the class divided by the correlation of the features with each other.

The Correlation Feature Selection (CFS) algorithm is developed, its results show great efficiency with different data sets with little or no loss of accuracy in classifiers.

The method allows forward and backward searches. The method consists in adding or eliminating a feature that increases merit and ends when merit decreases while removing or adding a feature, or there are no more features to evaluate.

The main limitation in this method is that although not all combinations of features are generated, too many comparisons are made between features, which could be expensive in a high dimensionality data set. Our proposed FSOC algorithm reduces these comparisons, thus running faster.

[²⁰] describe the method Fast Correlation-Based Filter (FCBF), that seeks primarily the answer to two questions: how to decide if a feature is relevant to discriminate instances with respect to the class (a relevance threshold δ is introduced), and how to decide if the relevant feature is redundant with some other feature in the complete feature set.

In order to answer this question, it uses the condition that the correlation between feature A and feature B is greater than or equal to the correlation between feature B and class feature.

The method first excludes from the complete set those non-relevant features, and then, every feature in the remaining subset is compared to all others in the subset, to find if there is a strong relationship between any of them.

In this case, it excludes the feature with less discriminatory power. FCBF has two disadvantages. It computes the correlations of the features with the class to provide an acceptable relevance threshold δ.

It excludes features whose correlation with the class are lower than δ. This is a disadvantage of the algorithm, since a feature that apparently is not very relevant (correlated) with the class, could be useful to avoid loss of classification accuracy (for example, when all the features are required to obtain the greatest discrimination power).

Another disadvantage is that it considers δ and redundancy sequentially. That is, it first filters out those features that are not relevant (have little discriminating power) and then proceeds to eliminate redundant features.

Although it is a very fast algorithm, the efficiency of the classifiers that use the selected subset of features decreases, which implies loss of discriminating power.

[¹⁶] defines four groups of features: (1) strongly relevant features, (2) relevant and non-redundant features, (3) relevant but redundant features and (4) weakly relevant and redundant features.

An optimal subset is one that has features of group 1 and group 2. Their ECMBF algorithm exploits these concepts with two parameters, α as the relevance threshold and β as the redundancy threshold.

The first step is to eliminate features that do not comply with α (group 4) and subsequently eliminates those that are redundant (group 3), prevailing those with greater relevance (groups 1 and 2). As in FCBF, considering the parameters α and β in isolation could cause loss of discriminative power.

Moreover, without a previous knowledge of the data set, an initial setting of α and β could be wrong, provoking poor classification accuracy when using the reduced feature set, as compared with using the complete set of features.

In [⁵] the ANCONE algorithm is developed, that employs the CFS method (Correlation Feature Selection, explained above when describing work [⁹]), it was used to find personal and socio demographic characteristics associated with the school performance of third grade Mexican High School students in Mathematics.

The complexity of the problem lies in the fact that the data sets to analyze contain approximately 52232 instances (students) and 232 features. Many of these features contain redundant information (Do you have internet at home? Do you have a home computer? Do you have electricity at home?).

From 232 features, 18 were identified as relevant by the CFS method, which are questions about the student’s academic record, the type of school, the educational level of the parents and the student’s academic aspirations. These features increased the efficiency of the classifier from 50% to 68%.

Although the CFS method is effective, when you have a large number of features the algorithm tends to have computationally high costs and requires substantial memory.

Deep learning can be used to extract high-dimensional features, which can be regarded as a complex combination of existing features. This can lead to a reduction of the needed features to accomplish a decent classification.

Therefore, deep learning can be used as a feature reduction method. Nevertheless, it is well known that deep learning takes a long time to converge, especially with massive amount of data having many features. In contrast to this, FSOC is characterized by a short processing time.

3 FSOC Algorithm

The FSOC algorithm uses the heuristic merit (MS) to select those relevant and non-redundant features (optimal subset) [⁹], which measures how ’good’ a set of features is (see Equation 1), the subset with highest merit will be the optimal subset.

In it, k is the number of features in the optimal subset, rcf is the average correlation between the features and the class feature (target feature), and rff is the average correlations between the features selected.

The same principle is used in test theory to design a composite test for predicting an external variable of interest, ’features’ are individual tests which measure traits related to the variable of interest (class or target feature).

If a group of components increase, it is unlikely that all of them are highly correlated with the target feature and at the same time bear low correlations with each other [¹⁹]:

3.1 Description of FSOC

Our algorithm (Algorithm 1, below), shows differences with previous state-of-the-art. FSOC starts by producing a set S of the correlations between each dependent feature and the dependent feature (class), and sorting set S in decreasing order.

Algorithm 1 FSOC algorithm 

Set S′ (initially empty) will contain the features selected as relevant and non-redundant. Subsequently, the first element is extracted (that feature having the highest correlation with the class) from the set S, add it to the set S′ and save the value of its correlation as the current merit.

Then FSOC evaluates in an orderly manner the inclusion of each element Xi of the set S in S′, by comparing the merit (given by Equation 1) of Xi∪S′ with the current merit.

The feature Xi that induces the highest merit (let us call it m) is added to S′ and removed from S, as long as that merit m is higher than the current merit. In addition, the current merit is set to m.

The addition of features from S to S′ continues until the merit of S′ is greater than the merit of Xi∪S′ (for any Xi∈S), or there are no more features to analyze. See Algorithm 1.

Two important differences between FSOC and CFS algorithms (Algorithm 2) involve the way in which the features to be included in the optimal subset are searched.

Algorithm 2 CFS algorithm 

The CFS algorithm searches the next feature to be added to the set S′ (the set of features selected as relevant and non-redundant) in all the set S (the set of features not yet included in S′).

If the size of S is large, this repeated search to the complete set S is costly. Instead, FSOC orders once the features in set S by decreasing correlation of each feature with the class feature. The search of the next feature to add to S′ stops sooner, due to this ordering.

The first difference is found in steps 4 to 9 of the FSOC algorithm, which obtain the correlation of each feature with the class feature and order them in decreasing order.

In algorithm CFS, its first iteration with the features (steps 7 to 20) also repeatedly seeks the feature Xi which obtains the highest merit of Xi∪S′, but it does this search without ordering the features by descending correlation with the class.

As it turns out, this step (ordering the features) is fundamental to reduce the computational cost. The second and biggest difference appears in steps 13 to 31 of algorithm 1, where two nested cycles are described.

The first cycle adds feature Xi to set S′ if the merit of Xi∪S′ is greater than the merit of S′. In other words, it tries to maximize the merit of S′.

The second cycle (steps 16 to 26) is internal. Since it searches each feature in decreasing order (of the correlation of the feature with the class), and stops as soon as the next candidate feature Xi fails to have the merit of Xi∪S′ higher than the merit of S′.

It is considered that the other features (“below” Xi in set S) could provide little information because they have less correlation with the class.

Instead, CFS evaluates the merits of all the features of S, and keeps doing so until there is no feature that increases the merit of S′.

Due to this early stop, FSOC performs fewer comparisons between features, and therefore fewer correlations between them. It is clear that fewer comparisons between features will produce a lower computational cost: lower CPU usage.

With respect to disk I/O, the training set has to be read once into main memory, either all of it at the same time (if it fits) or in batches of objects (if too large to fit in memory), in order to compute the correlations (lines 4 to 8 in algorithm 1; lines 8 to 16 in algorithm 2).

The pseudocode of algorithm CFS (Algorithm 2) does not make clear whether the merit calculation (line 9 in algorithm 2) causes the complete training set to be read for each feature Xi to be tested, or if some other method is used. In either case, FSOC has a lower or at least equal I/O cost than CFS.

The end result is that FSOC saves total computational cost = CPU time + I/O time. This improvement is very beneficial for data sets with large volumes of information and with a large number of features.

In addition, because of the way FSOC computes set S’ (algorithm 1), the relevant features in S’ are in ascending order of merit. In this manner, it is easy to reduce further the set of relevant features, in the case S’ is too large.

Now, let us compare how FSOC and ECMBF work, the main difference between FSOC and ECMBF are that ECMBF uses two thresholds; α (relevance) and β (redundancy). A poor setting of these thresholds could produce a set S′ with low classification accuracy.

The search space for these thresholds is two-dimensional in ranges of values in [0-1]; decreasing or increasing them independently does not guarantee that the combination found is ’good’, because the classification accuracy is not necessarily a monotonic function of either of them.

Testing different values of α and β and evaluating their behavior with some predictor (a classifier, for instance) could be impractical. FSOC avoids making comparisons where there is little predictive information, unlike ECMBF where the features that meet the α (relevance) threshold require a second redundancy filter (β), where comparisons between features are unavoidable.

Now, let us compare how FSOC and FCBF work, the main differences between FSOC and FCBF are that, although both algorithms order the features considering their correlation with the class, the two cycles described in steps 13 to 31 of algorithm 1 allow a faster stop and avoid making comparisons (correlations) between features, as opposed to FCBF, where the search is more exhaustive and therefore considers a greater number of comparisons.

In addition, the relevance parameter (δ) is not necessary in FSOC. This is a very important consideration, because poor values assigned to it could cause features to be incorrectly selected and prematurely discarded, resulting in lower precision when sorting with them. Moreover, it is difficult for the user to assign good values to δ.

The next section shows experiments with real data sets where it is observed that FSOC (mainly due to the ordering of features by their correlation with the class and the two nested cycles, already described) helps the reduction in computational costs and number of features selected.

4 Statistical Comparison of FSOC, CFS, ECMBF and FCBF Using Several Classifiers

This section compares FSOC with several feature selection methods, with respect to (1) accuracy (percentage of correct classifications), (2) computational cost (defined as number of necessary comparisons between features), and (3) reduction of features.

The experiments carried out use the accuracy and Kappa measures, since accuracy is an easy measure to understand and although it has a disadvantage when faced with unbalanced data sets, it is complemented by the Kappa measure, that improves on the accuracy measurement by measuring the agreement between predicted and real value, due to chance (the classifier does a random class assignment).

Statistical analysis consists in comparing the algorithms through multiple averages of random executions of data sets.

Our universe U (see Table 1) consists of 36 datasets with nominal, numerical and categorical features, the number of classes ranging from 2 to 26, and the number of instances or objects in the dataset is between 62 and 8,405,0979.

To reduce the possible bias introduced by a classifier, three classifiers were used in this analysis: A tree classifier (C4.5), an ensemble of tree classifiers (Random Forest), and a Naive Bayes classifier, in such a way that the averages by the central limit theorem normalize the results and they can be compared each other.

The pseudocode of the statistical algorithm used is shown in algorithm 3. For each feature selection algorithm perform randomly select a data set from U (refer to Algorithm 3), then randomly select a classifier (Random Forest, C4.5, Naive Bayes), make the feature selection of the selected data set and classify.

Algorithm 3 Statistical algorithm to compare feature selection algorithms 

Store the obtained value in T until it has at least 36 values. Then, the average of T will be stored in Y, this process will be carried out until the values obtained in Y form a Gaussian distribution.

According to the central limit theorem, a Gaussian distribution will be obtained when there are at least 5 observations in each decile and the normality test (a test to determine whether sample data has been drawn from a normally distributed population [within some tolerance]) has an error of 0.05 (This would be equivalent to say that there is a 5% probability that the distribution is not normal) X2≤5, if these properties are not maintained is necessary return to step 2 (see Algorithm 3).

Comparing the results of FSOC algorithm (Figure 2), when selecting and using the features identified as relevant slightly exceeds the average accuracy than when using the full data set (1.2%), as well as slightly beating the FCBF (3.08%) and ECMBF (1.37%) algorithms.

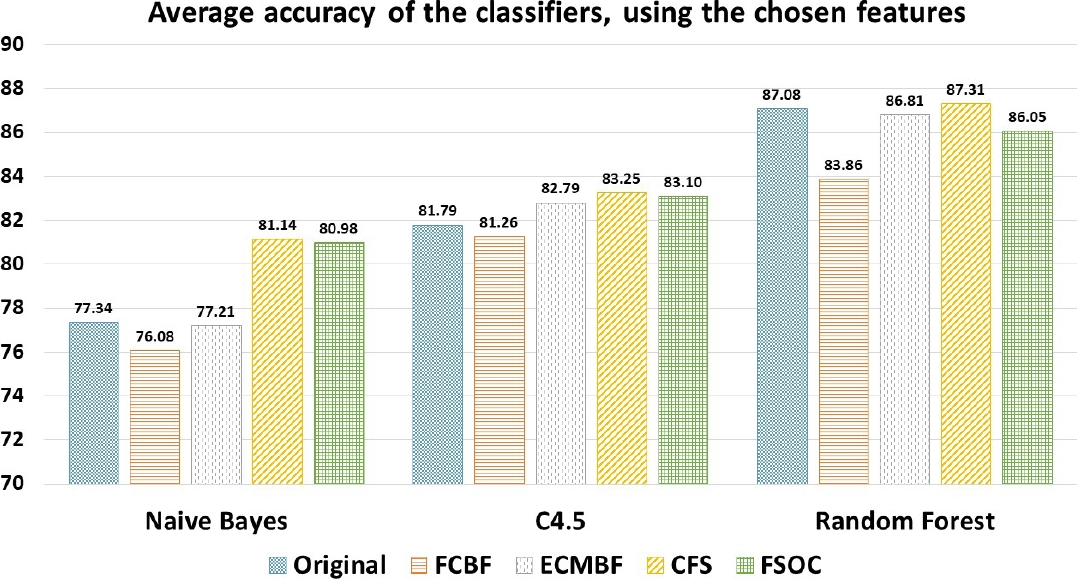
Fig. 1 Average accuracy percentage of the Random Forest, C4.5 and Naive Bayes classifiers for the 36 data sets, using the different features obtained from the feature selection algorithms. The vertical axis of the graph starts at number 68 to allow a greater appreciation of the results. The Feature Selection Ordered by Correlation (FSOC) algorithm has similar accuracy with Correlation Feature Selection (CFS), but with less features and computational cost, Efficient feature selection based on correlation measure (ECMBF) are slightly better just in Random Forest classifier while Fast Correlation-Based Filter (FCBF) is the lowest 

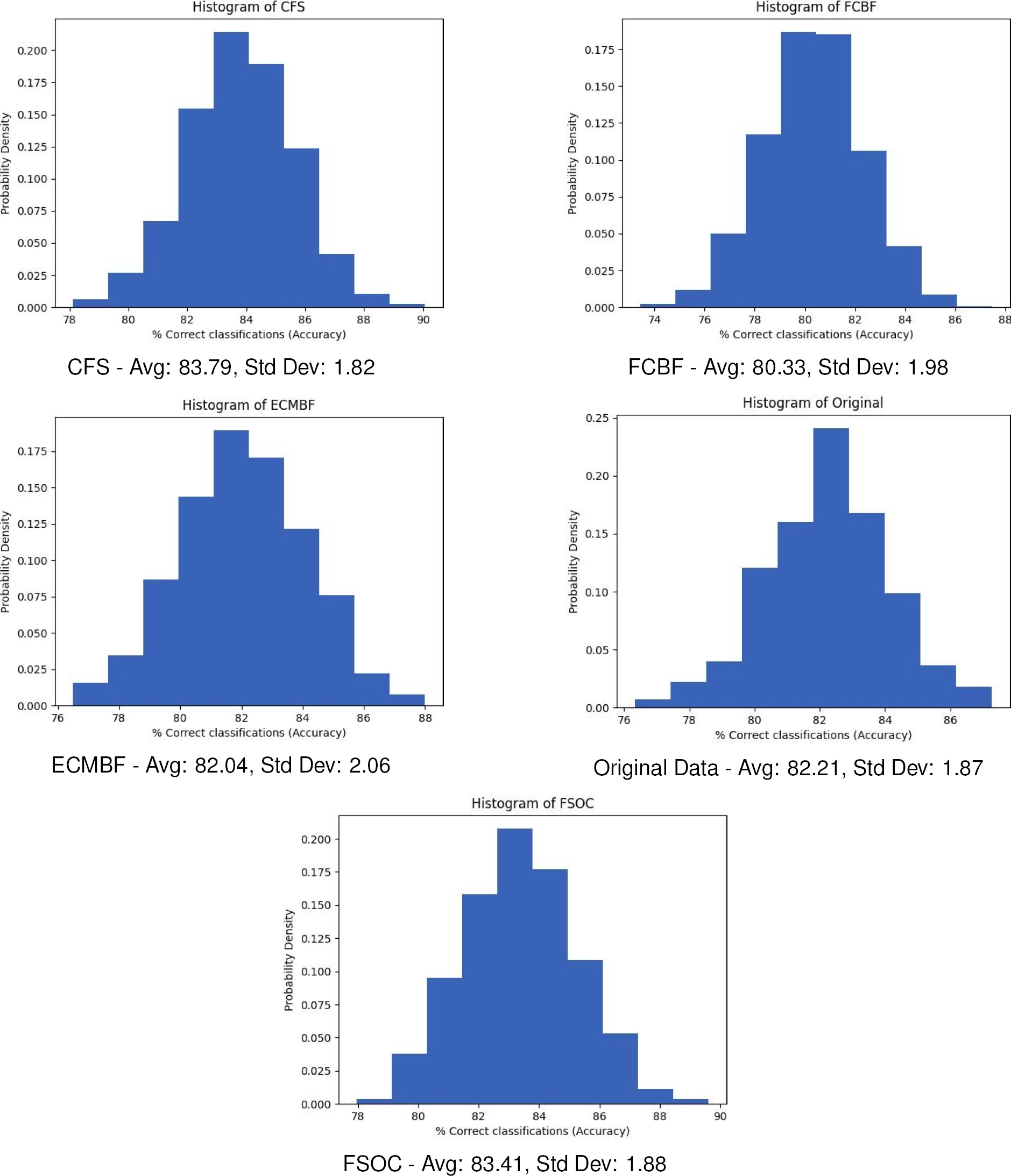
Fig. 2 Results of the statistical algorithm (Algorithm 3) applied to each feature selector algorithm. Gaussian-shaped histograms are displayed, allowing comparisons between them 

However, CFS is slightly higher than FSOC (0.38%). The difference of average accuracy between FSOC and the rest of the algorithms it is less than 1%, so we could say that it is practically the same or very similar (see Figure 2).

In addition to the previous results, the Chebyshev inequality [¹²] (see Equation 2) allows us to rank the algorithms by determining their probability that the percentage of correct classifications (y) is in the interval [μ−kσ, μ+kσ] of their distributions, where μ is the average accuracy, k is the number of standard deviations and σ is the value of the standard deviation:

If we establish a value of k=3.1623 we will know that the values of y will fall in this interval with the probability of p≈0.9. Therefore, the best (largest) value finding for the feature selection algorithms will be given by μ+kσ.

This is a way of measuring the performance or quality of the algorithm to solve the problems in U. Table 2 shows the algorithm with the corresponding values of μ+kσ, ordered from best to worst accuracy with a probability of falling in the interval (μ−kσ, μ+kσ) of 0.9.

All the algorithms show good average and upper bound in accuracy (greater than 80). While Table 3 shows the algorithms in order from less to high cost computational. Individual results by data set and classifier are placed in Tables 5, 6 and 7.

Table 4 shows the number of features selected by each feature selection algorithm. In addition, the number of comparisons necessary to obtain the subset. In addition, individual results by data set and classifier are placed in tables 5, 6 and 7.

Figure 1 compares the relative accuracy from individual experiments with the test data sets, as given by three different classifiers.

The FSOC algorithm gets less features than CFS, while FCBF and ECMBF select in average more features. Algorithms FCBF y ECMBF are the slowest for large features, followed by CFS and finally by FSOC (see Table 3).

It is interesting to see how FSOC behaves with large data sets (large number of instances), such as Poker, Susy, Mobile Health and Covid-19.

It can be seen that FSOC maintains classification efficiency by reducing the features of large data sets, which tend to generate very large models (mainly tree models) that sometimes cannot be stored in main memory.

The same is true for data sets of thousands of features, where very large and poorly understood models tend to be obtained.

Generating models with fewer features helps improve training and validation times, as well as reducing the space required to store models with little or no loss of predictive information.

In addition, if the reduced features are used for tree models, the tree becomes easier to understand. The algorithm with the lowest average in features and computational cost was FSOC.

Although CFS algorithm very slightly exceeds FSOC on the average of percentage of correct classifications and statistical kappa in the three classifiers, it also far exceeds the average of its computational cost compared to FSOC.

The FCBF algorithm has a low efficiency, it is below the rest of the algorithms, while the use of the complete set of features can cause some classifiers to be confused and overfit.

FSOC allows reducing the features to avoid analyzing statistical relationships that are not very discriminatory for the class (target) or the information contained in them are redundant.

In turn, it helps to eliminate those features that are unreliable because they were apparently answered randomly or based on a non-rational critic, helping to reduce data recovery and maintenance costs.

Could further reduction in time be achieved by parallelization? It is possible to further accelerate FSOC by simultaneously computing the correlation between feature Xi and the class feature C (lines 4 to 7 in algorithm 1), if there were many features.

To achieve this with several processors, the complete training set, as well as a fraction of the features, are given to each of them. Each processor will compute the correlation between the features given to it and the class feature C.

Nevertheless, the rest of the algorithm (lines 10 to 32, algorithm 1) can be run in just one processor, since the time spent by it is short.

5 Conclusions and Future Work

This article presents a method called FSOC that selects relevant features in a way to reduce the computational cost of its selection, with little or no loss of classification accuracy.

Statistical results comparing three well-known methods for feature selection with Feature Selection Ordered by Correlation (FSOC). It measures the computational cost to obtain such reduced set, and the efficiency (number of correct classifications) produced by the selected features.

The efficiency was obtained using classifiers C4.5, Random Forest (decision trees) and Naive Bayes (conditional probability), tested with a collection of 36 data sets available in the open literature.

The results show an efficiency very similar between FSOC and the best algorithm Correlation Feature Selection (CFS), but FSOC is 42 times cheaper with respect to CFS in the computational cost with null or very slight loss of discriminatory power.

Therefore, the FSOC method is especially relevant for high volumes (large data sets) and high dimensionality data (hundreds of thousands of features).

Even though Fast Correlation-Based Filter (FCBF) is fast, it needs to adjust a relevance threshold not to discard useful features. In addition, it classifies with less accuracy, and uses a number of features higher than FSOC does.

The Efficient feature selection based on correlation measure (ECMBF) algorithm is fast, but it is necessary to have a prior knowledge of the data sets, or to find (by trial and error) adequate values for the relevance and redundancy parameters. These extra classifications render it impractical.

Initial work with FSOC on data sets with large amounts of data and high dimensionality (Parkinson, Prostate_ge, Smk_Can, Yale, Gissete, Leukemia, Colon, Madelon, Pcmac, Basehock,Poker, Susy, Mobile Health and Covid-19, Tables 1 and 4, with up to 5,000,000 samples and up to 5,000 features) shows less features selected with no sacrifice in accuracy.

It is planned to perform further testing with additional high dimensionality data sets. It will also be interesting to integrate new ways to discretize numerical features or to find new measures to correlate nominal, numeric and mixed features.