1 Introduction
In the automotive manufacturing industry, there are different problems to solve, such as the design of new parts, optimization schedule times, new aerodynamic car designs, painting processes, and autonomous driving, among others.
The initial heuristic involves a double swap mechanism, requiring selecting two cities or nodes. These chosen cities exchange positions, creating a novel solution [46]. The algorithm is shown in 2.
Specifically, the painting process is one of the most common occurrences during car manufacturing and its use, as it becomes worn or damaged due to various factors. In the first case, when it comes to painting a car from the beginning, it is done with collaborative robots that work on specific work areas in most manufacturing companies.
The second case involves handmade workshop procedures with tools such as a compressor, airbrush, etc. For task assignment problems in collaborative robots, different algorithms help optimize the route and avoid possible collisions [67]. However, in most workshops, the car painters do not have performance methodologies that improve their work.
State of the art in metaheuristics, according to [23], has been applied to different problems such as scheduling [11], manufacturing and production, water management, oil and energy, traffic control, and among others.
Nevertheless, the actual problems in the industry are generally oriented to health, water, housing, education, and electromobility, and different artificial intelligence techniques can solve these problems. The most popular methods in recent research are neural networks [70], deep Learning [62], meta-learning [22], and others.
Therefore, there is a lot of research in the state of the art about the comparison of solving benchmark problems, artificial instances, or any other kind of problem [12, 27].
With these two contexts, metaheuristics can help solve industry problems, such as designing a route for collaborative robots or robots that work individually [28].
This work proposes a solution applicable to traditional painting workshops by designing a robotic arm with five degrees of freedom that can work in an
Our project aims to help the car painting process, where prolonged exposure to chemical paints causes serious human health problems (see section 3). Our proposal pays in the following points:
– Design of a robotic arm with five degrees of freedom adopted in a two-dimensional plane. The above is because, in the real application, it is easier and cheaper to implement.
– Integration of metaheuristics to design routes in the robot and parts.
– Methodology for recognizing parts and generating an optimized trajectory for your painting process.
The cost-benefit of the implementation of a Robotic Arm design and software for automotive painting processes are important since it covers the following aspects:
– Hardware and Software Acquisition Costs: The physical implementation of the prototype is much less expensive than that of a commercial robotic arm. Likewise, it contains the sensors, controllers, and materials necessary for its correct operation.
– Installation and Start-up Costs: The maximum costs for installation and testing range from $100 to $150 dollars, which makes it a viable option that is quite competitive with others that cost around $5,000.
– Use of Optimization Techniques. Optimization techniques can be used within the complete painting process to design the routes the robot must follow, decreasing the cost and time of this task.
The expected benefits of implementing the system include labor savings, increased productivity, reduced waste, improved quality, and occupational safety. The rest of this article is structured in 6 sections described below.
An extensive review of relevant literature was reported in the related works section 2. The theory section 3 presented main concepts and theoretical definitions, while the methodology section 5 detailed the procedures used in the research.
The results section 6 showed the findings obtained from the implemented methodology. Finally, in the conclusions and future work section 7, an analysis was carried out based on the results collected throughout the experimentation with metaheuristics.
2 Related Work
2.1 Car Painting Problem
An important step in the automotive production system is the aesthetic finish of the vehicle paint, which changes for the different models and colors of production and the availability and quantity of paint ovens. Consequently, the problem of scheduling and sequencing vehicle models that minimize the waiting problem in the painting system arises.
State of the art has addressed different lines of research for the solution of the vehicle painting problem: The first focuses on the general aspects of the problem in the context of painting times and model sequences and poses the problem as an optimization system, where Metaheuristic algorithms solve the scheduling [15]; Secondly, the research focuses on minimizing the error corrections in the painting process by studying the nozzle and stroke size [49]; thirdly, the literature proposes that the solution lies in the robot trajectories and the painting sequence, and generates a new optimization algorithm by resampling and speed calibration [2, 8].
In another perspective, the painting problem is manipulated by a set of nodes in the finishing and painting process network. In the network, each process configures a certain task; however, from the point of view of process planning and optimization, it needs to start from an initial point [32, 24].
To solve the optimal scheduling problem, research has adapted the concept of the Voronoi diagram, which consists of separating the space around the key points of the painting process. Consequently, Voronoi diagrams allow the creation of an environment of efficiency and optimization that avoids wasting time and speeds up the coverage of the painting process [55].
2.2 Collaborative Robotic Problem
In an automotive industrial system, one of the fundamental paradigms is Industry 4.0, where we highlight the concept of collaborative robotics. Using graph theory, research has addressed the issues arising from robot collaboration in a paint-finishing environment [58].
Accordingly, the robots in the collaborative network are represented as nodes, whereas the edges are the process connections between the robots. Tackling the problems derived from collaborative robotics through graphs obtains different benefits: it allows studying the dynamics of the collaborative network, the distribution of the nodes and their edge connection, process synchronization, and coordination of the primary tasks [59, 57, 66].
To study the dynamics of the collaborative robot ensemble, the Euler-Lagrange formulation allows the mathematical modeling of the movements in the robotic arms. In a general context, Euler-Lagrange considers the principle of minimum energy of the event; this approach leads directly to an optimization in the movements of the painting and finishing processes of the vehicles [71, 13].
An aspect to highlight of Euler-Lagrange is the pressure of the dynamic models since it is based on the minimum action and allows the deterministic design of electronic controllers that make the automotive processes more efficient [60, 31].
In comparison, different techniques have addressed the problem of coordination and optimization of collaborative robotic networks: research in the design of controllers that make the processes in the network more efficient, adaptation of the small gain theorem, which analyzes the steady states in the control system under a linear dynamics approach; application of shrinkage analysis dedicated to the treatment of nonlinear control problems [68, 69, 33].
In summary, research in a collaborative robotics environment considers three elements of its behavior: simple control, linear control, and nonlinear control.
The points mentioned above point to the complexity and diversity of problems and stochastic systems that collaborative robotics represents.
2.3 Health Risks During the Car Painting Process
The industry dedicated to vehicle painting plays a crucial role in enhancing the aesthetic appeal and providing protection to automobiles; however, this process entails significant health risks for workers exposed to the chemicals involved.
According to the World Health Organization (WHO), occupational exposure to chemicals found in paints and solvents affects approximately 11% of workers globally, including those exposed to organic solvents present in paints and varnishes [65].
These products often contain volatile organic compounds (VOCs) such as benzene, toluene, and xylene, which have been associated with mutagenic, carcinogenic, and teratogenic effects [43, 44, 48], as well as neurological disorders [61, 3, 36]. The International Agency for Research on Cancer (IARC) has classified some of the chemical components present in automobile paints as possible carcinogens [63], with benzene being linked to the development of leukemia.
Several reports have documented health issues experienced by automotive industry workers concerning their exposure to chemicals present in paints. For instance, Hammond et al. (2005) [20] report an increase in the incidence of asthma and chronic obstructive pulmonary disease, as well as an elevation in allergy-related symptoms such as eye and nose irritation, sinusitis, cough, and even heartburn.
Painters using aerosols have been observed to experience symptoms including excessive tearing, persistent cough, and short-term memory loss, along with a higher prevalence of respiratory symptoms, corneal opacity, and dry skin compared to the control group [40].
Furthermore, the risk is not confined solely to exposure to volatile organic compounds (VOCs), as it can also arise from contact or inhalation of metals such as cadmium, chromium, and nickel present in some paints. These metals can cause acute and chronic poisoning, as well as an increased risk of cancer [30, 39]. The primary Chemical Components Found in Paints Intended for the Automotive Industry and Their Health Effects are:
Cadmium. Acute and chronic poisonings, accumulation in kidneys, chronic decrement in renal, pulmonary, and hepatic function, causing ulcerations and perforations of the nasal septum, chronic bronchitis, decreased lung function, pneumonia, and other respiratory effects [6]. It exhibits impacts on bones, the respiratory system, the endocrine system, and the reproductive system [5]. Classified as carcinogenic to humans [53, 14].
-
Chromium. Allergic reactions and skin rashes, in addition to nasal irritation and bleeding [14]. Carcinogenic properties, hemolysis, and organ failure [38]. Genotoxic, toxic to reproduction and development [17].
-
Nickel. Systemic, immunological, neurological, reproductive, developmental distortion, and carcinogenic negative effects [9]. Accumulation in the kidney, inflammation of bronchioles, alveolar congestion, hyperplasia of alveolar cells [19].
It may cause dizziness, pulmonary embolism, and respiratory failure [47]. It also leads to congenital disabilities, asthma, chronic bronchitis, heart disorders, and allergic reactions such as skin rashes.
Associated with various types of lung, nasal, laryngeal, and prostate cancers. Induce various side effects, including allergies, cardiovascular and renal diseases, pulmonary fibrosis, and lung and nasal cancer. Epigenetic alterations are observed affecting genome level [16].
-
Benceno. Carcinogenic, causing cancer of the esophagus, ovaries, testicles, colon, and kidneys, as well as acute myeloid leukemia [52]. Induces dysbiosis of intestinal microbiota and metabolic disorders in mice [45, 18].
Additionally, it is associated with atopic dermatitis, irritant contact dermatitis, allergic dermatitis, neoplasms, infections, skin irritation, hypersensitivity, mucosal irritation, rash, redness, skin swelling, allergic hypersensitivity reactions, cutaneous melanoma, non-melanoma skin cancer, dry skin, itching, rash, red itchy blisters, and burns [72, 64, 37].
-
Tolueno. Neuronal inhibitor associated with progressive damage to the central and peripheral nervous system and memory loss. It can lead to neurological dysfunction and hematological damage. It directly affects the central nervous system, causing euphoria, confusion, depression, headache, dizziness, hallucinations, seizures, ataxia, stupor, and coma [35].
It may cause leukoencephalopathy and psychosis, as well as behavioral and functional abnormalities such as decreased memory capacity, cognitive impairment, and symptoms resembling depression [50].
-
Xileno. Neurotoxic effects, hepatotoxicity, and nephrotoxicity, leading to the formation of toxic intermediate and end products akin to those of benzene [21].
It may cause nausea, headache, a sense of ’euphoria,’ dizziness, weakness, irritability, vomiting, slow reaction time, confusion, clumsiness, difficulty speaking, loss of balance, ringing in the ears, drowsiness, loss of consciousness, and anemia. Results in fetotoxic effects such as delayed ossification [7, 26].
The reports above provide a clear and concerning perspective on the health hazards workers face exposed to chemicals in paints used in the automotive industry. These risks range from acute effects such as skin and respiratory tract irritation to more severe consequences, including the development of chronic respiratory diseases and an increased risk of cancer. Adopting appropriate safety practices, adequate training, and using protective equipment are crucial to minimize these risks and preserve the health of workers in this industry.
Furthermore, it is relevant to develop strategies to reduce human contact, and one of these strategies is introducing industry 4.0 technology, which enables remote execution of activities.
3 Theory
3.1 Heuristics and Metaheuristics
In our study, we employed the approach outlined by Ortiz et al. [41], which employs various frameworks for managing Constraint Satisfaction Problems (CSP). An initial solution is generated, refined, and applied perturbative heuristics.
A simple definition of CSP can be found in [42, 41], defined with
3.1.1 Heuristics
A simple definition given by [51] is ”Heuristic approach is based on trial and error to find or discover solutions to the problems”. Two types of heuristics are most commonly used in metaheuristics: construction and perturbation. According to those mentioned earlier, we define construction and perturbative heuristics used in this work. According to [29], two main techniques for building Traveling Salesman Problem (TSP) solutions are greedy heuristic or aleatory and the formal definition of TSP can be found in [25]. In this investigation, the aleatory heuristic was chosen to make the initial solutions (see Algorithm 1) and five perturbative heuristics described in algorithms 2, 3.
The second heuristic is the Crossover heuristic (
An arbitrary cutting point is chosen, where the first portion from Solution A forms the basis of the first offspring solution (SS1), complemented by the second segment from Solution B. The second offspring solution (SS2) is created by the initial part of Solution B combined with the latter segment of Solution A (see Algorithm 3).
The third heuristic, the Nearest Neighbor (
The fourth heuristic, known as K-OPT (
3.1.2 Metaheuristics
The metaheuristics are used to solve problems intelligently by choosing the best from a larger number of available solutions [23]. A metaheuristic algorithm lets one search for optimal solutions to a particular problem with some restrictions.
This searching process can involve some operators such as selection, mutation, improvement, crossover, and, in specific cases, a set of rules or mate mathematical equations that provide a guide during multiple iterations. These iterations are carried out until the solution found meets some criterion [23].
The Iterated Local Search algorithm (ILS) was used in the experimentation. This metaheuristic was proposed by Lourenço et al. [34], which constructs or modifies a solution through an embedded heuristic. The generated solutions are better than randomly generated or altered ones. This algorithm aims to intensify the initial solution by exploring its neighbors. The ILS algorithm is depicted in 6, taken from Talbi El-Ghazali [54].
3.2 Car Painting Problem
The car painting problem has had different variations, and according to [10], the problem above derives from the Paint Shop Problem for Words. In a paint shop, cars go through two painting steps. The first paint step applies a coat of filler paint, and the second one applies a coat of base paint depending on the final color of the car.
According to the type of filling, they are divided into white and black for each car model and each base color. Each of the two painting steps is done using separate spray nozzles, which must be cleaned before a new color can be applied, which can be expensive.
The above results in the definition of the Multi-Car Multi-Color Paint Shop Problem, whose objective is to find a color assignment in the sequence that minimizes the number of color changes for the fill paint nozzle and the paint nozzle base and that also satisfies the color demand required for the different models [10].
3.3 Trajectory Design in Car Painting Problem
With the previous context, this work proposes the design of routes for a robotic arm that can execute within a controlled environment. For our problem, we consider that a vehicle can be cleared into a
With the above, we seek to create a permutation of the
where:
– distance represents the calculated distance.
–
–
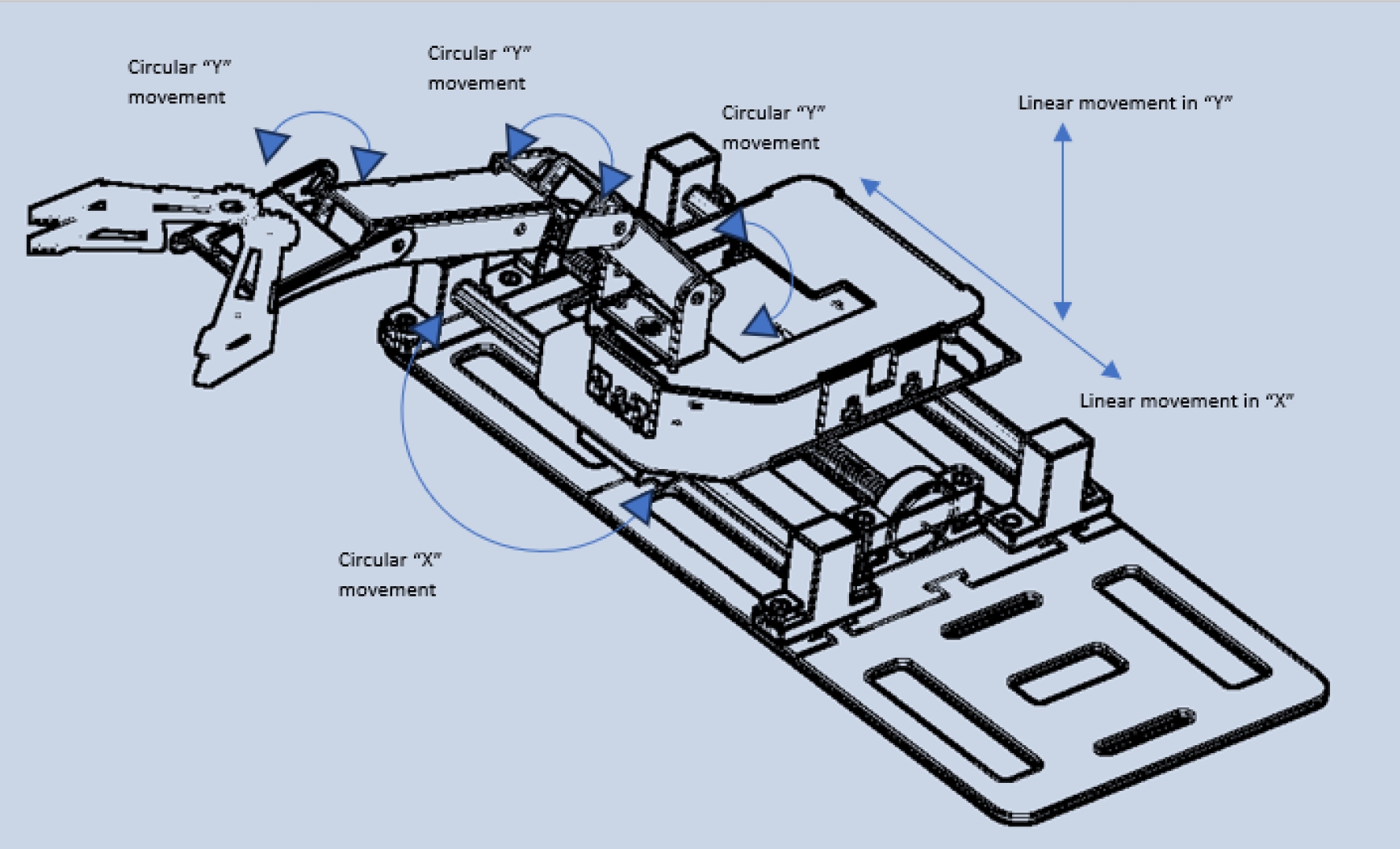
3.4 Robotic Arm Design
The arm design has two types of movements: circular and linear. Each modeled part was assembled using the Autodesk Inventor Professional 2023 software.
Using the restricted tools, their function coincides with the central axes of the cylindrical figures with which their same axes were joined.
Afterward, a matching function placed each piece glued to another. Once these assemblies were in place, the leveling function was used to overlap the bases of the robotic arm to match the upper parts at the same point as the fixation tool to prevent the piece from moving with the other assemblies. The final prototype can be seen in Figure 1. This work focuses exclusively on the development of metaheuristics for designing routes for the robotic arm; therefore, subsequent research will explain its design.
4 Methodology
The methodology developed in this work is described in the next sections.
-
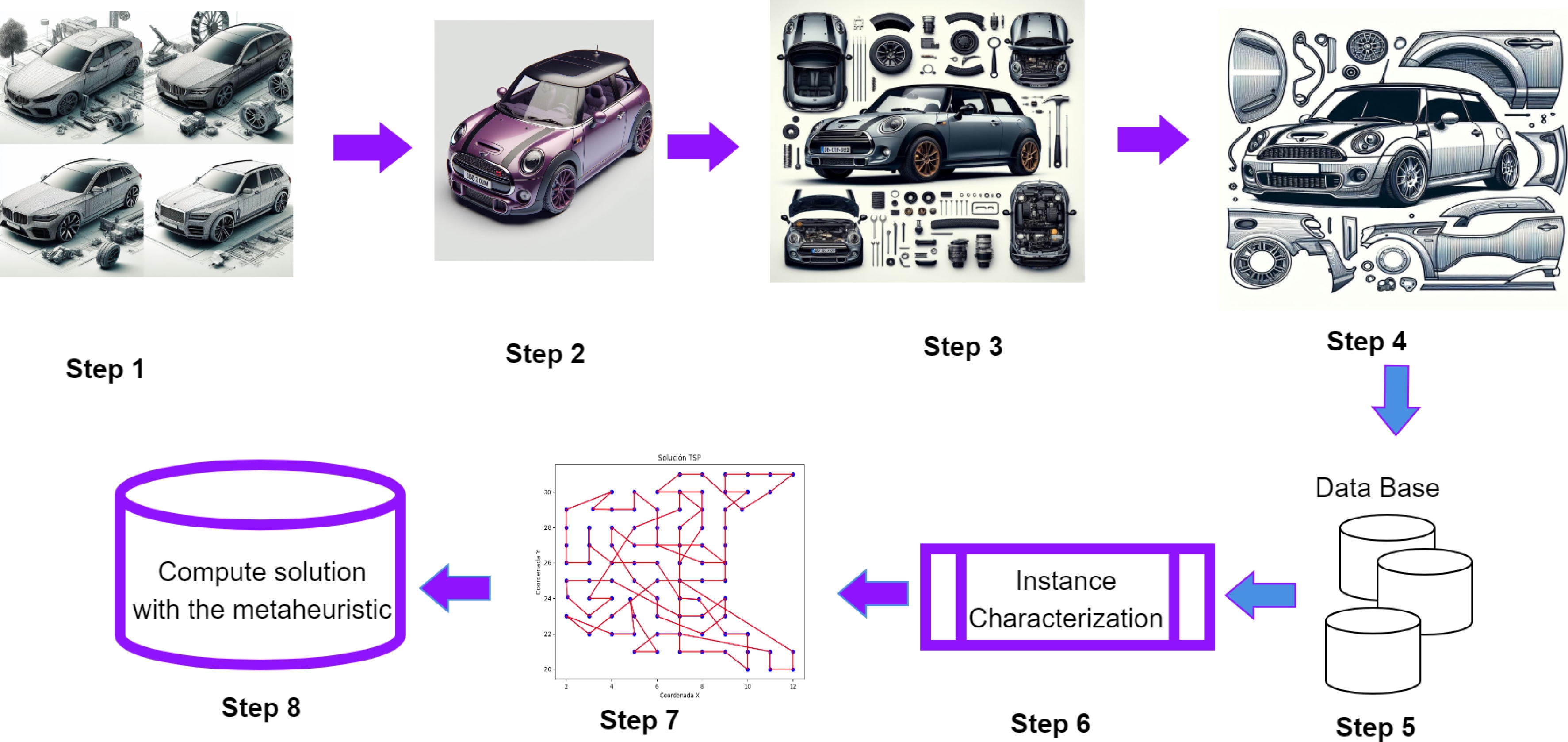
– Definition and Limitation of the Problem. The different cars will be chosen and designed in a CAD sketch in this stage. The type of car and the number of parts each drawing will include will be defined. We define the principal parts such as the roof, doors, bonnet, and bumper.
Subsequently, all completed designs will be collated to form a database of CAD models. This would represent steps 1 and 2 shown in figure 2. The cars considered for the database were selected among the most common models on the global market, such as Mazda, Ford, etc.
-
– Requirements Analysis. In Figure 2, steps 3 and 4 refer to the breakdown of the cars in their different views. Once each car instance has been obtained, the points of interest will be assigned to those through which the robotic arms must pass to paint each piece.
– Design. In the design phase, the robotic arms’ routes will be designed to respect all the restrictions posed in the problem limitation phase using heuristic construction techniques.
– Implementation. Once the routes have been designed, it will be validated which of them are feasible to be applied in a simulation (see Figure 2 in step 7 and step 8). A statistical comparison of the routes built will be made.
– Tests. In this phase, we move on to applying them either in a simulation or in a physical prototype. In addition, all tests and corrections will be made regarding the path of the robotic arms, either physically or through simulation.
5 Methodology
The methodology developed in this work is described in the next sections.
– Definition and Limitation of the Problem. The different cars will be chosen and designed in a CAD sketch in this stage. The type of car and the number of parts each drawing will include will be defined. We define the principal parts such as the roof, doors, bonnet, and bumper.
Subsequently, all completed designs will be collated to form a database of CAD models. This would represent steps 1 and 2 shown in figure 2. The cars considered for the database were selected among the most common models on the global market, such as Mazda, Ford, etc.
– Requirements Analysis. In Figure 2, steps 3 and 4 refer to the breakdown of the cars in their different views. Once each car instance has been obtained, the points of interest will be assigned to those through which the robotic arms must pass to paint each piece.
With this information, a database will be made (step 5), which will subsequently be characterized by instances (step 6).
– Design. In the design phase, the robotic arms’ routes will be designed to respect all the restrictions posed in the problem limitation phase using heuristic construction techniques.
– Implementation. Once the routes have been designed, it will be validated which of them are feasible to be applied in a simulation (see Figure 2 in step 7 and step 8). A statistical comparison of the routes built will be made.
– Tests. In this phase, we move on to applying them either in a simulation or in a physical prototype. In addition, all tests and corrections will be made regarding the path of the robotic arms, either physically or through simulation.
6 Results
Based on the criteria outlined in sections 3 and 5, the car painting problem demands a dedicated data structure as presented in [41]. For this instance set, our approach leaned towards employing the
These were selected based on their relevance and applicability within the problem’s framework, as detailed in the referenced work by Ortiz et al. (2023).
Different 3D models of vehicles were designed using the computer mechanical design software Inventor 3D. A set of 58 CAD designs was obtained according to various characteristics.
We grouped the cars according to the number of pieces counted, and the designs are described in table 1.
Table 1 Description of cars used for 3D modeling
| No. | Name | Points | Length Path | No. | Name | Points | Length Path | |
| 1 | AUDI-R8-CAPO-2024 | 90 | 93 | 30 | dodge-charger-1969-CARROCERIA | 165 | 192 | |
| 2 | AUDI-R8-CARROCERIA-2024 | 174 | 175.4 | 31 | dodge-charger-1969-PUERTAS | 53 | 54 | |
| 3 | AUDI-R8-PARTE TRASERA-2024 | 78 | 81 | 32 | FERRARI-CAPO | 84 | 83 | |
| 4 | AUDI-R8-PUERTAS-2024 | 42 | 41 | 33 | FERRARI-CARROCERIA | 250 | 309 | |
| 5 | AVEO-SEDAN-CAPO | 53 | 52 | 34 | FERRARI-PUERTAS | 38 | 37 | |
| 6 | AVEO-SEDAN-CARROCERIA | 136 | 176 | 35 | FORD F150 RAPTOR-CAPO | 107 | 107 | |
| 7 | AVEO-SEDAN-PARTE TRASERA | 58 | 57 | 36 | FORD F150 RAPTOR-PUERTA TRASERA | 55 | 54 | |
| 8 | AVEO-SEDAN-PUERTAS | 28 | 27 | 37 | FORD F150 RAPTOR-PUERTAS | 71 | 70 | |
| 9 | BUGATTI-CARROCERIA | 41 | 44 | 38 | FORD FIESTA MK3-4-CAPO | 54 | 53 | |
| 10 | BUGGATI CHIRON-CAPO | 35 | 34 | 39 | FORD FIESTA MK3-4-CARROCERIA | 120 | 134 | |
| 11 | BUGGATI CHIRON-CARROCERIA | 189 | 215.8 | 40 | FORD FIESTA MK3-4-PUERTA TRASERA | 86 | 85.4 | |
| 12 | BUGGATI CHIRON-PUERTA TRASERA | 45 | 48 | 41 | FORD FIESTA MK3-4-PUERTAS | 67 | 66 | |
| 13 | BUGGATI CHIRON-PUERTA | 62 | 61 | 42 | FORD GT40 -3-CAPO | 53 | 53 | |
| 14 | CADILLAC ELR-CAPO | 48 | 47 | 43 | FORD GT40 -3-CARROCERIA | 82 | 83.6 | |
| 15 | CADILLAC ELR-CARROCERIA | 52 | 54 | 44 | FORD GT40 -3-PUERTAS | 103 | 103 | |
| 16 | CADILLAC ELR-PUERTA TRASERA | 28 | 27 | 45 | FORD MUSTANG -3-CAPO | 83 | 82 | |
| 17 | CADILLAC ELR-PUERTA | 66 | 68.6 | 46 | FORD MUSTANG -3-CARROCERIA | 82 | 83 | |
| 18 | camaro-z-28-1969-CAPO | 132 | 131 | 47 | FORD MUSTANG -3-PUERTAS | 107 | 120 | |
| 19 | camaro-z-28-1969-CARROCERIA | 101 | 104 | 48 | FORD MUSTANG 1965 -4-CAJUELA | 36 | 35 | |
| 20 | camaro-z-28-1969-PUERTA | 64 | 65 | 49 | FORD MUSTANG 1965 -4-CAPO | 76 | 75 | |
| 21 | Chevrolet-Camaro-model-CAPO | 56 | 55 | 50 | FORD MUSTANG 1965 -4-CARROCERIA | 78 | 77 | |
| 22 | Chevrolet-Camaro-model-CARROCERIA | 44 | 49 | 51 | FORD MUSTANG 1965 -4-PUERTAS | 36 | 35 | |
| 23 | chevrolet-camaro-model-PARTE TRASERA | 24 | 23 | 52 | FORD MUSTANG 1967 -4-CAPO | 30 | 29 | |
| 24 | Chevrolet-Camaro-model-PUERTAS | 79 | 81.5 | 53 | FORD MUSTANG 1967 -4-CARROCERIA | 64 | 63 | |
| 25 | DATSUN 1500 PICK UP-CAPO | 48 | 47 | 54 | FORD MUSTANG 1967 -4-PUERTA TRASERA | 18 | 17 | |
| 26 | DATSUN 1500 PICK UP-CARROCERIA | 66 | 68 | 55 | FORD MUSTANG 1967 -4-PUERTAS | 34 | 33 | |
| 27 | DATSUN 1500 PICK UP-PUERTA TRASERA | 40 | 39 | 56 | FORD RANGER -3-CAJUELA | 18 | 17 | |
| 28 | DATSUN 1500 PICK UP-PUERTA | 41 | 40 | 57 | FORD RANGER -3-CARROCERIA | 84 | 83 | |
| 29 | dodge-charger-1969-CAPO | 47 | 46 | 58 | FORD RANGER -3-PUERTAS | 66 | 69 |
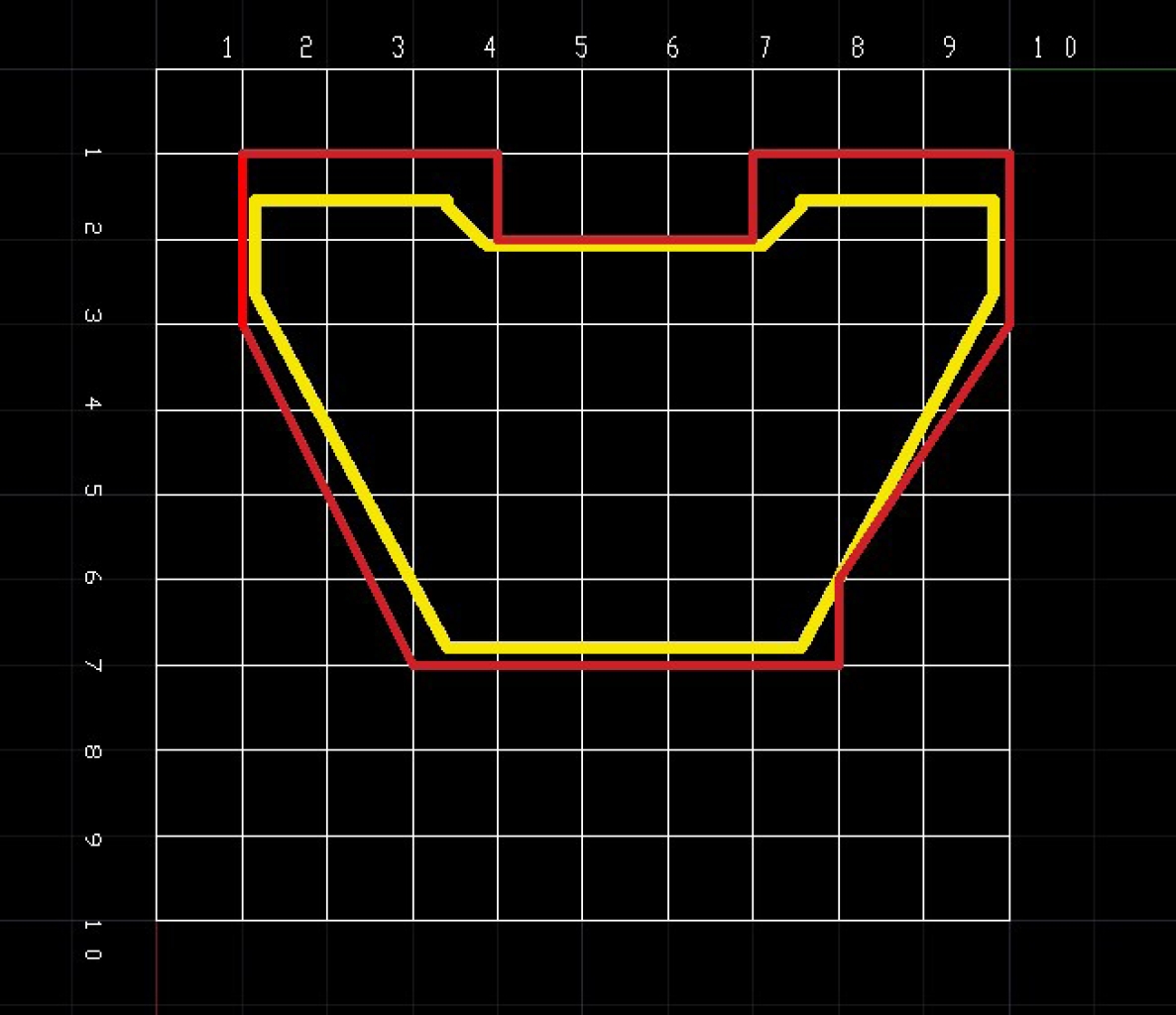
After selecting the vehicle 3D-CAD models, they were imported into Auto CAD to work in a 2D format. This is because if each piece has to be painted with a specific route, it needs to be in a two-dimensional plane to know the coordinate
Subsequently, a 20
With the help of our Cartesian coordinates application for Auto CAD loaded from the AP command, we will place the points that will be our coordinates in
6.1 Heuristics Results
We will describe the parameter configuration for each construction heuristics and explain the statistical tests used to compare the experiments. The experimentation involved testing Instances on a laptop with the following specifications: an Intel® Core™ i3-1005G1 CPU clocked at 1.20 GHz, 8 GB of RAM, and a 64-bit Windows 11 operating system.
The methodology was implemented using Python, and the experiments were iterated 31 times. Each heuristic experiment had a stipulated limit of 100,000 function calls per instance.
For the statistical analysis, first, the Shapiro-Wilks statistical test was applied to check if the data had a normal distribution, and the results indicated that the data did not follow a normal distribution; therefore, the median was chosen as the statistical representative.
We use the benchmark proposed in previous sections with 58 instances tested with 31 runs. We show our results in Table 2. The Friedman (FT), Alienated Friedman (AFT), and Quade (QT) statistical tests were applied to distinguish the performance of the heuristic set.
Table 2 Shapiro Wilks statistics for each heuristic
| Heuristic | Statistic | P-Value |
| 0.721222043 | 3.54E-09 | |
| 0.645808816 | 1.45E-10 | |
| 0.652767837 | 1.91E-10 | |
| 0.660536528 | 2.60E-10 | |
| 0.665777683 | 3.22E-10 |
We set
Table 3 Median for heuristics
| 1 | 131.6 | 383.1 | 210.7 | 135.9 | 161.8 | 30 | 308.7 | 1283.9 | 710.0 | 383.7 | 462.7 |
| 2 | 299.5 | 1114.1 | 551.1 | 356.5 | 429.6 | 31 | 73.2 | 189.3 | 112.3 | 68.4 | 78.1 |
| 3 | 112.8 | 314.9 | 172.8 | 114.0 | 129.4 | 32 | 117.8 | 320.0 | 173.8 | 119.1 | 138.6 |
| 4 | 50.9 | 103.8 | 62.7 | 48.7 | 52.7 | 33 | 570.0 | 2363.6 | 1194.0 | 714.2 | 860.3 |
| 5 | 67.5 | 152.2 | 91.2 | 64.6 | 71.8 | 34 | 46.0 | 87.2 | 57.8 | 43.5 | 45.5 |
| 6 | 249.0 | 894.5 | 499.3 | 271.9 | 343.5 | 35 | 158.2 | 494.3 | 244.2 | 170.1 | 202.5 |
| 7 | 73.3 | 175.5 | 101.0 | 72.0 | 82.8 | 36 | 71.7 | 171.2 | 99.8 | 67.3 | 77.4 |
| 8 | 31.1 | 52.6 | 36.4 | 30.4 | 30.7 | 37 | 97.6 | 266.6 | 140.1 | 102.3 | 117.7 |
| 9 | 54.0 | 121.5 | 71.1 | 51.9 | 56.6 | 38 | 66.6 | 157.6 | 91.6 | 65.3 | 74.5 |
| 10 | 40.4 | 75.9 | 49.5 | 40.3 | 42.0 | 39 | 194.6 | 663.8 | 350.5 | 214.3 | 255.7 |
| 11 | 346.2 | 1379.5 | 745.9 | 438.4 | 529.5 | 40 | 136.7 | 413.4 | 220.9 | 140.7 | 165.4 |
| 12 | 55.0 | 126.4 | 76.9 | 55.0 | 59.8 | 41 | 96.2 | 251.9 | 144.7 | 94.1 | 112.0 |
| 13 | 79.8 | 199.4 | 114.7 | 77.4 | 92.2 | 42 | 64.9 | 154.2 | 89.8 | 64.0 | 72.9 |
| 14 | 58.2 | 127.6 | 74.9 | 56.7 | 62.4 | 43 | 125.2 | 374.9 | 215.3 | 123.7 | 145.0 |
| 15 | 66.5 | 161.4 | 93.4 | 67.3 | 73.3 | 44 | 162.1 | 500.1 | 284.7 | 166.7 | 200.7 |
| 16 | 29.5 | 52.7 | 35.8 | 30.9 | 30.8 | 45 | 116.3 | 315.2 | 168.4 | 115.5 | 138.5 |
| 17 | 92.2 | 238.3 | 126.8 | 90.3 | 102.3 | 46 | 116.4 | 342.1 | 185.5 | 118.8 | 139.2 |
| 18 | 194.1 | 661.2 | 328.1 | 228.4 | 273.4 | 47 | 172.7 | 582.3 | 330.4 | 185.8 | 229.7 |
| 19 | 147.1 | 477.0 | 256.7 | 162.0 | 191.0 | 48 | 41.7 | 83.5 | 54.1 | 40.1 | 42.0 |
| 20 | 97.6 | 271.7 | 143.8 | 95.3 | 108.3 | 49 | 102.6 | 270.0 | 145.7 | 102.2 | 120.8 |
| 21 | 71.4 | 164.8 | 94.0 | 67.5 | 77.4 | 50 | 107.8 | 302.1 | 166.6 | 109.5 | 125.1 |
| 22 | 56.1 | 125.8 | 77.9 | 54.1 | 58.7 | 51 | 42.0 | 82.8 | 54.3 | 40.6 | 41.8 |
| 23 | 26.0 | 42.4 | 31.0 | 26.2 | 25.7 | 52 | 32.7 | 58.0 | 39.1 | 32.7 | 33.8 |
| 24 | 110.9 | 328.2 | 180.4 | 112.0 | 134.7 | 53 | 83.5 | 214.6 | 125.6 | 81.3 | 96.4 |
| 25 | 57.7 | 127.4 | 76.2 | 56.9 | 62.7 | 54 | 18.4 | 24.8 | 19.2 | 18.7 | 18.2 |
| 26 | 94.4 | 248.8 | 140.3 | 90.9 | 103.5 | 55 | 40.7 | 74.2 | 48.1 | 38.9 | 40.2 |
| 27 | 48.7 | 100.8 | 63.7 | 46.7 | 50.6 | 56 | 18.4 | 24.4 | 18.6 | 18.7 | 17.8 |
| 28 | 50.4 | 105.1 | 59.6 | 49.1 | 52.6 | 57 | 117.5 | 347.5 | 183.8 | 123.4 | 142.8 |
| 29 | 59.3 | 123.9 | 76.5 | 55.4 | 60.7 | 58 | 88.4 | 221.0 | 123.4 | 88.5 | 101.3 |
Table 4 Heuristics ranks per test
| FT | 1.7 | 5.0 | 4.0 | 1.6 | 2.8 |
| AFT | 1.7 | 5.0 | 4.0 | 1.6 | 2.8 |
| QT | 1.9 | 5.0 | 4.0 | 1.5 | 2.6 |
The results show that the best heuristic is
Therefore, no algorithm is best for all types of problems [1]. The experimentation present in this work is based on the characteristics of the problem, and we report the results fairly (the same function calls); in this case, the best heuristic was
With the above, the generality of the design and solution methodology for various combinatorial issues continues to be demonstrated.
7 Conclusion and Future Work
In the present work, state-of-the-art research was reviewed, focusing specifically on the problem of programming and sequencing vehicle models to minimize times in the painting system.
In addition, the health risks faced by workers exposed to chemical agents present in automotive paints were researched.
After carrying out this state-of-the-art study, the problem is usually solved with different techniques in a very complex way and sometimes very expensive in terms of algorithms.
Therefore, this area of opportunity was identified, in addition to the future vision of continuing with the prototype and testing it with pieces that can be painted by it and scaled.
Methodologically, the current research reviews and exposes the application of the methodology proposed in [41] to optimize the scheduling of vehicle painting tasks, thus addressing existing CAD designs and achieving a route design for its future simulation.
Analyzing the results obtained from the experimentation provides information on the effectiveness of the heuristics used to address the automobile painting problem.
Utilizing a variety of statistical tests, among which are Shapiro-Wilks and the Friedman, Friedman Aligned, and Quade tests for general comparison, significant variations in the performance of the heuristics (h1 to h5) are observed.
Due to the data do not follow a normal distribution, the median was chosen as the representative measure for statistical analysis. In particular, the
demonstrated superior performance in all statistical tests. Furthermore, this work reaffirms the applicability of the methodology proposed by Ortiz et al. (2023) by addressing different problems with combinatorial optimization constraints.
The findings contribute to a deeper understanding of the selection heuristics and the methodology’s effectiveness in solving complex constraint satisfaction problems. In this case, the study problem was the design of routes for the painting process in automobiles.











 nueva página del texto (beta)
nueva página del texto (beta)