1 Introduction
In recent years, the convergence of machine learning (ML) and metaheuristics has sparked great interest and innovation to address complex combinatorial optimization problems. Among these challenges, the Bin Packing Problem (BPP) and its various extensions are presented as complex problems that demand sophisticated solutions.
This paper presents a comprehensive exploration of the synergies between ML and metaheuristics, focusing on their application to efficiently solve BPP and its various variants, such as 2D-BPP, 3D-BPP, multi-objective BPP, and dynamic BPP.
BPP involves strategically packing items of different sizes into fixed-size containers to minimize the number of used containers. Despite decades of research and the existence of numerous heuristic algorithms, unresolved challenges remain in achieving optimal solutions. In response to the limitations of traditional heuristic approaches, there has been growing interest in leveraging ML strategies to improve problem-solving capabilities.
This study delves into the novel realm of employing ML techniques, exploring various optimization methods and problem variants within the domain of Bin Packing. This study is carried out by incorporating works from ten years ago to the present to analyze the evolution of the applied ML strategies. Preliminary results underscore the promising trajectory of ML in addressing complex optimization problems, shedding light on its potential to revolutionize not only BPP resolution but also similar intricate challenges.
We examine the interaction between ML and metaheuristics, analyzing how ML contributes to problem modeling, decision-making, and adaptive search strategies to identify potential applications and chart a course for future research and developments in the pursuit of optimal solutions for container packing problems.
2 Bin Packing Problem
The Bin Packing Problem (BPP) is a classic challenge in combinatorial optimization. This problem is categorized as NP-hard due to its complexity [1]. In its most basic formulation, it is known as 1D-BPP (One-dimensional bin packing problem) and is presented with a set of elements of different sizes that must be assigned to containers of fixed capacity, seeking to minimize the total number of containers used. This problem is formally defined as follows:
Given a set
This problem consists of assigning each item to a bin in such a way that the sum of the weights of the items in each bin does not exceed
Such as:
Eq. (1) represents the number of bins that are used to pack the set of
This problem, fundamental in logistics and planning, has generated an extensive field of research that covers various variants adapted to real-world situations [3]. Some of the variants of the BPP are defined below.
2.1 Problem Variants
Two-dimensional Bin Packing (2D-BPP)
In traditional BPP, elements are packed into a single dimension. However, in 2D-BPP are given a set of
Gilmore and Gomory [4] presented a mathematical formulation of 2D-BPP. They introduced a column generation strategy rooted in the exhaustive listing of all item subsets (known as patterns) that can be accommodated within a single bin. Here, let
The set of all admissible patterns is thus denoted by the matrix
Such as:
This variant has many industrial applications, especially in cutting (e.g., wood, glass, and paper industries) and packing (e.g., transportation, telecommunications, and warehousing) [6].
Three-dimensional Bin Packing (3D-BPP)
The 3D-BPP adds complexity by allowing the three-dimensional stacking of elements in three axes in bins. This results in greater flexibility in the arrangement of elements, but also poses new computational challenges when searching for the optimal three-dimensional configuration.
Martelo et al. [7] described the 3D-BPP as given a set of
Let
Such that:
Eq. (7) indicates that each element must be assigned to exactly one bin. Eq. (8), (9), and (10) respectively indicate that the sum of the widths, heights, and depths of the elements placed in a container cannot exceed the width, height, and depth of the bin.
Multi-objective Bin Packing Problem
The multi-objective variant of BPP (MOBPP) focuses on the simultaneous optimization of multiple criteria, such as minimizing the number of containers used, maximizing space utilization, and equitably distributing items among containers. This approach is especially relevant in situations where efficiency and performance objectives coexist and must be balanced.
Geiger [8] presented a problem formulation of MOBPP:
Given a number of
Such as:
Eq. (12) minimizes the number of bins and the second objective given in Eq. (12) minimizes the average heterogeneousness of the bins.
Dynamic Bin Packing Problem
Unlike static versions, Dynamic BPP addresses problems where elements arrive sequentially, and the layout must be adjusted dynamically as new elements are introduced. Instead of knowing all the elements in advance, the challenge lies in making packaging decisions as the elements present themselves, requiring adaptive and efficient strategies. This scenario more accurately reflects real-time logistics situations and adds a layer of complexity to problem resolution.
Coffman et al. [9] described Dynamic Bin Packing as an extension of the classical static 1D-BPP model. The items to be packed will be described by a finite sequence or list
Each item
Packaging rules denote that items cannot be moved from one bin to another once packed and operating online, i.e., items are packaged as they arrive without any knowledge of future arrivals. Therefore, the elements in
This section provides a solid conceptual framework for understanding BPP and its various variants, laying the foundation for exploring how Machine Learning strategies address these challenges in the next section.
3 Machine Learning in Metaheuristics
The employment of Machine Learning (ML) in combination with metaheuristics has emerged as an innovative and effective approach to address combinatorial optimization problems, including the challenging BPP and its variants. This section explores the convergence of ML and metaheuristics, presenting a detailed view of their integration and application in efficiently solving these problems.
Machine Learning focuses on the development of algorithms and models capable of learning patterns from data and dynamically adapting to new situations. This adaptive capacity is essential to address combinatorial optimization problems, where effective solutions must be discovered through the exploration and exploitation of multiple options.
The synergy between ML and metaheuristics lies in the ability of ML models to improve metaheuristic adaptive capabilities. By incorporating machine learning techniques, metaheuristics can learn and adjust their search strategies adaptively as they interact with the solution space.
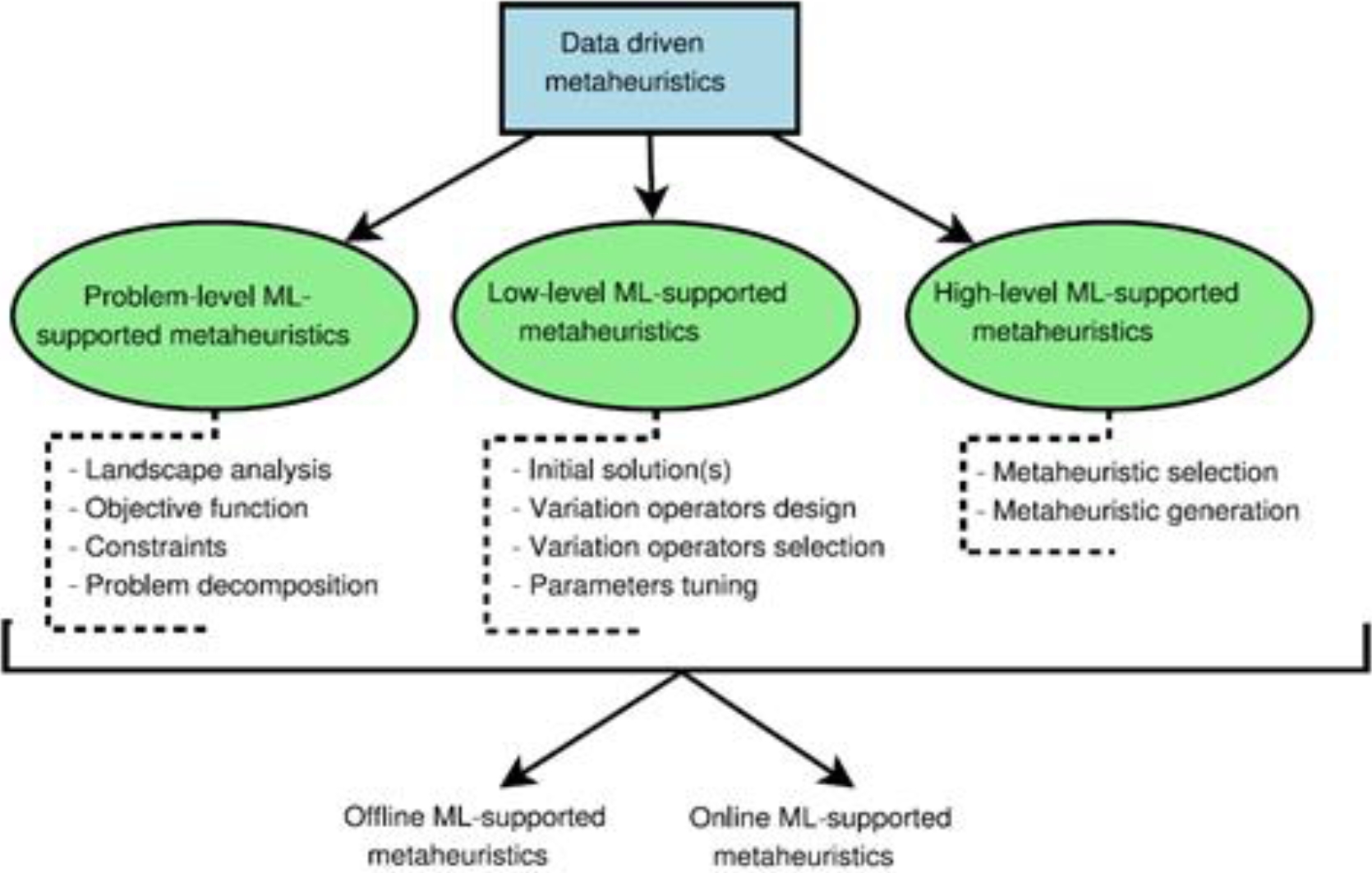
Talbi [10] presents a general taxonomy of how metaheuristics incorporate machine learning. Fig. 1., presents three ways of applying machine learning to a metaheuristic:
– Problem-level Machine Learning support in metaheuristics: Machine Learning can play a crucial role in modeling optimization problems, addressing aspects such as the objective function and constraints. In addition, it can contribute to the analysis of the problem landscape and its decomposition.
– Metaheuristics with low-level ML support: Metaheuristics are made up of various search components. In this context, Machine Learning can drive any search component, from solution initialization to search variation operators such as neighborhoods in local search, as well as mutation and crossover in evolutionary algorithms. Likewise, it can be used to adjust the different parameters of a metaheuristic.
– High-level ML-supported metaheuristics: This category focuses on the selection and generation of metaheuristics, as well as the design of hybrid strategies and cooperative metaheuristics in parallel.
At the same time, other criteria related to learning time are used. For offline ML-supported metaheuristics, the learning process is performed before the execution of the problem solver, this allows the model to be trained in advance.
On the other hand, in online ML-supported metaheuristics, the machine learning process is carried out concurrently with the search and resolution of the problem, allowing the model to accumulate knowledge in real time during the optimization process.
Among the machine learning techniques most used in metaheuristics, some strategies stand out:
-
– Supervised Learning: Uses labeled datasets to train models and guide adaptive capabilities in the metaheuristic.
-
– Unsupervised Learning: Explores patterns in unlabeled data, allowing the metaheuristic to discover hidden structures and adapt to problem complexity.
-
– Reinforcement Learning: Involves the dynamic interaction of the agent (metaheuristic) with the environment (optimization problem), aiming to maximize rewards over time.
-
– Deep Learning: Utilizes deep neural networks to learn complex representations and make predictions.
-
– Hyperparameter Optimization: Uses ML techniques to dynamically adjust metaheuristic parameters during the search.
-
– Artificial Neural Networks (ANN): Computational models inspired by the structure and function of the human brain, capable of learning complex patterns.
4 Hybrid Methods in BPP
Research aimed at addressing the challenges inherent in BPP has seen notable advances in recent years, especially with the incorporation of innovative strategies and advanced machine learning techniques. Over the years, various studies have significantly delved into these combinatorial optimization problems.
In this section, a summary of the literature that has used various ML techniques to address BPP from ten years ago to the present is presented. The twenty selected works have been organized according to the different techniques used by the authors, thus providing a detailed overview of the diversity of approaches applied in research on this topic.
4.1 Neural Networks
De Almeida and Steiner [11] address the 1D-BPP, exploring different configurations of AugNN. The study provides a comparative analysis between AugNN and Minimum Bin Slack (MBS), offering insights through experimental design and statistical analysis.
Sim et al. [12] present a hyperheuristic system that continuously learns over time to solve the 1D-BPP. The system continually generates new heuristics and shows problems in its environment; Representative problems and heuristics are incorporated into a self-sustaining network of interacting entities inspired by artificial immune system methods.
The network is plastic in both its structure and content, leading to the following properties: it exploits existing knowledge captured in the network to rapidly produce solutions; can adapt to new problems with very different characteristics; and is able to generalize over the problem space.
Laterre et al. [13] developed a ranked reward algorithm (R2) utilizing deep neural networks for solving the 2D and 3D Bin Packing Problems. The algorithm estimates a policy and a value function using deep neural networks, combined with Monte Carlo Tree Search (MCTS) for policy improvement.
Kroes et al. [14] utilize conventional neural networks to tackle the 1D-BPP. The study explores the hybridization of genetic algorithms and simulated annealing with traditional neural network heuristics for flexible container memory mapping.
4.2 Deep and Reinforcement Learning
Hu et al. [15] presented a new type of 3D-BPP, where a series of cuboid-shaped elements must be placed in an orthogonal-shaped container, one by one. The goal is to minimize the surface area of the container, reflecting real business scenarios where the cost of the container is proportional to its surface area. An approach based on Deep Reinforcement Learning (DRL), especially the Pointer Network, is applied to optimize the sequence of elements to be packed.
Mao et al. [16] introduce a deep learning approach to the Variable-Sized 1D Bin Packing Problem (1D-VSBPP), using a large training dataset and techniques for automatic feature selection and rapid labeling. They demonstrate how to build an adaptive system that can select the best heuristics to generate high-quality container packaging solutions.
Nanda and Hacker [17] employed deep reinforcement learning to consolidate active containers with different resource requirements into a minimal number of physical machines, proposing the RACC (Resource-Aware Container Consolidation) algorithm. Considers the resource demands of different types of tasks and the heterogeneity of physical machines.
Li and Hu [18] developed a deep reinforcement learning-based job scheduling algorithm for the container packing problem in cloud data centers. DeepJS can automatically obtain a fitness calculation method which will minimize the makespan (maximize the throughput) of a set of jobs directly from experience and the results prove that DeepJS outperforms the heuristic-based job scheduling algorithms.
Verma et al. [19] introduce a deep reinforcement learning algorithm for the online 3D Bin Packing Problem, focusing on decisions that can be physically implemented using a robotic loading arm.
This approach tackles a novel problem in two key aspects: Firstly, it assumes an unknown set of objects to be packed, with only a fixed number visible to the loading system upon arrival. Secondly, the objective is not merely to move objects but to optimize their location and orientation within the bin(s) to maximize packing efficiency.
Goyal and Deng [20] present PackIt, a virtual environment for evaluating and potentially learning the ability to perform geometric planning. It models the 3D-BPP, where an agent needs to sequence actions to pack a set of objects into a box with limited space. They construct challenging packing tasks using an evolutionary algorithm, including model-free and heuristic-based learning methods, as well as optimization methods based on searches assuming access to the environment model.
Silva-Gálvez et al. [21] introduced a solution model for the 1D-BPP that leverages unsupervised learning principles within a hyper-heuristic framework. The model dynamically selects from various heuristics during the search process, adapting to the problem state being explored.
By employing the k-means clustering algorithm, they identify action regions and recommend heuristics based on performance analysis within these regions. The hyper-heuristic determines the most appropriate heuristic to apply based on the current problem state.
Zhao et al. [22] present a restricted deep reinforcement learning method for the 3D Bin Packing Problem, using a feasibility predictor to modulate the output probabilities during training.
They introduced a prediction-and-projection scheme: The agent first predicts a feasibility mask for the placement actions as an auxiliary task and then uses the mask to modulate the action probabilities output by the actor during training. Such supervision and projection facilitate the agent to learn feasible policies very efficiently. The method can be easily extended to handle lookahead items, multi-bin packing, and item re- orienting.
Yang et al. [23] developed a flexible container packing framework based on slack, using reinforcement learning strategies to generate slack and improve container space efficiency.
The performance-driven rewards are used to capture the intuition of learning the current state of the container space, the action is the choice of the packing container, and the state is the remaining capacity after packing. During the construction of the slack, an instance-eigenvalue mapping process is designed and utilized to generate the representative and classified validate set
Zhang et al. [24] present an end-to-end learning model for bin packing using self-attention and deep reinforcement learning algorithms. They introduce the prioritized oversampling technique to accelerate policy learning. Their proposal is called Att2pack, which was initially proposed to address the offline 1D-BPP, however, they adapted it to the online BPP which also shows good performance.
Jiang and Zhang [25] develop an end-to-end multimodal deep reinforcement learning agent to solve the 3D-BPP, addressing sequence, orientation, and position tasks. They use a multimodal encoder and maintain lightweight computation to learn the packing policy.
Murdivien and Um [26] This study investigates the use of Deep Reinforcement Learning (DRL) to address dynamic logistics challenges, focusing on the real-time 3D sequential packing problem. It highlights the need for adaptive and autonomous manufacturing systems in the face of sudden changes in the supply chain. By employing neural networks in reinforcement learning, DRL shows promise in solving complex problems in manufacturing logistics. A game engine is used to train the DRL, allowing intuitive visualization of the learning process.
Fang et al. [27] introduce a reinforcement learning algorithm based on Monte Carlo (MC) learning, Q-learning, and Sarsa-learning to address a 2D irregular packing problem. The proposed algorithm adapts reward-return mechanisms and updates strategies based on the irregular piece-packing scenario.
Guerriero and Saccomanno [28] tackle the 1D-BPP using a reinforcement learning strategy aimed at training an agent to mimic a reference heuristic. In particular, the reward is proportional to the agent's ability to make the same decisions as a particular heuristic when applied to a specific problem state.
4.3 Others
Duan et al. [29] propose a multitask learning framework based on reinforcement learning for the Flexible 3D Bin Packing Problem (3D-FBPP). It focused on minimizing the plastic surface area used to wrap packages, which involves packing cuboid-shaped items in bins with the smallest possible surface area.
Instead of designing heuristics, they proposed a multi-task learning framework based on Selected Learning to learn a heuristic-like policy that generates the sequence and orientations of the elements to be packed simultaneously.
Mohiuddin et al. [30] focused on the challenges associated with cloud storage, such as inefficient use of resources and internal threats to stored data.
It proposes a distributed storage allocation architecture to ensure equitable use of storage resources and an integrated security framework to protect data at rest in cloud storage from insider threats. The goal is to effectively address challenges related to resource management and data security in the cloud.
The analysis of the works highlights the effectiveness of strategies based on neural networks, deep learning algorithms, and reinforcement learning methods to enhance the efficiency and quality of solutions in the field of container packaging.
However, it is crucial to note that the dynamic variants of this problem have received limited exploration so far. This research gap could represent a valuable area of opportunity for future studies, as the dynamics of ever-changing environments present additional challenges that could benefit from innovative approaches.
Additionally, it is worth noting that reinforcement learning (RL) and deep reinforcement learning (DRL) have emerged as preeminent strategies to address the challenges of container packaging, being recurrently used in the majority of the studies reviewed.
The combination of these approaches with other methodologies has been shown to offer promising results, underlining the versatility and effectiveness of these techniques in this domain.
5 Relevant State-of-the-Art Methods
The previous section provided an overview of work related to the BPP, exploring machine learning strategies and highlighting techniques employed by various researchers.
Now, we will immerse ourselves in a critical analysis, focusing on the selection of three representative works considering the number of citations of each one in the reviewed literature. These studies play a crucial role in the evolution of methods and approaches to optimize BPP.
We will examine the techniques and algorithms implemented in these works. This analysis will not only highlight the strengths and limitations of each approach but will also establish a solid framework for understanding the broader landscape of research in this field.
We also perform an in-depth examination of the practical implications and results obtained by the three selected methodologies for solving Bin Packing Problems. Table 1 presents the general characteristics of the three works selected as a case study.
Table 1 General characteristics of works representative of the state-of-the-art
| Algorithm | Year | Citations | BPP variant |
Strategies / methods |
| NELLI Sim et al. [11] | 2015 | 90 | 1D-BPP | Hyper-heuristic system (artificial immune system methods and neuronal network). |
| Packman Verma et al. [18] | 2020 | 40 | 3D-BPP | Deep reinforcement learning algorithm with a focus on robotic loading arm implementation. |
| RS Zhao et al., [21] | 2021 | 107 | 3D-BPP | Deep reinforcement learning with a feasibility predictor scheme. |
The name of the algorithm and author, year of publication, number of citations, BPP variant that is addressed, and the main ML strategies that apply are included.
5.1 A Lifelong Learning Hyper-heuristic Method for Bin Packing
Sim et al. [12] introduced a novel hyperheuristic approach designed to continuously learn and tackle combinatorial optimization problems. This system dynamically generates fresh heuristics when confronted with challenges in its environment.
Representative problems and heuristics become integral parts of an autonomous network of interacting entities, drawing inspiration from artificial immune system methods.
The flexibility in both structure and content within the network imparts noteworthy qualities: leveraging existing knowledge for swift solution generation, effective adaptation to new problems with diverse characteristics, and the ability to generalize within the problem space.
The system's efficacy is evaluated using an extensive dataset of one-dimensional bin packing problems (1D-BPP) and 1370 problems previously established in the literature. The results showcase exceptional performance in terms of solution quality across all datasets.
The system exhibits efficient adaptation to sets of problem instances undergoing dynamic changes, surpassing the performance of previous approaches.
The network's capacity to self-adjust and maintain a concise repertoire of problems and heuristics, functioning as a representative map of the problem space, underscores the computational efficiency and scalability of the system.
Algorithm 1 presents the pseudocode of the work (NELLI) proposed by Sim et al.
Algorithm 1. The pseudocode of the NELLI algorithm presented by Sim et al. [12]
The results reported by Sim et al. [12] include a comparison of the performance of the proposed algorithm (NELLI) against literature works previously developed by one of the collaborators: AIS I [31] and Island [32].
They used different instances to evaluate the Bin Packing Problem (BPP) such that Data Set 1, 2, 3 [33], Uniform, and Triplets [34].
Table 2 presents the results obtained by NELLI, AIS I, and Island for a set of 685 instances tested by the authors.
Table 2 NELLI results vs related works for a set of 685 instances [12]
Table 3 presents the evaluation of NELLI vs Island for 1370 instances, taking into account the minimum, maximum, mean, and standard deviation of each of the algorithms for both comparisons.
According to the analysis of Sim et al. [12] Tables 2 and 3 presents that both NELLI and Island systems generate solutions of identical quality on a data set of 685 and 1370 instances.
However, it is important to highlight that NELLI has several advantages compared to the evaluated approaches. Its scalability is greater since it significantly reduces the calculation time compared to the evaluated approaches.
Furthermore, NELLI has been shown to adapt efficiently to non-visible problems and dynamic environments, maintaining a memory of previous experiences.
5.2 A Generalized Reinforcement Learning Algorithm for Online 3D Bin-Packing
Verma et al. [18] introduced a Deep Reinforcement Learning (Deep RL) algorithm to tackle the challenge of online 3D bin packing (3D-BPP), accommodating a variable number and any container size. The approach focuses on decision-making that can be physically implemented through a robotic loading arm, validated using a laboratory prototype.
This problem presents innovation in two key aspects. Firstly, in contrast to the conventional 3D-BPP, it assumes that the complete set of objects to be packed is not known in advance. Instead, the loading system observes a fixed number of nearby objects and must load them in the order they arrive.
Secondly, the goal is not merely to move objects from one point to another through a feasible route, but to find the location and orientation for each object that maximizes the overall packing efficiency of the containers. Additionally, the learned model is designed to handle instances of problems of arbitrary size without the need for retraining.
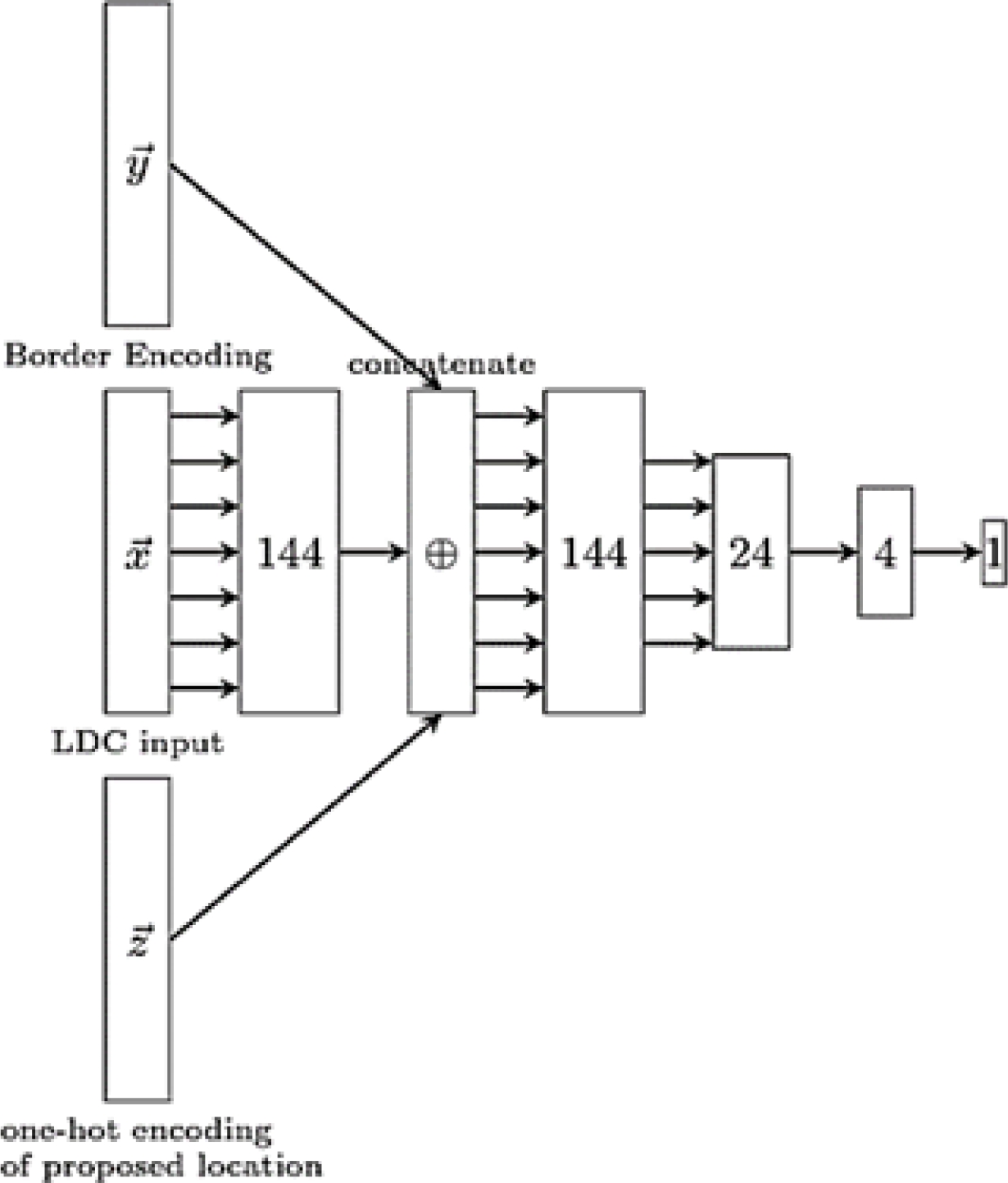
Simulation results indicate that the RL-based method outperforms state-of-the-art heuristics for online container packing, demonstrating improvements in terms of empirical competitive ratio and volume efficiency. The authors do not present the pseudocode of the proposed algorithm; however, they show the network architecture of the DQN agent used (Fig. 2).
Verma et al. [19] propose the PackMan algorithm, which was trained using synthetically generated data sets, which contain randomly generated dimension boxes. However, they made sure that the dimensions matched so that each container could be filled (100% fill fraction).
Each data set consists of 10 box bins
Table 4 compares the algorithms on the competitiveness ratiometric (
Table 4 Comparison of results on 100 episodes of test data between Packman vs other approaches from the literature [19]
| Algorithm | Comp. ratio |
Time per box (sec) | Avg. pack | Best Pack |
| AH | 1.58 | - | - | - |
| Floor building | 1.52 | 0.0002 | 81.0% | 5% |
| Column build | 1.46 | 0.0001 | 81.0% | 6% |
| First Fit | 1.47 | 0.0002 | 81.3% | 7% |
| WallE | 1.41 | 0.0106 | 81.8% | 25% |
| PackMan | 1.29 | 0.0342 | 82.8% | 57% |
Empirical results for robot stackable algorithms show that PackMan has the best empirical ratio of 1.29, averaging
The boxplot shown in Fig. 3. illustrates the differences between the algorithms. While floor and column construction have almost identical results for the test data sets, WallE returns the best results among the heuristics.
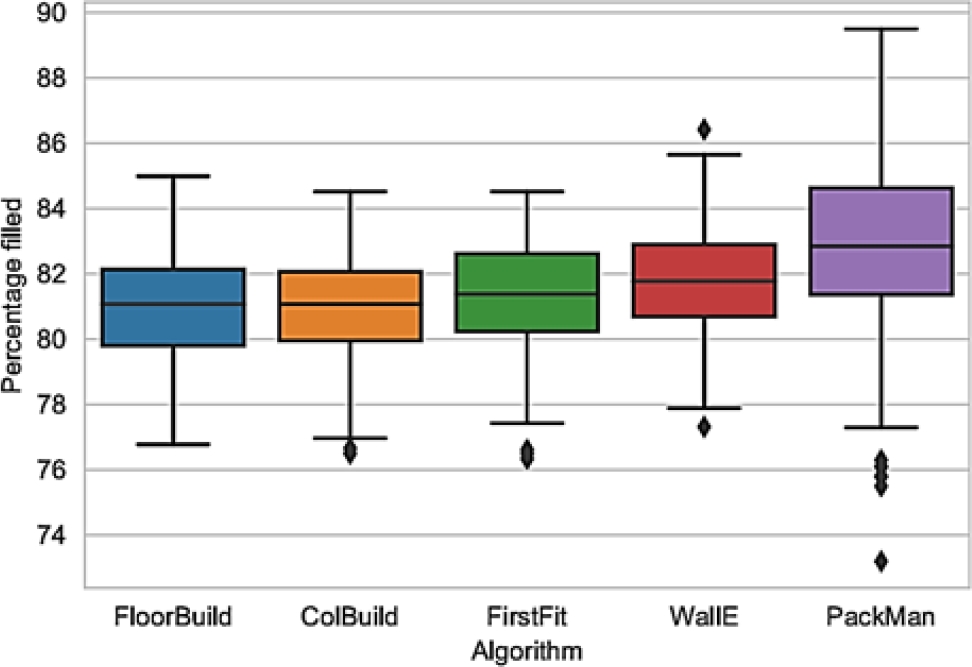
Fig. 3 Comparison of empirical compliance rates for the 5 algorithms, over 100 test data sets presented in [19]
This is a result of their balanced approach to box placement, with no singular emphasis on floor or column construction. The average packing efficiency for PackMan is higher than all heuristics but has a larger spread in outliers.
5.3 Online 3D Bin Packing with Constrained Deep Reinforcement Learning
Zhao et al. [22] address a variant of the challenging but highly practical 3D Container Packing Problem (3D-BPP). In the proposed scenario, the agent has limited information about the items that need to be packed into a single container, and each item must be placed immediately with no option to readjust later. The arrangement of items is also influenced by constraints related to order dependency and physical stability.
To address this online 3D-BPP, they propose a strategy based on the Constrained Markov Decision Process (CMDP). To solve this problem, they propose an efficient and easy-to-implement method based on constrained deep reinforcement learning (DRL), within the actor-critic framework. Specifically, they introduce a prediction and projection scheme: the agent initially anticipates a feasibility mask for location actions as an additional task and then uses this mask to adjust the action probabilities generated by the actor during training.
This monitoring and projection approach make it easier for the agent to learn viable policies in a highly efficient manner. The results of a comprehensive evaluation demonstrate that the learned policy significantly outperforms state-of-the-art methods in this context.
To validate their work called RS, Zhao et al. [22] carried out comparisons with two different methods. First, they evaluated their online approach against the BPH heuristic [35], which allows the agent to select the next best element among
In Table 5, it was specifically compared to the BPP-1 version of BPH. Also, in Fig. 4, the online BPH and the method under the BPP-
Table 5 Comparison of Zhao's proposal [22] against three online and offline approaches
| Method | # items / % space uti. | ||
| RS | CUT-I | CUT-2 | |
| Boundary rule (Online) | 8.7 / 34.9% | 10.8 / 41.2% | 11.1 / 40.8% |
| BPH (Online) | 8.7 / 35.4% | 13.5 / 51.9% | 13.1 / 49.2% |
| LBP (Offline) | 12.9 / 54.7% | 14.9 / 59.1% | 15.2 / 59.5% |
| Proposed BPP-1 (Online) | 12.2 / 50.5% | 19.1 / 73.4% | 17.5 / 66.9% |
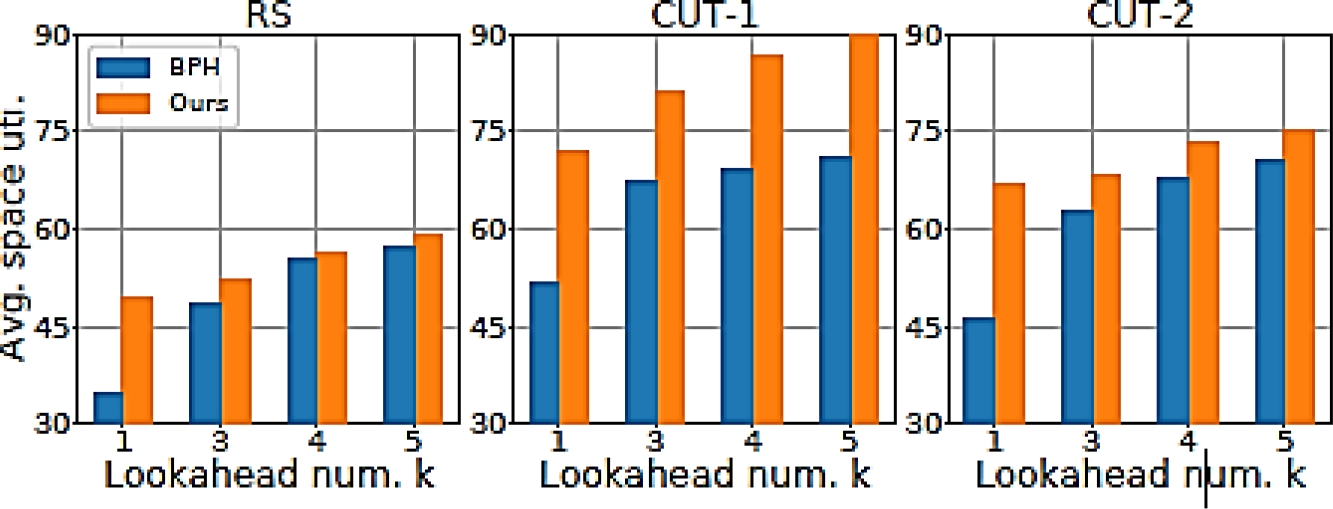
Fig. 4 Comparison with the online BPH method [28] in BPP-𝑘. BPH allows for the reordering of anticipated items, while the work of [18] does not
The latter imitates human behavior by trying to place a new item next to already packaged items, seeking to keep the packaging volume uniform. The comparison in Figure 8 reveals that the proposed method outperforms all online methods on all three benchmarks and surprisingly even outperforms the offline approach on CUT-1 and CUT-2.
Table 5 presents the method proposed by Zhao et al. [22] compared against three other approaches both online and offline, the number of objects and the percentage of space used by each approach are measured.
From the comparison in Table 5, the proposed method outperforms all alternative online methods on all three benchmarks and even beats the offline approach on CUT-1 and CUT-2.
Through examining the packing results visually, we find that our method automatically learns the above “boundary rule” even without imposing such constraints explicitly.
From Fig. 4, the method performs better than online BPH consistently with varying numbers of lookahead items even though BPH allows re-ordering of the lookahead items. They also conducted a preliminary comparison on a real robot test of BPP-1 (see our accompanying video). Over 50 random item sequences, our method achieves an average of 66.3% space utilization, much higher than the boundary rule (39.2%) and online BPH (43.2%).
The reviewed works have provided valuable insights into the realm of BPP, shedding light on machine learning strategies and diverse methodologies employed by researchers. The critical analysis of three representative works has contributed to a deeper understanding of the field's evolution and progress.
Sim et al. [12] approach introduces a groundbreaking hyperheuristic method, showcasing adaptability, swift problem-solving capabilities, and the ability to generalize within the problem space. The system's commendable performance across extensive datasets and dynamic problem instances underscores its computational efficiency and scalability.
Verma et al. [19] Deep RL algorithm for online 3D bin packing presents innovation by addressing unknown object sets and optimizing container packing efficiency. The model's ability to handle instances of varying sizes without retraining is a notable strength, outperforming existing heuristics in terms of competitive ratio and volume efficiency.
Zhao et al. [22] strategy for the 3D Container Packing Problem stands out in its approach to immediate item placement, constrained by limited information and influenced by order dependency and stability considerations. The proposed CMDP-based method, utilizing constrained DRL, exhibits remarkable efficiency in learning viable policies, surpassing state-of-the-art methods in the context of online 3D-BPP.
When comparing the three approaches in the literature, different aspects and performances stand out. NELLI [12] has demonstrated notable advantages in terms of scalability and adaptability to dynamic environments, outperforming other previous approaches. For its part, the PackMan algorithm [19] presents significant improvements in packaging efficiency, achieving more efficient space utilization.
However, it suffers from greater variability in results. Zhao et al. [22], with its reinforcement learning-based approach, exhibit outstanding superiority over online and offline methods, achieving efficient space utilization compared to traditional heuristics and even outperforming human players in certain scenarios.
Together, these results underscore the diversity of approaches and particular strengths of each algorithm. Considering the specific characteristics of each problem and the requirements of the environment, the choice of the most appropriate approach will depend on the specific objectives and constraints of the application.
In essence, these representative works contribute significantly to the ongoing advancements in BPP research, offering novel perspectives, innovative methodologies, and promising results.
The field continues to evolve, and these studies serve as crucial milestones in shaping the landscape of optimization strategies for Bin Packing Problems.
6 Conclusions and Future Directions
6.1 Conclusions
Despite promising advances in hybridizing machine learning strategies with the container packaging problem (BPP) and its variants, there are untapped areas of opportunity that deserve further exploration. Dynamic variants of BPPs emerge as relatively unexplored territory within this context, providing substantial space for future research and the development of novel hybrid strategies.
Furthermore, while deep reinforcement learning is an effective tool in most of the studies reviewed, there is a pressing need to deepen our understanding of their applicability in various BPP scenarios. Opportunities abound to investigate and improve learning adaptability to changing conditions, as well as explore its integration with other machine learning techniques and metaheuristics.
These areas of opportunity suggest that, despite commendable achievements to date, the trajectory of machine learning with BPP remains in a state of continuous evolution. The landscape continues to offer fertile ground for future research, driving continued refinement of the effectiveness and versatility of hybrid strategies.
6.2 Future Directions
The research landscape in the field of Bin Packing Problems (BPP) continues to evolve, driven by advancements in algorithms and methodologies. Building upon the insights gained from the analysis of the selected studies, several promising avenues for future research emerge.
1 Dynamic and Adaptive Algorithms: While some studies have touched upon dynamic aspects of BPP, there remains ample room for the development of algorithms that can dynamically adapt to changing scenarios. Future research could focus on the design of algorithms capable of adjusting their strategies in real-time as the packing environment evolves.
2 Integration of Hybrid Approaches: Combining the strengths of different algorithms and techniques can potentially lead to more robust and efficient solutions. Future research might explore the integration of machine learning, metaheuristics, and mathematical programming to create hybrid approaches that leverage the complementary advantages of these methods.
3 Scalability and Generalization: Many existing algorithms excel in specific scenarios but struggle with scalability or fail to generalize across diverse problem instances. Future work could concentrate on enhancing the scalability of algorithms, enabling them to handle larger problem sizes, and improving their generalization capabilities to address a broader range of BPP variants.
-
4 Real-world Implementation and Validation: As algorithms mature, practical implementation in real-world settings becomes crucial.
5 Incorporating Environmental Considerations: With a growing emphasis on sustainability, there is an opportunity to integrate environmental considerations into BPP algorithms. Future research might explore how to optimize packing solutions with a focus on reducing ecological impact, considering factors such as fuel efficiency in transportation or eco-friendly packaging materials.
6 User Interaction and Explainability: Developing algorithms that are interpretable and allow for user interaction can enhance their practical utility. Future research could delve into incorporating explainable AI principles and user-friendly interfaces, enabling stakeholders to understand and interact with the decision-making process.
7 Benchmark Datasets and Competitions: Establishing standardized benchmark datasets and organizing competitions can foster collaborative advancements in the field. Future efforts could focus on creating benchmark datasets that capture the complexities of real-world packing scenarios and organizing competitions to benchmark the performance of different algorithms on these datasets.
In pursuing these future directions, researchers can contribute to the continued evolution of BPP methodologies, addressing emerging challenges and ensuring the practical relevance of their findings.











 nueva página del texto (beta)
nueva página del texto (beta)