Investigación

 

Los conceptos relevantes en el aprendizaje de la graficación: un análisis a través de la estadística implicativa

 

María Trigueros G.* y Covadonga Escandón M.**

 

* Investigadora del Departamento de Matemáticas del Instituto Tecnológico Autónomo de México (ITAM). Río Hondo núm. 1, colonia Progreso Tizapán, México, DF, CP 01080. CE: trigue@itam.mx.

** Investigadora del Centro Geo-CONACyT. CE: escandon@centrogeo.org.mx.

 

Artículo recibido: 26 de abril de 2007
Dictaminado: 6 de agosto de 2007
Segunda versión: 30 de agosto de 2007
Aceptado: 24 de septiembre de 2007

 

Resumen

Diversos estudios muestran que los estudiantes tienen dificultades para entender conceptos específicos del cálculo diferencial. Algunos señalan los obstáculos que les representa la integración de los diferentes conceptos en la solución de problemas específicos, incluidos los de graficación de funciones. En este estudio se analizan las respuestas de un grupo de estudiantes cuando resuelven estos problemas utilizando como herramienta de análisis la estadística implicativa y cohesitiva. Los resultados muestran la importancia de la comprensión de la segunda derivada y de los intervalos en los que el dominio se subdivide en virtud de las propiedades de la función para la solución exitosa de los problemas. Se hace evidente que el uso de esta herramienta en este tipo de estudios resulta no sólo pertinente sino de gran utilidad.

Palabras clave: enseñanza de las matemáticas, educación superior, análisis estadístico, solución de problemas, México.

 

Abstract

Various studies show that students experience difficulties in understanding specific concepts of differential calculus. Some studies point to the obstacles represented by having to integrate different concepts into solving specific problems, including the writing of functions. The current study analyzes the responses of a group of students as they solve such problems by using implicative and cohesive statistics as an analytical tool. The results show the importance of understanding the second derivative and the intervals into which the domain is subdivided, due to the function's properties for successfully solving problems. It is evident that the use of this tool in such studies is not only pertinent but also highly useful.

Key words: teaching mathematics, higher education, statistical analysis, problem-solving, Mexico.

 

Antecedentes del problema de graficación

La literatura acerca de la forma en que los estudiantes resuelven problemas de cálculo diferencial es muy abundante. Varios autores hacen notar que los estudiantes tienen muchas dificultades con los conceptos del cálculo y que aun aquellos que son capaces de resolver hábilmente problemas rutinarios no lo son frente a los que se utilizan diferentes representaciones para presentar la información y cuando se cambia ligeramente el estilo de las preguntas (Selden et al., 1994). Algunos autores arguyen que estos problemas se deben a que los estudiantes no han profundizado en el concepto de función o que el aprendizaje concepto por concepto de manera relativamente aislada influye en que incorporen a su conocimiento construcciones matemáticas incorrectas y las mantengan durante algún tiempo (Orton, 1983; Selden et al., 1994, Cooley et al., 2007). Otros estudios han centrado la atención en la habilidad de visualización de los estudiantes y su posibilidad de relacionar la información acerca de la derivada en distintas representaciones (Aspinwall et al., 1997; Ferrini-Mundy y Graham, 1994; Asiala et al., 1996) o han encontrado que los estudiantes muestran concepciones débiles de la idea de derivada como razón de cambio, a pesar de haber terminado varios cursos de cálculo y de análisis, y que una de sus dificultades consiste en conceptualizar la derivada como una función en sí misma (Thompson, 1994). Esto último influye en los obstáculos que se presentan a los estudiantes para comprender algunas propiedades funcionales, como los puntos en los que la función es continua pero no derivable y, en general, las propiedades relacionadas con la continuidad (Slavit, 1995). En otras investigaciones se ha encontrado que en el proceso de solución de problemas de cálculo, los estudiantes toman en cuenta únicamente parte de la información que requieren y dejan de lado otra que sería indispensable para resolverlos con éxito Carlson et al., 2002 y 2003).

En una serie de trabajos, Baker, Cooley y Trigueros (Baker et al, 2000, Cooley et al., 2007) estudiaron, mediante la introducción del concepto de interacción entre esquemas en APOE (Acción, Proceso, Objeto, Esquema), las estructuras subyacentes a la comprensión de los problemas de graficación que requieren de conocimientos del cálculo diferencial y a la tematización del esquema. Utilizando una serie de problemas de graficación tanto convencionales como no convencionales, hallaron los obstáculos que encuentran los estudiantes cuando la solución de los problemas involucra la interrelación de diferentes propiedades de las funciones. Las mismas dificultades fueron observadas en otro trabajo que utilizó la misma serie de preguntas con estudiantes diferentes a los del segundo estudio (Cortés, 2004). El análisis de los resultados del primer trabajo condujo a la definición de un marco teórico, basado en la teoría APOE, donde se pone en evidencia que la posibilidad de establecer relaciones entre los conceptos del cálculo diferencial depende, por una parte, de la posibilidad de los estudiantes de establecer relaciones entre la forma en que las propiedades de una función, dadas en términos de límites, continuidad y primera y segunda derivadas, afectan el comportamiento de la misma y, por otra parte, de su posibilidad de dividir el dominio de la función en los subintervalos que corresponden a los diferentes comportamientos de la función. En ese mismo trabajo las autoras encontraron también que la mayoría de los estudiantes mostraban incomprensión del significado geométrico de la segunda derivada, de la interrelación de ésta con la primera, al establecer las implicaciones de la continuidad sobre la diferenciabilidad así como al interpretar la derivada cuando se presenta en términos de su definición.

En cuanto a las dudas manifestadas por los estudiantes, los resultados de estas investigaciones mostraron que ellos tenían mayor éxito al graficar una función cuando ésta se les presenta en forma analítica, es decir, cuando se conoce la regla analítica para la función. Los estudiantes mostraron menor entendimiento al tratar de integrar las propiedades de la función en su gráfica cuando se les proporcionan únicamente las condiciones que debe satisfacer la función.

El trabajo que aquí presentamos parte del cuestionario diseñado por Cortés y que se utilizó en dos de los estudios mencionados anteriormente (Cortés, 2004, Cooley et al, 2007). Mientras que dichos trabajos se centraron en las dificultades de los alumnos y en la posibilidad de tematizar un esquema, el presente tiene por objetivo el responder otras preguntas de investigación, a saber:

• ¿Cuáles conceptos, de entre los que se utilizan en la graficación de funciones resultan ser clave para que los estudiantes puedan establecer las relaciones que se requieren para resolver exitosamente este tipo de problemas?

• ¿Existe alguna estructura que tenga un papel dominante en la solución de los problemas?

• ¿Qué tipo de situaciones problemáticas pueden revelar las distintas concepciones de los alumnos?

La respuesta a estas preguntas permitirá sugerir algunas características que son relevantes para el diseño de situaciones didácticas que faciliten a los estudiantes relacionar sus conocimientos de manera significativa para resolver exitosamente los problemas de graficación.

 

Marco teórico

El marco teórico utilizado en el diseño y análisis de los instrumentos de esta investigación es la teoría APOE, que toma como referencia epistemológica la teoría de Piaget (Dubinsky, 1996; Czarnocha et al., 1999). A partir de las ideas piagetianas sobre la forma en que se pasa de un estado de conocimiento a otro, en la teoría APOE se hace una construcción para referirse únicamente a la forma en que las personas construyen conocimientos matemáticos, en particular aquellos que corresponden a la matemática que se introduce en la educación superior.

Desde el punto de vista de la teoría APOE, la construcción del conocimiento matemático pasa por tres etapas básicas: acción, proceso y objeto. El tránsito por estas tres etapas no es necesariamente secuencial; una persona puede pasar mucho tiempo en etapas intermedias e incluso estar en una fase de construcción para ciertos aspectos de un concepto y en otra para otros. Lo que sí puede afirmarse es que el manejo que una persona hace de un concepto ante distintas situaciones problemáticas es diferente cuando un individuo responde con una estructura caracterizada por un proceso en la teoría que cuando lo hace utilizando una estructura de tipo acción, y cuando es con una de tipo objeto que cuando se trata de una de tipo proceso. Es claro, además, que el tipo de respuesta del sujeto dependerá, en gran medida, de la demanda cognitiva del tipo de problema al que responde.

Al igual que en la teoría de Piaget, se considera que el mecanismo principal en la construcción de conocimiento matemático es la abstracción reflexiva (Dubinsky, 1991 a y b). Este mecanismo se activa a través de las acciones físicas o mentales que el sujeto hace sobre el objeto de conocimiento. En la teoría APOE se parte de un análisis de los conceptos matemáticos de interés en el que se ponen de relieve las construcciones cognitivas que pueden ser requeridas en su aprendizaje. A este análisis se le conoce como descomposición genética del concepto; es importante aclarar que no puede hablarse de una única descomposición genética, pues ésta depende de la formulación que ha hecho el investigador. Pueden coexistir varias descomposiciones genéticas de un mismo concepto. Lo que es importante es que cualquiera de ellas sea un instrumento que dé cuenta del comportamiento observable del sujeto y permita diseñar estrategias efectivas para su enseñanza.

En la teoría APOE, una acción es una transformación de un objeto que es percibida por el individuo como externa. Cuando una acción se repite y el individuo reflexiona sobre ella puede ser interiorizada en un proceso que es una transformación con base en una construcción interna, ya no dirigida por estímulos que el individuo percibe como externos. Cuando el individuo es consciente del proceso como una totalidad, puede pensar en él como un todo y es capaz de actuar sobre él, se dice que ha encapsulado el proceso y tiene una concepción objeto del concepto (Asiala et al., 1996).

En el proceso de aprendizaje de las matemáticas los estudiantes se enfrentan a conceptos complejos dentro de un área específica y a situaciones en las que requieren utilizar conjuntamente conceptos que provienen de distintas ramas de esta disciplina. En estos casos, la forma de trabajar con un concepto específico es insuficiente para describir lo que los individuos son capaces de hacer y la forma en la que lo hacen. Ante esta situación la descripción de las relaciones que se establecen entre los distintos conceptos y la forma en la que estas relaciones evolucionan se vuelve importante. La noción de esquema y los mecanismos de su evolución nos ayudan a dar cuenta de este tipo de situaciones.

La noción de esquema también proviene de las ideas de Piaget (1971, 1972) y, en la teoría APOE, se define como la colección de acciones, procesos, objetos y otros esquemas que están relacionados -consciente o inconscientemente- en la mente de un individuo en una estructura coherente y que pueden ser empleados en la solución de una situación problemática que involucre esa área de las matemáticas. Piaget habló de los esquemas en varias de sus obras, pero es en el trabajo conjunto con Rolando García, Psicogénesis e historia de la ciencia (Piaget y García, 1996), donde habla más explícitamente de la evolución de los esquemas y de los mecanismos involucrados en esta evolución. En ella proponen que los esquemas evolucionan y que se pueden distinguir tres fases o etapas que se caracterizan por el grado de construcción de relaciones entre los elementos constitutivos del esquema: intra-, inter- y trans- y proponen que estas etapas se pueden encontrar en cualquier proceso de construcción de conocimiento. En la etapa intra- se construyen relaciones internas al objeto o fenómeno; posteriormente ,se encuentra una inter-, donde el individuo constituye relaciones entre los objetos o fenómenos de conocimiento y, por último, una trans-, en la que las relaciones del nivel inter- adquieren mayor coherencia y se estructuran. En esta etapa el individuo puede trabajar con el esquema de una manera mucho más estructurada que cuando el esquema está en otras fases constitutivas, lo que no quiere decir que éste permanece inmóvil, pues sigue construyéndose y enriqueciéndose mediante nuevas relaciones con otros objetos u otros esquemas. La descripción de los esquemas en términos de las posibles coordinaciones entre acciones, procesos, objetos y otros esquemas se incluye también en la descomposición genética que describe su construcción.

La identificación de las transformaciones que intervienen en la evolución de los esquemas es una tarea compleja. En la teoría APOE lo interno o intra- de las relaciones se refiere a su construcción en términos de acciones, procesos y objetos relativos a un mismo concepto matemático; el inter-, a las relaciones entre diversos conceptos; y el trans-, a la posibilidad de tomar un conjunto de conceptos que pueden ser considerados como acciones, procesos, objetos o esquemas conjuntamente con sus relaciones como un objeto sobre el cual se pueden ejercer nuevas acciones (McDonald et al, 2000; Baker et al., 2000; Trigueros, 2000; Oktaç, Trigueros y Vargas, 2006).

Un resultado relevante de los trabajos anteriormente citados (Baker et al., 2000; Cooley et al., 2007) consiste en poner en evidencia que en la solución de algunos problemas matemáticos interaccionan diferentes esquemas. En particular en el problema de graficación que interesa en este estudio, los esquemas que interaccionan son el correspondiente a los intervalos y el de las propiedades de la función. Cada uno tiene su propio desarrollo por las etapas intra-, inter- y trans- pero en los problemas de graficación, como el que se estudia aquí, parecen interaccionar fuertemente, de manera que el desarrollo de uno puede interferir en el del otro. En los artículos mencionados se pone de manifiesto que los estudiantes que han cursado cálculo diferencial muestran conocimientos que evidencian distintas fases de evolución en cada uno de estos dos esquemas y que sus dificultades con la comprensión de las implicaciones de la derivada sobre el comportamiento de la función están relacionadas con el nivel de evolución de cada uno de ellos.

Para estudiar el problema de graficación, en el presente trabajo se utiliza una herramienta de análisis estadístico que fue diseñada para encontrar las posibles relaciones implicativas que existen detrás de las concepciones de los alumnos, así como entre ellas mismas y que es posible poner en evidencia cuando los estudiantes resuelven una serie de problemas relacionados con la graficación de funciones utilizando los conceptos del cálculo diferencial.

 

La estadística implicativa y cohesitiva

Los estudios que se han mencionado en los antecedentes dirigen su atención, por una parte, a las dificultades que presentan los estudiantes frente a los problemas de graficación y, por otra, a la importancia de considerar la posible interacción de esquemas en la construcción del conocimiento. Dejan abierta, sin embargo, la cuestión de profundizar en la estructura conceptual que subyace al esquema de graficación y que permitiría refinar la descomposición genética para acercarla a la forma en que los alumnos construyen el conocimiento. El análisis estadístico implicativo proporciona una herramienta particularmente eficaz para decantar posibles relaciones entre conceptos a partir de datos empíricos.

Según explica Gras (2005), el análisis estadístico implicativo se basa en que los conocimientos se forman principalmente a partir de hechos y de reglas que relacionan a los hechos o a las reglas mismas. Esos conocimientos se van formando así en estructuras de manera progresiva. Sin embargo, en el camino de esta construcción pueden aparecer ejemplos que contradicen las relaciones construidas previamente y es necesario reconsiderar, aunque sea inconscientemente, dichas estructuras para reconstruirlas en otras nuevas. La posición de Gras es congruente con el marco teórico descrito, pues permite hacer un análisis más detallado que influirá en el refinamiento de la descomposición genética del tema matemático.

Los métodos estadísticos tradicionales (análisis factorial de correspondencias, el análisis de similitud) hacen posible visualizar qué tanto se parecen ciertas variables. Sin embargo, estos métodos se basan en índices de similitud simétricos y permiten responder o predecir la forma en la que un individuo que ha respondido de cierta manera utilizando una variable, responderá a otra donde esa variable toma un papel determinante. Con el análisis estadístico implicativo se ha desarrollado una metodología estadística no simétrica para estudiar la relación entre las variables utilizando la idea de implicación del álgebra booleana.

Ante un conjunto de datos que incluyen múltiples categorías, los métodos estadísticos multivariados, como el análisis factorial o los métodos de clasificación, proporcionan herramientas para encontrar formas de orga-nizarlos. Estos métodos se basan principalmente en el hecho de que las variables de estudio están correlacionadas linealmente entre sí y, por ello, resultan poco informativos cuando lo que se pretende analizar son situaciones donde lo que interesa es la decisión de cuestionar o desechar una regla; por ejemplo, cuando lo que importa es encontrar cuántas excepciones hay a una regla dada para decidir si se cuestiona o, incluso, si se desecha. Como explica Gras (2005), cuando se encuentra un contraejemplo, los teoremas matemáticos se reformulan o la regla que se describe se descarta. En cambio, en las ciencias "suaves" siempre cabe la excepción que confirma la regla. En este caso, el conocimiento se forma inductivamente a partir de que se encuentra un número de éxitos que aseguran un cierto nivel de confianza en cierta regla. En el momento en que se alcanza ese nivel (subjetivo), la regla se acepta y se pone en práctica. Si se quiere modelar este tipo de construcción de reglas mediante el análisis estadístico de datos, el problema se convierte en encontrar un criterio cuantitativo relativamente consensuado que proporcione un nivel de confianza que corresponda a las exigencias del usuario. Este es justamente el objetivo del presente trabajo, encontrar reglas que permitan disminuir el número de categorías y que, al mismo tiempo, proporcionen información sobre los conceptos clave en la construcción de un tipo particular de conocimiento.

El método propuesto por Gras (1996, 2005), llamado análisis estadístico implicativo está basado en técnicas estadísticas, resultados de la inteligencia artificial y álgebra booleana, para modelar las situaciones descritas. Se basa en una elección epistemológica y puede ser refutable pero, ciertamente, hay un gran número de situaciones en las que se comprueba su pertinencia y fertilidad. El método presenta una resistencia no lineal al ruido (poco peso para los primeros contraejemplos y cae bruscamente cuando los contraejemplos se repiten suficientemente).

En la estadística implicativa, dada una población E (por ejemplo, alumnos u objetos) y un conjunto de variables V (por ejemplo ítems de un cuestionario o atributos), se busca dar sentido estadístico a una implicación no estricta a ⇒ b a partir de la observación excepcional en situaciones reales de implicación estricta de la variable a sobre la variable b. En este caso algunos individuos pueden verificar a y ¬b y es posible atribuir un valor a la veracidad de la implicación. La noción de implicación estadística, desarrollada por Gras (1996, 2005), se centra en una idea directriz que consiste en:

a) Encontrar un criterio que permita evaluar numéricamente la distancia entre el valor verdadero (en implicación estricta) del conjunto de circunstancias en las que los datos observados contradicen la implicación.

b) Propagar este estudio binario a todas las parejas de variables.

c) Organizar las variables en una gráfica no simétrica ponderada y transitiva que dé una imagen estructurada del conjunto de variables. Esta gráfica representa al conjunto de cuasi-teoremas empíricos de tipo a ⇒ b y la estructura puede ser interpretada como conjetura empírica de una teoría.

En esta metodología, la implicación a ⇒ b será admisible en una experiencia si el número de individuos de E que la contradicen es muy pequeño, en términos probabilísticos, en relación con el número de individuos esperado bajo la hipótesis de ausencia de relación. Si esto ocurre, se puede decir que A, que es el conjunto de observaciones que satisfacen la característica a, está "casi" contenido en B, el conjunto de observaciones que satisfacen la característica b, y que a ⇒ b (lo que equivale a a ∧ ¬b).

La noción central de la metodología es el índice de implicación (Gras, 1996). Para definir este índice se compara la distribución de los datos observados o medidos con la distribución de probabilidad que seguirían si se comportaran según la teoría. En la metodología de Gras es posible utilizar una distribución de tipo binomial, Poisson o normal, dependiendo del tipo de datos que se estén analizando.

Para hacer esa comparación, se toma aleatoriamente un subconjunto X del conjunto A y un subconjunto Y del conjunto B de tal manera que el número de elementos de X e Y sean proporcionales a la cardinalidad de A y de B, respectivamente. Se compara a continuación el índice teórico de implicación, Q, formado a partir de las cardinalidades de X e Y, con respecto al índice empírico de implicación, q, formado a partir de las cardinalidades de A y B.

Si se definen las variables n_a como la cardinalidad de A, n_¬b como la cardinalidad del conjunto complemento de B y n como la cardinalidad del conjunto E. Entonces Q y q quedan definidas por

y

 

El índice de implicación Q sigue una distribución de Poisson, para n suficientemente grande.

Se considera que la proposición a ⇒ b es admisible a un nivel de confianza 1- α a si y solamente si los índices de implicación cumplen con

φ (a, ¬b) = 1- Pr [Q (a, ¬b) < q (a, ¬b)] > 1- α

a la variable φ (a, ¬b), que sigue una distribución normal, se le llama la intensidad de la implicación de a sobre b.

Es importante resaltar que 0.5 < φ (a, ¬b) < 1 ⇔ q (a, ¬b) < 0 y que la implicación que se desea requiere de valores de φ (a, ¬b) cercanos a 1, es decir, que los valores de q(a, ¬b) sean negativos; por ejemplo se obtiene que φ (a, ¬b) > 0.95 ⇔ φ (a, ¬b) < -1.65.

A través de estas definiciones, el análisis estadístico implicativo garantiza la relación entre la lógica binaria y la implicación estadística. Además los índices q y Qson simétricos, o sea, q(a, ¬b) = q(¬b, a), Q(a, ¬b) = Q(¬b, a), lo que en lógica booleana equivale a [a ⇒ b ⇔ ¬b ⇒ ¬a]. Se establece también una relación entre a ⇒ b y b ⇒ a ya que si 0<n_a<n_b<n y n_an_¬b ≠ nn_{a ∧¬b}, entonces:

y además, si n_a< n_b⇒ Q(b,a) < Q(a,¬b).

Entre las propiedades importantes de estos índices resalta el hecho de que si n_an_¬b = nn_{a∧ ¬b} ⇒ q(a, ¬b) = 0 y q(¬a, b) = 0 entonces no hay implicación a ⇒ b ni b ⇒ a, de lo que se deduce que a y b son independientes y que las correspondientes q deben ser distintas de cero para que haya implicación. Cuando n_a< n_b, la implicación estadística más fuerte es a ⇒ b, lo cual no significa que no haya implicación en el otro sentido sino que no es simétrica, dado que n_bn_¬a > n_an_¬b.

El análisis de variables binarias arriba expuesto puede extenderse, siguiendo una perspectiva comparable, a variables modales o a la implicación entre clases de variables. En el caso de las clases, para reducir el efecto del encadenamiento que conduce a las asociaciones de variables, se consideran únicamente las clases que admiten lo que se denomina la "cohesión implicativa". La modelación de esta noción en el seno de una clase se hace de tal manera que dé cuenta de una orientación general de los elementos de dicha clase, considerando siempre que la orientación está determinada por la intensidad de implicación.

Es posible demostrar (Gras y Ratsimba-Rajhon, 1996) que existe una relación entre el índice q y la distribución χ², y entre el índice q y el coeficiente de correlación entre a y b; sin embargo, los conceptos utilizados en la definición de estos índices son muy distintos, dado que el estudio estadístico implicativo no es de la dependencia en el sentido estadístico habitual, en el que el índice de correlación es un indicador simétrico.

A partir de las nociones de la estadística implicativa es posible construir árboles de implicación y gráficas dirigidas que dan cuenta de los niveles significativos de implicación entre variables o clases y que permiten analizar la relación de causalidad entre las variables o clases consideradas, lo cual coincide con los objetivos de este trabajo. Con el fin de obtener este tipo de representaciones se desarrolló el programa computacional llamado Clasification Hiérarchique Implicative et Cohesitive (CHIC) (Couturier, 2001; Couturier et al., 2000).

 

Metodología

Para responder las preguntas planteadas en este estudio se utilizó un cuestionario de preguntas abiertas que demandan justificación, diseñado con base en el marco teórico y presentado por Cortés (2004) y utilizado también en otras investigaciones (Cooley et al., 2007). El cuestionario consta de diez preguntas relacionadas con la graficación de funciones utilizando los conceptos del cálculo diferencial, cuidadosamente elaboradas para obtener la mayor información posible de los alumnos y que, paulatinamente, incrementan el nivel de dificultad. En el análisis de las respuestas se centró la atención en la manera en que quien responde aborda los conceptos, con el fin de desentrañar el tipo de relaciones entre conceptos que utiliza y cuáles son sus dificultades.

El diseño de las preguntas incluyó la presentación de la información utilizando distintas formas de representación (ecuaciones, gráficas, propiedades de una función), de manera reiterativa para dar oportunidad a los estudiantes de reconsiderar respuestas a preguntas anteriores. El cuestionario se muestra en el anexo.

Por la manera en que están diseñadas las preguntas, con base en estudios cualitativos previos sobre las dificultades de los estudiantes, se espera que sea posible analizar, para cada uno que las responda, cómo utiliza su conocimiento para establecer la relación entre las distintas propiedades de la derivada que se requieren en la descripción de la función, así como la forma en que trabaja con los distintos conceptos.

El cuestionario se aplicó a 40 alumnos de una universidad privada que habían aprobado el curso de calculo diferencial; la selección se hizo a partir de un muestreo en diferentes grupos del curso y se incluyeron hombres y mujeres, estudiantes de distintas carreras y de distinto nivel de avance en sus estudios.

La aplicación del cuestionario tomó aproximadamente 90 minutos y se motivó a los estudiantes a responder a profundidad, proporcionando la mayor información posible en cada respuesta. El análisis de las respuestas se hizo alumno por alumno y se les identificó por número para evitar sesgos innecesarios.

A partir del análisis cualitativo de los resultados, Cortés, en el trabajo mencionado anteriormente, identificó 23 categorías que posibilitan describir en detalle el uso que los estudiantes hacen de los conceptos incluidos en el cuestionario. Estas categorías aparecen en varias preguntas, por lo que se pueden establecer criterios de calificación numéricos que describen el dominio del estudiante de cada una de ellas. Dichas categorías se refieren, por una parte, a las propiedades de las funciones y, por otra, al manejo de los intervalos del dominio de la función al sobreponer propiedades definidas mediante distintas condiciones. Una vez identificadas las categorías, es importante desentrañar su estructura, disminuir el número de categorías de modo que sean más asimilables, y jerarquizarlas para facilitar el diseño de instrucción. Las herramientas de la estadística implicativa difieren de la construcción de una estructura convencional de árbol, como ya se mencionó y permiten justamente conseguir estos objetivos.

Las siguientes categorías fueron definidas por Cortés (2004) como el resultado de un análisis cualitativo de entrevistas a estudiantes, basado en una primera descomposición genética del tema de graficación en cálculo:

A. Comprensión del significado de máximos y mínimos de una función

B. Comprensión del significado de los puntos de inflexión de una función

C. Comprensión del significado de la concavidad de una función

D. Comprensión del significado del crecimiento de una función

E. Comprensión del significado de la posibilidad de unicidad de una función relativa a sus propiedades

F. Comprensión del significado de la continuidad de una función

G. Comprensión de las implicaciones del signo de la primera derivada sobre las propiedades de la función

H. Comprensión de las implicaciones del signo de la segunda derivada sobre las propiedades de la función

I. Comprensión de las implicaciones de un límite infinito sobre la derivada de una función en un punto

J. Comprensión de las implicaciones de que la derivada de una función no esté definida en un punto

K. Capacidad de graficar una función a partir del conocimiento de sus propiedades

L. Capacidad de graficar una función a partir del conocimiento de la regla de la función

M. Capacidad de reconocer en la gráfica los intervalos donde la función crece o decrece

N. Capacidad de reconocer en la gráfica los intervalos donde la función tiene distintas concavidades

O. Capacidad de reconocer en la gráfica los intervalos donde la derivada de la función tiene signos distintos o es igual a cero

P. Capacidad de reconocer en la gráfica los intervalos donde la derivada de la función no está definida

Q. Capacidad de reconocer en la gráfica los intervalos donde la segunda derivada de la función tiene signos diferentes o es igual a cero

R. Capacidad de interpretar la gráfica de la función en general

S. Capacidad de trabajar con distintos intervalos del dominio de la función a partir de su definición

T. Capacidad de dividir una gráfica en distintos intervalos del dominio de la función según los crecimientos o concavidades de la función.

U. Capacidad de definir distintos intervalos del dominio de la función según sus crecimientos y concavidades

V. Capacidad de definir distintos intervalos en el dominio de la función según los crecimientos o concavidades de la misma cuando sus propiedades están dadas

W. Capacidad de reconocer la existencia de un punto en el dominio de la función que no comparte una propiedad dada con sus vecinos

Estas categorías se retoman en este trabajo como punto de partida para encontrar una posible estructura que permita refinar la descomposición genética y diseñar procesos de instrucción. Con este fin se realiza un estudio de las variables mediante los métodos del análisis implicativo y cohesitivo que se describe en el siguiente apartado.

 

Resultados del análisis implicativo

El análisis de los resultados de la clasificación de las respuestas de los estudiantes a las preguntas en distintas categorías se llevó a cabo mediante las tres herramientas que ofrece la estadística implicativa, los árboles de similitud, cohesitivo e implicativo.

En los estudios de didáctica de las matemáticas interesa, como se ha mencionado, identificar reglas que permitan dar cuenta de las estructuras que los alumnos han construido durante su aprendizaje. La estructuración del conocimiento no es, sin embargo, un proceso lineal de ensamblaje de partes para completar un todo significativo; tampoco es un proceso simétrico. Esta estructuración se presenta más bien de acuerdo con los esquemas siguientes (Gras, 2005): a) una regla del tipo a ⇒ b, en la que a y b pueden ser a su vez reglas, implica una variable c que puede ser interpretada como la consecuencia de esa regla; b) una variable a implica una regla b ⇒ c, que se puede interpretar como: de la observación de a se deduce la regla b implica c; y c) una regla a ⇒ b implica otra regla c ⇒ d, que puede compararse a aquella situación en la que un teorema tiene como corolario otro teorema. La estructura que responde a estas características es jerárquica, es orientada y no es simétrica. Esta es la estructura que puede obtenerse mediante el uso del análisis implicativo y con el paquete llamado Clasification Hiérarchique Implicative et Cohesitive (CHIC) (Couturier, 2001; Couturier et al., 2000). Con este análisis se puede obtener una gráfica jerárquica orientada, en la que los distintos niveles identifican las reglas que se forman a distintos niveles de implicación.

El árbol jerárquico de similitud, por otra parte, calcula, para cada par de variables, la similitud entre ellas y conforma las clases de variables. En el proceso de formación de clases se busca, en cada paso, el grupo optimal de esta relación, es decir, un conjunto de variables que contribuye más fuertemente a la formación de una relación que el conjunto de las demás variables. Así, es posible estudiar el impacto de las distintas variables en la formación de clases y detectar si una categoría contribuye más fuertemente que otras a la creación de una estructura. Esta información es de gran riqueza pues nos informa de las categorías de variables que están en la base de las estructuras obtenidas (Couturier, 2001).

Se aplicaron las técnicas de análisis estadístico implicativo descritas con anterioridad a los datos recogidos de la muestra de alumnos, usando el paquete CHIC 3.5 (Couturier, 2001; Couturier et al., 2000). Los resultados obtenidos se discuten a continuación.

Análisis del árbol de similitud

El árbol de similitud que se muestra en la figura 1 corresponde a las variables del problema en estudio. En él puede observarse que, en un primer nivel, las variables con mayor índice de similitud son aquellas que se refieren a la capacidad de los estudiantes de graficar una función cuando su expresión analítica está dada. El algoritmo continúa relacionando las variables por parejas hasta el nivel 5. Es importante destacar que en estos cuatro niveles se relacionan aquellos datos que manifiestan: la capacidad de los alumnos para graficar funciones independientemente de su representación (Q, R), la posibilidad de dividir la gráfica en intervalos según las propiedades de la función (N, P), reconocer los intervalos en el dominio de la función cuando no se ha presentado la gráfica (C, H) y la relación entre el punto de inflexión con tangente vertical y la concavidad de la gráfica (I, J). Es de notar que estas variables que están altamente relacionadas en este análisis separan claramente los tres tipos de actividad que se pedían en el cuestionario. A partir de ese nivel, se comienzan a agrupar lasnuevas variables con las clases ya formadas para, posteriormente, unir clases de variables por su similitud.

 

 

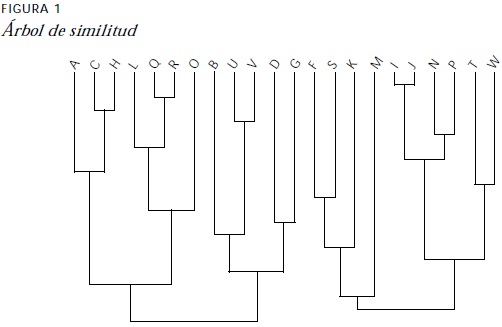
El análisis de las variables en cada una de las dos grandes clases que se forman muestra que el primer grupo corresponde a aquellas variables que indican que los alumnos comprenden el significado de la primera derivada (A, L, R, O, U, V, D, G); algunos manejan también la segunda derivada (C, H, Q, B, U, V), pero todos tienen problemas cuando aparecen puntos de inflexión donde la tangente es vertical (I, P, W). Dentro de este primer grupo se distinguen dos subgrupos. El primero incluye las variables que indican que los alumnos pueden reconocer un punto que no comparte las propiedades de los puntos en los intervalos contiguos y que interpretan correctamente la información presentada tanto gráfica como analíticamente. El segundo subgrupo queda conformado por variables que indican que los alumnos comprenden bien la primera derivada en general.

El segundo grupo reúne a las variables que indican una comprensión global del proceso de graficación en forma analítica, incluyendo a aquellas que se refieren a la capacidad de interpretar la información en forma gráfica (K, M, I, J, N, P, T, W). En este grupo destacan también dos subgrupos. El primero queda conformado básicamente por las variables que indican comprensión analítica pero no gráfica por parte de los alumnos (F, S, K, M), mientras que el segundo queda conformado por las variables que indican comprensión analítica y gráfica (I, J, N, P, T, W).

Los resultados del árbol de similitud nos permiten agrupar las variables originales en cuatro estructuras que ayudan a diferenciar la comprensión de los alumnos, a saber:

1) Comprensión de la primera derivada.

2) Comprensión de las propiedades de la función cuando la información se presenta de manera analítica.

3) Comprensión de las propiedades de la función, excepto en los casos que aparecen puntos en los que el comportamiento de la función difiere del comportamiento en los intervalos vecinos, cuando la información se presenta en cualquier representación.

4) Dominio de todas las relaciones implicadas entre los conceptos.

Análisis del árbol cohesitivo

Recordemos que el árbol cohesitivo está relacionado con la implicación entre las variables. En él, las clases de variables se constituyen a partir de la implicación entre ellas. En la figura 2 se muestra el árbol cohesitivo que se obtuvo en el estudio.

 

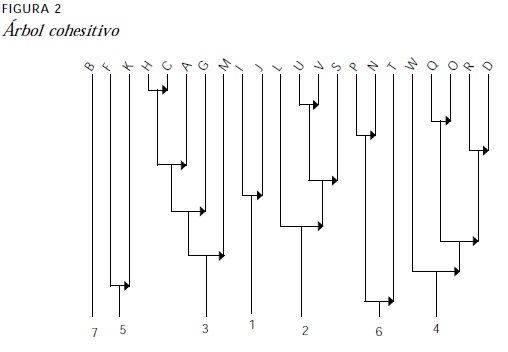
El primer nivel de este árbol, indica que la variable H implica a la C con un índice de implicación más fuerte que el de cualquier otro par de variables. Esto indica que cuando los estudiantes respondieron correctamente las preguntas relacionadas con los puntos de inflexión de la función en los que la recta tangente a la curva es vertical, es posible inferir que son capaces de responder, también correctamente, aquellas preguntas relacionadas con la concavidad de la función presentada gráficamente.

Posteriormente se observan 6 grupos de variables y una que queda sin agrupar. El análisis de estos grupos, en el orden en que se forman indica que:

• Si un alumno es capaz de interpretar la información presentada en términos de los intervalos que satisfacen determinadas propiedades, logrará graficar una función cuando se le presenta en forma analítica (grupo 1 en la gráfica).

• Si un alumno reconoce las concavidades en cualquier tipo de gráfica, es capaz de determinar los intervalos en que debe dividirse el dominio de la función de manera que ésta comparta las mismas propiedades en cada uno de ellos, independientemente de la representación en que se le presente la información (grupo 2).

• Si un alumno muestra problemas para interpretar el significado de la primera derivada cuando una función se le presenta en forma gráfica, no será capaz de interpretar el significado de la primera y de la segunda derivadas de la función cuando ésta se le presenta en forma analítica (grupo 3).

• Si un alumno es capaz de reconocer los puntos del dominio de la función que no tienen las mismas propiedades que los puntos contiguos, cuando la información se presenta utilizando cualquier representación, puede comprender sin dificultad el comportamiento de la función en términos de sus propiedades e intervalos. Nótese que este grupo y el segundo involucran las condiciones que satisfacen los alumnos que tienen un mejor dominio de la graficación de funciones en general; sin embargo, el segundo grupo se refiere a la interpretación de la concavidad en forma gráfica y su relación con los intervalos en que el dominio queda dividido de acuerdo con las propiedades de la función que se satisfacen, mientras que éste se refiere a los alumnos que distinguen todos los detalles de la gráfica de cualquier función (grupo 4).

• Si un alumno comprende las implicaciones del signo de la primera derivada, es capaz de reconocer, en la gráfica, los intervalos en los que la función crece o decrece. Nótese que la información proporcionada por el grupo 3 indica que lo contrario es también cierto, aunque añade información acerca de la comprensión de la segunda derivada (grupo 5).

• Si un alumno es capaz de dividir el dominio de la función en intervalos en los que la función comparte propiedades relacionadas con la primera y la segunda derivadas, independientemente de la representación en la que la información se presente, podrá determinar la existencia de un punto en el dominio de la función en el que ésta no comparte las propiedades que satisface en los puntos de los intervalos contiguos (grupo 6).

• La variable que queda aislada en el árbol corresponde al reconocimiento de los puntos de inflexión en cualquier representación (b). Esto refleja el hecho de que la mayoría de los alumnos que respondieron el cuestionario tuvo dificultades al interpretar la información en todas las preguntas que lo involucran (grupo 7).

Análisis del árbol implicativo

Por último, en la figura 3 se presenta el árbol implicativo para los datos:

Del análisis de esta figura se desprende que:

• Con 99% de confianza, si los alumnos comprenden las implicaciones gráficas y analíticas del límite sobre la primera derivada, no tienen dificultades con las concavidades de la función.

• Con 95% de confianza, si los alumnos comprenden las implicaciones gráficas y analíticas del límite sobre la primera derivada entonces son capaces de trabajar con la información definida en términos de intervalos.

• Con 95% de confianza, si los alumnos interpretan correctamente las concavidades de la función, son capaces de trabajar con la información definida en términos de intervalos en los que la función comparte propiedades específicas.

En resumen, este análisis nos indica que la comprensión profunda de los puntos de inflexión es un requisito indispensable para la comprensión del proceso de graficación en cálculo. Por otra parte, la posibilidad de dividir el dominio de la función en intervalos que comparten propiedades depende de manera importante de la comprensión profunda de la concavidad.

 

Discusión de los resultados

El análisis implicativo y cohesitivo de los datos nos proporciona información que puede ser interpretada en términos del marco teórico utilizado en el diseño del cuestionario. En la figura 4 se muestra una esquematización de los resultados obtenidos del árbol de similitud.

 

 

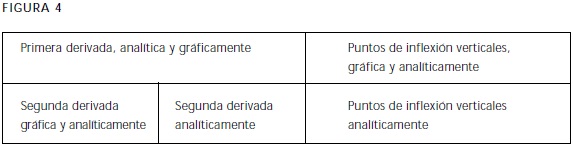
Es de notar en la figura anterior que los rectángulos señalados indican conjuntos de alumnos que fueron capaces de responder a las preguntas del cuestionario que involucran las propiedades que en ellos se incluyen. El conjunto completo se refiere a la posibilidad de los alumnos de construir e interpretar la gráfica de una función cualquiera cuando se le proporciona distinta información. Este conjunto queda dividido en dos subconjuntos muy claramente delimitados que corresponden a los que distinguen o no los puntos de inflexión verticales, es decir, que son capaces de interpretar límites sobre derivadas y su relación con la tangente a la curva. En términos del marco teórico esta división corresponde a aquellos alumnos que se encuentran en el nivel trans- propiedades, trans-intervalos, que en la figura están incluidos en el rectángulo completo de la derecha y aquellos que se encuentran en los otros niveles de la doble tríada en relación con las propiedades que en la figura se representan mediante el rectángulo completo a la izquierda.

Dentro de cada uno de estos rectángulos se encuentran nuevas divisiones. El de la izquierda queda conformado por dos subconjuntos, en el primero representado en la parte superior de la figura, se incluyen aquellos alumnos que únicamente son capaces de interpretar la primera derivada de la función, es decir, quienes no han construido relaciones entre las propiedades de la función y entre los intervalos del dominio de la función, por lo que puede considerarse que se encuentran en un nivel intra-propiedades, intra-intervalos en su construcción del esquema de graficación de funciones. Los estudiantes incluidos en el rectángulo inferior son aquellos que han empezado a construir relaciones entre la primera y la segunda derivadas y son capaces de interpretar analíticamente las implicaciones del signo de la segunda derivada y algunas operaciones entre intervalos. Puede considerarse por ello que estos alumnos se encuentran en un nivel inter-propiedades, intra-intervalos. Contenido en este rectángulo se encuentra un grupo de estudiantes, representado en la parte derecha inferior de esta parte de la figura, que además de lo anterior son capaces de interpretar las implicaciones de la segunda derivada tanto analítica como gráficamente. Se puede decir que, los alumnos que tienen esta capacidad, se encuentran en un nivel inter-propiedades, inter- intervalos de la triada.

En el rectángulo de la derecha se advierten también diferencias. Este conjunto queda dividido en dos: por una parte, en los alumnos que son capaces de interpretar toda la información únicamente cuando se presenta de manera analítica y que pueden considerarse en un nivel trans- propiedades, inter-intervalos de la triada y, por otra, aquellos que son capaces de interpretar la información independientemente de la forma en la que se les presenta, que corresponderían a aquellos estudiantes que se encuentran en el nivel trans-propiedades, trans-intervalos.

Por su parte, el árbol cohesitivo y la gráfica implicativa ponen de manifiesto la importancia de la comprensión de los puntos de inflexión, en particular de aquellos en los que la tangente a la curva es vertical y de los puntos en los que la función no comparte las propiedades que se cumplen en los intervalos contiguos en una comprensión sólida de los conceptos del cálculo involucrados en la graficación de funciones. También nos indican la fuerte relación de esta comprensión con la posibilidad de subdividir el dominio de la función en subintervalos de acuerdo con las propiedades de la misma. Esto pone de manifiesto la interacción entre las tríadas correspondientes a los intervalos y a las propiedades, interacción que se había ya encontrado mediante análisis cualitativos en algunos trabajos previos (Baker et al., 2000; Cooley et al., 2007).

Las seis reglas que se desprenden del árbol cohesitivo dan, por su parte, clara evidencia de que la comprensión del significado de la primera derivada de una función no es suficiente para interpretar correctamente el significado de la segunda derivada. Si bien a nivel operativo estas dos transformaciones están muy claramente relacionadas, sus interpretaciones geométricas y en cuanto a las propiedades de la función son muy diferentes.

 

Conclusiones

El análisis cualitativo es una herramienta invaluable en el análisis de los fenómenos relacionados con la educación matemática; sin embargo, este análisis resulta costoso y se dificulta cuando las poblaciones a estudiar son muy grandes. Durante muchos años se ha cuestionado el valor de la estadística multivariada en este tipo de estudios porque la información de los distintos métodos que se utilizan es muy general y no resulta útil para lograr un conocimiento a profundidad de los fenómenos relacionados con el aprendizaje de las matemáticas. En este trabajo se muestra que el uso del análisis estadístico implicativo y cohesitivo, desarrollado con base en el álgebra booleana y no en las correlaciones estadísticas, resulta pertinente y útil para el estudio de dichos fenómenos; también se ilustra cómo el uso de esta herramienta proporciona información consistente con la obtenida mediante análisis cualitativo, a la vez que permite el análisis de la información obtenida de poblaciones más grandes.

A partir de los resultados del presente trabajo se pone en evidencia que los conceptos que resultan ser clave en la posibilidad de los estudiantes de establecer las relaciones que se requieren para resolver con éxito problemas de graficación utilizando las herramientas del cálculo diferencial son los relacionados con la segunda derivada de la función, en particular, los puntos de inflexión, la relación de la continuidad con la primera derivada y la comprensión de la subdivisión del dominio de la función en intervalos determinados por la interrelación de las propiedades de la función definidas por la primera y la segunda derivadas. Los estudiantes en este estudio muestran una tendencia a guiarse únicamente por la primera derivada para completar o interpretar la gráfica de una función, lo que indica que ésta es la estructura dominante en sus procedimientos. La importancia que se le concede a la interpretación de la primera derivada de una función hace, probablemente que la interpretación de las implicaciones gráficas y analíticas de la segunda derivada sean comprendidas con mucha menor profundidad.

La mayoría de los estudiantes que resolvieron el cuestionario que se analizó en este estudio utilizan la información de la primera derivada como determinante en las decisiones que toman para graficar una función o para interpretar sus propiedades. Esta estructura tiene un papel dominante en la solución de los problemas y es importante; sin embargo, también parece actuar como obstáculo a la comprensión del papel que juega la segunda derivada y a la interrelación de ambas para determinar el comportamiento de una función.

Dada la importancia de la comprensión de la segunda derivada y de la relevancia de los intervalos en el dominio de la función, determinados por la relación entre propiedades, los datos de este análisis indican que para poner de manifiesto las concepciones de los alumnos es necesario plantear preguntas y situaciones problemáticas en las que la identificación de los puntos de inflexión, particularmente aquellos en donde la tangente a la curva es vertical, y de los puntos en los que la función es continua pero no derivable tomen un papel primordial. Estas son, asimismo, las propiedades que hacen que la subdivisión del domino de la función en los intervalos pertinentes sea relevante para la solución del problema.

La información que se obtiene de este trabajo muestra la necesidad de apoyar a los alumnos en la construcción de las relaciones entre conceptos. Suele pensarse que al estudiar cada concepto por separado los alumnos serán capaces de construir esas relaciones por ellos mismos, pero los resultados de este trabajo y de otros que lo anteceden ponen de manifiesto que esto no es así. Es necesario que estas relaciones se enseñen de manera explícita y ostensiva (Bosch y Chevallard, 1999), mediante el trabajo con información presentada en diferentes representaciones.

 

Anexo

 

Referencias

Asiala, M.; Brown, A.; DeVries, D. J.; Dubinsky, E.; Mathews, D., y Thomas, K. (1996). "A framework for research and curriculum development in undergraduate mathematics education", en J. Kaput, A. H. Schoenfeld, y E. Dubinsky (eds.), Research in collegiate mathematics Education, II, 1-32. Providence, R.I.: AMS y Washington D.C.: MAA.         [ Links ]

Aspinwall, L.; Shaw, K., y Presmeg, N. (1997). "Uncontrollable mental imagery: Graphical connections between a function and its derivative", Educational Studies in Mathematics, 33, 301-317.         [ Links ]

Baker, B.; Cooley, L, y Trigueros, M. (2000). "The schema triad - A calculus example", Journal for Research in Mathematics Education (JRME), 31(5), 557-578.         [ Links ]

Bosch, M. y Chevallard, Y. (1999). "La sensibilité de l'activité mathématique aux ostensifs", Recherches en didactique des mathématiques, 19 (1).         [ Links ]

Carlson, M. (1998). "A cross-sectional investigation of the development of the function concept", en E. Dubinsky, A. H. Schoenfeld y J.J. Kaput (eds.), Research in Collegiate Mathematics Education, III. Issues in Mathematics Education, 7, 115-162.         [ Links ]

Carlson, M.; Jacobs, S.; Coe, E.; Larsen, S. y Hsu, E. (2002). "Applying covariational reasoning while modeling dynamic events: A framework and a study", Journal for Research in Mathematics Education, 33(5), 352-378.         [ Links ]

Carlson, M. P.; Smith, N., y Persson, J. (2003). "Developing and connecting calculus students' notions of rate of change and accumulation: The fundamental theorem of calculus", en N.         [ Links ]

A. Pateman, B. J. Dougherty y J. T. Zilliox (eds.), Proceedings of the 2003Joint meeting of PME and PMENA, 2, Honolulu, HI: CRDG, College of Education, University of Hawaii, 165-172.         [ Links ]

Cooley, L.; Trigueros, M. y Baker, B (2007). "Schema thematization: a framework and an example", Journal for Research in Mathematics Education, 38(4), 370-392.         [ Links ]

Cortés, M. (2004). Integración de conceptos en la solución de problemas de cálculo diferencial, tesis de licenciatura en Matemáticas Aplicadas, México: ITAM.         [ Links ]

Couturier, R. (2001). "Traitement d l'analyse statistique dans CHIC", Actes des Journées sur la Fouille dans les données par la méthode d'analyse implicative, IUFM Caen,. 33-50 http://math.unipa.it/~grim/asi/asi_00_couturier.pdf, consultado febrero de 2006.         [ Links ]

Couturier, R.; Bodin, A. y Gras R. (2000). Classification Hiérarchique Implicative et Cohésitive,: Rennes: Association pour le Recherche en Didactique des Mathématiques.         [ Links ]

Czarnocha, B.; Dubinsky, E.; Prabhu, V. y Vidakovic, D. (1999). "One theoretical perspective in undergraduate mathematics education research", Proceedings of the xxiii pme International Conference, Israel.         [ Links ]

Dubinsky, E. (1996). "Una aplicación de la perspectiva piagetiana a la educación matemática post-secundaria", Educación Matemática, 8, (3), 24-45.         [ Links ]

Dubinsky, E. (1991a). "Reflective abstraction in advanced mathematical thinking", en D. Tall (ed.), Advanced Mathematical Thinking, Kluwer Academic Publishers, Dordrecht, 95-123.         [ Links ]

Dubinsky, E. (1991b). "The constructive aspects of reflective abstraction in advanced mathematics", en L.P. Steffe (ed.) Epistemological Foundations of Mathematical Experiences, New York: Springer-Verlag.         [ Links ]

Ferrini-Mundy, J. y Graham, K. (1994). "Research in calculus learning: understanding of limits, derivatives and integrals", en Kaput, J., Dubinsky, E. (eds) Research Issues in Undergraduate Mathematics Learning, Washington, DC: MAA.         [ Links ]

Gras, R. (1996). L'Implication Statistique. Nouvelle méthode exploratoire de données, La Pensée sauvage, éditions, Francia.         [ Links ]

Gras, R. (2005). Panorama du développement de l'A.S.I. à partir de situations fondatrices, Troisièmes Rencontres Internationales, Palermo, Italia http://math.unipa.it/~grim/asi/asi_05_gras_1.pdf, consultado: febrero de 2006        [ Links ]

Gras, R. y Ratsimba-Rajhon, H. (1996). "Analyse non symétrique de donnés par l'implication statistique", RAIRO. Recherche opérationnelle, vol. 30, n 3, pp. 217-232        [ Links ]

McDonald, M.; Mathews, D. y Strobel, K. (2000). "Understanding sequences: A tale of two objects", en E. Dubinsky, J. Kaput y A. Schoenfeld (eds.), Research in Collegiate Mathematics Education IV, 8,77-102. Providence, R.I: AMS/ Wash., DC: MAA.         [ Links ]

Oktaç, S. A.; Trigueros, M. y Vargas, X. N.(2006). "Understanding of vector spaces, a viewpoint from APOS Theory", Proceedings of the 3^rd International Conference on Undergraduate Mathematics Education. Estambul, Turquía, pp. 271-272        [ Links ]

Orton, A. (1983). "Students' understanding of differentiation", Educational Studies in Mathematics, 14, 235-250.         [ Links ]

Piaget, J. y García, R. (1996). Psicogénesis e historia de la ciencia, Cd. de México, México: Siglo XXI Editores.         [ Links ]

Piaget, J. (1970). Introducción a la epistemología genética (I-III), Madrid: Debate.         [ Links ]

Piaget, J. (1971). Psicología y epistemología, Buenos Aires. Emecé Editores.         [ Links ]

Selden, J.; Selden, A. y Mason, A. (1994). "Even good calculus students can't solve non-routine problems", Research Issues in Undergraduate Mathematics Learning, Notes, 33 (31-45). Washington, DC: Mathematical Association of America.         [ Links ]

Slavit, D. (1995). "A growth -oriented route to the reification of function", en D.T. Owens, M.K. Reid y G. M. Millsaps (Eds.), Proceedings of the seventeenth annual meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education (vol. 1, 284-290). Columbus, OH: edición de autor.         [ Links ]

Thompson, P. W. (1994). "Images of rate and operational understanding of the fundamental theorem of calculus", Educational Studies in Mathematics, 26, 229-274.         [ Links ]

Trigueros, M. (2000). "Students' conceptions of solution curves and equilibrium in systems of differential equations", Proceedings of the 22^nd annual meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education I, 93-97. Columbus, OH.         [ Links ]