Calibration of Parallel Manipulators and their Application to Machine Tools. A State of the Art Survey

 

Calibración de manipuladores paralelos y su aplicación a las máquinas herramienta. Un Estudio del estado del arte

 

Hernández–Martínez E.E.¹, López–Cajún C.S.² y Jáuregui–Correa J.C.³

 

¹ Facultad de Ingeniería. Universidad Autónoma de Querétaro, México. E–mail: e.hernandez@unicas.it

² Facultad de Ingeniería. Universidad Autónoma de Querétaro, México. E–mail: cajun@uaq.mx

³ CIATEQ E–mail: jcjaur@ciateq.mx

 

Recibido: diciembre de 2007
Aceptado: agosto de 2009

 

Abstract

Some of the main investigations on calibration methods of parallel mechanisms are briefly discussed in this work. Initially, the identification of errors in these structures applied to machine tools is presented, later the kinematics and the concept of parallel mechanisms calibration is introduced. Additionally, the main characteristics of the existing methods of calibration are discussed, such as the parametrical approaches, the calibration methods with internal/external measuring devices, innovative calibration methods and works that provide assistance to this aim.

Keywords: Parallel mechanisms, calibration, machine tools, inverse kinematics, forward kinematics.

 

Resumen

Las investigaciones más relevantes sobre métodos de calibración de mecanismos paralelos se discuten brevemente en este trabajo. Inicialmente se aborda la identificación de errores de estas estructuras como aplicación a las máquinas herramienta, después se introduce la cinemática y el concepto de calibración de los mecanismos paralelos. Adicionalmente, se discuten las principales características de los métodos de calibración existentes, tales como los métodos paramétricos, los métodos de calibración con dispositivos internos/externos de medición y trabajos adicionales que proporcionan ayuda para este fin.

Descriptores: mecanismos paralelos, calibración, máquinas–herramienta, cinemática inversa, cinemática directa.

 

Introduction

Parallel mechanisms present several advantages over serial mechanisms, such as high flexibility, high stiffness and elevated accuracy. For this reason, the interest on these structures has been increasing over the last few years. As a consequence, the number of works that deal with open problems of these mechanisms type has also grown. Nowadays, parallel mechanisms are starting to be used in industry such as machine tools, pick and place high velocity robots, and flight simulators, among other applications. This is so due to the high accuracy required for their processes. For the same reason, they are also used for medical applications and rehabilitation. A parallel mechanism has the main property of having its end–effector connected to the base through several serial (and/or parallel) kinematic chains. This allows the parallel mechanism to support heavy loads, high velocity operation and show a better repeatability (Merlet, 1997). However, its great number of links and passive joints offer limited performance in terms of accuracy (Wang and Masory, 1993). For this reason, the kinematic parameters of these mechanisms should be identified with the process called kinematic identification (or kinematic calibration). The objective of the robot kinematic calibration is to determine the exact kinematic parameters for improving its accuracy.

In order to be applied as a parallel kinematic machine (PKM) tool, calibration strategies for parallel mechanisms should be defined and consolidated, (Merlet, 2002). Conventional machine tools typically consist on three mutually orthogonal axes, each one controlled by a separate driver in linear guides. For a parallel mechanism of n degrees–of–freedom, the global pose depends on all its drivers. For this application, the global error at the end of the tool is the main concern. This error could be due to manufacturing tolerances or assembly errors in the parallel mechanism construction that can be used for tool or workpiece positioning. At high speed, control speed and accuracy play an important role in the overall final position.

In this work, a study on parallel mechanism calibration is presented, including some of the main works recently published and a discussion of the advantages and disadvantages of the calibration methods being used. In Section 2 the identification of PKM source errors is outlined, in Section 3 a mechanism kinematic is presented including the introduction of the calibration concept, and finally, beginning in Section 4, an actualized classification of the calibration methods of parallel structures is included.

Errors identification of parallel kinematic structures used as machine tools

In all manufactured machines or mechanisms a deviation from nominal design values occurs due to assembly or manufacture errors. Many works have been focused on error identification with the objective of improving the absolute accuracy of parallel mechanisms and their applications. In the PKMs, the factors listed below may cause positioning and orientation errors:

1. Parametric errors caused by geometrical deviation of the machine parts and errors in their assembly (i.e. manufacturing process of the machine components, which is known as tolerances);

2. Joint runout caused by geometrical deviation of the joint parts, which is caused by mechanism motion;

3. Elastic deformations of the links and the joints, which are generated by external forces or by displacement of the center of gravity;

4. Elastic deformation of the machine frame supporting the mechanism, which is caused by external forces or displacement of center of gravity;

5. Thermal expansion of the links and the frame, caused by temperature fluctuation.

The abovementioned factors (2–5) can be divided into two groups: mechanism errors and frame deformations. In figure 1a, the positioning error cases related to the tool and the workpiece for a conventional machine tool are shown; these errors also affect the PKMs accuracy. Some studies have been made in order to improve the PKM accuracy, Zhuang and Roth (1993) proposed a measurement method that consists of the separate estimate of parameters for each leg. In a machine tool of hexapod type, Ziegert (1996) attributed the source errors in the model to the uncertainties of the theoretical model, such as coordinates of the base joint center and moving platform, link length in the initial position, as well as tool length. Soons (1997) reported the measurement and analysis of the geometrical errors in a PKM, through its kinematic model and experimental measurements using conventional metrology tools. The research reported in (Rudder, 1997) was focused in error modeling, error computation and stiffness analysis.

Parenti–Castelli et al. (1998) emphasizes that kinematic and dynamic behavior of a PKM is strongly influenced by joint geometrical errors. Iowa and Tamaki (2000) reported that the spherical joints distance located at the leg end (which is the leg length) is fundamental for platform accuracy positioning. In (Cui et al., 2005) the kinematic and error modeling using Jacobian matrix method was established for TAU robot (Brogangrdh et al., 2002). In addition, that research introduced the Jacobian approximation method to calculate the forward kinematic problem instead of the Newton–Raphson method. The full size Jacobian matrix is used in order to estimate and identify the model parameters. Error compensation methods for PKMs have been described by Oiwa, (2005). He discussed the joint and link deformations caused by external forces and heat by working with two types of errors that establish the relative positioning between tool and workpiece for conventional machines, the mechanical errors and the frame deformation of the mechanism. Deblaise et al. (2004) studied the Delta robot and took into account errors due to the elasticity of the links.

Figure 1

Kinematics and calibration of parallel structures

The best known parallel mechanism is the Gough–Stew–art platform and it commonly has been applied as machine tool. This manipulator consists of two rigid bodies, called the base and moving platform, connected to the base by six legs, as shown in figure 1b. Each leg is, in turn, a six degree–of–freedom (dof) serial kinematic chain. These legs provide a sixth dof for any arbitrary pose (position and orientation) of the end–effector relative to the base that corresponds to the operation point, given as a vector p and the orientation imbedded in a rotation matrix Q. Thus, the pose x can be expressed as x=x(p,Q), which in turn, depends on the variations of each length of the prismatic joint, ci, for i = 1,...,6, which can be measured by internal sensors. Each leg is attached to the base by a universal joint and to the platform by a ball joint. Thus, there are 42 kinematic parameters –36 parameters for joints centers and six nominal lengths of the legs–, (Wang and Masory, 1993). In addition, the main error source in positioning is related to the limited knowledge of the joints center and a fraction of the size is not defined by the sensors. The kinematic models are essential for robot control, and produce the constraints used in calibration. By inverse kinematics, the length ci of the ith leg as a function of the desired pose can be computed as

where b_i and p_iare the position vectors of the attachment points of the legs on the base and platform, respectively, in a coordinate frame fixed to the base, meanwhile p'_i are the position vectors of platform points in a coordinate frame fixed to the platform. For the Gough–Stewart platform, the forward kinematics is more difficult to calculate since one must solve Eq. (1) for p given c_i for i = 1,... ,6 and the mechanism parameters. Clearly, the parallel mechanism configuration is related to the parameters of the kinematic structure through the equations of the kinematic model. The calibration proposal is the positioning error reduction of the end–effector using a precision identification of the kinematic parameters. It is known that the feasible and economical way to improve the parallel mechanism accuracy is by kinematic calibration. Calibration is crucial to any autonomous manipulator when high accuracy is required. Additionally, if the precise mathematical model is used as support, it can get an excellent positioning performance. Nowadays, a necessary condition to introduce the PKMs in the industrial context is to develop a fast calibration technique.

The calibration could be achieved measuring several mechanism configurations and identifying its respective kinematic parameters. The number of equations given by measurements is less than the number of unknown parameters. Data measurements are generally produced by a sensor, thus it is necessary to consider the noise associated to this device. The general parallel manipulator calibration includes the following tasks:

1. Platform kinematic modeling in order to know the main source of error;

2. Measurement of platform poses;

3. Error identification of platform kinematic parameters using measurement data;

4. Compensation of the platform accuracy using identified error parameters.

An important part of the calibration process is measuring the actual pose of some parts of the manipulator. A great variety of sensors have been used for this purpose. For some of them extra objects have to be installed on the manipulator, so it is possible to add extra accuracy problems. In accordance with the above four points of calibration tasks, a great variety of calibration algorithms has been developed according to specific requests. In Figure 2, several calibration methods for parallel manipulator calibration are shown, and discussed below.

Parametrical approaches

The classic methods for the calibration of parallel robots require extra sensor devices for the measurement of the pose of the moving platform and the values of the joint variables. Then, the calibration problem can be formulated to derive a residue, which is the difference between the measured variables and the calculated ones by using the kinematic model.

Parametrical approaches are also called model–based calibration strategies. Hollerbach et al., (1994) concluded an important principle for the calibration of parallel mechanisms: The calibration is possible if the number of joint sensors (including the measurement equipment), referred as the sensor degree, exceeds the mobility system to calibrate. They define the calibration index as the excess of sensors on the mobility of the mechanism. Furthermore, they established that the calibration index represents the number of independent equations by pose available for the calibration.

Some calibration methods are based on the forward kinematics model (FKM) and come up directly from the methods developed for serial mechanisms. Such methods reduce a nonlinear error between the pose measurement of the end–effector and its estimation of measurement values of the joint variables, (Wang and Masory, 1993). However, in general, a single numerical evaluation of the FKM for the parallel mechanism is obtained.

This could lead to numerical instabilities of the identification (Daney, 1999), and translated to the case of control, this result means that convergence cannot be guaranteed. Daney et al., (2005) proposed an algorithm based on a constrained optimization method, which allows to choose a set of measurement configurations. In (Daney et al., 2006) the dependency on the parameters of pose of a planar parallel manipulator calibration is eliminated; the FKM in the scheme of calibration is used. Since this model has different solutions, the authors set out two alternatives. One of them makes use of algebra to explain the relation between the set of sensors and the parameters, and the other one diminishes the residual errors of a restricted formulation of the FKM.

For solving the control problem, many investigators are innovating in the subject of structural synthesis, that is to say, they try this type of mechanisms with analytical or semi–analytical FKM. Redundant sensors for position have been used as an advisable way to solve the problem of forward kinematics. By reducing the number of necessary sensors, it is possible to overcome such problem. Nevertheless, for many applications of parallel manipulators, the problem of forward kinematics is a single small part of the control stage, used to obtain knowledge of the current manipulator position, but not in real time. A typical scheme control is represented in figure 3.

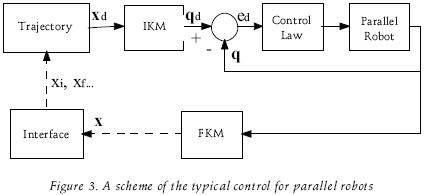
The trajectory is generated first in the Cartesian space; then, each Cartesian location is transformed to a position vector into the joint space via the inverse kinematics model (IKM). The control —–that is, the heavy part in real time of the process—– is obtained in the last space, the FKM frequently is implemented as a man–machine interface routine in the initial phase. Based on the error model, it is possible the mapping from the geometric errors to the pose error of a PKM. However, this mapping error could increase the global accuracy of the structure.

It is well known that for parallel mechanisms, the IKM can easily be derived. Then, the most natural method to develop the identification is to diminish an error between the measurements of the joint variables and their corresponding values, considering the pose measurement of the end–effector through the IKM. Last et al. (2005a) presented an IKM for the HEXA parallel robot which contains an increased number of geometric parameters as compared to the ideal geometric models while still being analytical solvable. Huang et al. (2005) presented an external–calibration–based approach that enables the geometric parameter errors of 6 dof PKM to be identified using a minimum set of pose error measurements.

With simulation results, they found strong correlations between all the parameters in the kinematic calibration of a Gough–Stewart platform. Sato et al. (2004) proposed to use a priori knowledge of the kinematic parameters to eliminate their correlation and to give robustness to the calibration. Using this knowledge through simulations, all kinematic parameters are identified in the artefact calibration without divergence.

The method of calibration based on IKM is seen more efficient in a numerical way in many of the identification algorithms for parallel mechanisms, but it is restricted by the necessity of precise measurements of all the poses of the end–effector, (Khalil and Besnard, 1999). In order to reduce the parametrical errors, some studies called parametrical calibrations have been performed.

These calibrations deal with static or kinematic systematic errors and do not allow the inclusion of unexpected disturbances or thermal fluctuation. Nevertheless, such non repetitive or geometrical errors should be compensated before kinematic calibration.

Calibration with additional internally measuring systems

The self calibration methods of parallel robots generally make use of extra sensors on the passive joints and allow the identification of the workspace. In this method, the values of the kinematic/geometrical parameters with the purpose of diminishing a remainder between the measured values and the calculated ones of the variables of the passive joints, are due to fit.

Approach of redundant sensors

In this approach it is necessary to have one or more sensors on the passive joint in an appropriate way, with the purpose of increasing the number of sensor degrees on the dof, so that the calibration algorithm can be applied. Yang et al., (2002) focus on the calibration of the base and tool. Sensors in the passive joints and the transformation kinematics of the base to the frame of the moving platform are used and calculated. The iterative algorithm of least squares is utilized to identify the errors of the parameters. In Zhuang and Liu, (1996), for calibrating the Gough–Stewart platform, three functions for rotational parametric identification are used by applying IKM and FKM with six encoders. In this same approach, in (Hollerbach et al., 1994) the calibration for a redundant parallel robot of 3 dof is reported. Multiple closed loops in the optimization method were used with least squares. In (Khalil and Besnard, 1999), a method for the kinematic calibration of 6 dof robots using two inclinometers is presented. The calibration model takes into account the error from the angle between the axes of the inclinometer. The estimation of the parameters is obtained using the Levenberg–Mar–quardt algorithm, (Marquardt, 1963).

With the use of additional sensors in the passive joints, the control functions, like calibration, supervision of the workspace and position control can be improved. In order to operate the potential of the concept of sensors in the passive joints, in (Hesselbach et al., 2005) calibration algorithms are developed to evaluate the additional information for certain functions of control, determining the necessary resolution of the sensors for a class of parallel robots. In (Zhang et al., 2007) based on the study of the relationship between the projected tracking error of the redundant joint angles, and the error of the sensor zero positions, the calibration of the sensor zero positions of a planar 2 dof parallel manipulator is studied. Two algorithms for the self–calibration of the joint angle offsets are proposed by (Yiu et al., 2003). The calibration is done by utilizing the redundancy sensor information, sampling over the workspace, and optimizing a cost function.

Ecorchard and Maurine (2005) proposed a geometrical self–calibration method for the Delta robot with compensation of the non–geometrical gravity effects, by using redundant sensors on its kinematic structure. For the HEXA parallel robot, Last et al., 2005b reported a technique to calibrate the structure by means of redundant angular sensors added to its passive joints. An important difference to previous work is the fact, that only angular measurements are available from both the actuator encoders as well as passive joints sensors. In order to consider the effect of measurement inaccuracies, they took the noise into account. The disadvantages of this approach are that sensors need high precision; it is not possible to place these sensors on all the passive joints and some kinematic parameters are dependent on the model error. Therefore, the tool position on the platform cannot be calibrated, (Zhuang and Liu, 1996). In addition, it is difficult to add extra sensors on the already existing mechanisms and sometimes almost impossible when ball joints exist

This approach offers an online calibration, which collects, evaluate data and return corrected parameters automatically to the control stage. In addition, the redundant sensors can be used to get an analytic and time–efficient solution of the direct kinematic problem. Moreover, the additional sensors are integrated to manipulator as durably parts, yet for commercial manipulators they increase the cost.

Singularity based calibration

In (Last et al., 2007) the singularity based calibration is presented and validated within simulated calibration studies. This technique allows parameter estimation without using any calibration equipment, the basic idea is to obtain redundant information from particular characteristics in singular configurations. It has been successfully adopted to a family of 3 dof planar parallel robots. Nevertheless, a parallel mechanism can be calibrated only if it permits singularities of second type in different places of the workspace.

Calibration with external devices

The self–calibration methods with external measuring systems can be divided in four categories: (1) calibration with vision as measurement device, (2) the approach of mobility restriction, (3) the approach of redundant leg, and (4) the approach with adapted device of measurement.

Calibration with vision as measurement device

Vision constitutes a suitable sensor, thus within these methods of calibration, the use of an external camera to obtain measurement of position or orientation can be considered. In (Renaud et al., 2002a) for a PKM, the calibration system by using IKM is formed by a simple camera and a calibration board generated on a LCD monitor. Precisions in the order of 1 micrometer for two translations and 0.001° for each of the three rotations are considered for a displacement of 400 mm. In (Renaud et al., 2002b) a criterion of pose selection for the kinematic calibration of an orthogonal mechanism is used, which necessarily implies to consider the measurement of the error amplification. In (Shaoping and Ming, 2002) a calibration method based on tool transformations is developed by virtue of optical position sensors. The pose measurement using a commercial 3D measurement system is also described.

For the kinematic calibration of parallel mechanisms with linear actuators in the base, in (Renaud et al., 2005) a camera is used without modifying the mechanism. With this system, the calibration can be done on line; the method is developed theoretically and experimentally applied to an I4 mechanism. Renaud et al., (2006a) sets out a device of measurement based on vision for a H4 parallel robot, introduces a monocular measurement device of high precision. The precision of the measurement device is evaluated on the order of 10 micrometers in position and 0.0005° in orientation. For the same robot, in (Daney et al., 2004) the calibration according to the method of the IKM is utilized too. Renaud et al. (2006b) provided a method for the complete identification of the physical model of a H4 robot. The researchers identify the parameters of the robot, describing the geometric parameters and the dynamic ones, with which they explained the effects of the masses, inertias and friction that act on the physical behavior. They used two algorithms of calibration based on vision, and two models, namely, the implicit model and the IKM.

Using a motion capture system in (Van Driel and Carretero, 2005), a kinematic calibration method for the 3–PRS parallel manipulator is presented. For medical application, Deblaise and Maurine, (2005) presented an effective and simple calibration method based on 1D and 3D measurements of a low cost artifact and validated on the Surgiscope, which is a structure based on a Delta robot used in neurosurgery. In addition, Ait–Aider et al. (2006) sets out a method to be applied in the dynamic identification. A camera is used to simultaneously measure the pose of the end–effector of the visual pattern calibrated and its Cartesian speed by using a single view. Chao et al., (2006) presents a calibration strategy according to the IKM method for a 3 dof flexure–based parallel manipulator by means of a camera. The algorithm does not identify directly the errors of geometry parameters, but finds the most appropriate control model taking all the errors into account.

For a Gough–Stewart platform, a technique of indirect calibration by using an omni–directional camera is considered in (Dallej et al., 2006). The tie points of the legs of the robot are considered on the base, which are the kinematic parameters that the control needs. Another form to compensate the low accuracy of the parallel manipulators is the use of a control law that is robust to calibration errors. The former approach is displayed in (Andreff and Martinet, 2006), the kinematic modeling based on vision and projected geometry is made through observation of the legs of a Gough–Stew–art platform and is extended to Orthoglide and I4L families. This way of modeling unifies and simplifies the stages of identification and control. The main advantage of this calibration method is the high precision that can be obtained. However, vision–based pose measuring can be considered as highly expensive and some particular knowledge should be take into count.

Approach of mobility restriction

The second category of calibration with external measuring systems is the approach of mobility restriction. Usually, the number of sensors in a manipulator is equal to the dof. Fixing one or more passive joints, or by partially restricting the dof of the manipulator, the mobility of the resulting system will be under the number of sensors. Consequently, the algorithm of calibration can be made (Khalil and Besnard, 1999). In the previous work the variables of the prismatic joints are used, and only correspond to the configurations where each universal joint or ball joint is fixed by a mechanical key, which fixes the corresponding leg with the fixed base or the moving platform. The simulations show that this calibration method can identify major errors in the kinematic parameters (almost 10% of error on the nominal values).

In (Sung et al., 2006) a method of global and completely observable calibration using a planar table and digital indicators is developed. The planar table is used as a mechanical installation to restrict the movement of the moving platform. The digital indicators are used as a sensor device, detecting if the restricted motion is satisfied. Consequently, the displacements of the active joints are acquired and applied to the kinematic model to calculate the theoretical motions. A calibration of a 6 dof fully parallel manipulators is presented in (Ryu and Rauf, 2001), the method uses a link of fixed length, having spherical joints at both of their ends, to restrain the motion of the end–effector over spherical surface with arbitrary orientations. With the same method, in (Rauf and Ryu, 2001) the kinematic calibration of parallel Hexa Slide manipulator is presented. Lee et al. (2003) developed a calibration algorithm implemented on a parallel manipulator constructed for a machining center tool. A single constraint plane is employed as a mechanical fixture to constrain the motion, and three digital indicators are used as the sensing devices to determine whether the constrained motion is satisfied.

Rauf et al. (2004) proposes a device to identify all kinematic parameters of a Hexa Slide manipulator. The device consists of a link with U joints on both sides and is equipped with a rotary sensor and a biaxial inclinometer. Numerical analyses of the Jacobian identification reveal that all parameters are identifiable.

However, intrinsic inaccuracies of the device can significantly deteriorate the calibration results. Consequently, a measurement procedure is proposed and cost functions are discussed to prevent propagation of the inaccuracies to the calibration results. Dayong and Junwei (2005) proposed an algorithm as part of a project aimed at developing a calibration method for a spacecraft docking simulator. To implement this algorithm, a calibration equation is built by generating the constraint conditions of the end–effector motion in the workspace using a three dimensional coordinate measuring machine.

The greater benefit of the mobility restriction approach is that neither require of additional sensors nor of metrology equipment; nevertheless, it is difficult to be implemented since it requires a mechanism to restrict the motions of the system.

This approach also undergoes the limitation of the pose. Thus, the machine tool platform cannot be calibrated, just as in the redundant sensor approach. In addition, some errors of parameters related to the immobilized joints can get to be non–observable to the algorithm of calibration due to the mobility restriction (Rauf et al., 2006). Moreover, such methods reduce the workspace and the efficiency of the identification (Besnard and Khalil, 2001). In order to apply this method, two conditions must be fulfilled: that passive joints are used and the possibility of putting a mechanical key on the robot.

Approach of redundant leg

This approach utilizes a redundant leg as the measurement device, it is a passive and unloaded strut separated from the driving mechanisms. In (Hsu and Chen 2004), the error analysis and calibration methodologies for a PKM called a Cartesian guided tripod (CGT) are proposed. The CGT has two kinds of functionally independent legs, the driving functional leg and the integrated Cartesian guiding/metrology functional leg, linked in–parallel to the platform. The platform displacements are guided and measured directly in a Cartesian coordinate system. Additionally, a calibration method that uses a redundant leg with a displacement sensor is presented in (Chiu and Perng, 2004), an end of the leg is joined to the base of the platform through a ball joint, while the other end is a precision adapter that can be joined to the axis or the clamp of the end–effector.

In summary, the implemented additional mechanical devices for calibration have the disadvantage of being expensive, presenting space of limited work, taking a considerable effort to place the end–effector on the additional installation. Besides, it requires different types of facilities for different types of manipulators; but mainly, it is difficult to collect precise measurement data. Nevertheless, this method gives better accuracy than the redundant sensor methods; little load and heat deformations are present on the passive redundant leg. Another merit is that, by putting the redundant leg on the platform centre, the metrology loop is much closer to the cutting tool position for a PKM.

Approach with adapted devices for measurement

Some adapted devices for measurement have been proposed, for example location systems by laser, (Koseki et al., 1998). In (Wei et al., 2001) during simulation of kinematic calibration of 6–PSS parallel manipulator, indirect method by photoelectric length gauge with a ball is used for pose measuring. Chai et al. (2002) proposed using an external laser measuring device to determine the actual accuracy of a Gough–Stewart platform. Daney (2003) presents the modeling and a unified scheme to identify the kinematic parameters of the last platform. The interest of this formulation is that it may be applied whatever information is available on the state of the robot (measurement or constraints) without using the kinematics to obtain the basic system of constraint equations. They experimented and compared three methods of calibration, using either (or both) external measurement and internal redundant sensors. Additionally, Jeong et al. (2002) present simulation and experimental results for kinematic calibration algorithms using a planar seven–bar 2 dof redundantly actuated parallel mechanism. Tool plate information is acquired using a laser ball bar and the parameters are identified using an optimization algorithm. For the constant joint offsets case introduced by internal forces the accuracy of the tool plate after calibration improved by 25%.

Ota et al. (2002) described a FKM based calibration method for a parallel–mechanism–based milling machine named HexaM that identifies the kinematic parameters using the positioning data measured by a Double Ball Bar (DBB) system. This work also describes a gravity compensation method, in which the parameters are updated gradually according to the travelling plate position. This provides real–time motion control with compensation. Oiwa and Kataoka, (2003) described a method using a DBB system with fixed ball distance for a coordinate measuring machine (CMM) based on a three dof parallel mechanism. The CMM with a touch trigger probe measures the moving ball of the DBB, and calculates position errors of the ball using kinematic parameters. Others CMM were studied in (Junhong et al., 2007) and (Yu et al., 2006), in last the plane equation was measured to gain the position of a 6 dof parallel robot and its error equations were established. Error parameters for the three planes method were obtained in order to implement error measurement and error compensation.

Takeda et al. (2004) proposed the use of a low order Fourier series obtained by transforming the data for circular measurement paths by using a 6 dof in–parallel actuated worktable. The errors of the realized paths were measured using a DBB system. An algorithm for determining adequate measurement paths and an optimal set of a specified number of paths using these indices was also proposed. With the same system, Huang et al. (2005) deal with the kinematic calibration of a 3 dof parallel mechanism. It forms the main body of a 5 dof reconfigurable hybrid robot named TriVariant that is a modified version of the Tricept, achieved by integrating one of its three active limbs into the passive one. The first order error mapping function is formulated to link the measured data and the geometric source errors affecting the compensatable pose accuracy.

In (Kim, 2005), a moving platform is connected to a fixed frame by three PRRR limbs to form the called Cartesian Parallel Manipulator which may be suitable for applications requiring high speed and accuracy. A simple FKM is derived and based on the error model, two calibration methods using full position and length measurements are developed by using a ball–bar. In (Liang Zhi et al., 2005) the calibration of a hybrid 5 dof manipulator based on a 3RPS in–actuated parallel manipulator is studied. A 2 dof serial working table is placed over the moving platform; the proposed method takes this device as a ruler and keeps the remaining end of the static end–effector with respect to the working table at different configurations. Nakagawa et al. (2001) described a method to obtain the kinematic parameters for a hexapod machine tool by using a telescope ball bar device. This method deals with length error of struts, position errors of base and platform joints as kinematic parameters.

For a Gantry hybrid machine tool, based on a 3 dof parallel mechanism and a long motion of the working table, the kinematic calibration methods based on estimation error and local measurement information is presented in (Tang et al., 2005). The first type of calibration method can easily improve the PKM accuracy quickly by estimating the errors trends. The second method includes the position errors and does not include the pose errors of the PKM. A micrometer, a leveling bar, and an optical grating ruler were used to measure the real machine tool errors in the Y and Z directions. Rauf et al. (2005) discussed the automation of calibration experiments for a parallel manipulator using a partial pose measurement device. A significant time saving was observed with the proposed automation. Furthermore, for Hexa Slide manipulator, the calibration with partial pose measurements, using a device that measures a rotation of the end–effector along with its position is done by Rauf et al. (2006). The device contains a Linear Variable Differential Transformer (LVDT), a biaxial inclinometer, and a rotary sensor.

The position of the Tool Center Point (TCP) of a PKM is traditionally being measured indirectly by means of the position measurement of the drives. Cutting– and acceleration forces cause displacements of the TCP, which cannot be detected from the position measurement of the drives. To improve the position accuracy of the TCP a force free add–on position measurement device is suggested in (Verl et al., 2006). Whereas, the interrelationship between optimal tolerance, model, and pose selection for calibration of the parallel manipulators is discussed by Boye et al., (2006).

The kinematics calibration of a planar parallel manipulator of 5–links, whose potential applications include micro–electromechanical systems (MEMS) assembling or bonding is developed in (Ji et al., 2006). A laser interferometer, whose resolution is about 10 nanometers, is adopted for measuring the kinematics model. In (Yu et al., 2007) a method was presented to calibrate a 2 dof parallel mechanism. Instead of measuring all or partial pose of the end–effector, the kinematic parameters of the mechanism were calibrated by measuring a serial of displacements of its end–effector. The universal tool microscope rather than extra sensors measured those displacements. The optimal kinematic parameters were obtained by minimizing the measurements error of the end–effector. This was done by solving an optimization model via nonlinear programming, using Matlab optimization toolbox.

The option of cable–based measuring systems can be considered as a feasible and cheap alternative for the identification of kinematic parameters on parallel structures. They present a good tradeoff between expected accuracy and low cost. At LARM Laboratory of Robotics and Mechatronics in Cassino, Catrasys has been used for the determination of workspace of robotic systems (Ottaviano et al., 2002). Another cable–based measuring system, called Milli–CaTraSys, has been used for pose measuring of a parallel manipulator (Conghui et al., 2009).

Numerical approaches

In (Hollerbach and Nahvi, 1995) the method of least squares is used to obtain a calibration approach. This method can be applied to handle the input and output noise in the calibration procedure. These methodologies are included into the so–called methods of implicit loop by Wampler et al. (1995). Based on the 6–TPS type PKM, a kinematic calibration method was studied by Zhong et al. (2005). Each kinematic structure parameter unit error of PKM was assumed, and then the influence coefficient matrix was constructed between the PKM terminal pose errors and structure errors by numerical methods using the measured data by the FKM.

A work to redefine the mathematical tools that helps calibration was developed in (Daney et al., 2004), demonstrating that the methods based on analysis of intervals can be used for the numerical certification of the calibration of parallel mechanisms.

The method gives an approach certified in the stage sensor for a set of measurements given with related uncertainties, providing a list of intervals for the kinematic parameters. Hence, any solution corresponding to an instance of the configuration satisfies the measurement that belongs to those intervals. In (Daney, 2004) methods of algebraic elimination for a general calibration of Gough–Stewart platform are implemented, emphasizing two approaches: algebraic elimination of variables and monomial linearization, which are compared to the classic technique of numerical optimization. The first one concludes that elimination methods are an important alternative to the established methods, and these methods do not require initial estimation, neither hypothesis on distribution of the noise. Numerical calibration methods are characterized by extremely high instrumentation expenditure and possess only local validity.

 

Conclusions

Some parallel structured machine tools are known as a new generation of multi–axis machining centre for the 21st Century manufacturing. They are mainly composed by parallel mechanisms. These kinematic structures are often claimed to be highly accurate, rigid machines, due to their closed loop structure and no error accumulation characteristics. Unfortunately, these generic thoughts have been challenged in the past few years, due to the growing need of high accuracy. In addition, because of the complex mechanisms their performance development is limited by the existing mathematical algorithms, measurement technique and calibration methods. For this reason, this paper was focused on the errors' source and calibration methodologies for PKMs. Different reported methods for calibration of parallel manipulators were presented. Moreover, this paper classifies the different robot calibration approaches and compares them to existing strategies. In general, the calibration methods showed the use of measurement devices, which require highly skills operators, are time consuming and expensive by adding redundant sensors, measurement devices or legs. Thus, it is apparent that inexpensive calibration methods are needed for successful applications of parallel mechanisms. Singularity based calibration and cable–based measuring systems promise good beginnings in this direction, taking into count their specific problematic.

 

Acknowledgements

The work reported was financially supported by CONACyT through a scholarship granted to the first author and the grant No. 51410Y.

 

References

Ait–Aider O., Andreff N., Martinet P. and Lavest J. Simultaneous Pose and Velocity Measurement by Vision for High–speed Robots. Proceedings of the International Conference on Robotics and Automation. Orlando Florida, 2006, pp. 3742– 3747.        [ Links ]

Andreff N., Martinet P. Vision–based Kinematic Modeling of Some Parallel Manipulators for Control Purposes. Proceedings of EuCoMeS, the First European Conference on Mechanism Science. Obergurgl, Austria, 2006.        [ Links ]

Besnard S., Khalil W. Identifiable Parameters for Parallel Robots Kinematic Calibration. International Conference on Robotics and Automation. Seoul, Korea, 2001, pp. 2859–2866.        [ Links ]

Boye T., Verl A., Pott A. Optimal Tolerance, Model and Pose Selection for Calibration of Parallel Manipulators. VDI Berichte, 1956:267. 2006.        [ Links ]

Brogangrdh T. Device for Relative Movement of Two Elements.         [ Links ] United States Patent 6425303, July 30. 2002.

Chai K.S., Young K., Tuerley I. A Practical Calibration Process using Partial Information for a Commercial Stewart Platform. Robotica. 20(3):315–322. 2002.        [ Links ]

Chao D., Zong G., Liu R., Yu J. A Novel Kinematic Calibration Method for a 3–dof Flexure–based Parallel Mechanism. IEEE International Conference on Intelligent Robots and Systems. Beijing, 2006, pp. 4660–4665.        [ Links ]

Chiu Y., Perng M. Self–calibration of a General Hexapod Manipulator with Enhaced Precision in 5 dof Motions. Mechanism and Machine Theory, 39:1–23. 2004.        [ Links ]

Cui H., Zhu Z., Gan Z., Brogardh T. Kinematics Analysis and Error Modeling of TAU Parallel Robot. Robotics and Computer–Integrated Manufacturing, 21:497–505. 2005.        [ Links ]

Conghui L., Hernandez–Martinez E., Carbone G., Ceccarelli M. A Comparison of Simulations and Experimental Tests on Operation Performance of CaPaMan2 bis. IEEE International Conference of Mechatronics and Automation. Changchun, 2009, pp. 430–436.        [ Links ]

Dallej T., Hadj–Abdelkader H., Andreff N., Martinet P. Kinematic Calibration of a Gough–Stewart Platform using an Omnidirectional Camera. Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems. Beijing China, 2006, pp. 4666–4671.        [ Links ]

Daney D. Self Calibration of Gough Platform Using Leg Mobility Constrains. World Congress on Theory of Machine and Mechanism. Oulu, Finland, 1999, pp. 104–109.        [ Links ]

Daney D. Kinematic Calibration of the Gough Platform. Robo–tica, 21(6):677–690. 2003.        [ Links ]

Daney D. Algebraic Elimination for Parallel Robot Calibration. Proceedings of the 11 World Congress in Mechanism and Machine Science, Tianjin China, 2004.        [ Links ]

Daney D., Papegay Y., Neumaier A. Interval Methods for Certification of the Kinematic Calibration of Parallel Robots. Proceedings of the International Conference on Robotics and Automation. New Orleans, LA., 2004. Vol. 2, pp. 1913– 1918.        [ Links ]

Daney D., Papegay Y., Madeline B. Choosing Measurement Poses for Robot Calibration with the Local Convergence Method and Tabu Search. International Journal of Robotics Research, 24(6):501–518. 2005.        [ Links ]

Daney D., Emiris I.Z., Papegay Y., Tsigaridas E., Merlet J.P. Calibration of Parallel Robots: on the Elimination of Pose–Dependent Parameters. Proceedings of EuCoMes. The First European Conference on Mechanism Science, Austria, 2006.        [ Links ]

Dayong Y., Junwei H. Kinematic Calibration of Parallel Robots. IEEE International Conference on Mechatronics and Automation. Ontario, 2005. Vol. 1, pp. 521–525.        [ Links ]

Deblaise D., Baradat C., Maurine P., Arekelian V. Improvement of Positioning of Delta Parallel Robot. XXI International Congress of Theoretical and Applied Mechanics, Warsaw, Poland, 2004.        [ Links ]

Deblaise D., Maurine P. Effective Geometrical Calibration of Delta Parallel Robot used in Neurosurgery. Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems. Edmonton, 2005, pp. 1313–1318.        [ Links ]

Ecorchard G., Maurine P. Self–calibration of Delta Parallel Robots with Elastic Deformation Compensation. Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems. Edmonton, 2005, pp. 1283–1288.        [ Links ]

Hesselbach J, Bier C., Pietsch I., Plitea N., Buttgenbach S., Wogersien A., Guttler J. Passive joint–Sensors for Parallel Robots. Mechatronics, 15:43–65. 2005.        [ Links ]

Hollerbach J.M., Nahvi A., Hayward V. Calibration of a Parallel Robot Using Multiple Kinematics Closed Loops. Proceedings of the IEEE International Conference on Robotics and Automation. San Diego, CA, 1994, pp. 407–413.        [ Links ]

Hollerbach J., Nahvi A. Total Least Squares in Robot Calibration. Experimental Robotics IV. The Fourth International Symposium. O. Khatib y J. K. Salisbury, eds., Springer, London, 1995, pp. 274–282, Palo Alto, CA.        [ Links ]

Hsu W., Chen J. Error Analysis and Auto–Calibration for a Cartesian–Guided Tripod Machine Tool. Int. J. Adv. Manufacturing Technology, 24:899–909. 2004.        [ Links ]

Huang T., Chetwynd D.G., Whitehouse D.J., Wang J. A General and Novel Approach for Parameter Identification of 6 dof Parallel Kinematic Machines. Mechanism and Machine Theory, 40(2):219–239. 2005.        [ Links ]

Huang T., Hong Z.Y., Mei J.P., Chetwynd D.G. Kinematic Calibration of the 3 dof Module of a 5 dof Reconfigurable Hybrid Robot using a Double–Ball–Bar System. IEEE/RSJ International Conference on Intelligent Robots and Systems, Beijing, 2006, pp. 508 – 512.        [ Links ]

Jeong J., Kang D., Iurascu C.C., Kim J. Kinematic Calibration for Redundantly Actuated Parallel Mechanisms. Proceedings of the ASME Design Engineering Technical Conference, 2002, pp. 1211–1217.        [ Links ]

Ji J., Zhu Y., Sun L. The Kinematics Calibration of a Planar Parallel Manipulator. VDI Berichte, 1956:295. 2006.        [ Links ]

Junhong J., Lining S., Lingtao Y. A New Pose Measuring and Kinematics Calibrating Method for Manipulators. IEEE International Conference on Robotics and Automation. Roma, 2007, pp. 4925–4930.        [ Links ]

Khalil W., Besnard S. Self–calibration of Stewart–Gough Parallel Robots Without Extra Sensors. IEEE Transactions on Robotics and Automation, 15(6):1116–1121. 1999.        [ Links ]

Kim H. S. Kinematic Calibration of a Cartesian Parallel Manipulator. International Journal of Control, Automation and Systems, 3(3):453–460. 2005.        [ Links ]

Koseki Y., Arai T., Sugimoto K., Takatuji T., Goto M. Design and Accuracy Evaluation of high–Speed and High Precision Parallel Mechanism. IEEE International Conference on Robotics and Automation. Leuven, 1998. Vol. 3, pp. 1340–1345.        [ Links ]

Last P., Hesselbach J., Plitea N. An Extended Inverse Kinematic Model of the HEXA–parallel–Robot for Calibration Purposes. IEEE International Conference Mechatronics and Automation. Ontario, 2005a. Vol. 3, pp. 1294–1299.        [ Links ]

Last P., Budde C., Hesselbach J. Self– Calibration of the HEXA–Parallel–Structure. Proceedings of the IEEE Conference on Automation Science and Engineering, IEEE–CASE. Article number 1506801, 2005b, pp. 393–398.        [ Links ]

Last P., Schutz D., Raatz A., Hesselbach J. Singularity Based Calibration of 3 dof Fully Parallel Planar Manipulators. 12^th IFToMM World Congress, Besacon, 2007.        [ Links ]

Lee M.K., Kim T.S., Park K.W., Kwon S.H. Constraint Operator for the Kinematic Calibration of a Parallel Mechanism. KSME International Journal, 17(1):23–31. 2003.        [ Links ]

LiangZhi F., Elatta A.Y., Xiaoping L. Kinematic Calibration for a Hybrid 5–D Manipulator Based on 3RPS In–actuated Parallel Manipulator. Int. J. Adv. Manufacturing Technology, 25:730–734. 2005.        [ Links ]

Marquardt D. An Algorithm for Least–squares Estimation of Nonlinear Parameters. SIAM J. Appl. Math., 11:431–441. 1963.        [ Links ]

Merlet J.P. Les Robots Paralleles. Hermes. Paris. 1997.        [ Links ]

Merlet J.P. Parallel Robots: Open Problems. ASME Conference DECT. Montreal, 2002.        [ Links ]

Nakagawa M., Matsushita T., Nashiki M., Kakino Y., Ihara Y. A Study on the Improvement of Motion Accuracy of Hexapod type Parallel Mechanism Machine tool the Method of Kinematic Calibration without Gravitational Deformation. Journal of the Japan Society for Precision Engineering, 67(8):1333–1337. 2001.        [ Links ]

Oiwa T., Tamaki M. Study on Abbe's Principle in Parallel Kinematics. Procedings of the 2nd Chemnitz Parallel Kinematics Seminar. Chemnitz, Germany, April 2000, pp. 354–352.        [ Links ]

Oiwa T., Kataoka Y. A Calibration Method for Coordinate Measuring Machine using Parallel Mechanism. Journal of the Japan Society for Precision Engineering, 69(2):222–226. 2003.        [ Links ]

Oiwa T. Error Compensation System for Joints, Links and Machine Frame of Parallel Kinematics Machines. The International Journal of Robotics Research, 24(12):1087–1102. 2005.        [ Links ]

Ota H., Shibukawa T., Tooyama T., Uchiyama M. Forward Kinematic Calibration and Gravity Compensation for Parallel–mechanism–based Machine Tools. IMechE Journal of Multi–body Dynamics 216(1):39–49. 2002.        [ Links ]

Ottaviano E., Ceccarelli M., Toti M., Avila–Carrasco C. Catrasys a Wire System for Experimental Evaluation of Workspace. Journal of Robotics and Mechatronics 14(1): 78–87. 2002.        [ Links ]

Parenti–Castelli V., Di Gregorio R., Lenarcic J. Sensitivity to Geometric Parameter Variation of a 3 dof Fully–Parallel Manipulator. Proceedings of 3rd International Conference on Advanced Mechatronics (JSME). Okayama, Japan, 1998, pp.364–369.        [ Links ]

Rauf A. and Ryu J. (2001). Fully Autonomous Calibration of Parallel Manipulators by Imposing Position Constraint. IEEE International conference on robotics and automation. Seoul, Vol. 3, pp. 2389–2394.        [ Links ]

Rauf A., Kim S.G., Ryu J. Complete Parameter Identification of Parallel Manipulators with Partial Pose Information using a New Measurement Device. Robotica, 22(6):689–695. 2004.        [ Links ]

Rauf A., Pervez A., Kim J.P., Ryu J. Automation of Calibration Experiments for Parallel Manipulators Using a Partial Pose Measurement Device. Proceedings of the SICE Annual Conference. 2005, pp. 3558–3563.        [ Links ]

Rauf A., Pervez A., Ryu J. Experimental Results for Kinematic Calibration of Parallel Manipulators Using a Partial Pose Measurements Device. IEEE Transactions on Robotics, 22(2). April 2006.        [ Links ]

Renaud P., Andreff N., Dhome M., Martinet P. Experimental Evaluation of a Vision–Based Measuring Device for Parallel Machine Tool Calibration. Proceedings of the IEEE/ RSJ International Conference on Intelligent Robots and Systems. Lausanne, Switzerland, 2002a. Vol. 2, pp 1868–1873.        [ Links ]

Renaud P., Andreff N., Dhome M., Gogu G. Optimal Pose Selection for Vision–based Kinematic Calibration of Parallel Mechanisms. Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems. Las Vegas Nevada, 2002b.Vol.3, pp. 2223– 2228.        [ Links ]

Renaud P., Andreff N., Martinet P., Gogu G. Kinematic Calibration of Parallel Mechanism: A Novel Approach Using Legs Observation. IEEE Transactions on Robotics, 21(4):529–538. 2005.        [ Links ]

Renaud P., Andreff N., Lavest J.M., Dhome M. Simplifying the Kinematic Calibration of Parallel Mechanisms Using Vision–based Metrology. IEEE Transactions on Robotics, 22(1):12–22. 2006a.        [ Links ]

Renaud P., Vivas A., Andreff N., Poignet P., Martinet P., Pierrot F., Company O. Kinematic and Dynamic Identification of Parallel Mechanisms. Control Engineering Practice, 14:1099–1109. 2006b.        [ Links ]

Rudder F.F. Thermal Expansion of Long Slender Rods with Forced Convection Cooling Along the Rod Length, Report NISTIR 5975, 1997, pp. 46.        [ Links ]

Ryu J., Rauf A. A New Method for Fully Autonomous Calibration of Parallel Manipulators using a Constraint Link. IEEE/ASME International Conference on Advanced Intelligent Mechatronics, 2001. Vol. 1, pp. 141–146.        [ Links ]

Sato O., Shimojima K., Furutani R., Takamasu K. Artefact Calibration of Parallel Mechanism, Kinematic Calibration with Apriori Knowledge. Measurement Science and Technology, 15(6):1158–1165. 2004.        [ Links ]

Shaoping B., Ming Y. Kinematic Calibration and Pose Measurement of a Medical Parallel Manipulator by Optical Position Sensors. 7^th International Conference on Control, Automation, Robotics and Vision, 2002. Vol. 1, pp. 419–424.        [ Links ]

Soons J.A. Error Analysis of a Hexapod Machine Tool. International Conference and Exhibition on Laser Metrology and Machine Performance. Huddersfield. 1997. W. Yorkshire, UK. Pp.12.        [ Links ]

Sung K.T., Park W., Lee K. Study on Observability of Parallel–typed Machining Center Using a Single Planar Table and Digital Indicators. Mechanism and Machine Theory, 41:1147–1156. 2006.        [ Links ]

Takeda Y., Shen G., Funabashi H. A DBB–based Kinematic Calibration Method for In–parallel Actuated Mechanisms using a Fourier Series. Journal of Mechanical Design, Transactions of the ASME, 126(5):856–865. 2004.        [ Links ]

Tang X., Wang J., Gao M. Kinematic Calibration of a Gantry Hybrid Machine Tool based on Estimation Error and Local Measurement Information. Int. J. Adv. Manufacturing Technology, 26:382–390. 2005.        [ Links ]

Van Driel C.G., Carretero J.A. Calibration of the 3–PRS Parallel Manipulator using a Motion Capture System. Transactions of the Canadian Society for Mechanical Engineering, 29(4):645–654. 2005.        [ Links ]

Verl A., Croon N., Kramer C., Garber T. Force Free add–on Position Measurement Device for the TCP of Parallel Kinematic Manipulators. CIRP Annals–Manufacturing Technology, 55(1):407–410. 2006.        [ Links ]

Wang J., Masory O. On the Accuracy of a Stewart Platform–Part I: The Effect of Manufacturing Tolerances. Proceedings of IEEE International Conference on Robotics and Automation. Atlanta, 1993, pp. 725–731.        [ Links ]

Wampler C.W., Hollerbach J., Arai T. An Implicit Loop Method for Kinematic Calibration and its Application to Closed–Chain Mechanism. IEEE Transactions on Robotics and Automation, 11:710–724. 1995.        [ Links ]

Wei S., Liao Q., Huang J. Simulation on the Kinematic Calibration of 6–pss form Parallel Manipulator. Machine Design and Research, 17(4):51–53. 2001.        [ Links ]

Yang G., Chen I.M., Lim K., Huat–Yeo S. Simultaneous Base and Tool Calibration of a Self–calibrated Modular Parallel Robot. Robotica, 20(4):367–374. 2002.        [ Links ]

Yiu Y., Meng J., Li Z. Auto–calibration for a Parallel Manipulator with Sensor Redundancy. Proceedings of the IEEE International Conference on Robotics and Automation. Taipei, 2003. Vol. 3, pp. 3660–3665.        [ Links ]

Yu L.T., Sun L.N., Du Z.J., Cai H.G. Three Planes Method on Measuring and Compensation of Parallel Robot. Journal of Harbin Engineering University, 27(5):671–675. 2006.        [ Links ]

Yu X., Chu L., Cen Y. Kinematics Calibration of a 2 dof Parallel Planar Mechanism. China Mechanical Engineering, 18(6):634–638. 2007.        [ Links ]

Zhang Y., Cong S., Li Z., Jiang S. Auto–Calibration of a Redundant Parallel Manipulator Based on the Projected Tracking Error. 12^th IFToMM World Congress, Besacon, 2007.        [ Links ]

Zhong S.S., Yang X.J., Wang Z.X. Research on Calibration Method based on 6–TPS type Parallel Machine Tool. Computer Integrated Manufacturing Systems, 10:1469–1474. 2005.        [ Links ]

Zhuang H., Roth Z. Method for Kinematic Calibration of Stewart Platforms. Journal of Robotic Systems, 10(3):391–405. 1993.        [ Links ]

Zhuang H., Liu L. Self–calibration of a Class of Parallel Manipulators. Proceedings of the IEEE International Conference on Robotics and Automation. Minneapolis, 1996, pp. 994–999.        [ Links ]

Ziegert J.C. Volumetric Performance of Hexapod Machine Tools. Hexapod Machine Tool Users Group Report, 1996, pp.13.        [ Links ]

 

About the autors

Eusebio E. Hernández–Martínez. Was born in Querétaro in 1978. He received his bachelor degree in electronic engineering from Instituto Tecnológico de Celaya in 2002. In 2004, he received his master degree in instrumentation and automatic control at Universidad Autónoma de Querétaro (UAQ). Currently he is a PhD candidate in the same university. He was a visiting PhD student at University of Cassino, Italy in the years 2008 and 2009. His research interests include kinematics, calibration and error modeling of parallel robots. He is author of 7 papers that have been published in proceedings of national and international conferences or in international journals. He is a member of SOMIM (Mexican Society of Mechanical Engineering).

Carlos S. López–Cajún. Received his BSME and MSME from Universidad Nacional Autónoma de México (UNAM) in 1969, 1977 and his PhD from Case Western Reserve University in 1982. He was professor at the UNAM, a visiting researcher at McGill University, and researcher at the Mexican Transportation Research Institute. Currently he is professor at UAQ. His research focuses on simulation, robotics, and mechanisms. He has published 20 journal papers, 30 conference extended publications, and 2 textbooks on kinematics. He is a Member of the Mexican Academy of Engineering and Member of the IFToMM Executive Council, and has been elected as secretary general, for the period 2008–2011.

Juan Carlos Jáuregui–Correa. Is director of CIATEQ, a research center in Queretaro. He obtained his bachelor and master's degree in mechanical engineering (ME) from UNAM and his PhD degree in ME from Wisconsin–Milwaukee University, USA, in 1986. He was assistant researcher at the same University and associate professor at the School of Engineering, UNAM. Currently, he is a top level member (III) of the National Researchers System in Mexico. He has been associated member of The American Society of Mechanical Engineers (ASME), Society of Automotive Engineers (SAE) and The Gear Research Institute. In recent years, more than forty papers have been published in scientific journals and/or scientific national and international conferences, and five Mexican patents have been conferred to him. In 1991 he won the Industrial Building award in Queretaro. He was distinguished as Honorary Research Associate, at Leicester University, England. He is currently interested in research topics such as, mechanical vibrations, mechanical design of machinery, parallel manipulators, and their applications.