Modelo geoestadístico y geotécnico de la generación de emanaciones de hidrocarburos en el fondo marino de la Sonda de Campeche, México

 

Geostatistical and Geotechnical Model of Hydrocarbon Leaking in the Seabed of Sonda de Campeche, Mexico

 

Galván–García E.¹ y Auvinet–Guichard G.²

 

¹ Instituto Mexicano del Petróleo. E–mail: egalvan@imp.mx

² Instituto de Ingeniería Universidad Nacional Autónoma de México. E–mail: gauvinetg@iingen.unam.mx

 

Información del artículo: recibido: junio de 2009.
Aceptado: agosto de 2010.

 

Resumen

Este artículo presenta un modelo de la formación de emanaciones de hidrocarburos en el fondo marino del Campo Cantarell en la Sonda de Campeche. El análisis se llevó a cabo recurriendo a la geoestadística y la geotecnia. Con la geoestadística, se estimó el espesor del estrato de suelo blando que constituye el fondo marino y se evaluó la variación espacial de las características físicas y mecánicas del suelo. Se encontró que la resistencia al corte del suelo se comporta como un "ruido blanco" espacial. Fue posible definir una frontera que subdivide al estrato arcilloso en dos subestratos: uno de consistencia blanda y otro de consistencia muy blanda. En el aspecto geomecánico, usando un modelo de elementos finitos, se evaluó el comportamiento del estrato arcilloso del fondo marino bajo el efecto de una subpresión que da origen a la falla de dicho estrato y a la generación de emanaciones. El modelo tiene valor explicativo y permite definir zonas de riesgo para la instalación de infraestructura petrolera, las cuales coinciden con las áreas de menor espesor del estrato arcilloso.

Descriptores: chapopotera, lecho marino, subpresión, campos aleatorios.

 

Abstract

This article introduces a model of the formation of hydrocarbon leaking in the seabed of Campo Cantarell in Sonda de Campeche, Mexico. The analysis was carried out appealing to geostatistics and geotechnics. Using geostatistics, the thickness of the stratum of soft soil that constitutes the marine bottom was estimated and the spatial variation of the physical and mechanical characteristics of the soil was assessed. It was found that soil shear strength behaves like a "white noise" spatial process. It was possible to define a boundary subdividing the clay stratum in two sublayers, one of soft and another of very soft consistency. A finite element geomechanical model was used to simulate the behavior of the sea bottom clayey stratum under the effect of a subpressure which induces failure of this stratum and leads to the generation of hydrocarbon leaking. The model has an explanatory value and allows defining risk zones for the oil facilities, which coincide with the areas of minor thickness of the clayey stratum.

Keywords: Chapopotera, seabed, soft soil, sub–pressure, random fields.

 

Introducción

En el Golfo de México, las manifestaciones de aceite flotante han sido observadas tanto en las costas del norte (Kennicutt et al., 1990) como en las del sur, en la Sonda de Campeche. En México, estas emanaciones naturales o descargas de hidrocarburos son conocidas como chapopoteras (González, 1997).

En los años 70s, el Sr. Cantarell (pescador) informó a PEMEX de la existencia en la Sonda de Campeche, de aceite y olor a gas en el mar, así como de la presencia de aceite y chapopote en las costas de Tabasco y Campeche, lo que propició y dio inicio a la exploración y explotación de hidrocarburos en el Campo Cantarell.

La construcción de la infraestructura petrolera en la Sonda de Campeche, se realiza así sobre un sitio donde existen emanaciones de hidrocarburos (González, 1997). La presencia de estas emanaciones constituye una fuente de riesgos mal identificados que justifica un estudio más detallado que los que a la fecha se han realizado (Mc Donald et al, 1993; Galván et al, 1998; González et al, 2002).

Sangrey (1977) señaló que las presiones de hidrocarburos superiores a la presión hidrostática pueden inducir excesos de presión de poro en los sedimentos. Estos materiales se encuentran entonces subconsolidados con reducción de la resistencia al corte e incremento de su compresibilidad.

Durante el desarrollo de la presente investigación, se consideró necesario examinar las condiciones en las que ocurre el fenómeno de generación de emanaciones e identificar los factores que lo favorecen. Para ello, se analizó la información geofísica y geotécnica somera disponible de una zona del Campo Cantarell y se realizó un estudio detallado de las variaciones espaciales de algunas propiedades relevantes del subsuelo.

Definido el medio en el que se presenta el fenómeno, se pudo entonces desarrollar un modelo geomecánico simple que explica la formación de las chapopoteras. Éste se basa en la hipótesis de que los incrementos de presiones que se desarrollan bajo el estrato arcilloso del fondo marino provocan la flexión y el fracturamiento del mismo con liberación de hidrocarburos. Los estudios geofísicos someros realizados en la Sonda de Campeche han mostrado que, en efecto, el estrato arcilloso del fondo marino funciona como estrato sello que impide la emanación libre de hidrocarburos, lo que implica el entrampamiento de estos y por ende, un empuje ascendente o subpresión bajo dicho estrato.

Los resultados del modelo mecánico permiten a su vez proponer una zonificación de los riesgos asociados a este fenómeno.

Análisis geoestadístico

Los estudios geofísicos someros y los geotécnicos desarrollados en la Sonda de Campeche, muestran que la estratigrafía de los suelos, hasta aproximadamente 150m de espesor, es variable, predominando en las zonas centro, sur, este y sureste intercalaciones de estratos de arcillas y arenas, que se transforman hacia al norte, oeste y noroeste en potentes estratos de arcillas.

La zona estudiada se localiza sobre el área de erraticidad estratigráfica con intercalaciones de estratos de arcillas y arenas. En el fondo marino, existe un estrato de arcilla de espesor variable que sobreyace un estrato de arena, debajo del cual continúa la secuencia de intercalaciones (Galván et al., 2000; Núñez et al., 2000a).

Para definir las variaciones espaciales del espesor y de las propiedades del suelo del estrato arcilloso del fondo marino, a partir de 30 sondeos realizados en el sitio, se aplicaron técnicas geoestadísticas basadas en la teoría de los campos aleatorios. El análisis se llevó a cabo sobre un modelo del suelo en 3D, con área en planta de ocho por ocho kilómetros, limitado en la parte superior por la superficie del fondo marino y en su base por un estrato de arena que constituye la frontera inferior del estrato arcilloso. Dentro de esta área se localiza una zona con emanación de hidrocarburos (chapopotera).

Se aceptó que las variables geométricas (estratigrafía) y físicas o mecánicas que caracterizan el estrato arcilloso pueden considerarse como campos aleatorios (Auvinet, 2002a; Auvinet, 2002b).

Si V(X) es una variable particular de interés, donde X representa las coordenadas de un punto del medio en 2D o 3D, (X R²o R³ ), el campo puede ser descrito mediante parámetros como el valor esperado E{V(X)}, la variancia σ_v²(X) y la función de autocovarianza C_v (X₁,X₂), o su equivalente el coeficiente de autocorrelación ρv(X₁,X₂) = (autocovarianza normalizada), que describe la correlación espacial existente entre los valores V₁ y V₂ de la propiedad en estudio en puntos distintos X₁ y X₂ del medio.

Tales parámetros pueden evaluarse a partir de la información existente (sondeos) mediante un análisis convencionalmente llamado estructural de tipo estadístico (Auvinet, 2002b). Definidos los parámetros del campo aleatorio, es posible estimar la propiedad de interés en puntos donde ésta no ha sido medida, recurriendo a estimadores insesgados de mínima varianza, usando la técnica del Kriging (Matheron, 1965).

Se considera que el tipo de interpolación anterior es preferible a otras técnicas puramente matemáticas (interpolación lineal, polinomios de Lagrange, funciones splines, etc.) que no toman explícitamente en cuenta la estructura del medio. Cuando existe una deriva o tendencia (campo no estacionario), es conveniente modelar como campo aleatorio el campo residual obtenido quitando la tendencia determinista de los valores del campo original.

Espesor del estrato arcilloso del fondo marino

Para definir la configuración de la frontera inferior del estrato arcilloso en la zona de interés (8x8 km), se consideraron inicialmente los resultados de los análisis geoestadísticos efectuados por Valdez (2002) en todo el Campo Cantarell (14x20 km) que permitieron, con una evaluación del contenido de agua (w) a partir de 89 sondeos geotécnicos, definir la configuración de dicha frontera, incluyendo la zona de interés.

En el presente estudio, para definir en forma más precisa la configuración de dicha frontera en la zona de interés, se realizó un nuevo análisis geoestadístico. Con la información de los 30 sondeos geotécnicos, se determinó la profundidad en la que el cambio de w indica la transición entre el estrato arcilloso del fondo marino y el de arena subyacente, obteniendo la configuración mostrada en la figura 1.

En la figura anterior, la profundidad de la frontera inferior del estrato arcilloso, que define el espesor del mismo, se definió tomando como referencia el fondo marino, cuya pendiente es sumamente baja (≈0.09%) y puede considerarse como horizontal. Se obtuvieron así las curvas de igual profundidad de la vista en 2D y el relieve mostrado en la vista 3D, donde la parte central (zona más obscura) corresponde a la zona de menor espesor, de forma alargada, con rumbo NW–E.

En la misma figura 1, es posible apreciar que, en la zona centro, donde se ubica la chapopotera, el espesor del estrato varía entre 8 y 10m. Se observa por otra parte, que el espesor máximo (17m) se localiza en los extremos SW y SE, pero que el espesor alcanza también valores elevados en el extremo NE.

Variación espacial de las propiedades mecánicas del suelo

Aplicando nuevamente técnicas geoestadísticas, se analizó la variación espacial dentro del estrato arcilloso de la resistencia al esfuerzo cortante, S, dada por los resultados de pruebas de veleta miniatura, debido a que no fue posible obtener muestras inalteradas para ensayes triaxiales y que estos valores se consideraron más confiables que los obtenidos con torcómetro (Galván et al., 1990a; Galván et al, 2000).

Verificando la compatibilidad de resultados entre los 30 sondeos considerados, se encontró que en cuatro de ellos había anomalías que propiciaron su eliminación y la reducción del número de sondeos aprovechables a 26 (Galván et al., 2004).

En la figura 2 se muestran los valores de S correspondientes a los 26 sondeos, así como su recta de tendencia, que indica que la resistencia aumenta con la profundidad. Se aprecia una fuerte dispersión resultando el coeficiente de correlación del orden de 0.84.

Un análisis estadístico más fino de los datos de S, mostró que pueden distinguirse dos poblaciones, una de 0 a 10.5 kPa y otra de 10.5 a 35 kPa que, de acuerdo con la tendencia mostrada en la figura 2, se ubican respectivamente en la parte superior e inferior del estrato.

Lo anterior permitió subdividir al estrato arcilloso en un subestrato muy blando y en otro blando y establecer de esta forma una frontera entre ambas poblaciones. En cada sondeo se determinó la profundidad de dicha frontera indicada en la tabla 1.

Con las profundidades de la tabla 1, se definió, mediante un análisis geoestadístico (Deutsch et al., 1998) la configuración de la frontera mostrada en la figura 3. La profundidad media resultó de 4.55 m. En la figura se aprecia que la frontera entre subestratos presenta una pendiente hacia el suroeste.

Analizando la variación espacial de la resistencia al corte S dentro de cada subestrato, se detectaron tendencias lineales (hiperplanos) que pueden representarse con las ecuaciones 1 y 2 para el subestrato superior e inferior respectivamente.

En las ecuaciones anteriores, las variables x y y corresponden a las coordenadas UTM de los sondeos y z a la profundidad. En la figura 4 se muestra una tendencia típica de la variación de la resistencia con la profundidad para un punto del dominio.

Para el análisis de la parte aleatoria de la variable (campo residual), se calcularon los coeficientes de auto–correlación vertical de cada sondeo en función de la distancia vertical correspondiente y de tales funciones, se obtuvo una curva de autocorrelación media (figura 5) a la que se ajustó el modelo exponencial dado por la ecuación 3, despreciando la ligera correlación negativa asociada con un comportamiento semi–armónico de la variación vertical de la resistencia.

donde 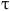es la distancia entre dos puntos ubicados en una misma vertical

La distancia de influencia, definida en forma convencional como el doble del área bajo la curva exponencial (Vanmarcke, 1983), resultó corta (0.91m).

Para evaluar la correlación horizontal se efectuó un análisis de correlación cruzada entre los 26 sondeos, obteniéndose la gráfica de la figura 6. La gran dispersión que se observa en dicha figura muestra que no existe correlación horizontal aparente, confirmando a su vez la erraticidad estratigráfica y concluyéndose que la parte aleatoria de S se comporta prácticamente como ruido blanco (white noise) (Bourke, 1998; Papoulis, 1972) con coeficiente de autocorrelación horizontal de tipo δ(X₁– X₂), siendo δ la Delta de Dirac. Algunos autores han propuesto considerar un coeficiente de este tipo para suelos como las arcillas del Valle de México (Reséndiz et al., 1969). Esto parece poco realista para suelos lacustres como los del valle en los que el proceso de sedimentación genera una fuerte correlación horizontal, pero resulta aparentemente más cercano a la realidad en el fondo marino donde el estrato arcilloso se ve afectado por corrientes aleatorias.

Despreciando la correlación vertical, el modelo de variación espacial de la resistencia quedó finalmente representado por las ecuaciones deterministas 1 y 2 y con ellas se trazaron perfiles como los de la figura (7) 8, cuya traza se muestra en la retícula de la figura 7 (perfiles Norte–Sur, A a E y Este–Oeste, 1 a 5).

En la figura 8 se muestran los perfiles centrales C y 3, con una longitud de 8 km y altura uniforme de 17 m. En la figura 7 se observa que estos perfiles se cruzan en el sitio de la chapopotera.

Asimismo, en la figura 8 se observan, al centro de ambos perfiles, una sobre–elevación de la frontera inferior y un menor espesor del estrato arcilloso. Puede pensarse que dicha sobre–elevación fue generada por la acción de la falla geológica que cruza la zona (figura 7).

Modelo geomecánico

Se simuló numéricamente, en los 30 sitios considerados inicialmente, la deformación y falla del estrato arcilloso del fondo marino sometido al efecto de una subpresión súbita generada por emanación de crudo, con la consecuente formación de una chapopotera (figura 9).

El análisis se llevó a cabo mediante un modelo de elementos finitos bidimensional a través del programa Plaxis V8 (Brinkgreve et al., 1998). Los elementos finitos fueron tipo Sepra triangulares con 15 nodos para desplazamientos y 12 puntos de integración Gaussiana para esfuerzos y deformaciones (puntos de esfuerzos). El análisis se realizó en deformación plana.

Para mejorar la representatividad del modelo, cada uno de los subestratos, muy blando y blando, se subdividió en dos más de igual espesor, subdividiendo así al estrato arcilloso en cuatro subestratos (figura 9).

En cada subestrato se consideró la resistencia al corte media definida en las ecuaciones 1 y 2. Los pesos volumétricos sumergidos medios de cada subestrato se obtuvieron de los reportes geotécnicos correspondientes a cada sitio o sondeo.

Para el planteamiento del modelo se fijaron las siguientes condiciones (figura 9):

• Suelo sumergido bajo el nivel medio del mar (NMM). El tirante de agua varía de 38m a 45.7m.

• Dos estratos, el arcilloso del fondo marino y la arena subyacente.

• Condiciones de fronteras perimetrales: desplazamientos horizontal y vertical restringidos.

• Aplicación súbita de la subpresión generada por emanación de crudo en una zona de 25m de largo.

• Longitud suficiente del modelo para evitar la influencia de las fronteras laterales. Longitud de 125m, con espesor variable del estrato arcilloso entre 7.3m y 18m.

• Propiedades mecánicas y características físicas obtenidas de los reportes geotécnicos y ajustadas mediante evaluaciones geoestadísticas.

El comportamiento del suelo se consideró como no–drenado, ya que al presentarse subpresiones súbitas por la baja permeabilidad del suelo y la alta velocidad de aplicación de la carga, el flujo del agua intersticial puede ser despreciado. El modelo de comportamiento del suelo adoptado fue el de Mohr–Coulomb.

Se consideró que el valor de la relación de Poisson v era de 0.495 para el estrato arcilloso y de 0.3 para el estrato de arena.

Dado que no fue posible medir los parámetros efectivos de estos suelos del lecho marino, el módulo de elasticidad efectivo E' se calculó a partir de la ecuación 4 en función del módulo de elasticidad no drenado, E_u obtenido a partir de las escasas (seis) pruebas triaxiales disponibles.

Los módulos de elasticidad no drenados E_u y efectivos (E') se dan en la tabla 2.

Los parámetros de resistencia al corte no drenado (c_u y Φ_u=0), se obtuvieron directamente de las pruebas de veleta miniatura.

Para definir el modelo de la figura 9, se hicieron varios análisis ajustando la longitud total y la de aplicación de la subpresión, pero dado que no se conocían las condiciones reales del fenómeno y que de los estudios geofísicos se sabía que la subpresión actuaba como presión uniforme, se optó por aplicar la subpresión en un ancho mayor al espesor del estrato, buscando con esto evitar su penetración como carga concentrada. Con el ajuste anterior se logró que no hubiera influencia de las fronteras laterales durante la deformación del modelo al aplicar la subpresión en los 25m centrales.

En el análisis se tomó en cuenta la resistencia del suelo a la tensión. Esta resistencia se definió en cada sitio y en cada subestrato considerando los resultados obtenidos por Marsal y Mazari, (1959), quienes, con ensayes de tensión en muestras de arcilla de la Ciudad de México, encontraron que, en arcillas con contenido de agua del 100% (contenido de agua similar al de las arcillas en estudio) la resistencia a tensión era del orden del 20% de la resistencia en compresión (ecuación 5).

En las simulaciones numéricas realizadas, al llevar la subpresión hasta su valor límite, se observaron dos tipos de falla del estrato arcilloso.

Uno de ellos fue de tipo dúctil (figura 10) con desplazamientos máximos al centro del modelo de 25 a 40cm. Este mecanismo se presentó en sitios con espesores del estrato arcilloso de más de 10.5m y con relaciones de espesores (muy blando/total) menores a 0.42 (tabla 3). En estos casos, el análisis se llevó hasta alcanzar la falla incipiente definida por la aparición en la parte superior del primer subestrato (lecho del fondo marino) de los primeros elementos que alcanzaban su resistencia a tensión límite.

El comportamiento de este modelo sugiere que la falla total se alcanza, después de presentarse la falla incipiente por un proceso en cadena en el que dejan de contribuir a la resistencia global los elementos que alcanzan su resistencia a tensión. El espesor del modelo se va reduciendo y por ende, también su resistencia, pudiendo al final coincidir el espesor mínimo resistente y la subpresión de colapso.

La primera imagen de la figura 10, correspondiente al sitio Nohf3, muestra el estrato arcilloso subdividido en sus cuatro subestratos y el estrato inferior de arena, quedando limitada por dos líneas verticales la zona central donde actúa la subpresión. En dicha figura se observan los elementos plastificados (puntos oscuros) en la condición de falla incipiente, los cuales ascienden desde las fronteras de la zona con subpresión, cruzan el cuarto subestrato y a la vez, se generan en el tercero y segundo subestratos. En el recuadro amplificado de la misma figura se indican con flechas diversos puntos blancos en los elementos finitos (fondo marino) que han alcanzado su resistencia a la tensión.

El segundo modo de falla fue de tipo frágil y en éste no fue posible definir una falla incipiente al presentarse bruscamente el colapso. Este modo de falla se presentó en espesores del estrato arcilloso menores de 10.5m, en la mayoría de los casos con desplazamientos pequeños y relaciones de espesores mayores de 0.4 con excepción de los sitios Akf y Gas1 con 0.37 y 0.36, respectivamente. En todos los casos, antes del colapso, algunos elementos se plastificaron como se muestra en ambos esquemas de la figura 11, observando que el número de éstos y su propagación ocurrieron únicamente en el cuarto subestrato.

El primer esquema de la figura 11 corresponde al sitio Akci con subpresión de 46.9 kPa, donde aun cuando se genera un desplazamiento severo (31.1cm) y el modelo está a punto del colapso (subpresión de 46.91 kPa), la plastificación no se propaga a todos los subestratos, como ocurrió en Nohf3.

El segundo esquema corresponde al sitio Akh con una subpresión de 37.95 kPa y desplazamiento de 2.1 cm. La subpresión de colapso fue de 38 kPa. En este caso se puede ver que el número de elementos plastificados es menor que en el de Akci.

En la tabla 3 se presentan los resultados obtenidos en los análisis de todos los modelos, separando con una raya horizontal los que presentaron falla frágil y los de falla dúctil. Los datos se ordenan en forma ascendente respecto a las subpresiones de fallas y se ve que, en la frontera, para generar una falla frágil se requiere aplicar una subpresión de hasta 51.1 kPa con un espesor del estrato arcilloso no mayor de 10.0m, como también puede ser constatado en la figura 12.

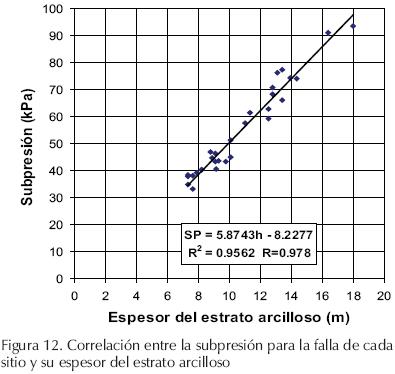
En la figura 12 se presenta una gráfica de correlación entre las subpresiones de falla y el espesor del estrato arcilloso de cada sitio. En ésta se puede distinguir la congruencia entre ambas variables, ya que al incrementar el espesor del estrato se requiere aplicar una subpresión mayor para alcanzar alguna de las fallas ya definidas (coeficiente de correlación R=0.978), asimismo en la gráfica es posible distinguir la frontera (líneas discontinuas) entre los grupos o poblaciones mostrados en la tabla 3 y la línea de tendencia que da indicios de la precisión del modelo.

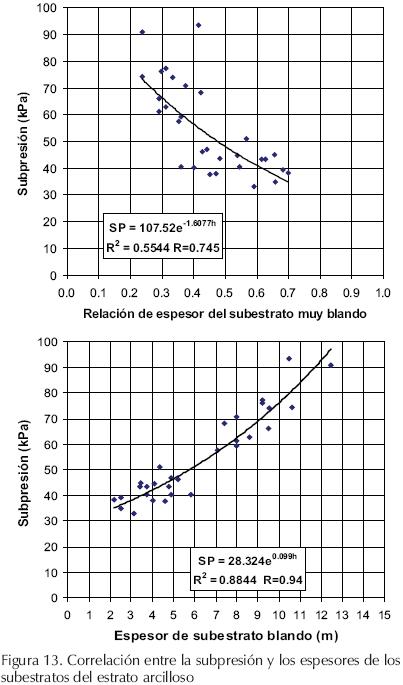
Siguiendo con el análisis de correlación entre las subpresiones de falla y el espesor del estrato arcilloso, en la figura 13 se presentan las gráficas de correlación entre la subpresión de falla y los espesores de los sub–estratos que conforman al estrato arcilloso. En la primera, se puede ver que la subpresión es inversamente proporcional a la relación del espesor del estrato muy blando, o sea, cuanto mayor es el espesor del subestrato muy blando, menor es la subpresión de falla del modelo. En la misma gráfica es posible distinguir las dos poblaciones de valores indicadas en la tabla 3, una con subpresión mayor de 57 kPa y relación de espesor menor de 0.42 y la otra con subpresión menor de 51.1 kPa y relaciones de espesores mayores de 0.40, con excepción de los casos ya mencionados.

En la segunda gráfica de la figura 13, se ve que, al igual que con el espesor total, la subpresión requerida para generar la falla correspondiente crece al incrementar el espesor del subestrato blando y que se aprecian las mismas dos poblaciones.

De lo anteriormente presentado se concluye que la magnitud de la subpresión depende principalmente del espesor del subestrato blando. Para que la subpresión de falla resulte alta, no es suficiente tener un espesor considerable del estrato arcilloso, sino también se requiere que el espesor del subestrato muy blando sea pequeño, como es el caso entre los sitios Aks3 y Ch101A, cuyas subpresiones límites son similares pero tienen espesores de 17.98m y 16.35m y relaciones de espesor del subestrato muy blando de 0.417 y 0.239, respectivamente.

Finalmente, para corroborar los resultados presentados en la figura 12, aplicando el método de kriging, se hizo un estimado de la variación espacial de las subpresiones de falla correspondientes, obteniendo las curvas de isovalores de la figura (13) 14.

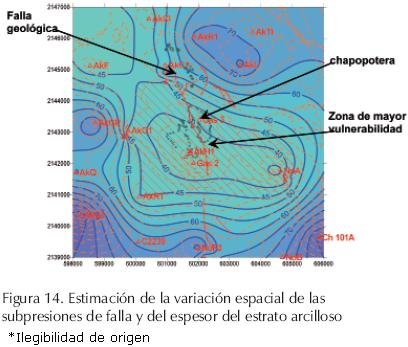
En esta última figura se presentan además las curvas de isovalores del espesor del estrato arcilloso (curvas discontinuas color naranja) presentadas en la figura 1 y se puede ver que, comparando ambos tipos de curvas, éstas presentan una tendencia y trayectoria muy similar; en algunas zonas son paralelas.

En la misma figura 14 se muestra una zona achurada que, aun cuando no corresponde con el área completa donde puede ocurrir una falla frágil, si corresponde con el área de menor espesor del estrato arcilloso y la zona de localización de la chapopotera. Por lo anterior se confirma que, la zona achurada es la zona de mayor vulnerabilidad para la generación de las emanaciones y consecuentemente la de mayor riesgo para la construcción de la infraestructura petrolera.

 

Conclusiones

La formación de emanaciones de hidrocarburos en el fondo marino del Campo Cantarell en la Sonda de Campeche tiene su origen en el escape de estos, a través de las fallas geológicas que cruzan la corteza terrestre desde la superficie del fondo marino hasta los yacimientos de petróleo de la zona.

En el análisis geoestadístico realizado, se estimó y definió la variación espacial del espesor del estrato arcilloso que constituye al fondo marino, estrato que conforma al sello que impide la emanación directa de hidrocarburos al ambiente marino. Con esta misma técnica se evaluó la variación espacial de la resistencia al corte en el mismo estrato, encontrando que se comporta como un "ruido blanco" espacial y que sólo es posible definir su variación espacial con la parte determinista. Asimismo con la geoestadística fue posible definir una frontera que subdivide al estrato arcilloso en dos subestratos, uno de consistencia blanda y otro de consistencia muy blanda, pero a su vez, conjuntando los resultados de las otras evaluaciones geoestadísticas, cada subestrato se subdividió en otros dos de igual espesor, permitiendo esto efectuar un análisis geomecánico de mayor precisión.

En el análisis geomecánico, usando un modelo de elementos finitos, se evaluó el comportamiento del estrato arcilloso del fondo marino sometido a una subpresión súbita propiciada por la emanación de hidrocarburos y que da origen a la falla de dicho estrato y la generación de emanaciones (chapopoteras). El modelo tiene un valor explicativo y permitió definir que los modos de falla que ocurren son de tipo dúctil y frágil. Se logró asimismo, por medio de las curvas de iso–subpresión, delimitar las zonas de ocurrencia de ambos modos de falla, pudiendo así verificar la correspondencia entre la zona de menor espesor, la de falla frágil y la de menor subpresión para la falla. Estos resultados permitieron a su vez definir la zona de mayor riesgo para la instalación de infraestructura petrolera, coincidiendo con el área de menor espesor del estrato arcilloso y la zona de la chapopotera.

Finalmente, se puede decir que la tendencia de propagación de los sitios con emanación (de acuerdo con los registros geofísicos) coincide con la trayectoria de la falla geológica hacia el norte, pero dado que en dicha dirección se incrementa el valor de las curvas de iso–espesor, las fallas tenderán a ser de tipo dúctil.

 

Agradecimientos

A PEMEX y el IMP, por la información proporcionada, al Instituto de Ingeniería de la UNAM por el apoyo para desarrollar los procesos y análisis requeridos.

 

Simbología

V(X) = variable que conforma al campo aleatorio

R ^p = espacio del campo aleatorio

E{V(X)}= esperanza del campo aleatorio

σ_v²(X) = varianza del campo aleatorio

C_V(X₁, X₂) = función de autocovarianza

ρ_V (X₁, X₂) = coeficiente de autocorrelación

S = resistencia al esfuerzo cortante

w = contenido de agua

x, y = coordenadas UTM

z = profundidad

E = módulo de elasticidad

v = relación de Poisson

c_u = cohesión no drenada

Φ_u =ángulo de fricción no drenado

h = espesor

SP =subpresión

q_t = resistencia del suelo a tensión

q_c = resistencia del suelo a compresión

 

Referencias

Auvinet–Guichard G. Incertidumbre en geotecnia. En: Reunión Nacional de Mecánica de Suelos (XXI, 2002, Querétaro, Qro.). Decimosexta conferencia Nabor Carrillo. México. Sociedad Mexicana de Mecánica de Suelos, A.C., 2002a.         [ Links ]

Auvinet–Guichard G. Confiabilidad y análisis de riesgos en geotecnia. 1a edición. DEPFI–UNAM, México, DF. 2002b.         [ Links ]

Bourke P. Generating Noise with Different Power Spectra Laws [en linea]. 1998 [fecha consulta 18/10/2004]. Disponible en: http://local.wasp.uwa.edu.au/.         [ Links ]

Brinkgreve R.B.J., Vermeer P.A. Plaxis manual. 7a. 320. A.A. Balkema/ Rotterdam/ Brookfield. Plaxis B. V., Netherlands. 1998.         [ Links ]

Deutsch C.V., Journel A.G. GSLIB, Geostatistical Software Library and user's Guide. 2ed ed, Oxford University Press, Inc. USA. 1998. P. 369.         [ Links ]

Galván–García E. et al. Implementación de un sistema de información geofísica y geotécnica de la sonda de Campeche (SIGGE). México DF. Instituto Mexicano del Petróleo, IMP–PEMEX, 1^s edición, 1990a. P. 220.         [ Links ]

Galván–García E., García V., González C. y Guzmán M. Estudio de las fuentes, distribución y efectos de hidrocarburos por arribazones en las costas de los estados de Veracruz, Tabasco y Campeche. México DF. Instituto Mexicano del Petróleo, IMP–PEMEX, 1^s edición, 1998.         [ Links ]

Galván–García E., Cruz–Roque D., Núñez–Farfán J. Sistema de información geofísica y geotécnica del Campo Cantarell. México DF. Instituto Mexicano del Petróleo, IMP–PEMEX, 1^s ed., 2000. P. 180.         [ Links ]

Galván–García E. y Auvinet–Guichard G. Caracterización geoesta–dística de la resistencia al corte del suelo en el fondo marino de la Sonda de Campeche. En: Reunión Nacional de Mecánica de Suelos (XXII, 2004, Guadalajara, Jal.). Sociedad Mexicana de Mecánica de Suelos, A.C. México. 2004.         [ Links ]

González C.M. Análisis de la comunidad bentónica en una chapopotera del Golfo de México y sus relaciones con la presencia crónica de hidrocarburos del petróleo. México DF. Facultad de Ciencias, UNAM, 1997.         [ Links ]

González C.M., Núñez–Farfán J., Cruz–Roque D., Cano–Martín G. Evaluación del volumen de hidrocarburos vertido por las emanaciones naturales en la Sonda de Campeche. México DF. Instituto Mexicano del Petróleo, PEMEX–RMNE–GESIPA–IMP. 2002.         [ Links ]

Kennicutt M.C. y Brooks J.M. Seepage of Gaseous and Liquid Petroleum in the Northern Gulf of Mexico. GCSSEPM Foundation Ninth Annual Research Conference Proceedings. Pp. 309–310. 1990.         [ Links ]

Marsal R.J. y Mazari M. El subsuelo de la Ciudad de México. Instituto de Ingeniería, UNAM, México. 1959.         [ Links ]

Matheron G. Les variables généralisées et leur estimation. Masson et Cie. France. 1965.         [ Links ]

McDonald I.R., Guinasso Jr. N.L., Ackleson S.G., Amos J.F., Duckworth R., Sassen R. y Brooks M. Natural Oil Slicks in the Gulf of Mexico Visible from Space. Journal of Geophysical Research. 98(C9): 16351–16354. 1993.         [ Links ]

Núñez–Farfán J., Cruz–Roque D., Cervantes–Martínez J., Alvarado J.G. GEOESTRAT: Programa para realizar cortes y sondeos estratigráficos de un volumen de terreno definido en 3D por superficies reticulares apiladas. México DF. Instituto Mexicano del Petróleo, IMP–PEMEX, 1^s edición, 2000a.         [ Links ]

Papoulis A. Probability, Random Variables, and Stochastic Processes. International student edition Kogakusha. McGraw Hill Ltd. 1972. Pp. 350–354.         [ Links ]

Reséndiz D. y Herrera I. A Probabilistic Formulation of Settlement Controlled Design. In: Proceedings, VII International Conference on soil mechanics and foundation engineering. Vol. II, 1969. Pp. 217–225, México.         [ Links ]

Sangrey D.A. Marine Geotechnology– State of the Art. Mar. Geotech. 2. 1977. Pp. 45–80.         [ Links ]

Valdez–Llamas P. Análisis geoestadístico de la estratigrafía del subsuelo marino en un área de la Sonda de Campeche. Tesis (Maestría en ingeniería). México DF. DEPFI–UNAM, 2002. 115 p.         [ Links ]

Vanmarcke E.H., Random Fields: Analysis and Synthesis. Cambridge Ma. MIT Press. 1983        [ Links ]

 

Semblanza de los autores

Eduardo Galván–García. Ingeniero civil graduado en el Instituto Politécnico Nacional en 1977. Obtuvo el grado de maestro en ciencias con especialidad en mecánica de suelos en 1994. Recibió el premio por la mejor tesis de posgrado 1994–95 en el área de ingeniería civil del IPN. Es candidato a doctor en ingeniería por la División de Estudios de Posgrado de la Facultad de Ingeniería de la UNAM. Fue profesor en la ESIA del IPN e impartió cursos de geotecnia a personal profesional de PEMEX. Ingresó al Instituto Mexicano del Petróleo en 1976 y ha participado en proyectos de geotecnia terrestre y marina para PEMEX.

Gabriel Auvinet–Guichard. Ingeniero civil originario de Francia y graduado en la Ecole Spéciale des Travaux Publics de Paris en 1964. Reside y trabaja en México desde 1966. Obtuvo el grado de doctor en ingeniería en la División de Estudios de Posgrado de la Facultad de Ingeniería de la UNAM en 1986. Es profesor en la misma División de Estudios de Posgrado desde 1968 a la fecha. Es Vicepresidente por Norteamérica de la Sociedad Internacional de Mecánica de Suelos e Ingeniería Geotécnica. Actualmente dirige el L–aboratorio de Geoinformática del Instituto de Ingeniería de la UNAM.