Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Ingeniería, investigación y tecnología
versión On-line ISSN 2594-0732versión impresa ISSN 1405-7743
Ing. invest. y tecnol. vol.12 no.3 Ciudad de México jul./sep. 2011
Identificación de regiones hidrológicas homogéneas mediante análisis multivariado
Identification of Homogeneous Hydrological Regions through Multivariate Analysis
Álvarez–Olguín G.1, Hotait–Salas N.2 y Sustaita–Rivera F.3
1 Instituto de Hidrología Universidad Tecnológica de la Mixteca. E–mail: galvarez@mixteco.utm.mx
2 Universidad Politécnica de Madrid. E–mail: nataliahs2@gmail.com
3 Instituto de Hidrología Universidad Tecnológica de la Mixteca. E–mail: sustaita@mixteco.utm.mx
Información del artículo: recibido: mayo de 2009.
Aceptado: septiembre de 2009.
Resumen
La regionalización hidrológica se utiliza para transferir información de cuencas aforadas a las no aforadas. Sin embargo, para obtener resultados confiables, las cuencas involucradas deben tener un comportamiento hidrológico semejante. El objetivo de este trabajo fue identificar zonas hidrológicamente homogéneas en la Mixteca oaxaqueña y zonas aledañas. El área de estudio comprendió 17 subcuencas para las que se cuantificaron 20 variables climáticas y fisiográficas potencialmente útiles en la predicción de gastos. La aplicación de técnicas estadísticas multivariadas, permitió identificar tres grupos de subcuencas hidrológicamente relacionadas. Se obtuvo un modelo regional para predecir gastos medios anuales, en el cual se determinó que las mejores variables explicativas son el área de la cuenca y la precipitación media anual. Los resultados obtenidos serán la base de futuras investigaciones para evaluar la disponibilidad del agua superficial en la región.
Descriptores: regionalización hidrológica, Mixteca Oaxaqueña, gráficas de Andrews, análisis de conglomerados, estimación de gastos, cuencas sin aforos.
Abstract
Hydrological regionalization is used to transfer information from gauged catchments to ungauged river basins. However, to obtain reliable results, the basins involved must have a similar hydrological behavior. The objective of this research was to identify hydrologically homogeneous regions in the Mixteca Oaxaqueña and surrounding areas. The area of study included 17 basins for which 20 climate and physiographic variables potentially useful in the prediction of flow were quantified. The applications of multivariate statistics techniques allowed us to identify three groups of basins hydrologically associated. A regional model was obtained to predict mean annual flow, which determined that the best predictive variables are the area and the average annual precipitation. The results will serve in future research to assess the availability of surface water in the region.
Keywords: hydrological regionalization, Mixteca Oaxaqueña, Andrews'curves, cluster analysis, estimation of flow, ungauged catchment.
Introducción
En las zonas donde el agua es insuficiente para satisfacer la demanda de las actividades humanas, la evaluación de la disponibilidad de este recurso, es un factor clave en la creación de estrategias eficientes para su aprovechamiento óptimo.
Al evaluar la disponibilidad de agua superficial de una cuenca, se requiere estimar el volumen medio anual de escurrimiento natural (CONAGUA, 2000). Sin embargo, la falta de información hidrométrica para cuantificar esta variable es común. La estimación de los escurrimientos en una cuenca sin registros de caudales es uno de los problemas principales de la ingeniería hidrológica (Hall et al, 1999).
La regionalización hidrológica es usada para facilitar la transferencia de información de sitios con registros a otros, en los cuales se requieren mediciones pero no existen (Nathan et al., 1990). Las metodologías de regionalización involucran dos etapas principales: la identificación de grupos de cuencas hidrológicamente homogéneas y la aplicación de un método regional para cada región homogénea (Ouarda et al., 2007).
La delimitación de regiones hidrológicas homogéneas constituye la etapa más difícil y uno de los obstáculos más serios para obtener una solución regional satisfactoria (Simithers et al., 2001; Gingras et al., 1993). En zonas montañosas, las características fisiográficas influyen en la distribución espacial irregular de las variables climáticas. Por lo que en estos sitios la división en regiones se debe realizar teniendo en cuenta tanto aspectos hidroclimáticos como fisiográficos, sin tomar en cuenta la continuidad geográfica de las cuencas. Nathan et al. (1990), mencionaron que regiones homogéneas definidas por la similitud hidrológica de las cuencas o las características de éstas, pueden no tener significancia geográfica.
La Mixteca Oaxaqueña es una región de relieve montañoso donde actualmente solo una estación hidrométrica se encuentra en operación; aunado a esto, existen zonas extensas sin aforar. El objetivo de este trabajo fue identificar zonas homogéneas dentro de la Mixteca, mediante la aplicación de técnicas estadísticas multivariadas. Además, se obtuvo un modelo regional, para la estimación de gastos medios. Los resultados servirán como punto de partida para evaluar la disponibilidad del agua superficial en la región.
Materiales y métodos
La zona de estudio tiene una superficie de 23,723 km2, y se localiza entre las coordenadas geográficas 16° 30' 24.3'', 18° 30' 51.7'' de latitud norte y 96°52'8.7'', 98°54'21.8'' de longitud oeste. Esta zona comprende 8 subcuencas del río Balsas, 5 del río Papaloapan y 4 de la región hidrológica Costa Chicarío Verde (figura 1).

Para las 17 subcuencas, se estimaron los valores del gasto medio anual (Q) y se cuantificaron los valores medios de 20 variables climáticas y fisiográficas potencialmente útiles para la predicción de gastos (tabla 1). Los registros hidrométricos utilizados corresponden a diferentes periodos de medición comprendidos entre los años 1953 y 1991, los cuales se extrajeron del Sistema de Información de Aguas Superficiales editado por el Instituto Mexicano de Tecnología del Agua, el cual permite consultar el Banco Nacional de Datos con información hidrométrica, sedimentos y de vasos de almacenamiento a cargo de la Comisión Nacional del Agua (CONAGUA). La lluvia media anual (LLUV), el coeficiente de Fournier (F) y la temperatura media anual (TEM), se obtuvieron de las series diarias de lluvia y temperatura extraídas del Extractor Rápido de Información Climatológica versión 3, que contiene los datos históricos del Servicio Meteorológico Nacional de la CONAGUA. La cobertura vegetal (VEG) se estimó a partir de imágenes LANDSAT del año de 1979. El tipo de suelo (S) se ponderó con base en su importancia para la retención de humedad, a partir de cartografía digital proporcionada por el Instituto de Geografía de la Universidad Nacional Autónoma de México. El resto de las variables se estimaron mediante el procesamiento de información topográfica obtenida del Instituto Nacional de Estadística Geografía e Informática.

Con el fin de corregir problemas de escala y unidades, los datos obtenidos se estandarizaron mediante la expresión siguiente:

donde:
Xij representa el valor de la j–ésima estación de la i–ésima variable,
Xi es la media de la variable Xij,
SX representa la desviación estándar de Xij,
Yij es la representación de la j–ésima observación de la i–ésima variable transformada.
Posteriormente, se obtuvo la matriz de correlación entre las variables predictoras y los coeficientes de correlación parcial con respecto al gasto medio (Q). Se excluyeron las variables que presentaron alta correlación con respecto a otras (mayor a 0.95) y menor correlación con respecto a Q.
Mediante el paquete estadístico SPSS versión 15, se aplicaron los procedimientos de eliminación hacia atrás (Backward elimination), selección hacia adelante (Ford–ward selection) y selección paso a paso (Stepwise selection), para identificar y seleccionar las variables que mejor describen a Q.
Con las variables seleccionadas, se aplicó una técnica gráfica (Andrews, 1972), que permite representar un punto de un espacio multidimensional en una curva de dos dimensiones mediante la función:
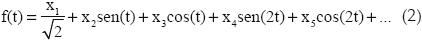
donde x1, x2,... representan las variables utilizadas para caracterizar las cuencas. La función se grafica en el rango –π a π.
Andrews (1972) mostró que la diferencia entre dos curvas es proporcional a la distancia euclideana, por lo que esta técnica permite comparar visualmente grupos homogéneos. De esta forma, grupos de cuencas similares se presentarán como una banda de curvas espacialmente cercanas (Nathan et al., 1990). De acuerdo con la metodología propuesta por Paris et al. (2004), el orden de estableció con base en las cargas obtenidas del análisis factorial.
De manera complementaria, se realizó un análisis de conglomerados, el cual tiene por objetivo agrupar elementos en grupos homogéneos, en función de las similitudes entre ellos. Los métodos de enlace utilizados fueron de promedios, completo, simple y de Ward (Peña, 2002).
La aplicación de las gráficas de Andrews y el análisis de conglomerados, dieron como resultado la división de regiones hidrológicamente homogéneas dentro de las cuales es válido transferir información; sin embargo, sólo en una de estas zonas el número de sub–cuencas fue adecuado para realizar un modelo de regresión lineal múltiple del gasto medio anual en función de las variables climáticas y fisiográficas.
Resultados y discusión
Los valores obtenidos de los coeficientes de correlación parcial con respecto a Q, se encuentran en la tabla 2. Se eliminaron Amax, LC, F, P, TC, LTC, debido a que presentan una colinealidad aproximada (mayor a 0.95) con Amed, LCP, PMA, A, LCP y A respectivamente y menores coeficientes de correlación parcial. Los métodos de selección paso a paso y selección hacia adelante identificaron a LCP y PMA como las variables significativas; sin embargo, el método de eliminación hacia atrás, seleccionó a A y PMA como las mejores variables predictoras. Dado que en ambos casos los modelos son estadísticamente significativos (α<0.001), se decidió utilizar LCP, A y PMA en los análisis subsecuentes.
Las tablas 3 y 4 contienen los resultados de aplicar el análisis factorial a las variables seleccionadas. Con una varianza de 79.4% y una comunalidad mínima (proporción mínima de la varianza que puede ser explicada por el modelo factorial obtenido) de 0.59, se seleccionó un factor principal.
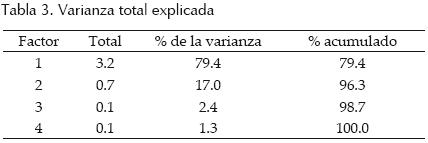
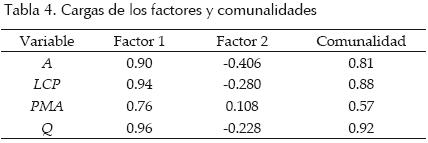
De acuerdo con los valores absolutos de las cargas, el orden de las variables para las gráficas de Andrews fue: Q, LCP, A y PMA. Con base en la similitud de las curvas (figura 2), se identificaron tres grupos de cuencas con un comportamiento hidrológico semejante.

Los cuatro métodos de enlace utilizados en el análisis de conglomerados, arrojaron resultados similares. En el dendograma de la figura 3, con un nivel de distancia de 2.39 se observan tres grupos de subcuencas asociadas.
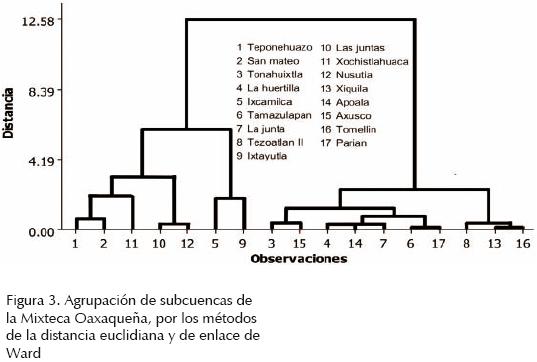
Tanto el método de Andrews como el de conglomerados, coinciden en la existencia de tres regiones homogéneas (figura 4): la región norte, que incluye a las subcuencas Tonahuixtla, Axusco, La Huertilla, Apoala, La Junta, Tamazulapan, Parian, Tezoatlan II, Xiquila y Tomellin; la región centro, conformada por Teponehuazo y San Mateo y la región sur que corresponde a Nusutia, Xochixtlahuaca y Las Juntas. Sin embargo, los resultados difieren para Ixcamilca e Ixtayutla, por lo que no se pudo definir la región hidrológica a la cual pertenecen.

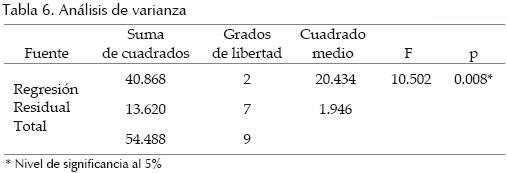
Dado que la región norte, es la única con un número viable de subcuencas para transferir información, se realizó un modelo regional para predecir gastos medios anuales dentro de la misma, cuyos resultados se resumen en la tabla 5. El modelo obtenido corresponde a la expresión (3) y es estadísticamente significativo en un nivel a de 0.05 (tabla 6). Las variables explicativas estadísticamente relacionadas con Q, son A y PMA (tabla 7).

donde Q estará dado en m3/s, A en km2 y PMA en mm.
Conclusiones
Con base en los resultados obtenidos, se determinó que las variables de mayor influencia en el comportamiento de los gastos medios de las 17 subcuencas analizadas, son: la longitud del cauce principal, el área de la cuenca y la precipitación media anual.
Existen tres regiones similares con respecto a sus características hidrológicas, dentro de las cuales es válido transferir información. Sin embargo, sólo para la región norte, que abarca 10 de las subcuencas analizadas, se obtuvo un modelo de predicción de gastos. Debido a esta situación, se propone ampliar el área de estudio, con la finalidad de lograr una regionalización hidrológica que incluya a la Mixteca Oaxaqueña en toda su extensión.
En la medida que se obtengan modelos regionales más precisos, se tendrá un punto de partida para cuantificar la disponibilidad de agua superficial en la región. Sin embargo, es necesario señalar que para comprender los procesos del ciclo hidrológico, es importante implementar una red eficiente de monitoreo de las variables hidrológicas, de esta forma se podrá conocer de manera precisa la calidad y cantidad del agua disponible y realizar estrategias adecuadas de manejo y planeación a nivel de cuencas.
Referencias
Andrews D.F. Plots of High Dimensional Data. Biometrics, 28:125136. Marzo de 1972. ISSN: 0006–34IX. [ Links ]
Gingras D. y Adamowski K. Homogeneous Region Delineation Bases on Annual Flood Generation Mechanism. Hydrological Sciences Journal, 38(2):103–121. Abril de 1993. ISSN: 0262–6667. [ Links ]
Hall M.J. y Minns A.W. The Classification of Hydrologically Homogeneous Regions, Hydrological Sciences Journal, 44(5):693–704. Octubre 1999. ISSN: 0262–6667. [ Links ]
Nathan R.J. y McMahon T.A. Identification of Homogeneous Regions for the Purposes of Regionalization. Journal of Hydrology, 121:217–238. Diciembre de 1990. ISSN: 0022–1694. [ Links ]
Comisión Nacional del Agua (CONAGUA). Norma Oficial Mexicana NOM–011–CNA–2000, Conservación del Recurso Agua –Que establece las especificaciones y el método para determinar la disponibilidad media anual de las aguas nacionales, Secretaría del Medio Ambiente y Recursos Naturales [en línea], 2002 [fecha de consulta 22 de abril de 2009]. Disponible en: http://www.semarnat.gob.mx/leyesynormas/normasoficialesmexicanasvigentes/CNA/NOM–011–CNA.pdf. [ Links ]
Ouarda T.B.M.J., Bâ K.M., Diaz–Delgado C., Cârsteanu A., Chokmani K., Gringras H., Quentin E., Trujillo E. y Bobée B. Intercomparison of Regional Flood Frequency Estimation Methods at Ungauged Sitios for a Mexican Case Study. Journal of Hydrology, 348:40–58. Enero 2008. ISSN: 0022–1694. [ Links ]
Paris M.C. y Zucarelli G.V. Regionalización de caudales. Propuesta metodológica para la identificación de regiones homogéneas. Ingeniería Hidráulica en México, XIX(4):5–19. Octubre–Diciembre 2004. ISSN: 0186–4076. [ Links ]
Peña D. Análisis de datos multivariantes. España. McGrawHill. 2002. pp. 219–243. [ Links ]
Smithers J.C. y Schulze R.E. A Methodology for the Estimation of Short Duration Design Storms in South Africa Using a Regional Approach Based on L–Moments. Journal of Hydrology, 241. pp. 42–52. Enero 2001. ISSN: 0022–1694. [ Links ]
Semblanza de los autores
Gabriela Álvarez–Olguín. Se título como ingeniera hidróloga en 2001 por la Universidad Autónoma Metropolitana y recibió la medalla al mérito universitario. En 2004, obtuvo el grado de maestría en ingeniería civil (hidráulica) en la División de Estudios de Posgrado de la Facultad de Ingeniería de la UNAM. Actualmente es profesora–investigadora del Instituto de Hidrología de la Universidad Tecnológica de la Mixteca, donde trabaja en la línea de investigación de sustentabilidad de cuencas hidrográficas y proporciona servicios de apoyo profesional a las comunidades rurales del estado de Oaxaca.
Natalia Hotait–Salas. Ingeniera de montes por la Universidad Politécnica de Madrid (UPM) en 2008. En 2007, realizó una estancia en México en la Universidad Tecnológica de la Mixteca, colaborando en el Instituto de Hidrología. Actualmente forma parte del departamento de aprovechamientos forestales de la Escuela Superior de Ingenieros de Montes de la U.P.M, donde participa en la evaluación del potencial de biomasa forestal en España para la elaboración del Plan de Energías Renovables 2011–2020 del Ministerio de Industria Turismo y Comercio de España.
Fidencio Sustaita–Rivera. En 1991 se gradúo como ingeniero agrónomo, especialista en suelos en la Universidad Autónoma Chapingo. Obtuvo el grado de maestro en ciencias en el Colegio de Posgraduados en 1998; año en el cual ingresó a la Universidad Tecnológica de la Mixteca como profesor–investigador. La línea de investigación que maneja es sustentabilidad de cuencas hidrográficas y pertenece al cuerpo académico de recursos naturales. Ha participado en diversos proyectos relacionados con el manejo sustentable de los recursos naturales en comunidades de la Mixteca Oaxaqueña. Actualmente realiza actividades de investigación para obtener el grado de doctor en ciencias.














