Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Ingeniería, investigación y tecnología
versión On-line ISSN 2594-0732versión impresa ISSN 1405-7743
Ing. invest. y tecnol. vol.15 no.2 Ciudad de México abr./jun. 2014
Fractional RC and LC Electrical Circuits
Circuitos eléctricos RC y LC fraccionarios
Gómez-Aguilar José Francisco1, Razo-Hernández José Roberto2, Rosales-García Juan3, Guía-Calderón Manuel4
1 Departamento de Ingeniería Eléctrica, División de Ingenierías Campus Irapuato-Salamanca, Universidad de Guanajuato, E-mail:jgomez@ugto.mx.
2 Departamento de Electromecánica, Instituto Tecnológico Superior de Irapuato, E-mail:jorazo@itesi.edu.mx.
3 Departamento de Ingeniería Eléctrica, División de Ingenierías Campus Irapuato-Salamanca, Universidad de Guanajuato, E-mail: rosales@ugto.mx.
4 Departamento de Ingeniería Eléctrica, División de Ingenierías Campus Irapuato-Salamanca, Universidad de Guanajuato, E-mail: guia@ugto.mx.
Abstract
In this paper we propose a fractional differential equation for the electrical RC and LC circuit in terms of the fractional time derivatives of the Caputo type. The order of the derivative being considered is 0 < γ ≤1. To keep the dimensionality of the physical parameters R, L, C the new parameter σ is introduced. This parameter characterizes the existence of fractional structures in the system. A relation between the fractional order time derivative γ and the new parameter σ is found. The numeric Laplace transform method was used for the simulation of the equations results. The results show that the fractional differential equations generalize the behavior of the charge, voltage and current depending of the values of γ. The classical cases are recovered by taking the limit when γ = 1. An analysis in the frequency domain of an RC circuit shows the application and use of fractional order differential equations.
Keywords: electrical circuits, fractional calculus, mittag-leffler functions, fractional structures.
Resumen
En este trabajo se propone una ecuación diferencial fraccionaria para los circuitos RC y LC en términos de la derivada fraccionaria en el tiempo del tipo Caputo. El orden considerado de la derivada es 0 < γ ≤ 1. Para mantener la dimensionalidad física de los parámetros R, L, C, se introduce un nuevo parámetro σ. Este parámetro caracteriza la existencia de estructuras fraccionarias en el sistema. Se encuentra la relación entre el orden de la derivada fraccionaria γ y el nuevo parámetro σ. El método de la transformada numérica de Laplace fue usado para la simulación de las ecuaciones resultantes. Los resultados muestran que las ecuaciones diferenciales fraccionarias generalizan el comportamiento de la carga, voltaje y corriente dependiendo de la elección de γ. Los casos clásicos se recuperan en el límite cuando γ = 1. Un análisis en el dominio de la frecuencia de un circuito RC muestra la aplicación y uso de ecuaciones diferenciales de orden fraccionario.
Descriptores: circuitos eléctricos, cálculo fraccionario, funciones de Mittag-Leffler, estructuras fraccionarias.
Introduction
Although the mathematical foundation of Fractional Calculus (FC) was established over 200 years ago, there remains a subject quite new to mathematicians. FC, involving derivatives and integrals of non-integer order, is the natural generalization of the classical calculus (Oldham and Spanier, 1974; Miller and Ross, 1993; Samko et al., 1993; Podlubny et al., 1999; Uchaikin, 2013). Many physical phenomena have "intrinsic" fractional order descriptions and so FC is necessary in order to explain them. In many applications FC provides more accurate models of the physical systems than ordinary calculus do. Since its success describing anomalous diffusion (Wyss et al., 1986; Hilfer, 2000), (Metzler and Klafter, 2000; Agrawal et al., 2004) non-integer order calculus both in one- and multi-dimensional spaces, it has become an important tool in many areas of physics, mechanics, chemistry, engineering, finances electromagnetism and bioengineering (Petras, 2010; Obeidat et al., 2011; Hilfer, 1974; West et al., 2003; Rosales et al., 2012; Magin et al., 2006; Gómez et al., 2012c; Gómez et al., 2012d; Caputo and Mainardi, 1971). Fundamental physical considerations in favor of the use of models based on derivatives of non-integer order are given in Westerlund (1994), Veliev (2004) and Baleanu et al. (2010). The advantage of using fractional order systems compared with systems of integer order is that the former has infinite memory, while others have finite memory. This is the main advantage of FC in comparison with the classical integer-order models, in which such effects are in fact neglected.
To analyze the dynamical behavior of a fractional system it is necessary to use an appropriate definition of the fractional derivative. In fact, the definitions of the fractional order derivative are not unique and there exist several definitions, including Grünwald-Letnikov, Riemann-Liouville, Weyl, Riesz, and the Caputo representation. In the Caputo case, the derivative of a constant is zero and we can properly define the initial conditions for the fractional differential equations so that they can be handled analogously to the classical integer case. Caputo derivative implies a memory effect by means of a convolution between the integer order derivative and a power of time (Podlubny, 1994; Gutiérrez et al., 2010). For these reasons, in this paper we prefer to use the Caputo fractional derivative defined by:

where n–1 < γ < n (n is N), and ƒ(n)(τ) represents the derivative of order n, real function evaluated in t. Working with this definition is important because of the ability to be implemented numerically (Podlubny, 1994). The Caputo derivative has the following property: if f(t) is a constant, then its derivative is zero. This does not happen with other representations. Another very important feature in the form of Caputo fractional derivative is that its Laplace transform is:

From equation (2), we can see that the representation of the Caputo derivative in Laplace domain using the initial conditions ƒ(k)(0) where k is integer. If the initial conditions are zero, this reduces to:

This is consistent with the usual definition of the Laplace transform when γ is an integer. In general, a fractional order differential equation has the form

where γk > γk–1 and αk are any real numbers, g(t) can be seen as the source of a dynamic system. Inverse transform 0 < γ ≤ 1 requires the introduction of a special function. The Mittag-Leffler function, where Γ is the gamma function, which is defined as

from (5) if a = 1, b = 1, we obtain the expression E1,1(t) = et. The Mittag-Leffler function is a generalization of the exponential function.
Numerical Laplace transform
The Laplace transform is a useful tool for analyzing linear systems because it simplifies the problem of dealing with differential equations in the time domain by converting them into algebraic equations within the frequency domain. The numerical Laplace transform (NLT) is essentially a modified discrete Fourier transform (DFT) through a windowing function (Gibbs phenomenon) and a stability factor (aliasing), (Proakis and Manolakis, 1996). Development of the NLT and its application to the analysis of systems has been well documented over the past 40 years (Ramirez et al., 2004; Wilcox and Gibson, 1998). However, its use has traditionally been limited to the analysis of problems where the result can be expressed in terms of simple functions that allow the use of tables of Laplace transforms (Moreno and Ramírez, 2008). When using discrete techniques in the frequency domain, computation time becomes an important factor since it requires a certain amount of time to transform the data from the frequency domain to the time domain or vice versa. However, by using the fast Fourier transform (FFT) the time necessary for computation is greatly reduced and as a result the techniques of analysis in the frequency domain become an attractive option.
Sheng investigated the validity of applying numerical inverse Laplace transform algorithms in fractional calculus (Sheng y Chen, 2011). In a paper of Gómez (2012b), an overview of a methodology based on the NLT and applied to the analysis of electromagnetic transient phenomena in power systems described by differential equations of fractional order, a Newton-type methodology to calculate either the transient or the periodic steady state is used and the definition of Caputo fractional derivative is applied to electrical networks including nonlinear reactors and electronic devices.
In the present work we are interested in the study of a simple electrical circuit consisting of a resistor, an inductor and a capacitor, in the framework of the fractional derivative applying the method of the NLT for the simulations.
Description
Using the Kirchhoff voltage law and the circuit of Figure 1, we have:


where E(t) is the source voltage, Ve(t) is the voltage in the fractal element and VC(t) is the voltage in the capacitor. The voltage in the fractal element is

where β{1, 2} is a parameter that determines whether the element e is a resistor or inductor, 0 < γ ≤ 1, the product βγ determines the order of the fractional differential equation e{R, L} defines the characteristics of e, σ is a parameter that determines the fractional structures of e.
Fractional electrical circuit RC
Taking in (7) e = R, β = 1, σe = σR, the fractional differential equation for RC circuit is

Recently Gómez et al. (2012a) proposed a systematic way to construct fractional differential equations for the physical systems. Such a way consists in analyzing the dimensionality of the ordinary derivative operator and trying to bring it to a fractional derivative operator consistently.
The introduction of the parameter σR allows dimensional consistency when [σR] = sec

with γ = 1 the equation (9) becomes an ordinary differential equation the first order with respect to time t. This is only true, as stated above, if σR has dimensions of seconds.
Using the expression (8), the fractional differential equation for a circuit of a capacitor and a resistor has the form

with

The constant τγ also can be called fractional time constant due to its dimensionality [sec]γ. When γ = 1, equation (11) recovers the ordinary time constant, ie., τ1 = τ = RC.
The γ parameter, which represents the order of the fractional time derivative in (10), can be related to the parameter σR, which characterizes the presence of fractional structures (fluctuations) in the system. In this case the empiric relationship is given by the expression

thus, the magnitude
δ = 1 – γ (13)
characterizes the existence of fractional structures in the system.
It can be seen this way: if γ = 1, then, from (12) we have σR = τ = RC and hence δ = 0 in (13), which means that the system does not have fractional structures, it is an ordinary RC circuit. However, in the range 0 < γ < 1, or 0 < σ < τ, the quantity δ increases and tends to unity, since in the system each is again a fractional structure.
Assuming zero initial conditions, q(0) = 0 and E(t) = sin ωt, the Laplace transform applied to (10) results in

The voltage in the capacitor is

The current can be obtained applying inverse numeric Laplace transform in (14) and differentiating with respect to time.
Fractional electrical circuit LC
Taking in (7) e = L, β = 2, σe = σL is obtained the fractional differential equation for the LC circuit is obtained.

Using the expression (16), the fractional differential equation for a circuit containing a capacitor and an inductor has the form

where

The constant τLγ also can be called fractional time constant due to its dimensionality [sec]. When γ = 1, from (18) recovers the ordinary time constant, this is, 
The γ parameter, as before, that represents the order of fractional time derivative in (17), can be related to the parameter σL, which characterizes the presence of fractional structures (fluctuations) in the system. In this case the empiric relationship is given by the expression

thus, the magnitude

characterize the existence of fractional structures in the system.
You can see it this way: if γ = 1, then, from (19) we have σL2 = LC and therefore δ = 0 in (20), which means that the system has no fractional structures, is an ordinary LC circuit. However, in the range  , (undamped natural frequency), the magnitude δ increases and tends to the unit, as in the system are increasingly found fractional structures.
, (undamped natural frequency), the magnitude δ increases and tends to the unit, as in the system are increasingly found fractional structures.
Assuming the initial conditions  and power supply E(t) = sin ω(t), the Laplace transform applied to (17) results,
and power supply E(t) = sin ω(t), the Laplace transform applied to (17) results,

The voltage in the capacitor is

The current can be obtained applying inverse numeric Laplace transform in (21) and differentiating with respect to time.
Results
All simulations used MATLAB 7.5. (R2007b), Figures 2, 3 and 4 show the simulation for RC circuit γ = 1, γ = 0.98, γ = 0.96, for the charge, voltage and current, respectively, using R = 1 pu, C = 0.1 pu and ω = 2π60.



Figure 5 show the simulation for LC circuit γ = 1, γ = 0.98, γ = 0.96, for the current, using L = 0.001 pu, C = 0.1 pu and ω = 2π60.

Spectroscopy applied to a RC circuit
The electrical impedance spectroscopy technique applies a potential difference between the two electrodes by passing a low power alternating current through the sample and this is compared with the voltage and current detected to the output. To obtain the electrical impedance spectra a Solartron® 1260 was used (Figure 6). The fidelity of the frequency sweep for these tests was important since it shows the characteristic spectrum of the sample, which is necessary for comparing with the electrical parameters of an equivalent circuit. The frequency range used was from 10 Hz to 100 kHz. Once the measurements were represented in a Nyquist diagram, we obtained representations of equivalent electrical circuits via the software ZView®. The method of "instant adjustment" was used to fit the data to predefined circuit models. A voltage of 25 mV was applied across the RC circuit.

To determine the equivalent equation, the impedance is determined, which is given by the following formula in the complex frequency domain.

Applying Kirchhoff laws to the circuit of Figure 1, we have:

Before applying the Laplace transform of (24) and (25) must make the following considerations

In applying the definition of fractional derivative (Podlubny, 1994), we have:

Substituting (28) and (29) into (25), we obtain:

Applying Laplace transform to (30) and (31) is obtained:

Finally from (32) and (33) we have:

If, s = (jω), we have:
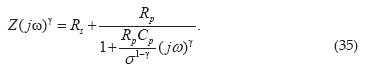
The equation (35) is the result of the fractional temporal operator in the equation for the RC equivalent circuit, this general formula includes an arbitrary constant sigma and in the case particular to take the value of σ = RPCP is reduced to the Cole model (1941) and Gómez et al. (2012). On the other hand, if we make γ = 1, we obtain the RC circuit ideal.
Figure 7 show the comparison of the Nyquist diagram resulting between integer order equation (23), the spectroscopy and fractional equation (35), fractional exponent γ = 0.9825. This value was obtained by a least-squares fit.

From the Figure 7, it can be seen that the fractional differential equation (35) obtained describes best the measurement of electrical impedance spectroscopy.
Discussion
The Figures 2 and 4 show the charge and current in the RC circuit, respectively. From Figure 3 can observe that as γ increases from 0.96 to 1, the fractal element behaves as a resistor of resistance R for γ = 1, intermediate values of γ determines behavior between a capacitor and a resistor. In the Figure 5 is observed a behavior inductive for γ = 1, intermediate values determine behavior between inductor and resistor.
It has been found that for every 0 < γ ≤ 1, the load stored in the RC circuit is directly proportional to the voltage on the capacitor; it follows that the behavior of the charge on the capacitor will give identical curves to those shown in Figure 3.
This current behavior can be induced from voltage in the capacitor, for γ = 1 will have a current value equal to the ratio between the supply voltage and resistance for t = 0, and will decrease with time until it reaches zero, a full-order RC circuit.
As to the fractional LC circuit, is observed in Figure 5, the current increases as the γ values decrease from 1 to 0.96 indicating losses in the LC series circuit, this can be seen because there is a damping voltage curves, typical of an RLC circuit with losses.
Conclusions
The fractional differential equation for the RC and LC circuits has been proposed. The relevant aspect of this work is the way to introduce the fractional derivatives operators, providing a systematic way to construct the fractional differential equations of any physical system keeping the dimensionality of the physical parameters. The order of the derivative being considered is 0 < γ ≤ 1. To keep the dimensionality of the physical parameters R, L, C the new parameter σ is introduced. This parameter characterizes the existence of fractal structures in the system (components that show an intermediate behavior between conservative and dissipative systems), the fractional time components change the time constant and affect the transient response of the system (Guía et al., 2013). A relation between the fractional order time derivative γ and the new parameter σ is found. The numeric Laplace transform method was used for the simulation of the equations results. The classical cases are recovered by taking the limit when γ = 1. Also, the concept of fractional time constant has been introduced.
From the description of the fractional differential equation models can be noted that the representation of the Cole model is generated to solve the RC circuit in the formalism of fractional calculus. The simulations obtained from the fractional representation showing a better description than those obtained by the equations of integer order. The exponent of the fractional differential equation that best fits the RC circuit is γ = 0.9825.
With the approach presented here, it will be possible to have a better study of the transient effects in the electrical systems. Also, the electrical circuit will provide a robust framework for studying the bioelectrical response to transient stimuli, when an equivalent electrical circuit has been used.
Acknowledgements
This research was supported by CONACYT.
References
Agrawal O.P., Tenreiro-Machado J.A., Sabatier I. Fractional Derivatives and Their Applications, Eds., Nonlinear Dynamics, vol. 38, Berlin, Springer-Verlag, 2004. [ Links ]
Baleanu D., Günvenc Z.B., Tenreiro-Machado J.A. New Trends in Nanotechnology and Fractional Calculus Applications, (Eds.), Springer 2010. [ Links ]
Caputo M., Mainardi F. Pure and Applied Geophysics, volume 91, 1971: 134-147. [ Links ]
Cole K.S. and Cole R.H. Dispersion and Absorption in Dielectrics: Alternating Current Characteristics. J. Chem. Phys., volume 9, 1941: 341-351. [ Links ]
Gómez-Aguilar J.F., Rosales-García J.J., Bernal-Alvarado J.J., Córdova-Fraga T., Guzmán-Cabrera R. Fractional Mechanical Oscillators. Revista Mexicana de Física, volume 58, 2012a: 524-537. [ Links ]
Gómez J.F., Rosales J.J., Bernal J.J., Guía M., Martinez J. Electromagnetic Transient Analysis of Networks Described by Equations of Fractional Order. Prespacetime Journal, volume 3 (issue 6), 2012b: 524-537. [ Links ]
Gómez-Aguilar F., Rosales-García J, Guía-Calderón M, Bernal-Alvarado J. Analysis of Equivalent Circuits for Cells: A Fractional Calculus Approach. Revista Ingeniería, Investigación y Tecnología, UNAM, volume XIII, 2012c: 375-384. [ Links ]
Gómez F., Bernal J., Rosales J., Córdova T. Modeling and Simulation of Equivalent Circuits in Description of Biological Systems- A Fractional Calculus Approach. Journal of Electrical Bioimpedance, volume 3 (issues 2-11), 2012d. [ Links ]
Guía M., Gómez F., Rosales J. Analysis on the Time and Frequency Domain for the RC Electric Circuit of Fractional Order. Cent. Eur. J. Phys., Springer, 2013. [ Links ]
Gutiérrez R.E., Rosário J.M., Tenreiro-Machado J.T. Fractional Order Calculus: Basic Concepts and Engineering Aplications, Hindawi Publishing Corporation, Mathematical Problems in Engineering, 2010. [ Links ]
Hilfer R. Applications of Fractional Calculus in Physics, Singapore, Ed. World Scientific, 2000. [ Links ]
Hilfer R. Phys. Chem. B, volume 104, 1974: 3914-3917. [ Links ]
Magin R.L. Fractional Calculus in Bioengineering, Begell House Publisher, Rodding, 2006. [ Links ]
Metzler R., Klafter J. Phys. Rep., volume 339, 2000: 1-77. [ Links ]
Miller K.S., Ross B. An Introduction to the Fractional Calculus and Fractional Differential Equations, Wiley, New York, 1993 [ Links ]
Moreno P and Ramirez A. Implementation of the Numerical Laplace Transform: a Review. IEEE Trans. Power Delivery, volume 23 (issue 4), 2008: 2599-2609. [ Links ]
Oldham K.B., Spanier J. The Fractional Calculus, Academic Press, New York, 1974. [ Links ]
Obeidat A., Gharibeh M., Al-Ali M., Rousan A. Evolution of a Current in a Resistor. Fract. Calc. App. Anal., Springer 2011, pp. 2-14. [ Links ]
Petras I. Fractional-Order Memristor-Based Chua's Circuit. IEEE Transactions on Circuits and Systems-II: Express Briefs, volume 57, 2010: 12. [ Links ]
Podlubny I. Fractional Differential Equations, San Diego, Academic Press, 1994. [ Links ]
Proakis J.G. and Manolakis D.G. Digital Signal Processing, in Principles, Algorithms and Applications, 3rd ed., Upper Saddle River, NJ, Prentice-Hall, 1996. [ Links ]
Ramirez A., Gómez P., Moreno P., Gutierrez A. Frequency Domain Analysis of Electromagnetic Transients Through the Numerical Laplace Transform, on: The IEEE General Meeting, Denver, CO, 2004. [ Links ]
Rosales J.J., Guía M., Gómez J.F., Tkach V.I. Fractional Electromagnetic Wave. Discontinuity, Nonlinearity and Complexity, volume 14, 2012: 325-335. [ Links ]
Samko S.G., Kilbas A.A., Maritchev O.I. Fractional Integrals and Derivatives, Theory and Applications, Gordon and Breach Science Publishers, Langhorne, PA, 1993. [ Links ]
Sheng H., Li Y., Chen Y.Q. Application of Numerical Inverse Laplace Transform Algorithms in Fractional Calculus. J. Franklin Inst., volume 348 (issue 2), 2011: 315-330. [ Links ]
Uchaikin V. Fractional Derivatives for Physicists and Engineers, Springer 2013. [ Links ]
Veliev E.I., Engheta N. Fractional Curl Operator in Reflection Problems, on: 10th Int. Conf. on Mathematical Methods in Electromagnetic Theory, Ukraine, September 2004, pp. 14-17. [ Links ]
West B.J., Bologna M., Grigolini P. Physics of Fractional Operators, Berlin, Springer-Verlag, 2003. [ Links ]
Westerlund S. Causality, Report no. 940426, University of Kalmar, 1994. [ Links ]
Wilcox D.J., Gibson I.S. Numerical Laplace Transformation and Inversion in the Analysis of Physical Systems. Int. J. Numer. Methods Eng., volume 20, 1984: 1507-1519. [ Links ]
Wyss W.J. Math. Phys., volume 27, 1986: 2782-2785. [ Links ]
About the authors
José Francisco Gómez-Aguilar. He obtained the degree of Doctor in Physics in the Division of Science and Engineering Campus León, University of Guanajuato. He currently works in the Department of Electrical Engineering, Division of Engineering, Campus Irapuato, Salamanca, University of Guanajuato. His interests are electromagnetic effects in biological systems, numerical methods applied to engineering, fractional calculus and its application to electrical circuit theory.
Roberto Razo-Hernandez. He obtained a Master degree in Electrical Engineering from the School of Mechanical Electrical and Electronics Engineering at the University of Guanajuato with specialization in Instrumentation and Digital Systems. He currently works in the Department of Electromechanical Engineering in the ITESI Irapuato. His interests are fractional calculus and its application to electrical circuit theory.
Juan Rosales-García. He obtained the degree of Doctor of Science in UAM Iztapalapa. He currently works in the Department of Electrical Engineering, Division of Engineering, Campus Irapuato, Salamanca, University of Guanajuato. His interests are fractional calculus and circuit theory.
Manuel Guía-Calderón. He obtained a Master degree in Electrical Engineering from the Faculty of Mechanical Engineering Electrical and Electronics, University of Guanajuato with specialization in Instrumentation and Digital Systems. He currently works in the Department of Electrical Engineering, Division of Engineering, Campus Irapuato, Salamanca, University of Guanajuato. His interests are numerical methods applied to engineering and fractional calculus.














