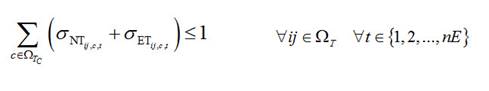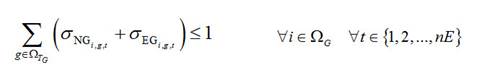Introducción
La alta dependencia de la energía eléctrica en la sociedad actual se refleja en el aumento acelerado que tiene su consumo en los últimos años, por lo que se espera que en 30 años el consumo de energía sea el doble del valor de la demanda consumida hoy en día (Paul Scherrer Institute, 2013). De acuerdo con lo anterior, cobra una gran importancia para el sector eléctrico el desarrollo de metodologías que permitan realizar planes adecuados de planeación y operación de los sistemas de distribución de una manera confiable y económica.
Tradicionalmente los sistemas de distribución se planearon considerando la instalación de elementos nuevos y el aumento de la capacidad de los existentes (subestaciones y tramos de red) (Miranda et al., 1994; Ramírez y Bernal, 1998; Lavorato et al., 2010; Rodrigues et al., 2013; Tabares et al. 2014).
Sin embargo, la evolución de las tecnologías basadas en componentes electrónicos en los últimos años, así como el desarrollo de estrategias que disminuyen impactos ambientales y la integración de Smart Grids en los sistemas eléctricos, han ocasionado la aparición de nuevas metodologías para planear estos sistemas. Dentro de este contexto, se encuentran los generadores distribuidos (GD), que se han empleado para mejorar condiciones operativas de los sistemas de distribución (pérdidas, confiabilidad, cargabilidad de elementos, regulación de tensión, etcétera) (Greatbanks et al., 2003; Shaaban et al., 2011; Nayanatara et al., 2014; Gopiya et al., 2015), y como estrategias adicionales dentro de las metodologías de planeación (El-Khattam y Salama, 2003; Mantway y Al-Muhaini, 2008; Zou et al., 2012; Popovic et al., 2014; Bagheri et al., 2015).
La inclusión de los GD en los trabajos relacionados con la planeación de sistemas de distribución, impacta los costos totales de los proyectos al disminuir las inversiones realizadas en la instalación de otros elementos. Generalmente estos GD se modelan como una inyección de potencia al sistema (nodos PQ), lo que no permite considerar generaciones que involucren máquinas síncronas como pequeñas centrales hidroeléctricas o basadas en gas natural (las cuales se deben modelar como nodos PV).
Por otro lado, en las formulaciones matemáticas empleadas en la planeación de los sistemas de distribución, se consideran diferentes horizontes de tiempo con el fin de involucrar el impacto de la demanda al corto, mediano y largo plazo. Dentro de este contexto, los modelos de planeamiento generalmente consideran metodologías con varias etapas (multi-etapa), destacándose los modelos multi-etapa no coordinados (pseudo-dinámico) y multi-etapa coordinados (dinámico), donde los primeros modelos se emplean tradicionalmente en la planeación de los sistemas de distribución.
El planeamiento multi-etapa no coordinado considera varias etapas de forma consecutiva, donde las acciones de planeación propuestas en una etapa se consideran como entrada para la siguiente etapa. A diferencia de esta metodología, el planeamiento multi-etapa coordinado considera las etapas de planeación de forma simultánea.
Con el fin de involucrar los aspectos mencionados previamente, en este artículo se presenta un nuevo modelo para la expansión de sistemas de distribución de energía eléctrica. A diferencia de los trabajos reportados en la literatura, se considera un planeamiento multi-etapa coordinado con penetración de generación distribuida. Los GD se modelan como nodos PQ o PV, lo cual permite generalizar el uso de cualquier tipo de generación basado en máquinas de inducción o síncronas.
Adicional al costo de instalación de GD, en la función objetivo del problema se considera el costo de instalación de nuevos elementos y la ampliación de existentes (tramos de red y subestaciones), y el costo de operación asociado a las pérdidas de energía del sistema. El conjunto de restricciones se compone por ecuaciones de carácter técnico y operativo.
Con el fin de realizar un análisis comparativo, se presentan tres casos de estudio. El Caso 1 considera un modelo de planeación multi-etapa no coordinado. El Caso 2 tiene en cuenta un modelo multi-etapa coordinado. Estos dos casos (1 y 2), no incluyen la instalación de GD. El caso 3 es un modelo de planeación multi-etapa coordinado que involucra la penetración de GD en el sistema de distribución. El horizonte de planeación tiene en cuenta tres etapas de cinco años.
Para solucionar el problema se emplea un algoritmo de búsqueda tabú (Glover y Laguna, 1997), que entrega buenos resultados en la solución de problemas del tipo NP-completo, como el de este trabajo.
Las principales contribuciones de este trabajo son:
Un modelo de planeamiento multi-etapa coordinado para sistemas de distribución. En este modelo todas las etapas se tratan de forma simultánea, permitiendo la evaluación de las acciones tomadas en cada etapa del planeamiento.
El modelo considera generación distribuida. Los GD se modelan como nodos PV o PQ, lo que permite usar cualquier tipo de tecnología de generación.
Se realiza una comparación con modelos de planeamiento multi-etapa no coordinado y coordinado, ambos sin GD. Para esta comparación se implementaron tres modelos de planeamiento multi-etapa: el modelo descrito en los dos ítems anteriores (coordinado con GD), coordinado sin GD y no coordinado sin GD.
Este artículo se organiza de la siguiente forma. En la sección 2 se presenta la formulación del problema. En la sección 3 se describe la metodología propuesta. En la sección 4 se muestran las pruebas y los resultados numéricos. Finalmente en la sección 5 se presentan las conclusiones derivadas de este trabajo.
Formulación del problema
El planeamiento de sistemas de distribución de energía eléctrica tiene como enfoque principal la minimización de los costos de inversión y operación en un periodo de planeamiento específico, sujeto a un conjunto de restricciones técnicas y operativas. Los costos de inversión se relacionan con la instalación de nuevos elementos y la ampliación de los existentes (tramos de red, subestaciones y generadores distribuidos). Los costos de operación son el valor de las pérdidas de energía durante el periodo de planeamiento. El modelo matemático empleado para describir el problema es del tipo no lineal entero mixto, que se soluciona bajo un esquema de planeamiento coordinado.
A continuación se describe en forma detallada cada componente del modelo matemático, así como una explicación de cómo se involucra el horizonte de planeamiento.
Horizonte de planeamiento
Tradicionalmente la planeación de los sistemas de distribución se soluciona considerando una etapa (mono-etapa o estático) o varias etapas (multi-etapa). En los modelos estáticos la inversión se asume al inicio del periodo de estudio, esta debe atender las necesidades de la demanda hasta el final del periodo analizado. En los modelos multi-etapa el horizonte de tiempo se divide en varias etapas para el estudio, donde cada uno de estos periodos considera un crecimiento de la demanda. Estos modelos se dividen en dos categorías: planeamiento multi-etapa no coordinado y coordinado (Figura 1).
En el planeamiento multi-etapa no coordinado se consideran un número n de etapas, donde la solución final de cada etapa se usa como configuración inicial para la siguiente etapa. En este caso en cada configuración (comienzo de cada etapa), la demanda se incrementa por la tasa predefinida por la empresa. Este procedimiento se repite para cada etapa n, es decir, realmente se realizan n procesos de optimización de forma separada. La solución de la última etapa se considera como la solución final para todo el problema; sin embargo, el costo total involucra el valor de cada etapa expresado en valor presente.
A diferencia del planeamiento anterior (multi-etapa no coordinado), en el planeamiento multi-etapa coordinado, las n etapas se consideran de forma simultánea. En otras palabras, en lugar de n procesos de optimización, solamente se realiza uno, con todas las etapas consideradas al mismo tiempo.
Formulación matemática
El problema del planeamiento de sistemas de distribución se formula como un modelo de programación no lineal entero mixto. La función objetivo a ser minimizada se presenta en la ecuación (1). El conjunto de restricciones presentado en las ecuaciones (2)-(9) considera aspectos físicos, técnicos y operativos. La nomenclatura empleada en este artículo se puede consultar en el Apéndice.
Función objetivo
La función objetivo (ecuación 1) se compone por siete términos. Los dos primeros términos son los costos de instalación de nuevos tramos de red y ampliación de los tramos existentes, respectivamente. Los términos tres y cuatro son los costos de instalación de nuevas subestaciones y ampliación de existentes, respectivamente. Los términos cinco y seis son los costos de instalación de nuevos generadores distribuidos y ampliación de existentes. El último término (séptimo término) es el costo de las pérdidas de energía eléctrica en los tramos de red del sistema, los cuales se expresan en valor presente.
Note que los primeros seis términos de la ecuación (1) tiene una doble sumatoria, las cuales representan la localización y el tipo de un elemento, respectivamente. Respecto a la primera sumatoria, los términos tres al seis tienen solamente un subíndice, debido a que se asocia a la ubicación de subestaciones o generadores distribuidos (i o j). Por otro lado, los términos uno y dos tienen dos subíndices, debido a que se encuentran relacionados con los dos nodos de un tramo de red (ij). La segunda sumatoria en estos seis términos se asocia a la capacidad (tipo) de un tramo de red, subestación o GD (c, s o g).
A diferencia de los primeros seis términos, el séptimo término tiene tres sumatorias. La primera sumatoria hace referencia al nivel de la curva de duración de carga, la segunda sumatoria se asocia a un tramo de red i-j y la tercera sumatoria al calibre asociado al conductor de dicho tramo de red.
Conjunto de restricciones
El conjunto de restricciones se presenta en las ecuaciones (2) a (9). La ecuación 2 es el balance de potencia en todos los nodos del sistema. Las ecuaciones (3), (4) y (5) aseguran que no se presenten sobrecargas en tramos de red, subestaciones y GD, respectivamente. La ecuación (6) evita que los límites de la magnitud de la tensión se violen. Las ecuaciones (7), (8) y (9) garantizan que solamente un tipo de conductor, subestación o GD se instale en una sección o nodo de la red, respectivamente.
Metodología propuesta
En este artículo el problema del planeamiento de sistemas de distribución se soluciona usando un algoritmo de búsqueda tabú. Los principales aspectos de este algoritmo y su implementación al problema se describen a continuación.
Técnica de solución
Búsqueda Tabú (BT) es una técnica metaheurística de optimización, que surge de la inteligencia artificial, ya que emplea conceptos de memoria adaptativa y exploración sensible. Se propuso por Fred Glover en la década de los 80 y se ha utilizado para resolver problemas de diferentes disciplinas, presentando buenos resultados (Glover y Laguna, 1997; Gallego et al., 2008).
Este algoritmo implementa una estrategia de búsqueda local eficiente alrededor de una solución encontrada, donde dicha búsqueda se asocia a un conjunto de soluciones vecinas, que permiten en pasos pequeños pasar a la configuración vecina más adecuada.
Debido a que una búsqueda exhaustiva de vecinos alrededor de una configuración puede acarrear tiempos computacionales elevados, es necesario recurrir a un vecindario reducido mediante índices de sensibilidad, que se eligen según las características del problema.
Una vez seleccionada la configuración de la próxima iteración, se actualizan las listas tabú, bloqueando por las próximas iteraciones los atributos modificados, es decir, que no se regrese a soluciones visitadas. En este paso también se actualiza la incumbente local, la lista élite local y el contador de repeticiones de la incumbente. El algoritmo se detiene cuando se cumple el criterio de parada, que se da por un número máximo de iteraciones o por un número de iteraciones sin mejorar la incumbente.
El pseudocódigo del algoritmo BT se presenta en la Figura 2. Mayor información sobre el funcionamiento de este algoritmo, se puede encontrar en Glover y Laguna (1997).
Codificación del problema
En este artículo se presenta una codificación vectorial de variables enteras, con la que es posible representar la topología y tipo de elementos del sistema de distribución. Este vector se divide en tres partes, las cuales se asocian a los elementos del sistema. Por lo tanto, cada etapa de planeamiento tiene un vector de tamaño igual al número de subestaciones, tramos de red y generadores distribuidos, tanto existentes como nuevos.
De acuerdo con lo anterior, cada posición del vector se relaciona con un elemento del sistema. Si en una posición aparece un cero, indica que dicho elemento no se propone para su instalación. Si aparece un número entero indica que se propone su instalación con el tipo (capacidad) asociado a dicho número. Por ejemplo, los números 1 y 2 se pueden asociar a subestaciones con capacidades de 5 y 10 MVA, respectivamente.
En cada una de las n etapas del modelo de planeamiento pseudo-dinámico, se tiene un vector como el descrito previamente. Sin embargo, en el modelo dinámico se tiene un vector que considera n subvectores de forma simultánea, donde cada subvector es del tamaño de un vector empleado por el modelo anterior. Debido a esto, el modelo dinámico considera un número mayor de variables que el modelo pseudo-dinámico, al considerar todas las etapas de forma simultánea.
Flujo de carga
Para evaluar las configuraciones generadas por el algoritmo BT, es necesario emplear un flujo de carga que permita determinar de manera eficiente y rápida el valor de su función objetivo y el cumplimiento del conjunto de restricciones.
Sin embargo, es importante tener en cuenta que al conectar un GD al sistema de distribución se pierde la radialidad de la red, al circular corrientes en ambos sentidos. De acuerdo con esto, es necesario utilizar un flujo de carga que se adapte a estas características operativas. En este artículo se emplea un flujo de carga para redes levemente enmalladas (Shirmohammadi y Hong, 1988).
Integración del algoritmo bt a la solución del problema
La metodología propuesta en este artículo emplea una estrategia maestro-esclavo. La estrategia maestro (problema de inversión) se soluciona con el algoritmo BT. La estrategia esclavo (problema operativo) se resuelve con el flujo de carga. Cada configuración propuesta por la técnica de solución (configuración del vecindario generado) se evalúa por medio de la aplicación del flujo de carga, el cual permite hallar el valor de la función objetivo y validar la factibilidad. Una vez determinados estos valores, el algoritmo BT continúa su proceso, hasta que el algoritmo alcanza el criterio de parada.
Pruebas y resultados
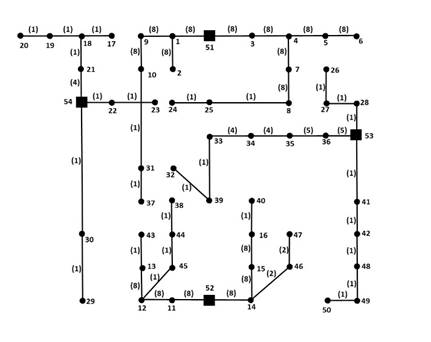
La metodología propuesta se aplica a un sistema de prueba de 54 nodos (Miranda et al., 1994), el cual se modifica para permitir la localización de generadores distribuidos (Figura 3). En este sistema los cuadrados negros corresponden a subestaciones existentes (nodos 51 y 52) y los blancos a propuestas (nodos 53 y 54). Las líneas continuas son tramos de red existentes y las líneas punteadas son tramos de red propuestos. Los puntos negros son nodos de paso y de carga. Los lugares candidatos para ubicar generadores distribuidos son los nodos 6, 18, 31, 36 y 45. Los datos de conductores, subestaciones y generadores distribuidos se encuentran en las Tablas 1, 2 y 3, respectivamente. La base de datos de la topología del sistema se puede consultar con los autores.
El horizonte de planeamiento se dividió en tres etapas de cinco años, en las cuales se consideró una tasa de crecimiento anual de la demanda de 2%. Se considera una curva de duración de carga de 100%, 70% y 40% del valor nominal de la demanda, con una duración de 1000, 5760 y 2000 horas, respectivamente (Figura 4). La tasa de descuento es de 10% y el precio de la energía $250 [kWh].
La metodología se implementó en Fortran 90 en un computador con procesador Intel Core i7-3612QM CPU2.10GHz x 8, con 6GB de memoria RAM bajo sistema operativo UNIX.
Con el fin de verificar el comportamiento de la metodología propuesta, en esta sección se realiza el análisis comparativo bajo tres escenarios de planeación. El primer escenario considera un modelo de planeación multi-etapa no coordinado sin generación distribuida (pseudo-dinámico sin GD - caso 1). El segundo escenario emplea un planeamiento multi-etapa coordinado sin generación distribuida (dinámico sin GD - caso 2). El tercer escenario resuelve el problema bajo un planeamiento multi-etapa coordinado con generación distribuida (dinámico con GD - caso 3). Para los tres casos se empleó el mismo horizonte de planeamiento.
Después de aplicar la metodología propuesta se obtuvieron los resultados presentados en la Tabla 4. Las configuraciones finales de cada caso (después de la etapa 3) se presentan en las Figuras 5, 6 y 7. Los calibres seleccionados se observan entre paréntesis al lado de cada tramo de red respectivo.
De los tres casos implementados, el caso 1 es el más fácil de implementar. En este las etapas se resuelven de manera consecutiva, donde su complejidad matemática es de una sola etapa, por lo tanto, el tiempo de cómputo es el más bajo de los tres casos. Sin embargo, la calidad de la respuesta es de peor calidad, respecto a los obtenidos en los otros dos casos. En el caso 2 las etapas se estudian de manera simultánea, incrementando ostensiblemente su complejidad matemática y por ende, el tiempo de cómputo requerido para su solución. A diferencia del caso anterior (caso 1), se obtienen redes de menor costo, ya que requiere menos elementos al efectuar una adecuada distribución de los mismos en el tiempo. En relación al caso 3, además de considerar un planeamiento coordinado, considera en su estudio la generación distribuida, incrementando su complejidad matemática y con ello el tiempo de cómputo. Por otro lado, la generación distribuida impacta positivamente la distribución de flujos en la red, llevándolos a valores que resultan favorables tanto en lo relacionado con las pérdidas de energía, como en la carga por los conductores. Estos aspectos favorecen positivamente los costos en inversión y operación, como se puede observar en la Tabla 4, en los casos 1, 2 y 3, respectivamente.
De la Tabla 4 se observa que el mayor costo de inversión en subestaciones se presenta en el caso 1 (M$8424.10), que es mayor a los casos 2 y 3 un 5.03% y 52.51%, respectivamente. En el caso 1 se propone la instalación de las dos nuevas subestaciones (tipo 1), ya que las dos subestaciones existentes no son capaces de alimentar el crecimiento de la demanda. Adicionalmente una subestación existente aumenta de capacidad al tipo 2. En el caso 2, también se construyen las dos nuevas subestaciones; sin embargo, no aumentan capacidad las otras subestaciones. En el caso 3 solamente se construye una subestación tipo 1 en el nodo 53.
Respecto a los generadores distribuidos, en el caso 3 se instalan tres generadores de tipo 1 en los nodos 18, 31 y 45, con un costo de M$975.
Adicionalmente se observa que el caso 3 tiene el mayor costo de inversión (M$8043,5) en tramos de red. Los casos 1 y 2 son menores un 5.09% y 2.75%, respectivamente. Esto se debe a que en el caso 3 se instalan conductores de mayor capacidad, respecto a los otros dos casos.
Por otro lado los menores costos de pérdidas de energía se obtienen en el caso 3 (M$4128,42), que es menor a los casos 1 y 2 un 11.02% y 6,52%, respectivamente. Este comportamiento se ocasiona por el calibre de los conductores y la instalación de los generadores distribuidos en el sistema. Al aumentar el calibre del conductor, disminuye su valor de resistencia, lo cual impacta en la reducción de las pérdidas de red. Adicionalmente al ubicar los generadores distribuidos, el nivel de corriente que circula por los tramos de red disminuye, lo que también ocasiona una disminución en las pérdidas técnicas.
Finalmente se nota que el menor costo total se obtiene con el caso 3 (M$17146,92), el cual reduce la inversión total de los casos 1 y 2 en un 20.37% y 17.91%, respectivamente.
En otras palabras, el análisis costo/beneficio de emplear un planeamiento multi-etapa coordinado con penetración de generadores distribuidos (caso 3), puede encontrar soluciones con costos totales más bajos que los modelos de planeamiento multi-etapa no coordinado y coordinado sin generación distribuida (casos 1 y 2, respectivamente).
Conclusiones
En este artículo se presenta una metodología para solucionar el problema de la expansión de sistemas de distribución de energía eléctrica, usando como técnica de solución un algoritmo de búsqueda tabú. El problema se soluciona usando un planeamiento multi-etapa coordinado, considerando la penetración de generación distribuida. Como análisis comparativo se realizan otros dos casos de prueba, los cuales consideran modelos de planeamiento multi-etapa no coordinado y coordinado (ambos sin GD). Los resultados obtenidos muestran que al emplear un modelo de planeamiento como el propuesto en este artículo (multi-etapa coordinado con GD), se reducen los costos totales de inversión al compararse con los otros dos modelos de planeamiento (planeamiento multi-etapa no coordinado y coordinado sin GD).
La metodología propuesta es útil para las empresas distribuidoras de energía eléctrica debido a que la inversión realizada en elementos de red (tramos de red, subestaciones y generadores distribuidos), se compensa en el tiempo con la disminución en el valor de las pérdidas de energía, lo cual garantiza una mejor relación costo/beneficio. Adicionalmente esta metodología se puede emplear para sistemas con diferentes condiciones operativas, ya que permite modelar los GD como nodos PV o PQ, dependiendo de la tecnología considerada.
Debido a las características de la metodología propuesta se puede aplicar en sistemas de distribución de diferentes tamaños, características operativas, con redes levemente enmalladas o inclusión de generación distribuida, lo cual la hace atractiva para las empresas del sector eléctrico al permitir su adaptación a sistemas de distribución bajo un ambiente de redes inteligentes (Smart Grids).











 nueva página del texto (beta)
nueva página del texto (beta)