Introducción
En los últimos años, la simulación de los sistemas de ventilación de invernaderos por dinámica de fluidos computacional (CFD) se ha incrementado considerablemente, mediante esta técnica es posible estimar la tasa de ventilación, así como la caracterización del campo de flujo dentro y fuera del invernadero (Teitel et al., 2008; Teitel y Wenger 2014). Además, se han desarrollado diversos modelos para optimizar el comportamiento de diferentes fluidos y se han logrado reducir los costos experimentales que en la mayoría de los casos requieren también de costosas instalaciones (Bournet y Boulard, 2010).
Diversos grupos de investigadores intentan presentar diferentes sistemas de conversión de energía eólica que sean rentables y confiables (Frikha et al., 2016), donde la dirección del flujo de aire es paralela y constante en el espacio. Existen diferentes propuestas para aprovechar la energía del flujo de aire saliente de diferentes dispositivos, por ejemplo: una solicitud de patente de la Universidad Autónoma Chapingo (UACh) para ubicar la posición de instalación de un aerogenerador y un recuperador de potencia del aire propuesto por Romantchik y Ríos (2017), además de otros trabajos como la patente Anon (2013) en torres de aire; en estos casos, el flujo de aire no es constante en la dirección ni espacio.
Diferentes autores han efectuado simulaciones y experimentos por CFD en túneles de viento como medio de circulación del aire, por ejemplo, Driss et al. (2014) realizaron un experimento en un túnel equipado con un rotor eólico tipo Savonius para validar el método numérico. Por otra parte Saha et al. (2008) realizaron un análisis por CFD y pruebas en un túnel de viento para evaluar el rendimiento aerodinámico de los sistemas Savonius para tres configuraciones diferentes. D’Alessandro et al. (2010) desarrollaron un modelo matemático para analizar la interacción entre el campo de flujo y las palas de un rotor eólico Savonius, representar el campo de flujo desarrollado alrededor del mecanismo y evaluar su rendimiento. Khorsand et al. (2008) analizaron el patrón de flujo y la pérdida de presión en una turbina de gas con el objetivo de optimizar la pérdida de presión y las características de flujo en la entrada del compresor de la turbina. Similares trabajos de análisis aerodinámico por CFD presentaron Scotto di Perta et al. (2016) en túneles de viento.
En cuanto a la geometría del sistema de ventilación Driss et al. (2015) compararon por CFD diferentes diseños de rotores con cuatro ángulos de aspa (60, 75, 90 y 130°). Además Frikha et al. (2015) estudiaron cuatro tipos de difusores utilizando diferentes ángulos de inclinación de aspas para visualizar la temperatura, velocidad y presión total del sistema entre otros parámetros de flujo. Hughes y Ghani (2010) investigaron el efecto de modificar el ángulo externo de las persianas de un sistema de ventilación contra la presión interna y la velocidad dentro del dispositivo, así como la velocidad del microclima, el objetivo de la investigación fue obtener el ángulo con la menor pérdida de presión para optimizar la velocidad de suministro de aire fresco al espacio ocupado.
Este estudio se basó en la visualización y análisis de los resultados mediante SolidWorks Flow Simulation, software ocupado debido a su practicidad en cuanto a la creación de la geometría y mallado del sistema de extracción de aire. Este programa combina un alto nivel de funcionalidad y precisión mediante un código basado en la resolución numérica de las ecuaciones de flujo de Navier-Stokes para fluidos newtonianos (ecuación 1) bajo un régimen predeterminado de solución del problema que vincula los tipos de flujo laminar y turbulento, con un método de discretización de volumen finito en un mallado de forma rectangular (Dhanushkodi et al., 2015; Driss et al., 2014).
donde
ρ (kg·m-3) = densidad del fluido
v (m) = velocidad de flujo del fluido
p (Pa) = presión del fluido
µ (Pa·s) = viscosidad dinámica del fluido (Çengel y Cimbala, 2014).
El cálculo se realiza en un prisma rectangular conocido como dominio computacional. Los planos de frontera que comprende el dominio computacional son ortogonales a los ejes del sistema cartesiano de coordenadas, envolviendo por completo el volumen del fluido que comprende el modelo. La técnica consiste en dividir el dominio computacional en volúmenes elementales alrededor de cada nodo en el mallado; esto asegura la continuidad del flujo entre nodos. La discretización espacial se obtiene de acuerdo con un procedimiento de interpolación tetraédrica. En cuanto a la discretización temporal, se adopta la formulación implícita. La ecuación de transporte es integrada sobre el volumen de control (Driss et al., 2010; Ammar et al., 2011; Driss y Abid, 2012). Para efectuar la simulación computacional primero se procede a diseñar el modelo tridimensional en el software SolidWorks, a continuación, se crea un proyecto en Flow Simulation para un análisis interno de flujo y se establecen las condiciones de flujo y de frontera del sistema, y se procede a generar el mallado del sólido, este componente se genera automáticamente por la computadora al subdividir el modelo y el dominio computacional en celdas computacionales. Con lo anterior, se procede a ejecutar la simulación de flujo y se verifica la convergencia del modelo de acuerdo con los parámetros de flujo como la velocidad o presión, esto conforme al número de iteraciones o respecto al tiempo. Al finalizar el cálculo se puede consultar un informe general de la simulación en un archivo de texto o una hoja de cálculo que incluye gráficos de corte en puntos específicos del sólido, así como vistas isométricas y animaciones del fluido (Dhanushkodi et al., 2015). Noh et al. (2012) efectuaron un análisis por CFD con este software para visualizar el flujo de aire en unas persianas colocadas a la entrada de un ducto instalado en una turbina, variando el ángulo de ataque (25, 35 y 45°). Por su parte, Herrera et al. (2017) analizaron la variación de la velocidad de salida del aire en el extractor y el flujo en un pulverizador agrícola operando a diferentes velocidades, mientras que Tsay et al. (2004) llevaron a cabo un trabajo en un sistema de pulverización asistida por aire.
Este documento está conformado por dos secciones: En la primera parte se presenta el diseño de un conjunto de extractores con diferente número de aspas y ángulo de ataque del aire, con los que se analizó el patrón de flujo del aire generado por simulaciones CFD al interior de un túnel de viento. Enseguida, se presentan los resultados de la simulación y el análisis del comportamiento de la velocidad del aire dentro del sistema.
Desarrollo
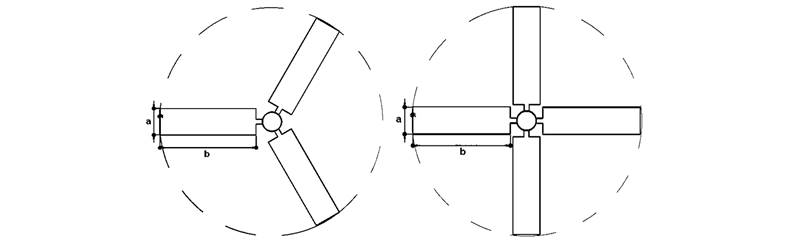
El experimento se basó en un diseño completamente al azar con arreglo multifactorial, considerando el número, n, y ancho de aspas, α, la frecuencia de rotación del sistema de ventilación, ω, y el ángulo de ataque del aire del extractor, α, generando 48 tratamientos, es decir 48 unidades experimentales (Figura 1), donde las variables respuesta fueron el ángulo de apertura del aire a la salida del extractor, β, el ángulo de flujo al interior del ducto, ϕ, la velocidad de salida, v, y presión total del aire, pt.
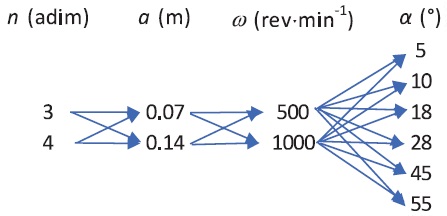
Figura 1 Unidades experimentales respecto al número y ancho de aspas, frecuencia de rotación del sistema de ventilación y ángulo de ataque del aire del extractor
Inicialmente, con el software SolidWorks se diseñó un conjunto de extractores (Ø 1.2 m) con diferente ángulo de ataque del aire, número y ancho de las aspas, y mediante el complemento Flow Simulation, incluido en el programa, se efectuó un conjunto de simulaciones por CFD de estado estable para analizar el flujo de aire en el sistema de ventilación de un invernadero.
Modelo geométrico
Primero se diseñaron 24 extractores respecto a n y a (Figura 2), variando α (5, 10, 18, 28, 45 y 55°) (Figura 3). Además, en todas las variantes, el eje de rotación midió Ø100mm.
Para efectuar la simulación, cada extractor se acopló a la parte central de un túnel de viento (Ø 3 m x 6 m), cuyo diámetro se redujo acorde con la geometría del mecanismo (Figura 4).
Condiciones de frontera
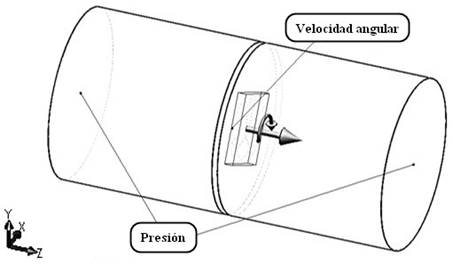
Posteriormente, se efectuó la simulación del sistema sometiéndolo a las siguientes condiciones de frontera: presión del aire (total, estática), frecuencia de rotación del eje del motor y geometría del extractor (ancho, número de aspas y ángulo de ataque del aire).
Respecto a la primera condición, en el ducto de ventilación (aperturas circulares de entrada y salida del aire) (Figura 5), el software considera el valor de la presión ambiental (pa=101325 Pa) como el equivalente de la presión total, pt, para el flujo de aire que ingresa al sistema (Ecuación 2), en cambio, este mismo valor representa la presión estática, pe, para el flujo de aire en la salida del túnel (ecuación 3) (Systems, 2012). Es decir:
Condiciones de entrada: pa = pt (2)
Condiciones de salida: pa = pe y (3)
donde pd, (Pa) es la presión dinámica del sistema.
Para los experimentos se establecieron dos valores de ( a 500 y 1000 revˑmin-1, es decir, 52.35 y 104.72 radˑs-1, y el eje de giro de cada extractor se ubicó en el eje “z” con rotación en sentido horario (Figura 5).
Análisis de independencia de malla
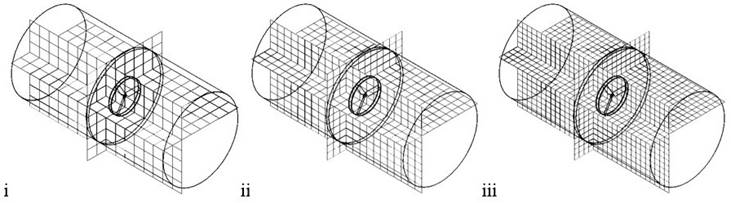
Al ejecutar las simulaciones por CFD, la precisión de los resultados incrementa al diseñar un mallado considerablemente denso, sin embargo, también aumenta la duración del cálculo. Por tal motivo, antes de presentar los resultados de la simulación, se efectuó un análisis de independencia de malla de acuerdo con tres tamaños de rejilla y la frecuencia de rotación del extractor de aire para verificar el refinamiento del sistema, donde el número de celdas osciló entre 1313 y 8303 elementos (Figura 6).
Las tres configuraciones de malla analizadas mostraron un efecto diferente en los perfiles de velocidad del aire, donde los valores promedio fueron de (144.82, 2.33 y 2.39) m·s-1, presentando una variación porcentual de (98.39 y 2.58%). Además, los valores de presión fueron de (1369659.76, 101322.43 y 101321.57) Pa, con una variación de (92.60 y 0.001%).
De acuerdo con lo anterior, para el presente estudio se implementó el mallado ii con 3562 elementos por mantener un equilibrio entre precisión y duración de la simulación por CFD. Este último aspecto se consideró para resolver oportunamente las 48 variantes.
Funcionamiento del sistema de ventilación en la simulación por CFD
El movimiento de aire en el sistema se genera debido a la cantidad de pt que ingresa al ducto, así como por la geometría de los extractores y la frecuencia de rotación aplicada al eje del motor por cada variante (condiciones de frontera). El aire ingresa al ducto por una apertura circular de Ø 3 m y recorre una distancia de 6 m hacia el extremo opuesto debido al movimiento de aspas generado por el extractor, ubicado a 3 m de la entrada del sistema.
Del análisis de las simulaciones por CFD se obtuvieron los datos de velocidad del aire, v, y la presión, pt, al interior del túnel con los que se estimó el caudal, Q, y potencia, P, del sistema de extracción. Para correlacionar los valores de v y pt con el ángulo de ataque de aire del extractor, α, se efectuó el ajuste de las curvas v y pt respecto a α, posteriormente se generó una ecuación polinómica de segundo orden por cada variante de estudio.
El análisis estadístico y ajuste de datos se efectuó con la herramienta Curve Fitting Tool incluida en el software Matlab v. 8.0. Para comprobar la bondad de ajuste de las curvas pt - v respecto a α se ubicó el mayor valor del coeficiente de determinación, R2, así como los menores valores de RMSE y SSE. Con esta información se obtuvieron los coeficientes de la regresión efectuada. El intervalo de confianza de la modelación matemática fue de 95%.
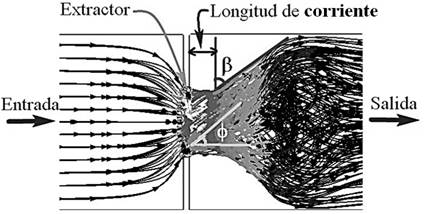
Posteriormente se analizó la corriente interna de aire generada por el extractor a través del túnel de viento mediante dos curvas con los ángulos: β y ϕ (Figura 7), donde β es el ángulo que describe la forma de la corriente, el cual fue medido en intervalos de 0.5 m desde la salida del extractor hasta el extremo del ducto, con los valores acumulados se construyó la curva β respecto a la distancia de salida del ducto, y con los valores de ϕ, que es el ángulo interno de la columna de aire para la misma sección, se construyó la curva ϕ respecto a la distancia de salida del ducto.
Discusión y análisis de resultados
Se efectuaron 48 simulaciones por CFD de flujo turbulento del aire en un sistema de ventilación con un mallado promedio del modelo de 3550 celdas, con los resultados se obtuvieron 48 imágenes en 2D y 48 en 3D del flujo de aire por cada variante, con estas imágenes se estimaron los valores del ángulo de apertura del aire a la salida del extractor, β, y del ángulo de flujo al interior del ducto. Además, se generaron 8 curvas de v y pt respecto a α conformadas por un conjunto de 6 datos.
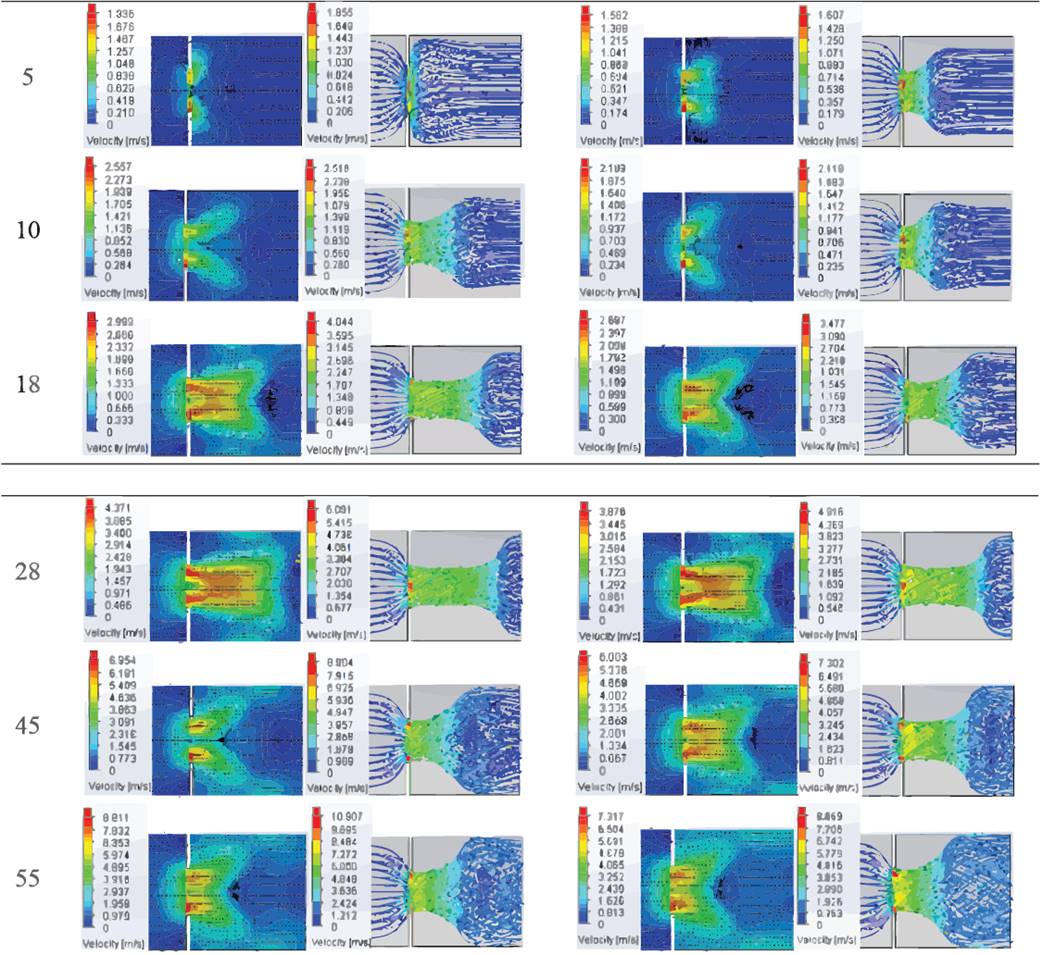
A continuación, se muestran 8 simulaciones representativas de las 48 efectuadas, donde se presentan los valores y dirección de la corriente de aire en la entrada y salida del ducto, los ángulos del cono formado por la misma corriente, además de los perfiles de velocidad y su longitud para un análisis de flujo (Tabla 1). Para identificar las variantes de estudio, a cada simulación se asignó un nombre de acuerdo con n, a, ω y α, por ejemplo, 3145005 significa n=3, a=0.14 m, ω=500 revˑmin-1 y α=5°.
Tabla 1 Contornos de velocidad (2D) y líneas de corriente (3D) del sistema de ventilación respecto a: n, a, ( y α de los extractores de aire
Las figuras en la parte izquierda representan los contornos de velocidad y distribución de los perfiles simulados, y en las figuras de la derecha se presentan los resultados de las líneas de corriente del aire, así como el cambio de longitud y ángulo del cono formado por la corriente.
Aunque los resultados mostrados en la Tabla 1 representan el mismo caso de estudio por cada variante, la escala de valores fue diferente debido a que en las imágenes de los contornos de velocidad se presentan la magnitud y vectores de v para el corte longitudinal del ducto, mientras que en las imágenes de las líneas de corriente del aire los valores de este parámetro se relacionan con el volumen total del solido de interés.
La velocidad del aire en los contornos de velocidad del túnel fue menor que en las imágenes de las líneas de corriente, donde se presentaron mayores valores de v en la periferia. En general, los valores de v en la periferia de la corriente oscilaron entre 12 y 15 mˑs-1. La velocidad máxima fue de 22.16 mˑs-1 para el caso 314100055, en los contornos de velocidad puede apreciarse que este parámetro se obtuvo al interior de la corriente, en el periférico de las aspas del extractor, y disminuyó conforme se aproximaba a la salida del ducto.
Además, los perfiles de velocidad desde la entrada del túnel y hasta pasar por el extractor en general fueron homogéneos, es decir, hasta este punto no influyó la forma geométrica de dicho componente.
En general, la distribución del aire fue similar para las combinaciones entre n y ( conforme incrementaron los valores de α, por lo que únicamente se muestra en la Tabla 2 un caso representativo de las simulaciones para la variante n=3 y ω=500 revˑmin-1. Además, se pudo comprobar que la velocidad promedio de salida del aire, v, incrementó a mayores valores de α, por ejemplo, para α(5°) y α(55°), los valores de v comprendieron entre (1.50 y 11) mˑs-1.
Los valores de β fluctuaron entre 16.49 y 76.03°, donde el menor valor se obtuvo para α(28°) ubicado a 2.5 m de la salida del extractor, y el mayor valor para α(5°) se obtuvo a 0.2 m del mismo punto de referencia. Puede apreciarse que cuanto mayor fue el ancho de aspas y menor el valor de α, el valor del ángulo β fue mayor, esto independientemente de n y ω del mecanismo de ventilación. Mientras los valores de β se mantuvieron constantes en la salida del ducto hasta obtener sus valores máximos, la longitud del perfil de salida de la velocidad del aire en esta sección osciló entre 1 m para α(5, 10°) y hasta 2.5 m en las variantes con α(28°).
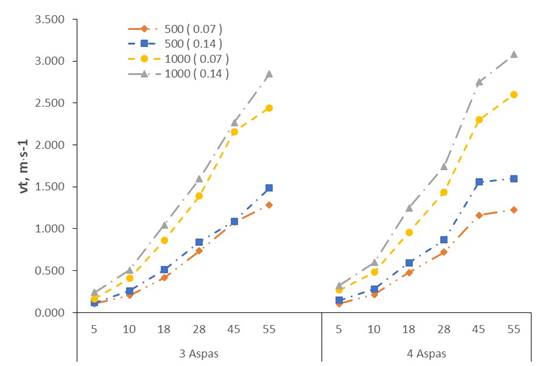
De las simulaciones por CFD y el análisis de los datos obtenidos, se generaron las curvas de cambio de velocidad promedio de la superficie de salida v respecto a α para los valores establecidos de n, ω y a (Figura 8), con estos datos se puede calcular el flujo total del aire al interior del túnel. Los máximos y mínimos de velocidad fueron 3.08 y 0.11 mˑs-1, ubicados en las variantes 4141000 y 37500 para α(5) y α(55).
Al comparar los resultados de la velocidad promedio del aire respecto al diferente número de aspas del extractor, para las mismas condiciones de a y ω, se obtuvo un incremento máximo de v de 64.63% en la curva 471000 respecto de la variante 371000.
En cambio, al contrastar los valores de v respecto a los valores de ω, para las mismas condiciones de n y a, es decir, 37500-371000, 314500-3141000, 47500-471000 y 414500-4141000, el incremento máximo en la velocidad del aire fue de 149.77% para el tercer caso, en la curva 471000, respecto de la variante 47500, presentando un valor promedio de 114.06% para todos los valores de α. En general, en este conjunto de 8 comparaciones el incremento de v respecto a ω fue superior a 100%. Es decir, al incrementar al doble la frecuencia de rotación del motor para el mismo tipo de extractor, se duplicó la velocidad del aire producida por el mecanismo de ventilación.
Para correlacionar v y el ángulo de aspas bajo las condiciones de ventilación, se aplicó una regresión polinómica de segundo orden mediante la ecuación 5:
donde A, B y C (adimensional) son constantes. Analizando la Tabla 3 se obtuvo que los valores promedio de R2 = 99.40% indican la bondad de ajuste de la relación empírica de la variación de v respecto a α.
Tabla 3: Estadísticos y coeficientes de modelación de v en el sistema de ventilación respecto a α, considerando el mayor valor de R2. Intervalo de confianza = 95%
| Variante | SSE | R2 | RMSE | A | B | C |
|---|---|---|---|---|---|---|
| v371000 | 0.0042 | 0.9990 | 0.0373 | -0.0003 | 0.0644 | -0.1810 |
| v471000 | 0.0085 | 0.9981 | 0.0534 | -0.0002 | 0.0603 | -0.0622 |
| v4141000 | 0.0163 | 0.9974 | 0.0737 | -0.0004 | 0.0774 | -0.0857 |
| v37500 | 0.0034 | 0.9970 | 0.0339 | -0.0001 | 0.0301 | -0.0646 |
| v3141000 | 0.0183 | 0.9964 | 0.0781 | -0.0002 | 0.0634 | -0.0689 |
| v47500 | 0.0068 | 0.9939 | 0.0477 | -0.0002 | 0.0356 | -0.0939 |
| v414500 | 0.0290 | 0.9851 | 0.0983 | -0.0002 | 0.0421 | -0.0977 |
| v314500 | 0.0207 | 0.9847 | 0.0831 | -0.0001 | 0.0304 | -0.0224 |
Asimismo, la variante 371000 presentó la mejor bondad de ajuste a los datos con SSE = 0.0042, R2 = 0.9990 y RMSE = 0.0373; seguida por las variantes 471000 y 4141000 con SSE (0.0085 y 0.0163), R2 (0.9981 y 0.9974) y RMSE (0.0534 y 0.0737). En cambio, la variante 314500 fue la que presentó el menor ajuste con SSE = 0.207, R2 = 0.9847 y RMSE = 0.0831. Con la tabla anterior, se puede determinar la velocidad del aire para diferentes valores de α comprendidos entre 5-55°.
Estos resultados se compararon con el funcionamiento de un extractor de aire Multifan 130 instalado en un invernadero experimental de la UACh, para las mismas condiciones de n y ω (3 y 500 rev·min-1). En este caso, las velocidades del aire fueron de (1.08 y 1.39) m·s-1, obtenidas en los diseños de extractor con α = (45 y 55°), mientras que en la ficha técnica del extractor se indica un valor de 1.29 m·s-1, presentando una variación porcentual del (16.28 y 7.75%). Con base en la información anterior se ratificó la fiabilidad de los resultados.
Además, de acuerdo con los valores de v y aplicando la ecuación 6, en este artículo se trabajó en un rango de número de Reynolds de (0.22 y 6.28) E05. Este parámetro confirma el régimen turbulento mediante el cual fue resuelto el problema.
donde
Re (adimensional) = número de Reynolds
D (m) = diámetro del túnel de viento y
µ (Pa·s) = viscosidad dinámica del aire
Posteriormente se generaron las curvas de cambio de la presión total del aire, pt, respecto a α a lo largo del tubo de salida para estimar la distribución de la presión (Figura 9). Donde los valores máximos y mínimos fueron de (101.329 y 101.324) kPa, ubicados en las variantes 4141000 y 3141000 para α(5) y α(55).
A continuación, se estimaron los valores de potencia del extractor de aire de acuerdo con la frecuencia de rotación y torque del sistema, ecuación 7.
donde
P (W) = potencia y
ω (Nˑm) = torque
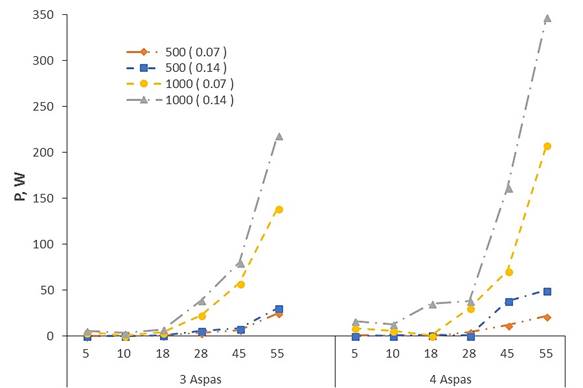
El valor máximo de potencia fue de 347.49 W y se obtuvo en la variante 4141000. Por el contrario, los valores mínimos se ubicaron en la variante 37500 y fueron menores a 0.36 W (Figura 10). Esto indica que a mayores valores de α y ω, también incrementa la potencia del motor.
El comportamiento de la corriente de aire generada por el extractor al interior del túnel se analizó con los ángulos β y ϕ, medidos en las imágenes 3D desde la salida del extractor hasta el extremo de ducto, ubicado a 3 m. Para su mejor interpretación, los datos se agruparon en un conjunto de 8 gráficos de β y ϕ respecto a la longitud del túnel hacia la salida del sistema, y acorde con los valores de n, ω y a (Figuras 11 y 12).
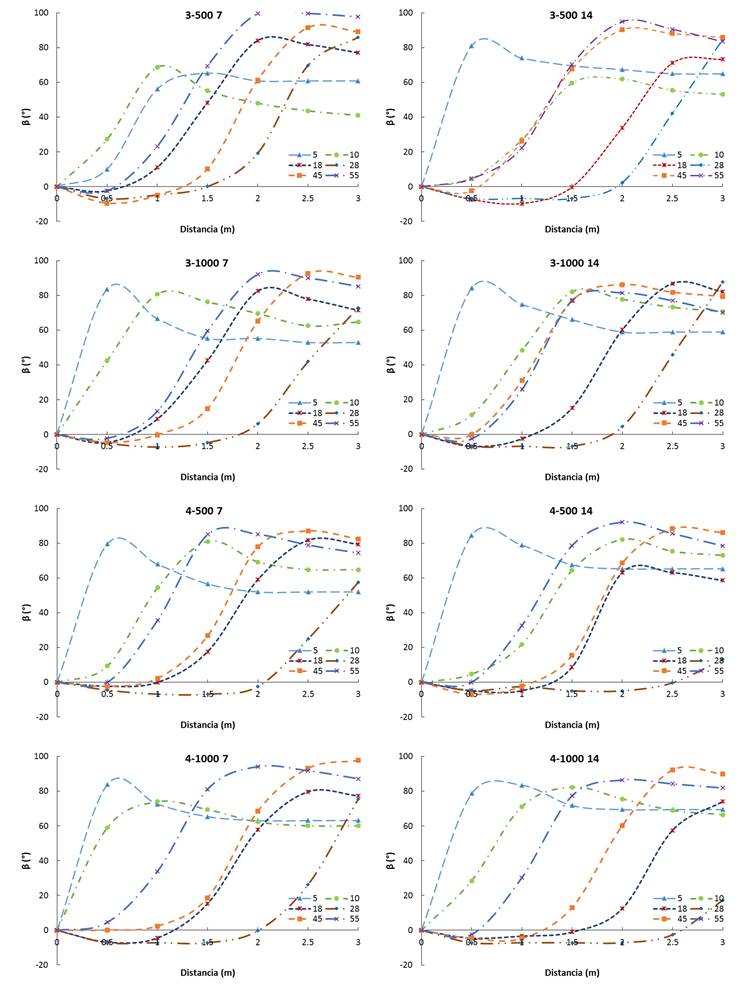
Figura 11 Curvas del ángulo de apertura del aire a la salida del extractor (β) respecto a la longitud del túnel hacia la salida del sistema para diferentes valores de n, ω y a
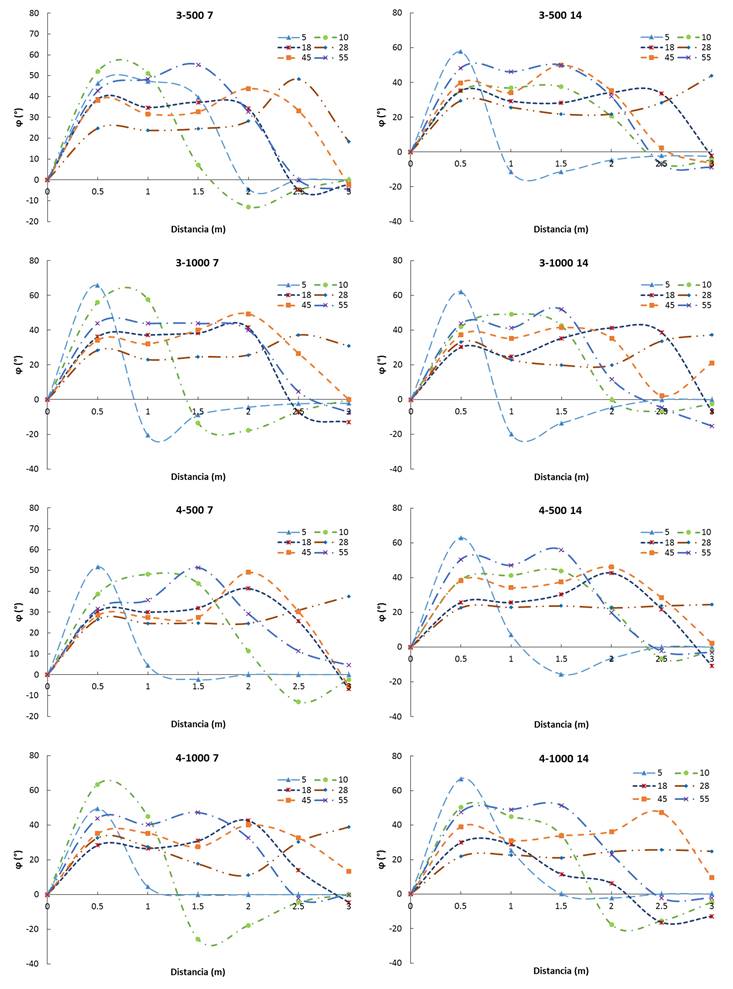
Figura 12 Curvas del ángulo de flujo al interior del ducto (ϕ) respecto a la longitud del ducto para diferentes valores de n, ω y a
Los valores de β oscilaron entre -9.72° para la variante 31450018, y 99.63° para 3750055 (Figura 11), donde se presentó la apertura máxima del cono formado por la corriente de aire.
A excepción de las curvas con α(5, 10), en la mayoría de las simulaciones la apertura del cono se generó entre 1.5 y 2 m, esto significa que hasta esta distancia la corriente del aire mantuvo una forma compacta debido a la geometría del sistema de extracción.
Los valores de ϕ oscilaron entre -25.64° para la variante 47100010, y 66.80° para 41410005 (Figura 12). En general, los valores de ϕ fluctuaron entre 20 y 60° a lo largo del túnel de viento. En la mayoría de los casos la pérdida de energía por rotación del aire en el sistema, ϕ ≤ 0, se dio entre 1.5 y 2.5 m, es decir, ocurrió un efecto de disipación de energía entre el aire y la superficie de contacto con el ducto, además, en las curvas α(5, 10) el valor del ángulo ϕ disminuyó a una menor distancia (0.5 y 1m).
La relación entre los valores del ángulo ϕ fue inversamente proporcional a los resultados del ángulo β, por tanto, a menores valores de ϕ se obtuvieron mayores valores de β, es decir, cuando en la corriente de aire no hubo pérdidas de energía por contacto con la superficie del ducto, los valores de ϕ incrementaron hasta el tiempo en que β alcanzó su valor máximo.
Conclusiones
Se analizó un conjunto de extractores con diferente número de aspas y ángulo de ataque del aire, con los que se efectuó un conjunto de simulaciones por dinámica de fluidos computacional bajo diferentes condiciones de frontera, para analizar el flujo de aire en el sistema extractor de un invernadero.
Se simuló por dinámica de fluidos computacional el comportamiento de la corriente de aire al interior del ducto generada por los extractores, diseñados en función del ancho, número de aspas, frecuencia de rotación y ángulo de ataque del extractor.
Se definieron las ecuaciones de las curvas que describieran el movimiento del aire.
Se presentaron los perfiles de salida de aire de los extractores estimados con los ángulos de apertura del aire en la salida del extractor y el ángulo de flujo al interior del ducto acorde con los perfiles de los contornos de velocidad y las líneas de corriente del aire generadas.
Al obtener los valores de velocidad y flujo en los extractores de aire, se podrá estimar la cantidad de renovaciones del volumen de aire dentro de los invernaderos, lo cual permitirá controlar el gradiente térmico, humedad y presión del aire en este tipo de estructuras.
Con la información obtenida se podrá establecer la relación de parámetros geométricos de los extractores (número y ancho de aspas, ángulo de ataque y velocidad de rotación), acorde a los requerimientos de velocidad o caudal del aire en la aplicación a instalar.
Lo anterior demuestra el potencial que tienen los modelos computacionales para diseñar o mejorar los sistemas de ventilación bajo invernadero conforme a las condiciones requeridas.











 nueva página del texto (beta)
nueva página del texto (beta)