Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista electrónica de investigación educativa
versión On-line ISSN 1607-4041
REDIE vol.13 no.2 Ensenada ene. 2011
Artículos arbitrados
Calibración de una prueba de química por el modelo de Rasch
Calibration of a Chemistry Test Using the Rasch Model
Nancy Martín Guaregua1, Consuelo Díaz Torres2, Gilberto Córdoba Herrera1, Michel Picquart3
1 Universidad Autónoma Metropolitana-Iztapalapa Departamento de Química mgnc@xanum.uam.mx gil@xanum.uam.mx
2 Departamento de Matemáticas ditc@xanum.uam.mx
3 Departamento de Física Av. San Rafael Atlixco 186. C.P. 09340 D. F., México mp@xanum.uam.mx
Recibido: 9 de diciembre de 2010;
aceptado para su publicación: 29 de julio de 2011
Resumen
Se aplicó el modelo de Rasch para calibrar una prueba de química general con el fin de analizar las ventajas y la información que proporciona el modelo. La muestra fue de 219 alumnos del primer año universitario. Se logró un buen ajuste del modelo en 10 reactivos de un total de 12. Además se evidenció que la prueba cuenta con reactivos de diferentes índices de dificultad, con intervalos vacíos en la escala para los que se tendrán que diseñar nuevos reactivos para que la prueba sea completa.
Palabras clave: Teoría de Respuesta al Reactivo (TRR), modelo de Rasch, Curva Característica del Reactivo (CCR), química.
Abstract
The Rasch model was used to calibrate a general chemistry test for the purpose of analyzing the advantages and information the model provides. The sample was composed of 219 college freshmen. Of the 12 questions used, good fit was achieved in 10. The evaluation shows that although there are items of variable difficulty, there are gaps on the scale; in order to make the test complete, it will be necessary to design new items to fill in these gaps.
Key words: Item Response Theory (IRT); Rasch model; Characteristic Graphical of Item (CGI), chemistry.
I. Introducción
Un instrumento de medición de buena calidad debe tener validez, confiabilidad y objetividad. Tiene validez si mide lo que se pretende medir, es confiable si es independiente del tiempo y es objetivo si es independiente de evaluadores y evaluados. Por lo tanto, la validez, la confiabilidad y la objetividad de una prueba son aspectos importantes a considerar cuando se lleva a cabo su elaboración. En educación se considera al instrumento de medición como el medio a través del cual se recaba información y se registran los datos que permiten una valoración sobre la habilidad o el conocimiento de los alumnos.
Entre las diferentes pruebas de evaluación que existen están: oral, escrito y práctico-procedimental. Todos ellos pueden ser complementarios. La evaluación escrita es la más comúnmente usada como prueba de conocimiento y dentro de esta clasificación, se pueden mencionar, a las pruebas abiertas, las de opción múltiple, estudios de casos, etc.
Las pruebas de opción múltiple están compuestas por reactivos o ítems cerrados con varias opciones de respuesta de las que una sola es correcta y las otras son distractores. Éstas presentan ciertas ventajas sobre las pruebas abiertas en que permiten rapidez al calificar y pueden ser aplicadas a grupos grandes de alumnos. Entre las desventajas están, que pueden ser respondidas al azar y la dificultad para diseñar reactivos de buena calidad.
De allí, la importancia que tiene la calibración de la pruebas de evaluación que se aplica a fin de asegurar su calidad, de forma que se pueda evaluar con eficiencia el conocimiento.
En la Universidad Autónoma Metropolitana-Iztapalapa (UAMI) no se tiene establecido ningún tipo de norma para el diseño de los exámenes. Tampoco se aplica ningún tipo de valoración o análisis que permita comprobar la validez y la confiabilidad de la evaluación que hacemos a los alumnos.
El propósito del presente estudio es analizar y calibrar los reactivos de una prueba de opción múltiple usada como examen diagnóstico de química general en los alumnos del primer año universitario de la División de Ciencias Básicas e Ingeniería (DCBI) de la UAMI. Después de la revisión de los diferentes métodos que existen para el análisis de instrumentos se decidió aplicar el modelo de Rasch con el fin de analizar el modelo y su ajuste a los reactivos de esta prueba.
II. Antecedentes
Entre los modelos estadísticos más antiguos para análisis de instrumentos está el de la Teoría Clásica de la Medida (TCM) desarrollado por Spearman (Spearman, 1904, Stevens, 1946, Muñiz, 1997), el cual es un modelo de regresión lineal que ha sido aplicado a pruebas sicométricas. (Embretson y Reise, 1986).
La principal limitación de la TCM consiste en que las características de la prueba y las puntuaciones de los evaluados no pueden ser separadas, ya que las características de los reactivos dependen del grupo de personas al que se han aplicado y la puntuación de una persona depende del conjunto particular de reactivos utilizados.
Estas limitaciones han llevado a la propuesta de modelos alternativos. Uno de ellos, surgido en los años 60 para complementar el primero es el atribuido a Cronbach (1971) y llamado de la generalizabilidad, el cual gracias al uso específico del análisis de variancia hace posible analizar las distintas fuentes de error que se presentan en los puntajes mediante el concepto de faceta, término introducido por Cronbach para designar cada una de las características de la medición y puede modificarse de una ocasión a otra; por tanto, hace variar los resultados obtenidos (por ejemplo, los reactivos de una prueba, las formas de codificar las respuestas, los tipos de examen, etc.).
Un método adicional para la validación de un instrumento de opción múltiple es el de Sympson y Haladyna (1988) quienes desarrollaron un método de ponderación múltiple de las respuestas a los reactivos de una prueba (Backhoff, 2000).
Un enfoque más reciente es el de la Teoría de la Respuesta al Reactivo (TRR) (Hambleton y Swaminathan, 1985, Embretson y Reise, 2000) que se centra más en las propiedades de los reactivos individuales que en las propiedades globales de la prueba. Se trata de llegar a la elaboración de instrumentos de medición cuyas características no sean demasiado influenciadas por un grupo de referencia dado. Se basa en el postulado de que la respuesta de un individuo al reactivo, en particular su probabilidad de dar una respuesta correcta, está determinada por dos tipos de factores: por una parte, algunos atributos del sujeto, su competencia por ejemplo, que no son directamente accesibles a la observación y a la medición y que son generalmente calificados de rasgos latentes y por otra, las propiedades del reactivo, en particular su dificultad, su poder de discriminación o el azar en algunos casos. Por lo tanto, se considera la respuesta al reactivo como una función de las características del individuo y las del reactivo.
La propiedad de invarianza es la característica principal de la TRR. Nos dice que las estimaciones relativas a los reactivos (parámetro de dificultad, de discriminación y de azar) son independientes de la muestra particular de individuos y que las estimaciones relativas a los individuos (nivel de competencia, de habilidad) son independientes de la muestra de reactivos utilizada. Por esto se tiene que asegurar que el ajuste de los datos al modelo sea satisfactorio. Así, la relación matemática se puede representar como la probabilidad de contestar satisfactoriamente el reactivo i en función del nivel de habilidad (θs) para un sujeto s. El índice de discriminación del reactivo se define como una medida para determinar si las competencias o habilidades que mide la prueba también las mide el reactivo. Un buen reactivo debe discriminar entre aquéllos que obtuvieron altas calificaciones en la prueba y aquéllos que obtuvieron bajas calificaciones.
La relación anterior se expresa por una función matemática logística (función característica del reactivo) representada por una gráfica de forma de sigmoides (Rojas y col. 2004). En la figura 1 se representa un ejemplo de este tipo de gráfica llamada Curva Característica del Reactivo (CCR) que muestra la función de probabilidad (Pis) en función de la habilidad (θs). Las tres curvas presentan diferentes pendientes que corresponden a diferentes índices de discriminación. Las curvas deseables son las que presentan una forma de "S", como las 2 y 3, lo que implica que el paso de acertar o fallar debe ser gradual. En tanto que, la curva 1, de forma lineal, es la menos discriminatoria y menos deseable. Estas curvas pueden variar según el ajuste del modelo.

El Modelo de Rasch
El modelo matemático más sencillo en el marco de la TRR, es el propuesto por Georg Rasch (1960), conocido como modelo de un parámetro. Es un modelo matemático sencillo que permite analizar la medición conjunta en una misma escala, de las personas y de las puntuaciones obtenidas en una prueba dada.
Las ventajas del modelo de Rasch con respecto a otros modelos de la TRR es que es muy simple de aplicar. Otra característica, es que permite analizar las interacciones entre los alumnos y los reactivos. Además, las medidas que se obtienen no dependen de las condiciones específicas de cómo son obtenidas. Otra propiedad, es la unidimensionalidad del instrumento, es decir, que todos los reactivos que lo componen contribuyan a evaluar una sola característica o competencia. Finalmente, la independencia local postula que la respuesta a un reactivo no está influenciada por las respuestas a los otros reactivos del instrumento.
El modelo propuesto por Rasch proporciona una solución para calibrar pruebas de evaluación y se basa en las siguientes suposiciones: a) el instrumento a medir se representa en una dimensión, en la que se ubican de manera conjunta a los alumnos y a los reactivos de la prueba; b) el nivel del alumno en el instrumento y la dificultad del reactivo determinan la probabilidad de que la respuesta sea correcta.
Haciendo un ajuste adecuado de los datos es posible obtener pruebas más eficientes. La relación matemática se puede representar como la probabilidad de que un reactivo i tenga una respuesta satisfactoria, para un nivel de habilidad θs del sujeto s, según:

La ecuación (1) se puede representar como el cociente entre la probabilidad de una respuesta correcta a un reactivo Pis y la probabilidad de una respuesta incorrecta (1-Pis) y la diferencia entre el nivel de habilidad de una persona (θs) y el nivel de dificultad de un reactivo (βi):

Entonces, cuando una persona responde a un reactivo equivalente a su umbral de competencia (o habilidad), tendrá la misma probabilidad de una respuesta correcta y de una respuesta incorrecta. Esto es, [Pis/(1-Pis)] = 0.50/0.50 = 1.0. En este caso, se tiene que la dificultad del reactivo es equivalente al nivel de la habilidad de la persona (θs-βi) = 0. Si la habilidad de la persona es mayor que la requerida por el reactivo la probabilidad de una respuesta correcta será mayor que la de una respuesta incorrecta [(θs-βi)>0]. Por el contrario, si la habilidad de la persona es menor que la requerida por el reactivo la probabilidad de respuesta correcta será menor que la de una respuesta incorrecta [(θs-βi)<0)]. Este modelo ha sido aplicado acertadamente en muchas áreas como, psicología, educación, medicina y socio-economía (Golia, 2011). Un buen ajuste de las medidas obtenidas depende de las suposiciones planteadas y la calidad de la prueba.
Existen distintas escalas métricas de los valores de las personas y los reactivos. La más utilizada es la escala lógitos, que es el Ln[Pis/(1-Pis)], es decir (θs-βi). La localización del punto cero de la escala es arbitraria, pero por tradición el punto cero indica la habilidad media de los sujetos (Embretson y Reise, 2000). El intervalo de probabilidad, en la gran mayoría de los casos, se ubica entre -5 y 5.
Por tanto, el interés es estimar a los parámetros, (θs) habilidad de las personas, (βi) índice de dificultad e índice de discriminación de los reactivos. Como el ajuste es a un solo parámetro, el índice de discriminación toma un valor de uno y el índice de dificultad (βi) es el que se estima en el modelo para explicar las características de cada reactivo. La interpretación de la prueba se fundamenta en la probabilidad, alta o baja, que tiene un alumno de contestar correctamente un reactivo. Los procedimientos de cálculo de éstos son largos por lo que es necesario usar programas de computadora como, Winsteps, Bigsteps o Rascal, entre otros. Los procedimientos de análisis permiten detectar a los reactivos y a los alumnos que no se ajustan al modelo.
Por tanto, además de estimar los parámetros antes mencionados es necesario determinar el grado en que los datos obtenidos se ajustan al modelo. Existen dos medidas de bondad de ajuste en el modelo de Rasch: el INFIT que se interpreta como ajuste interno, es un valor sensible al comportamiento inesperado que afecta a los reactivos cuya dificultad está cerca del nivel de habilidad de una persona y el OUTFIT que se interpreta como ajuste externo, es un valor sensible al comportamiento inesperado que afecta a los reactivos cuya dificultad está lejos del nivel de habilidad de una persona. Estos estadísticos se reportan como medias cuadráticas de residuales (MNSQ) y como residuales estandarizados (ZSTD). En la práctica el criterio que se aplica es que los valores de la media cuadrática deben estar entre 0.8 y 1.3 y los valores estandarizados deben estar entre -2 y 2, lo cual indica un ajuste razonable (González, 2008). Los valores INFIT o OUTFIT fuera de este intervalo indican una falta de ajuste al modelo, valores de la media cuadrática menores a 0.8 o valores estandarizados menores a –2 indican datos con demasiado determinismo o poco estocásticos, mientras que valores de la media cuadrática mayores a 1.3 o valores estandarizados mayores a 2 indican alta posibilidad de azar (Tristán, 1998).
Otro estadístico útil en la calibración de los reactivos es el coeficiente de correlación punto-media que mide el grado de asociación entre el puntaje particular observado para el reactivo individual y el puntaje total observado en la prueba. Valores altos de esta correlación indican que el reactivo "trabaja en la misma dirección que el conjunto de reactivos" al que pertenece la prueba (González, 2008).
III. Metodología
Con el fin de realizar un diagnóstico de ideas básicas en química general se diseñó un examen diagnóstico (Anexo 1) con algunas preguntas tomadas del Journal of Chemical Education (JCE) y otras tomadas de libros de texto correspondientes a los temas de los primeros cursos de química de la UAMI. Los temas que se incluyeron fueron: concepto de mol, relaciones molares, nomenclatura de sales, teoría cinética de los gases, conservación de la masa y transformación de fases.
La prueba fue de opción múltiple con 12 reactivos y 5 opciones de respuestas cada una. Sólo se tenía una respuesta correcta y cuatro distractores. Se dio un tiempo de 40 minutos para la resolución de la prueba, el cual se consideró suficiente dado que el 95% de los participantes terminó en ese tiempo.
Participó una muestra de 219 alumnos del primer año universitario de la DCBI de la UAMI. La aplicación de la prueba tuvo lugar durante primavera de 2009. Los resultados fueron recopilados en una base de datos.
IV. Resultados y Discusión
En primer lugar, se calcularon estadísticos descriptivos con los datos obtenidos de la aplicación de la prueba de evaluación (Anexo 1) con el fin de conocer los resultados del grupo (N=219). Se considera este tamaño de muestra (N>100) apropiado para su análisis estadístico
La prueba fue de 12 reactivos, los cuales fueron clasificados en aciertos y desaciertos, a través de un conjunto de "distractores" o respuestas incorrectas. La prueba no fue planificada con pesos relativos a los aciertos en los diferentes reactivos. Al respecto, se ha reportado (Golia, 2011) que la precisión del modelo de Rasch va en relación lineal con el tamaño de la prueba. Esto es, al aumentar el número de reactivos, se logra un mejor ajuste. Sin embargo, el autor demostró con una prueba con 10 reactivos que el modelo produce medidas de ajuste precisas y estables.
En la Figura 2 se presenta la distribución de frecuencia porcentual de aciertos de los alumnos del grupo en cada reactivo. El grupo obtuvo un promedio de aciertos de 45% con una desviación estándar de 19.7%. Cabe mencionar que hubo un menor número de aciertos que en grupos previamente evaluados (50%) (Martín et al., 2009).
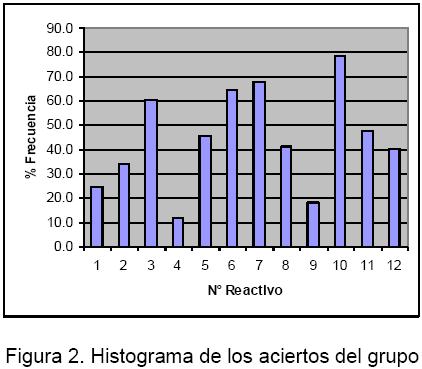
Como se expuso anteriormente lo que se busca es la objetividad de la prueba, en consecuencia, se procedió a analizar el ajuste de estos datos con el modelo de Rasch mediante el programa Winsteps versión 3.69.1.4.
Se estimaron los índices de dificultad (βi) de los 12 reactivos del examen diagnóstico (Anexo), así como los valores INFIT y OUTFIT y la correlación punto-media. En la Tabla I se muestran los resultados obtenidos al ajustar el modelo a los datos, los reactivos están ordenados, de acuerdo al índice de dificultad (βi), de mayor a menor valor.
Se observa que 10 de los 12 reactivos de la prueba presentan valores INFIT dentro de los intervalos descritos anteriormente, de 0.8 a 1.3 para la media cuadrática y de -2 y 2 para los valores estandarizados. Sin embargo, el reactivo 12 presenta un valor estandarizado INFIT mayor a 2, lo que indica una falta de ajuste debido a respuestas al azar ó a una falta de precisión en el enunciado, mientras que el reactivo 9 presenta un valor OUTFIT mayor a 1.3 para la media cuadrática y en el límite para el valor estandarizado. También se puede observar en la Tabla I que estos dos reactivos son los que tienen una correlación punto-media más baja, 0.21 y 0.10 respectivamente, mientras que los demás reactivos muestran correlaciones mayores a 0.30. Es decir, que es conveniente revisarlos ya que no se ajustan adecuadamente al modelo.
Con el fin de analizar, del punto de vista de las respuestas, a los reactivos 9 y 12, en la Figura 3 se muestran las gráficas que corresponden al análisis de distractores (o desaciertos) de estos dos reactivos. Se observa la falta de ajuste de los datos de los dos reactivos al modelo. En ambas curvas (respuesta correcta y distractores) los datos están muy dispersos y se alejan de la curva de ajuste.
Cabe mencionar, que estos reactivos corresponden a los temas de nomenclatura y relación de moles, respectivamente, los cuales se suponen son conocidos por los alumnos. En el reactivo 9 la opción (B) que es incorrecta, es la que responden con mayor frecuencia, esto es, que no tienen conocimientos de las cargas de los elementos químicos. En tanto que el reactivo 12, sobre relación molar, parece que si discrimina pues los alumnos con mayor habilidad eligen la respuesta correcta, sin embargo, no se ajusta al modelo de Rasch. Por tanto, es importante hacer un análisis más profundo de estos dos reactivos tomando en consideración además de los aciertos, a cada uno de los distractores de los reactivos y al enunciado de los mismos.
Se repitió el análisis sin considerar a los reactivos 9 y 12, los cuales como comentamos antes, deben ser revisados. Los resultados se muestran en la tabla II. Se observa que con los 10 reactivos los valores INFIT y OUTFIT están dentro de los límites establecidos, lo que indica un ajuste razonable al modelo, y las correlaciones son mayores a 0.30. Por otro lado, los índices de dificultad de los reactivos toman valores de -1.84 (más fácil) a 2.35 (más difícil) con un promedio de 0 y una desviación estándar de 1.17.
La Figura 4 es una representación gráfica del escalamiento de la dificultad de los reactivos y de los alumnos en una sola escala (-3 a +3 lógitos) y es llamada mapa de alineación de los reactivos y alumnos del grupo evaluado. Del lado izquierdo están representados los alumnos y del lado derecho los reactivos.
La estimación de la habilidad de los alumnos está entre -2.66 lógitos (menor habilidad) a 2.73 lógitos (mayor habilidad), con un promedio de -0.12 y una desviación estándar de 1.21. Se observa que la distribución de la habilidad de los alumnos es aproximadamente normal, que la diferencia entre la media de habilidad de los alumnos y la media de dificultad de los reactivos es pequeña y que hay alumnos con habilidad por debajo de la dificultad de los reactivos y también por arriba. Además, la dificultad de los reactivos no es uniforme, ya que se observan huecos entre los reactivos 10 y 7, 3 y 11, así como entre los reactivos 1 y 4. Esto es, que es necesario ampliar la prueba diseñando más reactivos.
Es evidente que, un examen que sea 100% confiable no es siempre posible de alcanzar, de allí que sea necesario complementar la evaluación de los conocimientos de los alumnos con otros tipos de evaluación y que sean continuamente analizadas. De igual forma, aun cuando se demostró la utilidad del modelo de Rash como una herramienta que permite conocer a la habilidad que tiene el alumno en responder a los reactivos que diseñamos, como una función de su dificultad, también permite visualizar factores que con frecuencia ignoramos como son, la elaboración de un buen enunciado y respuestas y distractores adecuados.
En la UAMI, no se tiene la costumbre de analizar los exámenes que se aplican. Siempre se consideran como buenos. Sin embargo, no siempre se tienen exámenes homogéneos y confiables que sean aplicables a cualquier grupo, con cualquier profesor y en cualquier momento; de allí, que sea necesaria su valoración continua.
V. Conclusiones
El grupo obtuvo un porcentaje promedio de 45% de aciertos con una desviación estándar de 19.7%.
A través del modelo de Rasch fue posible conocer la calidad de los reactivos de nuestra prueba mediante los datos estadísticos que reporta el paquete. Se comprobó que sólo dos de los reactivos (9 y 12), de un total de 12 del instrumento de medición, no se ajustaron al modelo de Rasch, los cuales deben revisarse y analizarlos con mayor profundidad a través de los distractores de cada uno para lograr mejorarlos y reutilizarlos.
Además, el análisis permitió comprobar que los reactivos usados presentaron diferentes grados de dificultad, los cuales estuvieron en función de la habilidad de los alumnos del grupo evaluado. Asimismo, se detectó la ausencia de reactivos en algunos intervalos de la escala de índices de dificultad, por lo que deben agregarse nuevos reactivos a la prueba de evaluación para lograr que éste sea más completo.
Es importante señalar que la aplicación del método de Rasch para evaluar la calidad de los exámenes, además de servir para poder mejorar el instrumento, que a veces se considera muy bueno, permite realizar una evaluación más confiable de los estudiantes. En resumen, el modelo de Rasch es una herramienta valiosa para la calibración de pruebas de evaluación.
Referencias
Backhoff E., Larrazolo N. y Rosas N. (2000). Nivel de dificultad y poder de discriminación del examen de habilidades y conocimientos básicos (EXHCOBA). Revista Electrónica de Investigación Educativa, 2(1). [ Links ]
Backhoff, E., Tirado F. y Larrazolo N. (2001). Ponderación diferencial de reactivos para mejorar la validez de una prueba de ingreso a la universidad. RevistaElectrónica de Investigación Educativa, 3(1). [ Links ]
Budescu, D. V. (1979). Differential weighting of multiple choice items. Princeton: Educational Testing Service. [ Links ]
Cronbach, L. J. (1971). Test validation. En R. L. Thorndike (Ed.), Educational measurement (2a. ed.). Washington: Consejo Americano en Educación. [ Links ]
Embretson S. E. y Reise S. P. (2000). Item response theory for psychologists. Mahwah, NJ: LEA. [ Links ]
Golia, S. (2011). The impact of questionnaire size on the accurace of the Rasch measure. Journalof Applied Science, 11(4), 707-712. [ Links ]
González M., M. J. (2008). El análisis de reactivos en el modelo de Rasch. Manual Técnico A. Serie Medición y Metodología. México: Universidad de Sonora, Instituto Nacional para la Evaluación de la Educación. [ Links ]
Hambleton, R. K. y Swaminathan, H. (1985). Item Response Theory: Principles and applications. Boston, MA: Kluwer-Nijhoff Publishing. [ Links ]
Martin-Guaregua, N., Córdoba-Herrrera, G., Lomas-Romero, L., Rojas H. A. y Picquart, M. (2009). Errores conceptuales de química básica en alumnos delprimer año universitario. Enseñanza de la ciencias, VIII CIDEC, pp. 950-951. http://ensciencias.uab.es/congreso09/numeroextra/art-950-951.pdf [ Links ]
Muñiz, J. (1997). Introducción a la Teoría de Respuestas a los Ítems. Madrid: Pirámide. [ Links ]
Planinic, M., Ivanjek, L. y Susac, A. (2009). The Rasch model based analysis of the Force Concept Iventory. Physical Review Special Topics-Physics Education Research, 6(1), 1-9. [ Links ]
Prieto, G. y Delgado A. R. (2003). Análisis de un test mediante el modelo de Rasch. Psicothema, 15(1), 94-100. [ Links ]
Rasch, G. (1960). Probabilistic models for some intelligence and attainment tests. Copenague: Danish Institute for Educational Research. [ Links ]
Rojas, R. M., Manriquez LL., G., Gatica A., Y. y Salcedo A, L. P. (2004). Curso de UML Multiplataforma Adaptativo basado en la Teoría de Respuesta al Item. Revista Ingeniería Informática, 10. [ Links ]
Spearman, C. E. (1904). The proof and measurement of association between two things, American Journal of Psychology, 15, 75-101. [ Links ]
Stevens, S. S. (1946). On the theory of scales of measurement. Science, 103, 667-680. [ Links ]
Sympson, J. B. y Haladyna, T. M. (1988). An evaluation of "polyweighting" in domain referenced testing. Trabajo presentado en la Reunión Anual de la American Educational Research Association, Nueva Orleans, EE.UU. [ Links ]
Tristán L. A. (2001). Análisis de Rasch para todos: una guía simplificada para evaluadores educativos. México: Centro Nacional de Evaluación. [ Links ]














