Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Economía mexicana. Nueva época
versión impresa ISSN 1665-2045
Econ. mex. Nueva época vol.22 no.1 Ciudad de México ene. 2013
Artículos
Capacidad predictiva de los índices cíclicos compuestos para los puntos de giro de la economía mexicana
Predictive Ability of the Composed Cyclical Indices for the Turning Points of the Mexican Economy
Víctor M. Guerrero*
* Profesor de tiempo completo, Departamento de Estadística, Instituto Tecnológico Autónomo de México (ITAM), México. guerrero@itam.mx.
Fecha de recepción: 26 de mayo de 2011;
Fecha de aceptación: 17 de abril de 2012.
Resumen
Este trabajo presenta un análisis de la capacidad predictiva de algunos índices cíclicos para los puntos de giro de la economía mexicana. El enfoque es de ciclo de crecimiento, el cual requiere eliminar la tendencia de las series; por ello se probaron diversos métodos y se determinó que el filtro de Hodrick-Prescott aplicado dos veces es el mejor, en términos de revisiones. Después, los índices coincidentes y adelantados se estimaron con tres métodos distintos: 1) del NBER, 2) de la OCDE y 3) de Stock-Watson. Los índices coincidentes producen resultados similares y aceptables, pero los adelantados no brindan resultados satisfactorios.
Palabras clave: ciclos de crecimiento, estimación de tendencias, filtro de Hodrick-Prescott, indicador adelantado, indicador coincidente.
Abstract
This work analyzes the predictive ability of some cyclical indices for the turning points of the Mexican economy. The growth cycle approach adopted requires working with detrended series, and so several detrending methods were tried. A double Hodrick-Prescott filter application produced the best results in terms of revisions. Then, the coincident and leading indices were estimated with three different methods: 1) NBER, 2) OECD and 3) Stock-Watson's. The resulting coincident indices produce similar and acceptable results, but the leading ones do not work as expected.
Keywords: growth cycles, trend estimation, Hodrick-Prescott filter, leading index, coincident index.
Clasificación JEL: C43, E30, E32, E37.
Introducción
El estado de la economía es un concepto general que abarca diversos aspectos de las condiciones prevalecientes en un sistema económico. Uno de tales aspectos es la producción de bienes y servicios, representado por la variable producto interno bruto (PIB), que es una de las más relevantes, pero no deja de ser sólo una de las posibles variables que deben tenerse en cuenta al efectuar un análisis de la situación económica de un país. De hecho, la medición del estado de la economía ha conducido a los analistas a construir indicadores compuestos, con los cuales se pretende capturar los movimientos de diversas variables económicas. Esto ha originado los indicadores coincidente y adelantado, cuya finalidad principal es resumir la información más relevante sobre el sistema económico, especialmente en relación con los ciclos y los puntos de giro de la economía. Un indicador coincidente debe ser capaz de mostrar el estado agregado de la economía en el momento presente y con oportunidad, mientras que un indicador adelantado debe anticipar los movimientos, en particular los puntos de giro, del estado de la economía.
Existen diversos métodos para construir los indicadores coincidente y adelantado, y no hay consenso acerca de cuál es el más apropiado. Por ello los analistas de la coyuntura económica eligen un método específico para construir los indicadores, de acuerdo con criterios variados y subjetivos. En el caso de México, el Instituto Nacional de Estadística y Geografía (INEGI) desarrolló el Sistema de Indicadores Compuestos Coincidente y Adelantado (SICCA) que en 2010 usa indicadores construidos con la metodología del National Bureau of Economic Research (NBER) de Estados Unidos. Esta metodología tiene gran aceptación a nivel mundial y se caracteriza por ser de relativamente fácil aplicación, pero no es la única que podría utilizarse. Asimismo, en el INEGI se encuentra en proceso de implementación el procedimiento desarrollado por la Organización para la Cooperación y el Desarrollo Económicos (OCDE).
Conviene comparar los resultados que producen las metodologías citadas, y los de otras, dentro de las que sobresale la de Stock-Watson, que se basa explícitamente en un modelo estadístico de factores comunes cuyo fundamento teórico es sólido y que se ha utilizado con éxito en diversos países. Así pues, el presente estudio pretende ayudar a determinar una metodología que brinde resultados adecuados, particularmente en relación con la anticipación de los puntos de giro de la situación económica mexicana.
Pronosticar un punto de giro equivale a pronosticar la ocurrencia de un evento (una variable categórica) más que la magnitud de una variable cuantitativa, lo cual hace que las herramientas tradicionales de pronóstico, basadas en modelos lineales y en criterios como el del Error Cuadrático Medio Mínimo, no sean apropiadas. Específicamente, lo que se pretende saber es si se puede anticipar la ocurrencia de una recesión en el futuro próximo. La creencia popular tiende a expresar lo que es una recesión en términos del crecimiento del PIB; por ejemplo, en Estados Unidos se considera que si el PIB registró crecimiento negativo durante dos trimestres consecutivos la economía entró en una etapa de recesión. Hay autores que discrepan de esta regla, e.g. Bandholz y Funke (2003), quienes señalan que "podría tener más sentido definir una recesión como el periodo durante el cual el PIB cae de manera significativa por debajo de su tendencia potencial". Sin embargo, no sólo debe contemplarse el PIB para decidir si ha ocurrido o no una recesión, sino que es el retroceso en el estado de la economía lo que indica que tal cosa sucede. De hecho, una recesión se presenta como consecuencia de choques (tanto exógenos como endógenos) al sistema económico, que se reflejan como caídas en el ingreso real, en las ventas, en la producción y en el empleo, lo cual origina un círculo vicioso, sin que sea claro dónde y cuándo inicia dicho círculo. Por ello, un indicador coincidente del estado de la economía debe incluir, entre otras, alguna forma de expresión de estas variables.
Para referirse a la situación o estado de la economía, se debe definir primero un índice que refleje el comportamiento de esa variable. Tal índice se denomina coincidente si refleja las contracciones y expansiones "que se sabe" han ocurrido durante el periodo de estudio. A otro índice que muestre con antelación los movimientos de contracción y expansión de la economía se le llama indicador adelantado. De manera similar se podría hablar de un indicador retrasado, cuyo uso permitiría confirmar los movimientos cíclicos después de que ya ocurrieron, pero en este trabajo únicamente se consideran los índices coincidente y adelantado. Dentro de las referencias sobre el tema de la construcción de este tipo de índices económicos para México se encuentran los trabajos de Pérez (2001), Ruiz (2006) y Fernández (2008).
Los índices coincidente y adelantado parten de la idea de que "se sabe", es decir, que la sabiduría popular reconoce de alguna manera cuándo se encuentra la economía en cada una de las distintas fases que forman un ciclo económico, o sea, cuándo se encuentra la actividad económica en expansión, en desaceleración, en recesión o en recuperación, y se pretende que los índices reflejen dicha sabiduría popular. En el presente caso se hace mención de los índices cíclicos, con los cuales se ubica el estado de la economía dentro de alguna de las fases del ciclo. Usar un índice compuesto (que incorpora diversas variables) es preferible a utilizar en forma aislada cada una de las variables que lo componen para anticipar las fases de los ciclos, y, por ende, los puntos de giro de la economía. La razón es que cada ciclo tiene sus características propias, aunque se parezca a otros ciclos previamente observados, pero no es razonable pensar en una causa única de la actividad cíclica, y tampoco es razonable atribuir a una sola variable la capacidad anticipatoria de los puntos de giro. Es necesario incorporar diversas variables que pueden ser útiles como predictoras individuales, en partes específicas del ciclo, y tratar de combinar su potencial predictivo en un solo índice. Además, los índices coincidentes y adelantados deben construirse de acuerdo a la estructura económica que se desea estudiar, ya que los índices basados en variables que funcionan bien para la economía de un país no necesariamente tienen que funcionar bien al utilizar las mismas variables con datos de otro país (véanse al respecto las recomendaciones del documento OECD, 1997). Sin embargo, las metodologías para la construcción de los índices sí son aplicables en forma general.
De las metodologías que se usan en la actualidad sobresale la del Conference Board (CB) de Estados Unidos (organización privada fundada en 1916, que es una asociación internacional de investigación sin fines lucrativos y de interés público). En 1995 el U. S. Department of Commerce asignó al CB la responsabilidad de ser la fuente oficial de los índices compuestos y de dar mantenimiento a los Business Cycle Indicators. La metodología que usa el CB es la del NBER para el ciclo clásico, y así genera los indicadores: adelantado (conformado por 10 variables), coincidente (con cuatro variables) y retrasado (con siete variables). Para más información sobre el CB y los índices que produce se recomienda consultar la dirección electrónica http://www.conference-board.org.
Por su lado, la OCDE genera un Indicador Compuesto Adelantado, diseñado para dar señales tempranas sobre la situación de la economía global en cuanto a sus puntos de giro. El procedimiento de cálculo de tal indicador lo empezó a desarrollar la OCDE en la década de 1970, y actualmente está referido a las tres diferentes formas del ciclo: clásico, de crecimiento y de tasa de crecimiento, según se menciona a continuación. Cabe notar que los indicadores correspondientes al ciclo clásico se pueden obtener a partir del ciclo de crecimiento al restaurar la tendencia. Los indicadores de ciclo de crecimiento se estiman actualmente para 29 países miembros de la OCDE, seis países no miembros y siete agrupaciones de la Eurozona. A finales de 2008 se hicieron modificaciones a la metodología (véase el sitio http://www.oecd.org/std/cli); el cambio fundamental es que ahora se usa el filtro de Hodrick-Prescott para extraer la tendencia y antes se usaba el método PAT. Estos métodos se describen en la siguiente sección.
Tanto el ciclo clásico como el de crecimiento se usan en diversos países para referirse al estado de la economía. Por ejemplo, el CB usa la definición de ciclo clásico de negocios, mientras que la OCDE utiliza la de ciclo de crecimiento. En este trabajo se hace referencia al ciclo de crecimiento, pero conviene saber que el ciclo clásico o de negocios se refiere al hecho de que la actividad de negocios disminuye y después se recupera, no respecto a su tendencia, sino en relación con el nivel alcanzado. Desde luego, los dos tipos de ciclo están relacionados, según lo muestra el esquema ABCD presentado por Anas y Ferrara (2004), así como por Mazzi y Moauro (2009). Los puntos A y B de la gráfica 1 indican una fase de desaceleración, tanto del ciclo clásico como del de crecimiento; los puntos A y B corresponden a crestas, mientras que C y D son valles. Además, un ciclo está constituido por dos fases, la ascendente o de expansión (de valle a cresta) y la descendente o de contracción (de cresta a valle), así como por los puntos de giro asociados con las fases. Se aprecia que una cresta del ciclo de crecimiento anticipa el valor máximo en el ciclo clásico, y el valor mínimo del ciclo clásico anticipa un valle en el ciclo de crecimiento. Sin embargo, en el ciclo de crecimiento el interés radica en los puntos A y D, y para ir de A a D se debe pasar por una etapa de contracción, mientras que el paso de D a A transcurre por una etapa de expansión. Por otro lado, como hacen notar Mazzi y Moauro (2009), se podría presentar una fluctuación en el ciclo de crecimiento sin que exista la correspondiente fluctuación en el ciclo clásico; por ejemplo, cuando la serie muestre menor pendiente en su tendencia (lo que se conoce como doble declive).
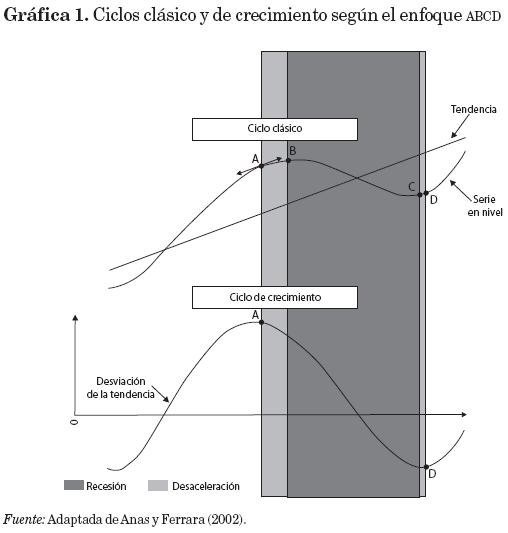
Para otras distinciones entre ciclos de crecimiento y clásicos se recomienda consultar el artículo de García-Ferrer et al. (2001). Asimismo, existe el ciclo de aceleración o de tasa de crecimiento (ya que considera los cambios en el ciclo de crecimiento). Este tipo de ciclo no se usa en el presente trabajo y, en general, es menos utilizado que los ciclos clásico y de crecimiento debido a que está sujeto a fluctuaciones erráticas y de corta duración, lo cual hace que produzca muchas falsas alarmas (véase Anas y Ferrara, 2004).
La sección siguiente presenta una breve definición de los métodos para estimar tendencia y ciclo que aquí se comparan: el PAT del NBER (que utiliza el SICCA y está asociado al ciclo de crecimiento), el filtro de Hodrick-Prescott con dos propuestas de aplicación doble (la propuesta por la OCDE y otra que controla la suavidad de la tendencia) y el filtro de paso de banda de Christiano y Fitzgerald, que utiliza EUROSTAT. La sección II compara los distintos métodos para estimar tendencia y ciclo. Los criterios para llevar a cabo las comparaciones miden el desempeño de los métodos en función de las revisiones de los componentes cíclicos que genera cada uno de ellos. En esta sección se presenta un ejemplo numérico que ilustra los resultados que se obtienen al realizar las comparaciones con datos de la economía mexicana. Como resultado se concluye que el método usado en la OCDE, con aplicación doble del filtro de Hodrick-Prescott, es el que proporciona mejores resultados para estimar tendencias y ciclos.
En la sección III se describen los métodos del NBER, de la OCDE y de Stock-Watson para estimar los índices cíclicos. Se usan los componentes cíclicos de las series coincidentes y adelantadas previamente definidos, de manera que las diferencias en los índices cíclicos sean atribuibles solamente al método de cálculo de los índices compuestos correspondientes. Mientras los métodos del NBER y de la OCDE son casi mecánicos, el de Stock-Watson requiere de mayor esfuerzo para su aplicación. La sección IV presenta una aplicación de las tres metodologías para generar los índices cíclicos compuestos. Los índices coincidentes proporcionan resultados semejantes entre sí, mientras que los índices adelantados difieren, tanto entre ellos como con referencia a la cronología para las crestas y los valles que obtuvo el INEGI. La última sección muestra algunas conclusiones, cómo es que se pudo determinar el método más apropiado para estimar tendencias y ciclos de las series coincidentes y adelantadas. Asimismo, el método de la OCDE para generar los índices compuestos brinda los mejores resultados para la economía mexicana, pero aun con ello, no es factible predecir apropiadamente las recesiones.
I. Métodos para estimar tendencia y ciclo
El enfoque de análisis de ciclo de crecimiento (conocido también como "desviación de la tendencia") requiere que cada una de las series del indicador sea estacionaria de segundo orden, de manera que la tendencia de la serie debe eliminarse al iniciar el estudio del ciclo. Después de ajustar la serie de tiempo en estudio por efectos estacionales, se supone que está formada sólo por tendencia y ciclo, así que la parte de la serie que no sea considerada tendencia debe ser ciclo, y viceversa. Para formalizar esta idea se representa la serie como un modelo de componentes no observables, es decir, si {Yt} es la serie observada en t = 1, ..., N, {τt} es su componente de tendencia (no observable directamente) y {ct} es el ciclo (no observable); entonces se tiene que

donde no necesariamente se piensa que la serie observada fue generada de esta manera, sino que ésta es una forma que captura la esencia de los datos. La estimación y posterior eliminación de la tendencia resulta un paso necesario para detectar y estimar el componente cíclico de la serie, así como para identificar los puntos de giro de la misma.
En este trabajo se comparan los siguientes métodos para estimar la tendencia y el ciclo: 1) el método de Tendencia con Promedio de Fases (PAT por sus siglas en inglés), usado por el NBER y también en asociación con el SICCA para considerar ciclos de crecimiento; 2) el filtro de Hodrick-Prescott (HP) doble, propuesto por la OCDE; 3) el filtro HP doble semejante al anterior, excepto porque la primera aplicación del filtro se hace con suavidad controlada por el usuario; y 4) el filtro de Christiano y Fitzgerald (CF), que utiliza EUROSTAT y permite elegir el paso de banda para la frecuencia de los ciclos.
I.1. Método PAT del NBER (utilizado en el SICCA para el ciclo de crecimiento)
Este método separa la serie observada en distintas fases, de acuerdo con las fechas de las crestas y los valles en la serie de desviaciones respecto a un promedio móvil (MA por sus siglas en inglés) de 75 meses centrado. El método consiste en varias operaciones que se realizan en forma secuen-cial, así que una vez que se tienen las desviaciones señaladas: 1) se corrigen los valores extremos; 2) se calculan los valores medios de la serie para cada una de las fases sucesivas de expansión y contracción detectadas por el algoritmo de Bry-Boschan, diseñado para tal fin; 3) se suavizan los valores mediante promedios móviles de dos o tres fases adyacentes, y la tendencia PAT se obtiene al conectar los puntos medios; 4) se extrapolan los 37 valores perdidos en cada extremo de la serie para compensar por el efecto de aplicar el MA centrado.
El método carece de la sencillez de los métodos que se expresan mediante fórmulas, y aunque es no-lineal su complejidad es sólo aparente, pues los cálculos que involucra son en realidad relativamente simples, y es muy flexible. La esencia del método consiste en reemplazar las fluctuaciones grandes de la serie por movimientos graduales y persistentes, que es lo esperable en una serie de tendencia.
Debido a que está basado en los datos, más que en un modelo, los cálculos se realizan mediante un procedimiento de tipo "enlatado", aunque no todos los pasos se realizan de manera automática sino que existen opciones que elige el usuario en forma manual. Por ejemplo, se puede usar una opción para proporcionar los puntos de giro de la serie sin usar el algoritmo de Bry-Boschan. Adicionalmente, la parte del suavizamiento del método usa el criterio del Mes para Dominancia del Ciclo (MCD por sus siglas en inglés) que permite asignar aproximadamente la misma suavidad a todas las series a las que se aplica el método. Este criterio se define en términos del cambio absoluto mensual de cada uno de los componentes, irregular (I) y de tendencia-ciclo (C) de la serie. Se busca así que el cociente I/C sea menor que la unidad para definir entonces la longitud de un promedio móvil que se aplica para suavizar y que se denomina ma para el periodo del MCD. Comúnmente se pone un tope de seis meses para el valor máximo de esta longitud, y en la práctica es común que se use un MA de longitud de tres meses. Para más información y argumentos a favor del método PAT véase Zarnowitz y Ozyildirim (2002), y para conocer algunas críticas del procedimiento se recomienda consultar el trabajo de Nilsson y Gyomai (2008).
I.2. Filtro de Hodrick-Prescott
El filtro HP propuesto por Hodrick y Prescott (1997) sirve para estimar una serie de tendencia y surge al minimizar la función

con λ > 0 una constante que establece un balance entre la fidelidad de la tendencia a los datos y su suavidad. O sea, al escribir

se observa que conforme λ ↓ 0, M(λ) sólo tiene en cuenta la fidelidad (F) a los datos (o sea, τt → Yt para toda t = 1, N), de manera que no hay suavidad (S), mientras que lo contrario ocurre si λ ↑ ∞, en cuyo caso la tendencia se comporta aproximadamente como una línea recta (descrita por τt = 2 τt-1 - τt-2 para t = 3, ..., N), sin apegarse necesariamente a los datos observados. El uso indiscriminado del filtro HP ha sido criticado por diversos autores, e. g. Cogley y Nason (1995) y Park (1996), ya que puede inducir ciclos espurios. Pero en otros trabajos se ha justificado su uso, ya que se ha demostrado que funciona mejor que otras alternativas; por ejemplo, Pedersen (2001) menciona que la definición misma de efecto espurio es la que podría estar equivocada. En la práctica, el problema por resolver para usar el filtro HP es la elección de la constante de suavizamiento. Para ello se puede optar por el enfoque del dominio de las frecuencias, que conduce a determinar primero las frecuencias que se desea eliminar con el filtro, o bien se puede elegir el valor de λ que produzca un porcentaje de suavidad deseado para la tendencia. Estas dos opciones dan origen a las propuestas que se indican a continuación.
I.3. Filtro HP doble, propuesto por la OCDE
Con respecto a la elección de la constante de suavizamiento, la monografía de Kaiser y Maravall (2001) sugiere elegirla en función del periodo de actividad cíclica que se desea analizar, es decir, en función del corte de las frecuencias bajas. La frecuencia de corte se define como aquella que permite pasar 50 por ciento de la ganancia original del ciclo y retiene el otro 50 por ciento. Si se desea un corte de las frecuencias de manera que el ciclo de referencia se complete en T meses, la fórmula a utilizar es (véase Maravall y del Río, 2007).
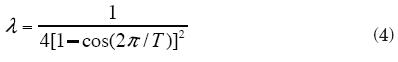
Para este trabajo se eligió un punto de corte para las frecuencias de T = 120 meses, por lo que la constante que resulta para eliminar la tendencia, expresada como fluctuaciones de baja frecuencia (aquellas que se repiten cada 120 meses), es λ = 133,107.9.
Una segunda aplicación del filtro HP se utiliza para suavizar el componente cíclico por fluctuaciones de alta frecuencia que no se consideran de carácter cíclico. Para ello se usa un corte de T = 12 meses, lo cual conduce a usar λ = 13.9. En consecuencia, al aplicar dos veces el filtro HP se produce un filtro de tipo paso de banda, y la serie resultante se queda con fluctuaciones cíclicas que van de 12 a 120 meses. Una justificación de este procedimiento secuencial del filtro HP y su interpretación como paso de banda se encuentra en Pedersen (2004).
I.4. Filtro HP doble con tendencia de suavidad controlada
La elección de la constante de suavizamiento con enfoque de suavidad deseada surge de una idea expuesta en principio por Prescott (1986), quien menciona que si la curva de tendencia es suave los hechos clave del ciclo no son sensibles al procedimiento usado para cancelarla. Con esta base, se propone usar el método propuesto en Guerrero (2008), el cual indica fijar primero un porcentaje de suavidad, expresado como S(λ; N)%, en donde se aprecia que la suavidad es una función de tal constante y del tamaño de la serie. Así pues, para una serie de longitud determinada por la muestra de datos disponible, una vez que se elige una suavidad deseada, se obtiene como resultado el valor de λ. La relación entre suavidad y constante de suavizamiento está dada por

con K2 como matriz de segundas diferencias, mediante la cual se expresa la suavidad mencionada en (3), y tr[.] es la operación traza de una matriz cuadrada. Aunque la relación entre S(λ; N) y λ es relativamente simple y de fácil cálculo numérico, no es posible expresar analíticamente λ como función de S(λ; N). En el artículo de Guerrero (2008) se encuentra la justificación de (5) y también mayores detalles acerca del uso del método.
El filtro HP con porcentaje de suavidad elegido por el usuario se presentó originalmente para series de tiempo trimestrales, que es con el cual trabajaron Hodrick y Prescott. Sin embargo, en las aplicaciones de este trabajo las series son mensuales, por lo que se requiere adecuar el valor de la constante de suavizamiento. En Guerrero (2011) se deduce la adecuación necesaria, que consiste en elegir primero la constante que produce la suavidad deseada para una serie trimestral, digamos λ*, y calcular después la constante equivalente para una serie mensual  3 mediante la expresión
3 mediante la expresión

Por ejemplo, para estimar la tendencia de una serie de tiempo de flujos con 16 años de datos (N = 192) y 90 por ciento de suavidad, se obtiene primero el valor de la constante de suavizamiento para la serie trimestral (con 64 trimestres), o sea λ* = 180.1. A partir de este valor se obtiene la constante  3 = 12 687 equivalente para datos mensuales. Nuevamente, una segunda aplicación del filtro HP se usa para suavizar el componente cíclico, igual que en el método anterior. En resumen, primero se estima la tendencia con un porcentaje de suavidad deseado y después se suaviza el ciclo para cancelar las fluctuaciones de corto plazo, consideradas como parte de la irregularidad.
3 = 12 687 equivalente para datos mensuales. Nuevamente, una segunda aplicación del filtro HP se usa para suavizar el componente cíclico, igual que en el método anterior. En resumen, primero se estima la tendencia con un porcentaje de suavidad deseado y después se suaviza el ciclo para cancelar las fluctuaciones de corto plazo, consideradas como parte de la irregularidad.
I.5. Filtro de Christiano y Fitzgerald
Este filtro surge de la idea de que se puede construir un filtro ideal que permita pasar solamente un cierto tipo de frecuencias de la serie observada, para separarla en diversos componentes, a los que se asocie con movimientos de mayor o menor frecuencia de aparición en el periodo de observación. El filtro ideal es en realidad una transformación lineal de los datos observados, que no altera los componentes con frecuencia dentro de la banda y elimina los demás. Ese filtro supone teóricamente un tamaño de serie infinito, así que en la práctica se aplica alguna aproximación y la serie debe admitir una representación de tipo Caminata Aleatoria sin deriva (el filtro es óptimo sólo para este tipo de series), y si existiera deriva en la serie en estudio debería cancelarse antes de usar el filtro. Esta técnica se utiliza en EUROSTAT por su flexibilidad para adecuarse a distintos tipos de series.
Para usar el filtro CF se debe definir el periodo de oscilación del componente que se desea aislar, asociado con los periodos bajo pl y alto pu que satisfacen 2 < pl < pu < ∞. Con esta definición se preservan los ciclos de longitud mayor que pl y menor que pu, de manera que permanecen en el ciclo estimado. Así pues, para estimar el ciclo {ct} de acuerdo con el modelo (1), la fórmula de filtrado de la serie {Yt}, con t = 1, ..., N, es

donde los coeficientes que aparecen en esta fórmula son, para t = 3, ..., N-2,

Mientras que

y  es la suma de las bj' s para j = t-1, t, ... Para conocer la derivación del filtro y detalles de su uso se recomienda consultar el artículo de Christiano y Fitzgerald (2003).
es la suma de las bj' s para j = t-1, t, ... Para conocer la derivación del filtro y detalles de su uso se recomienda consultar el artículo de Christiano y Fitzgerald (2003).
II. Comparación de métodos para estimar tendencias y ciclos
La manera como se comparan los filtros es a través del comportamiento que siguen las revisiones del componente cíclico, según se añaden nuevos datos a la serie en estudio. El objetivo es encontrar un método robusto que brinde señales tempranas y estables de los puntos de giro. Nilsson y Gyomai (2008) compararon diversos métodos, dentro de los cuales se encuentran el método usado por el NBER, el filtro HP doble que se utiliza en la OCDE y el filtro CF que se usa en EUROSTAT. El método de NBER resultó mejor en lo que respecta a la estabilidad de la señal del punto de giro, mientras que el de CF dio resultados preferibles en términos de precisión numérica. Además, encontraron adecuado que el filtro HP doble tuviera parámetros de suavidad elegidos para eliminar el componente de tendencia con longitud de ciclo mayor a 120 meses y el ruido de alta frecuencia de la serie con longitud menor a 12 meses. En el presente estudio la comparación de métodos para las series de la economía mexicana incluyen el filtro HP doble, con la primera aplicación del filtro HP que produce la suavidad deseada para la tendencia y la segunda aplicación que suaviza el ruido con frecuencia menor a 12 meses.
II.1. Series a utilizar y fechado de ciclos
La comparación de métodos se realiza después de aplicar cada una de las metodologías para estimar tendencia y ciclo a un grupo de variables coincidentes o adelantadas respecto al ciclo económico de México. La elección de estas variables es un trabajo muy laborioso y detallado que no fue necesario realizar, porque en el INEGI ya se tenían decididas las variables a usar para el cálculo de los indicadores compuestos con la metodología de la OCDE. En el cuadro 1 se muestran las series, para las cuales se eligió una muestra inicial de datos que va de enero de 19801 a diciembre de 1995, mientras que las revisiones se efectúan con los datos de enero de 1996 al último mes disponible en el momento de iniciar este estudio (en la mayoría de los casos fue mayo de 2010).

En México no existe una entidad o árbitro que determine oficialmente la entrada a, o la salida de, los periodos de recesión, como ocurre en Estados Unidos con el comité encargado de fechar los ciclos económicos. Un recuento de cómo el NBER realiza la definición y fechado de los ciclos económicos se encuentra en Moore y Zarnowitz (1986). Por esta razón, como lo más cercano a un fechado oficial de los ciclos económicos, se adopta en México la cronología utilizada en el INEGI, la cual surgió del análisis de los resultados del SICCA con referencia al ciclo clásico de negocios. Luego el INEGI obtuvo un nuevo fechado para el indicador coincidente, con la idea de adoptar la metodología propuesta por la OCDE y las variables del cuadro 1. Las fechas de las crestas y los valles con las que se determinan los ciclos económicos, definidos ahora como ciclos de crecimiento, se presentan en el cuadro 2. En lo que sigue de este trabajo la cronología de este cuadro se considera como ciclo de referencia "oficial" para México.

Para apreciar mejor el comportamiento de la serie referida como estado de la economía, en la gráfica 2 se presenta el índice coincidente respectivo. Este índice se obtuvo al aplicar, primero, el método del NBER (con enfoque de ciclo clásico) para obtener el índice coincidente, y después aplicarle a la serie de ese índice el método del NBER, con enfoque de ciclo de crecimiento y donde se aplicó el método PAT para estimar la tendencia y el ciclo.
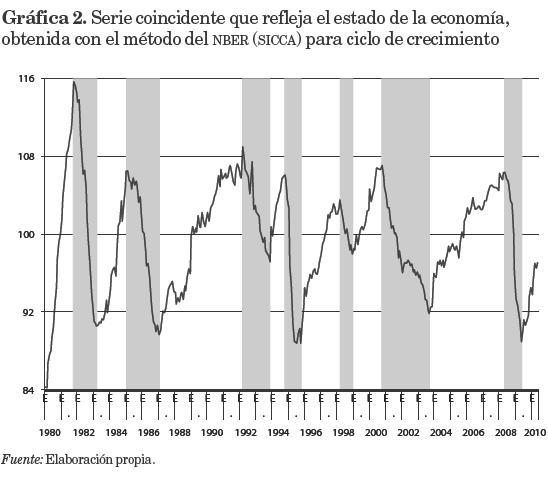
Con el fin de tener una serie de referencia para el indicador adelantado que brinde una cronología de crestas y valles y que pueda considerarse cercana a lo "oficial", en el cuadro 3 se muestran las crestas y los valles del índice adelantado. Ahí se ven los meses con que el indicador adelantado anticipa al coincidente; el adelantado se retrasa respecto al coincidente en una cresta y en un valle, pero en los casos en que sí anticipa adecuadamente lo hace en promedio con seis meses a las crestas y cinco a los valles. La gráfica 3 complementa el cuadro 3 al mostrar la serie del indicador adelantado equivalente al de la gráfica 2.


Es de subrayar que las series que se usan al estimar tendencias surgen del procedimiento de ajuste estacional; posteriormente se ajustan por valores extremos y acto seguido se expresan en logaritmos, excepto cuando la serie contiene valores negativos (que es el caso de TEM) o cuando la variable es ya una tasa (TDU y TIIE). Las tendencias se obtienen con el procedimiento que se haya elegido para este fin, y la serie de tendencia en la escala original se obtiene al aplicar el antilogaritmo a los datos previos (si es que antes se aplicó el logaritmo). En cambio, el ciclo que surge de quitarle la tendencia a la serie en logaritmos es el que se utiliza para calcular los índices coincidente y adelantado con los métodos de NBER y OCDE.
II.2. Criterios para efectuar las comparaciones
Para comparar los métodos de estimación de tendencia y extracción de ciclo, los criterios que se usan en este trabajo son los recomendados por Di Fonzo (2005) y empleados por Nilsson y Gyomai (2008). Éstos permiten contrastar empíricamente los métodos a través del comportamiento de las revisiones en el ciclo estimado, conforme se incluyen nuevos datos en el cálculo. El valor estimado del ciclo para el periodo t, que utiliza información hasta el tiempo t+i, está dado por  t, t+i, de manera que la revisión de la estimación realizada con información disponible en el periodo t+i-1, es
t, t+i, de manera que la revisión de la estimación realizada con información disponible en el periodo t+i-1, es
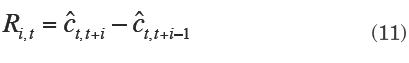
Así, para cada valor de i se tiene una nueva "cosecha" de datos y de revisiones. Se supone que existen suficientes cosechas de revisiones (i = 1, ..., n) como para efectuar un análisis de las mismas. Otra forma de cálculo de revisiones se basa en la expresión de la revisión acumulada a partir del primer periodo en que se efectuó la estimación del ciclo

Las comparaciones se basan en las siguientes medidas, resumen del comportamiento de las revisiones, conforme se añaden nuevos datos a la serie y se vuelve a estimar el ciclo.
Revisión Media: 
Revisión Absoluta Media: 
Desviación Estándar de las Revisiones: 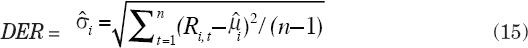
Revisión Absoluta Acumulada: 
Autocorrelación de las Revisiones: 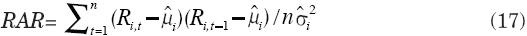
Estadístico t corregido2: 
con 
Sesgo condicional (centrado): 
con sgn(.) la función que asigna el signo al argumento entre paréntesis.
Cambio de signo: 
donde #[.] asigna el número de elementos que tiene el conjunto dentro de las llaves.
Cambio de dirección: 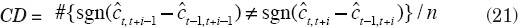
Para establecer las comparaciones se forman tres bloques de medidas referidos como: 1) tamaño de las revisiones; 2) sesgo y autocorrelación en las revisiones; 3) señal contenida en el ciclo. El primero de estos bloques considera las medidas: RAM, que mide el tamaño de las revisiones sin considerar el signo, e incluye sesgo potencial por no estar centrada en la media; DER, que mide la dispersión global de las revisiones y corrige el sesgo potencial que pudiera existir en ellas, además de enfatizar más los valores extremos en comparación con RAM; y RAA, que mide la magnitud acumulada de las revisiones desde la primera estimación del ciclo que se realice, y que no tiene corrección por sesgo.
El segundo bloque incluye medidas acerca de la calidad de los ciclos, es decir: RM es un reflejo del sesgo que pudiera presentarse al estimar el ciclo y que debería ser cercano a cero para que el método sea adecuado; tHA tiene como distribución asintótica la Normal estándar y permite probar la hipótesis nula de que la media de las revisiones no difiere de cero, es decir, que el sesgo no es significativo en términos estadísticos; RAR indica la existencia de información desaprovechada en las revisiones pasadas, por lo cual un método con valores grandes de RAR se considera ineficiente; SC mide el tamaño promedio de las revisiones y asigna a las revisiones por arriba de la tendencia el signo contrario que a las revisiones por debajo de ella, así que valores positivos indican sesgo hacia la tendencia y negativos indican que las revisiones tienden a alejarse de ésta.
El tercer bloque de medidas considera cambios, tanto de signo (CS) como de dirección (CD), en las señales generadas por los ciclos. CS permite determinar las fases del ciclo, es decir, cuántas veces la revisión de la estimación inicial cambia de abajo hacia arriba de la tendencia y cuántas veces lo hace a la inversa. Por su parte, CD se mide en porcentaje y mide las veces que el componente cíclico de la serie cambia de creciente a decreciente, y lo mismo en sentido inverso.
Los cálculos de los diversos criterios de comparación se efectuaron con el programa Cyclical Analysis and Composite Indicators Software (CACIS), desarrollado por la OCDE (véase Nilsson y Gyomai, 2008). Primero se hace el ajuste estacional de cada una de las series en consideración, y para ello se elige una descomposición multiplicativa o aditiva. El programa CACIS se usa dentro del marco del ajuste estacional del paquete TRAMO-SEATS, así que se efectuó la corrección de observaciones extremas y se eligió de manera automática la descomposición multiplicativa para casi todas las series, excepto IMPT, IVFP y TEM.
II.3. Ejemplo ilustrativo de las comparaciones realizadas
Los resultados de las comparaciones efectuadas se presentan a través de gráficas como las que se muestran a continuación para el IVFP. Los cálculos y las correspondientes gráficas para las demás series, tanto coincidentes como adelantadas, fueron realizados por la Dirección de Estudios Econométricos de la Dirección General del Servicio Público de Información del INEGI, y el lector interesado en obtenerlas deberá solicitarlas a esa Dirección. El periodo mensual de 1980:01 a 1995:12 se utiliza en este caso para efectuar la estimación inicial de la tendencia y el ciclo. Al ciclo se le estandariza primero y se le suma 100 para que fluctúe alrededor de este valor. Conforme se incrementa el tamaño de muestra (mes a mes, según se incluyen nuevas cosechas de datos) se repite el procedimiento de estimación y estandarización del ciclo. Esto se hace en el presente caso para los meses de 1996:01 a 2010:03 y se realiza entonces el análisis de las revisiones.
La comparación de los distintos métodos se efectúa para elegir el que brinde respuesta más rápida para detectar puntos de giro, que presente menos revisiones y que éstas sean pequeñas y tempranas. En las gráficas 4a y 4b se muestran los resultados para el bloque de medidas del tamaño de las revisiones; allí se debe poner atención en lo que ocurre en la parte central, porque los extremos están muy influenciados por el número de datos usado en las comparaciones. Por ello conviene concentrase en el patrón mostrado por las cosechas de datos (numeradas en el eje horizontal), entre 30 y 140. En estos casos, las menores RAM y DER surgen con los filtros HP dobles, mientras que la menor RAA surge con el método CF.

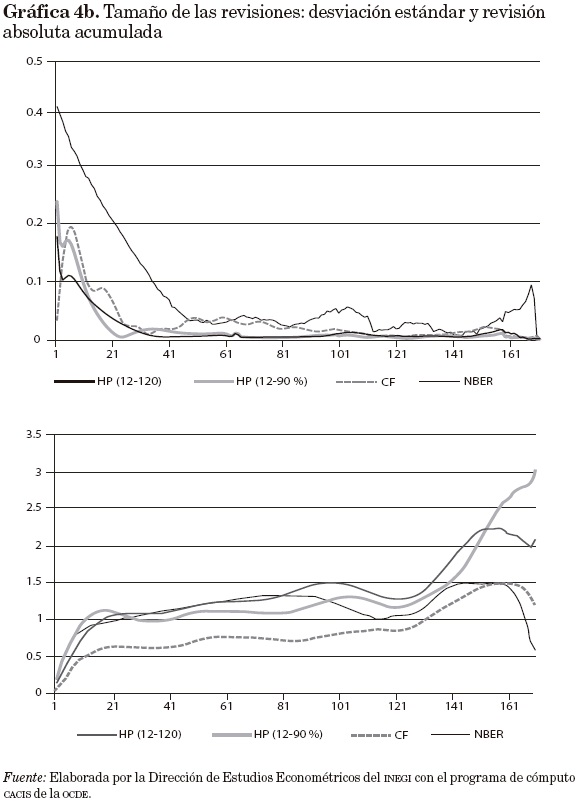
Respecto al bloque de medidas sobre la calidad de los ciclos de las gráficas 5a y 5b, la RM más cercana a cero se obtiene con el método HP (12, 90%); el criterio tHA tiende a mantenerse dentro del intervalo (-2, 2) para todos los métodos, excepto en el caso de las últimas cosechas; la menor RAR corresponde a los métodos CF y de NBER; y estos dos métodos muestran sesgo condicional (SC) más volátil en general.
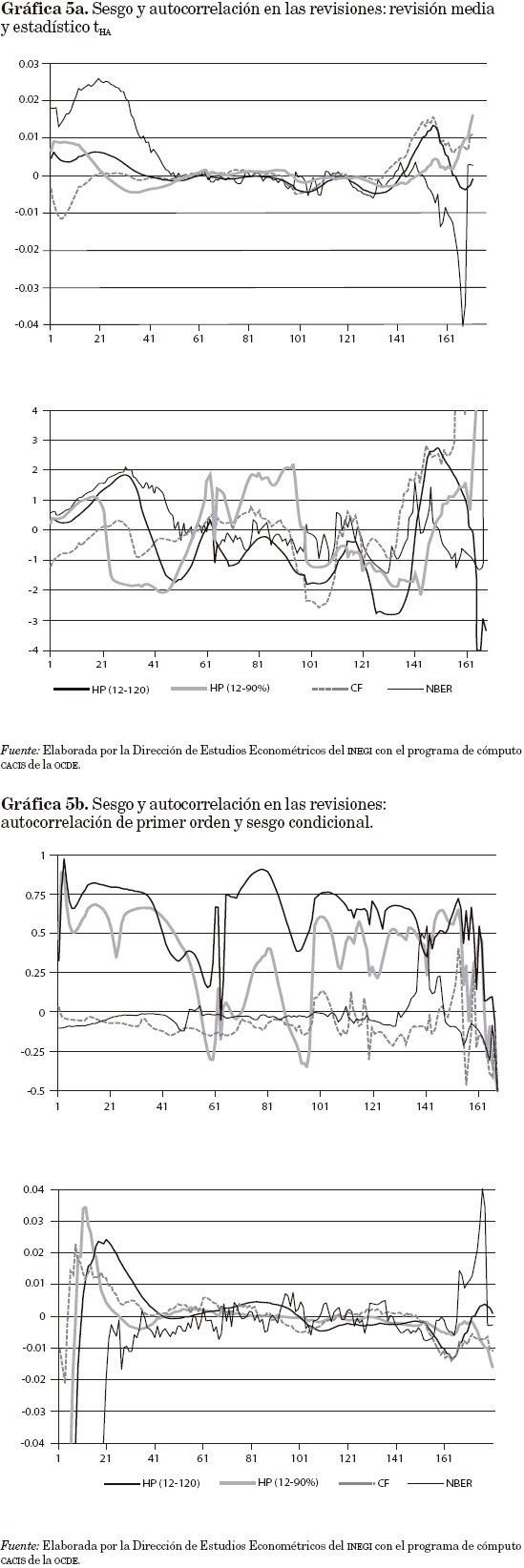
Las gráficas 6a y 6b permiten apreciar el comportamiento de las medidas del tercer bloque, es decir, de los cambios CS y CD, y es claro que las mejores señales son las de los ciclos generados con los métodos HP doble. Incluso se aprecia que el método HP (12, 120) genera señales más estables que las de HP (12, 90%).

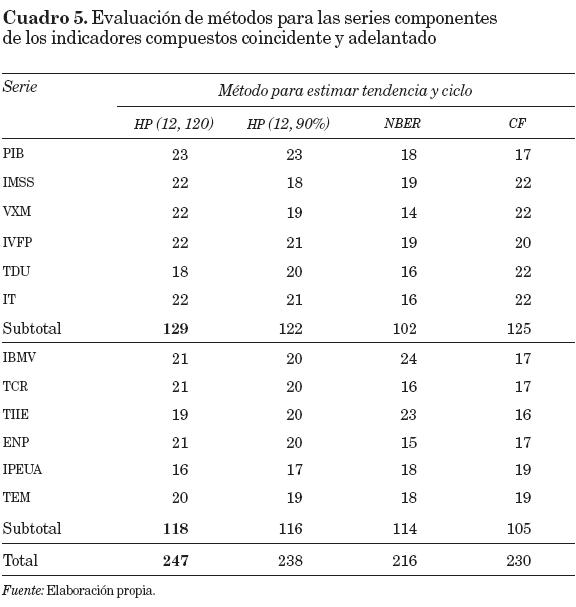
Con el fin de esclarecer las comparaciones se optó por asignar una calificación numérica a los diversos criterios utilizados, según se muestra en el cuadro 4 donde se observan las puntuaciones asignadas en una escala del 1 (malo) al 3 (bueno).

Puntuaciones similares a las del cuadro 4 para cada una de las series que conforman los indicadores compuestos coincidente y adelantado condujeron al resumen de resultados del cuadro 5. A partir de este resumen de resultados se decidió que la metodología para estimar las tendencias y los ciclos de las series mexicanas en estudio debería ser la que se basa en HP (12, 120). Es con este método que se obtuvieron las series de tendencia y ciclo mostradas en las gráficas 7a, 7b y 7c para las series coincidentes, así como las gráficas 8a, 8b y 8c para las series adelantadas. Cabe notar que en tales gráficas el eje del lado derecho corresponde al ciclo.
III. Métodos para estimar los índices cíclicos
Para generar los índices compuestos, en este trabajo se hace uso de las metodologías del NBER, de la OCDE y de Stock-Watson, descritas a continuación.
III.1. Método del NBER
En este caso, el método del NBER se utiliza después de eliminar la tendencia de las series previamente desestacionalizadas. El diagrama 1 muestra los pasos que se siguen para obtener el índice compuesto.

Ya que se tienen separados los componentes de tendencia y ciclo, se trabaja con este último. Se utiliza la misma nomenclatura que en el procedimiento del NBER para ciclo clásico; la referencia de donde se obtuvieron las expresiones que se enumeran a continuación es INEGI (2010). Para comenzar, primero se calculan los cambios mes a mes de cada una de las series zi,t con i = 1, ..., k (k = 6 debido a que estas son las series que componen los índices compuestos coincidente y adelantado) mediante la fórmula de cambio porcentual simétrico

o bien, si la serie es un porcentaje o una tasa, como

donde ci,t es el componente cíclico de la serie i en el tiempo t = 1, N. En caso de que la serie muestre un patrón contrario al ciclo de la actividad económica se aplican las expresiones (22) con signo negativo. Después se estandarizan los cambios conforme a
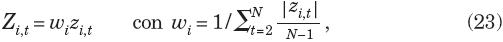
donde wi es el factor de estandarización.
Posteriormente se agregan las series al promediar los cambios mes a mes, o sea

donde kt indica el número de series disponibles en el mes t, que puede ser menor que k. Este resultado también se estandariza y se ajusta por amplitud para obtener

con P el promedio de los valores absolutos de los cambios del índice de producción industrial para un periodo determinado. Se obtiene así un índice cíclico ICt que toma el valor 100 para t = 1 y de ahí en adelante se calcula recursivamente como

Finalmente, para una mejor interpretación, el índice cíclico se rebasifica con la base 2003 = 100 al dividir entre el promedio de los valores del índice anterior para el año 2003 y multiplicar por 100.
III.2. Método de la OCDE
Al igual que con la metodología anterior, la de la OCDE puede mostrarse esquemáticamente de acuerdo con el diagrama 2, en donde las series del ciclo que se usan son las que resultan de eliminar la tendencia de las series ajustadas por estacionalidad.

Después de separar los componentes de tendencia y ciclo se estandariza este último, ya que las series componentes tienen diferentes unidades de medición y variabilidad. La expresión que se usa es

donde  es el promedio del ciclo para cada una de las variables i = 1,..., k (con k = 6). Una vez estandarizada cada serie, se agregan todas ellas por medio de las tasas de crecimiento promedio entre dos periodos consecutivos, como sigue
es el promedio del ciclo para cada una de las variables i = 1,..., k (con k = 6). Una vez estandarizada cada serie, se agregan todas ellas por medio de las tasas de crecimiento promedio entre dos periodos consecutivos, como sigue

donde δi,t, es una variable indicadora que toma el valor 1 si se cuenta con el dato para la variable Zi,t, y es 0 en otro caso. Por último, con fines prácticos, se estandariza el indicador de tal manera que los resultados fluctúen alrededor de 100 mediante la expresión

Para mayores detalles se recomienda consultar la monografía OECD (2008).
III.3. Método de Stock-Watson
El enfoque de Stock y Watson (1989, 1991) permite obtener los índices compuesto y adelantado a partir de desarrollos basados en modelos estadísticos formales. Según este enfoque, las variables macroeconómicas tienen un movimiento común que denota el estado global de la economía y que puede ser capturado por un factor latente, que no es observable directamente. El problema consiste en estimar el estado de la economía en el momento actual, a partir de su relación contemporánea con diversas variables macroeconómicas mediante un índice coincidente. Por su lado, el indicador adelantado se obtiene como pronóstico del estado de la economía.
El modelo propuesto por Stock y Watson (1991) para el índice coincidente se expresa mediante el siguiente sistema de ecuaciones, donde aparecen las variables X1, ..., Xk, que se suponen integradas de orden 1, de manera que son estacionarias en diferencias, así como el factor común Ct que se desea estimar para el periodo muestral, t = 1, ...,N,

La constante βi también se estima a partir de los datos observados y el error aleatorio se supone que forma una sucesión {ui, t} cuyo comportamiento se describe como

para i = 1, ..., k, en donde los di son los parámetros de los k modelos de tipo Auto-Regresivo (AR) involucrados, los cuales deben ser estimados. {ei,t} es una sucesión de choques aleatorios no correlacionados entre sí e idénticamente distribuidos como N(0, σi2), que además son mutuamente no-correlacionados con {ej,t}, para i ≠ j (esto implica no-correlación mutua entre las sucesiones {ui,t}). A su vez, el factor común se supone que se puede representar en forma AR, como

con δ y Φ parámetros por estimar, y {ηt} es otra sucesión de choques aleatorios no autocorrelacionados y mutuamente no-correlacionados con los errores {ei,t}, i = 1, ..., k.
En este estudio, las Xi de (30) son consideradas en forma de componente cíclico, de manera que, contrario a la especificación de Stock y Watson (1991), no es necesario suponer que son integradas de orden 1, y serán referidas a las correspondientes k = 6 variables coincidentes: X1 = ciclo de PIB, X2 = ciclo de IMSS, X3 = ciclo de VXM, X4 = ciclo de IVFP, X5 = ciclo de TDU y X6 = ciclo de IT. Por lo tanto, C no es integrada de orden 1, sino un factor estacionario que es común a todas las variables. Al método asociado con este modelo se le llama sw de aquí en adelante.
Las series adelantadas se agregan al modelo para ayudar a predecir el estado de la economía; para ello se reemplaza la ecuación (32) por el sistema de ecuaciones

donde Yj,t son los componentes cíclicos de las variables adelantadas, es decir: Y1 = ciclo de IBMV; Y2 = ciclo de TCR; Y3 = ciclo de TIIE; Y4 = ciclo de ENP; Y5 = ciclo de IPEUA; y Y6 = ciclo de TEM. Por su lado, λcc, λcj, λjc y λjj son coeficientes que ponderan las variables retrasadas un periodo, mientras que μc y μj son constantes que reflejan el nivel de las respectivas variables. Además, vc,t y vj,t son errores aleatorios que cumplen con ser no autocorrelacionados y mutuamente no-correlacionados.
Las ecuaciones anteriores no se estiman en la forma como se acaban de presentar, debido a que (30) contiene dos parámetros que no pueden estimarse por separado pues están ligados mediante E(Xi) = βi + yiδ. Por tal motivo, para realizar la estimación por máxima verosimilitud conviene que las variables se expresen en forma estandarizada. Como las variables en realidad son componentes cíclicos con media 100, se estandarizan mediante xi,t = (Xi,t - 100)/sXi y yj,t = (Yj,t - 100)/sY j, con sXi y sY j las desviaciones estándar muestrales de las variables respectivas. De esta manera, el modelo se expresa como

donde el índice coincidente es ahora  . Conviene notar que en (35), además del componente ct, común a todas las variables pero que se pondera de manera distinta en cada ecuación, hay un elemento idiosincrático, ui,t, propio de cada una de ellas. Se desea estimar el valor ct a partir de los datos de las variables observadas hasta el tiempo t, o sea, de la sucesión de vectores xt = (x1,t, ..., x6,t )' y yt = (y1,t, ..., y6,t)' con t = 1, ..., N, lo que implica obtener la esperanza condicional E(ct |x1, ..., xN,, y1, ..., yN) para lograr la estimación lineal óptima en el sentido de Error Cuadrático Medio mínimo. Para ello se usa el filtro de Kalman, que requiere expresar el modelo como un sistema de espacio de estados. Dicho sistema consta de dos ecuaciones, una de observación (o medición) y otra de estado (o de transición); la primera relaciona las variables observadas con el vector de estados y la segunda muestra la evolución de dicho vector. El vector de estados es αt = (ct, y't, u't)' y la ecuación de observación se escribe como
. Conviene notar que en (35), además del componente ct, común a todas las variables pero que se pondera de manera distinta en cada ecuación, hay un elemento idiosincrático, ui,t, propio de cada una de ellas. Se desea estimar el valor ct a partir de los datos de las variables observadas hasta el tiempo t, o sea, de la sucesión de vectores xt = (x1,t, ..., x6,t )' y yt = (y1,t, ..., y6,t)' con t = 1, ..., N, lo que implica obtener la esperanza condicional E(ct |x1, ..., xN,, y1, ..., yN) para lograr la estimación lineal óptima en el sentido de Error Cuadrático Medio mínimo. Para ello se usa el filtro de Kalman, que requiere expresar el modelo como un sistema de espacio de estados. Dicho sistema consta de dos ecuaciones, una de observación (o medición) y otra de estado (o de transición); la primera relaciona las variables observadas con el vector de estados y la segunda muestra la evolución de dicho vector. El vector de estados es αt = (ct, y't, u't)' y la ecuación de observación se escribe como

que premultiplica el vector de estados por la matriz Z, de dimensión 12 × 13, dada por

La ecuación de transición toma la forma

con wt (vc,t, v1,t, v2,t, v3,t, v4,t, v5,t, v6,t, e1,t, e2,t, e3,t, e4,t, e5,t, e6,t)', mientras que la matriz T es de dimensión 13 × 13 y está definida como

Al expresar el sistema de esta manera, el filtro de Kalman permite estimar los parámetros y el índice coincidente. Luego debería realizarse un análisis de los residuos del modelo para verificar su adecuación a los datos disponibles. Sin embargo, la evidencia empírica acumulada indica que estos modelos presentan violaciones a los supuestos aunque sus resultados desde el punto de vista del fenómeno que se estudia sean razonables (véase al respecto Carriero y Marcellino, 2007). Por otro lado, conviene citar a Kim y Nelson (1999, p. 53) donde se demuestra que la ganancia de Kal-man converge a su valor de equilibrio debido a que las variables entran en forma estandarizada (en Kim y Nelson sólo se pide que estén expresadas como desviaciones respecto a sus medias), así que la aplicación del filtro de Kalman es apropiada en el presente caso.
Conviene señalar que el modelo de espacio de estados es invariante en el tiempo (en el sentido de Harvey, 1994, cap. 3). De hecho, si las variables coincidentes entraran en el modelo en niveles, el modelo original de Stock y Watson carecería de la propiedad de "estado estable", la cual se requiere para que la función de verosimilitud del modelo de espacio de estados pueda maximizarse, en términos numéricos, así como para interpretar de manera formal los resultados del modelo. Esto fue subrayado en los trabajos de Nieto y Melo (2001) y Melo et al. (2002). Sin embargo, en el primero de esos artículos se demuestra que si las variables son integradas de orden cero, el modelo sí tiene la propiedad de estado estable y eso es lo que ocurre en la aplicación al caso que aquí se presenta para México, al igual que en el modelo que utilizaron Kim y Nelson (1999).
Los problemas prácticos de estos modelos incluyen la falta de especificación, para lo cual se ha propuesto usar métodos no-paramétricos y obtener índices cíclicos distintos a los aquí mostrados. También se puede recurrir a la robustez de los resultados respecto a la similitud de patrones que surgen con distintas especificaciones, de manera que no se juzgue la especificación y se considere el modelo como un filtro diseñado para generar los índices cíclicos. Este último razonamiento se aplica en este trabajo para mantener como válida la especificación AR de orden 1 de la expresión (36), sin cuestionar siquiera la necesidad de usar un mayor número de retrasos.
Un problema adicional se presenta cuando el índice incorpora tres o más variables, ya que al maximizar la función de verosimilitud se encuentra que tiene muchos máximos locales o es plana en algunas regiones, como lo señala Nieto (2003). Esto mismo ocurrió en los trabajos de Ruiz (2006) y Fernández (2008) al estimar los modelos respectivos. Por esto se han buscado estrategias alternativas para la estimación, como la de Castillo y Nieto (2008) quienes aplicaron el muestreador de Gibbs que se usa en Estadística Bayesiana. En los casos citados las series se encuentran expresadas en niveles, no en cambios como en el presente estudio; sin embargo, también aquí se enfrentaron dificultades al estimar el modelo por máxima verosimilitud y se requirió de un gran esfuerzo para elegir valores iniciales apropiados para los parámetros en la subrutina de estimación no-lineal empleada. Asimismo, a sugerencia de un árbitro, conviene recordar que las series de tiempo carecen de efectos estacionales porque contienen solamente la parte cíclica de los indicadores respectivos (libres por lo tanto de estacionalidad y tendencia).
IV. Aplicación a las series de la economía mexicana
Esta sección presenta los resultados de la aplicación de los métodos de cálculo del NBER, de la OCDE y de SW a las series de la economía mexicana. Los cálculos requeridos por los métodos del NBER y de la OCDE son de fácil realización y no se presentó ninguna situación extraordinaria. En cambio, la especificación de la ecuación (38) para el método de SW se tuvo que modificar debido a que la estimación de los parámetros λjj arrojó valores prácticamente iguales a la unidad en las seis ecuaciones correspondientes (j = 1, ..., 6), motivo por el cual se reestimó el modelo con esa restricción, y es por ello que no se presentan dichos coeficientes estimados. Los resultados de la estimación del modelo se resumen en los cuadros 6 a 9 (7-8), aunque debe recordarse que todas las ecuaciones se estimaron en forma simultánea.

La estimación se realizó con un programa similar al empleado por Fernández (2008) en el paquete computacional RATS, Versión 7.2 (distribuido por la empresa Estima, http://www.estima.com). La subrutina de estimación no-lineal empleada fue la de Broyden, Fletcher, Goldfarb y Shanno, y la convergencia de los coeficientes estimados se logró a las 117 iteraciones, con lo cual se obtuvo el valor 2609.253 para la log-verosimilitud. Cabe recordar que no se presenta la verificación de los supuestos del modelo de SW debido a que se trata esta metodología de manera semejante a las otras dos, es decir, como un algoritmo de cálculo cuya validez se juzga en relación con los resultados que produce. En este caso la validación se efectúa respecto a la adecuación del índice para representar el estado presente de la economía (índice coincidente) y su respectiva anticipación con el índice adelantado.
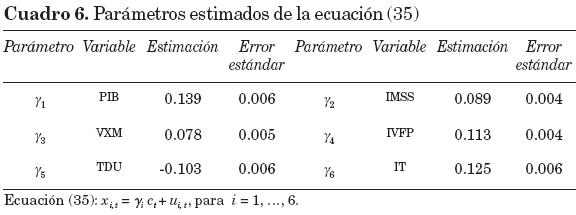
IV.1. Obtención de índices coincidentes
El cuadro 6 presenta los resultados de la estimación de la ecuación (35). Se ve que las ponderaciones asociadas a cada una de las variables en la expresión del índice coincidente son significativamente diferentes de cero, de manera que todas ellas afectan el índice, pero la mayor influencia la ejercen PIB, IT e IVFP (esto se concluye porque los componentes cíclicos de las variables entran al modelo en forma estandarizada).
Los resultados de la estimación de la ecuación (36) se observan en el cuadro 7, donde se aprecia que todos los coeficientes son cercanos a la unidad, pero aun así producen representaciones estacionarias para los respectivos modelos AR.
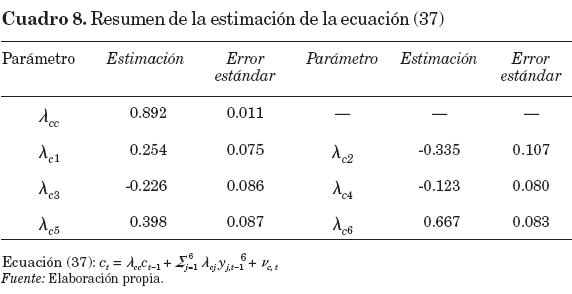
La estimación de la ecuación (37) se resume en el cuadro 8 y puede verse que el índice coincidente tiene una inercia muy alta ( cc = 0.892) pero con patrón estacionario; asimismo, los efectos de las variables adelantadas, excepto la 4, son todos significativos, y las variables 2, 3 y 4 (TCR, TIIE y ENP) contribuyen negativamente a la explicación de ct.
cc = 0.892) pero con patrón estacionario; asimismo, los efectos de las variables adelantadas, excepto la 4, son todos significativos, y las variables 2, 3 y 4 (TCR, TIIE y ENP) contribuyen negativamente a la explicación de ct.
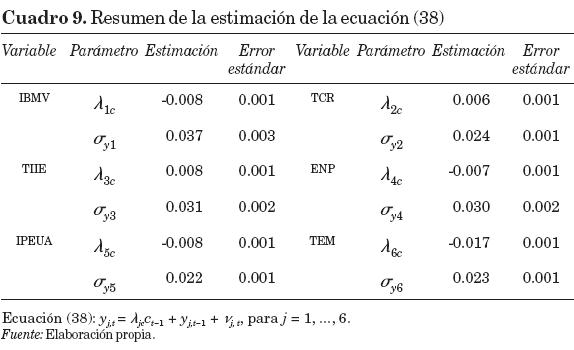
La estimación de la ecuación (38) se resume en el cuadro 9, donde se aprecia que el índice coincidente afecta significativamente cada una de las variables adelantadas.
Una manera sencilla de mostrar los resultados logrados con los diferentes métodos es con gráficas de las series de los índices coincidente y adelantado para cada método. Las series de índices coincidentes aparecen en la gráfica 9, donde al índice surgido del modelo SW se le sumó 100 para hacerlo comparable con los otros dos índices. La inspección visual de esta gráfica permite apreciar que los tres métodos brindan resultados parecidos, aunque el índice del NBER tiene más fluctuaciones hacia arriba que los otros dos, cuyos comportamientos son semejantes a simple vista.

Por otro lado, el cuadro 10 muestra las diferencias en los puntos de giro de los tres métodos en consideración, en relación con las fechas "oficiales" para el estado de la economía mexicana. Los tres índices compuestos producen cronologías cíclicas semejantes a la "oficial", pero los resultados del NBER y de la OCDE son mejores que los de SW por la menor discrepancia media que producen. Es notorio que los tres índices señalan un ciclo faltante en la cronología "oficial", con cresta y valle ubicados entre octubre (o noviembre) de 1987 y mayo (o julio) de 1988, lo cual podría deberse a la cercanía de fechas y a la poca profundidad mostrada por el ciclo. Quizá convendría incluir en la cronología "oficial" para el estado de la economía (o índice coincidente) dicho ciclo complementario.

IV.2 Obtención de índices adelantados
Los resultados de los índices adelantados se muestran en la gráfica 10. En el caso del método SW, el índice se obtuvo mediante pronósticos seis periodos hacia adelante del respectivo índice coincidente y, posiblemente debido a la falta de especificación del modelo de espacio de estados, los resultados dejan que desear en lo que toca a la anticipación, pues se observa retrasado respecto a los índices adelantados construidos con los métodos NBER y OCDE. En contraste, al comparar el índice adelantado de la OCDE con el respectivo índice coincidente de la gráfica 9, se observa que sí anticipa a dicho índice coincidente, el cual se vio anteriormente que sigue un patrón semejante al de la cronología "oficial". El índice adelantado del NBER también anticipa a su respectivo índice coincidente, pero sus fluctuaciones son mayores que las de los otros índices en estudio.

El cuadro 11 presenta los resultados equivalentes a los del cuadro 10, pero ahora para los índices adelantados. Se puede concluir con facilidad que la metodología de la OCDE es la que brinda mejores resultados para generar el índice cíclico adelantado, ya que la gráfica 10 permite apreciar que su comportamiento es menos volátil que el de los otros dos, y en el cuadro se observa que discrepa en promedio -0.1 meses respecto a las crestas y 4.3 meses respecto a los valles. En contraste, el índice adelantado de SW proporciona resultados desalentadores pues sus discrepancias son mayores: en promedio son de -2.7 meses respecto a las crestas y 4.8 meses para los valles.

La capacidad predictiva de los índices adelantados respecto a la cronología "oficial" es baja en general, pues aun el índice de la OCDE (el mejor de los tres índices) se retrasa en algunos casos, tanto en crestas (81:05, 89:07, 97:11) como en valles (82:09, 95:04, 98:11); en otros casos se adelanta en crestas (84:06, 00:05, 02:03 y 07:08) al igual que en valles (86:07, 90:12, 03:02, 05:04 y 09:02); y descubre un ciclo difícil de interpretar que no existe en la cronología "oficial" (92:03 a 92:12). Una parte de este comportamiento es atribuible a que tal cronología no es necesariamente verdadera, ni totalmente confiable.
Conclusiones
El presente trabajo debe considerarse un primer acercamiento al análisis detallado de los indicadores cíclicos para México. La intención es mostrar que existen diversos métodos que pueden aplicarse en las distintas etapas de la construcción de los índices cíclicos, pero que no existe consenso respecto a cuál es el mejor método en general, y que el caso particular de México no es la excepción. Los esfuerzos realizados con anterioridad para crear y dar mantenimiento al SICCA en el INEGI son encomiables (estos incluyen la determinación de las variables coincidentes o adelantadas). Contar con esa base permite avanzar en el estudio de nuevas técnicas que podrían ser aplicables en México, ya sea en forma complementaria o como sustitutas de las que actualmente se usan. Una primera conclusión es que la técnica basada en la aplicación del filtro HP (12, 120) proporciona mejores resultados que las otras técnicas consideradas para estimar tendencias. Esto es relevante para proseguir con el estudio de la mejor metodología que pudiera detectar y anticipar los puntos de giro. Dicha labor es complicada, en principio por la falta de consenso respecto a la definición misma de un punto de giro, como se mencionó en la introducción y como fue enfatizado por Hamilton y Pérez-Quiros (1996).
De las tres metodologías que se estudiaron con detalle, la que resultó con mejores propiedades fue la de la OCDE, mientras que el método SW, aun cuando tiene mejores bases de teoría estadística, resultó difícil de implementar y aunque sus resultados para el índice coincidente no son malos, los del índice adelantado dejan mucho que desear. Un punto interesante es que la cronología que aquí se consideró "oficial" parece estar omitiendo un ciclo entre octubre de 1987 y julio de 1988 (la cresta podría estar relacionada con causas externas, como la crisis ocurrida en Wall Street, mientras que el valle podría reflejar circunstancias internas del país). En resumen, la recomendación que surge de este análisis es que se utilice el método de la OCDE, tanto para estimar tendencias y ciclos como para generar los índices cíclicos coincidente y adelantado. Sin embargo, se visualizan muchas rutas futuras de investigación, como son: incluir otras variables con capacidad anticipatoria del estado de la economía mexicana, dentro de las que se encuentran los indicadores de opinión (una vez que se tengan series de tiempo de longitud suficientemente larga de estos indicadores); buscar la manera de que la suavidad de la tendencia se complemente con la suavidad del ciclo, para mejorar la estimación de ambos componentes (tendencia y ciclo) en función del control de sus respectivas suavidades; mejorar la especificación del modelo SW (quizás al incluir más retrasos para el modelo de pronóstico del indicador coincidente, de manera que mejore su capacidad predictiva); y finalmente, si se continúa con la idea de usar el modelo de SW, incorporar la técnica de Markov-switching para detectar y pronosticar los puntos de giro.
Lo que podría considerarse como utilidad principal del índice adelantado que surge de este trabajo es tener una señal de alerta temprana del estado futuro de la economía, que no es seguro que corresponderá con la entrada a (o salida de) una recesión, pero que vale la pena tener en cuenta por sus consecuencias negativas sobre la actividad económica. Es decir, si el índice adelantado detecta una recesión que en realidad no se presenta, las consecuencias de no haberla previsto son más dañinas que las de no haberla anticipado.
Referencias bibliográficas
Anas, J. y L. Ferrara (2004), "Detecting Cyclical Turning Points: The ABCD Approach and Two Probabilistic Indicators", Journal of Business Cycle Measurement and Analysis, OECD Publishing, CIRET, 2, pp. 193-225. [ Links ]
Bandholz, H. y M. Funke (2003), "In Search of Leading Indicators of Economic Activity in Germany", Journal of Forecasting, 22 (4), pp. 277-297. [ Links ]
Carriero, A. y M. Marcellino (2007), "A Comparison of Methods for the Construction of Composite Coincident and Leading Indexes for the UK", working paper 590, Queen Mary, University of London, Department of Economics. [ Links ]
Castillo, L. E. y F. H. Nieto (2008), "Using the Gibbs Sampler for Obtaining a Coincident Economic Index: A Model-based Approach", ESTADÍSTICA 60 (174-175), pp. 19-42. [ Links ]
Christiano, L. J. y T. J. Fitzgerald (2003), "The Band Pass Filter", International Economic Review, 44 (2), pp. 435-465. [ Links ]
Cogley, T. y J. M. Nason (1995), "Effects of the Hodrick-Prescott Filter on Trend and Difference Stationary Time Series: Implications for Business Cycle Research", Journal of Economics and Dynamic Control, 19 (1-2), pp. 253-278. [ Links ]
Di Fonzo, T. (2005), "The OECD Project on Revisions Analysis: First Elements for Discussion", ponencia presentada en la OECD steseg Meeting, 27-28 de junio, París, disponible en: http://www.oecd.org/dataoecd/55/17/35010765.pdf [fecha de consulta: noviembre de 2012] [ Links ].
Fernández, M. X. (2008), "Comparing Composite Leading Indexes for the Mexican Economy", dissertation in Statistics and Econometrics, University of Essex, Department of Mathematical Sciences. [ Links ]
García-Ferrer, A., R. Queralt y C. Blázquez (2001), "A Growth Cycle Characterisation of the Spanish Economy: 1970-1988", International Journal of Forecasting, 17, pp. 517-532. [ Links ]
Guerrero, V. M. (2008), "Estimating Trends with Percentage of Smoothness Chosen by the User", International Statistical Review, 76, pp. 187-202. [ Links ]
Guerrero, G. V. M. (2011), "Medición de la tendencia y el ciclo de una serie de tiempo económica desde una perspectiva estadística", Realidad, Datos y Espacio: Revista Internacional de Estadística y Geografía, 2 (2), pp. 50-73. [ Links ]
Hamilton, J. D. y G. Pérez-Quiros (1996), "What Do the Leading Indicators Lead?", Journal of Business, 69 (1), pp. 27-49. [ Links ]
Harvey, A. C. (1994), Forecasting, Structural Time Series Models and the Kalman Filter, Cambridge, Cambridge University Press. [ Links ]
Hodrick, R. J. y E. C. Prescott (1997), "Postwar U.S. Business Cycles: An Empirical Investigation", Journal of Money, Credit and Banking, 29 (1), pp. 1-16. [ Links ]
INEGI (Instituto Nacional de Geografía y Estadística) (2010), Nota metodológica. Sistema de indicadores compuestos: Coincidente y adelantado, Aguascalientes, México, Instituto Nacional de Estadística y Geografía, disponible en: www.inegi.org.mx/prod_serv/contenidos/espanol/bvinegi/productos/derivada/coyuntura/sicca/sicca.pdf [fecha de consulta: noviembre de 2012] [ Links ].
Kaiser, R. y A. Maravall (2001), Measuring Business Cycles in Economic Time Series: Lecture Notes in Statistics 154, Nueva York, Springer-Verlag. [ Links ]
Kim, Ch-J. y Ch. R. Nelson (1999), State-space Models with Regime Switching, Cambridge, Ma., The MIT Press. [ Links ]
Maravall, A. y A. del Río (2007), "Temporal Aggregation, Systematic Sampling and the Hodrick-Prescott Filter", Computational Statistics and Data Analysis, 52 (2), pp. 975-998. [ Links ]
Mazzi, G. L. y F. Moauro (2009), "Monthly Assessment of the Euro Area Cyclical Situation", ponencia presentada en el International Seminar on Early Warning and Business Cycle Indicators, 14-16 de diciembre, Scheveningen, The Netherlands, disponible en: http://unstats.un.org/unsd/nationalaccount/workshops/2009/netherlands/ac202-2.asp [fecha de consulta: noviembre de 2012] [ Links ].
Melo, L. F., F. H. Nieto, C. E. Posada, Y. R. Betancourt y J. D. Barón (2002), "Un índice coincidente para la actividad económica de Colombia", Ensayos sobre Política Económica, 40, Bogotá, Banco de la República, pp. 46-68. [ Links ]
Moore, G. H. y V. Zarnowitz (1986), "The Development and Role of the National Bureau of Economic Research's Business Cycle Chronologies", en R. J. Gordon, The American Business Cycle: Continuity and Change, Chicago, University of Chicago Press. [ Links ]
Newey, W. y K. West (1987), "A Simple Positive Semi-Definite, Heterosce-dasticity and Autocorrelation Consistent Covariance Matrix", Econometrica, 55 (3), pp. 703-708. [ Links ]
Nieto, F. H. (2003), "Identifiability of a Coincident Index Model for the Colombian Economy", Borradores Semanales de Economía, 242, Bogotá, Banco de la República. [ Links ]
Nieto, F. H. y L. F. Melo (2001), "About a Coincident Index of the State of the Economy", Borradores Semanales de Economía, 194, Bogotá, Banco de la República. [ Links ]
Nilsson, R. y G. Gyomai (2008), "Cycle Extraction: A Comparison of the Phase-Average Trend Method, the Hodrick-Prescott and Christiano-Fitzgerald Filters", reporte técnico, París, OCDE. [ Links ]
OECD (1997), Cyclical Indicators and Business Tendency Surveys, documento OCDE/GD (97), París, OCDE. [ Links ]
----------, (2008), Handbook on Constructing Composite Indicators: Methodology and User Guide, París, OECD, disponible en: http://www.oecd.org/dataOECD/37/42/42495745.pdf [fecha de consulta: noviembre de 2012] [ Links ].
Park, G. (1996), "The Role of Detrending Methods in a Model of Real Business Cycles", Journal of Macroeconomics, 18 (3), pp. 479-501. [ Links ]
Pedersen, T. M. (2001), "The Hodrick-Prescott Filter, the Slutzky Effect, and the Distortionary Effect of Filters", Journal of Economics and Dynamic Control, 25 (8), pp. 1081-1101. [ Links ]
----------, (2004), "Alternative Linear and Non-Linear Detrending Techniques: A Comparative Analysis Based on Euro-zone Data", en G. L. Mazzi y G. Savio (eds.), Monographs of Official Statistics, document del Third EUROSTAT Colloquium on Modern Tools for Business Cycle Analysis, Luxemburgo, EUROSTAT, pp. 51-85. [ Links ]
Pérez, A. F. (2001), "Indicadores cíclicos: Un indicador adelantado para la economía mexicana", tesina de licenciatura en Economía, México, ITAM. [ Links ]
Prescott, E. C. (1986), "Theory ahead of Business Cycle Measurement", Carnegie-Rochester Conference Series on Public Policy, 25 (1), pp. 11-44. [ Links ]
Ruiz, R. C. D. (2006), "Índices coincidente y adelantado para la economía mexicana: Una aplicación del método de Stock y Watson", tesis de licenciatura en Actuaría, México, ITAM. [ Links ]
Stock, J. y M. Watson (1989), "New Indexes of Coincident and Leading Economic Indicators", NBER Macroeconomics Annual, pp. 351-394. [ Links ]
----------, (1991), "A Probability Model of the Coincident Economic Indicators", en G. Moore y K. Lahiri (eds.), The Leading Economic Indicators: New Approaches and Forecasting Records, Cambridge, Cambridge University Press. [ Links ]
Zarnowitz, V. y A. Ozyildirim (2002), "Time Series Decomposition and Measurement of Business Cycles, Trends and Growth Cycles", working paper 8736, National Bureau of Economic Research, disponible en: http://www.nber.org/papers/w8736 [fecha de consulta: noviembre de 2012] [ Links ].
Este proyecto se pudo llevar a cabo gracias a la colaboración brindada por personal del INEGI. Sobresale en este sentido Andrea C. García, de la Dirección de Desarrollo de Modelos Econométricos Especiales. Asimismo, se agradece la participación de B. R. Sainz, directora de Estudios Econométricos, y de L. Montoya y J. Martínez, de la misma dirección. También es de agradecer el apoyo brindado por Y. Yabuta, directora general adjunta, por E. Ordaz, director general del Servicio Público de Información, y por el mismo E. Sojo, presidente del INEGI. Los comentarios de E. Sainz ayudaron a mejorar la presentación de este documento. Se agradecen también los comentarios y sugerencias de dos árbitros anónimos, y del editor y el secretario editorial de esta revista. La participación de Víctor M. Guerrero fue posible gracias a un periodo sabático otorgado por el ITAM, y a la Cátedra de Análisis y Pronóstico de Series de Tiempo Económicas, asignada por la Asociación Mexicana de Cultura, A.C.
1 Algunas series tienen datos faltantes en los primeros meses, pero el cálculo del índice puede realizarse con sólo 60 por ciento de los datos.
2 Con corrección por heteroscedasticidad y autocorrelación de primer orden, según Newey y West (1987).














