Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista latinoamericana de investigación en matemática educativa
versión On-line ISSN 2007-6819versión impresa ISSN 1665-2436
Relime vol.9 no.2 Ciudad de México jul. 2006
Formación de un discurso escolar: el caso del máximo de una función en la obra de L'Hospital y Maria G. Agnesi
Apolo Castañeda 1
1 Centro de Investigación en Ciencia Aplicada y Tecnología Avanzada del IPN, México. E–mail: apcastane@gmail.com
Fecha de recepción: Abril de 2006
Fecha de aceptación: Enero de 2006
RESUMEN
Este trabajo analiza los aspectos que configuran el discurso matemático escolar de la idea de máximo a través de un estudio socioepistemológico a las obras de L'Hospital y Maria G. Agnesi. Se destaca el proceso en la formación del discurso, los elementos que lo puntualizan, así como el tratamiento a la matemática en cuanto a la forma de definirla, caracterizarla y usarla. El análisis se apoya en los resultados de la investigación de Castañeda (2004) relativa al análisis de obras de texto de antaño, a su tratamiento didáctico y al fenómeno de difusión del saber con relación a la idea de máximo de una función.
PALABRAS CLAVE: Discurso matemático escolar, socioepistemología, máximo de una función.
ABSTRACT
This work analyzes the aspects that configure the school mathematical speech of the idea of maximum, through a socioepistemologic study of the works of L' Hospital and Maria G. Agnesi. The process in the constiyution of the speech is emphasized, the elements that point it out, as well as the treatment to the mathematics regarding the way to define it, to characterize it and to use it. The analysis is supported by the results of the research content in Castañeda (2004) relative to the ancient text analysis, to its didactic handling and the dissusion phenomenon of the knowledge with relation to the idea of maximum of a function.
KEYWORDS: School mathematical speech, socioepistemology, maximum of a function.
RÉSUMÉ
Ce travail analyse les aspects qui donnent forme au discours mathématique scolaire de l'idée du maximum à travers une étude socioépistémologique des oeuvres de L'Hospital et de Maria G. Agnesi. Le processus de la formation du discours se distingue ainsi que les éléments qui le précisent, et que le traitement de la mathématique en ce qui concerne la façon de la définir, de la caractériser et de l'utiliser. L'analyse se soutien sur les résultats de la recherche de Castañeda (2004) concernant l'analyse des oeuvres de textes anciens, son traitement didactique et les phénomène de diffusion du savoir en relation a l'idée du maximum d'une fonction.
MOTS CLÉS: Discours mathématique scolaire, socioépistémologie,maximum d'une fonction.
RESUMO
Este trabalho analisa os aspectos que configuram no discurso matemático escolar da idéia de máximo através de um estudo socioepistemológico das obras de L'Hospital e Maria G. Agnesi. Destaca–se o processo na formação do discurso, os elementos que o caracterizam, assim como o tratamento da matemática enquanto forma de defini–la, caracterizá–la e usá–la. A análise se apóia nos resultados da investigação de Castañeda (2004) relativa à análise de obras de texto antigos, em seu tratamento didático e no fenômeno de difusão do saber em relação a idéia de máximo de uma função.
PALAVRAS CHAVE: Discurso matemático escolar, socioepistemologia, máximo de uma função.
ANTECEDENTES
El libro de texto en el ámbito escolar cumple, entre otras funciones, la de fuente de consulta del saber que se estudia, así como la de organizador en la creación de programas de estudio, estructuración de cursos y seminarios, o de situaciones específicas en la preparación de clases, elaboración de problemarios, guías de estudio o exámenes. Con una mirada más profunda, se puede advertir una doble naturaleza en las obras de texto: como una obra de texto, referida a los elementos de estructura y organización, y a aquellos tocantes a su contenido, es decir, al discurso que contiene.
En este artículo nos referimos a esta segunda componente, e identificamos algunos elementos que caracterizan un discurso matemático escolar, considerando el tipo de actividades matemáticas, las prácticas que involucra (entendidas como cierto tipo de actividades que en el ámbito escolar no son rutinarias, las cuales contienen aspectos procedentes del entorno social y cultural, y aportan significado a los conceptos matemáticos), así como el enfoque, la perspectiva e ideología que asume el autor en relación con el saber matemático.
Las preguntas referidas a la naturaleza del saber, a su estructuración didáctica y a las componentes del discurso (Van Dijk, 1998) se ubican en los ámbitos didáctico y epistemológico. Por ello, nuestra investigación se apoya en el análisis de libros, específicamente en obras de antaño sobre cálculo diferencial, para explicar el proceso de construcción del discurso de la matemática escolar2 del máximo de una función. Nos apoyamos en los resultados de investigación socioepistemológica de Castañeda (2004), donde se aborda el estudio de la evolución del tratamiento didáctico del punto de inflexión en las obras de L'Hosptial y Maria G. Agnesi, y se destaca ampliamente el tratamiento que estos autores le dan a ciertas ideas, como la de máximo de una función.
UN ACERCAMIENTO A LA NOCIÓN DE DISCURSO
Marta Marcolini y Javier Perales (2005), quienes citan a Cantoral, señalan que el discurso matemático escolar es aquel que atiende a la formación de consensos en la noosfera en torno a un saber escolar y a aspectos relativos a su tratamiento y características, incluyendo aspectos de organización temática y profundidad expositiva. Dos elementos que definen al discurso matemático escolar (Buendía, 2004) son, por una parte, los libros de texto en los que se apoya la enseñanza; por otra, el tipo de explicaciones que usa el docente en clase, las cuales se suelen basar en experiencias cercanas del individuo para referirse a un fenómeno.
Las obras escolares son un apartado del discurso matemático escolar, por lo cual están sujetas a las restricciones de la noosfera y moldean su contenido de acuerdo con las exigencias de la sociedad (Chevallard, 1991). Es posible encontrar diferencias en el análisis que hacen los libros, pues aún tratándose de los mismos contenidos hay notables diferencias en cuanto al tipo de explicaciones, metáforas, tipo de ejemplos, clases de problemas, actividades, mientras que en cuanto a la componente epistemológica, existen diferencias en el tipo de argumentos, manejo de conceptos, definiciones, teoremas, etc. Observemos, por ejemplo, el tipo de resultados que presenta R. Martínez (2005) en su estudio de corte didáctico sobre la idea de pendiente en dos libros de texto: el primer caso (geometría elemental de Hemmerling) distingue el carácter invariante de la pendiente como argumento para definirle; en el segundo (álgebra de Leithold) denota a la pendiente como una razón de cambio.
Por otra parte, suele creerse que el discurso escolar se elabora de una fuente matemática que es inmutable al tiempo y al espacio; de ahí que el saber escolar adquiera una idea de preexistencia y tienda a creerse que los esfuerzos didácticos no deben ni siquiera pensar en modificar este discurso. Sin embargo, trabajos socioepistemológicos como los de Cantoral (1990), Cordero (1994) y Buendía (2004) refuerzan la idea de que ciertas prácticas, como la predicción, son fuente de la reorganización de la obra matemática y permiten el rediseño del discurso matemático escolar.
El trabajo de Cantoral (2001) ilustra con un resultado, de carácter epistemológico, la formación de un discurso escolar a partir de la reinterpretación de los significados en torno al concepto de integral. Afiirma que la integral puede entenderse de diferentes maneras, según se trate el programa teórico desde donde se está definiendo: la de Cauchy–Riemann, la de Newton–Leibniz y la de Wallis. "Las tres presentaciones (..) no sólo difieren por la época en la que fueron desarrolladas, sino también respecto de las explicaciones de las que echan mano"(Cantoral, 2001).
Actualmente, estas visiones no coexisten dentro del discurso escolar, pues ha ocurrido una especie de consenso sobre el modelo de Cauchy–Riemann; todos los profesores lo usan en clase. Las preguntas que surgen al respecto son: ¿Cuál de las tres formulaciones de la integral favorece el aprendizaje de los alumnos? ¿Cómo ocurrió esta elección? Tales preguntas problematizan el saber matemático y plantean la posibilidad de reorganizar el discurso.
Los resultados de la investigación epistemología constituyen una fuente de información para conocer la naturaleza de las ideas. Además, permiten reconocer el hecho de que la matemática ha sido construida ajena a los sistemas de enseñanza, cumpliendo con intereses y expectativas específicas, por lo que su introducción en los sistemas de enseñanza obliga a un conjunto de transformaciones adaptativas (Chevallard, 1991). En tal proceso ocurre un fenómeno al que Chevallard llama despersonalización, donde un saber se le desasocia de las problemáticas originales y situaciones que le daban sentido y razón de ser. De ello resulta un nuevo saber, pero desprendido de sus orígenes, pues queda reducido sólo a definiciones y teoremas que lo presentan como un saber finamente construido; no permite recrear los conflictos, conjeturas e interpretaciones originales de donde surgieron sus primeros significados. No obstante, la tesis socioepistemológica que se desarrolla en Castañeda (2004) muestra que no se produce una despersonalización absoluta, ya que en una transposición didáctica permanecen ciertas practicas de referencia.
Una forma de despersonalización es lo que Chevallard llama la textualización del saber, en el que se identifica una primera ruta que conduce a la formación un discurso matemático escolar; los saberes se organizan, sistematizan y, en el caso de las obras con carácter escolar, se le incorpora una génesis ficticia con el propósito de facilitar su estudio.
El caso de la formación de un discurso escolar
El trabajo de Castañeda (2004) presentó un estudio sobre el intrincado proceso en la construcción del discurso escolar del cálculo en dos obras de difusión: el Analyse des infiniment petits, del marqués L'Hospital, y el Analitiche Institutioni, de Maria Gaetana Agnesi3. En estos libros, el saber que se dispuso para la difusión no sólo resultó de una selección arbitraria por parte de los autores, sino que la comunidad académica participó legitimando ese saber mediante una especie de consenso, al validarlas y reconocer su importancia.
También aparecieron diversas justificaciones, desde el ámbito sociocultural, que se vertieron para definir y configurar ese saber. Por ejemplo, las explicaciones de carácter geométrico que contienen dichas obras tienen una raíz histórica en Descartes, ya que su pensamiento analítico se ve reflejado en las explicaciones sobre el comportamiento diferencial en una curva, primero en L'Hospital y cincuenta años después en Agnesi. Este fenómeno de consenso muestra la existencia de acuerdos y criterios unificados, es decir, un primer rasgo de institucionalización; además, el discurso institucionalizado tiende a reproducirse por una especie de acción hegemónica que sistematiza el saber matemático. La obra de L'Hospital es un claro ejemplo de la sistematización del saber bajo un esquema de obra de difusión y, más aún, legitimado por la institución científica más importante de aquella época: la Academia de Ciencias de París.
El ambiente de difusión, que encabezó Fontenelle4, resaltó la importancia de la publicación como medio para la comunicación de las ideas. De este modo, las obras promovieron la divulgación de los trabajos de las comunidades académicas y configuraron un nuevo tipo de obras con contenidos adaptados a las nuevas circunstancias de difusión, en las que se usaron nuevas formas de estructurar y organizar el conocimiento con una evidente preocupación por exponer un discurso claro.
La formulación del discurso escolar del cálculo no sólo proviene de la transposición didáctica del saber erudito, sino que involucra otros factores ajenos a la noosfera para la selección y conformación de un saber a enseñar; entre ellas, están las prácticas socialmente compartidas que se toman en cuenta para adaptar un saber a su versión didáctica. L'Hospital asumió la estructuración de un nuevo discurso del cálculo, ya que intentó dotar de claridad al discurso mediante un lenguaje accesible a la población no especializada. Esto produjo una transposición didáctica del cálculo en el que las ideas aparecieron adaptadas a una circunstancia específica –la difusión– y se organizaron en una secuenciación lógica, atendiendo a la evolución y profundidad de las ideas. Por tanto, no se entendió el ejercicio de difusión como la reimpresión y publicación a gran escala de los originales de Leibniz; L'Hospital no redujo la tarea a una trascripción fiel de Leibniz ni compiló sus escritos, sino también hubo consideraciones teóricas reconocidas como ideas propias.5
EL CASO DE LA IDEA DE MÁXIMO
La tarea de fortalecer el discurso matemático escolar no se reduce a una tarea de ampliación de los conceptos, debido a que los resultados de carácter didáctico y epistemológico aportan elementos para una tarea de reorganización y/o reconstrucción del discurso. La epistemología en general se propone revisar la ciencia para definir su origen, determinar sus criterios de validez, revisar su consistencia lógica y predecir sucesos, entre otras acciones (Albert, 1998). Sin embargo, es posible llevar esta práctica hasta niveles más específicos que las disciplinas científicas exigen y, al menos para los matemáticos educativos, esta disciplina puede proveer de explicaciones detalladas sobre los procesos por los que se desarrolla una idea matemática, observando las condiciones y contextos pasados, los estancamientos, los momentos donde se agregan significados –con lo que se amplían campos de estudio–o los puntos en la historia en que se descartan ideas asociadas a los conceptos en cuestión (Sierpinska & Lerman, 1996).
Aunque un estudio histórico nos aproxima al origen de las ideas, este acercamiento no permite interpretaciones más finas de aquellas situaciones, explicaciones y conjeturas que validaron y reorientaron las ideas. Si se analizan con más detalle las circunstancias que posibilitaron el origen de un saber, se reconocen nuevos elementos que intervienen como variables en las investigaciones epistemológicas: los aspectos sociales y culturales que inciden en la construcción del conocimiento.
Para los socioepistemólogos, la búsqueda de evidencias no termina con ubicar la serie de sucesos que culminaron con una idea, sino con la determinación de aquellas prácticas asociadas al conocimiento matemático, que proceden de los ámbitos social y cultural. Con esta idea, en Castañeda (2004) se analizó la obra de L'Hospital para identificar, entre otras cosas, las formas usadas para caracterizar las ideas, los argumentos para exponer y definir los conceptos.
Leibniz (1684) hace una amplia descripción del comportamiento infinitesimal, en el que caracteriza al máximo por un mismo argumento geométrico, usando dos diferentes criterios. El primero, a través de la comparación de estados, donde precisa que el máximo queda determinado por la línea GF (ubica la mayor de las ordenadas de todas las posibles; obsérvese que en la imagen aparecen otras dos ordenadas, CD y LN). El segundo, a través de una condición geométrica, explica que la tangente sobre la curva en el punto máximo es paralela al eje de las abscisas (Figura 1).

Más adelante, aborda una caracterización a través del método algebraico de las diferencias.
En las obras de L'Hospital (1696) y Agnesi (1748) se presenta una nueva versión del cálculo para su difusión, que se distingue de la expuesta por Leibniz, debido a la intencionalidad con la que fueron escritas. El discurso de L'Hospital y Maria G. Agnesi incorpora, además de las reglas concernientes al método del cálculo, explicaciones sobre el comportamiento variacional de las curvas. Por ejemplo, las representaciones gráficas de la naturaleza poligonal de las curvas, la magnitud de las diferencias de orden superior o explicaciones verbales del comportamiento de la curva en vecindades infinitesimales.
Sin embargo, este discurso no sólo enuncia definiciones. L'Hospital y Maria G. Agnesi conforman un formato presentar las ideas matemáticas, caracterizado por un orden y una secuencia lógica en la exposición de los contenidos6. Así, se puede leer en la introducción a la obra de Agnesi su intención por abordar ideas en forma clara y accesible, señalando "los beneficios con ese orden natural que proporciona, quizás el de mejor instrucción y agrandar más la luz". La visión didáctica del cálculo en estas obras se identifica al hallar múltiples explicaciones sobre una misma idea, pero desde diferentes acercamientos, para ofrecer una noción más elaborada. Este tratamiento se mantiene a lo largo de estos libros, incluyendo la sección de problemas, donde se observa un planteamiento diversificado de los problemas más representativos7. L'Hospital aclara en su introducción "hago solamente algunos ejemplos seleccionados", dejando en evidencia el ejercicio de selección para organizar el contenido de su libro.
La tercera sección del libro de L'Hospital, titulada "Uso del cálculo de las diferencias para encontrar las ordenadas mayores y las menores, a lo que se reducen los problemas de máximos y mínimos", revela un interés geométrico por hallar las ordenadas que cumplan con esta propiedad. Podemos distinguir en sus argumentaciones al menos tres aproximaciones distintas que muestran el significado asociado a la noción de máximo o mínimo.
La primera argumentación está basada en la noción de tamaño. Centra su propiedad en discriminar, entre un conjunto de ordenadas, la que cumpla con la característica de ser la más grande o más pequeña. L'Hospital explica:
Sea MDM una línea curva cuyas ordenadas PM, ED y PM sean paralelas entre sí, tal que al incrementarse continuamente la abscisa AP, la ordenada PM crece también hasta cierto punto E, después del cual disminuye. Entonces, la línea ED será denominada la mayor o la menor ordenada (Figura 2) [L'Hospital, 1696, p. 41. Traducción libre]
La segunda se fundamenta en identificar el signo de las diferencias, en una región muy cercana al máximo.
Si al crecer AP PM también crece, es evidente que su diferencia Rm será positiva con relación a la de AP y que, por lo contrario, cuando PM disminuya al crecer la abscisa AP, su diferencia será negativa (Figura 3) [L'Hospital, 1696, pp. 41–42. Traducción libre].
Afirma L'Hospital que una diferencia no puede convertirse de positiva a negativa si no se hace pasar por cero, o por infinito.
De esta manera, el máximo es nombrado como un punto por el que las diferencias cambian de signo.
El tercer argumento se sustenta en observar la posición relativa que guarda la subtangente y la tangente, a medida que se consideran nuevos puntos en la curva. El máximo se alcanza cuando la tangente se vuelve horizontal y paralela a la subtangente; de manera análoga, esto pasa con el mínimo.
L'Hospital explica: supóngase una tangente en el punto M, y su respectiva subtangente PT (Figura 4).

Si la subtangente PT aumenta [hacia la izquierda] a medida que MP se acerca a DE, es claro que cuando se construya la tangente en el punto D, la subtangente tiene una magnitud infinita. De esta forma, cuando AP rebasa a AE, la subtangente PT se vuelve negativa de positiva, o al contrario.
L'Hospital agrega una nueva componente a su obra, que consiste en problemas resueltos a modo de ejemplo, los cuales aparecen al final del apartado. En ello se observa un énfasis sobre el manejo algebraico para la solución (propiedades infinitesimales), como ilustra la Figura 5.

Supposons que x3 + y3 = axy (AP= x, PM= y y AB = a), exprime la nature de la courbe MDM (L'Hospital. 1696, p. 42).
Al tomar las diferencias, tenemos 
para que la diferencia dy= 0, consideramos que el numerador sea igual a cero:

al sustituir en la ecuación inicial, se halla el valor para AE, 
En el capítulo tercero del libro de Maria Agnesi, que lleva como título "Donde se estudia el método para el cálculo de máximos y mínimos", se distinguen cuatro caracterizaciones sobre estas ideas. La primera hace un reconocimiento de lo variacional; en la segunda aparece nuevamente la idea presentada por L'Hospital sobre el comportamiento de la subtangente; la tercera está referida a una propiedad de las diferencias, y la cuarta realiza una puntualización sobre una propiedad analítica.
Sobre la primera caracterización, a la que hemos denominado sobre la naturaleza dinámica de las curvas, Agnesi dice que el máximo en una curva se alcanza cuando en una sucesión de ordenadas se alcanza la mayor y para el mínimo, la menor.
72. Se in una curva qualunque, le di cui ordinate sieno parallele, crescendo la assisse BC continovamente, cresca altresì l'ordinata CG sino ad un certo punto E dopo di cui vada calando, o non vi sia più ordinata di sorta alcuna; o pure al contrario crescendo l'assissa, l'ordinata CG vada continivamente calando sino ad un certo punto E, dopo di cui, o cresca, o più non vi sia; l'ordinata EF si chiama la Massima, o la Minima (Agnesi, 1748, p. 527).
Una segunda caracterización se basa en la propiedad geométrica que guarda la subtangente respecto a la curva. Es claro que, al aproximarse CG a EF, la subtangente AC será siempre la mayor, y cuando CG cae en EF, la tangente será paralela a BC; por consecuencia, la subtangente será infinita (Figura 6).

La tercera caracterización identifica las propiedades infinitesimales: al ser semejantes los triángulos ACG y GIH, se determina la relación AC : CG :. GI : IH. Al dejar fluir las ordenadas, el triángulo GIH se acercará hacia el punto F(en este caso, el máximo), CG permanecerá finita, pero GI e IH tendrán valores cada vez más pequeños. Cuando una nueva ordenada coincide con EF, entonces tenemos dy=0 . Este es el punto máximo (Figura 6).
La cuarta caracterización se sustenta en un principio analítico expresado como regla: el lugar donde dy=0 o dy = ∞ bien se determina un máximo o mínimo. Por consiguiente, dada la ecuación de la curva, para determinar un máximo o un mínimo se deberá diferenciar bajo el supuesto de que dy = 0 o dy=∞ ; de esta forma se obtendrá el valor de la abscisa x, al punto en el que corresponde la máxima o mínima ordenada.
Agnesi concluye este apartado con la presentación de un ejemplo, pero agrega una variante más, ya que muestra un problema de optimización. Dado el rectángulo ADCB , se requiere la recta mínima QH que pase por el punto C del ángulo QAH.

Sea AB = a, BC = b, BH = x, de lo que se obtiene  .Por triángulos semejantes, HBC, HAQ, se determina
.Por triángulos semejantes, HBC, HAQ, se determina
la relación  , esto es
, esto es 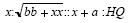 . Al despejar, resulta que
. Al despejar, resulta que  .
.
Antes de este problema, se han analizado aspectos de optimización en una situación similar. Para este caso, explica que HQ puede considerarse como la ordenada de una curva, por lo cual es posible HQ = y. Al sustituir de la ecuación anterior, se tiene que  . Al diferenciar, resulta
. Al diferenciar, resulta 
Para que sea cero la expresión  , es suficiente que x3 – abb=0, por lo que al considerar la suposición de dy = 0, saldrá
, es suficiente que x3 – abb=0, por lo que al considerar la suposición de dy = 0, saldrá  y, por tanto, BH =
y, por tanto, BH =  , la cual determina la magnitud del segmento para que HCQ sea el segmento de longitud mínima. Por el contrario, al considerar el supuesto que dy = ∞ , se obtendrá que
, la cual determina la magnitud del segmento para que HCQ sea el segmento de longitud mínima. Por el contrario, al considerar el supuesto que dy = ∞ , se obtendrá que  determina una cantidad imaginaria, que no nos dará el mínimo.
determina una cantidad imaginaria, que no nos dará el mínimo.
RESULTADOS DEL ANÁLISIS
Se identificaron tres áreas que estructuran los capítulos tocantes al estudio del máximo y mínimo en las obras de L'Hospital y Agnesi: 1) las formas de caracterización del saber, referido a las razonamientos y explicaciones que conducen a una definición; 2) el manejo operatorio, que atañe al uso de las técnicas y procedimientos algebraicos, y 3) los problemas, que se muestran como ejemplos o problemas resueltos.
En torno a las caracterizaciones, L'Hospital presenta tres formulaciones a la idea de máximo. La primera está basada en la noción de tamaño (argumento geométrico), que retoma de Leibniz; la segunda, concerniente a la naturaleza dinámica de las curvas (argumento geométrico con referente analítico), parte de reconocer al máximo desde una exploración geométrica, pero se acompaña de un planteamiento variacional; la tercera, referente a la subtangente de magnitud infinita (geométrico–analítico), define el comportamiento de la subtangente a partir de la variación de las abscisas.
Agnesi, por su parte, expone cuatro caracterizaciones. La primera se argumenta con la idea de variación; la segunda, a la que llamamos signo de las diferencias infinitesimales (sobre un argumento analítico), destaca que muy cerca del máximo las diferencias pasan de un signo a otro; la tercera alude a la propiedad infinitesimal (analítico), donde explica que cerca del máximo ocurren las variaciones más pequeñas, mientras que la cuarta, denominada propiedad analítica, explica una regla: en un máximo se determinan diferencias nulas o infinitas.
La existencia de varios argumentos acerca de una misma idea es un rasgo que distingue al discurso de L'Hospital y Agnesi. Sobresale el tratamiento geométrico–analítico, en el que se explica el comportamiento de las diferencias en vecindades muy pequeñas sobre las curvas geométricas, donde aparecen descripciones muy detalladas del comportamiento infinitesimal, que también se explica, y se identifican regularidades.
En Leibniz se identifican tres caracterizaciones: las dos primeras son de naturaleza geométrica, mientras que la tercera, de corte analítico, hace mención al método. Por su parte, en L'Hospital y Agnesi se abunda en las explicaciones, se agregan nuevas, se organiza este saber dentro de un esquema evolutivo y lógico de las ideas, lo cual se percibe a lo largo de estos libros –en Castañeda (2004) se explica con mayor detalle– y se agregan más imágenes, que también cumplen una función didáctica. No se abandona el paradigma leibniziano, pero es notable el nuevo tratamiento del cálculo orientado a la difusión.
COMENTARIOS FINALES
La exposición de L'Hospital y Agnesi no se reduce a la formulación de una definición, sino se acepta una necesidad de los autores por explicar una misma idea con varias argumentaciones, ya sean verbales, geométricas, algebraicas y analíticas, o bien una combinación de todas ellas. En Castañeda (2004) se sostiene que el carácter de estas obras de difusión hizo necesario que el saber a exponer contara con más formas de caracterizarlo para garantizar que los lectores, no necesariamente expertos, pudieran acercarse a estas novedosas ideas.
El tratamiento a través de múltiples caracterizaciones constituye un elemento determinante para estudiar regularidades; así, las gráficas, las explicaciones verbales, los ejemplos, etc., convergen a una misma idea. Con ello, en teoría las ideas adquieren significados más amplios.
La presentación de los contenidos no es aleatoria. Tanto Agnesi como L'Hospital exponen las ideas matemáticas atendiendo a una secuencia lógica, producto de un interés explícito por organizar y presentar las ideas en forma didáctica; desde las más simples hasta las más complejas. Un rasgo notable es la inclusión de ejemplos comentados y, en el caso de Agnesi, de algunos problemas resueltos, con el objetivo de movilizar al lector para que usara las ideas matemáticas estudiadas y las aplicara en situaciones concretas.
Por el carácter innovador de estas obras, por el ambiente de difusión que se vivía en esa época, por la publicación masiva –a diferencia de los artículos de Leibniz, que fueron publicados en el Acta Eroditorum–, los libros de L'Hospital y Agnesi tuvieron amplia aceptación. Así lo constatan pasajes históricos donde se narra que la Academia de Ciencias de París avaló estas publicaciones y reconoció en ellas un esfuerzo muy importante para la difusión. Fontenelle, secretario de la Académie des Sciences, ante la aceptación que gozaba el texto de L'Hospital, trató de enfrentar a la oposición haciendo notar dos ideas importantes; el carácter esclarecedor de la obra ante las cuestiones del infinito y la postura de L'Hospital como redactor del libro:
"El señor L'Hospital decidió comunicar sin reserva los secretos ocultos de la nueva geometría, y lo hizo en el famoso libro Analyse des infiniment petits, que publicó en 1696. En él fueron revelados todos los secretos del infinito geométrico y del infinito; en una palabra, de todos estos diferentes órdenes de infinitos que se levantan los unos por encima de los otros, y forman un edificio más asombroso y más audaz que la mente humana jamás se haya atrevido a imaginar" (Cambray, 1998)
A la obra de L'Hospital siguió la de Reyneau8, titulada Analiza démontrée, que apareció en 1708; después, en 1745, Agnesi escribió su libro con un esquema muy cercano al de L'Hospital. No hubo una declaración explícita acerca de los contenidos y de la manera en que Agnesi los abordara, pero fue claro se estableció una especie de consenso con relación a la forma de tratar el saber, incluyendo aspectos de organización temática y profundidad expositiva.
REFERENCIAS BIBLIOGRÁFICAS
Albert, A. (1998). Introducción a la epistemología. En R. Farfán (Coord. y Ed.), Antologías Número II (pp. 1–28). México: Cinvestav (Programa Editorial, Área de Educación Superior, Departamento de Matemática Educativa). [ Links ]
Agnesi, M. G. (1748). Instituzioni analitiche ad uso della gioventú italiana (tomo I). Milano, Italia: Nella Regia Ducal Corte. [ Links ]
Arrieta, J. (2003). Las prácticas de modelación como proceso de matematización en el aula. Tesis de doctorado, Cinvestav, México. [ Links ]
Arsac, G. (1992). L'evolution d'une théorie en didactique: l'exemple de la transposition didactique. Recherches en Didactique des Mathematiques, 12 (1), 7–32. [ Links ]
Buendía, G. (2004). Una epistemología del aspecto periódico de las funciones en un marco de prácticas sociales. Tesis de doctorado, Cinvestav, México. [ Links ]
Cambray, R. (1998). Introducción: L'Hospital y el primer libro de texto de cálculo diferencial. En Carlos Álvarez y Rafael Martínez (Eds.), Análisis de los infinitamente pequeños para el estudio de las líneas curvas (pp. 1–14). México: Coordinación de Servicios Editoriales, Facultad de Ciencias de la UNAM, Col. Mathema. [ Links ]
Cantoral, R. (2001). Sobre la articulación del discurso matemático escolar y sus efectos didácticos. En G. Beitia (Ed.), Acta Latinoamericana de Matemática Educativa, 14 (1), 64–75. [ Links ]
Cantoral, R. (1990). Categorías relativas a la apropiación de una base de significados propios del pensamiento físico de la teoría elemental de las funciones analíticas. Tesis de doctorado, Cinvestav, México. [ Links ]
Castañeda, A. (2004). Una aproximación a la construcción social del conocimiento. Estudio de la evolución didáctica del punto de inflexión. Tesis de doctorado, Cicata, México. [ Links ]
Castañeda, A. (2002). Estudio de la evolución didáctica del punto de inflexión: una aproximación socioepistemológica. Revista Latinoamericana de Investigación en Matemática Educativa, 5 (2), 27–44. [ Links ]
Cordero, F. (1994). Cognición de la integral y la construcción de sus significados (un estudio del discurso matemático escolar). Tesis de doctorado, Cinvestav, México. [ Links ]
Chevallard, Y. (1991). La transposición didáctica. Del saber sabio al saber enseñado. Buenos Aires, Argentina: Aique Grupo Editor. [ Links ]
Leibniz, G. (1684). Nova methodus determinandi maxima & minima. Acta Eruditorum. E.T. Guntheal. [ Links ]
L'Hospital, A. (1696). Analyse des infiniment Petits pour l'intelligence des lignes courbes Paris, France, ACL–Editions (reimpresión, 1988. [ Links ]
Marcolini, M. y Perales, J. (2005). La noción de predicción: Análisis y propuesta didáctica para la educación universitaria. Revista Latinoamericana de Investigación en Matemática Educativa, 8 (1), 25–68. [ Links ]
Martínez Sierra, G. (2005). Los procesos de convención matemática como generadores de conocimiento. Revista Latinoamericana de Investigación en Matemática Educativa, 8 (2), 195–218. [ Links ]
Martínez, R. (2005). La pendiente y su variación: un estudio didáctico y cognitivo. Tesis de maestría, Cimate–Facultad de Matemáticas, Universidad Autónoma de Guerrero. México. [ Links ]
Malet, A. (2002). Divulgación y popularización científica en el siglo XVIII: entre la apología cristiana y la propaganda ilustrada. Quark. Divulgadores de la Ciencia 26. Obtenido de www.prbb.org/quark/26/default.htm. [ Links ]
Sierpinska, A. & Lerman, S. (1996). Epistemologies of mathematics and of mathematics education. En A. J. Bishop et al. (Eds.), Internacional Hanndbool of Mathematics Education (pp. 827–876). Dordrecht, Holland: Kluwer, AP. [ Links ]
Van Dijk, T. (1998). Ideología. Barcelona, España: Gedisa. [ Links ]
2 A principios del siglo XVIII no existía el libro escolar como tal. Habían libros de difusión, cuya intención era divulgar los conocimientos matemáticos que los círculos académicos producían. Estos libros se estructuraban a manera de curso y contenían ejercicios y problemas.
3 Existe una traducción al inglés de la obra Maria Gaetana Agnesi, Analytical Institutions, realizada por John Colson, y que en 1801 publicó en Londres la editorial Taylor and Wilks.
4 Secretario perpetuo de la Academia de Ciencias de París. I nició sus funciones en 1699, su cargo era vitalicio y tenía como función redactar los resúmenes anuales de la actividad de la Academia, así como los Éloges o necrológicas oficiales (Malet, 2002).
5 Se puede encontrar una amplia discusión en el índice de biografías de la Facultad de Matemáticas y Estadística de la Universidad de St Andrews, Escocia, que puede consultarse en la página electrónica http://www–groups.dcs.st–and.ac.uk/~history/BiogIndex.html.
6 Este orden responde a un criterio del autor.
7 Existió un interés generalizado en el ambiente académico de aquella época por la resolución de problemas de geometría relativos a máximos y mínimo, así como de tangentes y subtangentes.
8 Reyneau estuvo allegado a debates del cálculo organizados por Rolle en París cuando escribió su libro Analice démontrée, publicado en 1708. Reyneau obtuvo una copia de lecciones que Bernoulli preparó para L'Hospital.
















