El uso de las gráficas en el discurso matemático escolar. Un estudio socioepistemológico en el nivel básico a través de los libros de texto ¹

 

Francisco Cordero ² Rebeca Flores ³

 

² Departamento de Matemática Educativa DME – Cinvestav–IPN. En estancia sabática en la Universidad Católica de Valparaiso. Chile (julio 2006–julio 2007). México, D.F. E–mail: fcordero@cinvestav.mx

³ Centro de Formación Básica y Sensibilización Artística México E–mail: rebefe87@hotmail.com

 

Fecha de recepción: 16 de abril de 2006
Fecha de aceptación: 26 de enero de 2007.

 

RESUMEN

La siguiente investigación contribuye al planteamiento fundacional de la aproximación socioepistemológica, la cual consiste en considerar a las prácticas sociales como los elementos constituyentes del conocimiento matemático: ¿qué es lo que norma lo que se construye como conocimiento matemático? Tal planteamiento ofrece indicadores para desarrollar una matemática funcional en el sistema educativo. Realizamos así un estudio del uso de las gráficas en el discurso matemático escolar (dme), el cual consiste en comprender a la graficación como una práctica social en su proceso institucional y no como una representación del concepto de función. Dicho estudio lo realizamos a través de los libros de texto del nivel básico para ir creando un marco de referencia que ayude a resignificar el conocimiento matemático en cuestión.

PALABRAS CLAVE: Uso de las gráficas, resignificación y discurso matemático escolar.

 

ABSTRACT

The following research contributes to the foundational formulation of the socioepistemologic approach, which consists of considering the social practices as the constituents of the mathematical knowledge: What is what rules the construction of the mathematical knowledge? Such formulation offers indicators to develop a functional mathematics in the educational system. We carry out thus a study of the use of the graphics in the school mathematical speech (dme), which consists of understanding the graphics as a social practice in its institutional process and not like a representation of the concept of function. We carry out the study through the textbooks of basic level to create a reference frame that helps assign a new meaning to the mathematical knowledge in question.

KEY WORDS: Use of graphics, assign new meaning, school mathematical speech

 

RESUMO

A seguinte investigação contribui ao planejamento fundamental da aproximação socioepistemológica, a qual consiste em considerar as práticas sociais como os elementos constituintes do conhecimento matemático: Que é o que normatiza, o que se constrói como conhecimento matemático? Tal planejamento oferece indicadores para desenvolver uma matemática funcional no sistema educativo. Realizamos, assim, um estudo do uso dos gráficos no discurso matemático escolar (dme), no qual consiste em compreender os gráficos como uma prática social, em seu processo institucional, e não como uma representação do conceito de função. Realizamos esse estudo através dos livros de texto, do nível básico, para ir criando um marco de referência que ajude a resignificar o conhecimento matemático em questão.

PALAVRAS CHAVE: Uso de gráficos, resignificação e discurso matemático escolar.

 

RÉSUMÉ

La recherche suivante contribue à l'exposé des fondements de l'approche socioépis–témologique, laquelle consiste à considérer les pratiques sociales comme éléments constituants de la connaissance mathématique: Qu'est–ce qui norme ce qui est construit en tant que connaissance mathématique? Cet exposé offre des indicateurs pour développer une mathématique fonctionnelle dans le système éducatif. Nous réalisons dans ce cadre une étude de l'usage des graphiques dans le discours mathématique scolaire (dms), lequel consiste à comprendre la graphication en tant que pratique sociale dans son processus institutionnel et pas comme une représentation du concept de fonction. Nous avons réalisé cette étude à travers des manuels de niveau basique à fin de créer un cadre de référence qui aide à la re–signification de la connaissance mathématique en question.

MOTS CLÉS: Usage de graphiques, re–signification et discours mathématique scolaire.

 

INTRODUCCIÓN

En este artículo reportamos los resultados de una investigación cuyo propósito fue ofrecer indicadores que contribuyan a favorecer el desarrollo de una matemática funcional⁴ en el sistema educativo. La relevancia de la investigación está en los aspectos teóricos–metodológicos que se formularon. Para la consecución del objetivo del estudio se estableció el concepto "uso de las gráficas" como parte del marco teórico de la investigación a partir del que se hace un estudio del discurso matemático escolar (dme) ⁵ mediante el análisis de libros de texto del nivel básico, donde se comprende (hipotéticamente) a la graficación como una práctica social en su proceso institucional.

La metodología para vigilar dicha hipótesis fue analizar, en el discurso de los libros de texto del nivel básico (primaria y secundaria), el "uso" que se le da a las gráficas con respecto a sus funcionamientos y sus formas según las situaciones específicas.

Como resultado de la investigación se identificaron y caracterizaron tres momentos del uso de las gráficas:

• El uso del síntoma de la gráfica de la función.

• El del uso de la gráfica de la función.

• El del uso de la curva.

Estos momentos expresan un desarrollo del uso de las gráficas en el que el funcionamiento y formas de las gráficas en juego dependen de los procesos institucionales, como es el caso de esta investigación, en nivel básico.

Presentamos a continuación la formulación de la investigación y sus resultados, articulando los conceptos "discurso matemático escolar", "resignificación" y "uso de las gráficas^" en la aproximación socioepistemológica.

 

LA INVESTIGACIÓN

Se parte de diversas consideraciones. Una de ellas está relacionada con la problemática de la enseñanza y el aprendizaje de la matemática en educación superior, que se ocupa del problema que plantea la constitución social del saber matemático avanzado y su ingreso al sistema didáctico (Cantoral & Farfán, 2003). En esta problemática, el rol que comúnmente juega el Calculus es como la materia medular en el currículo de las matemáticas, define una parte anterior y posterior: el precálculo y la matemática avanzada (Cordero, 2003, 2005 y 2006a). Con dicho rol las gráficas de las funciones han sido tratadas, en la disciplina de la matemática educativa, a través de diferentes programas de investigación, con enfoques a la visualización, a la integración de la tecnología en la educación y a la construcción de un lenguaje gráfico (Cordero, 2006b).

En esta investigación consideramos a las gráficas de las funciones como argumentaciones⁶ del Calculus (Suárez, 2006, Buendía & Cordero 2005, Buendía, 2004, Cordero & Solís, 2001; Cordero, 1998, 2001 y 2003; Rosado, 2004; Hernández, 2004; Campos, 2003 y Domínguez, 2003), donde pretendemos sean el resultado de ciertas prácticas sociales que ha generado el conocimiento del Calculus. Por lo que convenimos centrar la atención en el uso de las gráficas con el propósito de articular dos categorías: la resignificación y la justificación funcional, de las que expresamos sus acepciones de la manera siguiente:

a) La resignificación. Esta categoría muestra la función de la práctica social y el desarrollo del uso del conocimiento en situaciones específicas, y;

b) La justificación funcional. Esta categoría se refiere a que los mecanismos de desarrollo del uso del conocimiento en la situación específica son funcionales como contra parte de una justificación razonada, es decir, lo que norma la justificación no es una proposición lógica sino aquello que le es de utilidad a lo humano.

Los elementos anteriores fortalecen la hipótesis de investigación formulada en términos de convenir la comprensión de la graficación como una práctica social en su proceso institucional que se desarrolla en el discurso matemático escolar y no solamente como representación del concepto de función.

La metodología para atender la hipótesis consiste en estudiar, en el discurso de los libros de texto del nivel básico (primaria y secundaria), el uso que se le da a las gráficas con respecto a sus funcionamientos y sus formas según la diversidad de situaciones específicas. Todo ello para apreciar el desarrollo de sus usos en los libros de texto mencionados.

 

LA PROBLEMÁTICA

Las investigaciones de las gráficas de las funciones, en Matemática Educativa, tradicionalmente han tenido un tratamiento privilegiado como representación del concepto de función. Tal vez porque el modelo teórico que subyace en dichas investigaciones arroja resultados acerca de generar habilidades cognitivas para mejorar los entendimientos de los conceptos matemáticos, conlleva centrar a los conceptos en las reconstrucciones o reorganizaciones matemáticas y anclarlos en el dominio matemático. Asimismo este modelo teórico genera un discurso matemático escolar que privilegia a los conceptos matemáticos como lo más importante del conocimiento matemático. Como un resultado de este modelo, es que centra la problemática de enseñanza y aprendizaje en los conceptos matemáticos, pero más aún, la considera únicamente en el dominio matemático, soslayando otros marcos de referencia.

Por el contrario, esta investigación se propone brindar un modelo en oposición a dicha centración en los conceptos. Es decir, precisar otro marco de referencia enfocado a lo que pudiera ser el conocimiento institucional que explique a las gráficas de las funciones como una manifestación de los usos del conocimiento en el discurso matemático escolar, donde se resignifican al debatir entre sus funcionamientos y sus formas al paso de la vivencia escolar. En ese sentido lo institucional será aquello que hace que la graficación se desarrolle y se acepte como producto material social que tenemos que enseñar y aprender.

La hipótesis formulada conlleva a cuestionar cómo vive la graficación en el discurso matemático escolar por lo que se convinieron dos direcciones:

a) evidenciar dicha hipótesis en los libros de texto escolar por su rol en el discurso matemático escolar y,

b) formular la génesis del uso de las gráficas en el discurso matemático escolar.

De este modo, se presenta un estudio de los libros de texto del nivel básico (educación primaria y secundaria) en el marco de los contenidos curriculares de los textos para cada grado escolar.

 

LAS GRÁFICAS EN EL CURRÍCULO

Curricularmente las gráficas de las funciones en el Sistema Educativo Nacional ⁷ son abordadas en el nivel básico, iniciando en la educación secundaria, como lo indican el Plan y el Programa de estudios elaborados por la Secretaría de Educación Pública para la educación primaria y secundaria (SEP, 1993a y 1993b).

Es importante mencionar que en educación primaria las gráficas de las funciones no son consideradas curricularmente, pero a cambio se realizan ciertos tratamientos temáticos sobre gráficas sin hacer alusión explícitamente al concepto de función. Describimos enseguida los temas de las gráficas según los grados escolares:

En los tres primero grados de la educación primaria se abordan pictogramas sencillos, como ilustraciones para el planteamiento y resolución de problemas, en los que se requiere de la recolección, la organización y la interpretación de información contenida en registros. En cuarto grado se plantea la recolección y el registro de datos provenientes de la observación o de pequeñas encuestas, representados en tablas de frecuencia y en gráficas de barras para proceder al análisis de acuerdo a ciertos cuestionamientos. En este grado también se introduce al alumno a la elaboración de tablas para el registro de la variación proporcional y la representación de experimentos aleatorios en tablas y gráficas. En quinto y sexto grados se recopila y organiza la información de diversas fuentes mediante tablas, diagramas, gráficas de barras o pictogramas para analizar las tendencias: promedios, valor más frecuente y la mediana. También se introduce al estudiante al planteamiento y resolución de problemas que impliquen la elaboración de tablas y gráficas de variación proporcional y no proporcional. En estos últimos grados escolares aparecen los ejes coordenados para ubicar elementos, dependiendo del contexto del problema.

En lo que respecta a la educación secundaria, en primer grado se plantea la lectura y elaboración de tablas y gráficas construidas a partir de un enunciado con la temática presentación y tratamiento de la información, con ciertas situaciones de la geometría, de la física y de datos recolectados por los alumnos, asi como la exploración de cantidades que varían de manera proporcional. En segundo grado, en las áreas de álgebra se aborda la localization de puntos en el plano cartesiano, la representación de regiones, los conjuntos de puntos que satisfacen ciertas condiciones y la representación de sistemas de primer grado, las ecuaciones lineales y las cuadráticas. En el área de presentación y tratamiento de la información se aborda la organización y representación de datos en las tablas, en las gráficas de frecuencias absolutas y relativas, en los pictogramas, en los diagramas de barras, de sectores y en otras gráficas de uso común de la estadística y la probabilidad. También se introduce la noción de función como una relación entre dos cantidades por medio de tablas, gráficas y fórmulas pasando de un contexto a otro (funciones de la forma y–mx, y = mx+b, xy=k). En el tercer grado se aborda a las gráficas en el área de álgebra con temas como el plano cartesiano para ubicar los puntos y regiones que satisfacen sistemas de ecuaciones y desigualdades lineales, el estudio de las gráficas de funciones y el comportamiento local de funciones de la forma:

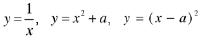
así como el estudio de familias de gráficas de la forma y = mx + a. En el área de presentación y tratamiento de la información se aborda el estudio de fenómenos que varían a tasa constante, con crecimiento aritmético y crecimiento geométrico, representados en gráficas comunes de la estadística y de la probabilidad para estudiar la moda, la media y la mediana, así como la dispersión de los mismos.

Un análisis de estos textos centrado en el concepto de función exigiría concluir que las gráficas son abordadas, desde ciertos grados del nivel básico, como una representación del concepto de función. Sin embargo, el concepto de función no existe en el currículo sino hasta la educación secundaria. La centración en tal concepto crea necesariamente secuencias insoslayables que en el mejor de los casos hacen que emerja el concepto, en consecuencia se obscurecen los significados situacionales manifestados según el uso del conocimiento. Definitivamente, creemos que la mayoría de los marcos teóricos de la disciplina no modelan el desarrollo del uso del conocimiento. Por ello, la socioepistemología se propone construir modelos del "uso del conocimiento". A continuación, en las siguientes secciones, presentamos un avance de esta tarea.

 

LA INSTITUCIONALIZACIÓN COMO UNIDAD DE ANÁLISIS

Un saber, ante todo, es un producto material continuo. Pudiéramos no dominarlo, pero socialmente se acepta que es un conocimiento, como es el caso de la matemática: lo continuo refleja su permanencia en la vida que es transformada por la matemática y, a la vez. la matemática es transformada. Tal continuo no se destruye porque hay ciertas formas de actuar impuestas o sugeridas desde afuera del individuo (Durkheim, 1982), las cuales son encarnados en sucesos individuales. Tales formas son las instituciones.

Creemos que el "uso de las gráficas" pudiera adquirir la categoría de un producto material continuo, puesto que permanece en la vida que es transformada y a la vez el producto es transformado. Por lo que el "uso" deberá tener un "desarrollo" de tal suerte que exprese cierto dominio (mejores ejecuciones, por ejemplo) de las gráficas. En ese sentido hablamos de "desarrollo del uso de las gráficas" en el cual las gráficas se resignifican en una situación específica.

El planteamiento anterior no soslaya los conceptos, por el contrario se les ubica en un mejor estatus epistemológico en el modelo del conocimiento consistente con la intervención de la práctica social, ya que dicha intervención ayudará a poner al descubierto las causas reales del desarrollo social de tal conocimiento, y que pudieran ser los procesos institucionales. Con ello la resignificación no sería otra cosa que la construcción del conocimiento mismo en la organización del grupo humano, normado por lo institucional.

Un escenario que el programa socioepistemológico ha formulado para dar evidencia de la aseveración anterior consiste en investigar y dar respuestas del uso del conocimiento en una situación específica. En particular se está trabajando sobre el uso de las gráficas en el discurso del Cálculo escolar. Para ello estamos formulando una epistemología al respecto, donde los usos tienen funciones específicas que dependen de la situación y que conllevan formas específicas. Ambos aspectos necesariamente debaten acorde con lo que organizan los participantes en la situación (Cordero, 2006a).

 

LA FUNCIÓN Y LA FORMA DEL USO DE LAS GRÁFICAS

Se trata de formular una epistemología del "uso de las gráficas^" que determine su desarrollo institucional ante situaciones específicas. El "uso" es la función orgánica de la situación que se manifiesta por las "tareas" que componen la situación, y la forma del ^"uso^" serán la clase de esas "tareas^". Las tareas pueden ser actividades, acciones, ejecuciones y alternancias de dominios. Cuando la alternancia de tareas sucede se genera una nueva función orgánica que debatirá con las formas de los usos. A este acto de "uso" se le llamará resignificación de la gráfica de la función en el marco socioepistemológico del Cálculo (Cordero, 2006a), donde la graficación es la modelación de los comportamientos tendenciales de las funciones (Cordero, 2006b). Esta modelación estará influida por justificaciones funcionales.

Presentamos a continuación a los libros de texto como un escenario para investigar y dar respuesta del uso de las gráficas en situaciones específicas, según los grados escolares del nivel básico, en los cuales identificamos diferentes momentos de uso que ayudan a entender el desarrollo del uso de las gráficas y su génesis en el dme, precisamente, en los libros de texto del nivel educativo mencionado.

 

ESTATUS DEL USO DE LAS GRÁFICAS EN LOS LIBROS DE TEXTO

El discurso matemático escolar es la manifestación del conocimiento matemático normado por creencias de los actores del sistema didáctico de lo que es la enseñanza y lo que es la matemática. Se ejerce la enseñanza–aprendizaje, por un lado, considerando a la matemática como un conocimiento acabado y por el otro, tratando a los conceptos matemáticos en las acciones de enseñar como actos repetitivos o de memorización. Estos hechos han definido la enseñanza tradicional de las matemáticas, cuya característica esencial es que se ha limitado al plano del lenguaje (modelo racional de la ciencia) y ha dejado de lado el papel de las acciones (los sentidos de los participantes) (Cordero, 2003). En el discurso, el libro de texto juega un papel importante puesto que prácticamente norma todas las acciones de enseñanza y aprendizaje o por lo menos tiene una gran influencia en ellas. Las selecciones del conocimiento que el docente hace en su práctica de enseñar son tomadas, precisamente, de los libros. El libro de texto es un marco de referencia insoslayable para el profesor y para el estudiante, genera el discurso matemático que se manifiesta en la práctica del docente (reflexiones al respecto se pueden consultar en Cantoral et al., 1990).

Con esta formulación, el libro de texto es una componente insoslayable en los estudios de los usos del conocimiento en el sistema didáctico. Por ello decidimos considerar el discurso matemático escolar en los libros de texto, en el cual también es parte del discurso del profesor y del alumno. En ese sentido se realizó el estudio de libros de texto del nivel básico, considerando la educación primaria y secundaria.

Se analizaron los libros de texto gratuitos de matemáticas y de ciencias naturales del nivel básico para la educación primaria, que fueron distribuidos por la Secretaría de Educación Pública (SEP) en el ciclo escolar 2003–2004. También se analizaron algunos libros de texto del nivel básico para la educación secundaria de matemáticas de los grados primero, segundo y tercero, de los cuales se consideraron tres series compuestas de tres ejemplares que corresponden a cada uno de los grados escolares. Estas series fueron creadas de acuerdo a los lineamientos expuestos en el Plan y programas de estudios autorizados por la SEP y corresponden al ciclo escolar 2003–2004.

En la investigación observamos que las gráficas son usadas en diversas actividades, aún sin ser un concepto curricular. Convenimos en considerar este hecho como un síntoma del uso de las gráficas de las funciones en el mismo sentido que Yoschkevitech (1976) lo hace para entender los diversos momentos del concepto de función. A continuación explicamos algunos aspectos al respecto.

Youschkevitech (1976) realiza un estudio sobre el concepto de función y reporta que tuvo un largo desarrollo para consolidarse en el siglo XVII, identifica tres etapas principales de su desarrollo:

• La antigüedad. Etapa en la que se hacen estudios de casos particulares de dependencia entre dos cantidades. Aparece el uso de tablas sexagesimales, de cuadrados y raíces cuadradas, de cubos y raíces cúbicas. Se elaboran empíricamente tablas de efemérides del sol, la luna y los planetas, que se convirtieron en cimientos matemáticos del desarrollo subsiguiente de la astronomía. Los griegos determinan leyes sencillas de la acústica, como la relación entre las longitudes y los tonos de las notas emitidas por cuerdas de la misma especie al ser pulsadas bajo tensiones iguales. En la época de Alejandría se desarrolló toda una trigonometría de las cuerdas correspondientes a una circunferencia de radio fijo, que equivalen a las tablas del seno de los Hindúes de unos cuantos siglos más tarde.

• La edad media (siglo XIV). Las nociones generales se expresaron por primera vez de modo definido, mediante formas geométricas y mecánicas, pero al igual que en la antigüedad, cada caso concreto de dependencia entre dos cantidades era definido por una expresión verbal de su propiedad específica, o por medio de una gráfica. También se fueron perfeccionando métodos de tabulación, introduciendo así funciones trigonométricas importantes.

• El periodo moderno (siglo XVI, y especialmente durante el siglo XVII). Empiezan a prevalecer las expresiones analíticas de las funciones. Al situarnos en el periodo moderno se tiene que el lenguaje matemático, de la latitud y la longitud, al igual que las semicuerdas y segmentos de diámetros que correspondían a las secciones cónicas de la antigüedad bien se podrían denominar la ordenada y la abscisa, respectivamente, en donde es necesario resaltar que las coordenadas en el siglo XIV siempre se referían a puntos de alguna curva y no puntos arbitrarios del plano (Youschkevitech, 1976; Campos, 2003).

Youschkevitech recoge estos tres aspectos en una idea que no coincide con otras aportaciones del desarrollo conceptual del concepto de función. Esta idea consiste en no considerar el nacimiento del concepto de función antes del momento (histórico) donde los grupos humanos enfocaron su atención al movimiento, y por ende a las cantidades de variación continua, justo ahí nace el concepto de función. Todo momento anterior lo denomina síntoma del concepto de función.

Para el caso que nos ocupa, en los libros de texto del nivel básico aparecen gráficas sin ser a priori una representación del concepto de función, curricularmente hablando, más tarde, de la misma manera, sin hacer mención al concepto de función, aparece la palabra "gráfica^", para que posteriormente se presente de manera curricular el concepto de función ejemplificado con gráficas para responder a discusiones que tienen que ver con comportamientos de las curvas.

Es así como este desarrollo formula una epistemología del uso de las gráficas, donde los funcionamientos y formas de las gráficas son identificados en el marco de dos momentos en el discurso de los libros de texto de matemáticas y de las ciencias naturales para la educación primaria. Reinterpretando a Youschkevitech, enfocamos la atención hacia el uso de las gráficas para determinar que cualquier uso de gráfica del espacio (mapas, ilustraciones, planos, cuadrículas y trayectorias), antes de ser especificada curricularmente la gráfica de la función, se le llamará el síntoma del uso de la gráfica de la función y una vez que la gráfica de la función es declarada curricularmente se le llamará el uso de la gráfica de la función. Sin embargo, en los libros de texto de educación secundaria aparece un momento tercero alusivo a la gráfica de una función de una curva específica, no como la unión arbitraria de puntos en un sistema de coordenadas, el cual se le llamó uso de la curva. Todo ello compone un marco de referencia del uso de las gráficas para analizar la resignificación de las gráficas en escenarios de gráficas cartesianas y su reorganización en el discurso matemático escolar.

A continuación describimos los momentos mencionados con detalle.

 

MOMENTO DEL SÍNTOMA DEL USO DE LA GRÁFICA DE LA FUNCIÓN

Curricularmente no se define el concepto de gráfica, ni el de función. Sin embargo, en el contenido de los libros aparecen actividades que usan gráficas del espacio "alusivas" a lo que posteriormente (en el currículo escolar, específicamente en educación secundaria) se le llamará gráfica de una función. Estos usos de gráficas manifiestan formas con relación a ciertas clase de tareas en mapas, ilustraciones, planos (ver Figura 1 .a), y cuadrículas con funcionamientos como ubicación, comparación y "optimización" de trayectorias (ver Figura 1b), asi como también aparecen formas con relación a una clase de tareas en diversidad de retículas donde su funcionamiento es la reproducción de figuras (ver Figura 1.c). Finalmente se usan tablas de barras con ciertos indicadores que implican conteo y cardinalidad con preferencia en el primer cuadrante (ver Figura 1.d). Este momento se presenta en todos los grados escolares de la educación primaria.

 

MOMENTO DEL USO DE LA GRÁFICA DE LA FUNCIÓN

Curricularmente se alude a la palabra gráfica sin hacer alusión al concepto de función. Sin embargo se dibujan gráficas de funciones. En los libros aparecen actividades en las que se incorpora la palabra gráfica, cuyos usos manifiestan formas como: tablas, pictogramas, gráficas de barras, gráficas poligonales y de sectores con escalas en los ejes de referencia (ver Figura 2.e y 2.f), así como también puntos en planos con ejes cartesianos cuyos funcionamientos consisten en establecer sus coordenadas (ver Figura 2g). Además, usos de gráficas cuyas formas son curvas contiguas con funcionamientos para analizar la distribución de puntos (ver Figura 2.h). En esta categoría de uso, precisamente, aparece "la palabra gráfica" sin que el concepto de función curricularmente sea mencionada para hacer referencia a las formas y funcionamientos respectivos. Dicha categoría aparece desde el tercer grado de la primaria para presentarse más tarde en los tres años escolares de la secundaria, donde curricularmente es declarado el concepto de función y su gráfica.

Los dos momentos ofrecen usos de las gráficas cuyas formas norman los funcionamientos de las gráficas según la clase de tareas que propone el libro de texto. Los momentos mismos nos ayudan a identificar desarrollos de usos de las gráficas, por ejemplo, en las Figuras 1.b y 2.h aparecen gráficas cuyos funcionamientos en las actividades consisten, para la primera, en la comparación de trayectorias para después reproducirlas en retículas cuadradas, y para la segunda, la comparación de las gráficas a partir de ciertos valores numéricos analizados a través de la distribución de los puntos en el plano cartesiano. Estos funcionamientos debaten con formas establecidas como la presencia o ausencia de retículas, de los ejes cartesianos y las escalas. Así, los momentos proveen diferentes categorías de uso de las gráficas que se van desarrollando en los contenidos de los libros de texto a través de los diferentes niveles escolares.

 

LOS LIBROS DE TEXTOS DE LA PRIMARIA Y SUS CATEGORÍAS DE USO DE GRÁFICA

Los contenidos matemáticos, de los libros de texto, en los diferentes grados escolares de la primaria se organizan en torno a seis ejes, considerando los procesos de aprendizaje de los alumnos, según la reforma de la SEP (SEP, 1993a): los números, sus relaciones y sus operaciones, medición, geometría, tratamiento de la información, procesos de cambio, la predicción y el azar. Y los programas de la escuela primaria se distribuyen en tres ciclos, cada uno compuesto de dos grados escolares cuya característica es considerar temas similares durante los dos años escolares: 1) ciclo uno: primero y segundo grado escolar; 2) ciclo dos: tercero y cuarto grado escolar y 3) ciclo tres: quinto y sexto grado escolar (SEP, 1994).

Cada grado escolar tiene su propósito que determina la propuesta del libro de texto, la cual gira en torno a algunos o todos los ejes anteriormente mencionados. Los contenidos de los textos se agrupan en cinco bloques, compuestos por lecciones que abarcan uno o varios incisos. Tales contenidos están ligados a temáticas, las cuales son tratadas por medio de actividades y tareas para el alumno.

Siguiendo la secuencia de los ciclos escolares se analizaron los libros que en un a priori surgieron interrogantes sobre el uso de las gráficas por cada ciclo: ¿a qué se le llama gráfica en cada grado escolar?, ¿cuáles son los tipos de gráficas y sus usos?, ¿cómo son los usos en los diferentes grados escolares?, ¿cuándo aparece el plano cartesiano?, y ¿cuándo las curvas cartesianas?

En el análisis de los textos se clasificó el uso que se le da a las gráficas según las clases de tareas y la función de la gráfica derivada por la clase. Sin embargo, para distinguir la clase fue necesario identificar un patrón de tarea, el cual define el nombre de la categoría cuya caracterización se valió de tres aspectos: gráfica de la tarea alusiva, ubicación y descripción de las tareas, así como también, se consideró prudente indicar el número de tareas (la frecuencia) propuestas en cada uno de los libros (ver Tabla I). Cada uno de los aspectos fueron definidos de la siguiente manera: a) Categoría. Determina el patrón de tarea para describir el uso de las gráficas por medio de los funcionamientos y formas de la gráfica en cuestión; b) Gráfica de la tarea alusiva. Se muestra una imagen de la gráfica de la tarea alusiva a la categoría, para evidenciar la forma de la gráfica usada; c) Ubicación de la tarea. Se ubican las tareas alusivas para crear un marco de referencia curricular que permita señalar aspectos del desarrollo del uso de las gráficas; d) Descripción de la tarea. Se describe el contenido de la tarea para analizar los significados y procedimientos del uso de las gráficas; y e) Número de tareas. Se especifica el número de tareas propuestas en cada libro de texto ubicadas en las categorías para evidenciar los usos más frecuentes.

A continuación se despliegan en la Tabla I las distintas categorías encontradas en cada uno de los libros de texto de matemáticas.

 

A continuación se explica el contenido de la Tabla I por cada uno de los ciclos.

Ciclo uno. Los textos analizados en el primer ciclo comprenden los grados escolares primero y segundo. La organización de sus contenidos gira entorno a los cuatro primeros ejes descritos anteriormente. En este primer ciclo el uso de las gráficas se manifiestan únicamente por el primer momento, el síntoma del uso de la gráfica de la función, ya que el concepto de "gráfica de una función^" no está descrito curricularmente. Sin embargo el momento se hace evidente a modo de síntoma en tareas donde las gráficas tienen funcionamientos distintos que definen las categorías de usos como son la reproducción y comparación de trayectorias de cierto móvil con un estado inicial y final de manera puntual, la reproducción de figuras con un estado inicial y final de cada una de sus partes, el análisis de información a partir de ciertos datos cualitativos y la ubicación y desplazamiento de ciertos puntos y móviles. Las formas de las gráficas establecidas por la clase de tareas son retículas (punteadas, cuadriculadas o triangulares), tablas, registros o cuadros con gráfica de barras con retícula rectangular y con ciertos indicadores (dibujos de animales, alimentos, objetos), así como también ilustraciones de mapas. Las gráficas referentes a la categoría reproducción de figuras son más frecuentes (en número) en todo el contenido de los dos libros de texto, utilizando retículas diversas: cuadriculadas, triangulares y punteadas.

Ciclo dos. Los textos analizados del segundo ciclo comprenden los grados escolares tercero y cuarto. La organización de sus contenidos gira entorno a los cuatro primeros ejes descritos anteriormente, sin embargo en el cuarto grado se introducen actividades correspondientes al eje de Procesos de cambios. Los usos de las gráficas en los cincos bloques de estos dos libros manifiestan la presencia de los dos momentos: el síntoma del uso de la gráfica de la función y el uso de la gráfica de la función. El primero caracterizado por la clase de tareas que conlleva la forma de las gráficas en retículas, con ejes de referencia, ilustraciones de mapas o planos con los puntos cardinales y, registros como tablas, cuadros o gráficas con indicadores (en este caso dibujos alusivos a los datos), cuyos funcionamientos gráficos consisten en la reproducción de figuras, la ubicación y desplazamiento y el análisis de información. El segundo momento es caracterizado por las gráficas que posteriormente, en el currículo escolar de la educación secundaria, corresponderán al concepto de gráfica de una función. La clase de tareas conllevaron la forma de la gráfica en tablas, pictogramas o gráficas de barras con escalas o datos cualitativos en los ejes de referencia y planos cartesianos con cuadrículas y escalas en los ejes de referencia privilegiando el primer cuadrante cuyos funcionamientos gráficos consistieron en el análisis de información a partir del registro de ciertos datos cualitativos y cuantitativos, la ubicación y desplazamiento de puntos y móviles por medio de claves (coordenadas). La frecuencia de los usos de las gráficas no tiene diferencias significativas como lo fue en el ciclo anterior. De alguna manera podríamos decir que en este ciclo hay una tendencia a equilibrar los usos.

Ciclo tres. Los textos analizados en el tercer ciclo comprenden los grados escolares quinto y sexto. La organización de sus contenidos gira entorno a los seis ejes descritos anteriormente. Los usos de las gráficas fueron manifestados por los dos momentos: el síntoma del uso de la gráfica de la función y el del uso de la gráfica de la función. El primero caracterizado por la clase de tareas que conllevan la forma de la gráfica en retículas cuadriculadas con ejes de referencia e ilustraciones de mapas o planos con los puntos cardinales, cuyos funcionamientos gráficos consistieron en la reproducción de figuras y, la ubicación y desplazamiento. El segundo momento es caracterizado por la clase de tareas que conllevan la forma de la gráfica en tablas, pictogramas, gráficas de barras, gráficas poligonales y de sectores con escalas en los ejes de referencia, planos coordenados con cuadriculas y ejes de referencia mostrando los cuatro cuadrantes, así como curvas contiguas en planos coordenados con escalas en los ejes de referencia sin cuadrículas, cuyos funcionamientos gráficos consisten en el análisis de información a partir de tablas de frecuencia, la ubicación y desplazamiento de puntos y móviles a partir de coordenadas y la distribución de puntos enfocado en la variación (proporcional y no proporcional) de dichos puntos. En este ciclo las gráficas referentes a la categoría reproducción de figuras son las menos frecuentes (en número) en todo el contenido de los dos libros. Sin embargo, el uso de gráficas referentes a las categorías análisis de información, ubicación y desplazamiento y distribución de puntos presentan cierto equilibrio con relación a su frecuencia.

Resumiendo. En la Tabla I se muestran las categorías de uso de las gráficas en los libros de texto, considerando sus dos momentos: síntoma del uso de la gráfica de la función y uso de la gráfica de la función. Para ganar precisión, en términos genéricos describimos a las categorías y sucintamente las presentamos en el Esquema I:

a) Reproducción y comparación de trayectorias: patrón de tareas que usan gráficas en las cuales se plasman, reproducen o comparan trayectorias en retículas cuadriculadas;

b) Análisis de información: patrón de tareas en la cual se recopilan, organizan, comparan e interpretan, datos e información, usando tablas, pictogramas, histogramas, y gráficas de barras, poligonales y de sectores;

c) Reproducción de figuras: patrón de tareas en la cual se reproducen figuras en retículas cuadriculadas, triangulares o punteadas con ausencia o presencia de ejes de referencia;

d) Ubicación y desplazamiento: patrón de tareas en la cual se realizan ubicaciones y desplazamientos en planos, mapas o planos cartesianos de móviles y puntos, y;

e) Distribución de puntos: patrón de tareas en la cual se usan y comparan tablas y gráficas contiguas, de puntos que se distribuyen y varían de cierta manera.

 

LOS LIBROS DE TEXTO DE CIENCIAS NATURALES DE LA PRIMARIA Y SUS CATEGORÍAS DE USO DE GRÁFICA

Se analizaron los contenidos de los libros de texto gratuitos de ciencias naturales del grado tercero al sexto y los libros integrados correspondientes al grado primero y segundo, todos ellos de la educación primaria y fueron distribuidos por la SEP en el ciclo escolar 2003–2004. Las ciencias naturales se integra en los dos primeros grados de primaria, según el plan de estudios vigentes de la SEP (SEP, 1993a). Esto a través de la asignatura denominada Conocimiento del Medio, la cual trata aprendizajes de nociones de historia, geografía y educación cívica, cuyo elemento articulador es el conocimiento del medio natural y social que rodea al niño. Mientras que a partir del tercer grado los alumnos estudian ciencias naturales como asignatura independiente y continúan con el estudio de los contenidos correspondientes de cada grado, los cuales se han organizado en cinco ejes temáticos: los seres vivos; el cuerpo humano y la salud; el ambiente y su protección; materia, energía y cambio; y ciencia, tecnología y sociedad.

La enseñanza de las ciencias naturales está vinculada con otras asignaturas del plan de estudios, como es el caso de la matemática, en donde la lectura, la elaboración y el análisis de tablas y gráficas, el uso de unidades de longitud, peso y capacidad son indispensables en el tratamiento de algunos contenidos (García, et al, 1997). El contenido de los textos se agrupa de la misma manera que en los libros de texto de matemáticas, a diferencia de los textos de primer y segundo grado que contienen ocho bloques.

En el análisis de los libros el "uso de las gráficas de las funciones^" se clasificó de acuerdo a las clases de tareas como se realizó para los libros de matemáticas. A continuación se despliegan las tablas que caracterizan las categorías encontradas en cada uno de los libros de texto.

En este primer ciclo la clase de tareas conllevan las formas de las gráficas en cuadrículas y planos o mapas con una tendencia más de figura, cuyos funcionamientos consisten en la reproducción de figuras, la ubicación y el desplazamiento. El concepto de función y gráfica no está declarado en el currículo, por ello se consideró el momento del síntoma del uso de la gráfica de la función. Se encontró mayor número de tareas que usan gráficas con funcionamientos de ubicación y desplazamiento.

En el segundo ciclo la clase de tareas conllevó formas de gráficas en barras y gráfica de puntos donde se discute la variación entre los puntos o valores, cuyos funcionamientos de las gráficas fueron el análisis de información y la distribución de puntos. La categoría de usos manifiesta el momento del uso de la gráfica de la función, donde existe un mayor número de tareas que usan gráficas con funcionamientos consistentes en el análisis de información.

En el tercer ciclo las clases de tareas conllevaron formas de las gráficas en barras con datos cuantitativos y gráficas contiguas para discutir la variación entre puntos, cuyos funcionamientos de gráficas consisten en el análisis de información y la distribución de puntos. Las categorías manifiestan el momento del uso de la gráfica de la función, encontrando un mayor número de tareas que usan gráficas con funcionamientos consistentes en el análisis de información.

En las Tablas de II.1 a II.6, (Tabla II.1, II.2, II.3, II.4, II.5 y II.6) en forma sucinta, se exhiben las categorías de uso de la gráfica considerando sus momentos respectivos. Con respecto a los momentos el uso de las gráficas en los libros mencionados se exhibe en el Esquema II. De alguna manera los usos son similares salvo las tendencias de hacer figuras y la ausencia de la categoría "reproducción y comparación de trayectorias". Todo ello puede deberse a la integración de programas de la educación básica, lo cual ayuda a normar el discurso matemático escolar, situación que es diferente en educación superior.

La similitud de las categorías a través de los dos momentos (síntoma del uso de la gráfica de la función y el del uso de la gráfica de la función) en los dos dominios (matemáticas y ciencias naturales) pudiera formular un marco de referencia sobre el desarrollo del uso de las gráficas de las funciones en el discurso matemático escolar, en la educación primaria. De esta manera los usos de las gráficas se manifestarían por medio de las categorías de reproducción y comparación de trayectorias, de reproducción de figuras, de ubicación y de desplazamiento, del análisis de información y de la distribución de puntos. Si esto fuera así, querrá decir que los estudiantes con ese marco de referencia resignificarán las gráficas de las funciones más adelante en el sistema educativo.

El análisis de los libros de texto de nivel secundaria clasificó el uso de las gráficas en los momentos que se presentaron en la educación primaria. Sin embargo, apareció un tercer momento, que decidimos llamarle "momento del uso de la curva^", con tres direcciones (comportamientos de cantidades discretas, comportamientos geométricos y comportamientos de cantidades continuas). Tal momento es el distintivo de la educación secundaria con el de la primaria, pero no quiere decir que haya ausencia de los momentos primero y segundo caracterizados anteriormente en la educación primaria, aunque sí se percibieron sólo algunas categorías del segundo momento.

A continuación describimos los momentos significativos del desarrollo del uso de las gráficas en los libros de texto de la educación secundaria.

 

LOS LIBROS DE TEXTO DE MATEMÁTICAS DE LA EDUCACIÓN SECUNDARIA

Se analizaron los contenidos de libros de texto del nivel básico para la educación secundaria en los grados primero, segundo y tercero. Las tres series analizadas están compuestas, a su vez, de tres ejemplares que corresponden a cada uno de los grados escolares. Estas series fueron creadas de acuerdo a los lineamientos expuestos en el plan y programas de estudios autorizados por la SEP y corresponden al ciclo escolar 2003–2004. Todo ello como resultado de un prolongado proceso de consulta, diagnóstico y elaboración iniciado en 1989, en el cual fueron incluidos de manera conjunta los niveles de educación preescolar, primaria y secundaria. Así, el nuevo plan de estudios se convirtió en un instrumento para organizar el trabajo escolar y lograr el avance cualitativo. Para que sus propósitos se cumplieran se integró a un proceso general de mejoramiento donde los alumnos aprendan a utilizar la matemática para resolver problemas, no solamente los que resuelven en la escuela, sino también aquellos cuyo descubrimiento y solución requieren de la curiosidad y la imaginación creativa. En ese sentido, la enseñanza de las matemáticas en la escuela secundaria tiene como propósito general el desarrollo de las habilidades operatorias, comunicativas y de descubrimiento de los alumnos. Para ello la organización de los temas del programa están agrupados en cinco áreas para los tres grados escolares: aritmética, álgebra, geometría (en el tercer grado se agrega trigonometría, presentación y tratamiento de la información y nociones de probabilidad).

Los libros de texto utilizados en las escuelas secundarias del país son los autorizados por la SEP, los cuales fueron dictaminados en los lineamientos para la evaluación de libros de texto el 18 de diciembre de 1997. Del conjunto de libros autorizados, el maestro puede elegir con toda libertad el que mejor responda a las necesidades educativas de sus alumnos, según el grado y asignatura correspondiente (SEP, 2004). En nuestro caso, los ejemplares analizados forman parte del Programa de Distribución de Libros de Texto de Educación Secundaria de la SEP. La estructura de sus contenidos de cada uno de los tres grados varían entre ellos: a) el libro Matemáticas 1, 2 y 3 tiene una estructura conformada de unidades, cada una dividida en temas, los cuales a su vez presentan una serie de lecciones relacionadas entre si, que ofrecen cierto desarrollo teórico y una serie de ejercicios. Al final de cada unidad se presenta una sección de ejercicio de unidad, una recopilación de ideas principales y finalmente una sección de recreación matemática; b) el libro Matemáticas en contexto 1, 2 y 3 tiene su estructura organizada en unidades, cada una dividida en lecciones, las cuales cubren un contenido principal y uno o más contenidos relacionados. Dichas lecciones constan de las siguientes partes. Situación problema, estrategia de solución, formalización y aplicación. Al final de cada unidad se presenta una sección de ejercicios semejantes a los tratados en las lecciones, lectura complementaria y finalmente una sección de pistas; y c) el libro Descubre y aprende Matemáticas 1, 2 y 3, igual que los anteriores tiene una estructura organizada en unidades, cada una dividida en lecciones, las cuales comienzan planteando un problema, un juego, o la teoría directamente, al final de las lecciones se propone una serie de ejercicios. Al término de cada unidad se sugieren actividades relacionadas con todas las lecciones.

 

MOMENTO DEL USO DE LA GRÁFICA DE LA FUNCIÓN EN LA SECUNDARIA

El momento del uso de la gráfica de la función se presenta también en los libros de texto de secundaria a través de clases de tareas que conllevan formas de gráficas en tablas, pictogramas, gráficas de barras, gráficas poligonales y de sectores o de pastel e histogramas con escalas en los ejes de referencia con funcionamientos para analizar datos e información (ver Figura 3.i), así como puntos en planos cartesianos con funcionamientos para establecer sus coordenadas (ver Figura 3.j) y finalmente gráficas con curvas contiguas con funcionamientos para analizar la distribución de puntos (ver Figura 3.k). Cabe mencionar que la palabra gráfica (sin ser explícitamente un concepto de función curricular), es mencionada para hacer referencia a aquellas formas y funcionamientos expuestos anteriormente, dicho momento se presenta en los tres grados escolares de la educación secundaria.

 

MOMENTO DEL USO DE LA CURVA

El "uso de las curvas^" manifiesta el comportamiento de las curvas de las funciones (curricularmente es declarado el concepto de función). Todo ello sucede en tres direcciones: los comportamientos de cantidades discretas, los comportamientos geométricos y los comportamientos de cantidades continuas.

a) En las discusiones del texto sobre los comportamientos de cantidades discretas los funcionamientos enfocan la atención hacia la curva para explicar el comportamiento de las cantidades que arrojan los datos, censos y registros vaciados en tablas y gráficas. Observamos que el interés está en discutir la variación con la estrategia de comparación, la cual asocia la acción de establecer diferencias entre los estados, algunos de los términos usados son el decrecimiento y crecimiento, el valor máximo, mínimo y medio, otra estrategia de discusión es la estimación la cual se parte del hecho de conocer estados cambiantes, sin embargo en este caso no se busca un patrón que pudiera seguir, si no más bien se proponen nuevos estados a corto plazo como es el análisis del crecimiento de población, como lo indica Salinas (2003).

b) Con lo que respecta a las discusiones sobre los comportamientos geométricos los funcionamientos de las gráficas enfocan la atención hacia la curva para entender cómo se dan las transformaciones de funciones. Las cuales consisten en obtener nuevas funciones a partir de una conocida, ya sea por traslación, estiramiento o reflexión de las gráficas correspondientes. Desde el contexto algebraico la transformación es presentada con la introducción de un parámetro a la expresión algebraica de la función dada, lo cual se puede ver en las gráficas de las funciones mediante un desplazamiento de la gráfica original en el plano cartesiano x–y, hacia arriba o hacia abajo, hacia la izquierda o hacia la derecha; la contracción de la gráfica, el estiramiento o una reflexión de la gráfica original, como lo indica Campos (2003).

c) Con lo que respecta a las discusiones sobre los comportamientos de cantidades continuas los funcionamientos enfocan la atención hacia la curva para explicar el comportamiento de las cantidades continuas que se obtienen de funciones y fenómenos interpretados por tablas y gráficas. Observamos que el interés está en discutir la variación con la estrategia de predicción. Estrategia asociada a la acción de poder intuir después de analizar algunos estados cuales son los estados posteriores. Por ejemplo dada una tabla de cantidades establecer el patrón que cumple la variación, como lo indica Salinas (2003).

Este tercer momento con las tres direcciones formula funcionamientos y formas de las gráficas que describen las categorías de usos. En seguida describimos algunos aspectos al respecto.

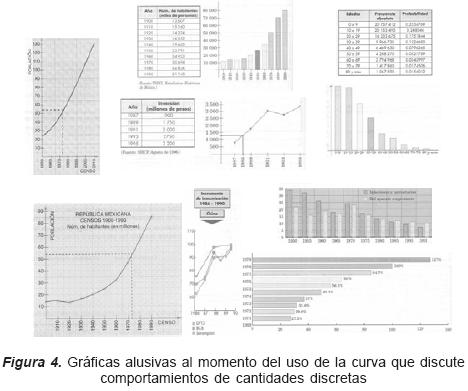
Las formas de las gráficas con relación a los comportamientos de cantidades discretas, son el resultado de una clase de tareas que tienden a privilegiar el primer cuadrante con ejes de referencia y escalas con presencia o ausencia de cuadrículas, así como tablas, gráficas de barras, poligonales e histogramas, cuyos funcionamientos son el análisis de información con datos cuantitativos y cualitatativos así como la distribución de puntos de acuerdo a la variación de los datos y tivos así como la distribución de puntos registros (ver Figura 4).

En el caso del uso de las gráficas con relación a los comportamientos geométrico, las formas de las gráficas resultan de la clase de tareas con relación a dibujar gráficas en los planos cartesianos con uno o los cuatro cuadrantes, con escalas en los ejes de referencia, con ausencia o presencia de cuadrículas, así como tablas y fórmulas asociadas a las curvas contiguas que se obtiene de esas tablas. Sus funcionamientos consisten en la ubicación y desplazamiento de puntos y de móviles a partir de coordenadas y la asociación curva–expresión algebraica en la cual se plasman gráficas con curvas que se asocian con una expresión algebraica (ver Figura 5 m y n).

En el uso de las gráficas con relación a los comportamientos de cantidades continuas las formas de las gráficas resultan de la clase de tareas que privilegian el dibujo de gráficas en el primer cuadrante con ejes de referencia y escalas con presencia o ausencia de cuadrículas, así como tablas y fórmulas asociadas a las curvas. Sus funcionamientos consisten en la distribución de puntos de acuerdo a la variación de los datos y la asociación curva–expresión algebraica en la cual se plasman gráficas con curvas que se asocian con una expresión algebraica (ver Figura 6).

Cada una de las categorías encontradas en el momento de uso de las curva describen respectivamente los funcionamientos y formas de las gráficas. La caracterización de tales categorías se basa en los mismos aspectos considerados para los textos de la primaria: patrón de tareas, gráficas de la tarea alusiva, ubicación de la tarea y descripción de la tarea. Sin embargo se identificó que cada categoría dirige la discusión de la tarea a un aspecto específico: comportamiento de cantidades discretas, comportamientos geométricos y comportamientos de cantidades continuas. A cada uno de estos aspectos se les llamó "dirección de la discusión^".

A continuación se despliega la Tabla III que caracterizan las categorías y la dirección de la discusión encontradas en cada uno de los libros de texto.

 

A MANERA DE CONCLUSIÓN

Las categorías de uso de las gráficas discutidas anteriormente proporcionan un marco de referencia para responder a las interrogantes que surgieron en el transcurso de nuestra investigación en torno al uso de las gráficas en los ciclos de la educación primaria y secundaria. Con ello se entendió a lo que se le llama gráfica en los diferentes grados escolares del nivel básico, los tipos de gráficas y sus usos, los usos en los distintos grados escolares, la aparición del plano cartesiano y de las curvas cartesianas, respectivamente en el dme de los libros de texto.

Es importante destacar que los datos plasmados en las tablas anteriores dan evidencia de la relación estrecha entre las categorías resignificación y justificación funcional. De alguna manera esta última proveyó el hecho de que las gráficas, de acuerdo a las tareas, aparecen desde el primer año de primaria (momento del síntoma de uso de la gráfica de la función) sin ser un concepto en el currículo. Posteriormente aparece en los libros y en el currículo la palabra gráfica sin aludirlo al concepto de función. Y no es sino hasta la educación secundaria que explícitamente aparece en el currículo y en los libros el concepto de función, el cual se le describe y ejemplifica con gráficas cartesianas para responder a los comportamientos de las curvas. Este hecho es relevante porque está señalando que en la "génesis" del uso de las gráficas de las "funciones^", en el dme de los libros de texto del nivel básico, se anticipa la "gráfica" al concepto mismo de "función^", pero la alternancia de las tareas resignifican los usos de las gráficas hasta desarrollar explícitamente el uso de las gráficas cartesianas .

La naturaleza de estos datos da la pauta para continuar con investigaciones que comprendan a la graficación como una práctica social en su proceso institucional, en este caso educativo.

Desde la educación primaria hasta la secundaria hay un desarrollo del uso de las gráficas, donde las gráficas (y en su momento el concepto de función) deberán resignificarse puesto que los funcionamientos y las formas de las gráficas debaten para reorganizar nuevos funcionamientos y formas de las gráficas. De ahí la importancia de las categorías formuladas para cada grado escolar. Sin embargo, para formular, en futuras investigaciones, el estatus del uso de las gráficas en los libros será conveniente valerse de los tres momentos: el uso del síntoma de la gráfica de la función, el uso de la gráfica de la función y el uso de la curva. Habrá que hacer estudio de ello, pero se tendrá que considerar que la resignificación es normada por lo institucional donde las prácticas (sociales), en algún aspecto, se manifestarán en el discurso matemático escolar en expresiones como los libros escolares. Esta investigación provee información sistemática al respecto y en una forma sucinta se expresa en el siguiente esquema (ver Esquema III).

El contenido del Esquema III integra aspectos que pudieran señalar el desarrollo del uso de las gráficas en el dme en la visión socioepistemológica. Estos aspectos se refieren a (a) lo que norma la institución, y (b) las comprensiones según sus prácticas y sus instituciones.

A continuación desarrollamos las conclusiones de acuerdo a los aspectos señalados.

(a) El rol del libro de texto en el dme nos provee ciertos indicadores sobre lo que norma la institución. Esto es, los nuevos significados que arroja el hecho de haber encontrado los tres momentos (el uso del síntoma de la gráfica de la función, el uso de la gráfica de la función y el uso de la curva.) consisten en cuestionar la centración de los conceptos matemáticos, como la única fuente para reconstruir el conocimiento matemático y abre otro camino más amplio, donde las prácticas sociales son los elementos medulares para tal reconstrucción del conocimiento matemático. Esto conlleva cuestionar ¿por qué lo matemático es referido a objetos y no "aquello" que norman la construcción de los objetos matemáticos? En ese sentido hemos querido llamar la atención en la resignificación que manifiesta el uso del conocimiento en una situación especifica, donde el uso es desarrollado a través de justificaciones funcionales orgánicas de la situación, según la alternancia de las tareas.

(b) Como lo dijimos con anterioridad en esta investigación consideramos, a las gráficas de las funciones como argumentaciones del Calculus, las cuales serían el resultado de ciertas prácticas sociales que han generado el conocimiento del Calculus. Con ello, en el estudio del uso de las gráficas en el dme, quisimos ver las compresiones de las gráficas según las prácticas y las instituciones que entran en juego. Por eso los tres momentos y las categorías de uso de las gráficas conllevan la articulación de las categorías, anteriormente mencionadas, resignificación y justificación funcional. Lo que destaca las características de las tareas donde la graficación pueda llevar a cabo múltiples realizaciones y hacer ajustes en su estructura para producir un patrón o generalización deseable, crearle un medio que soporta el desarrollo del razonamiento y de la argumentación, entendiéndola como prácticas gráficas, retóricas y argumentativas, en diversas situaciones donde son resignificadas al debatir entre el funcionamiento y la forma de la graficación misma.

De esta manera el estatus epistemológico del uso de la gráfica lo ubica como un producto material continuo, es decir, institucional en el sentido que lo establece Durkheim (1982), como ya hemos señalado. La argumentación gráfica en las diversas situaciones de uso, tanto en los libros de texto como en los trabajos antecedentes de nuestra investigación mencionados, es un indicativo que pudiera permitir el continuo. Para que el continuo no se destruya se requiere lograr un estatus cultural de la argumentación gráfica. De aquí la conveniencia de pensar a la graficación como una práctica social tarea que tendríamos que saber desarrollar en el sistema educativo. Para ello, se requiere ir integrando en secuencia didáctica tal estatus epistemológico del uso de las gráficas centrando la atención en los momentos donde se pondrán en juego los funcionamientos y formas para mirar las distintas resignificaciones institucionales en las argumentaciones de los alumnos que se sometan a la situación.

En términos generales la investigación nos brinda los referentes para comprender que la graficación como una argumentación del Cálculo exige reflexionar sobre las epistemologías que hasta ahora se han tratado en la Matemática Educativa, las que responden a conceptos matemáticos. No obstante, "graficación" propiamente no es un concepto, sino una práctica o uso ante una situación de construcción, de ahí el interés por abrir un espectro hacia otras epistemologías.

El marco de referencia (o los indicadores para tal fin) del uso de las gráficas es la contribución del trabajo de investigación que trata este artículo, el que integraremos en futuras investigaciones, hacia la resignificación de la gráfica, lo que contribuye al rediseño del discurso de la matemática escolar.

¹ Esta investigación está financiada por CONACYT con el Proyecto Estudio de las gráficas de las funciones como prácticas institucionales. Una gestión escolar para el Nivel Superior. Clave: No. 47045. regresar

 

BIBLIOGRAFÍA

Buendía, G. & Cordero, F. (2005). Prediction and the periodical aspect as generators of knowledge in a social practice framework. A socioepistemological study. Educational Studies in Mathematics 58(3), 299–333.        [ Links ]

Buendía, G. (2004). Una epistemología del aspecto periódico de las funciones en un marco de prácticas sociales (Un estudio socioepistemológico). Tesis de doctorado no publicada. Departamento de Matemática Educativa, Cinvestav–IPN, México.        [ Links ]

Campos, C. (2003). La argumentación gráfica en la transformación de funciones cuadráticas. Una aproximación socioepistemológica. Tesis de maestría no publicada, Departamento de Matemática Educativa, Cinvestav–IPN, México.        [ Links ]

Cantoral, R., Cordero, F., Farfán, R. & Imaz, C. (1990). Calculus–Análisis: Una revisión de las Investigaciones recientes en Educación. En R. Cantoral, F. Cordero, R. Farfán & C. Imaz (Ed.), Memorias del Segundo Simposio Internacional sobre Investigación en Educación Matemática (pp. 55–69). Cuernavaca, Morelos. México.        [ Links ]

Cantoral, R. & Farfán, R. (2003). Matemática Educativa: Una visión de su evolución. Revista Latinoamericana de Investigación en Matemática Educativa 6(1), 27–40.        [ Links ]

Cordero, F. (1998). El entendimiento de algunas categorías del conocimiento del cálculo y análisis: el caso de comportamiento tendencial de las funciones. Revista Latinoamericana de Investigación en Matemática Educativa 2(1), 56–74.        [ Links ]

Cordero, F. (2001). La distinción entre construcciones del cálculo. Una epistemología a través de la actividad humana. Revista Latinoamericana de Investigación en Matemática Educativa 4(2), 103–128.        [ Links ]

Cordero, F. (2003). Reconstrucción de significados del Cálculo Integral: La noción de acumulación como una argumentación. México, D.F.: Grupo Editorial Iberoamérica.        [ Links ]

Cordero, F. (2005). El rol de algunas categorías el conocimiento matemático en educación superior. Una socioepistemología de la integral. Revista Latinoamericana de Investigación en Matemática Educativa 8(3), 203–228.        [ Links ]

Cordero, F. (2006a). El uso de las gráficas en el discurso del cálculo escolar. Una visión socioepistemológica. En R. Cantoral, O. Covián, R. M. Farfán, J. Lezama & A. Romo (Ed.), Investigaciones sobre enseñanza y aprendizaje de las matemáticas: un reporte Iberoamericano (pp. 265–286). D.F., México: Díaz de Santos–Comité Latinoamericano de Matemática Educativa. A. C.        [ Links ]

Cordero, F. (2006b). La modellazione e la rappresentazione grafica nell'insegnamento–apprendimento della matematica. La Matematica e la sua Didattica 20(1), 59–79.        [ Links ]

Cordero, F. & Solís, M. (2001). Las gráficas de las funciones como una argumentación del Cálculo. Serie: Cuadernos de Didáctica. Grupo Editorial Iberoamérica. Edición especial CASIO. Tercera edición.        [ Links ]

Domínguez, I. (2003). La resignificación de lo asintótico en una aproximación socioepistemológica. Tesis de maestría no publicada, Departamento de Matemática Educativa, Cinvestav–IPN, México.        [ Links ]

Durkheim, E. (1982). The Rules of Sociological Method and Selected Texts on Sociology and its Method. N. Y., USA: Free Press.        [ Links ]

García, N., Guerra, M. T., Mayén, A. & Villavicencio, R. (1997). Libro para el maestro. Ciencias Naturales. Tercer grado (2ª reimpr. 2ª ed. rev). México, D.F.: SEP.        [ Links ]

Hernández, D. (2004). Las argumentaciones gráficas de los estudiantes en las relaciones de f y f' para las funciones x, x² y x³. Tesis de Maestría no publicada, Departamento de Matemática Educativa, Cinvestav–IPN, México.        [ Links ]

Rosado, P. (2004). Una resignificación de la derivada. El caso de la linealidad del polinomio en la aproximación socioepistemológica. Tesis de Maestría no publicada, Departamento de Matemática Educativa, Cinvestav–IPN, México.        [ Links ]

Salinas, C. (2003). Un estudio sobre la evolución de ideas variacionales en los cursos introductorios del cálculo. Tesis de Maestría no publicada, Departamento de Matemática Educativa, Cinvestav–IPN, México.        [ Links ]

Secretaría de Educación Pública. (1993a). Plan y Programas de estudio. Educación básica. Primaria (1ª reimpr.). México D.F.: Autor.        [ Links ]

Secretaría de Educación Pública. (1993b). Plan y Programas de estudio. Educación básica. Secundaria (2ª ed.). México D.F.: Autor.        [ Links ]

Secretaría de Educación Pública. (1994). Libro para el maestro. Matemáticas. Segundo grado (3ª reimpr. 1ª ed. rev). México D.F.: Autor.        [ Links ]

Suárez, L. (2006). Uso de las gráficas en la modelación del cambio. Un estudio socioepistemológico. Memoria predoctoral. Departamento de Matemática Educativa, Cinvestav–IPN, México.        [ Links ]

Youschkevitech, A.P. (1976). The concept of function up to the middle of the 19th century (Trad. R. M. Farfán). Serie: Antologías 1 (pp. 99–145). México: Cinvestav–IPN (Programa Editorial, Área de Educación Superior, Departamento de Matemática Educativa).        [ Links ]

 

NOTAS

⁴ Matemática funcional quiere decir un conocimiento incorporado orgánicamente en el humano que lo transforma y que le transforma su realidad. Todo ello en oposición al conocimiento utilitario. regresar

⁵ El discurso matemático escolar es la manifestación del conocimiento matemático normado por creencias de los actores del sistema didáctico de lo que es la enseñanza y lo que es la matemática. Discutimos un poco más al respecto en la sección 'Estatus del uso de las gráficas en los libros de texto' de este artículo. regresar

⁶ Las argumentaciones de las gráficas de las funciones, en la aproximación socioepistemológica, se refiere a la argumentación de la situación de transformación de funciones (situación de modelación). Ahí se resignifica el uso de las gráficas debatiendo entre su funcionamiento y forma: las curvas de movimiento y geométricas son resignificadas como patrones de comportamientos gráficos y analíticos, y comportamientos tendenciales de las funciones generando procedimientos que consisten en identificar y variar los parámetros de las funciones, construyendo procesos y objetos de instrucciones que organizan comportamientos: se considera una función f para que sea transformada a la función Y=Af(Bx+C)+D ( Ver Cordero, 2006a). regresar

⁷ Nos referimos al Sistema Educativo Nacional de México regresar