Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista latinoamericana de investigación en matemática educativa
versión On-line ISSN 2007-6819versión impresa ISSN 1665-2436
Relime vol.14 no.2 Ciudad de México jul. 2011
Artículos
Las tres dimensiones fundamentales de un problema didáctico. El caso del álgebra elemental
The three fundamental dimensions of a didactic problem, the case of elemental algebra
Josep Gascón
Departamento de Matemáticas. Universitat Autònoma de Barcelona, gascon@mat.uab.cat
Recepción: Junio 19, 2010.
Aceptación: Febrero 17, 2011.
RESUMEN
Con el fin de caracterizar el objeto de estudio de la Didáctica de las Matemáticas, proponemos un patrón heurístico del desarrollo de los problemas didácticos y lo ejemplificamos con el álgebra elemental. El patrón está estructurado en torno a las tres dimensiones básicas o fundamentales de dichos problemas cuando son construidos en el ámbito de la Teoría Antropológica de lo Didáctico: la epistemológica, que sitúa a lo matemático en el corazón del problema; la económico–institucional, que despersonaliza la problemática didáctica y delimita la unidad mínima de análisis de los procesos de estudio, y la ecológica, que enfatiza las condiciones necesarias para que sea posible el estudio institucionalizado de las matemáticas y pone de manifiesto las restricciones de todo tipo que inciden sobre dicho estudio.
PALABRAS CLAVE: Teoría Antropológica de lo Didáctico (TAD), Dimensiones de un problema didáctico (epistemológica, económico – institucional y ecológica), Problema del álgebra elemental.
ABSTRACT
In order to illustrate the purpose of the Didactics of Mathematics study, we suggest a heuristic pattern for the development of didactic problems demonstrated with elemental algebra. The pattern is structured around three basic or fundamental dimensions of said problems when they are constructed in the field of the Anthropological Theory of Didactics: epistemológica!, which puts mathematics at the heart of the problem; economic–institutional, which depersonalizes the didactic set of problems and delimits the minimum unit of analysis of the processes of study, and ecological, which emphasizes the conditions required so that the institutionalized study of mathematics is possible and reveals obvious restrictions of any kind that have an effect on said study.
KEYWORDS: Anthropological Theory of Didactics (ATD), Dimensions of a didactic problem (epistemológical, economic – institutional and ecological), Problem of elemental algebra.
RESUMO
Com a finalidade de caracterizar o objeto de estudo da Didática da Matemática, sugerimos um padão heurístico do desenvolvimento dos problemas didáticos e o exemplificamos com a álgebra elementar. O padrão está estruturado ao redor das três dimensões básicas ou fundamentáis de tais problemas quando são construidos no horizonte da Teoria Antropológica do Didático: a epistemológica, que sitúa aquilo que é matemático no coração do problema; a econômico–institucional, que despersonaliza a problemática didática e delimita a unidade mínima de análise dos processos de estudo, e a ecológica, que dá ênfase às condições necessárias para que o estudo institucionalizado da matemática seja possível e coloca de maneira manifesta as restrições de todos os tipos que incidem sobre tal estudo.
PALAVRAS CHAVE: Teoria Antropológicado Didático (TAD), Dimensões de um problema didático (epistemológica, econômico – institucional e ecológica), Problema da álgebra elementar.
RÉSUMÉ
Afin de caractériser l'objet d'étude qui est celui de la Didactique des Mathématiques, nous proposons dans cet article un patron heuristique du développement des problèmes didactiques et nous l'illustrons en prenant comme exemple l'algèbre élémentaire. La structure de ce patron est axée sur les trois dimensions basiques et fondamentales desdits problèmes lorsqu'ils sont abordés dans le cadre de la Théorie anthropologique du didactique: la dimension épistémologique, qui place l'aspect mathématique au coeur du problème, la dimension économico–institutionnelle, qui dépersonnalise la problématique didactique et circonscrit l'unité minimale de l'analyse des processus d'étude et la dimension écologique qui met en relief les conditions nécessaires pour qu'une telle étude institutionnalisée des mathématiques soit possible et qui fait ressortir les contraintes en tout genre ayant une incidence sur l'étude en question.
MOTS CLÉS: Théorie anthropologique du didactique (TAD), Dimensions d'un problème didactique (épistémologique, économico – institutionnelle et écologique), Problème d'algèbre élémentaire.
1. EL OBJETO DE ESTUDIO DE LA DIDÁCTICA DE LAS MATEMÁTICAS
En este trabajo describiremos las tres dimensiones básicas o fundamentales que distinguen a los problemas de investigación en Didáctica de las Matemáticas cuando son enunciados y propuestos —construidos— en el ámbito de la Teoría Antropológica de lo Didáctico (en adelante, TAD). De este modo, postulamos una primera caracterización del objeto de estudio de la Didáctica de las Matemáticas y, en consecuencia, de esta disciplina, bajo el enfoque de la TAD1.
Sin embargo, no pretendemos caracterizar de manera absoluta el objeto de estudio de la Didáctica de las Matemáticas, ya que esta disciplina se encuentra todavía en una etapa histórica fundacional y, en cierta manera, pre–paradigmática (Kuhn, 1962).
Únicamente trataremos de analizar y relacionar entre sí a las tres características fundamentales de los que consideramos como problemas didácticos2.
Esas tres dimensiones, que describiremos con cierto detalle y posteriormente ejemplificaremos con el caso del problema del álgebra elemental, no deben tomarse como propiedades obtenidas de un análisis a posteriori sobre los problemas didácticos previamente definidos o establecidos, sino como características definitorias y constitutivas de la noción de problema didáctico, según el punto de vista de la TAD.
Lo anterior significa que, en lugar de empezar suponiendo queja sabemos ¡o que son los problemas didácticos (a los que se identifica, por ejemplo, con los problemas relativos a la enseñanza y el aprendizaje de las matemáticas) y proponer luego una lista de características de los mismos, nosotros actuaremos al revés. Asumimos el principio epistemológico general que señala que los problemas científicos no están dados de antemano, sino que se generan y evolucionan conjuntamente con la disciplina que los construye (Gascón, 1993); en nuestro caso, construiremos y enunciaremos los problemas didácticos con las herramientas que nos proporciona la TAD en su estado actual de desarrollo.
2. PATRÓN HEURÍSTICO DEL DESARROLLO DE LOS PROBLEMAS DIDÁCTICOS
En forma esquemática, el desarrollo virtual de un problema didáctico (que no es necesariamente histórico) puede representarse como sigue:

Donde P1, P2 y P3 representan las dimensiones fundamentales del problema, mientras que P0 juega un papel especial porque, como veremos, es una formulación inicial, en cierta forma precientífica, de algunos tipos de problemas didácticos, a la que hemos denominado problema docente (Gascón 1999b). Veremos que, aunque P0 es especialmente visible en las primeras etapas del desarrollo de la Didáctica de las Matemáticas —en las que nos encontramos actualmente—, no consideramos que constituya una dimensión que esté necesariamente presente en todos los problemas didácticos. El símbolo 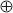 alude a que P0 es un problema didáctico incompleto y que es necesario añadirle, al menos, la dimensión epistemológica P1 para que pueda ser considerado como problema.
alude a que P0 es un problema didáctico incompleto y que es necesario añadirle, al menos, la dimensión epistemológica P1 para que pueda ser considerado como problema.
El símbolo  no debe interpretarse como una inclusión; más bien, indica que cada una de las dimensiones Pi es lógicamente anterior a la dimensión Pi+1, al menos, que "Pi va antes que Pi+1" en un hipotético desarrollo virtual del problema. También podría decirse que una formulación completa de Pi+1 requiere de cierta formulación previa —aunque sea implícita— de Pi.
no debe interpretarse como una inclusión; más bien, indica que cada una de las dimensiones Pi es lógicamente anterior a la dimensión Pi+1, al menos, que "Pi va antes que Pi+1" en un hipotético desarrollo virtual del problema. También podría decirse que una formulación completa de Pi+1 requiere de cierta formulación previa —aunque sea implícita— de Pi.
En cuanto a Pδ, se le puede llamar simplemente problema didáctico y considerarlo como una formulación (que puede ser virtual) donde están contenidas las tres dimensiones fundamentales del problema, las relaciones entre ellas y algunas cuestiones nuevas que no aparecían explícitamente en ninguna de aquellas.
Aquí es importante subrayar dos características del desarrollo histórico efectivo, esto es, de la historia real de la investigación didáctica:
a) En la práctica científica normal —independientemente del enfoque teórico que se adopte— no se suelen explicitar todas las dimensiones de los problemas didácticos; normalmente se estudia un aspecto de alguna de las dimensiones del problema. El desarrollo posterior de la investigación puede dar origen a la formulación y al estudio de otros aspectos de alguna de las restantes dimensiones, así como a su conexión con otros problemas didácticos.
b) El desarrollo histórico de la investigación didáctica no siempre se atiene ni respeta de manera estricta el patrón heurístico, ya que en la historia real puede cambiar el orden en que se estudian algunas de las dimensiones básicas de un problema didáctico. Además, pueden valorarse como principales o prioritarias a las dimensiones que aquí consideramos secundarias —por ejemplo, las dimensiones cognitiva, personal, ostensiva, instrumental, etc.— y, desde luego, puede quedar implícita y no ser ni siquiera planteada alguna dimensión que desde la TAD se juzgue como básica o fundamental, como la epistemológica. Se confirma así la afirmación de Lakatos (1971): la historia real es una caricatura de sus reconstrucciones racionales.
A fin de dar una formulación general sobre las dimensiones básicas de un problema didáctico y empezar a clarificar el objeto de estudio de la Didáctica de las Matemáticas, asignaremos una denominación a cada una de ellas y la acompañaremos de una breve descripción.
2.1. Los problemas docentes como posible punto departida
Llamamos problemas docentes a los que se plantea el profesor como tal profesor cuando tiene que enseñar un tema matemático a sus alumnos. Los problemas docentes se formulan con las nociones disponibles en la cultura escolar, que en muchas ocasiones son importadas de los documentos curriculares (por ejemplo, las nociones de motivación, aprendizaje significativo, individualización de la enseñanza, adquisición de un concepto, abstracción o competencia). Tanto las nociones como las ideas dominantes de la cultura escolar no se cuestionan. Un prototipo de problema docente genérico puede expresarse en los siguientes términos:
P0: ¿Qué tengo que enseñar a mis alumnos y cómo tengo que enseñarlo a propósito de la geometría, de la estadística, del cálculo diferencial o de la proporcionalidad?
Los problemas docentes admiten formulaciones más específicas, que suelen aludir a algún aspecto particular del problema. Por ejemplo:
P0: ¿Cómo puedo motivar a mis alumnos, aumentar su interés por el estudio y mejorar su actitud en relación con cierto ámbito de las matemáticas? O también, ¿cómo puedo utilizar las TIC a fin de mejorar el proceso de enseñanza de dicho ámbito? ¿Cómo individualizar la enseñanza de tal o cual concepto?
Hay que señalar, de nuevo, que no todo problema didáctico parte necesariamente de un problema docente, aunque históricamente la problemática docente ha constituido la problemática didáctica inicial. Pero a medida que una disciplina se desarrolla, su objeto de estudio evoluciona de modo paralelo.
[...] no debería sorprendernos que, a medida que evoluciona la Didáctica de las Matemáticas, los diferentes tipos de problemas que van apareciendo queden, aparentemente, cada vez más alejados de la problemática inicial. De hecho, esto es lo que ha sucedido y sigue sucediendo en todas las disciplinas científicas desde la física, la química, la biología, la psicología y la economía, hasta las propias matemáticas.
[...] El alejamiento que sufren los problemas didácticos respecto de la problemática docente inicial no debería interpretarse como un olvido de ésta, sino como una reformulación que puede ser muy profunda e inesperada y que está propiciada por la elaboración de nuevos instrumentos teóricos y técnicos. (Gascón 1999b,p. 135)
Sin embargo, actualmente muchos de los problemas didácticos que aparecen en la bibliografía se siguen formulando de un modo relativamente próximo a los problemas docentes. Esto se pone de manifiesto en que algunas investigaciones didácticas no cuestionan el ámbito de la actividad matemática que está involucrado en el problema didáctico; en consecuencia tampoco consideran la relatividad institucional del saber matemático. Por ejemplo, si el problema didáctico atañe a la enseñanza de la geometría, no es habitual que se tome como parte del problema la dilucidación de lo que se entiende por geometría en la institución de referencia —donde se ha planteado el problema— ni que se sienta la necesidad de elaborar un modelo epistemológico de la geometría para utilizarlo en el estudio del problema.
Dicho cuestionamiento, según la perspectiva de la TAD, es imprescindible. Para que un problema didáctico pueda ser considerado como tal debemos empezar explicitando, su dimensión epistemológica.
2.2. Dimensión epistemológica de un problema didáctico
En la formulación de cualquier problema didáctico, el didacta siempre utiliza, aunque sólo sea implícitamente, una descripción y una interpretación —es decir, un modelo epistemológico— del ámbito matemático que está enjuego. La TAD ha subrayado desde el principio la necesidad de explicitar dicho modelo y utilizarlo como referencia para analizar los hechos didáctico–matemáticos (Gascón, 1993, 1994, 1998, 1999a, 2001a). Actualmente se le llama modelo epistemológico de referencia (MER) y tiene un carácter siempre provisional. Con base en el MER, el didacta puede deconstruir y reconstruir las praxeologías cuya difusión intrainstitucional e interinstitucional pretende analizar.
La Teoría de la Transposición Didáctica (Chevallard, 1991, 1997) nos enseña que no existe un sistema de referencia privilegiado a partir del cual se observe, analice y juzgue el mundo de los saberes. Pero la ausencia de un sistema de referencia absoluto no hace menos imprescindible —de forma bastante análoga a lo que pasa en la mecánica— la utilización de sistemas de referencia relativos, adecuados a cada problema y situación (Bosch & Gascón, 2005). Queremos insistir una vez más en que los modelos epistemológicos que construye la Didáctica de las Matemáticas deben tomarse como hipótesis de trabajo y, como tales, deben ser constantemente contrastados y revisados. Es en este punto donde toma pleno sentido el nombre de epistemología experimental, que Guy Brousseau dio inicialmente a la Didáctica de las Matemáticas.
El MER también es necesario para estudiar el saber matemático antes de que se transforme para ser enseñado. Sólo así podremos dar cuenta no sólo de la forma en que se interpreta la proporcionalidad, la geometría o la topología dentro del sistema de enseñanza, sino también del porqué es posible encontrar en dicho sistema unos objetos matemáticos y no otros. Por ejemplo, podremos identificar el porqué de la insistencia actual en enseñar la proporcionalidad y porqué en un momento histórico reciente desapareció la geometría euclidiana del corpus de la matemática enseñada (y porqué ha vuelto a aparecer, aunque tímidamente, en la Enseñanza Secundaria Obligatoria de España). En cualquier caso, es importante que el MER que se utiliza en una investigación didáctica sea explícito —o potencialmente explicitable—, ya que condicionará decisivamente:
a) La amplitud del ámbito matemático más adecuada para plantear el problema didáctico en cuestión. Por ejemplo, si un problema didáctico hace referencia a los límites de funciones, el didacta deberá utilizar un MER más o menos amplio, que contenga o no las problemáticas de la existencia del límite, la continuidad o la derivabilidad (Barbé, Bosch, Espinoza & Gascón,_2005).
b) Los fenómenos3 didácticos que serán visibles para el investigador. Si se considera, por ejemplo, que el saber matemático es una construcción axiomática, será muy difícil detectar fenómenos didácticos ligados con la actividad de resolución de problemas.
c) Los tipos de problemas de investigación que se pueden plantear. Para los investigadores en didáctica que toman el saber matemático como un sistema conceptual es muy difícil proponer problemas didácticos fuera de un marco —normalmente psicologista— en el que aprender matemáticas se identifica con adquirir conceptos.
d) Las explicaciones tentativas que se podrán proponer, esto es, el tipo de soluciones que se considerarán admisibles (Bosch & Gascón, 2007). Por ejemplo, si el modelo epistemológico asumido considera al saber matemático como un lenguaje, entonces las explicaciones relativas a las dificultades en el aprendizaje del álgebra elemental se plantearán forzosamente en términos de adquisición y utilización del lenguaje algebraico.
En resumen, la dimensión epistemológica de un problema didáctico es una dimensión nuclear puesto que, como veremos, impregna y condiciona fuertemente al resto de las dimensiones. Y esto sucede incluso en las investigaciones didácticas donde las cuestiones relativas a esta dimensión son más o menos transparentes y, en consecuencia, no se consideran de manera explícita.
Cuando la dimensión epistemológica se pone en primer plano, como se muestra en los enfoques que se sitúan en el Programa Epistemológico de Investigación en Didáctica de las Matemáticas4, entonces se hace un esfuerzo por explicitar el MER —sea con este nombre o con otro— y aparecen cuestiones relativas a la forma de describir e interpretar los conocimientos matemáticos. En forma más concreta, los tipos de preguntas que integran la dimensión epistemológica de un problema didáctico son los siguientes:
a) ¿Qué es el conocimiento matemático? Esto es, ¿cómo se interpreta y cómo se describe el conocimiento matemático? ¿Cuáles son sus componentes y cómo se estructuran?
b) ¿Cómo pueden modelizarse, desde la posición del didacta, los conocimientos matemáticos (modelo epistemológico general) y cada uno de los ámbitos de la actividad matemática (modelos epistemológicos específicos)?
c) ¿Cuál es su razón de ser? Esto es, ¿cuáles son las cuestiones matemáticas o extramatemáticas a las que responde cada uno de los ámbitos de la actividad matemática?
d) ¿Qué se entiende por hacer matemáticas y por adquirir, comunicar, aprender, enseñar o aplicar los conocimientos matemáticos?
e) ¿Cómo se generan y cómo se desarrollan los conocimientos matemáticos? ¿Cómo se transforman al emigrar entre las diferentes instituciones?
f) ¿Cuál es la amplitud del ámbito matemático más adecuada para plantear un problema didáctico determinado?
Dichas cuestiones están siempre presentes en el trasfondo de los problemas didácticos, incluso en el caso de que estos sólo se refieran explícitamente a otros de sus aspectos o dimensiones. Además, las respuestas a estas cuestiones que propone o asume implícitamente cada enfoque en Didáctica de las Matemáticas condicionan completamente a la problemática didáctica.
En cualquier caso, las preguntas que forman parte de la dimensión epistemológica dejan entrever que esta no sólo ocupa una posición privilegiada en todo problema didáctico, sino que además es inseparable de las restantes dimensiones (la económico–institucional y la ecológica), que analizaremos a continuación.
Dado que las preguntas de carácter epistemológico son las fundamentales de la teoría del conocimiento, podemos afirmar que la dimensión epistemológica de un problema didáctico es más básica o fundamental que la que podríamos llamar dimensión cognitiva. Por ello, la TAD no considera que las cuestiones directamente relacionadas con lo cognitivo (en el sentido de la psicología cognitiva) integren una de las dimensiones fundamentales o básicas de un problema didáctico, sino que formen parte de una dimensión secundaria, aunque no por ello menos importante.
Para tomar en cuenta la dimensión epistemológica de un problema didáctico, el didacta debe construir efectivamente —y, de preferencia, en forma explícita— un MER relativo al ámbito de la actividad matemática que está en juego en dicho problema. Este MER, de alcance local o regional, debe ser compatible con el modelo epistemológico general de la actividad matemática que, en el caso de la TAD, se formula en términos de organizaciones praxeológicas o praxeologías5.
Esto significa que los MER deben describirse conforme a la génesis y el desarrollo (incluyendo ampliaciones y completaciones progresivas) de determinadas praxeologías matemáticas.
En este punto, aparecen como inseparables las dos caras de la actividad matemática: el proceso de estudio (lo didáctico) y el producto o resultado de esa construcción (lo matemático, en sentido clásico). El proceso de estudio, al ser una actividad humana, también puede ser modelizado en términos de praxeologías que serán llamadas didácticas (Chevallard, 1999). La noción de estudio integra todos los procesos de manipulación de las matemáticas en las diversas instituciones sociales, ya sean de producción, difusión, utilización o enseñanza (Chevallard, Bosch & Gascón, 1997). El objeto de estudio de la Didáctica de las Matemáticas puede formularse ahora con la noción de praxeología:
El concepto de praxeología nos permite formular completamente el objeto de la didáctica: la didáctica se preocupa por el estudio de las condiciones y restricciones bajo las cuales las praxeologías comienzan su vida, migran, cambian, funcionan, mueren, desaparecen, reviven, etc., dentro de los grupos humanos. Por supuesto, esto conlleva una considerable ampliación del campo de investigación de la didáctica: la didáctica estudia lo didáctico, en cualquier forma que pueda aparecer. Dándose el objeto de estudio adecuado, la didáctica aumenta progresivamente sus esperanzas de evitar quedar dominada por campos disciplinares establecidos en la escuela. (Chevallard, 2005)
Como dice Chevallard, el estudio de la transposición didáctica, y añadimos, el análisis de los MER que este estudio requiere y permite construir, son los instrumentos que han permitido a la Didáctica de las Matemáticas romper con la didáctica clásica y construir su propio objeto de estudio, integrando definitivamente al saber matemático.
[...] en la medida en que el "saber" deviene para ella problemático puede figurar, en adelante, como un término en el enunciado de problemas (nuevos o simplemente reformulados) y en su solución. (Chevallard, 1997, p. 16)
Para formular un problema didáctico en términos de la TAD se requiere tomar un MER como sistema de referencia. Dicho en forma breve, al plantear un problema didáctico es imprescindible tomar en cuenta su dimensión epistemológica porque esta tiene un carácter nuclear. Toma así pleno sentido la idea tan repetida de Guy Brousseau, la cual señala que todo problema didáctico tiene un componente matemático esencial, al tiempo que se subraya, una vez más, la importante ampliación de lo matemático, defendida por el programa epistemológico de investigación en Didáctica de las Matemáticas, al integrar de manera inseparable en la dimensión epistemológica la génesis, el desarrollo, el estudio, la utilización y la transposición institucional del saber matemático (Gascón, 1993, pp. 299–300).
2.3. Dimensión económico–institucional de un problema didáctico y unidad mínima de análisis de los procesos de estudio
De manera coloquial, podemos decir que la dimensión económico–institucional de un problema didáctico incluye cuestiones que giran en torno a la pregunta ¿cómo son las cosas (las OMy las OD) en la contingencia institucional? Con ello, abarca al sistema de reglas y principios (nomos) que regulan –en una institución determinada– la organización y el funcionamiento de las OM y las OD involucradas en el problema didáctico.
Cabe mencionar que cualquier respuesta que pretendamos dar a la citada pregunta deberá apoyarse en un MER y en un modelo didáctico de referencia (MDR) sustentado por dicho MER. Además, no hay que olvidar que cuando nos preguntamos cómo son las cosas aparecen cuestiones que sólo pueden responderse investigando lo que sucede cuando intentamos cambiar las cosas en una dirección determinada. En resumen, podríamos decir que la actividad que se ha de llevar a cabo para responder las preguntas tocantes a la dimensión económico–institucional de un problema didáctico está muy ligada a lo que Chevallard (2010, en prensa) designó como el análisis clínico de la didáctica, y que engloba lo que suele denominarse ingeniería didáctica. Dicho análisis incluye la observación y la descripción detallada de las OM y las OD que existen efectivamente en determinadas instituciones (utilizando como referencia determinados MER y MDR), así como el diseño, experimentación y evaluación de nuevas OD, construidas con los criterios mencionados. Este análisis pretende, por una parte, estudiar los hechos didácticos que se producen en los sistemas docentes cuando se introducen cambios didácticos controlados, al igual que su viabilidad; por otra, contrastar determinados fenómenos didácticos previamente formulados y explicitados en forma teórica.
Dado que el MER se estructura mediante una sucesión creciente de praxeologías matemáticas, ningún problema didáctico puede abordarse haciendo referencia a una OM puntual6, esto es, que haya sido generada únicamente por un concepto, una técnica o un tipo de problemas matemáticos.
En forma análoga, y teniendo en cuenta de nuevo que en la construcción de un MER hay que atender a los datos empíricos que provienen de todas y cada una de las instituciones que intervienen en el proceso de transposición didáctica (ver Figura 1), ningún problema didáctico podrá considerar únicamente los datos que emanan de una sola institución —por ejemplo, el aula o la institución escolar—, y mucho menos podemos restringirnos a los datos que emanan del comportamiento individual de los sujetos de una o más instituciones.

Desde el punto de vista de la TAD, todo problema didáctico tiene que hacer referencia, en forma más o menos explícita, a todas las etapas de la transposición didáctica y debe contener una praxeología matemática suficientemente amplia. Hay que recordar que la unidad mínima de análisis de los procesos didácticos (Bosch & Gascón, 2005) debe contener el proceso de estudio institucional de una OM local relativamente completa (Bosch, Fonseca & Gascón, 2004). En realidad, la unidad mínima de análisis de los procesos didácticos es una organización didáctica asociada a una OM local.
Es en este contexto donde tiene sentido plantear la dialéctica entre lo personal y lo institucional, tal como la considera la TAD. En efecto, al aceptar la citada unidad mínima de análisis de los procesos didácticos se señala la preeminencia de lo institucional sobre lo personal, tanto en la descripción de los fenómenos didácticos como en la formulación de los problemas de investigación didáctica y hasta en el tipo de respuestas admisibles.
Para la TAD, no hay fenómenos ni problemas didácticos que se refieran en última instancia a la relación personal con un ámbito del saber matemático, puesto que dicha relación está en gran medida determinada —y, en consecuencia, puede ser explicada— a partir de la relación institucional. Por ejemplo, la relación personal de un alumno con la proporcionalidad o, mejor, con una praxeología matemática determinada que vive en cierta institución, la cual incluye a la noción de proporcionalidad, depende en gran medida y puede explicarse en última instancia a partir de la relación institucional a dicha praxeología, esto es, a partir del tipo de actividades matemáticas que es posible llevar a cabo en torno a la proporcionalidad en la institución de referencia, sin que esto niegue las diferencias evidentes entre las diversas relaciones personales a una praxeología determinada.
Es por ello que en la TAD se considera la relación institucional a una OM, y en forma más amplia, la vida institucional de una OM, esto es, la génesis, el desarrollo, la difusión intrainstitucional, la migración a otras instituciones y la desaparición institucional de las praxeologías matemáticas, como objeto primario de estudio, mientras que la relación personal es vista como objeto secundario, aunque no por ello menos importante. Así, la TAD no toma en cuenta a la dimensión personal como fundamental o básica en un problema didáctico.
Las cuestiones que forman parte de la dimensión económico–institucional de un problema didáctico requieren que se explique previamente la dimensión epistemológica. En particular, el MER resulta imprescindible para analizar el saber matemático, tal como aparece y es interpretado en cada una de las instituciones que intervienen en las sucesivas etapas del proceso de transposición. Por ejemplo, para estudiar la forma como se interpretan los números decimales, el álgebra elemental o la derivación de funciones en un determinado sistema de enseñanza, el didacta necesita utilizar un MER específico de cada uno de esos ámbitos del saber matemático.
Si, por ejemplo, queremos estudiar lo que algunos autores llaman el razonamiento proporcional de los estudiantes y los fenómenos didácticos que se le asocian, es imprescindible partir de un análisis de cómo es interpretada ¡a proporcionalidad en la institución docente. Esto implica ahondar en las prácticas matemáticas que es posible llevar a cabo en dicha institución sobre la proporcionalidad. Pero este análisis es todavía insuficiente. Será necesario, además, situar la proporcionalidad en una OM local relativamente completa que, a su vez, deberá integrarse en una OM regional y, sobre todo, estudiar todas y cada una de las etapas de los fenómenos transpositivos, los cuales han dado como resultado las OM en torno a la proporcionalidad que aparecen efectivamente en las instituciones escolares.
En resumen, la dimensión económico–institucional de un problema didáctico plantea cuestiones sobre el resultado que, en un periodo histórico determinado, ha producido la acción de la transposición didáctica en las praxeologías matemáticas y didácticas. Los tipos de problemas que forman parte de dicha dimensión son los siguientes7:
a) ¿Cuál es el ámbito institucional que hemos de tomar en consideración para estudiar el problema didáctico en cuestión?
b) ¿Qué características presentan determinadas OM, y las OD asociadas, en una institución y en un periodo histórico determinados?
c) ¿Cómo se considera en cada institución un ámbito concreto de la actividad matemática? (es decir, cómo se describe y cómo la interpretan los sujetos de la misma).
d) ¿Qué tipos de prácticas matemáticas pueden llevarse a cabo en una institución determinada en relación con un ámbito particular de la actividad matemática?
e) ¿Cuál es, en definitiva, el modelo epistemológico de las matemáticas (específico de un ámbito) y el modelo didáctico asociado dominantes en una institución dada?
f) ¿Qué dificultades aparecen cuando se pretende modificar las OD en una dirección determinada dentro de una institución dada?
Todo problema didáctico hace referencia a la forma de organizar el estudio de ciertas OM en determinas instituciones; esto es, alude a una OD institucional. En consecuencia, el didacta necesita instrumentos para describir y analizar las características de dichas OD, los cuales se los proporcionará un modelo de referencia de las OD posibles que, al igual que el MER, debe ser preferiblemente explícito. En el caso de la TAD, el modelo didáctico de referencia (MDR) se expresa en términos de la teoría de los momentos o dimensiones de la actividad matemática, que permite describir la dinámica de las OD (Chevallard, 1999), así como de los tipos ideales de OD. Dado que cada OD empírica —históricamente existente en una institución— está basada en el modelo epistemológico de las matemáticas que domina en dicha institución, la descripción de las OD empíricas debe incluir una caracterización del modelo epistemológico de las matemáticas en que cada una de ellas se sustenta. En definitiva, el MDR tiene que establecer una profunda relación entre las características del proceso (OD) y el producto (OM) de la actividad matemática institucionalizada (Gascón, 2001a).
2.4. Dimensión ecológica de un problema didáctico: niveles de codeterminación matemático–didáctica
De forma muy simplificada, podría decirse que la dimensión ecológica de un problema didáctico contiene las cuestiones que giran en torno a la siguiente pregunta: ¿por qué las cosas (las OMy las OD) son como son en la contingencia institucional y qué condiciones se requerirían para fuesen de otra forma dentro del universo de lo posible?
Como la dimensión ecológica de todo problema didáctico incluye en cierta forma las dimensiones epistemológica y económico–institucional, se puede afirmar bajo el enfoque de la TAD que todo problema didáctico es, en alguna medida, un problema de ecología praxeológica o, con más precisión, que la didáctica se preocupa por el estudio de la ecología institucional de las praxeologías matemáticas y didácticas (Bosch & Gascón, 2007) Por ello, es preciso tomar en consideración las restricciones y condiciones impuestas sobre las praxeologías en todos los niveles de co–determinación didáctica, desde los más genéricos, como la sociedad y la civilización, a los más específicos, como el tema y la cuestión matemática concreta.
La Teoría Antropológica de lo Didáctico propone una jerarquía de niveles de co–determinación didáctica (Chevallard, 2001, 2002a, 2002b) entre las OM y sus correspondientes OD, estructurada mediante una sucesión de niveles, y en cada uno surgen dependencias mutuas entre las OM y las OD:

Cada nivel contribuye a determinar la ecología institucional de las OM y las OD, tanto por los puntos de apoyo que ofrece como por las restricciones que impone. En cada nivel se producen restricciones entre las OM y las OD que tienen carácter recíproco: la interpretación y la estructuración de las OM en cada nivel de la jerarquía condicionan las formas posibles de organizar su estudio, mientras que, recíprocamente, la naturaleza y las funciones de los dispositivos didácticos existentes en cada nivel determinan, en gran medida, el tipo de OM que será posible reconstruir.
Toda cuestión —en este caso, matemática— que genera un proceso de estudio en una institución didáctica forma parte de un tema que pertenece a un sector, el cual queda incluido en un área de una cierta disciplina. Si esta disciplina son las matemáticas, llamaremos a estos niveles matemáticos. En contraposición, los niveles más allá de la disciplina, que se denominan genéricos, son considerados culturalmente como niveles pedagógicos en el sentido de no matemáticos; sin embargo, incluyen restricciones que tienen fuerte incidencia en la matemática escolar y, por tanto, deben formar parte del objeto de estudio de la Didáctica de las Matemáticas.
Por ejemplo, la pregunta ¿cuáles son las simetrías de un rectángulo no cuadrado? es considerada en la mayoría de los sistemas escolares de la siguiente manera: pertenece al tema simetrías de polígonos, que se incluye en el sector de transformaciones del plano; éste a su vez concierne al área de la geometría, que forma parte de la disciplina matemáticas (Chevallard, 2001).
Sin embargo, el hecho de que se construya esta jerarquía disciplinar no garantiza la calidad del estudio de la pregunta en cuestión. Para que una cuestión matemática pueda estudiarse con sentido en la escuela, señala Gascón (2003b), es necesario:
1) Que provenga de cuestiones que la sociedad propone para que se estudien en la escuela (legitimidad cultural o social).
2) Que aparezca en ciertas situaciones umbilicales de las matemáticas, esto es, ubicadas en la raíz central de las matemáticas (legitimidad matemática).
3) Que conduzca a alguna parte, esto es, que esté relacionada con otras cuestiones que se estudian en la escuela, sean matemáticas o de otras disciplinas (legitimidad funcional).
Si para una cuestión determinada no se elabora una jerarquía de niveles que cumpla con dichas condiciones, entonces carece de sentido porque que ha desaparecido la razón de ser de su estudio en la escuela. En este caso, se dice que es una cuestión encerrada en sí misma o una cuestión muerta (Chevallard, Bosch & Gascón, 1997).
De esta manera se amplía y precisa la antigua ecología de los saberes (Chevallard, 1992). Es más precisa porque la estructura de las praxeologías se describe en forma mucho más detallada que la de los saberes y porque las restricciones están concretadas en los diferentes niveles de codeterminación didáctica. También la problemática ecológica se amplía debido a que incluye las praxeologías didácticas, además de las matemáticas.
En la nueva ecología praxeológica es necesario priorizar y jerarquizar las restricciones que tomaremos en cuenta, ya que no todas tienen la misma importancia ni la misma relevancia. Así, puede suceder que una restricción concreta sea tan decisiva que anule o convierta en prácticamente irrelevantes a las otras.
A manera de resumen, diremos que la dimensión ecológica de un problema didáctico abarca cuestiones que pretenden indagar qué tipo de restricciones, y de qué nivel proceden, son cruciales para la ecología de las praxeologías matemáticas y didácticas. En forma más concreta:
a) ¿Cuáles son las condiciones que permiten dar cuenta del estado actual —o en un periodo histórico determinado— de las OM y de las OD asociadas en una institución determinada?
b) ¿Qué restricciones dificultan o impiden que determinadas características de las OM y de las OD se desarrollen en una institución? ¿En qué niveles de la jerarquía surgen esas restricciones?
c) ¿Qué condiciones se deberían instaurar, y en qué niveles de la jerarquía, para que fuese posible la vida de ciertas OM y OD con unas características determinadas?
d) El modelo epistemológico específico de un ámbito de la actividad matemática dominante en una institución I, ¿cómo condiciona la forma de organizar la enseñanza (y, más en general, el estudio) de dicho ámbito en I? (Gascón, 2001a)
Las investigaciones sobre la problemática ecológica ponen de manifiesto que las restricciones que determinan las características de las praxeologías institucionales —sean matemáticas, didácticas o de cualquier otro tipo— son, en general, independientes de la voluntad de los sujetos que participan en ellas. Esto no significa que las restricciones sean inamovibles ni que los sujetos no tengan responsabilidad alguna. Por el contrario, existen restricciones que pueden ser modificadas desde cierta posición institucional, como la de profesor o la de director de un centro educativo. Cuando una restricción es modificable desde una posición institucional (por ejemplo, la de profesor o la de alumno) diremos que se trata de una condición mirada desde —o relativa a— dicha posición.
3. A MODO DE EJEMPLO: LAS DIMENSIONES DEL PROBLEMA DIDÁCTICO DEL ÁLGEBRA ELEMENTAL FORMULADO EN EL ÁMBITO DE LA TAAD8
Para fijar ideas, vamos a describir las dimensiones fundamentales del problema didáctico del álgebra elemental y las relaciones entre ellas, con base en el siguiente esquema:

3.1. Problema docente del álgebra elemental: P0(A)
El problema docente P0(A) puede enunciarse del siguiente modo: ¿Qué tengo que enseñar a mis alumnos en relación al álgebra elemental y cómo tengo que enseñarlo?
En las investigaciones sobre el álgebra elemental conforme a la perspectiva antropológica hay una primera etapa que culmina con la publicación, a finales de 1989, de la nota de síntesis hecha por Chevallard (1990b), la cual incluye un conjunto de sus trabajos (destacamos los de 1985, 1989 y 1990a). Dicho escrito puede considerarse, globalmente, como la construcción de un dominio de investigación didáctica, y ofrece la base en la que se sustentan las investigaciones posteriores en relación al problema didáctico del álgebra elemental por parte de nuestro grupo de investigación.
Conforme a este punto de vista antropológico, nuestras primeras investigaciones relativas al problema del álgebra elemental (Gascón, 1989, 1993, 1993–94, 1999a) pusieron de manifiesto la necesidad de dar un paso atrás desde la problemática docente y plantear una cuestión más fundamental sobre la naturaleza del álgebra elemental, que suele quedar implícita en muchos estudios debido a su transparencia.
Por ello, nos vimos llevados a cuestionar el modelo epistemológico del álgebra elemental que dominaba no sólo en las instituciones escolares, sino también en la noosfera9 y hasta en muchas investigaciones sobre el álgebra elemental. En este sentido, antes de intentar dar ni tan sólo una respuesta provisional a P0(A) nos planteamos un problema de ingeniería matemática: la elaboración, desde la didáctica, de un modelo epistemológico específico del álgebra elemental.
3.2. Dimensión epistemológica del problema del álgebra elemental: P1 (A)
Elaboramos un MER del álgebra elemental como una alternativa a la interpretación que se hace de ella cuando se la identifica con una especie de aritmética generalizada, que constituye el modelo dominante en las instituciones escolares. Nuestro modelo identifica, en primera instancia, el álgebra elemental con un instrumento de modelización de todo tipo de OM. Para la TAD, la modelización algebraica —y, en realidad, todo tipo de modelización matemática— posee un carácter constitutivo del sistema que modeliza. Por ejemplo, el cálculo algebraico como actividad matemática es un elemento esencial de la construcción de lo numérico, tanto en la génesis histórica como en la teoría matemática, que rebasa la concepción de que lo algebraico es un simple epifenómeno de lo numérico. Se pone de manifiesto una nueva manera de interpretar las relaciones entre lo algebraico y lo numérico.
Además, el MER del álgebra elemental que propusimos hizo que se ampliara el problema didáctico del álgebra elemental, con la construcción de nociones como proceso de algebrización de las matemáticas escolares y grado de algebrización de una OM (Bolea, Bosch & Gascón, 2001a, 2001b).
En resumen, el tipo de cuestiones y problemas didácticos relativos a la dimensión epistemológica del problema del álgebra elemental son, entre otros, los siguientes:
a) ¿Qué es el álgebra elemental y qué papel juega en la actividad matemática?
b) ¿Cómo puede describirse el álgebra elemental mediante un MER compatible con el modelo epistemológico general de la actividad matemática que propone la TAD?
c) ¿Cuáles son las relaciones posibles entre lo algebraico y lo numérico en la enseñanza obligatoria?
d) ¿Es posible la introducción del álgebra elemental en un marco diferente del marco aritmético habitual, en el que lo algebraico es considerado como un epifenómeno de lo numérico?
e) ¿En qué consiste la actividad algebraica y cómo se puede interpretar el denominado pensamiento algebraico con las herramientas que proporciona el MER?
f) ¿Cuáles son las cuestiones a las que responde el álgebra elemental, esto es, cuál es su razón de ser?
g) ¿Cuál es la amplitud del ámbito matemático más adecuada para plantear el problema didáctico del álgebra elemental: la variable, el signo igual, el significado de las expresiones simbólicas, los conceptos, las ecuaciones? O, por el contrario, ¿debemos plantear el problema a un nivel más amplio que abarque el papel de los problemas verbales y de la modelización matemática en la enseñanza secundaria?
Si se toma el MER del álgebra elemental que construimos como un sistema de referencia provisional y relativo pueden plantearse, en términos de la TAD, nuevas cuestiones que relacionan la dimensión epistemológica descrita con la dimensión económico–institucional del problema del álgebra elemental que describiremos a continuación.
3.3. Dimensión económico–institucional y unidad de análisis del problema del álgebra elemental: P2(A)
Al considerar en el MER propuesto a la actividad algebraica como un instrumento de modelización matemática, y después de cuestionar la amplitud del ámbito matemático más adecuada para plantear el problema didáctico del álgebra elemental, surge la cuestión de la unidad de análisis:
a) ¿Cuál es la unidad de análisis adecuada para estudiar el problema del álgebra elemental? Con más precisión: ¿qué ámbito institucional hemos de tomar en consideración: el aula, la escuela, el sistema de enseñanza de las matemáticas, la sociedad o incluso la civilización?
El estudio de este problema puso de manifiesto que para entender lo que sucede en los sistemas didácticos es preciso tomar en cuenta el sistema de enseñanza de las matemáticas en su conjunto y la noosfera, que incluye a la sociedad y su cultura. El desarrollo de dicho trabajo constituyó el primer ejemplo de análisis (macro)ecológico sobre las condiciones de posibilidad de un tipo dado de fenómenos didácticos en un entorno institucional determinado. Este tipo de análisis hizo hincapié en la relatividad institucional de los conocimientos matemáticos y originó una crítica de la presunta universalidad abstracta y a–institucional de los conceptos (Chevallard, 1990b).
Surgen así nuevas cuestiones para indagar cuál es el papel y la función del álgebra elemental en las diferentes instituciones (lo que hemos denominado relación institucional a lo algebraico), las cuales también forman parte de la dimensión económico–institucional del problema del álgebra elemental:
b) ¿Cómo se considera, cómo se describe, cómo se interpreta y qué características presenta el álgebra elemental actualmente en cada una de las instituciones que intervienen en el proceso de transposición?
c) ¿Qué tipos de actividades consideradas como algebraicas (en el MER) pueden llevarse a cabo en la Enseñanza Secundaria Obligatoria (ESO), que comprende a alumnos del2al6 años?
d) ¿Cómo se puede caracterizar el grado de algebrización de las OM que viven en las instituciones escolares?
e) El modelo epistemológico dominante en una institución escolar, ¿cómo condiciona la forma de organizar la enseñanza del álgebra elemental en dicha institución? ¿Qué se entiende en las instituciones docentes por enseñar álgebra elemental?
f) ¿Qué dificultades aparecen cuando se pretende introducir en la ESO el álgebra como un instrumento de modelización? ¿Qué posibilidades nuevas emergen? ¿Qué hechos didácticos se ponen de manifiesto?
Con ayuda del MER elaborado como respuesta a Pj(A),es posible observar el fenómeno de la desalgebrización de las matemáticas escolares y analizar sus consecuencias didácticas (Bolea, 2003; Bolea, Bosch & Gascón, 2001a; Gascón, 2001b).
3.4. Dimensión ecológica del problema del álgebra elemental: P3(A)
Las cuestiones que atañen a la dimensión ecológica del problema del álgebra elemental constituyen la problemática en torno al por qué la relación institucional a lo algebraico es como es y qué condiciones se requerirían para modificarla en una dirección determinada. En el marco de la TAD, el estudio de la relación personal del alumno a lo algebraico es prácticamente fundamental, pero resulta epistemológicamente secundario para la Didáctica de las Matemáticas.
Para llevar a cabo el análisis de la ecología de lo algebraico en los sistemas didácticos se utilizan diversos materiales empíricos —los manuales, los textos oficiales, las clases, las respuestas de alumnos y profesores a determinados cuestionarios— y se subrayan las diferencias respecto al funcionamiento de lo algebraico como objeto de saber. Esto es, se atiende a las diferencias entre el álgebra en las instituciones escolares y el álgebra en las instituciones productoras del conocimiento matemático.
Este análisis sobre algunos rasgos de la ecología de lo algebraico en los sistemas didácticos sugiere un fuerte grado de desalgebrización del curriculum escolar, y plantea una problemática cuyo alcance desborda ampliamente los sistemas didácticos: las condiciones de vida de lo algebraico en los sistemas didácticos, tal como han sido descritas, ¿son absolutamente necesarias o, por el contrario, son contingentes y pueden ser modificadas?
Aparece, de nuevo, la necesidad de realizar un estudio ecológico que considere la naturaleza abierta del sistema didáctico para identificar las relaciones de lo algebraico con la matemática sabia, la cultura, las prácticas sociales, la noosfera y el sistema de enseñanza, formulando las siguientes preguntas:
a) ¿Por qué la modelización algebraica está ausente en la matemática de la ESO? ¿Cuáles son las causas últimas de la desalgebrización del curriculum escolar?
b) ¿Qué papel juegan la noosfera, la sociedad y la cultura en la construcción de la relación escolar al álgebra elemental? ¿Cómo es considerada el álgebra en la cultura occidental?
c) ¿Cómo organizar el estudio del álgebra elemental de manera que permita implantar en las primeras etapas de la ESO el uso funcional del instrumento algebraico y el desarrollo progresivo de la modelización algebraica?
d) ¿Qué condiciones se deberían instaurar para que fuese posible la vida de determinadas OM con cierto grado de algebrización?
La hipotética algebrización de las OM escolares como, por ejemplo, la OM en torno a la divisibilidad (Gascón, 2001b), ¿de qué manera transformaría las posibles formas de estudiarlas?
e) ¿En qué niveles de la escala de co–determinación didáctica surgen las restricciones que dificultan el proceso de algebrización de las matemáticas escolares (por ejemplo, en la ESO)?
f) ¿Qué dispositivos didácticos se requieren para construir la infraestructura didáctico–matemática necesaria para organizar el estudio de las OM de la ESO previamente algebrizadas?
Como ya hemos señalado, uno de los principios básicos del estudio de la problemática ecológica —o, si se quiere, de la dimensión ecológica de los problemas didácticos— puede formularse diciendo que las características de las OM y las OD que viven en una institución determinada no pueden cambiarse como consecuencia exclusiva de la voluntad de los agentes, sean profesores, autores de cualquier tipo de materiales escolares o autoridades educativas. En particular, la algebrización de las OM escolares no puede imponerse de un modo puramente voluntarista (Bolea, Bosch & Gascón, 2004).
4. OTROS TIPOS DE PROBLEMAS DIDÁCTICOS RELACIONADOS CON EL PROBLEMA DEL ÁLGEBRA ELEMENTAL
Los problemas científicos no se desarrollan en forma aislada e independiente, sino que integran diferentes tipos de problemas. A lo largo de su desarrollo, los problemas didácticos se relacionan no sólo con problemas de su misma índole, sino también con otros que en apariencia están muy alejados.
En el caso de nuestro ejemplo, ya hemos visto que el problema didáctico del álgebra elemental se desarrolló para dar origen a un primer tipo de problemas que giraban en torno al proceso de algebrización de las matemáticas escolares (Bolea, 2003). Investigaciones posteriores mostraron que dicho tipo de problemas estaba profundamente relacionado con el problema didáctico de la proporcionalidad que, a su vez, se amplió radicalmente para situarse en el ámbito del problema de las relaciones funcionales elementales (García, 2005; García, Gascón, Ruiz Higueras & Bosch, 2006).
Después de los trabajos de tesis de Pilar Bolea y Javier García surgió la necesidad de estudiar el problema ecológico de la modelización funcional.
La investigación, hecha conforme a nuestro patrón virtual del desarrollo de un problema didáctico, requirió la elaboración previa de un MER de esa modelización funcional en el bachillerato español, que comprende a alumnos de 16 a 18 años. Pudimos abordar de este modo el correspondiente problema de ingeniería didáctica —que constituye un aspecto esencial de la dimensión económico–institucional— mediante el diseño y experimentación de una organización didáctica que hiciese posible la vida de la modelización funcional en el bachillerato. El análisis de esta experimentación mostró la existencia de múltiples restricciones,entre las que destacó el carácter preaígebraico de la matemática escolar (Ruiz Munzón, Bosch & Gascón, 2007a, 2007b, 2010).
Por ello, surgió la necesidad de diseñar un MER que fuera capaz de articular globalmente la introducción del álgebra elemental en los primeros cursos de la ESO, en donde aparecen el lenguaje algebraico y los números negativos (Cid, Bosch, Gascón & Ruiz Munzón, 2010 en prensa), con el desarrollo del instrumento algebraico en la segunda etapa de la ESO (alumnos de 14 a 16 años) y la modelización funcional en el bachillerato (alumnos de 16 a 18 años). Dicho MER se formuló en términos de una sucesión de OM cada vez más amplias y completas, de tal manera que cada una de las OM que aparecen puede considerarse como un modelo matemático de la anterior (Ruiz Munzón, 2010). Tal integración de los sucesivos tipos de problemas y su desarrollo conjunto es otro síntoma de madurez de una disciplina científica.
5. CONCLUSIÓN: ¿CÓMO SE ELIGE Y DELIMITA UN PROBLEMA DIDÁCTICO?
Hemos mencionado que una investigación didáctica no se inicia necesariamente con un problema docente y que el patrón virtual propuesto no coincide forzosamente con el orden temporal en el que se desarrolla la historia real de la investigación sobre las diferentes dimensiones de un problema didáctico.

Este patrón heurístico ideal pretende únicamente poner de manifiesto las principales dimensiones de un problema didáctico, bajo el enfoque de la TAD, así como la relación funcional entre ellas. Además, como hemos mostrado en el caso del álgebra elemental, una misma dimensión del problema puede ser estudiada en diversos momentos del proceso de investigación.
Por todo lo dicho, queda claro que tampoco es seguro que cada dimensión Pi provoque efectivamente la emergencia de ¡a dimensión Pi+1 del problema, en el sentido de que la comunidad científica se vea forzada a formular y estudiar dicha dimensión. Aunque las respuestas provisionales a la dimensión P permitan virtualmente que las cuestiones relativas a la dimensión P sean planteadas y estudiadas —e incluso constituyan una condición necesaria para ello—, no nos tiempo prudencial.
Y, por último, es obvio que el patrón no ayuda a seleccionar los problemas didácticos relevantes, puesto que esto es una prerrogativa de la comunidad científica. Se trata únicamente de un patrón ideal que esquematiza una reconstrucción racional (Lakatos, 1976) de la evolución histórica de los problemas didácticos.
En consecuencia, para elegir y delimitar un problema de investigación en Didáctica de las Matemáticas se necesita tomar una gran cantidad de decisiones que no vienen determinadas de antemano, y que muy difícilmente puede afrontar un investigador en solitario. Para que dichas elecciones sean fecundas y acaben constituyendo una aportación relevante al desarrollo del conocimiento didáctico deben estar guiadas por los criterios emanados de la comunidad científica.
De acuerdo con las tres dimensiones fundamentales de un problema didáctico que hemos descrito, presentamos algunas de las cuestiones principales que deberán ser consideradas para elegir y delimitar adecuadamente un problema didáctico:
1) ¿Cómo recortar el ámbito de la actividad matemática que está en juego? ¿Cómo describir, con qué nociones básicas y con qué modelo epistemológico dicho ámbito recortado de la actividad matemática? ¿Qué es lo primariamente problemático y, por tanto, lo que la Didáctica de las Matemáticas debe modelizar en primer término?
2) ¿Qué referencia empírica deben tener los problemas didácticos? Esto es, ¿cuál es el universo empírico o el espacio institucional del que deberán extraerse los datos empíricos? ¿Cuál es la unidad mínima de análisis de los procesos didácticos?
3) ¿Qué tipos de problemas pueden plantearse en Didáctica de las Matemáticas? ¿Los problemas a tratar deben hacer una referencia prioritaria a la actividad matemática individual o a las condiciones y restricciones ecológicas institucionales que la hacen posible, al tiempo que la condicionan? ¿Qué tipos de respuestas a dichas cuestiones serán admisibles?
Y, en cualquier caso, ¿qué papel debe jugar el marco teórico, esto es, la teoría didáctica que proporciona los criterios para tomar cada una de las decisiones que hemos descrito como necesarias para delimitar un problema de investigación didáctica?
Podemos concluir que de lo anterior se deducen dos tesis y un corolario en relación con la cuestión de cómo elegir y delimitar un problema de investigación en Didáctica de las Matemáticas:
Tesis 1. Las elecciones básicas (de la unidad de análisis, de la problemática primaria, del objeto de estudio, del ámbito empírico a tomar en consideración) son responsabilidad de la comunidad de investigadores, no de un investigador aislado.
Tesis 2: Dichas elecciones definen y están determinadas por un paradigma —o programa de investigación— que caracteriza en cada momento histórico a la disciplina científica en cuestión.
Corolario: No es el investigador quien de manera individual elige los problemas. Cuando un paradigma o una teoría científica incluida en él se encuentran suficientemente desarrollados es la comunidad científica la que elige los tipos de problemas que pueden abordarse en cada momento histórico, la que determina su potencial relevancia y la que delimita dichos problemas en coherencia con sus postulados básicos y con ayuda de las herramientas que la propia teoría proporciona.
Hasta tal punto esto es así que, metafóricamente, no sólo podríamos decir que no es el investigador el que elige los problemas que estudiará, sino que son los propios problemas los que se imponen al investigador en tanto que es miembro de una comunidad científica. Se pone de manifiesto la importancia metodológica y filosófica de lo que Kuhn (1962) denominó estructura comunitaria de la ciencia.
RECONOCIMIENTOS
Este trabajo fue realizado en el marco del Proyecto I+D+i EDU2008–02750/EDUC, del Ministerio de Ciencia e Innovación de España.
Algunas de las ideas que aquí se desarrollan fueron expuestas, en una versión provisional, durante un seminario impartido en la Universidad de Jaén, en mayo de 2009.
REFERENCIAS BIBLIOGRÁFICAS
Artigue, M.; Bosch, M. & Gascón, J. (2011, en prensa). Research praxeologies and networking theories. In T. Rowland et al. (Eds.), Proceedings of the 7th Congress of the European Society for Research in Mathematics Education (CERME 7). Rzeszów, Poland: University of Rzeszów. [ Links ]
Bolea, P. (2003). El proceso de algebrización de organizaciones matemáticas escolares. Monografía del Seminario Matemático García de Galdeano, No. 29. Zaragoza, España: Departamento de Matemáticas, Universidad de Zaragoza. [ Links ]
Bolea, P.; Bosch, M. & Gascón, J. (2001a). La transposición didáctica de organizaciones matemáticas en proceso de algebrización. El caso de la proporcionalidad. Recherches en Didactique des Mathématiques 21 (3), 247–304. [ Links ]
Bolea, P.; Bosch, M. & Gascón, J. (2001b). ¿Cómo se construyen los problemas en Didáctica de las Matemáticas? Educación Matemática 13 (3), 22–63. [ Links ]
Bolea, P.; Bosch, M. & Gascón, J. (2004). Why is modelling not included in the teaching of algebra at secondary school? Quaderni diRicerca in Didattica 14, 125–133. [ Links ]
Barbé, J.; Bosch, M.; Espinoza, L. & Gascón, J. (2005). Didactic restrictions on the teacher's practice: the case of limits of functions at Spanish high schools. Educational Studies in Mathematics 59 (1), 235–268. doi: 10.1007/sl0649–005–5889–z. [ Links ]
Bosch, M.; Fonseca, C. & Gascón, J. (2004). Incompletitud de las organizaciones matemáticas locales en las instituciones escolares. Recherches en Didactique des Mathématiques 24 (2), 205–250. [ Links ]
Bosch, M. & Gascón, J. (2005). La praxéologie comme unité d'analyse des processus didactiques. In A. Mercier et C. Margolinas (Coords.), Balises en Didactique des Mathématiques (pp. 107–122). Grenoble, France: La Pensée Sauvage. [ Links ]
Bosch, M. & Gascón, J. (2007). 25 años de Transposición Didáctica. En L. Ruiz–Higueras, A. Estepa y F. J. García (Eds.), Sociedad, escuela y matemáticas. Aportaciones de la Teoría Antropológica de lo Didáctico (pp. 385–406), Jaén, España: Universidad de Jaén. [ Links ]
Brousseau, G. (1997). Theory of didactical situations in mathematics. Didactique des Mathématiques: 1970–1990. Dordrecht, Netherlands: Kluwer Academic Publishers. [ Links ]
Cid, E.; Bosch, M.; Gascón, J. & Ruiz Munzón, N. (2010, en prensa). Actividades de estudio e investigación para introducir los números negativos en un entorno algebraico. Trabajo presentado en 3rd Conference on the Anthropological Theory of the Didactic. Barcelona, España: Sant Hilari Sacalm. [ Links ]
Chevallard, Y. (1985). Le passage de l'arithmétique à l'algébre dans l'enseignement des mathématiques au collège: l'évolution de la transposition didactique. Petit x 5, 51–94. [ Links ]
Chevallard, Y. (1989). Le passage de l'arithmétique à l'algébrique dans l'enseignement des mathématiques au collège. Deuxième partie. Perspectives curriculaires: la notion de modelisation. Petit x 19, 45–75. [ Links ]
Chevallard, Y. (1990a). Le passage de l'arithmétique á l'algébrique dans l'enseignement des mathématiques au collège. Troisième partie. Perspectives curriculaires: voies d'attaque et problèmes didactiques. Petitx, 23, 5–38. [ Links ]
Chevallard, Y. (1990b). Aspects d'un travail de théorisation de la didactique des mathématiques. Etude du cas de l'algèbre élémentaire. Nota de síntesis disponible en el IREM d'Aix–Marseille. [ Links ]
Chevallard, Y. (1991). La Transposition Didactique. Du savoir savant au savoir enseigné. (2da. ed.) Grenoble, France: La Pensée Sauvage. [ Links ]
Chevallard, Y. (1992). Fundamental concepts in didactics: perspectives provided by an anthropological approach. In R. Douady & A. Mercier (Eds.), Research in Didactique of Mathematics. Selected Papers (pp. 131–167). Grenoble, France: La Pensée Sauvage. [ Links ]
Chevallard, Y. (1997). La transposición didáctica. Del saber sabio al saber enseñado. Buenos Aires, Argentina: Aique. [ Links ]
Chevallard, Y. (1999). L'analyse des pratiques enseignantes en théorie anthropologique du didactique. Recherches en Didactique des Mathématiques 19 (2), 221–265. [ Links ]
Chevallard, Y. (2001). Aspectos problemáticos de la formación docente. Conferencia impartida en las XVI Jornadas del Seminario Interuniversitario de Investigación en Didáctica de las Matemáticas, Huesca, España: Consultado en la página web http://www.ugr.es/local/jgodino/siidm.htm. [ Links ]
Chevallard, Y.(2002a). Organiser l'étude 1. Structures et fonctions. In Dorier, J.–L. , Artaud, M., Artigue, M., Berthelot, r., Floris, R. (Eds.), Actes de la 11e Ecole d'Eté de Didactique des Mathématiques (pp. 3–22). Grenoble, France: La Pensée Sauvage. [ Links ]
Chevallard, Y. (2002b). Organiser l'étude 3. Écologie & régulation. In Dorier, J.–L., Artaud, M., Artigue, M., Berthelot, r., Floris, R. (Eds.), Actes de la 11e École d'Eté de Didactique des Mathématiques (pp. 41–56). Grenoble, France: La Pensée Sauvage. [ Links ]
Chevallard, Y. (2005). La didactique dans la cite avec les autres sciences. Trabajo presentado en el Symposium de Didactique Comparée. Montpellier, Francia: Université Montpellier. [ Links ]
Chevallard Y. (2010, en prensa). La notion d'ingénierie didactique, un concept à refonder. Actes de la XXVe École d'Eté de Didactique des Mathématiques. Clermont–Ferrand, France: IREM de Clermont–Ferrand. [ Links ]
Chevallard, Y.; Bosch, M. & Gascón, J. (1997). Estudiar matemáticas. El eslabón perdido entre la enseñanza y el aprendizaje. Barcelona: ICE/Horsori. [ Links ]
Fonseca, C. (2004). Discontinuidades matemáticas y didácticas entre la secundaria y la universidad. Tesis de doctorado no publicada, Universidad de Vigo, España. [ Links ]
García, J. (2005). La modelización como herramienta de articulación de la matemática escolar. De la proporcionalidad a las relaciones funcionales. Tesis de doctorado no publicada, Universidad de Jaén, España. [ Links ]
García, F. J.; Gascón, J.; Ruiz Higueras, L. & Bosch, M. (2006). Mathematical modelling as a tool for the connection of school mathematics. Zentralblatt für Didaktik der Mathematik 38 (3), 226–246. [ Links ]
Gascón, J. (1989). El aprendizaje de métodos de resolución de problemas de matemáticas. Tesis de doctorado, Universitat Autónoma de Barcelona, España. [ Links ]
Gascón, J. (1993). Desarrollo del conocimiento matemático y análisis didáctico: Del patrón análisis–síntesis a la génesis del lenguaje algebraico. Recherches en Didactique des Mathématiques 13 (3), 295–332. [ Links ]
Gascón, J. (1993–1994). Un nouveau modele de l'algébre élémentaire comme alternative à l' <<arithmétique généralisée>>. Petit x 37, 43–63. [ Links ]
Gascón, J. (1994). El papel de la resolución de problemas en la enseñanza de las matemáticas. Educación Matemática 6 (3), 37–51. [ Links ]
Gascón, J. (1998). Evolución de la didáctica de las matemáticas como disciplina científica. Recherches en Didactique des Mathématiques 18 (1), 7–34. [ Links ]
Gascón, J. (1999a). La naturaleza prealgebraica de la matemática escolar. Educación Matemática 11 (1), 77–88. [ Links ]
Gascón, J. (1999b). Fenómenos y problemas en Didáctica de las Matemáticas. En T. Ortega, (Ed.), Actas del III Simposio de la SEIEM (pp. 129–150). Valladolid, España: SEIEM. [ Links ]
Gascón, J. (2001a). Incidencia del modelo epistemológico de las matemáticas sobre las prácticas docentes. Revista Latinoamericana de Investigación en Matemática Educativa 4 (2), 129–159. [ Links ]
Gascón, J. (2001b). Reconstrucción de la divisibilidad en la Enseñanza Secundaria. Quadrante. Revista de Investigação em Educacão Matemática 10 (2), 33–66. [ Links ]
Gascón, J. (2002). El problema de la Educación Matemática y la doble ruptura de la Didáctica de las Matemáticas. Gaceta de la Real Sociedad Matemática Española 5 (3), 673–702. [ Links ]
Gascón, J. (2003a). From the cognitive to the epistemological programme in the Didactics of Mathematics: two incommensurable scientific research programmes? For the Learning of Mathematics 23 (2), 44–55. [ Links ]
Gascón, J. (2003b). La pedagogía y la didáctica frente a la problemática del profesorado. Conferencia presentada en el Congreso de la Asociación dos Ensinantes de Ciencias de Galicia (ENCIGA). Pontevedra, España: Cangas do Morrazo. [ Links ]
Gascón, J. (2011). ¿Qué problema se plantea el enfoque por competencias? Un análisis desde la Teoría Antropológica de lo Didáctico. Recherches en Didactique des Mathématiques 31 (1), 9–50. [ Links ]
Kuhn, T. S. (1962). The structure of scientific revolutions. Chicago, USA: University of Chicago Press. [ Links ]
Lakatos, I. (1971). History of science and its rational reconstructions. In R. C. Buck & R. S. Cohen (Eds.), PSA 1970. Boston Studies in the Philosophy of Science (Vol. VIII, pp. 91135). Dordrecht, Netherlands: Reidel [Traducción española. Historia de la ciencia y sus reconstrucciones racionales. Madrid, Tecnos, 1974] [ Links ].
Lakatos, I. (1976). Proofs and refutations: the logic of mathematical discovery. Cambridge, USA: Cambridge University Press. [ Links ]
Ruiz Munzón, N; Bosch, M. & Gascón, J. (2007a). Modelización funcional con parámetros en un taller de matemáticas con WIRIS. En L. Ruiz–Higueras, A. Estepa y F. J. García (Eds.), Sociedad, escuela y matemáticas. Aportaciones de la Teoría Antropológica de lo Didáctico (pp. 677–702). Jaén, España: Universidad de Jaén. [ Links ]
Ruiz Munzón, N; Bosch, M. & Gascón, J. (2007b). The functional algebraic modelling at secondary level. In D. Pitta–Panzati & G. Philippou (Eds.), Proceedings of the Fifth Congress of the European Society for Research in Mathematics Education (pp. 2170–2179). Nicosie, Chypre: University of Chypre. [ Links ]
Ruiz–Munzón, N; Bosch, M. & Gascón, J. (2010). La algebrización de los programas de cálculo aritmético y la introducción del álgebra en secundaria. In A. Bronner, M. Larguier, M. Artaud, M. Bosch, Y. Chevallard, G. Cirade & C. Ladage (Eds), Diffuser les mathématiques (et les autres savoirs) comme outils de connaissance et d'action. (pp. 655–676). Montpellier, France: IUFM de l'Académie de Montpellier. [ Links ]
Ruiz Munzón, N. (2010). La introducción del álgebra elemental y su desarrollo hacia la modelización funcional. Tesis de doctorado no publicada, Universitat Autónoma de Barcelona, España. [ Links ]
1 En adelante daremos por sentado que este artículo se inscribe en el ámbito de la Teoría Antropológica de lo Didáctico (TAD) para no tener que repetir constantemente aunque a veces será inevitable expresiones del tipo —"en el ámbito de la TAD", —"de acuerdo con la interpretación de la TAD" y otras similares.
2 En este texto utilizaremos problema didáctico como sinónimo de problema de investigación en Didáctica de las Matemáticas.
3 En este trabajo utilizaremos la noción de fenómeno didáctico como un término primitivo, tal como suele hacerse cuando se habla As fenómenos físicos, fenómenos biológicos o fenómenos sociológicos. El análisis sobre cómo una teoría didáctica construye los fenómenos didácticos y cómo los utiliza merece un estudio en profundidad que no podemos hacer aquí (ver Gascón, 2011; Artigue, Bosch & Gascón, 2011).
4 Guy Brousseau (1997) denominó inicialmente didáctica fundamental al nuevo punto de vista en Didáctica de las Matemáticas que surgió a principios de los años 70 del siglo pasado. El nuevo enfoque provocó una ampliación inesperada de la problemática didáctica debido, principalmente, a que incluía al conocimiento matemático como objeto primario de investigación. En Gascón (1998) se analiza la evolución de la didáctica hasta desembocar en la didáctica fundamental, y en Gascón (2002, 2003a) se habla abiertamente de un nuevo programa de investigación en Didáctica de las Matemáticas: el programa epistemológico.
5 La TAD introduce una conceptualization unitaria en términos de praxeologías –unión de los términos griegos praxís y logos– para referirse a esa unidad indivisible formada por la actividad y el conocimiento humanos. Se parte del postulado que afirma que toda actividad humana se puede describir como la activación de praxeologías, asumiendo así que toda práctica o saber hacer (praxis) aparece siempre acompañada de un discurso o saber (logos); es decir, una descripción, explicación o racionalidad mínima sobre lo que se hace, el cómo se hace y el porqué de lo que se hace. La praxis está formada, a su vez, por dos componentes, [T/τ] un tipo de tareas T una técnica τ o manera institucionalizada y compartida de llevar a cabo las tareas del tipo T en cierta institución. El logos, a su vez, tiene otras dos componentes [θ/Θ], una tecnología θ o discurso razonado (logos) sobre la técnica (para hacer inteligible la técnica τ como medio para realizar T) y un componente teórico Θ que rige la propia tecnología θ, aportando elementos descriptivos, justificativos y generativos de los demás componentes de la praxeología. Al unir la praxis y el logos tenemos la praxeología, que se designa como [T/τ/θ/Θ]. Hablaremos así de praxeologías matemáticas (u organizaciones matemáticas, OM) y praxeologías didácticas (u organizaciones didácticas, OD). (Chevallard, 1999).
6 La caracterización de una OM como puntual, local o regional no es absoluta, ya que depende de lo que en cada institución se considere como un único tipo de tareas matemáticas, y del ámbito que abarque el discurso tecnológico que se le asocie. Se puede mostrar (Fonseca, 2004; Bosch, Fonseca & Gascón, 2004) que una de las discontinuidades didácticas que se aprecian en la articulación entre la enseñanza secundaria y la universitaria es la dificultad para hacer vivir en la enseñanza secundaria las OM locales relativamente completas y la consiguiente ausencia en la universidad de OM locales que sean capaces, a su vez, de constituir el punto de partida para la construcción de las OM de nivel superior (regionales y globales) de una forma no meramente teoricista (Gascón, 2001a).
7 Este tipo de problemas didácticos no se suelen plantear cuando la problemática didáctica se mantiene muy próxima a la problemática docente puesto que el profesor, como tal profesor, tiene que negar la existencia de los procesos transpositivos para preservar la legitimidad de la matemática enseñada, manteniendo así la ilusión de la existencia de un único saber matemático que, naturalmente, coincidiría con el que se enseña en la escuela (Chevallard, 1991).
8 En este apartado no se pretende abordar explícitamente ninguna de las cuestiones que se derivan del problema didáctico del álgebra elemental. Únicamente se persigue formularexplícitamente los componentes de cada una de las dimensiones de dicho problema. Aunque es cierto que se podría haber tomado como ejemplo cualquier otro problema didáctico (esta es, precisamente, una de las tesis del presente trabajo) la elección no ha sido casual. Se debe a que el problema del álgebra elemental ha sido estudiado profusamente en el ámbito de la TAD a lo largo de los últimos 30 años y, en consecuencia, disponemos de múltiples trabajos donde se explicitan y relacionan entre sí las cuestiones que constituyen cada una de sus tres dimensiones fundamentales.
9 La noción noosfera del sistema de enseñanza fue introducida por Chevallard (1991) en el contexto de la Teoría de la Transposición Didáctica para designar la esfera en la que se piensa el funcionamiento del sistema didáctico. Se trata del verdadero tamiz por donde opera la interacción entre el sistema de enseñanza y el medio social. Como hemos visto en la Figura 1, que esquematiza las etapas de la transposición didáctica, la noosfera vincula la institución productora del saber con la escuela. Las producciones de la noosfera (programas oficiales, libros de texto, recomendaciones para profesores, materiales didácticos, etc.) condicionan fuertemente las características y hasta la naturaleza del conocimiento que debe ser enseñado en la escuela.














