Artículos

 

Sentido estructural de estudiantes de bachillerato en tareas de simplificación de fracciones algebraicas que involucran igualdades notables

 

High school students' structural sense in the context of simplification of algebraic fractions that involve notable equations

 

Danellys Vega-Castro*, Marta Molina**, Encarnación Castro***

 

* Universidad de Granada. danelly@correo.ugr.es

** Universidad de Granada. martamg@ugr.es

*** Universidad de Granada. encastro@ugr.es

 

Recepción: Mayo 11, 2011
Aceptación: Mayo 15, 2012.

 

RESUMEN 

En este artículo se analiza el sentido estructural que estudiantes de primero de bachillerato (de 16 a 18 años) ponen de manifiesto al trabajar con expresiones algebraicas simples y complejas, en el contexto de la simplificación de fracciones algebraicas que involucran las igualdades notables: cuadrado de la suma, cuadrado de la diferencia, diferencia de cuadrados y propiedad distributiva o factor común. Por medio de una prueba escrita elaborada para tal fin, se detecta un amplio espectro de niveles de sentido estructural. Estos niveles dan cuenta de la aplicabilidad del conocimiento sobre igualdades notables de dichos estudiantes. El análisis realizado permite avanzar en la comprensión del constructo sentido estructural identificando algunas de las habilidades que lo componen y su papel en las tareas propuestas.

PALABRAS CLAVE: Igualdades notables, Expresiones algebraicas, Sentido estructural, Estrategias, Simplificación.

 

ABSTRACT

This article analyzes the structural sense that high school students (16 to 18 years old) demonstrate when working with simple and complex algebraic expressions, in the context of simplification of algebraic fractions that involve notable equations: square of the sum, square of the difference, difference of squares and distributive property or common factor. A written test prepared for this purpose detects a wide spectrum of levels of structural sense. These levels reveal the relevance of students' knowledge of notable equations. The analysis carried out allows us to make progress in understanding the construct structural sense by identifying some of its component skills and its role in the proposed tasks.

KEY WORDS: Notable equations, Algebraic expressions, Structural sense, Strategies Simplification.

 

RESUMO

Neste artigo, analisa-se o sentido estrutural que estudantes de segundo grau (de 16 a 18 anos) manifestam ao trabalhar com expressões algébricas simples e complexas, no contexto da simplificação de frações algébricas que envolvam as igualdades notáveis: o quadrado da soma, o quadrado da diferença, diferença de quadrados e propriedade da distributiva ou fator comum. Através de uma prova escrita elaborada para tal fim, é detectado um amplo espectro de níveis de sentido estrutural. Estes níveis são responsáveis pela aplicação do conhecimento sobre igualdades notáveis por tais estudantes. A análise realizada permite avançar na compreensão do constructo sentido estrutural identificando algumas das habilidades que o componem e seu papel nas tarefas propostas.

PALAVRAS CHAVE: Igualdades notáveis, Expressões algébricas, Sentido estrutural, Estratégias, Simplificaçâo.

 

RÉSUMÉ

Cet article est une analyse du sens structurel que des lycéens (âgés de 16 à 18 ans) expriment lors qu'ils travaillent sur des expressions algébriques simples et complexes et qu'ils doivent simplifier des fractions algébriques qui impliquent des égalités remarquables : carré de la somme, carré de la différence, différence des carrés, propriété distributive et facteur commun. Par l'intermédiaire d'une épreuve écrite conçue dans ce but, un grand nombre de niveaux de sens structurels est détecté. Tous ces niveaux révèlent les différents degrés de validité des connaissances en ce qui concerne les égalités remarquables de la part de ces étudiants. L'analyse réalisée permet ainsi d'avancer dans la compréhension de la construction du sens structurel en identifiant quelques-unes des aptitudes qui le composent et le rôle joué par ce dernier lors des travaux réalisés par les lycéens.

MOTS CLES: Egalités remarquables, Expressions algébriques, Sens structurel, Stratégies, Simplification.

 

1. INTRODUCCIÓN

Existe gran coincidencia entre diversos autores (Cerdán, 2010; Hoch & Dreyfus, 2005, 2006; Nortes & Nortes, 2010; Novotná & Hoch, 2008) en destacar la falta de capacidad de los estudiantes de educación secundaria y bachillerato (de 12 a 18 años) para aplicar las técnicas algebraicas básicas en contextos distintos de los que han experimentado. En especial se pone énfasis en las dificultades 'manifestadas por los alumnos para reconocer y generar formas equivalentes de expresiones algebraicas comprendiendo su significado. Ambas capacidades, la de reconocer y la de generar dichas expresiones, están relacionadas con los objetivos de aprendizaje de la educación matemática en educación secundaria (Ministerio de Educación y Ciencia, 2006; NCTM, 2000). La reiterada percepción de las dificultades señaladas, así como otras puestas de manifiesto por los estudiantes en el aprendizaje del álgebra, han ocasionado un interés creciente en la investigación en Educación Matemática por conocer cuál es el conocimiento sobre el álgebra escolar que poseen o desarrollan los estudiantes de educación secundaria y cómo éste se lleva a cabo (Demby, 1997; Hoch & Dreyfus, 2005, 2006; Kieran, 1989, 2006, 2007; Kirshner & Awtry, 2004; Sfard & Linchevsky, 1994; Ruano, Socas & Palarea, 2008; Trujillo, Castro & Molina, 2009). Esta misma preocupación ha dado lugar al surgimiento del constructo ''sentido estructural'', que busca precisar las habilidades necesarias para hacer un uso eficiente, en tareas escolares, de las técnicas algebraicas aprendidas. En esta línea de trabajo se enmarca el estudio que aquí presentamos, en el que analizamos el sentido estructural que ponen de manifiesto estudiantes de primer curso de bachillerato (de 16-17 años) en la simplificación de fracciones algebraicas que involucran igualdades notables. En primer lugar planteamos la problemática en la que se enmarca este estudio, pasando a centrar nuestra atención en el constructo sentido estructural y en el estudio empírico realizado.

 

2. DIFICULTADES EN EL APRENDIZAJE DEL ÁLGEBRA

Tradicionalmente el álgebra es introducida como generalización de la aritmética y las representaciones algebraicas se tratan como generalizaciones de las operaciones aritméticas, las cuales son evaluadas para valores concretos de las variables¹ (Kieran, 1992). Se sigue un enfoque inductivo-se espera que los alumnos adquieran conocimiento de la estructura de las operaciones a partir de su aprendizaje de la aritmética- y a continuación las representaciones algebraicas se consideran como objetos matemáticos en los cuales se llevan a cabo operaciones estructurales, por ejemplo, la combinación de términos lineales, la factorización y la operación miembro a miembro de una ecuación (Kieran, 1992).

Este enfoque asume que las relaciones matemáticas, que son el verdadero objeto de la representación algebraica, son familiares al alumno debido a su aprendizaje de la aritmética, por lo cual durante la enseñanza del álgebra se les presta poca atención. Sin embargo, diversos estudios muestran que muchos alumnos poseen una pobre comprensión de las relaciones y estructuras matemáticas (Booth, 1982; Kieran, 1989; MacGregor, 1996; Schifter, 1999) y muestran una falta de relación entre sus conocimientos aritméticos y sus conocimientos algebraicos (Carpenter & Franke, 2001; Warren, 2001, 2004). Dichos trabajos evidencian que esta forma tradicional de introducir el álgebra no es eficaz en el desarrollo de las habilidades de los alumnos para reconocer y usar la estructura matemática. A esto Kieran (1992) añade la comprensión del significado de las letras y el cambio de convenciones, como otras de las principales dificultades en la introducción del álgebra.

El énfasis de la enseñanza de la aritmética en ''encontrar la respuesta'' hace que los alumnos consigan desenvolverse con procesos intuitivos e informales evitando el uso y reconocimiento de la estructura, que es esencial en el aprendizaje del álgebra (Kieran, 1989). Para explicar esta transición, Sfard (1991), Sfard y Linchevski (1994), Gray y Tall (1994) y Kieran (1991) utilizan la dualidad proceso-objeto². Según estos autores, una de las grandes diferencias entre estas subáreas de las matemáticas, la aritmética y el álgebra, es que en la primera de ellas las expresiones simbólicas (en este caso numéricas) son interpretadas como procesos; mientras que en la segunda, han de interpretarse como procesos y como objetos. Ver una entidad matemática como un objeto requiere ser capaz de referirse a ella como si fuera una cosa real y manipularla como una unidad global. En cambio, interpretar una entidad matemática como un proceso implica considerarla como algo potencial constituido por una secuencia de acciones, en lugar de una verdadera entidad (Sfard, 1991).

Desde esta perspectiva, el estudio del álgebra escolar se entiende como una serie de ajustes proceso-objeto que los alumnos deben realizar para poder comprender los aspectos estructurales del álgebra. Progresivamente se va desarrollando la habilidad de ver una cadena de símbolos como un nombre para un número, más adelante se llega a considerar las letras en una fórmula como variables en vez de incógnitas, y finalmente se perciben las funciones que se esconden tras las fórmulas.

En el trabajo con expresiones algébricas es frecuente que los estudiantes actúen ''sin pensar'', trasformando las expresiones por medio de técnicas algebraicas aprendidas e ignorando sus significados, pero es esencial tener la capacidad de recuperar los significados de dichas expresiones cuando sea necesario. Un buen dominio del álgebra requiere comprender ambas concepciones de las expresiones algebraicas (objeto y proceso) y flexibilidad en el paso de una a otra en la resolución de tareas según sea necesario. De este modo, el trabajo con expresiones algebraicas requiere la conjugación flexible de conocimiento procedimental y conceptual³ (Hiebert & Lefevre, 1986). El primero de ellos permite aprovechar el poder de abstracción del lenguaje algebraico y el segundo informa para la toma de decisiones sobre las manipulaciones a realizar y la interpretación de los resultados obtenidos.

Los estudios empíricos realizados ponen de manifiesto la falta de dominio del álgebra por parte de los estudiantes, señalando como causas una concepción exclusivamente procedimental de las expresiones algebraicas y la falta de conocimiento conceptual que sustente la ejecución de dichos procedimientos. Las dificultades que los estudiantes manifiestan con la estructura algebraica fueron inicialmente estudiadas por Booth (1982), Wagner, Rachlin y Jensen (1984) y por Steinberg, Sleeman y Ktorza (1990), quienes pusieron de manifiesto que alumnos de educación secundaria tenían dificultades para concebir una expresión compleja como un todo y reconocer semejanzas en las estructuras de ecuaciones equivalentes, pese a mostrar facilidad para resolver dichas ecuaciones siguiendo procedimientos estándares. Booth (1982) investigó el tipo de expresiones algebraicas que los alumnos consideraban equivalentes y observó que interpretaban las expresiones de manera diferente según el contexto aplicando la siguiente regla: ''Una expresión algebraica se resuelve siempre de izquierda a derecha, a menos que el contexto especifique que debe realizarse previamente otra operación''. Según esta regla, un par de expresiones pueden ser equivalentes en un contexto y no serlo en otro.

En el contexto de las ecuaciones, Sfard y Linchevski (1994) observan que los estudiantes no suelen aplicar la definición formal de equivalencia de ecuaciones (igual conjunto de soluciones) sino que tienden a utilizar el criterio de poder trasformar una ecuación en otra. Pirie y Martin (1997) señalan la tendencia de los alumnos a interpretar las ecuaciones como sucesos temporales, no estáticos y a leerlos de izquierda a derecha. Además confunden los conceptos de equivalencia numérica y equivalencia algebraica y no muestran capacidad para juzgar la equivalencia entre expresiones numéricas sin la realización del cálculo de las operaciones implicadas (Liebenberg, Sasman & Olivier, 1999). Los trabajos de Herscovics y Linchevski (Herscovics & Linchevski 1994; 'Linchevski & Herscovics 1994) y Ruano et al. (2008) señalan algunas de las dificultades y errores concretos que manifiestan los estudiantes al transformar expresiones algebraicas tales como la necesidad de clausura que muestran los alumnos, la particularización de expresiones algebraicas donde les dan valores numéricos al no encontrar sentido en el uso del lenguaje algebraico en algunos contextos, el uso inadecuado o la ausencia de paréntesis, la concatenación de igualdades, el fallo en la percepción de la cancelación de expresiones, la sobre-generalización de la propiedad distributiva del producto respecto de la suma a la operación multiplicación, la falta de aceptación del signo igual como expresión de una equivalencia, un orden incorrecto de las operaciones y la separación de un número del signo operacional que le precede.

Trabajos más recientes que analizan específicamente el sentido estructural (Hoch & Dreyfus, 2004; 2005, 2006) destacan el escaso uso que hacen del mismo estudiantes de entre 16 y 17 años al resolver ecuaciones algebraicas especialmente diseñadas para facilitar su resolución a partir de la apreciación de subestructuras dentro de la ecuación, o de uno de sus miembros y de relaciones entre ellas, por ejemplo . El uso del sentido estructural 'fue algo mayor en el caso de alumnos de un curso previo que habían trabajado más recientemente la resolución de ecuaciones lineales, lo cual sugiere que la enseñanza tiene efecto en el desarrollo del mismo. Los autores citados identificaron la presencia de la variable en ambos miembros de la igualdad, así como la presencia de paréntesis, como elementos facilitadores de la percepción de estructuras por parte de los estudiantes. También observan un bajo sentido estructural en tareas de factorización de expresiones complejas utilizando la igualdad notable a²-b²=(a-b)(a+b), en las que los estudiantes mostraron falta de capacidad para aplicar una fórmula conocida cuando los términos implicados eran compuestos (Hoch & Dreyfus, 2005). Detectaron cierta correlación entre el sentido estructural y la habilidad para la manipulación de expresiones algebraicas (despreciando errores menores), en especial en niveles bajos de ambos, y observaron que los alumnos que utilizan sentido estructural cometen menos errores de manipulación (Hoch & Dreyfus, 2006; Novotná & Hoch, 2008).

 

3. SENTIDO ESTRUCTURAL

Al centrar nuestra atención en las habilidades de los sujetos que intervienen en el trabajo con expresiones algebraicas, resulta pertinente destacar los trabajos que Hoch y sus colaboradores (Hoch, 2003; Hoch & Dreyfus, 2004, 2005, '2006; Novotná & Hoch, 2008) han desarrollado en la última década en torno a la noción de ''sentido estructural''. Dicha noción surge del análisis del trabajo con expresiones algebraicas, al distinguir entre las posibles actuaciones aquellas que hacen un uso efectivo de la estructura particular de las expresiones y de las técnicas algebraicas aprendidas previamente. El término ''sentido estructural'' refiere, de forma general, a una colección de habilidades relacionadas con transformar expresiones algebraicas, que permite a un alumno hacer un mejor uso de las técnicas algebraicas aprendidas (Linchevski & Livneh, 1999). No se trata de un concepto nuevo, sino que enfatiza cierta forma de ''poseer'' el conocimiento. Se manifiesta a través de unos signos externos cuando el sujeto trabaja con expresiones aritméticas y sobre todo algebraicas.

La Figura 1 muestra la resolución de dos ecuaciones lineales que, al contraponerse con la resolución de ecuaciones basada en el procedimiento estándar de abrir paréntesis, obtener común denominador, operar numeradores y despejar la incógnita, sugiere el tipo de habilidades a las que refiere este término.

El término sentido estructural, junto a los de sentido numérico (Sowder, 1992), sentido operacional (Slavit, 1998) y sentido simbólico (Arcavi, 1994), son términos asociados a una visión de la enseñanza y del aprendizaje centrada en promover la comprensión de las matemáticas, que parte de la consideración de los alumnos como pensadores, como personas capaces de comprender los dominios matemáticos (Molina, 2006). Estos constructos se enmarcan dentro de una concepción pedagógica del aprendizaje en la que se considera que un conocimiento no puede ser funcional sino en la medida en que es portador de sentido para quien lo posee, es decir, en la medida en que el sujeto es capaz de identificar un campo de aplicación de este conocimiento (Peltier, 2003).

Las habilidades que componen el sentido estructural son componentes del conocimiento algebraico que se espera desarrollen los estudiantes de educación secundaria. Su uso o aplicación implica una concepción estructural de las expresiones algebraicas (más o menos desarrollada) para ser capaz de percibir, comparar y relacionar la estructura de diferentes expresiones -o subexpresiones-algebraicas y utilizar esta información para la toma de decisiones sobre la manipulación de las mismas.

El término ''estructura'' se utiliza en este contexto para referir a los términos que componen la expresión, los signos que los relacionan, el orden de los diferentes elementos y las relaciones que existen entre ellos (Molina, 2010). Se refiere a la forma gramatical de las expresiones en términos de Esty (1992), la denominada estructura superficial de una expresión en palabras de Kieran (1991) o la estructura sintáctica, según Kirshner (1989). Desde un punto de vista amplio, se puede decir que el término estructura refiere a la forma en que una entidad se compone de partes, en la que existen conexiones o relaciones entre las partes que la componen.

3.1. Descriptores del sentido estructural

En 2006, Hoch y Dreyfus presentaron una caracterización operacional de sentido estructural, por medio de tres descriptores, los cuales permiten identificar si se utiliza sentido estructural en el contexto de una tarea algebraica. Dicen que un alumno muestra sentido estructural en dicho contexto si es capaz de:

SS1 Reconocer una estructura familiar en su forma más simple,

SS2 Tratar con un término compuesto como una única entidad y reconocer una estructura familiar en una forma más compleja,

SS3 Elegir manipulaciones apropiadas para hacer el mejor uso de una estructura.

En función de la complejidad de los términos que componen las expresiones con las que se esté trabajando, los autores subdividen los descriptores SS2 y SS3 en dos y tres sub-descriptores respectivamente:

SS2.a Donde el término compuesto contiene un producto o potencia pero no una suma / resta

SS2. b Donde el término compuesto contiene una suma / resta y posiblemente 'también un producto o potencia

SS3. a Donde la estructura está en su forma más simple

SS3.b Donde el término compuesto contiene un producto o potencia pero no una suma/resta

SS3.c Donde el término compuesto contiene una suma / resta y posiblemente también un producto o potencia

Lo que caracteriza a SS2.a, SS2.b, SS3.b. y SS3.c es la necesidad de tratar términos compuestos como una entidad. Los siguientes son ejemplos relacionados con la expresión a²- b² para cada uno de estos descriptores del sentido estructural. En la tarea de factorizar la expresión 81- x², reconocer dicha expresión como una diferencia de cuadrados e identificar los factores correspondería al descriptor SS1. En la tarea de factorizar (x-3)⁴- (x+3)⁴, tratar cada uno de los binomios (x - 3)² y (x+3)² como una sola entidad, reconocer dicha expresión como una diferencia de cuadrados e identificar los factores implicados, correspondería a SS2. El descriptor SS3 intervendría en ambas tareas al aplicar la igualdad notable a²- b² = (a - b) (a+b) para factorizar dichas expresiones.

 

4. ESTUDIO EMPÍRICO

El trabajo que aquí presentamos es un estudio exploratorio dirigido a analizar el sentido estructural que ponen de manifiesto estudiantes de 1° de bachillerato al simplificar fracciones algebraicas que involucran, implícita o explícitamente, igualdades notables. Nos basamos para ello en los descriptores propuestos por Hoch y Dreyfus (2006) anteriormente recogidos.

Focalizamos nuestra atención en las igualdades notables debido a la diversidad de dificultades que confrontan estudiantes de secundaria cuando resuelven tareas que involucran estas expresiones (Chang & Tsai, 2005) y a su destacada presencia en los programas de estudio de matemáticas a nivel de educación secundaria como consecuencia de sus frecuentes aplicaciones en otros contenidos matemáticos (por ejemplo la simplificación de expresiones, operaciones con fracciones algebraicas o el cálculo de límites), en otras áreas como la física y en estudios superiores o de nivel universitario.

4.1. Participantes

La recogida de datos se realizó durante el curso académico 2009-2010 en dos centros de educación secundaria españoles. Los sujetos que intervinieron en el estudio fueron tres grupos de estudiantes de edades comprendidas entre 15 y 18 años. Estos estudiantes fueron elegidos intencionalmente por el nivel educativo que cursaban y por su disponibilidad para participar en el estudio.

Los grupos de estudiantes cumplieron una función diferente dentro del proceso de la investigación. Los dos primeros grupos, de 4° curso de educación secundaria obligatoria, permitieron poner a punto el instrumento de recogida de datos e identificar la necesidad de trabajar con alumnos de un curso posterior para que el instrumento proporcionara más información. El tercer grupo (estudiantes de 1° de bachillerato) nos permitió recoger los datos empíricos sobre los que realizamos el análisis que aquí presentamos. Este grupo consta de treinta y tres estudiantes de entre 16 y 18 años, diecinueve chicas y catorce chicos, con un rendimiento académico variado en matemáticas. Como muestra de ello, señalamos que ocho de los estudiantes suspendieron la asignatura de matemáticas en el curso 2009 - 2010, dieciséis aprobaron con baja calificación (5 o 6), seis estudiantes tuvieron una calificación media (7 u 8) y tres estudiantes destacaron con calificación muy alta (9 o 10). Así mismo señalamos que estos estudiantes habían trabajado, en dicho curso y en cursos previos, el uso de las igualdades notables para simplificar, factorizar y desarrollar expresiones algebraicas.

4.2. Diseño y aplicación del instrumento

Elaboramos una prueba escrita compuesta por cuatro tareas en las que se proponía a los estudiantes realizar actuaciones análogas en cada tarea. Se presentaba una fracción algebraica (ver Tabla I) con las siguientes indicaciones:

a) Modifica esta expresión para obtener una expresión equivalente más sencilla,

b) Explica lo que has hecho.

El diseño de la prueba estuvo guiado por los descriptores de sentido estructural que señalan Hoch y Dreyfus (2006) (ver Tabla I). El tercero de dichos descriptores (SS3) nos guió a seleccionar la simplificación de fracciones algebraicas por ser un contexto en el cual tiene un propósito explícito plantear la manipulación de expresiones algebraicas involucrando las igualdades notables seleccionadas. En este contexto la aplicación de las igualdades notables es necesaria para simplificar las fracciones propuestas, pues a diferencia de las tareas consideradas en estudios previos sobre uso de sentido estructural (Hoch & Dreyfus, 2004, 2005) los términos a simplificar no aparecen expresados de la misma forma. Los otros dos indicadores, SS1 y SS2, se consideran adicionalmente, de forma separada, en el diseño de las tareas. La primera de las tareas propuestas está compuesta por una expresión algebraica en su forma más simple (SS1) y las tres tareas restantes están compuestas por expresiones cuya estructura está en una forma más compleja (SS2).

Una de las variables consideradas en el diseño de las tareas es el tipo de igualdad notable incluida (ver Tabla I). Las tres primeras fracciones consideradas involucran una de las igualdades notables y la cuarta dos, aunque sólo una de ellas resulta de utilidad para la simplificación de la fracción. Si bien las expresiones planteadas tenían ciertas restricciones en su dominio, este hecho no se mencionó en la formulación de la tarea.

Esta prueba se aplicó al grupo de estudiantes, de forma individual, durante una hora de clase de matemáticas, sin previo aviso, y bajo la presencia de una de las investigadoras y la profesora habitual del grupo.

 

5. ANÁLISIS DE LOS DATOS

En este apartado recogemos el análisis realizado de las producciones de los estudiantes. En primer lugar identificamos las estrategias que utilizaron. Entendemos por estrategia cualquier procedimiento o regla de acción que permite 'obtener una conclusión o responder a una cuestión haciendo uso de relaciones y conceptos, generales o específicos, de una determinada estructura conceptual (Rico, Castro, Castro, Coriat, Martín, Puig, et al., 1997). A continuación clasificamos las estrategias identificadas en tres modelos de actuación. Estos modelos evidencian diferentes grados de uso de sentido estructural, lo que nos permite establecer niveles en el sentido estructural puesto de manifiesto por los estudiantes.

5.1. Rendimiento de los estudiantes

Para describir el rendimiento de los estudiantes en cada tarea distinguimos entre estrategias exitosas y no exitosas, de acuerdo a si los procedimientos utilizados por los estudiantes conducen o no a la simplificación de la fracción algebraica dada, acción en la que se basaba la tarea. Dentro de las estrategias exitosas diferenciamos tres tipos: irreducible, interrumpida y con errores. La diferencia entre los dos primeros tipos radica en que el estudiante alcance o no la fracción irreducible equivalente a la fracción dada; en ambos casos no se producen errores en la trasformaciones de las expresiones y se utiliza una estrategia conducente a la simplificación de la fracción. Se obtiene así una fracción equivalente a la inicial en el rango de valores en los que ésta Ultima está definida. Las estrategias exitosas con errores corresponden a aquellos casos en los que los estudiantes obtienen una fracción algebraica no equivalente a la dada debido a que comenten algún error en la trasformación de las expresiones pese a utilizar un procedimiento adecuado para la simplificación a realizar (ver ejemplos en la Figura 2).

La Tabla II muestra el número y porcentaje de estudiantes que evidencian cada tipo de estrategia. La codificación de las producciones de los estudiantes, según estas categorías, fue realizada por el equipo de investigación formado por las autoras de este trabajo en donde se discutieron individualmente los casos en los que existía desacuerdo hasta llegar a una interpretación consensuada.

 

El número de estrategias exitosas utilizadas fue muy alto en las tareas 1 y 3: 29 de los 33 estudiantes; un 88 por ciento. En la tarea 3 fue mayor el número de estudiantes que interrumpieron dichas estrategias o cometieron algún error en la manipulación, posiblemente debido a la dificultad de trabajar con términos compuestos (en este caso, potencias). En las tareas 2 y 4 el número de estrategias exitosas utilizadas fue de 23 y 15 respectivamente (70 y 45 por ciento). En la tarea 2 el 30 por ciento de los estudiantes se limitaron a simplificar parcialmente la fracción algebraica, también hubo un alto número de estudiantes que cometieron errores en la manipulación de las expresiones. Cabe destacar el alto número de estrategias no exitosas utilizadas por los estudiantes en la tarea 4. La complejidad de esta tarea radica en que además de requerir trabajar con términos compuestos, involucra dos igualdades notables, pero sólo la aplicación de una de ellas conduce a la simplificación de la fracción dada. No obstante, sólo dos estudiantes aplicaron la igualdad notable (cuadrado de una diferencia) que no les permitía simplificar la fracción dada.

5.2. Modelos de actuación de los estudiantes

Una vez identificados los tipos de estrategias empleadas por los estudiantes, organizamos dicha información de acuerdo con patrones de comportamiento observados que nos permitieron distinguir tres modelos de actuación puestos de manifiesto por los estudiantes. El uso de procedimientos de cálculo es creciente en estos tres modelos.

- El modelo A implica la aplicación directa de una igualdad notable — cuadrado de una diferencia, suma por diferencia, propiedad distributiva / factor común y cuadrado de una suma— tras reconocer el alumno, en el numerador o el denominador, una de las partes de dicha igualdad. Esta transformación permite al estudiante abordar la simplificación de la fracción al obtener una fracción equivalente a la inicial en la cuál es explícita la existencia de factores comunes entre el numerador y el denominador, al aparecer expresados de igual forma, y por tanto la posibilidad de realizar una cancelación de los mismos (Ver Figura 3). Este modelo de actuación se presentó en las cuatro tareas propuestas.

– En el modelo B, en cambio, el estudiante no aplica igualdades notables sino que ejecuta un procedimiento estándar que conduce al desarrollo o factorización de alguna de las expresiones (por ejemplo, aplicar Ruffini, desarrollar el producto o potencia de binomios) hasta alcanzar, al igual que en el modelo A, una fracción equivalente a la dada en la que se manifiesta con mayor claridad la posibilidad de cancelación de algunos términos (ver Figura 4). Las estrategias correspondientes al modelo B son también exitosas en la simplificación de la fracción dada. Este tipo de estrategias tuvieron lugar en las tareas 1 y 3. Las dos estrategias presentadas en la tarea 1 corresponden a la factorización del numerador ya sea mediante la técnica de Ruffini o mediante el uso de la fórmula de la ecuación cuadrática. En la tarea 3 las estrategias difieren en si la manipulación afecta únicamente al denominador o también al numerador, distinguiéndose dos casos. En el primer caso la estrategia consiste en el uso de la propiedad distributiva para desarrollar el denominador y, en el segundo, implica además el desarrollo del producto de suma por diferencia que aparece en el numerador. La figura 4 muestra ejemplos de estas estrategias.

- Por último, distinguimos el modelo c que engloba casuísticas diversas. a diferencia de los otros dos modelos, éste no conduce a una simplificación de la fracción dada, debido a que algunas de las transformaciones realizadas en la expresión no permiten detectar factores comunes entre numerador y denominador, o no son correctas. Este modelo de actuación es puesto de manifiesto por el uso de estrategias no exitosas (ver Figura 5). En este caso, el estudiante realiza transformaciones que no parecen estar guiadas por ninguna anticipación de una posible simplificación de la expresión (pues no permiten identificar factores comunes en el numerador y denominador), o bien comete errores en la manipulación de las expresiones que le conducen a expresiones no equivalentes a las dadas. Este modelo de actuación se puso de manifiesto en las cuatro tareas propuestas.

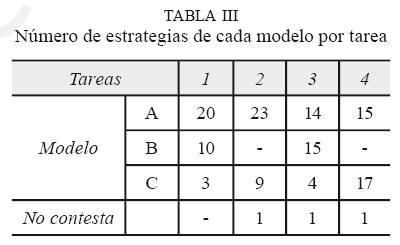
Las diferentes estrategias que se distinguen en las producciones de los alumnos se enmarcan dentro de alguno de los tres modelos, con la distribución que se muestra en la Tabla III. Para hacer esta clasificación, hemos obviado errores de manipulación de las expresiones por lo que todas las estrategias exitosas, independientemente de si han sido irreducibles, interrumpidas o con errores, han quedado clasificadas dentro de los modelos A y B.

5.3. Niveles de sentido estructural

Los tres modelos de actuación nos ayudan a analizar el sentido estructural puesto de manifiesto por los estudiantes y clasificar sus producciones en relación al mismo. Entendemos que las estrategias correspondientes al modelo A evidencian un buen sentido estructural pues, al basarse en la aplicación directa de una igualdad notable, evidencian el reconocimiento por el alumno de una estructura familiar (la de dicha igualdad notable), la percepción de subestructuras de dichas expresiones como entidades (por ejemplo, así ocurre con las expresiones 2x o 5a² en las tareas 3 y 4, respectivamente) tanto para reconocer la estructura de la expresión como para identificar términos susceptibles de cancelarse, así como la elección de manipulaciones apropiadas para hacer uso de dicha estructura de forma eficiente anticipando o intuyendo que van a ser útiles para obtener una expresión más simple de la fracción. Se hace un escaso uso de procedimientos de cálculo.

Por otra parte, las estrategias correspondientes al modelo B evidencian cierto uso de sentido estructural pero menor al de las estrategias del modelo A pues el alumno no reconoce en las expresiones la estructura de ninguna igualdad notable (las cuales le son familiares de su trabajo previo en el aula) sino que inicialmente recurre a desarrollar o factorizar alguna de las expresiones que aparecen en la expresión por medio de manipulaciones estándares en el trabajo con expresiones algebraicas. La información de las producciones de los estudiantes que hemos recogido no nos permite distinguir si el estudiante anticipaba la utilidad de dicha transformación o, por el contrario, estaba procediendo por ensayo y error; ambas son acciones que denotan diferentes desarrollos de sentido estructural. No obstante, el estudiante evidencia cierto sentido estructural al decidir desarrollar o factorizar algunas de las expresiones (ambos pasos clave en la simplificación de fracciones algebraicas) y al reconocer factores comunes en denominador y numerador tras haber realizado alguna trasformación. El reconocimiento de dicha posibilidad de cancelación implica identificar subestructuras dentro de las expresiones que componen el numerador y el denominador, concebirlas como entidades y detectar la relación de igualdad entre ellas.

Por último, las estrategias que se recogen dentro del modelo C evidencian un bajo o nulo nivel de sentido estructural pues el estudiante no hace uso de la estructura particular de las expresiones que componen la fracción para elegir las manipulaciones a realizar, lleva a cabo varios cálculos que no conducen a una 'situación útil para simplificar. En este tipo de estrategias algunos de los errores cometidos en la manipulación de las expresiones actuaron como limitantes de un posible uso de sentido estructural.

En sus producciones los estudiantes no hacen referencia alguna al dominio de definición de la fracción algebraica dada (el cuál no se les explicitaba) ni al de la fracción obtenida, ni al rango de valores de la variable para el cual son ciertas las equivalencias obtenidas al simplificar las fracciones dadas. Por este motivo, en el análisis de los datos y en particular en el análisis del sentido estructural puesto de manifiesto por los estudiantes, no atendemos al reconocimiento de lo que Mason, Graham y Johnston-Wilder (2005) denominan el ''rango de cambio permisible'' en las variables que intervienen en una expresión algebraica.

A partir de estas consideraciones y según el modo de actuación observado en el desempeño de cada una de las tareas, percibimos diferentes niveles de sentido estructural puestos de manifiesto por los estudiantes (ver Figura 6).

La Figura 6 permite mostrar una amplia variabilidad en el desempeño de las tareas por los estudiantes. Ordenadas las actuaciones de los estudiantes de izquierda a derecha según la frecuencia de uso de estrategias de cada modelo, se aprecia que el nivel de sentido estructural manifestado decrece conforme avanzamos hacia la derecha. Se observa que los primeros trece alumnos (40 por ciento) muestran un buen sentido estructural pues al menos tres de sus actuaciones corresponden al modelo A (n° 4, 24, 32, 12, 30, 21, 23, 8, 22, 7, 14, 29, 18). Otros ocho estudiantes (24 por ciento) evidencian nivel intermedio de sentido estructural pues en dos de las tareas utilizan estrategias del modelo A (n° 28, 5, 6, 11, 27, 9, 17, 33). El nivel de sentido estructural puesto de manifiesto por el resto de los estudiantes (36 por ciento) es relativamente bajo, siendo dos los estudiantes que no hacen uso de las igualdades numéricas en ninguna de las tareas propuestas y cuatro los que solo manifiesta dicho uso en la tarea 1 (única en la que no aparecen términos compuestos).

 

6. DISCUSIÓN Y CONCLUSIONES

El objetivo de este estudio es analizar el sentido estructural que ponen de manifiesto estudiantes de 1° de bachillerato en la simplificación de fracciones algebraicas que involucran igualdades notables. Para este objetivo, la prueba diseñada ha sido de utilidad, dado que permite distinguir diferentes niveles de sentido estructural a partir de las producciones de los estudiantes. También nos ha informado sobre algunas de las dificultades que los estudiantes encuentran en la tarea propuesta para hacer uso de sentido estructural y sobre la diferente influencia de las características de las expresiones algebraicas, en las estrategias empleadas por los estudiantes. El análisis de los datos nos conduce a plantear cuestiones abiertas de interés para avanzar en la comprensión del conocimiento algebraico necesario para un trabajo eficiente con expresiones algebraicas y de la forma en que diferentes componentes del mismo se ponen en juego en actividades algebraicas particulares. Comentamos a continuación los resultados obtenidos y planteamos dichas cuestiones.

Con la excepción de dos estudiantes, todos aplicaron igualdades notables en al menos una de las tareas (estrategias del modelo A), siendo este uso más frecuente en la primera y segunda tarea. Ambas tareas fueron, asimismo, las que presentaron un mayor número de estrategias no exitosas (modelo C). Este último resultado puede haberse debido a las características particulares de ambas tareas, en las cuales no existía una estrategia exitosa alternativa a la aplicación de la igualdad notable. En la tarea 4 existe la posibilidad de aplicar dos igualdades notables en la resolución, lo que dificulta la tarea al hacer necesario valorar cuál de las transformaciones es más útil realizar.

Los datos obtenidos sugieren que los estudiantes pusieron de manifiesto un mayor uso de sentido estructural cuando las expresiones no incluían términos compuestos (tarea 1) o la igualdad notable implicada era la propiedad distributiva / factor común (tarea 2). Por tanto se observa que, de entre las igualdades seleccionadas, la propiedad distributiva / factor común es la que los estudiantes tienen mayor facilidad en aplicar y reconocer incluso cuando las expresiones incluyen términos compuestos. Asimismo, los datos muestran que un 70 por ciento de los estudiantes son capaces de concebir términos compuestos como una entidad, al menos cuando la estructura de la expresión les es familiar. No obstante, la presencia de términos compuestos sí supuso una fuente de dificultad, pues fue en esos casos donde un mayor número de estudiantes cometieron errores al manipular las expresiones que componen la fracción y un menor número de estudiantes reconocieron la posibilidad de cancelar términos 'tras haber realizado trasformaciones en la fracción. Estos resultados plantean la necesidad de seguir indagando en el sentido estructural de los estudiantes en situaciones que no requieran la transformación de expresiones (por ejemplo, agrupar expresiones de igual estructura o reproducir la estructura de una expresión dada) para evitar la interferencia de la fluidez en el cálculo con expresiones algebraicas, en el análisis de algunas de las habilidades que componen el sentido estructural. Aunque hay evidencias de que bajos niveles de sentido estructural están asociados a bajos niveles de fluidez en la manipulación, queda por explorar cuál de ambos elementos del conocimiento algebraico (y de qué modo) es el que actúa como limitante del otro cuando se trabaja con términos compuestos.

Es de llamar la atención que ningún estudiante intentó formas alterativas de abordar una misma tarea, lo que sugiere falta de persistencia y flexibilidad en su modo de actuar. Este resultado destaca una de las deficiencias más importantes detectadas en los estudiantes. Se considera necesario fomentar en las aulas ambas cualidades, la persistencia y la flexibilidad, a la hora de abordar la simplificación de expresiones, dado que la utilidad de las transformaciones realizables en una expresión no es en ocasiones clara hasta que se inician dichas transformaciones. Asimismo, el hecho de que los estudiantes no realizaran más de un intento de simplificar la fracción, enfatiza la importancia del sentido estructural, dado que para anticipar o reconocer la utilidad de una manipulación es clave analizar la estructura de las expresiones y relacionarla con estructuras conocidas, así como identificar subestructuras en la expresión y buscar relaciones entre las mismas.

Los estudiantes tampoco dieron muestras de reconocer restricciones en el rango de las variables en que están definidas las fracciones utilizadas o para el cual se cumple la equivalencia obtenida como resultado del proceso de simplificación. Autores como Mason, Graham y Wilder (2005) y Caraça (1998) han destacado la importancia de reconocer el ''rango de cambio permisible'' en las variables que intervienen en una expresión algebraica como componente de la competencia algebraica de un estudiante. En el caso de la simplificación de expresiones, esta información es relevante ya que para ciertos valores la equivalencia puede no ser cierta. Entendemos que una de las causas por las que ningún estudiante expresa esta restricción puede ser no haberlo pedido de manera explícita en la tarea. La experiencia nos dice que en la práctica docente estas restricciones son más frecuentemente explicitadas por los docentes cuando se trabaja con incógnitas en tareas de resolución de ecuaciones o inecuaciones debido a que las trasformaciones pueden conducir a una solución equivocada, pero no tanto en tareas como la simplificación de expresiones algebraicas que no requieren alcanzar un valor numérico.

En la recogida de datos realizada hemos detectado un variado espectro de niveles de sentido estructural que sugiere diferentes niveles de desarrollo de las habilidades a las que éste término refiere. Un 40 por ciento de los estudiantes evidenciaron un buen sentido estructural y otro 24 por ciento pusieron de manifiesto un sentido estructural intermedio al hacer uso de estrategias del modelo A en al menos la mitad de las tareas. El sentido estructural de al menos seis estudiantes es muy bajo. El uso de sentido estructural permitió a los estudiantes obtener la respuesta de forma más rápida, evitando transformaciones largas en las que hay más oportunidades para cometer errores. Según hemos visto en las producciones de los estudiantes, hicieron uso de su sentido estructural al abordar inicialmente la expresión a simplificar o bien tras realizar alguna transformación basada en el uso de procedimientos estándares como aplicar la propiedad distributiva para eliminar paréntesis y desarrollar un producto. Los modelos de actuación identificados nos informan del sentido estructural que demandan las tareas propuestas y permiten percibir que diferentes niveles de sentido estructural son compatibles con una exitosa resolución de las tareas, aunque los procedimientos empleados difieren en su rapidez y en la cantidad de transformaciones a realizar. Entendemos que mayores niveles de sentido estructural, junto con el conocimiento de técnicas algebraicas, dotan a los estudiantes de mayor flexibilidad procedimental -una componente crítica de la competencia matemática destacada por Kilpatrick, Swafford y Findell (2001) - dado que les permite reconocer mayor diversidad de estrategias a utilizar y elegir entre ellas la más eficiente.

Destacamos que al cruzar los diferentes niveles de sentido estructural detectados con el sexo, la edad y el rendimiento académico de los estudiantes en la asignatura, corroboramos que ninguna de estas variables influyó directamente en el nivel de sentido estructural manifestado por los estudiantes.

El sentido estructural se manifiesta en este estudio como un constructo útil para profundizar en la complejidad de los aprendizajes necesarios para abordar tareas algebraicas escolares. Sugerimos considerar también como descriptores del sentido estructural los siguientes: considerar formas alternativas de trasformar una expresión algebraica, anticipar la utilidad de transformaciones algebraicas en una expresión, reconocer relaciones (por ejemplo, de igualdad, ser factor o múltiplo, etc.) entre subestructuras e identificar el rango de variación permisible para las variables involucradas. Estas habilidades son necesarias para hacer un uso eficiente de las técnicas algebraicas básicas en el contexto de las tareas aquí propuestas. El modo en que se aborde el trabajo algebraico en la educación secundaria y en bachillerato condicionará el grado de desarrollo de las mismas. Las igualdades notables suelen ser tratadas como reglas fijas a memorizar, lo que conduce a un conocimiento inerte; el sentido estructural destaca como un 'elemento clave que condiciona la utilidad y la aplicabilidad de dicho conocimiento y su transferencia a nuevos contextos o situaciones.

Con el propósito de contribuir a que los aprendizajes que van acumulando los estudiantes potencien su intuición y su capacidad de resolver problemas - uno de los objetivos primordiales de la didáctica de la matemática (Malaespina, 2007) - se consideran necesarios futuros trabajos para informar sobre cómo promover el desarrollo del sentido estructural en la educación obligatoria y seguir avanzando en la caracterización de dicho constructo a partir de la identificación de las habilidades que lo componen. Para ello proponemos la consideración de otros tipos de contextos y tareas, en particular tareas que no requieran transformar expresiones, pero sí su consideración como objetos y el análisis de sus estructuras, para evitar la influencia de la fluidez de los estudiantes en la ejecución de operaciones con expresiones algebraicas e indagar en algunas de las cuestiones ya explicitadas que surgen a partir de este trabajo. Asimismo, tomando esta investigación como punto de partida y siguiendo el esquema de otros trabajos tales como Molina, Ambrose, Castro y Castro (2009) y Molina y Mason (2009) centrados en un constructo relacionado, el pensamiento relacional, nos proponemos continuar este estudio indagando en los elementos que condicionan el uso del sentido estructural ya sean variables de tarea (por ejemplo, estructura o complejidad de las expresiones involucradas), aspectos cognitivos (por ejemplo, demanda cognitiva de la tarea, conocimiento previo del alumno) o elementos relativos a la cultura o normas socioculturales del aula.

 

AGRADECIMIENTOS

Este trabajo se ha desarrollado en el marco del proyecto de investigación EDU2009-11337 ''Modelización y representaciones en educación matemática'' del Plan Nacional de Investigación, Desarrollo e Innovación 2010-2012 del Ministerio de Ciencia e Innovación de España y con el apoyo otorgado a la primera autora por el Programa de Becas Doctorales que patrocina la Secretaría Nacional de Ciencia, Tecnología e Innovación (SENACYT) de la República de Panamá.

Agradecemos a los revisores anónimos su crítica constructiva que ha contribuido muy significativamente a la mejora de este artículo.

 

REFERENCIAS BIBLIOGRÁFICAS

Arcavi, A. (1994). Symbol sense: informal sense-making in formal mathematics. For the Learning 'of Mathematics 14 (3), 24-35.         [ Links ]

Booth, L. R (1982). Ordering your operations. Mathematics in School 11 (3), 5-6.         [ Links ]

Caraça, B. J. (1998). Conceitos Fundamentais da Matemática. Lisboa, Portugal: Gradiva.         [ Links ]

Carpenter, T. P. & Franke, M. L. (2001). Developing algebraic reasoning in the elementary school: 'generalization and proof. In H. Chick, K. Stacey, J. Vincent & J. Vincent (Eds.), Proceedings 'of the 12^th ICMI Study Conference. The Future of the Teaching and Learning of Algebra '(pp.155-162). Melbourne, Australia: University of Melbourne.         [ Links ]

Cerdán, F. (2010). Las igualdades incorrectas producidas en el proceso de traducción algebraico: 'un catálogo de errores. PNA 4 (3), 99-110.         [ Links ]

Chang, C. K. & Tsai, Y. L. (2005). An alternative Approach for the Learning of (a+b)²=a²+2ab+b². 'Electronic Proceedings the 3^rd East Asia Regional Conference in Mathematics Education '(pp. 7-12), 7-12 august 2005, Shanghai, China. Avaliable http://www.sciedu.ncue.edu.tw/teacher–in.php?ts=3        [ Links ]

Demby, A. (1997). Algebraic procedures used by 13-to-15-years-olds. Educational Studies in Mathematics 33 (1), 45-70. DOI: 10.1023/A:1002963922234        [ Links ]

Esty, W. W. (1992). Language concepts of mathematics. Focus on Learning Problems in Mathematics 14 (4), 31-54.         [ Links ]

Gray, E. M. & Tall, D. O. (1994). Duality, Ambiguity and Flexibility: A Proceptual View of Simple Arithmetic. Journal for Research in Mathematics Education 26 (2), 115-141.         [ Links ]

Herscovics, N. & Linchevski, L. (1994). A cognitive gap between arithmetic and algebra. Educational Studies in Mathematics 27 (1), 59-78. DOI: 10.1007/BF01284528        [ Links ]

Hiebert, J., & Lefevre, P. (1986). Conceptual and procedural knowledge in mathematics: An introductory analysis. In J. Hiebert (Ed.), Conceptual and procedural knowledge: The case of mathematics (pp. 1-27). Hillsdale, NJ: Lawrence Erlbaum Associates.         [ Links ]

Hoch, M. (2003). Structure sense. In M. A. Mariotti (Ed.), Proceedings of the 3^rd Conference for European Research in Mathematics Education (CD). Bellaria, Italy: ERME.         [ Links ]

Hoch, M. & Dreyfus, T. (2004). Structure sense in high school algebra: The effect of brackets. In M. J. Heines & A. B. Fuglestad (Eds.), Proceedings of the 28^th Conference of the International Group for the Psychology ofMathematics Education (Vol.3, pp. 49-56). Bergen, Norway: Bergen University College.         [ Links ]

Hoch, M. & Dreyfus, T. (2005). Students' difficulties with applying a familiar formula in an unfamiliar context. In H. L. Chick & J. L. Vincent (Eds.), Proceedings of the 29^th Conference of the International Group for the Psychology of Mathematics Education (Vol. 3, pp. 145152). Melbourne, Australia: University of Melbourne.         [ Links ]

Hoch, M. & Dreyfus, T. (2006). Structure sense versus manipulation skills: an unexpected result. In J. Novotná, H. Moraová, M. Krátká & N. Stehlíková (Eds.), Proceedings of the 30^th conference of the International Group for the Psychology of Mathematics Education (Vol.3, pp. 305-312). Prague, Czech Republic: Faculty of Education, Charles University in Prague.         [ Links ]

Kieran, C. (1989). The early learning of algebra: A structural perspective. In S. Wanger & C. Kieran (Eds.), Research Issues in the Learning and Teaching of Algebra (Vol. 4, pp. 33-59). Reston, VA.: Lawrence Erlbaum Associates y NCTM.         [ Links ]

Kieran, C. (1991). A procedural-structural perspective on Algebra Research. In F. Furinghetti (Ed), Proceedings of the 15^th International Conference for the Psychology of Mathematics Education (Vol. 2, pp. 245-253). Assisi, Italy: PME Program Committee.         [ Links ]

Kieran, C. (1992). The learning and teaching of school algebra. In A. Grouws, Handbook of Research on Mathematics Teaching and Learning (A project of the NCTM) (pp. 390-419). New York, U.S.A.: Macmillan.         [ Links ]

Kieran, C. (2006). Research on the learning and teaching of algebra. A broadening of sources of meaning. In A. Gutiérrez & P. Boero (Eds.), Handbook of Research on the Psychology ofMathematics Education: Past, Present and Future. (pp. 11-49). Rotterdam, Netherlands: Sense Publishers.         [ Links ]

Kieran, C. (2007). Learning and teaching algebra at the middle school through college levels: building meaning for symbols and their manipulation. In F. Lester (Ed.), Second Handbook of Research on Mathematics Teaching and Learning. (pp. 707-762). Charlotte, USA: National Council of Teachers of Mathematics.         [ Links ]

Kilpatrick, J., Swafford, J. O. & Findell, B. (Eds.). (2001). Adding it up: Helping children learn mathematics. Washington, DC: National Academy Press.         [ Links ]

Kirshner, P. (1989). The Visual Sintax of Algebra. Journalfor Research in Mathematics Education '20 (3), 274-287.         [ Links ]

Kirshner, D. & Awtry, T. (2004). The visual salience of algebraic transformations. Journal for Research in Mathematics Education 35 (4), 224-257.         [ Links ]

Liebenberg, R., Sasman, M. & Olivier, A. (1999). From Numerical Equivalence To Algebraic Equivalence. Mathematics Learning and Teaching Initiative (MALATI). Proceedings of the 1^th Annual Congress of the Association for Mathematics Education of South Africa (Vol. 2, pp. 173-183). Port Elizabeth, South Africa: Port Elizabeth Technikon.         [ Links ]

Linchevski, L. & Herscovics, D. (1994). Cognitive obstacles in pre-algebra. In J. P. Ponte & J. F. Martos (Eds), Proceedings of the 18^th International Conference for the Psychology of Mathematics Education (Vol. 3, pp. 176-183). Lisboa, Portugal: Universidad de Lisboa.         [ Links ]

Linchevski, L. & Livneh, D. (1999) Structure sense: the relationship between algebraic and numerical contexts. Educational Studies in Mathematics 40 (2), 173-196. DOI: 10.1023/A:1003606308064        [ Links ]

Malaespina, U. (2007). Intuición, rigor y resolución de problemas de optimización. Revista 'Latinoamericana de Investigación en Matemática Educativa 10 (3), 365-399.         [ Links ]

MacGregor, M. (1996). Aspectos curriculares en las materias aritmética y álgebra. UNO Revista de 'Didáctica de las Matemáticas 9, 65-69.         [ Links ]

Mason, J., Graham, A. & Wilder, J. S. (2005). Developing thinking in algebra. Londres, Reino 'Unido: The Open University.         [ Links ]

Ministerio de Educación & Ciencia (2006). Real Decreto 1631/2006 de 29 de diciembre, por el 'que se establecen las enseñanzas mínimas correspondientes a la Educación Secundaria 'Obligatoria. Boletín Oficial del Estado (BOE) 5, 677-773.         [ Links ]

Molina, M. (2006). Desarrollo de pensamiento relacional y comprensión del signo igual por 'alumnos de tercero de Primaria. Tesis doctoral, Universidad de Granada, Granada, España. 'Disponible en http://funes.uniandes.edu.co/544/         [ Links ]

Molina, M. (2009). Una Propuesta de Cambio Curricular: Integración del Pensamiento Algebraico 'en Educación Primaria. PNA 3 (3), 135-156.         [ Links ]

Molina, M. (2010). Una visión estructural del trabajo con expresiones aritméticas y algebraicas. 'Suma 65, 7-15.         [ Links ]

Molina, M., Ambrose, R., Castro, E. & Castro, E. (2009). Breaking the addition addiction: creating the conditions for knowing-to act in early algebra. In S. Lerman & B. Davis (Eds.), Mathematical Action & Structures Of Noticing: Studies inspired by John Mason (pp. 121134). Rotterdam, The Netherlands: Sense Publisher.         [ Links ]

Molina, M. & Mason, J. (2009). Justifications-on-demand as a device to promote shifts of attention associated with relational thinking in elementary arithmetic. Canadian Journal of Science, Mathematics and Technology Education 9 (4), 224-242.         [ Links ]

NCTM (2000). Principios y Estándares para la Educación Matemática. Sevilla, España: Sociedad Andaluza de Educación Matemática Thales.         [ Links ]

Nortes, A. y Nortes, R. (2010). Resolución de Problemas de Matemáticas en las pruebas de acceso a la Universidad. Errores significativos. Educatio SigloXXI28 (1), 317-342.         [ Links ]

Novotná, J. & Hoch, M. (2008). How Structure sense for algebraic expression or equations is related to structure sense for abstract algebra. Mathematics Education Research Journal '20 (2), 93-104.         [ Links ]

Peltier, M. (2003). Problemas aritméticos. Articulación, significados y procedimiento de resolución. 'Educación Matemática 15 (3), 29-55.         [ Links ]

Pirie, S. & Martin, L. (1997). The equation, the whole equation and nothing but the equation! One 'approach to the teaching of linear equations. Educational Studies in Mathematics 34 (2), 159-181. DOI: 10.1023/A:1003051829991         [ Links ]

Rico, L., Castro, E., Castro, E., Coriat, M., Marín, A., Puig, L. et al. (1997). La educación 'matemática en la enseñanza secundaria. Barcelona, España: Editorial Horsori e Institut de Ciéncies de l'Educació         [ Links ].

Ruano, R. M., Socas, M. M. y Palarea, M. M. (2008). Análisis y clasificación de errores 'cometidos por alumnos de secundaria en los procesos de sustitución formal, generalización 'y modelización en álgebra. PNA 2 (2), 61-74.         [ Links ]

Schifter, D. (1999). Reasoning about operations. Early algebraic thinking in grades K-6. In L. 'V. Stiff & F. R. Curcio (Eds.), Developing mathematical reasoning in grades K-12. NCTM 'Yearbook (pp. 62-81). Reston, VA: NCTM.         [ Links ]

Sfard, A. (1991). On the dual nature of mathematical conceptions: reflections and objects as different sides of the same coin. Educational Studies in Mathematics 22 (1), 1-36. DOI: 10.1007/BF00302715.         [ Links ]

Sfard, A. & Linchevski, L. (1994). The gains and the pitfalls of reification: The case of algebra. 'Educational Studies in Mathematics 26 (2-3), 191-228. DOI: 10.1007/BF01273663.         [ Links ]

Skemp, R. R. (1978). Relational understanding and instrumental understanding. Arithmetic 'Teacher 26 (3), 9-15.         [ Links ]

Slavit, D. (1998). The role of operation sense in transitions from arithmetic to algebraic thought. Educational Studies in Mathematics, 37 (3), 251-274. DOI: 10.1023/A:1003602322232.         [ Links ]

Sowder, J. (1992). Estimation and Number Sense. En D. A. Grouws (Ed.), Handbook of research on 'mathematics teaching and learning (pp. 371-389). New York, U.S.A.: Macmillan Publishing 'Company y NCTM.         [ Links ]

Steinberg, R. M., Sleeman, D. H. & Ktorza, D. (1990). Algebra students' knowledge of equivalence of equations. Journal for Research in Mathematics Education 22 (2), 112-121.         [ Links ]

Tall, D., Thomas, M., Davis, G., Gray E. & Simpson, A. (2000). What is the object of the encapsulation of a process? Journal of Mathematical Behavior 18 (2), 223-241.         [ Links ]

Trujillo, P. A., Castro, E. y Molina, M. (2009). Un estudio de casos sobre el proceso de generalización. En M. J. González, M. T. González y J. Murillo (Eds.), Investigación en Educación Matemática XIII (pp. 511-521). Santander: Sociedad Española de Investigación en Educación Matemática.         [ Links ]

Wagner, S., Rachlin, S. L. & Jensen, R.J. (1984). Algebra learning project: Final report. Athens, Greece: University of Georgia.         [ Links ]

Warren, E. (2001). Algebraic understanding and the importance of operation sense. In M. Heuvel-Penhuizen (Ed.), Proceedings of the 25^th International Group for the Psychology of Mathematics Education (Vol. 4, pp. 399-406). Utrecht, The Netherlands: Freudenthal Institute.         [ Links ]

Warren, E. (2004). Generalizing arithmetic: supporting the process in the early years. In M. Johnsen y A. Berit (Eds.), Proceedings of the 28^th International Group for the Psychology of Mathematics Education (Vol. 4 pp. 417-424). Bergen, Norway: Bergen University College.         [ Links ]

 

Notas

¹ En la actualidad y desde hace algo más de una década, existe una propuesta de introducción del álgebra alternativa a la que aquí se trata, denominada Early-Algebra, que propone la integración del pensamiento algebraico en la Educación Primaria (ver Molina, 2009).

² Según Tall, Thomas, Davis, Gray y Simpson (2000), esta idea de la dualidad proceso/objeto surgió, en los años 50, a partir del trabajo de Piaget. Las ideas de Piaget sobre las acciones y operaciones que se convierten en objeto de pensamiento y asimilación han sido extendidas más allá de las matemáticas elementales.

³ Conocimiento instrumental y relacional en términos de Skemp (1978).