1. Introducción
En un contexto globalizado y altamente tecnologizado en el que la educación STEM (Science Technology Engenering Maththematics) empieza a ser el centro de interés de todas las políticas supranacionales, centrar la formación del futuro profesorado de primaria en las competencias genéricas más valoradas en los países con fuertes puntuaciones en conocimientos STEM, se convierte en una necesidad para nuestro actual sistema educativo, esto es, investigación, resolución de problemas, pensamiento crítico, innovación y creatividad (Lyn y Kishmer, 2016; López, Couso y Simarro, 2020; Valero-Matas y Cocas, 2021).
Sin embargo, la formación inicial del profesorado para el proceso de enseñanza / aprendizaje en educación matemática se ha cuestionado, especialmente a partir de los resultados evidenciados en pruebas internacionales como el Programme for International Student Assessment (PISA), Trends in International Mathematics and Science Study (TIMSS) o Teacher education and development study in mathematics (TEDS-M) (Socas, 2011; Muñiz - Rodríguez, Alonso, Rodríguez - Muñiz y Valckle, 2016).
Al realizar una aproximación a la formación inicial del profesorado de Educación Primaria, algunos trabajos expresan una considerable falta de confianza por parte de los futuros maestros y maestras en su propio conocimiento y comprensión de las matemáticas. Obviamente, no se puede enseñar lo que no se sabe por mucha motivación que uno tenga (Anderson y Kim, 2003) y lo cierto es que la etapa de Educación Primaria, siguiendo a Socas (2011), es “…una parte esencial de la Educación Obligatoria, y consideraremos al profesorado de esta etapa como un elemento básico, …, para mejorar y conseguir un aprendizaje de calidad (cognoscitivo, significativo y efectivo) en Matemáticas” (p. 200); entre otras cosas, porque en esta etapa es cuando se establecen los hábitos de razonamiento matemático de lo que depende el éxito posterior en la competencia matemática. Esta realidad, ampliamente compartida por los profesionales de la educación, ha despertado nuestro interés en conocer cómo es el perfil de los futuros maestros y maestras y cómo acceden a los estudios universitarios. Estudios previos como el realizado por Monge (1993) muestran que la mitad del alumnado elegía la profesión docente porque le gustaba. Tras cursar la titulación, a más de la mitad de la muestra le gustaba más y sólo al 11% menos. Cabe señalar, asimismo, que el porcentaje de alumnado que considera ejercer la profesión docente al finalizar los estudios se situaba en el 52%, mientras que el 39% optaba por continuar los estudios.
En esta misma línea, Sánchez (2009) ha evidenciado que una de las motivaciones de la elección de la carrera era su corta duración y que, en consonancia con el trabajo anterior, facilitaba la continuación de los estudios. Esta autora señala como factores motivantes en la elección: el salario, las vacaciones, la duración de la carrera, los insignificantes requisitos para el acceso y la vocación.
No obstante, Ruiz, García y Sarasua (2013) en su estudio orientado a conocer la perspectiva de los futuros maestros y maestros de Educación Primaria sobre educación matemática y su importancia en la formación, muestran resultados diferentes. Señalan que los estudios son fundamentalmente vocacionales, siendo seleccionados como primera opción por el 89% del alumnado; además, explican que la demanda para cursarlos se ve incrementada en la actualidad, lo que se refleja en una mayor competitividad en la entrada evidenciada en la nota de corte requerida para su acceso. En relación con el acceso a la titulación, la mayor parte del alumnado procede del bachillerato de ciencias sociales (60%), mientras que el científico - tecnológico (16%) y ciencias de la salud (24%), habiendo cursado matemáticas el 76% de la muestra en segundo de Bachillerato.
Los autores distinguen tres perfiles a partir de los resultados obtenidos. Un primer grupo de alumnado más motivado, caracterizado por haber cursado un bachillerato distinto al de ciencias sociales, que entiende que las matemáticas es una de las materias más importantes en Educación Primaria. En consecuencia, deben profundizar en su conocimiento, valoran la materia tan importante como las demás, consideran que ser buen docente es complejo y que el título contribuirá de distintas formas a su formación.
El segundo grupo que considera que ser buen docente en matemáticas es fácil, no estiman necesaria la preparación universitaria para la profesión, pero esperan que una formación de tipo pedagógico y didáctica basada en enseñar a enseñar y conocer el desarrollo evolutivo de los niños y las niñas. No perciben que más conocimientos contribuyan a ser mejores docentes y, por tanto, creen que no es necesario dominar más matemáticas de las que van a enseñar.
Por último, un tercer perfil que no es tan claro y presenta unas características intermedias entre los anteriores.
Por otra parte, la propuesta de Díaz, de la Torre y Guerrero (2006) sobre la formación inicial incide en la necesidad de un conocimiento profundo de la disciplina (contenidos matemáticos y métodos de obtención del conocimiento matemático, así como de los recursos didácticos y los procesos de matematización de distintos ámbitos: ciencias de la naturaleza, ciencias sociales…).
Aunque la formación actual que reciben los estudiantes para maestros en las universidades españolas los debe capacitar profesionalmente para impartir docencia en cualquier materia de la Educación Primaria, la estructura que se puede contemplar en los diferentes planes de estudio no es consecuente con esa tarea. En general se ha puesto un énfasis muy claro en materias que se interesan por la cuestión educativa (pedagogía, psicología, sociología, historia de la educación, etc.), reduciendo el espacio de formación específica para cada una de las materias curriculares y su correspondiente didáctica (Díaz, de la Torre y Guerrero, 2006).
Siguiendo a Blanco (1996), la formación de maestros/as de Educación Primaria en el área de matemáticas se ve afectada por tres aspectos fundamentales: las transformaciones en el curriculum, las contribuciones que se han realizado para el aprendizaje de las matemáticas, y el contexto en el que tiene lugar el proceso de enseñanza - aprendizaje. En esta dirección, se pueden observar dos ámbitos sobre los que se estructura la formación inicial: la Didáctica, sobre la que descansa el curriculum, y el Contenido Matemático, sobre el que se establece la disciplina.
Socas (2011) plantea la representación de los diferentes ámbitos del contenido matemático y su vinculación con los aspectos didácticos y de contenido, diferenciando contenido matemático disciplinar, curricular y de enseñanza, señalando cuatro ejes en la formación en Educación Matemática: las matemáticas para los maestros, el análisis e interpretación de las producciones del alumnado, la didáctica de las matemáticas y la gestión del contenido matemático en el aula.
Ante la necesidad de alcanzar un modelo integrador entre los diferentes ámbitos del contenido matemático, este estudio se ha focalizado en el análisis de los programas que recogen la formación de futuros docentes de Educación Primaria. En España, los programas académicos de Grado se desarrollan bajo un marco orientativo del gobierno central que luego cada comunidad autónoma concreta, siendo las propias universidades en virtud de su autonomía, quienes configuran el plan de estudios de la formación del futuro docente de Educación Primaria.
2. Problema de investigación y marco teórico
El propósito principal de este trabajo ha sido analizar el tipo de conocimiento matemático que se refleja en los planes de estudio de las titulaciones de Grado en Educación Primaria en las universidades públicas españolas. Para ello se ha realizado una aproximación comparada de las guías docentes de las materias del área de Didáctica de las Matemáticas. Concretamente, se ha llevado a cabo un estudio exploratorio de carácter comparado nacional que tiene como objetivo conocer las tendencias y la estructura de los programas académicos en la formación inicial en el campo de la educación matemática, así como las diferencias que se pueden observar en los mismos.
Los programas de formación del profesorado en los que trabajamos se basan en un modelo propuesto en el marco de la convergencia en Europa. Se ha tomado como referencia el trabajo realizado por Rico, Gómez y Cañadas (2014) sobre los programas de la formación inicial en relación con el estudio TEDS -M (Tatto, Schwille, Senk, Ingvarson, Peck y Rowley, 2012) con carácter previo a la reforma curricular de la Ley Orgánica 8/2013, de Mejora de la Calidad en Educación y a la aprobación de los nuevos planes de estudio para los maestros de Educación Primaria, que se aprobaron y publicaron principalmente a partir del 2010.
Nuestro encuadre teórico se contextualiza en la perspectiva sociocultural de la matemática educativa al asumir las practicas sociales como la base de la construcción del conocimiento matemático en los futuros profesores de primaria, en tanto en cuanto, los objetivos del presente estudio no se focalizan en el estudio de la matemática como disciplina científica, sino en el cuestionamiento sobre el saber matemático que se está enseñando a los futuros maestros y maestras de educación primaria en las facultades de ciencias de la educación (Reyes-Gasperini y Cantoral, 2014; Guerrero, 2021).
Recientes estudios (Ball, 2000; Anderson y Kim, 2003; Morales, Anderson y McGowan, 2003; Hill, Ball y Schilling, 2008; Appova y Taylor, 2020) nos proporcionan una importante distinción entre saber matemáticas y la manera en que se capacita su uso en la práctica. Esta idea es clave para entender como el conocimiento de las matemáticas se transforma en una buena enseñanza. No se trata sólo de saber lo que los profesores de primaria saben de matemáticas, sino también de cómo lo saben y cuáles son sus creencias sobre la disciplina que enseñan.
A partir de la clasificación de los tipos de conocimiento de Shulman (1986, 1987), Carrillo et al. (2018) nos informan de la existencia de diferentes modelos enfocados en conceptualizar y caracterizar el conocimiento necesario para el profesorado. Entre los modelos destacados se encuentra el Mathematics Teacher’s Specialised Knowledge (MTSK) (Carrillo et al., 2018) . Este modelo es definido por los propios autores como una conceptualización del conocimiento del profesor que presta atención al carácter especializado de las matemáticas, además del conocimiento que le es útil y necesario al profesorado de matemáticas y su relación con el proceso de su enseñanza y aprendizaje. De esta forma, el MTSK considera los siguientes dominios: Conocimiento Matemático (Mathematical Knowledge, MK); Conocimiento Didáctico del Contenido (Pedagogical Content Knowledge, PCK), y, además el dominio Creencias sobre la matemática y sobre su enseñanza y aprendizaje.
De acuerdo con Carrillo et al. (2018), el carácter especializado del conocimiento del profesor se encuentra en la integración y las relaciones entre los diferentes conocimientos en distintas dimensiones, lo que deriva de su labor docente. Sin embargo, tal y como señalan Anderson y Kim (2003), faltan estudios concluyentes que conecten la necesidad del conocimiento del contenido matemático (Mathematical Content Knowledge, MCK) y el PCK con los logros en matemáticas del alumnado.
Con relación a las creencias y la solidez en las mismas, los perfiles se aproximan a los resultados de Latorre y Pérez (2005). Estas autoras realizan su investigación a partir de su acercamiento al ámbito laboral, diferenciando los que no habían cursado las prácticas de los que lo habían hecho. Con respecto al primer grupo, aunque todos comparten un planteamiento positivo con respecto a la aproximación a la práctica docente, se pueden diferenciar dos perfiles, mientras que un grupo se siente más comprometido y con creencias más sólidas y sostenidas; el otro grupo demuestra una actitud más cómoda y laxa. En relación con los que no han cursado prácticas, se aprecian también dos perfiles diferenciados por su intensidad en las creencias y compromiso con las cuestiones planteadas.
De acuerdo con su perfil y creencias sobre las competencias matemáticas, Escolano, Gairín, Jiménez-Gestal, Murillo y Roncal (2012) estudian tres variables: competencia matemática, dificultad en matemáticas y capacidad para comprender cómo enseñar matemáticas. Sus resultados muestran que el perfil de alumnado que presenta dificultades con las matemáticas manifiesta su capacidad para entender los elementos clave de cómo enseñarlas. Incluso un 10% del alumnado de este perfil, pese a su escasa competencia matemática, afirman no tener inseguridad para explicarlas.
Por otra parte, las experiencias escolares que han tenido los futuros maestros y maestras de primaria en relación a esta disciplina van a influir también en su efectividad a la hora de enseñarla. Una buena preparación docente, promoverá una disposición positiva hacia las matemáticas (Bambico, 2003; Barrantes y Blanco, 2006; Cardetti y Truxaw, 2014).
En esta línea, Polly et al. (2013) citando a Askew, Browon, Rhodes, Johnson y Williams (1997) menciona la importancia que tienen las creencias del profesorado sobre las matemáticas y su forma de enseñarlas distinguiendo tres orientaciones: transmisión, descubrimiento y conectividad. De esta manera, el profesorado vinculado al modelo transmisor cree que las matemáticas son un conjunto de reglas fijas que deben transmitirse o presentarse a los estudiantes. No obstante, aquel vinculado al modelo por descubrimiento concibe las matemáticas como un conjunto de conocimientos que se aprenden mejor a través de la exploración guiada del estudiante. Por su parte, el docente orientado por la teoría de la conectividad concibe las matemáticas como un conjunto de conceptos entrelazados y se basa en las experiencias previas para ayudar a los estudiantes a aprender a hacer relaciones entre los distintos tópicos matemáticos.
En lo referido al proceso de aprendizaje del conocimiento de la disciplina, los resultados en PISA concluyen que la memorización en matemáticas es importante para resolver problemas sencillos, pero si se trata de asuntos complejos, el alumnado español tiene cuatro veces menos probabilidad de éxito que los estudiantes de Shanghái o Hong-Kong (Hsieh et al., 2011). Sin embargo, un alto porcentaje de futuros maestros y maestras creen que necesitan explicar matemáticas a los estudiantes con procedimiento matemáticos. Vienen de aprender matemáticas con modelos transmisivos, centrados en el profesorado y en donde los errores se traducen en una falta de interés del que aprende.
El estudio de Escolano et al. (2012) revela el predominio de la Aritmética sobre la Geometría en los procesos de aprendizaje de competencia matemática de los futuros docentes. En Geometría presentan una mayor dificultad para la comprensión de conceptos. Asimismo, evidencia que la competencia matemática de los futuros maestros y maestras es un elemento que vertebra sus creencias sobre la Educación Matemática y sobre el desarrollo profesional docente. En consecuencia, si no se cambia el modelo formativo es muy probable que opten por la reproducción del modelo aprendido.
Paradójicamente, Sellers (2004), explica que investigaciones sobre la enseñanza-aprendizaje de las matemáticas nos informan que los niños y las niñas no entienden las matemáticas cuando sólo se les da instrucciones para hacer un problema o memorizar un procedimiento. El método del libro de texto, “mostrar, contar y demostrar” parece no ser suficiente. Una enseñanza de las matemáticas efectiva exige que los estudiantes de primaria piensen y razonen, que investiguen y exploren diferentes métodos.
Por ello, estudiar las relaciones entre el perfil de profesor de matemáticas de primaria, la calidad de la enseñanza de las matemáticas y las relaciones entre el MCK y el PCK, se convierte en una prioridad política y social. Sin embargo, todavía no existe consenso sobre qué contenidos o conocimientos en educación matemática son necesarios para la formación de un maestro/a (Copur-Gencturk y Lubienski, 2013). De esta manera, se hace necesario repensar la formación inicial y el peso que en ella tiene el PCK al entender que este tipo de conocimiento es clave para que el conocimiento de las matemáticas se transforme en una buena enseñanza. Norton (2020) o Cardetti y Truxaw (2014) señalan que lo que no se ha descubierto claramente es cómo el profesorado adquiere el conocimiento matemático para enseñar, destacando insuficiencias en la formación universitaria en este sentido.
La necesidad de confluir hacia una formación común del profesorado de Primaria en el conjunto de los países europeos impone que los programas de formación del profesorado deberán capacitar al profesorado para desempeñar su trabajo en cualquier estado de la Unión Europea, además de facilitar la movilidad del estudiantado durante la realización de sus estudios superiores. De ahí que todas las titulaciones de la Unión Europea tengan la necesidad de cuantificar sus materias de la misma forma, y surge por ello el crédito ECTS (European Credit Transfer and Accumulation System). Se pretende no sólo reformar los títulos, sino lograr un modelo atractivo y exportable, una educación de calidad y universal. La nueva estructura de educación superior se organiza en tres ciclos: Grado (240 ECTS), Máster (60 ECTS) y Doctorado (60 ECTS de formación y tesis doctoral).
Para configurar estos planes de estudios se crea en España en el año 2003 la llamada “red de Magisterio” establecida como consecuencia de una convocatoria de la Agencia Nacional de Evaluación de la Calidad y Acreditación (ANECA), para incorporar los estudios de Magisterio a la normativa de Bolonia. Esta red, de la que formaban parte prácticamente todos los directores y directoras de las Escuelas de Magisterio y los decanatos de las Facultades de Educación (en total eran 44 participantes) publica el Libro Blanco de la Titulación de Magisterio (ANECA, 2005), donde se proponen dos titulaciones. Una de Maestro/a de Educación Infantil y otra de Maestro/a de Educación Primaria (con carácter generalista y al mismo tiempo especializado) con una duración de 240 ECTS (distribuidos en cuatro cursos). Se establece un bloque de materias troncales (en torno al 70% de la titulación) y cuatro itinerarios formativos (Lengua Extranjera, Educación Física, Educación Musical y Educación Especial) especializados en el caso de Educación Primaria. La formación práctica recibe 42 ECTS y las materias básicas del currículo pasan a tener un peso de 102 ECTS.
En cuanto a las materias, se organizaron en distintos bloques: materias comunes (psico-socio-pedagógicas), materias comunes de áreas del currículo (Matemáticas, Lengua, Ciencias, Geografía e Historia y Educación Artística-plástica), materias específicas de cada itinerario (Educación Física, Educación Musical, Educación Especial o Lengua Extranjera), prácticas docentes (Prácticum) y créditos de libre disposición.
La distribución de asignaturas y créditos en estos títulos sería de 240 ECTS totales, distribuidos en 180 correspondientes a la formación básica y 60 destinados a la formación adicional de orientación académica o profesional (Tabla I).
Tabla I Contenidos formativos comunes recogidos en el Libro Blanco de Magisterio
| Denominación de las materias de Maestro Educación Primaria | Nº mínimo de ECTS |
| Enseñanza y aprendizaje de las Ciencias Experimentales | 14 |
| Enseñanza y aprendizaje de las Ciencias Sociales | 14 |
| Enseñanza y aprendizaje de las Matemáticas | 20 |
| Enseñanza y aprendizaje de las Lenguas | 22 |
| Enseñanza y aprendizaje de los ámbitos musical, plástico y visual | 10 |
| Enseñanza y aprendizaje de la Educación Física | 8 |
| Procesos y contextos educativos | 14 |
| Aprendizaje y desarrollo de la personalidad (6-12 años) | 10 |
| Familia y escuela | 8 |
Fuente: Agencia Nacional de Evaluación de la Calidad y Acreditación (2005)
La Ley Orgánica 4/2007, de 12 de abril, por la que se modifica la Ley Orgánica 6/2001, de 21 de diciembre de Universidades, facilita a las propias universidades la creación de las enseñanzas y títulos que se hayan de impartir y expedir, sin sujeción a la existencia de un catálogo previo establecido por el Gobierno, como hasta ahora era obligado. También se flexibiliza la organización de las enseñanzas universitarias, promoviendo la diversificación curricular y permitiendo que las universidades aprovechen su capacidad de innovación, sus fortalezas y oportunidades.
Por otra parte, la nueva organización de las enseñanzas universitarias responde no sólo a un cambio estructural, sino que además impulsa un cambio en las metodologías docentes centrando, el objetivo en el proceso de aprendizaje del estudiante, en un contexto que se extiende a lo largo de la vida. En particular, la principal característica de este nuevo modelo radica en la pretensión de promover el trabajo autónomo del alumnado, al que se quiere implicar de forma más activa en el proceso de aprendizaje; y en una atención más individualizada a los estudiantes. En este sentido, las clases expositivas son complementadas por otras de carácter interactivo y, en caso de existir capacidad docente suficiente, por clases tutorizadas. Otras novedades consisten en la obligatoriedad de realizar y defender un trabajo de fin de grado y en la potenciación de prácticas externas orientadas a familiarizar al estudiantado con el mundo profesional.
Para conseguir estos objetivos, en el plan de estudios de una titulación de Grado deben reflejarse más elementos que la mera descripción de los contenidos formativos. Este nuevo modelo concibe el plan de estudios como un proyecto de implantación de una enseñanza universitaria. Como tal proyecto, para su aprobación se requiere la aportación de nuevos elementos como: justificación, objetivos, admisión de estudiantes, contenidos, planificación, recursos, resultados previstos y sistema de garantía de calidad. Los planes de estudio conducentes a la obtención de un título deberán, por tanto, tener en el centro de sus objetivos la adquisición de competencias por parte de los estudiantes, ampliando, sin excluir, el tradicional enfoque basado en contenidos y horas lectivas. Se debe hacer énfasis en los métodos de aprendizaje de dichas competencias, así como en los procedimientos para evaluar su adquisición.
La ORDEN ECI/3857/2007, de 27 de diciembre, establecen los requisitos para la verificación de los títulos universitarios oficiales que habiliten para el ejercicio de la profesión de Maestro/a en Educación Primaria:
Conocer las áreas curriculares de la Educación Primaria, la relación interdisciplinar entre ellas, los criterios de evaluación y el cuerpo de conocimientos didácticos en torno a los procedimientos de enseñanza y aprendizaje respectivos.
Diseñar, planificar y evaluar procesos de enseñanza y aprendizaje, tanto individualmente como en colaboración con otros docentes y profesionales del centro.
Abordar con eficacia situaciones de aprendizaje de lenguas en contextos multiculturales y plurilingües. Fomentar la lectura y el comentario crítico de textos de los diversos dominios científicos y culturales contenidos en el currículo escolar.
Diseñar y regular espacios de aprendizaje en contextos de diversidad y que atiendan a la igualdad de género, a la equidad y al respeto a los derechos humanos que conformen los valores de la formación ciudadana.
Fomentar la convivencia en el aula y fuera de ella, resolver problemas de disciplina y contribuir a la resolución pacífica de conflictos. Estimular y valorar el esfuerzo, la constancia y la disciplina personal en los estudiantes.
Conocer la organización de los colegios de Educación Primaria y la diversidad de acciones que comprende su funcionamiento. Desempeñar las funciones de tutoría y de orientación con los estudiantes y sus familias, atendiendo las singulares necesidades educativas de los estudiantes. Asumir que el ejercicio de la función docente ha de ir perfeccionándose y adaptándose a los cambios científicos, pedagógicos y sociales a lo largo de la vida.
Colaborar con los distintos sectores de la comunidad educativa y del entorno social. Asumir la dimensión educadora de la función docente y fomentar la educación democrática para una ciudadanía activa.
Mantener una relación crítica y autónoma respecto de los saberes, los valores y las instituciones sociales públicas y privadas.
Valorar la responsabilidad individual y colectiva en la consecución de un futuro sostenible.
Reflexionar sobre las prácticas de aula para innovar y mejorar la labor docente. Adquirir hábitos y destrezas para el aprendizaje autónomo y cooperativo y promoverlo entre los estudiantes.
Conocer y aplicar en las aulas las tecnologías de la información y de la comunicación. Discernir selectivamente la información audiovisual que contribuya a los aprendizajes, a la formación cívica y a la riqueza cultural.
Comprender la función, las posibilidades y los límites de la educación en la sociedad actual y las competencias fundamentales que afectan a los colegios de Educación Primaria y a sus profesionales. Conocer modelos de mejora de la calidad con aplicación a los centros educativos.
3. Metodología
Con el fin de conocer en mayor profundidad la literatura científica sobre la temática abordada, se ha realizado una revisión bibliográfica con las siguientes palabras clave: “Preservice Teacher Education”, “Mathematics Education” y “Primary Education”. Se ha indagado en cuatro bases de datos de relevancia en el ámbito educativo, tres internacionales (APA PsycInfo, ERIC y Psychology Database) y en una nacional (DIALNET). Como filtros se ha aplicado un límite temporal de los últimos diez años y se han incluido los artículos evaluados por expertos y publicados en revistas científicas. Como resultado se han obtenido 19 artículos, de los cuales por su pertinencia en relación con este estudio se han seleccionado dos, que hemos complementado con otros trabajos que sustentan teóricamente nuestra propuesta.
La revisión bibliográfica llevada a cabo ha evidenciado la demanda de seguir investigando sobre educación matemática y la formación docente (Blanco, 1996; Anderson y Kim, 2003; Palarea, 2011; Shain y Soylu, 2017; Da Silva y Zeichner, 2021). Esta necesidad ha sido corroborada por distintos trabajos como el de Norton (2020), Muñiz- Rodríguez, Aguilar-González, Rodríguez-Muñiz (2020) y González y Sánchez (2020).
Se ha realizado un análisis exploratorio descriptivo comparado con el objetivo de extraer toda la información que hiciera referencia a las materias relacionadas con la Educación Matemática (Matemáticas y Didáctica de las Matemáticas) de los planes de estudio de la titulación del Grado en Educación Primaria, siguiendo el modelo de Clasificación Internacional Normalizada de la Educación (CINE 1) (UNESCO, 2013).
La aproximación metodológica comparada se ha planteado utilizando fuentes primarias de 39 universidades públicas españolas. Las fases de investigación han sido: selección y definición del problema, formulación de la hipótesis de partida y elección de la unidad de análisis (Rasmussen y Zou, 2014; Caballero, Manso, Matarranz y Valle, 2016; Egido y Martínez-Usarralde, 2019). El acceso a estas fuentes se ha realizado a través de las páginas web oficiales de cada una de estas universidades.
El parámetro de comparación y los indicadores se han establecido a partir del marco recogido en el informe TEDS -M International (2012). El primer parámetro es el conocimiento del contenido matemático (MCK) con dos dominios: el dominio de contenido con cuatro subdominios: Números y operaciones, Geometría y medida, Álgebra y funciones y Estadística y probabilidad; y el dominio cognitivo con tres subdominios: Conocimiento, Aplicación y Razonamiento.
El segundo parámetro es el conocimiento del contenido pedagógico de matemáticas (PCK), en el que se diferencian tres subdominios: Conocimiento del curriculum de matemáticas, Conocimiento para la planificación del proceso de enseñanza-aprendizaje en matemáticas y Promoción de las matemáticas para la enseñanza y aprendizaje.
Se ha utilizado como indicadores del estudio comparado el curso, el número de créditos y el carácter (formación básica, obligatoria y optativa). Para la recogida de la información, se ha confeccionado una base de datos ad hoc, asignando el valor de 0 a la ausencia de los parámetros con sus subdominios y el valor de 1 a su presencia en los planes de estudio.
Se han establecido las siguientes preguntas de investigación:
- P1. En la formación de la educación matemática, ¿el MCK predomina sobre el PCK? ¿Predomina del mismo modo tanto en la formación obligatoria, como en la formación optativa?
- P2. En los planes de estudio, ¿dentro del MCK cómo se trabajan los dominios de contenido y cognitivo? ¿qué subdominios predominan?
- P3. En los planes de estudio donde se trabaja el PCK, ¿qué subdominio predomina?
4. Resultados
Teniendo en cuenta los objetivos propuestos de investigación se inicia el análisis de los resultados, presentando los ECTS obligatorios y optativos que ofrecen las distintas universidades públicas españolas en formación de Educación Matemática (se puede consultar en la Tabla II). Se puede observar que la oferta difiere tanto entre comunidades autónomas, como entre las propias universidades dentro de una misma comunidad autónoma. Tampoco hay una tendencia homogénea en el número de créditos. Más bien podemos observar una gran diversidad y heterogeneidad, ya que tenemos universidades con planes de estudio que recogen únicamente 12 créditos obligatorios en formación matemática, mientras otras ofrecen 24 créditos. De forma similar ocurre con los créditos optativos, nos podemos encontrar con universidades que no ofrecen ningún crédito optativo en formación matemática y otras que ofrecen hasta 33 créditos.
Tabla II Distribución de obligatoriedad y optatividad de los ECTS de las universidades españolas
| Comunidad Autónoma |
ECTS obligatorios |
ECTS optativos |
Total de ECTS |
| Andalucía | 166 | 12 | 178 |
| Universidad de Almería | 24 | 24 | |
| Universidad de Cádiz | 24 | 6 | 30 |
| Universidad de Córdoba | 18 | 18 | |
| Universidad de Granada | 22 | 6 | 28 |
| Universidad de Huelva | 21 | 21 | |
| Universidad de Jaén | 18 | 18 | |
| Universidad de Málaga | 21 | 21 | |
| Universidad de Sevilla | 18 | 18 | |
| Asturias (Universidad de Oviedo) | 18 | 18 | |
| Canarias | 39 | 15 | 54 |
| Universidad de La Laguna | 20 | 9 | 29 |
| Universidad de Las Palmas de Gran Canaria | 19 | 6 | 25 |
| Cantabria (Universidad de Cantabria) | 18 | 6 | 24 |
|
Castilla la Mancha (Universidad de Castilla-La Mancha) |
18 | 18 | |
| Castilla y León | 65 | 32 | 97 |
| Universidad de Burgos | 18 | 18 | |
| Universidad de León | 12 | 8 | 20 |
| Universidad de Salamanca | 17 | 12 | 29 |
| Universidad de Valladolid | 18 | 12 | 30 |
| Cataluña | 89 | 63 | 152 |
| Universidad Autónoma de Barcelona | 17 | 30 | 47 |
| Universidad de Barcelona | 18 | 12 | 30 |
| Universidad de Girona | 16 | 21 | 37 |
| Universidad Rovira i Virgili | 18 | 18 | |
| Universitat de Lleida | 20 | 20 | |
| Comunidad de Madrid | 72 | 57 | 129 |
| Universidad Autónoma de Madrid | 18 | 33 | 51 |
| Universidad Complutense de Madrid | 18 | 24 | 42 |
| Universidad de Alcalá | 18 | 18 | |
| Universidad Rey Juan Carlos | 18 | 18 | |
| Extremadura (Universidad de Extremadura) | 18 | 18 | |
| Galicia | 48 | 10,5 | 58,5 |
| Universidad de A Coruña | 18 | 4,5 | 22,5 |
| Universidad de Santiago de Compostela | 18 | 18 | |
| Universidade de Vigo | 12 | 6 | 18 |
| Islas Baleares (Universitat de las Illes Balears) | 18 | 18 | |
| La Rioja (Universidad de La Rioja) | 18 | 4,5 | 22,5 |
| Murcia (Universidad de Murcia) | 21 | 3 | 24 |
| Navarra (Universidad Pública de Navarra) | 18 | 18 | |
| País Vasco (Universidad del País Vasco) | 15 | 6 | 21 |
| Valencia | 57 | 42 | 99 |
| Universidad de Alicante | 18 | 6 | 24 |
| Universitat de València | 21 | 30 | 51 |
| Universitat Jaume I de Castellón | 18 | 6 | 24 |
| Aragón (Universidad de Zaragoza) | 18 | 6 | 18 |
| Total general | 716 | 257 | 973 |
Fuente: Elaboración propia
Sólo hemos encontrado dos comunidades autónomas, Canarias y Comunidad Valenciana, que ofrecen en todas sus universidades tanto formación obligatoria, como optativa; aunque la oferta de la primera es más uniforme que la de la segunda.
En cuanto a la distribución de créditos por curso y carácter de la materia (Figura 1), teniendo en cuenta el diseño de los planes de estudio, la mayor carga de créditos obligatorios está en los dos primeros cursos (1º y 2º), concentrándose mayoritariamente la oferta optativa en 3º y 4º curso. Si bien, hay universidades que ofrecen esta formación ya desde 2º curso, y la obligatoriedad se extiende entre los cuatro cursos, siendo su concentración mayor en 1º, 2º y 3º.
En general, se puede observar una tendencia en la formación de mantener un cierto equilibrio entre el parámetro del MCK con el parámetro del PCK, si bien con un relativo predominio del primero sobre el segundo en dos comunidades autónomas (País Vasco y la Rioja, Figura 2).
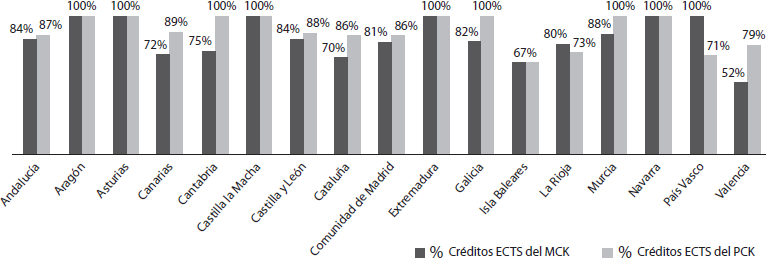
En particular, si analizamos esta situación comparando la oferta obligatoria de créditos y la optativa se puede observar que en seis comunidades autónomas los conocimientos PCK y MCK están igualmente presentes en la oferta obligatoria, y cuando esta situación de igualdad no se da, predomina el MCK (Figura 3).
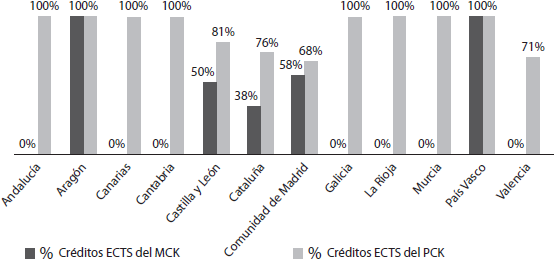
Mientras, en la oferta optativa (Figura 4), el conocimiento que más presencia tiene es el PCK, estando exclusivamente presente en siete comunidades autónomas.
En relación al curso, podemos comprobar una tendencia opuesta en el comportamiento de ambos parámetros. Así, mientras que el MCK va disminuyendo su presencia a medida que avanzamos en el curso, el PCK va aumentando progresivamente hasta decaer levemente en cuarto curso (Figura 5).
Como podemos ver en la Tabla II hay nueve universidades con una oferta de formación matemática obligatoria con un número mayor o igual a veinte ECTS. Se puede observar que el MCK es igual o predominante con respecto al PCK, excepto en un caso (Figura 6).

Figura 6 Porcentaje de la distribución de ECTS por parámetro: MCK y PCK en las comunidades autónomas que tienen universidades con una formación matemática mayor o igual a 20 créditos
Con respecto a la segunda pregunta de investigación, si estudiamos los dominios del MCK, podemos ver en la Figura 7 como en siete comunidades autónomas (Aragón, Asturias, Canarias, Castilla la Mancha, Comunidad de Madrid, Extremadura y Galicia) el Dominio Cognitivo del MCK prevalece (su presencia es más del doble) sobre el Dominio de Contenido, siendo esta presencia en el resto de comunidades mayor, pero no tan acusada, excepto en el País Vasco que su presencia es igual (67%).
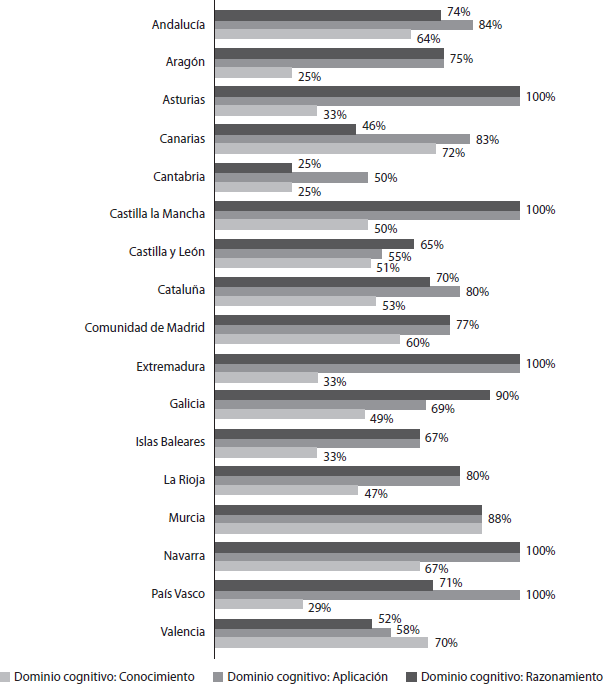
En cuanto al Dominio Cognitivo del MCK, se puede observar una tendencia en la distribución de sus subdominos (Figura 8), evidenciándose una menor presencia del subdominio cognitivo de razonamiento frente a los subdominios de conocimiento y de aplicación.
Si analizamos los subdominios del dominio del contenido del MCK se puede observar que el de Números y operaciones es el dominante en Aragón, Galicia y País Vasco; mientras que el de Geometría y medida tiene mayor presencia en Andalucía, Asturias, Castilla y León, Cataluña y Comunidad de Madrid. Es destacable también que Canarias presente el subdominio de Algebra y funciones como el predominante, siendo éste el minoritario en el resto de las comunidades autónomas. También se puede observar que Castilla la Mancha, Extremadura, Islas Baleares y Murcia, presentan el mismo peso porcentual en los tres subdominios que tienen y Cantabria en sus dos subdominos (Figura 9).
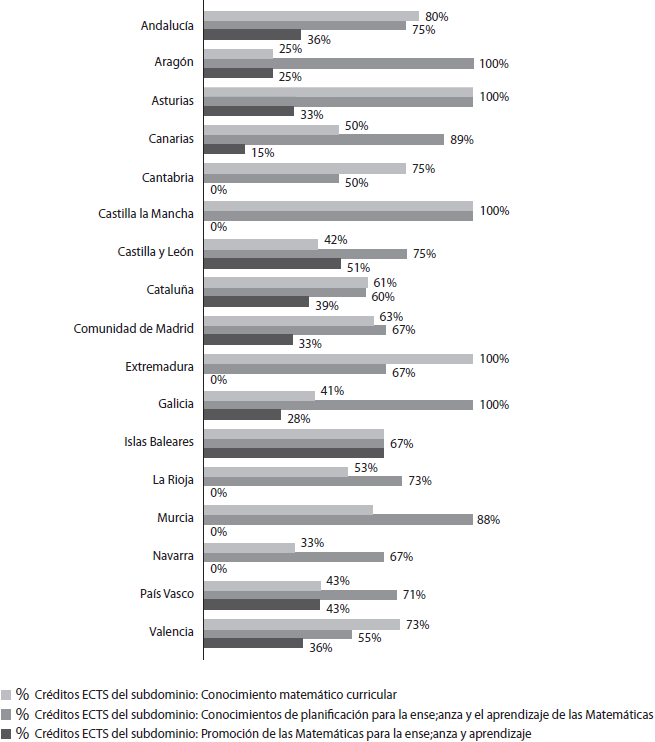
En lo que respecta a la tercera pregunta que nos hemos planteado, seis comunidades autónomas no desarrollan el subdominio Promoción de las matemáticas para la enseñanza y el aprendizaje, siendo únicamente en la comunidad autónoma de las Islas Baleares donde existe un equilibrio entre los tres subdominios. Es destacable una cierta variabilidad en el porcentaje de los otros dos subdominios (Conocimiento matemático curricular y Conocimientos de planificación para la enseñanza y el aprendizaje de las matemáticas), siendo el segundo el de mayor presencia en la mayoría de las comunidades autónomas (Figura 10).
5. Discusión y conclusiones
Considerando los objetivos de investigación, los primeros resultados obtenidos apuntan a una formación matemática en el estado español muy dispar, tanto por comunidades autónomas con competencias en materia educativa, como por universidades dentro de cada comunidad. Esto se refleja por un lado en las materias obligatorias que deben cursar, cuya configuración en el número de créditos puede variar desde los 12 hasta 24, con una media de 18,36 créditos obligatorios y una desviación típica de 2,38. Esta formación obligatoria se puede complementar con una formación optativa en universidades donde ofrecen un mínimo de 4,5 créditos y un máximo de 33 créditos, con una media de 6,43 y desviación típica de 9,18. También es reseñable que las universidades que tienen un mayor número de créditos obligatorios, no son las que ofrecen un mayor número de créditos optativos. Ni tampoco, las que tienen mayor número de créditos optativos, son las que mayor número de créditos obligatorios tienen.
Esta conclusión se evidencia en la Tabla II, recogida en los resultados, y reafirma las conclusiones de Rico, Gómez y Cañadas (2014), que manifiestan “una incipiente diversificación de las materias orientadas hacia la formación del maestro como profesor de matemáticas” (p.55). Sin embargo, no se puede constatar que se mantengan las recomendaciones nacionales como evidenciaban estos autores en el citado trabajo. Si se tienen en cuenta las recomendaciones recogidas en el Libro Blanco (ANECA, 2015), la formación en Educación Matemática de un futuro docente debería tener al menos 20 ECTS obligatorios. No obstante, la media de créditos no cumple esta recomendación ya que sólo 9 de las 39 universidades ofrecen como mínimo ese número de créditos, es decir aproximadamente el 23,1%.
En este sentido, coincidiendo con los resultados de otros estudios (Palarea, 2011; Copur-Gencturk y Lubienski, 2013; Rico, Gómez y Cañadas, 2014), no se ha identificado una tendencia, pudiéndose observar divergencias en la oferta de formación inicial en cuanto al número de créditos. Por el contrario, sí parece haber una tendencia más homogénea en cuanto al carácter de las materias ofertadas y su distribución por cursos en la formación optativa y obligatoria. En los primeros cursos tiene lugar la formación obligatoria y en los últimos cursos la optativa.
Esta cuestión que puede parecer a simple vista una obviedad, por ser un consenso entre universidades, puede tener efectos en la distribución del peso otorgado al PCK y al MCK en la formación. De esta manera, en relación a la primera pregunta de nuestra investigación, nuestros resultados afirman que el MCK domina en la formación obligatoria, mientras que el PCK tiene una mayor presencia en la optatividad. Esta realidad puede inferir lo expuesto en el estudio de Anderson y Kim (2003), previamente es necesario afianzar el dominio de la disciplina para poder enseñarla posteriormente, y, por tanto, podría decirse que los planes de estudio se elaboran desde este supuesto.
La respuesta a la segunda pregunta de la investigación con respecto a los dominios del MCK que predominan en los planes de estudio del futuro docente de primaria, los resultados obtenidos evidencian que, mayoritariamente, el dominio cognitivo prevalece sobre el dominio de contenido. Particularmente, en el Dominio Cognitivo del MCK, los subdominios más trabajados son los que potencian un pensamiento más concreto: el de Conocimiento y Aplicación; frente al subdominio más abstracto de Razonamiento, que es significativamente el menos empleado en la formación de los futuros maestros y maestras de Educación Primaria. En la línea de los estudios de Polly et al. (2013), este resultado puede corroborar la presencia aun dominante del modelo de formación transmisor que concibe las matemáticas como un conjunto de reglas fijas que deben transmitirse a los estudiantes. Como afirman Bosch y Gascón (2005) se observa una influencia creciente del tecnicismo que identifica implícitamente “enseñar y aprender matemáticas” con “enseñar y aprender técnicas simples”.
Cabe preguntarse si un modelo de formación inicial con estas características responde a la propuesta planteada por Sellers (2004) en el que asocia una enseñanza de las matemáticas efectiva con el pensamiento y el razonamiento lo que conlleva necesariamente a explorar nuevos modelos de formación docente más vinculados con el modelo de aprendizaje por descubrimiento y de una enseñanza interdisciplinar que conecte los nuevos conocimientos con los conocimientos previos, que contextualice el aprendizaje y enseñe a establecer relaciones entre los distintos subdominios matemáticos.
Esta conclusión, podría estar relacionada con el estudio de Hsieh et al. (2011) y presenta una línea de investigación futura, donde se asocian los dominios cognitivos, el rendimiento de los estudiantes y la preparación docente, ya que, si la formación inicial del profesorado muestra una menor presencia del subdominio de Razonamiento, quizás podría darse una menor preparación de nuestro alumnado de Educación Primaria en este sentido.
Por otra parte, teniendo en cuenta el domino de contenido del MCK, podemos concluir que el subdomino de Álgebra y Funciones casi no está presente, al no ser un conocimiento curricular propio de la etapa de Educación Primaria. También se puede destacar que el subdominio de Estadística y Probabilidad es de los menos trabajados en consonancia con el desarrollo curricular actual de esta etapa educativa (Educación Primaria). Tal vez esto sucede porque como se demuestra en el estudio de Escolano et al. (2012), la dificultad para la comprensión de determinados conceptos matemáticos por parte de los futuros maestros y maestras puede estar condicionando el predominio de un subdominio sobre otro a la hora de elaborar los planes de estudio de las respectivas universidades. Así, tal y como apuntan Bosch y Gascón (2004) se mantiene la tendencia en los planes de estudios a “atomizar” los contenidos matemáticos, ya que no existe un consenso sobre qué contenidos son necesarios para la formación de un/a maestro/a como ya afirmaban Copur-Gencturk y Lubienski (2013).
Por lo que respecta a la tercera pregunta de investigación que nos hemos planteado, en lo relativo al segundo parámetro, el PCK , el subdominio de Promoción de las matemáticas para la enseñanza y el aprendizaje es el menos enseñado en la formación de los futuros docentes. De esta forma, se explicita la necesidad de explorar nuevos métodos que enseñen a los/as futuros/as maestros/as a conectar el MCK con el PCK y conseguir así mejores resultados en los futuros estudiantes de primaria. El modelo de formación debería enseñar a los futuros docentes a aprender a aprender matemáticas desde un modelo que integre reflexión- conocimiento-acción (Schön, 1992), porque no se trata sólo de saber lo qué el profesorado sabe de matemáticas, sino cómo lo saben y qué pueden movilizar matemáticamente durante su proceso de enseñanza (Chick y Harris, 2007). Como señala Reyes-Gasperini y Cantoral (2014) el problema de la enseñanza y aprendizaje de las matemáticas va más allá de las explicaciones didácticas o a rellenar los agujeros de contenidos matemáticos entre estudiantes y profesores, se trata del cuestionamiento del saber matemático escolar inmerso en la vida del sistema didáctico.
Desde la perspectiva de la educación matemática y ante la necesidad manifestada por Cardetti y Truxaw (2014) este trabajo pretende situar como parte de la discusión científica una revisión de la formación para que los futuros docentes sean capaces de ver el valor de la educación matemática desde un modelo integrador de las diferentes dimensiones de los conocimientos matemáticos abordados (Hsieh et al., 2011). En este sentido, nuestro estudio de carácter institucional sigue la línea propuesta por la Sociedad Española de Investigación en Educación Matemática (SEIEM) al plantear la necesidad de repensar una nueva organización curricular en la formación de los/as docentes de Educación Primaria más homogénea y con una mayor articulación entre el MCK y el PCK capaz de satisfacer las nuevas exigencias globales y altamente tecnologizadas de la sociedad del conocimiento.
En cualquier caso, se sugiere la necesidad de completar estos resultados con estudios de corte más cualitativo que nos permitan analizar las propuestas pedagógicas de la educación matemática dentro del aula universitaria mediante técnicas de observación directa y triángulación de perspectivas docentes, discentes e investigadoras.











 nueva página del texto (beta)
nueva página del texto (beta)