1. Introducción
En los últimos 40 años la investigación de las matemáticas situadas ha evidenciado al menos tres focos en el ámbito educativo: a) construcción de curriculum flexibles a las demandas de una ciudadanía críticar, b) promoción de cambios didácticos en la forma de enseñar las matemáticas escolares centrada en lo local, y c) dificultades para establecer metodologías de modelamiento matemático que incluya la resolución de problemas desde una perspectiva intercultural (Bernardi y Caldeira, 2012; Greer, 2013). Esto evidencia que, si bien existe la intención de fortalecer las matemáticas situadas, la interculturalidad desafía a las propuestas metodológicas. Al respecto, Greer (2013) y Pais (2011) concuerdan que las intervenciones en el aula intercultural suelen acabar perdiendo el objetivo situado, al valorar únicamente las matemáticas occidentales. Lo cual ha generado en las comunidades indígenas un rechazo absoluto a las nuevas propuestas, al considerarlas verdaderas “encomiendas” para invadir, conquistar y servirse del conocimiento cultural (Semali, Hristova y Owiny, 2015).
Este continuo intento de abordar la enseñanza de las matemáticas de forma situada en el aula intercultural ha dejado en evidencia diferentes barreras, tales como: a) políticas centradas solo en la promoción y rescate de la lengua indígena en el aula, sin la formación necesaria para los docentes y educadores tradicionales (Peña-Cortes, Huiliñir-Curío, Pincheira-Ulbrich, Quintriqueo, Quilaqueo, Gutiérrez y Morales, 2018). Lo cual se traduce en carencia de metodologías y estrategias didácticas para integrar el conocimiento y cultura de los pueblos indígenas y el occidental; b) predominio de un currículo occidental y monocultural (Mansilla Llancavi, Mieres y Montanares, 2016); c) falta de reconocimiento y participación de la comunidad y familia (Williamson, 2008), d) menoscabo de la integración de relatos orales y el conocimiento territorial; e) recursos didácticos o pedagógicos que subordinan los contenidos de los pueblos al currículo occidental (Peña-Cortes et al., 2018). Sin embargo, estas dificultades se convierten en oportunidades para los modelos de educación intercultural de integración paralela, los cuales comprenden el aula como un fenómeno de interacción entre dos espacios que se intersecan en un tercero (Aikenhead, 1997; Bhabha, 1994; Mpofu, Otulaja y Mushayikwa, 2014).
En este esfuerzo por comprender el fenómeno del aula intercultural, y aunque puede ser limitado por las posiciones y disposiciones de los autores y la complejidad del fenómeno (Wences, 2021), el modelo del tercer espacio afirma que las culturas que interactúan en el aula presentan elementos comunes (Bhabha, 1994). Aunque algunos más críticos, plantean que la intersección no es más que la interpretación de una misma realidad, pero desde diferentes culturas y marcos conceptuales (Aikenhead, 1997; Walsh, 2015). En este sentido, se reconoce la complejidad del sistema de conocimiento indígena como la comprensión local exclusiva de una cultura que se ha adquirido a través de la acumulación de experiencias y percepciones íntimas con el entorno. Este se ha perpetuado a través de prácticas desarrolladas por cada pueblo al interactuar con su medio natural, y desempaquetado en un conglomerado de subsistemas de conocimiento que va desde las ciencias, tecnología, religión, lenguaje, filosofía, matemática, política a sistemas duales como el socioeconómico (Ogunniyi, 2007).
Esta comprensión converge con las orientaciones sobre la exigencia de un diálogo descolonizador no jerarquizado y dominante, que reconoce la necesidad de una simetría de las culturas en el aula intercultural (Wences, 2021), y que va más allá de las políticas interculturales estandarizadas al servicio de las imposiciones neoliberales (Zuchel y Henríquez, 2020). Así, el modelo resultante comprende las limitaciones, alcances y la movilidad de la cultura para expresar las tecnologías dispuestas en las prácticas de los pueblos indígenas como el mapuche (Walsh, 2018), pero visualiza en ésta una forma de contribuir al desarrollo de las culturas indígenas dentro de las aulas de clases.
En educación matemática, uno de los modelos que sigue una orientación del tercer espacio es la Enseñanza de las Matemáticas Culturalmente Responsable definida por Bonner (2014), quien la describe como aquella que provee acceso a ideas matemáticas, mediante el conocimiento de la cultura y su identidad en cada comunidad. Esto implica, que las competencias profesionales del docente incorporen el conocer metodologías de aproximación a la comunidad y a su cultura, y metodologías didácticas para crear un tercer espacio justo dentro de sus procesos de enseñanza escolar (Mpofu et al., 2014).
Chile, reconocido como laboratorio neoliberal, ha establecido una serie de políticas educativas para la integración cultural en el aula (Zuchel y Henríquez, 2020). Sin embargo, éstas carecen de orientaciones que capaciten y entreguen herramientas al sistema escolar para construir una escuela intercultural. Lo cual ha invisibilizado la discriminación y reproduciendo de nociones hegemónicas de la cultura occidental, imposibilitando la condición de igualdad necesaria para sustentar un proyecto intercultural (Stefoni, Stang y Riedemann, 2016).
En esta misma línea, las propuestas en Educación Matemática han presentando movilización únicamente desde las traducciones al mapudungun del conocimiento matemático curricular escolar, sin cuestionar su pertenencia a la cultura del pueblo tanto local como temporal de la praxis de éstos (Huencho, Chandia, Rojas y Williamson, 2021). En la actualidad, la Educación Matemática de Chile carece de una política de formación inicial y continua de docentes y educadores tradicionales al alcance de un tercer espacio.
Así, esta investigación aborda la necesidad de generar un tercer espacio, tomando en cuenta el conocimiento y cultura del pueblo mapuche, específicamente el situado en la región rural de la Araucanía. Por tanto, el propósito es generar una propuesta de comprensión dispuesto en un modelo de integración cultural basado en la Enseñanza de las Matemáticas Culturalmente Responsable, que permita crear condiciones para fortalecer las capacidades de los docentes que están en contextos de interculturalidad con foco el diseño de tareas matemáticas. Con esto, la propuesta resultante no trata de homogeneizar las culturas que se encuentran en el aula intercultural, ni establecer una relación funcional, si no que reconoce la desigualdad existente y redistribuye el conocimiento en función de un Tercer Espacio justo para la comunidad escolar (Zuckel y Henríquez, 2020).
De esta forma, en el marco conceptual de este reporte de investigación se presentan los tópicos referidos a la Enseñanza Culturalmente Responsable, para luego adentrarse en la Educación Matemática bajo esta premisa. En la metodología, se describe las comunidades donde se llevó a cabo el estudio, las técnicas de recolección y análisis de los datos. En los resultados, se describen las dimensiones de análisis: Definición de una tarea matemática con responsabilidad cultural, Implementación de la tarea y Pertinencia situada. Por último, se encuentra el apartado de discusiones y conclusiones, donde se establece un modelo en consecuencia de la comprensión de los resultados del estudio.
2. Marco conceptual
Una perspectiva cultural de la enseñanza y aprendizaje de las matemáticas parte con reconocer que la clase de matemática está inserta en un cuerpo educativo y contexto educacional que forma las oportunidades de aprender de los estudiantes. Esta comprensión ha llevado a explicar, representar y comprender el proceso observado en diferentes niveles educativos y culturales en las últimas tres décadas ( Blömeke, Gustafsson y Shavelson, 2015; Brousseau, 2007; Shulman, 1987). Así, cada una de estas formas ha establecido aproximaciones de como se desarrolla la enseñanza y el aprendizaje en situaciones específicas para propósitos establecidos, es decir, han caracterizado un modelo explicativo de este (Borromeo y Lesh, 2013). Por tanto, cualquier forma de comprensión, como modelo, requiere de un marco conceptual para lograr establecer interpretaciones y representaciones del fenómeno observado. Marco que actúa como filtro para seleccionar, organizar, transformar o inferir patrones y regularidades bajo la superficie de lo que se quiere modelar (Lesh y Lehrer, 2003). De este modo, la perspectiva cultural e intercultural es modelable desde diferentes puntos de vista de los investigadores. Entre las diferentes aproximaciones, destacan aquellas que establecen un modelo desde perspectivas teóricas (Blömeke et al., 2015; Depaepe y König, 2018) y aquellas que lo establecen relacionando aspectos teóricos con empíricos de investigación (Shulman, 1987). Ejemplo de este último son los modelos de enseñanza culturalmente responsable (ECR).
2.1. Enseñanza Culturalmente Responsable
Operacionalizar la Enseñanza Culturalmente Responsable (ECR) implica el desarrollo de un perfil efectivo de enseñanza, que se contrapone al aula tradicional, donde es el profesor quién define lo que es central, apropiado y aceptable (Bishop, Berryman, Cavanagh y Teddy, 2009). La ECR va más allá de determinar qué y cómo se debe enseñar, ésta reconoce el rol que cumple la interacción social en el desarrollo cognitivo del estudiante (Boon y Lewthwaite, 2015).
El modelo de enseñanza bajo el enfoque ECR se constituye como un espacio donde los estudiantes y el conocimiento de su cultura es provocado e incorporado a la clase, aceptado y oficializado como objetivo de enseñanza, enmarcando procesos de gestión con sentido. De tal manera, el capital cultural de los estudiantes es el que proporciona la base del aprendizaje, el que se expande a nuevos campos de conocimiento a través de interacciones estructuradas con personas significativas del entorno (Bishop et al., 2009). La ECR se considera como un constructo multidimensional que toma en cuenta el contenido curricular, estrategias instruccionales, evaluación del logro y el clima de clase de un aula diversa culturalmente (Gay, 2010), considerando como base la idea de que la enseñanza y el aprendizaje son influenciados por la cultura del profesor, de la clase, de los estudiantes, de la escuela, y de la comunidad donde están insertas (Parker, Bartell y Novak, 2017). De este modo, Gay (2002) describe algunas prácticas observables en la ECR: Consciencia cultural crítica, donde el profesor es consciente de la cultura y del efecto que esta tiene en su conducta como profesional de la educación; clima de clase, donde se remueven los estereotipos y se crean condiciones de equilibrio y reconocimiento; comunidades de aprendizaje, donde se desarrolla un sentido de interdependencia, además de sentimientos de comunidad en la cual los estudiantes comprenden que sus vidas y destinos son cercanos, adquiriendo una obligación moral y política de responsabilidad de ayudar a sus pares a aprender; currículo Multicultural e instrucción culturalmente congruente, donde se apela a que el aprendizaje de los estudiantes mejora cuando el contenido es familiar, tiene alto interés para ellos, es desafiante, está directamente relacionado a su conocimiento prioritario y esta presentado en la forma de su modelo de aprendizaje de la cultura. De forma particular, la ECR se puede observar en cada uno de los actores del aula escolar, así como en el ambiente de aprendizaje.
2.2. Enseñanza de las Matemáticas Culturalmente Responsable
El reconocimiento de la ECR permitió a los investigadores Nasir, Hand y Taylor (2008) afirmar que el conocimiento matemático está inherentemente relacionado a las prácticas culturales, identificando tres niveles de vinculación: (a) el conocimiento de las matemáticas como actividad cultural (las estructuras y el discurso de las matemáticas cotidianas frente a las matemáticas escolares), (b) el aprendizaje de las matemáticas como una empresa cultural (las estructuras y el discurso del aula frente al hogar y la comunidad local de los estudiantes), y (c) el sistema de educación matemática como sistema cultural (acceso y posicionamiento en el campo de las matemáticas).
A partir de esto, Bonner (2014) define la Enseñanza Matemática Culturalmente Responsable (EMCR) como aquella que provee acceso a las ideas matemáticas mediante la cultura y su identidad. El autor plantea que entre las prácticas precursoras de EMCR se encuentran el establecer relaciones entre el profesor, los estudiantes, la comunidad y la familia, para obtener conocimiento de su cultura y así incorporar en las prácticas del aula el conocimiento de la cultura de forma pedagógica. Para adquirir este tipo de conocimiento, los profesores deberían constantemente conversar con los estudiantes sobre sus modos de vida, lenguaje, valores, creencias y conocimiento adquirido para luego integrarlo al conocimiento clásico y así evidenciarlos en sus prácticas.
De esta forma, propone 5 dimensiones para el modelo EMCR: a) comunicación, donde los profesores reconocen que ellos deben ser capaces de comunicarse con los estudiantes, para dar acceso a las matemáticas, b) reflexión y revisión cultural, donde el profesor continuamente evalúa sus prácticas y revisa la conexión que tiene con la cultura de los estudiantes y la comunidad donde está inserta la escuela, c) pedagogía y disciplina, donde el profesor evoca los elementos de su competencia profesional, d) empoderamiento del estudiante, donde el profesor provee de oportunidades para que el estudiante consolide su conocimiento e identidad cultural en la clase, y e) establecimiento de espacios para el desarrollo y mantención de la identidad racial y cultural.
Así, y dado que el diseño de la tarea matemática a implementar es la que concreta el propósito de la enseñanza (Chandía, Huencho, Rivas y Ortíz, 2018), la EMCR se alcanzaría al diseñar y ejecutar tareas matemáticas con responsabilidad cultural.
3. Metodología
Para el desarrollo de esta investigación se contempló una metodología cualitativa bajo el marco de los Ciclos de Investigación y Desarrollo (CID) (Goodchild, 2014) y el proceso de Investigación Acción Participativa (IAP) (Susman, 1983), en comunidades indígenas territorialmente circunscritas a tres escuelas primarias reconocidas por el estado chileno, lo cual se fundamenta en el hecho de que los métodos permiten hacer interactuar a las comunidades indígenas, la comunidad escolar e investigadores. En este sentido, el investigador actúa como pivote de situaciones y mediador para un proceso de integración paralela, así como recolectores de los elementos que debería tener el Tercer Espacio.
Participantes
En cada una de las tres escuelas participa su director, los profesores que realizan clases de matemáticas, los educadores tradicionales, todos los estudiantes y sus respectivas familias, quienes firmaron el consentimiento de participación, se describen en la Tabla I.
Tabla I Participantes por comunidad y escuela
| Escuela | Comunidad | Director | Docentes |
Educadores tradicionales |
Estudiantes | Familias |
| Botronhue | Lladquihue Norte, Labranza |
1 | 1 | 1 | 7 | 7 |
| San José | Lladquihue Sur, Labranza |
1 | 2 | 1 | 14 | 14 |
| Vega Larga | Peuman Mapu, Lautaro |
1 | 2 | 1 | 24 | 24 |
Fuente: elaboración propia
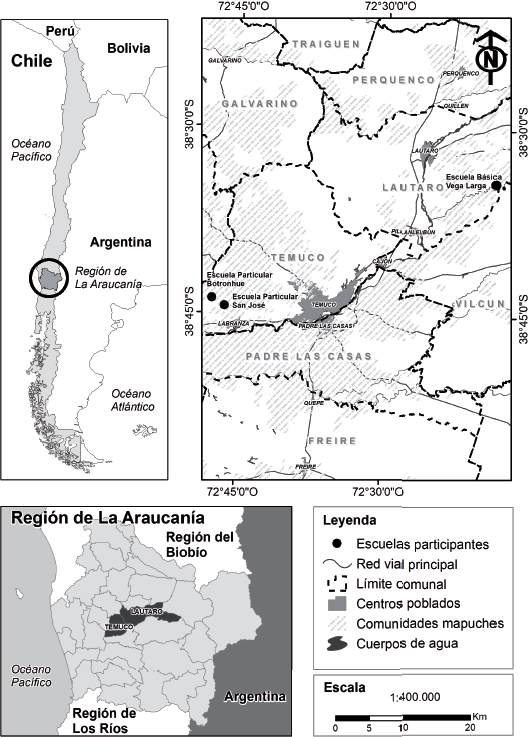
La disposición geográfica de las comunidades donde se encuentran las escuelas da variabilidad (Peña-Cortes et al., 2018) a los posibles elementos del Tercer Espacio (ver Figura 1).
Procedimiento
Con el objeto de identificar los elementos del Tercer Espacio, se hizo necesario hacer interactuar a representantes de la cultura escolar, directivos y docentes, y de la cultura mapuche, estudiantes, familia de los estudiantes y educadores tradicionales. Para facilitar la interacción, participa un investigador quién favorece el diálogo y el establecimiento de acuerdos. En cada sesión el investigador incita el diálogo entre las partes con preguntas orientadoras. Cada pregunta sitúa y hace reflexionar sobre algún aspecto de la cultura local, o bien, en aspectos de la cultura escolar para el diseño y ejecución de tareas. Producido el diálogo, se trata de determinar los elementos del Tercer Espacio mediante la regulación cultural de acción participativa, elemento ajustado de los procesos de IAP. Con esta estructura se ejecuta un total de 54 sesiones de entre 2 y 4 horas distribuidas en tres etapas considerando los CID como se visualiza en la Figura 2.
- La primera etapa constituye un primer ciclo de un CID y tiene como objetivo acercarse al proceso de matematización compartido a partir del significado construido por las comunidades mapuche y por las escuelas, donde teorías locales (conocimiento construido por las comunidades) y globales (marco teórico del investigador y la cultura establecida por la escuela) se complementan para definir necesidades y demandas al proceso educativo de las matemáticas, y así construir una propuesta didáctica que los solvente.
- La segunda etapa corresponde a un ciclo de desarrollo del CID, donde la teoría se transforma por medio de la reflexión sobre los objetos de aprendizaje y el análisis epistemológico de las matemáticas locales y escolares, y se generan planes de acción a implementar. Entonces, de forma colaborativa, se implementa con los estudiantes una unidad didáctica en colaboración con sus familias. Posteriormente, se realiza una revisión y reflexión crítica del proceso para contrastar y fortalecer el modelo con un nuevo ciclo de desarrollo, lo que implica enfrentar la primera hipótesis del modelo teórico con el desarrollo de ésta y así construir una mejorada, es decir, un modelo con sustento práctico.
- La tercera etapa corresponde a un nuevo ciclo de investigación del CID con el objeto de valorar el modelo elaborado desde los ciclos de investigación y desarrollo anteriores. El objetivo de esta etapa es evaluar cómo los productos obtenidos en la etapa de investigación y desarrollo se consideran un aporte al contexto educativo y social. Esta tercera etapa da sentido al criterio de validez científico para investigaciones cualitativas desarrolladas en entornos de comunidades específicas, donde la comunidad debe configurarse como árbitro de calidad del proyecto.
Recolección y análisis de datos
Desde el planteamiento de las preguntas orientadoras hasta el establecimiento de acuerdos, se reflejan las etapas de visualización, reflexión y acción de la IAP. Así, en cada sesión y de forma colaborativa se determinan a) los focos a visibilizar en el contexto propuesto, preguntas que guían cada sesión, necesidades entre los sujetos y la interacción y negociación de demandas; b) se generan reflexiones por medio de la interacción dialógica que permite saturación de ideas; y c) se establecen acciones, como acuerdos o desacuerdos resultantes del diálogo establecido. Esto permite recolectar los datos y analizarlos en las mismas sesiones entre todos los miembros representantes de ambas culturas.
4. Resultados
4.1. Definición de una Tarea Matemática con Responsabilidad Cultural (TMRC)
Para definir una TMRC pertinente a las necesidades del territorio se establece una primera Etapa de Investigación del Ciclo de Goodchild (2014), con el objeto de construir un prototipo que las aborde. Así, se desarrollan dos grupos de acciones denominadas “Organizando una TMRC” y “Co-construcción de la TMRC: Prototipo y modelación”.
4.1.1. Organizando una TMRC
Las cuatro sesiones de Organización desarrolladas en cada una de las tres comunidades establecen un conjunto de necesidades que responden al ámbito local y global en el área académica de la educación matemática. El primer conjunto de necesidades hace referencia al nulo impacto que el aprendizaje de las matemáticas evidencia en el cotidiano de las actividades locales. Se explicita la distancia entre lo que se aprende en la escuela y las relaciones lógicas, tangibles y cotidianas que se realizan habitualmente en la comunidad, lo que se sustenta desde las apreciaciones dadas por los adultos de la comunidad:
“Le digo que me corte un pedazo de madera que mida lo mismo que este coligue (madera) y él utiliza una huincha, mide el coligue y luego con la huincha pone la medida en el palo y en todo eso le queda más largo o más corto (…), no pueden resolver situaciones del día, se les debe dar la instrucción completa de lo que uno quiere que haga y cómo quiere que lo haga y como nunca están con nosotros, viendo lo que hacemos, no saben cómo hacer.” (CM222)
Otra necesidad es la contribución de la asignatura lengua indígena3, con foco en la lengua y cultura territorial, a las otras asignaturas de currículo, incluida la educación matemática.
“No tenemos orientaciones para enseñar nuestra matemática (desde lo curricular). A lo más unas páginas donde se tratan los números en mapudungun (lengua mapuche) para aprender de memoria, es más vocabulario que otra cosa. (…) somos una isla, no conectamos ni tributamos a otra asignatura” (ET3)
En el mismo sentido, los docentes no visualizan el efecto de los recursos, metodologías y estrategias tradicionales de la enseñanza de las matemáticas en el aprendizaje de los estudiantes. Advierten que los esfuerzos desplegados no han movilizado el aprendizaje ni el gusto por la asignatura.
“Nosotros tenemos recursos manipulativos para los estudiantes, usamos bloques, (…), autitos de diferentes colores (…) les decimos, si José tienen 4 autitos azules y Valeria tiene 3 autitos verdes, ¿cuántos autitos más tiene José?, y no hay caso, ellos suman todo, la palabra más (de la pregunta) los confunde, le hacemos la pregunta tal como viene en el libro, donde se muestran dibujados los autitos, cambiamos a bloques de color, autitos de juguete y nada…, no sabemos qué más hacer (…). luego viene SIMCE4 y salimos mal.” (PM1)
Dada la sistematización del proceso etnográfico previo al diseño de una TMRC, y su sociabilización en la comunidad escolar, se observa que el pueblo mapuche posee conocimiento matemático implícito en sus actividades cotidianas y metodologías de enseñanza, las cuales podrían ser tratadas como actividades escolares. También acuerdan que este tipo de prácticas contribuiría al logro de los aprendizajes matemáticos escolares junto con fortalecer el conocimiento local y la identidad del educando.
“El püron (nudo en lana) para registrar la edad de las personas (…) la luz y las estrellas nos determinan etapas del año y del tiempo dentro del día (…). El mapuche debe propiciar el rakizuam (desarrollo del conocimiento, resolver un problema) en el aprendiz, no sólo que copie y repita, sino que pueda apropiarse del concepto y su proceso y lo ponga a prueba y generar algo propio, nuevo, (pausa en silencio) así lo hacia la familia antes.” (CM50)
Finalmente, las escuelas están dispuestas a generar estrategias educativas en matemáticas con RC siempre que se cumplan ciertas condiciones, como el acceso a información clave en la materia; recursos y medios para su enseñanza; apoyo desde la familia frente a las producciones escolares que fortalezcan y mantengan la pertinencia dentro de la lógica cultural situada; y gestionar un ambiente de aprendizaje recíproco.
4.1.2. Co-construcción de la TMRC: Prototipo y modelación
En siete sesiones de trabajo en cada establecimiento, se elaboró un prototipo de unidad didáctica en Matemáticas con Responsabilidad Cultural, que contempla una tarea matemática y su forma de enseñanza. Desde las sesiones emerge la riqueza de la enseñanza por proyectos desarrollados de forma colaborativa, donde la diversidad de habilidades dadas por los roles de cada integrante permite enriquecer las estrategias y alcanzar la meta establecida, tal como lo plantea un Educador Tradicional:
“El mapuche, antes, hacia todo en comunidad, el territorio era importante, nada se hacía de forma individual y cada participante era reconocido por su conocimiento o habilidad en la tarea o por ser un apoyo, cualquier cosa era importante y se reconocía por igual…” (ET1).
De esta manera, los ET y profesores de matemáticas decidieron escoger una actividad cultural situada desarrollada con un artefacto matemático propio. Para esto, lo primero fue identificar las matemáticas que involucran conexiones con el conocimiento de la comunidad local, determinando artefactos matemáticos culturales (AMC) que se impregnan de procesos matemáticos con sentido en la vida cotidiana. Luego, se establece un propósito para favorecer las oportunidades de alcanzar la comprensión y el desarrollo de esta matemática con apoyo del conocimiento curricular a través del AMC.
“El püron es pura matemática, es nuestra forma de escribir los números, por lo que puede ser más fácil conectarlo con la lengua mapuche y la asignatura de matemática. Es una forma que ya no se suele ver entre nuestra gente y necesitamos darle uso para el hoy, que sea importante hoy.” (ET1)
Así, el proyecto educativo se planeó en base a caracterizar el entorno escolar por medio de un sistema de registro numérico a través del püron, donde el conocimiento matemático presente en el AMC se establece como una variable mediadora entre el conocimiento cultural y el conocimiento curricular.
Con el objetivo de enseñanza planteado y el artefacto matemático cultural explícito en él, se determinan actividades, preguntas orientadoras, tiempo, lugar y forma en que el proceso de enseñanza se desplegará en concordancia con las demandas que el AMC requiera para su desarrollo. El marco que determina la tarea tiene relación con generar oportunidades de alcanzar el rakizuam pero considerando los elementos curriculares, evidenciando una interacción dialógica entre comunidad y escuela.
ET2: el territorio ya lo dijo, la gente dijo que la forma es el rakizuam.
PM2: si, y me parece bien, pero ¿cómo lo hacemos?
ET2: deben participar todos los niños (1ro a 6to básico) en algo común, que tenga sentido para ellos. Yo me acuerdo que antes si había que construir una ruka, todo el territorio se reunía a construirla, todos apoyaban, no se construía nada de forma individual. (…) obvio que las cosas se complican y se deben resolver situaciones y eso se resuelve con más de una cabeza pensando.
(pausa de silencio)
ET2: entonces, todos los estudiantes de 1ro a 6to básico deberían trabajar bajo un mismo objetivo y sus productos debieran servir para un producto mayor, uno como colegio.
PM2: me parece bien (sonriendo), pero cómo generamos que creen, que creen (repite para enfatizar) nuevo conocimiento desde el püron.
INV: ¿Qué registros son los que reconocemos en el püron? y ¿Cuáles parecen no tener solución a simple vista?
ET2: sabemos números chicos, yo no recuerdo nada que supere el 10
PM2: pero si el nudo es para registrar los números del mapuche y podemos decir números más grandes que 10 éstos se pueden registrar con nudos también ¿o no?
ET2: yo creo que sí, porque si se usaba para contar animales y antes el mapuche tenía muchos animales, así que se debiera poder, pero no sé cómo.
De la interacción, se establece la metodología, la estrategia y las actividades de enseñanza. La metodología se basará en proyectos. El inicio del proyecto se gestiona desde el educador tradicional quien ubica el artefacto dentro del pueblo respondiendo a quién, para qué y cómo lo usa/usaba, desde la manipulación del artefacto y el relato de historias. El desarrollo del proyecto se articula desde el profesor de matemáticas que establece demandas con objeto de replicar y reconstruir un elemento matemático dentro del margen operacional del artefacto. El cierre del proyecto se articula en colaboración entre el profesor y el educador tradicional con objeto de provocar la comunicación y argumentación matemática del estudiante en torno a los productos alcanzados y su uso en la comunidad local.
“Dado que el foco es que ellos construyan algo que nosotros no les hemos dicho como es o cómo puede ser, necesitamos pensar en las posibles soluciones que consideraremos correctas dentro de la lógica mapuche (…) por varias razones, entre ellas que la familia será un validador de las estrategias que el estudiante establezca (…) necesitamos saber si la proyección matemática que estamos pensando es adecuada para los parámetros de uso, (…) es vital el apoyo de nuestro educador tradicional.” (PM3)
Establecidas las condiciones del proyecto, se generan estrategias de interacción entre el docente, los estudiantes y sus familias, de manera que promueva la negociación de significados, el aprovechamiento del error y el pensar desde la lengua. La interacción se gestiona desde un set de interrogantes que simplifican o amplifican la demanda con el fin de poner a prueba la argumentación lógica matemática detrás del producto establecido y orquestar la generalización de procesos.
Aunque la interacción permitió definir de forma proyectiva toda la clase, los docentes presentaron dudas de su propia gestión, “Tenemos todo lo necesario para desarrollar nuestras clases, tanto en el rol del educador tradicional, como el mío (profesor de matemática), pero no sé cómo actuar en la clase…” (PM1). Ante esto, la investigadora realiza una modelación de la totalidad de los procesos establecidos en la etapa de co-construcción, permitiendo conocer la trayectoria de producción de las respuesta que se esperan alcanzar; regular el nivel de desafío cognitivo de las demandas establecidas y de las que emergen producto de las contingencias del proceso; enriquecer conceptos matemáticos de la comunidad local usando el purön como medio; confirmar el alcance de los objetivos educativos planteados; evaluar el alcance del artefacto matemático cultural y su efecto en el aprendizaje.
4.2. Implementación de una TMRC
Una segunda Etapa denominada Desarrollo dentro del Ciclo de Goodchild (2014), pone en práctica el prototipo de TMRC diseñado. Así, se crean dos grupos de acciones denominadas “Aplicación y valoración de una TMRC” y “Artefacto y modelo de la TMRC”.
4.2.1. Aplicación y valoración de una TMRC
El proceso práctico de la etapa de desarrollo se realiza en cuatro sesiones de aplicación en aula y cuatro sesiones de valoración desde el contexto familiar en el hogar. Este proceso mostró un amplio entusiasmo e interés por el artefacto matemático situado en una práctica cotidiana antigua de gran valor histórico y social.
La clave de los productos alcanzados por los estudiantes se sustenta en la observación y escucha de relatos que posicionan al artefacto en un punto clave y mediático dentro del pueblo. La recreación y análisis de la situación, posicionan al AMC en demandas matemáticas complejas que impregna al grupo de estudiantes en un ambiente que desafía y motiva su actuar.
Así, el desarrollo del conocimiento matemático se orquesta desde la oportunidad de construir conocimiento dentro de una lógica estructural con sentido local, reconociendo los límites y alcances de las matemáticas con el artefacto. De esta manera, la construcción se desenvuelve en un ambiente de monitoreo constante, debido a la diversidad de caminos y productos que los estudiantes pueden escoger para resolver el desafío planteado. Por ejemplo, luego de solicitar el registro de la edad de una persona mayor en su hogar, se produce la siguiente interacción:
ET2: Amulen, ¿me enseñas lo que has registrado?
E6: (acción de entregar una lana con nudos)
ET2: Dame información que me permita leer tú registro
E6: tiene püron (nudo) grandes y simples, los grandes valen 10 y los simples 1
ET2: muy bien, entonces acá tenemos mari (10), epu mari (20), küla mari (30), (…) pura mari kiñe (91), pura mari epu (92), pura mari küla (93), (tocando cada nudo mientras realizaba el conteo) ¿es correcto?
E6: Sí.
ET2: la edad de quién es
E6: de mi abuelo José
ET2: ah, muy bien. ¿porqué tiene estos nudos aquí? (refiriéndose a nudos simple entre los nudos grueso)
E6: Me falto lana y allí me quedaba un espacio vacío.
ET2: Entiendo, muy bien hecho.
PEM2: Amulen, ¿influye en algo que los nudos se mezclen, gruesos con simple en la lana?
E6: no, no influye.
El docente se anticipa a dos trayectos posibles: extraviar el objetivo de la demanda, o responder dentro de un proceso carente de lógica matemática. Para el docente, la primera situación comprende advertir y tratar, reinterpretando la demanda original; en cambio, en la segunda situación comprende entender hasta qué punto la toma de decisiones es coherente y planteando desafíos que los ayude a re-pensar la decisión tomada.
Por último, se gestionaron espacios de vinculación con el conocimiento familiar, recreándoles los productos generados, solicitándoles otras técnicas para una misma demanda, u otras demandas donde el artefacto tiene sentido. Los resultados muestran complicaciones por desconocimiento y desuso del artefacto, lo que llevó a las familias a reconocer entre ellas a las más conocedoras, para establecer vínculos, comunicarse y enriquecer el conocimiento local. Los abuelos tuvieron un mayor acercamiento a la práctica, validando la información que sustenta el artefacto y nutriendo a los estudiantes con nuevas historias familiares-locales asociadas. Por ejemplo, el padre de uno de los estudiantes indicó lo siguiente:
“Mi abuelita era partera y yo sé que ella usaba una lana con nudos y con eso ella guiaba el tema del embarazo, la fecha de nacimiento, y permitía preparar la fecha de parto.” (AM8)
4.2.2. Artefacto y modelo de la TMRC
Los Educadores Tradicionales coinciden en la satisfacción de promover un conocimiento que aporte a actividades de otras asignaturas, lo que otorga valor a su conocimiento y desempeño en el contexto escolar: “cuando iba a pensar que me iban a pedir apoyo para las matemáticas, me siento importante, se valora nuestro conocimiento” (ET2). Por su parte, el profesor de matemáticas reflexiona sobre el impacto del artefacto y las demandas planificadas para su desarrollo, el razonamiento matemático de los estudiantes, los procedimientos lógicos, la argumentación sobre la heurística, y las contingencias consideradas para resolver las diferentes problemáticas: “todo lo que pueden construir a partir de nudos y las formas en que argumentan sus productos los obliga siempre a moverse de su estatus de confort, debido a las tareas que les damos (…) solo apoyamos su proceso” (PM1). Concluyen con la idea que esta forma de hacer matemática moviliza al estudiante a esferas donde pone a prueba su conocimiento y su labor se centra en apoyar la continuidad del objetivo de trabajo planeado.
En cuanto a la percepción de las familias, en un inicio se cuestionaba el tratamiento de artefactos mapuche para enseñar matemáticas, aludiendo a que en clases se deben enseñar las matemática winca (no mapuche) “porqué les están enseñando eso, yo quiero que aprenda que el winca aprende” (AM12). Sin embargo, luego de la aplicación del diseño vinculado a los hogares de los estudiantes, su percepción se tornó positiva para los objetivos educativos planteados.
El equipo de trabajo acuerda que la TMRC propuesta, es una fuente innegable de aprendizaje matemático que potencia los resultados favorables en pruebas estandarizadas nacionales, dado el fortalecimiento del razonamiento matemático desplegado. Sin embargo, advierten la necesidad de focalizar la TM dentro del formato lineal y parcelado del conocimiento dispuesto en el currículo escolar.
4.3. Pertinencia situada de la TMRC
Continuando con el ciclo, se despliega una nueva etapa de Investigación que se sustenta en las acciones generadas en el ciclo de desarrollo. Esta denominada Etapa 3 propone organizar un proceso coherente de exposición de la metodología de co-construcción, el método de enseñanza y los productos creados por los estudiantes dada la TMRC, para posibilitar el intercambio de opiniones, sugerencias y aportes de la comunidad local.
4.3.1. Análisis de pertinencia situada de una TMRC
Para desarrollar el intercambio de sugerencias desde la comunidad local, se planea el ilustrar secciones vivenciadas en el aula, expuestas por la comunidad escolar, en un ambiente natural para el pueblo mapuche como es la ruka (casa mapuche).
Iniciado el encuentro y en relación del AMC, la comunidad expresó gran interés en la representación utilizada para pequeñas cantidades “¡así lo usaba mi mamá! (…) hasta para enseñarme a tejer a telar, me dejaba nudos para saber cuántas hebras de cada color me faltaban” (CM40), frente a la exposición de lanas donde cada nudo representaba una unidad; para grandes cantidades, en cambio, surgieron dudas sobre el registro, siendo los estudiantes quienes debieron transmitir la forma de decodificar un número dentro de la unidad de mil. Los miembros de la comunidad se prestaron atentos, escuchando y replicando la manipulación del artefacto, expresando el desuso del artefacto dada la capacidad de registrar números en símbolos arábicos. Expresan que comprenden la lógica del código presentado, su coherencia lingüística con la lengua mapuche, la proyección que posee dentro del sistema numérico del pueblo y el sentido de lo que expresa, “nosotros ya no lo usamos, (…) los nudos están ordenados de la misma forma en que los decimos en mapudungun, (…) sirve para números más grandes aun” (CM2).
Las interacciones orales argumentativas sobre el AMC y el error en el constructo de nuevos contextos de uso, exige una labor docente centrada en guiar, movilizar las formas de razonar y promover múltiples respuestas acertadas. Los docentes explicitan la capacidad de elaborar argumentos sustentados en razonamiento lógico matemático: “los niños pueden argumentar, hablar de producciones matemáticas, de razonamiento lógico, y lograron amplificar y generalizar en función de las tareas planeadas” (M2). Lo anterior, es evaluado dentro de las normas que posibilitan al estudiante vivenciar el rakizuam del pueblo. Así, la familia mapuche valora el diálogo entre el conocimiento conceptual y procedimental local con el escolar: “esto es lo que queremos, no sólo lo mapuche, queremos que aprendan la matemática del mapuche y del winca (persona no mapuche). Que se potencien.” (AM5).
Se valora la metodología de trabajo desarrollada desde lo local, su conocimiento ancestral y las formas en que se transmite para enriquecer la enseñanza académica. El educador tradicional y su labor dentro del proyecto, genera tranquilidad y cercanía dentro de la comunidad local, lo cual fortalece su posición al interior de la comunidad escolar. Destaca el compartir y opinar sobre los productos que se generan utilizando el conocimiento local al interior de la escuela,
“Esto es bueno, lo que hicieron en clase es bueno, que ahora nos muestren lo realizado nos ayuda a fortalecer lo que ya casi hemos olvidado. Es importante que nuestros niños, nos ayuden a no olvidar.” (CM7)
“Esto de contarles a todos mi historia, la que antes le conté sobre los nudos y cómo me enseñaron a mi, me llena de orgullo, me siento reconocido.” (CM10)
Finalmente, se concuerda que la forma de sustentar cada decisión del proyecto basado en las historias de vida de la comunidad mapuche de hoy y ayer, le otorga valor a su conocimiento y fortalece la identidad de los participantes de la sesión.
5. Discusión y Conclusiones
Las implicancias de los resultados que emergen del diseño, aplicación y valoración de una TMRC, fueron estableciendo una serie de hitos, secuencias y conexiones que determinan el modelo que define y sustenta una TMRC como el principal componente del Tercer Espacio. Al interactuar comunidades locales y escolares, se encuentran sus culturas en un proceso de Investigación Acción Participativa, logrando con ello una integración paralela no dominante (Mpofu, et al., 2014). Luego, y para avanzar en la construcción, los ciclos de investigación y desarrollo, permiten la reflexión y la práctica en el diseño y ejecución de las TMRC (Goodchild, 2014). Esta metodología de diálogo, moviliza el conocimiento matemático hacia un producto de trascendencia temporal y social que construye una visión multicultural de su misma realidad, enriqueciendo ambas culturas y creando elementos de intersección (Bhabha, 1994; Wences, 2021).
Como parte de la intersección, el modelo centra su interés en el actuar del docente en su interacción constante con el contexto sociocultural que lo rodea, lo cual se evidencia en la fase de Organización y Co-construcción de la TMRC. Aquí, las necesidades/demandas del contexto y la generación de propuestas de actividades matemáticas situadas, permiten movilizar el conocimiento local hacia demandas locales y globales. Además, la participación de la comunidad local indígena facilita la caracterización del modelo de aula, dada la recreación tradicional e histórica de las formas de enseñanza del conocimiento en sus familias (Peña-Cortes et al., 2018). Ahora bien, pese a la valoración dada por la comunidad en el reconocimiento de su cultura, éstas validan la imposición histórica de un currículo monocultural, que les otorga una proyección social y económica, por lo que reconocen la influencia positiva que tiene en las trayectorias de vida de sus hijos e hijas (Mansilla et al., 2016).
En este sentido, el diseño y la ejecución de la TMRC cumple un rol formador de los actores de ambas culturas, dada la interacción de las mismas en cada una de las instancias de trabajo, respondiendo a una de las principales dificultades que enfrenta el aula multicultural (Peña-Cortes et al., 2018; Semali et al., 2015). Así mismo, tales instancias permiten crear un currículo que comprende un conocimiento desde una perspectiva multicultural (Williamson, 2008), impidiendo el dominio de alguna mediante la co-construcción de los objetivos matemáticos culturales y el diseño de las TMRC.
De esta manera, se establece un modelo (Ver Figura 3) que inicia con el reconocimiento de Prácticas Socioculturales (PS) con matemáticas intrínsecas en ellas, aquí es fundamental comprender la lógica de la praxis con un sentido matemático, dado que guiará las demandas conceptuales o procedimentales de un objeto denominado “Artefacto Matemático Cultural (AMC)” de aspecto tangible y/o conceptual, donde se involucran las matemáticas desde las visiones académicas escolares y socioculturales (Cantoral, Montiel y Reyes-Gasperini, 2015). Así, la necesidad de acudir a los insumos matemáticos propios del currículo escolar dependerá del conocimiento local que posea quien diseña las tareas matemáticas. Esto plantea un desafío, ya que en cuanto mayor sea la distancia respecto del conocimiento cultural local que tenga quién diseña, más requerirá del apoyo de un asesor cultural, de metodologías para el acceso a este conocimiento, y/o la creación de comunidades que se integran por actores representantes de ambas culturas y el establecimiento de diálogos en base a propósitos pertinentes y comunes (Zuchel y Henríquez, 2020). Esto permite comprender la lógica matemática de la PS y el AMC emergente, como primer elemento del Tercer Espacio, columna central del modelo.
El ciclo continúa relacionando el AMC con las matemáticas escolar, para posicionarla dentro de niveles educativos, ejes temáticos, contenidos específicos, y/o objetivos de enseñanza acordes a su estructura conceptual y procedimental. Esto facilita su desarrollo y proyección a nivel de aula. Llegado a este punto, se debe considerar el riesgo de visualizar el AMC solamente para el beneficio del currículo escolar, por lo que es fundamental acudir al conocimiento práctico que condiciona la acción de él, para así establecer un objetivo conceptual y/o procedimental pertinente a las lógicas matemáticas propias, territoriales y temporales. Aquí nace el segundo componente del Tercer Espacio, el Objetivo de Aprendizaje Matemático Cultural (OApMC), compuesto por un contenido y una acción que responde a los requerimientos escolares y locales integrando los objetivos de aprendizajes propios del currículo dentro de una forma de proceder y razonar local.
Al diseñar un OApMC pueden ocurrir dos eventos diferentes, que la acción de la PS coincida con la solicitud curricular, o que se diferencien. En el primer caso se fortalece el conocimiento local y escolar. El segundo caso responde a una necesidad local, su conexión curricular se centra en habilidades matemáticas y/o en contenido desde formas lógicas locales, lo que permite tratar el conocimiento curricular nutriendo de significado lo conceptual y re-valorando lo local y por ende, enriqueciendo el contenido de manera multicultural (Aikenhead, 1997; Wences, 2021; Zuchel y Henríquez, 2020). En ambos casos se tratan las lógicas de razonamiento matemático locales, se actualizan los métodos de enseñanza y los contenidos matemáticos específicos escolares, tal como se desarrolló con la construcción de un código de representación numérica a través de nudos, püron, y su conexión con el sistema numérico mapuche.
Con el OApMC y el AMC explícito en él, se procede a configurar un posible set de actividades para los estudiantes que propicien el logro del objetivo planteado. Para ello se acude a las disposiciones inherentes a la Didáctica de las Matemáticas y a cada una de las dimensiones que determinan la construcción de una actividad. Como teorías de aprendizaje, demandas cognitivas, procesos instruccionales y gestión, modelos de interacción, recursos didácticos, etc., que proporcionan un marco de opciones de instrucción que condicionan los tipos de actividad y el conocimiento como Objeto de Enseñanza local (Huencho, Rojas y Webb, 2017). De lo anterior, se definen las Actividades Matemáticas Culturales (AcMC), como aquellas centradas en la enseñanza de la práctica sociocultural enfocada en el AMC, desde donde se configura un set de demandas que movilizan los diversas conceptos y propiedades inherentes al artefacto, determinando así, el tercer elemento del Tercer Espacio.
Definida la AcMC se procede a determinar cómo se gestionará el proceso de enseñanza. Se consideran las Disposiciones Instruccionales propias de los docentes y los contratos didácticos del aula escolar (Brousseau, 2007), proponiendo un margen de elementos a los que se accede. Además, se requiere de las Disposición de la práctica de la enseñanza sociocultural para definir cuál es la gestión de la AcMC y así responder a las lógicas del AMC, la práctica sociocultural y la comunidad escolar. Esto determina el último componente del Tercer Espacio para el modelo de diseño de TMRC, la Gestión de la Actividad Matemática Cultural (GAcMC). Esta determina la organización general del tiempo, espacio, lugar y estrategias de interacción entre el docente, los estudiantes y sus familias, para promover la negociación de significados, el aprovechamiento del error y la promoción del pensamiento a través de la lengua indígena. La GAcMC modifica la disposición instruccional habitual del docente y de su clase, actualizando las formas de enseñanza tradicionales dentro de la clase. Los contratos didácticos tendrán presencia con un foco integrador, validado por un asesor cultural, la familia y su interacción con la AcMC.
Estos cuatro elementos constituyen el Tercer Espacio para el diseño de TMRC, construidos por el diálogo de representantes de cada cultura en un proceso sistemático de interacción con el objeto de determinarlos en una integración paralela, no dominante. De esta manera, se responde a las principales dificultades que han presentado quienes han tratado de abordar el aula intercultural, mostrando una alternativa viable para la enseñanza de las matemáticas, y porque no decir, para otras disciplinas, siendo ineludible comprender las múltiples visiones de un mismo conocimiento por pueblos con trayectorias disimiles.
Finalmente queremos declarar que tal como todos los esfuerzos de comprensión de la interculturalidad, este modelo está fuertemente anclado al acceso a las comunidades indígenas, y a su disposición para interactuar con la comunidad escolar, además de tener como base conceptual la aproximación no paralela del Tercer Espacio bajo el concepto de Responsabilidad Cultural en Educación Matemática, lo cual puede restringir y posiblemente dejar de considerar variables, que en función de otros marcos o comunidades pueden ser viables o factibles de analizar e incorporar al modelo.











 nueva página del texto (beta)
nueva página del texto (beta)