INTRODUCCIÓN
El conocimiento se genera a partir de un proceso de transformación de la información (Ramírez & García, 2018), y su representación es esencial en el progreso del ser humano. Existen diferentes técnicas para representar el conocimiento (Han & Ellis, 2020; Lei et al., 2019; Lu et al., 2020; Wang et al., 2019; Yang et al., 2020; Zhang et al., 2020) y una de ellas está atrayendo a los investigadores del ámbito de la educación, la comunicación y de la industria: el grafo de conocimiento (GC) (Li et al., 2019; Mosquera & Piedra, 2018; Yoo & Jeong, 2020; Yu et al., 2017; Zárate et al., 2019; Zhao et al., 2019).
En los últimos años, el GC ha recibido mayor atención en el ámbito educativo (Cope et al., 2020; He et al., 2019; Wang, Ding & Yu, 2019), debido a que se requiere descubrir, medir o compartir el conocimiento de los estudiantes en cada área disciplinar (AD) (Shi et al., 2020). En este sentido, el GC provee una estructura matemática robusta para representar el conocimiento de cualquier AD, por ejemplo, matemáticas, física, química, contaduría, entre otras.
Un AD se compone de gran cantidad de temas que están interrelacionados con base en su complejidad. De acuerdo con el número de temas dominados es posible determinar el grado de conocimiento de un estudiante. Aunque se han hecho esfuerzos por representar el conocimiento de distintas formas (Ivinson, 2020; Paulius & Sun, 2019; Puustinen & Khawaja, 2020), en la actualidad es aún una tarea desafiante que exige procesos y métodos innovadores (Bloodgood, 2019; Guan et al., 2019; Long et al., 2020) para evitar la evaluación exhustiva y procurar la precisión.
Por lo tanto, el conocimiento pueden representarse mediante colecciones interrelacionadas de temas en un ámbito determinado. En este sentido, el GC establece relaciones causales entre los temas previos y posteriores de un AD (Rantanen, Hyttinen & Järvisalo, 2020; Shin & Jeong, 2021). Así, la no evaluación exhaustiva se justifica al evitar la evaluación de todos los temas de un AD; es decir, al suponer tres temas interrelacionados por su complejidad A>B>C, si al evaluar el tema B se determina 100% de dominio, entonces se asume que el tema A es dominado totalmente, lo que determinaría también parte del conocimiento que se tiene del tema C.
En el presente artículo mostramos los avances iniciales sobre el diseño de un método que clasifica y pondera los nodos (temas) de un GC en un AD. El método tiene dos enfoques: evitar la evaluación exhaustiva de los nodos y examinar los nodos con precisión adecuada. El método se compone de tres fases que se fundamentan en reglas, las cuales determinan los lineamientos para clasificar y ponderar un nodo de forma objetiva mediante la evidencia proporcionada por el estudiante sobre el dominio de un tema en particular. Después, el grafo es actualizado de forma subjetiva, primero descendente y en seguida ascendente, a partir del efecto causal del nodo antes indicado. Por último, las tres fases son iteradas hasta que el GC es obtenido.
A manera de ilustración, se presenta un estudio de caso que muestra cómo el método propuesto permite obtener un GC del AD de matemáticas. En cada fase del método se considera el enfoque que evita la evaluación exhaustiva de los múltiples temas (nodos) del AD y procura la precisión en la ponderación de los nodos.
El artículo está organizado de la siguiente manera: después de la introducción, se presenta la revisión de la literatura; posteriormente, se indica la metodología que sustenta el diseño del método propuesto. También se muestran los resultados del estudio de caso y, finalmente, las discusiones y conclusiones.
REVISIÓN DE LA LITERATURA
Hay gran cantidad de investigaciones que aplican el GC para representar el conocimiento (Bellomarini et al., 2020; Jia et al., 2017; Krenn & Zeilinger, 2020; Lin et al., 2017; Zhu et al., 2019). La estructura del GC facilita la utilización de ponderaciones que permiten obtener nuevo conocimiento y conclusiones de datos existentes (Chen et al., 2020; Li & Madden, 2019; Wang et al., 2019). Los nodos del GC representan entidades o temas relevantes de un dominio y los bordes (flechas) determinan dependencias, prerrequisitos, relaciones y frecuencia de coocurrencia entre los nodos.
La mayoría de las aplicaciones de GC se enfocan a la extracción de asociaciones de entidades, como is-a y part-of (Seo et al., 2020; Wang et al., 2019). En contraste, otros estudios consideran como base las diferencias del dominio de los estudiantes para representar, en un GC, las relaciones de prerrequisitos entre los puntos de conocimiento y la recomendación de ejercicios (Lv et al., 2018; Meneses et al., 2020); sin embargo, ellos solo proponen un método que examina los nodos del GC basados en el comportamiento de datos de un estudiante, colectados mediante un sistema de evaluación, pero no utilizan la evidencia proporcionada por el estudiante sobre el dominio de un AD para evitar la exhaustividad en la evaluación.
Oramas et al. (2017) y Qiao y Hu (2020) propusieron un método que enriquece la descripción de los nodos en un GC con información semántica. Emplearon dos enfoques diferentes para codificar la información del GC dentro de una representación lineal de las características. Liang et al. (2018) destacan el diseño de un esquema de entidad relación para modelar asociaciones y propiedades de diferentes objetos. A partir del esquema se genera el GC, cuya estructura facilita el aprendizaje en el área del diseño de interiores mediante la ponderación de sus nodos.
Chen et al. (2018) proponen un sistema que construye un GC de forma automática en el contexto educativo, combina fuentes de datos heterogéneas para obtener conceptos instruccionales (nodos) e infiere relaciones entre los nodos. Wang et al. (2018) representan el conocimiento del AD de geociencias mediante un GC, donde los nodos simbolizan palabras de contenido y la frecuencia de coocurrencia se muestra como borde. En ambos casos, se propone un método compuesto de fases para representar el conocimiento mediante un GC de un AD; cada nodo es etiquetado y ponderado de acuerdo con su influencia entre los temas relevantes. Ninguno de ellos clasifica los nodos para evitar su evaluación exhaustiva como en el caso de Liu et al. (2020) y tampoco examina los nodos con una precisión adecuada (Chen et al., 2020).
Las propuestas de Chen et al. (2018), Long et al. (2020), Shi et al. (2020) y Wang et al. (2018) se enfocan en integrar fuentes de datos heterogéneas para aplicar principalmente técnicas de procesamiento de lenguaje natural, clasificación o redes neuronales de acuerdo con el contexto del problema; sin embargo, la mayoría evidencia áreas de oportunidad en su aplicación práctica porque la ponderación de los nodos de la red requiere largos tiempos de procesamiento o entrenamiento para representar el conocimiento mediante el GC. Por esta razón, se propone un método que clasifica los nodos del GC que evitan la exhaustividad y los pondera con una precisión adecuada, a partir de la evidencia proporcionada por el estudiante sobre el dominio de los temas de un AD en particular.
METODOLOGÍA
Un AD involucra gran cantidad de temas que son interrelacionados de acuerdo con las dependencias de sus complejidades, las cuales se pueden representar como nodos y bordes (flechas), respectivamente, en un diagrama llamado grafo del experto. El método propuesto clasifica y pondera los temas (nodos), a partir del grafo del experto, para obtener un GC que representa el dominio de un estudiante sobre los temas de un AD.
En la figura 1 se muestran las tres fases iterativas (proceso) que componen el método propuesto. La entrada para las fases es el grafo del experto, el cual es construido por un experto del AD. En este grafo se establecen las interrelaciones de dependencias mediante bordes (flechas), de acuerdo con la complejidad de los temas (nodos). Así, en la parte superior, es decir, en el primer nivel, se indica el nombre del AD; en el segundo nivel se determinan las áreas del AD; mientras que el tercer nivel presenta los temas (nodo) raíz de las áreas porque son los de menor complejidad.
A partir del tercer nivel hacia abajo se especifican los temas, de esta forma, la complejidad de uno de ellos es mayor entre más alejado se encuentre de su tema (nodo) raíz. Las fases se repiten cada vez que se realiza una evaluación objetiva del estudiante. Después de que las iteraciones de las fases concluyen, se obtiene el GC como salida del método. En la salida de la figura 1 se han resaltado algunos valores y nodos de diferentes tipos, con el fin de mejorar la apreciación visual. Por lo tanto, el tamaño de estos no es relevante.
Para pasar del grafo del experto (entrada) al GC (salida), los nodos son clasificados en los cinco tipos mostrados en la tabla 1. Por lo tanto, los nodos que aparecen en el GC de la figura 1 son definidos en la tabla 1.
Tabla 1 Clasificación de los nodos del GC
| TIPO | DESCRIPCIÓN |
|---|---|
| V | Nodo virgen: todos los nodos del grafo del experto son del tipo V y no tienen ponderación. Este tipo de nodo tiene la menor prioridad en el grafo. Es de color negro |
| SV | Nodo subjetivo virgen: en la fase 1 los nodos se convierten al tipo SV, cada uno con ponderación de 3 para representar un grado de dominio bajo. El nodo SV sustituye a un nodo de tipo V. Es de color gris |
| O | Nodo objetivo: es determinado cuando se obtiene la evidencia del dominio del tema (nodo) por parte de un estudiante mediante un cuestionario con un valor mínimo de 0 y máximo de 100. El nodo O impactará a sus nodos interrelacionados de forma ascendiente y descendiente. Este tipo de nodo tiene la mayor prioridad en el grafo; por lo tanto, puede sustituir a un nodo de cualquier tipo: SV, S y SL. Es de color azul |
| S | Nodo subjetivo: se genera a partir del efecto causal del nodo O. Un nodo S forma parte de los nodos ascendientes y descendientes que están interrelacionados al nodo O. El valor del nodo S es calculado subjetivamente a partir del valor del nodo O. El nodo S puede sustituir a un nodo de tipo SV o SL. Es de color verde |
| SL | Nodo subjetivo lejano: se genera a partir del efecto causal del nodo O. Un nodo SL forma parte de los nodos descendientes que están interrelacionados al nodo O a partir del cuarto nivel de complejidad hacia abajo. Debido a que un nodo SL se encuentra lejano del nodo O, su ponderación tiene más incertidumbre que el nodo S; por lo tanto, el nodo SL tendrá una ponderación constante de 2 para representar un grado de dominio bajo. El nodo SL puede sustituir a un nodo de tipo SV. Es de color amarillo |
Fuente: elaboración propia.
Cada tipo de nodo, excepto el V, tendrá una ponderación actual (PA) que representa el dominio de un estudiante sobre el tema en el GC. Los nodos O y S pueden tener una PA de 0 a 100. La PA del nodo O se determina a partir de la evaluación objetiva de un estudiante mediante un cuestionario con n preguntas o problemas sobre el tema del nodo O. Por lo tanto, la PA del nodo O es el porcentaje de aciertos que un estudiante ha obtenido de la evaluación objetiva. Por esta razón, cada estudiante tendrá un GC diferente en función de su dominio del AD.
Los nodos de tipo SV y SL tendrán una PA constante de 3 y 2, respectivamente, mientras que el nodo V no tiene PA porque forma parte del grafo del experto. Así, el cálculo de la PA se realiza en las tres fases del método, es decir, en el proceso mostrado en la figura 1.
En seguida se detallan las tres fases del método propuesto y las reglas que las fundamentan.
Fase 1. Establecer nodo O
En esta fase se determina un nodo del tipo O al que se le asocia la PA obtenida de la evaluación objetiva del estudiante. Las reglas de esta fase son:
F1.R1) El nodo O sustituye a un nodo de tipo SV, S y SL. F1.R2) Un nodo O se establece aleatoriamente sobre un nodo que se encuentre debajo de los primeros dos niveles del grafo (el primer nivel es el AD y el segundo nivel son las áreas del AD). Además, los tres primeros nodos O deberán estar antes de los dos últimos niveles del grafo (los temas más complejos). Esta regla asegura que los nodos O se establezcan exclusivamente en un tema (no en el nodo que representa el AD ni en los nodos que representan las áreas del AD). Además, asegura que los tres primeros nodos O presenten temas de mediana complejidad.
F1.R3) Un nodo O no puede ser sustituido por ningún tipo de nodo.
F1.R4) Un nodo O es evaluado objetivamente una sola ocasión.
A continuación, se describen los pasos de la fase 1, los cuales respetan las reglas mencionadas:
F1.P1) Los nodos V se convierten al tipo SV, cada uno con ponderación de 3 para representar un grado de dominio bajo.
F1.P2) Se elige un nodo aleatoriamente.
F1.P3) Si el nodo elegido es de tipo S, SL o SV, se sustituye por el nodo O. De lo contrario, regresa al paso F1.P2. F1.P4) Al nodo O se le asigna la PA obtenida de la evaluación objetiva del estudiante. De esta forma, se obtiene la evidencia proporcionada por el estudiante sobre el dominio de un tema (nodo) en particular. F1.P5) El color del nodo O se establece azul.
En la figura 2 se muestra un ejemplo de referencia de cómo se actualiza el grafo en cada fase durante una iteración. En la figura 2 (a) se muestra el estado inicial del grafo del experto (entrada). En la figura 2 (b) se aprecia la transición cuando el nodo O ha sido establecido con una ponderación de 80 (PA=80), es decir, cuando la fase 1 ha concluido. Los valores mostrados son la PA de cada nodo.
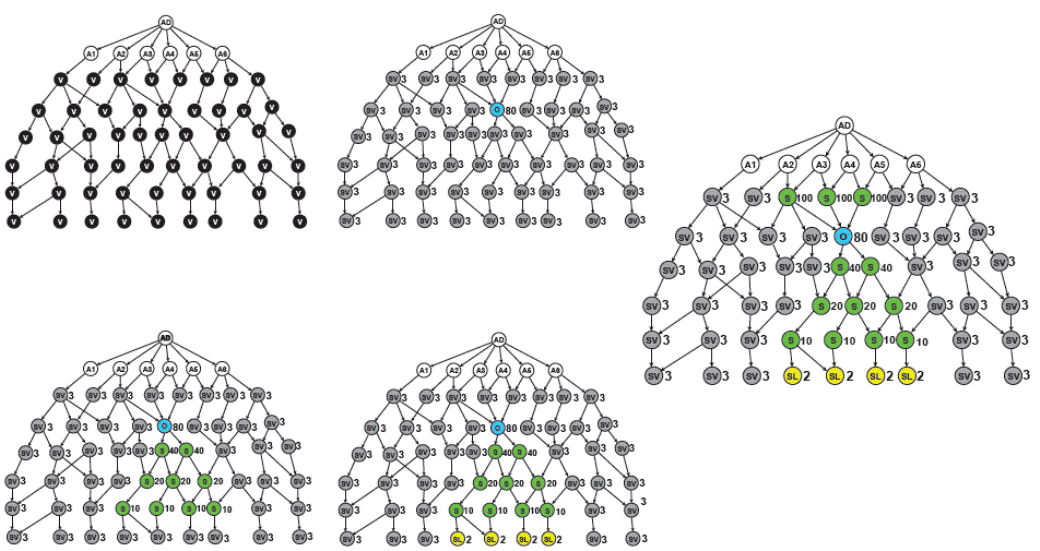
Fuente: elaboración propia
Figura 2 Actualización del grafo a través de las tres fases del método: ejemplo de una iteración.
En las reglas de la fase 2 y fase 3 se especifican valores y porcentajes que hemos propuesto para que el método evite la evaluación exhaustiva de los nodos y realice la ponderación con una precisión adecuada. Aunque esta es una propuesta de los autores, se ha tomado en cuenta la relación causal entre los diferentes niveles de conocimiento en un AD con su grado de complejidad respecto a los conocimientos previos y posteriores (Nie, Shi & Li, 2020; Rantanen, Hyttinen & Järvisalo, 2020; Shin & Jeong, 2021).
Fase 2. Ponderar los nodos descendientes
En esta fase se ponderan los nodos descendientes que están interrelacionados al nodo O. Así, el efecto causal del nodo O impacta a los nodos (temas) con mayor complejidad que el mismo. Los nodos impactados serán sustituidos por nodos del tipo S o SL. Las reglas de la fase 2 son:
F2.R1) El efecto causal del nodo O impacta a sus nodos hijos, nietos y bisnietos. En otras palabras, son los nodos que están a máximo tres saltos del nodo O. Estos nodos son clasificados como tipo S.
F2.R2) Los nodos S clasificados en el paso anterior, reciben una ponderación de 50% de su padre. Por lo tanto, un hijo del nodo O recibe 50% de la PA del nodo O. Un nieto del nodo O recibe 50% de la PA de su padre (hijo del nodo O). Un bisnieto del nodo O recibe 50% de la PA de su padre (nieto del nodo O). Esta regla se debe a que los nodos S, antes indicados, representan temas más complejos que el tema del nodo O, por consecuencia a partir de la evidencia del nodo O el método asume que el estudiante domina el nodo siguiente en complejidad (hijo del nodo O) en 50% de la PA del nodo O, y así sucesivamente.
F2.R3) La PA de un nodo S es el promedio de las ponderaciones que recibe sucesivamente. En la ecuación 1 se muestra la expresión para calcular la PA de un nodo S:
Donde P son las ponderaciones recibidas en el nodo S y NP es el número de ponderaciones recibidas en el nodo S.
F2.R4) El efecto causal del nodo O impacta a los nodos posteriores de sus bisnietos. En otras palabras, son los nodos que están a partir del cuarto salto del nodo O. Estos nodos son clasificados como tipo SL.
F2.R5) La PA de un nodo SL es de 2 porque se asume que el estudiante tiene un grado de dominio bajo de este tema (nodo). Aunque el nodo SL está interrelacionado con el nodo O, el efecto causal del nodo O no impacta al nodo SL tanto como al nodo S (con 50% de la PA de su padre). Lo anterior se justifica por la distancia lejana del nodo SL con respecto al nodo O.
A continuación, se describen los pasos de la fase 2, los cuales respetan las reglas mencionadas:
F2.P1) Se determinan los caminos que tienen nodos interrelacionados, a máximo tres saltos, al nodo O descendientemente. Un camino puede tener nodos que han sido considerados en otros caminos.
F2.P2) Los caminos son ordenados de manera ascendente de acuerdo con su número de nodos. De esta forma, el camino con menos nodos es el primero en el orden.
F2.P3) Si existen n caminos que tienen el mismo número de nodos, los n caminos son ordenados de manera descendente de acuerdo con el número de nodos S que tiene cada uno de los n caminos. De esta forma, el camino con más nodos S será el primero en el orden de los n caminos.
F2.P4) Si existen n caminos que tengan el mismo número de nodos y el mismo número de nodos S no se realiza ordenamiento en los n caminos.
F2.P5) Se obtiene la PA de los nodos interrelacionados en cada uno de los caminos que han sido ordenados mediante los cuatro pasos anteriores. El primer camino para ponderar los nodos es el primero en el orden obtenido, y así sucesivamente. En cada camino se pondera primero el hijo, luego el nieto y por último el bisnieto, todos con respecto al nodo O, según corresponda. Esta ponderación se fundamenta en las reglas F2.R1 a la F2.R3. F2.P6) El color del nodo S se establece en verde.
F2.P7) Se determinan los nodos SL interrelacionados al nodo O descendientemente. Los nodos SL están a partir del cuarto salto del nodo O.
F2.P8) A cada nodo SL se le asigna una PA de 2.
F2.P9) El color del nodo SL se establece amarillo.
En la figura 2 (c) y (d) se muestran los nodos S y SL, respectivamente, clasificados y ponderados al finalizar la fase 2. Los valores mostrados son la PA de cada nodo.
Fase 3. Ponderar los nodos ascendientes
En esta fase se ponderan los nodos ascendientes que están interrelacionados al nodo O. Así, el efecto causal del nodo O impacta a los nodos (temas) con menor complejidad que el mismo. Los nodos impactados serán sustituidos por nodos del tipo S. Las reglas de la fase 3 son:
F3.R1) Un tema (nodo) raíz se encuentra después del segundo nivel del grafo; por lo tanto, es hijo de un AD.
F3.R2) El efecto causal del nodo O impacta a sus nodos padres, abuelos y así sucesivamente hasta llegar al tema (nodo) raíz. En otras palabras, son los temas (nodos) interrelacionados que anteceden al nodo O. Estos nodos son clasificados como tipo S.
F3.R3) Los nodos S clasificados en el paso anterior reciben una ponderación de 25% más de la PA de su hijo. En la ecuación 2 se muestra la expresión para calcular la ponderación que recibe un nodo S en la fase 3.
Donde PR es una ponderación recibida en el nodo S durante la fase 3 y PA es la ponderación actual del hijo del nodo S. Esta regla se debe a que los nodos S en la fase 3 representan temas menos complejos que el tema del nodo O; por consecuencia, a partir de la evidencia del nodo O se asume que el estudiante domina el nodo anterior en complejidad (padre del nodo O) en 25% más que la PA del nodo O, y así de manera sucesiva.
F3.R4) La PA de un nodo S es el promedio de las ponderaciones que recibe de manera consecutiva. En la ecuación 1 se muestra la expresión para calcular la PA de un nodo S.
F3.R5) Si la PA del nodo S es mayor que 100, la PA se actualiza a 100 para mantener el límite máximo de ponderación.
A continuación, se describen los pasos de la fase 3, los cuales respetan las reglas mencionadas:
F3.P1) Se determinan los caminos que tienen nodos ascendientes a partir del nodo O hasta el tema (nodo) raíz. Un camino puede tener nodos que han sido considerados en otros caminos.
F3.P2) Se realizan los pasos F2.P2, F2.P3 y por último el F2.P4.
F3.P3) Se obtiene la PA de los nodos interrelacionados en cada uno de los caminos que han sido ordenados mediante los pasos F3.P1 y F3.P2. El primer camino para ponderar los nodos es el primero en el orden obtenido, y así sucesivamente. En cada camino se pondera primero el padre y luego el abuelo, ambos con respecto al nodo O, y así de manera consecutiva hasta llegar al tema (nodo) raíz, según corresponda. Esta ponderación se fundamenta de las reglas F3.R1 a la F3.R5. F3.P4) Se realiza el paso F2.P6.
En la figura 2 (e) se muestran los nodos S clasificados y ponderados al finalizar la fase 3. Los valores mostrados son la PA de cada nodo.
Al terminar la fase 3, se ha concluido una iteración. En seguida, se itera a la fase 1 para establecer el siguiente nodo O. Después de concluir las iteraciones de las fases, se obtiene el GC que representa el dominio del estudiante sobre los temas de un AD.
ESTUDIO DE CASO
Como ya se mencionó, el dominio educativo necesita representar el conocimiento de los estudiantes mediante procesos y métodos innovadores (Guan et al., 2019; Long et al., 2020) que eviten la evaluación exhaustiva (Liu et al., 2020) y procuren la precisión (Chen et al., 2020). El presente estudio de caso describe cómo se puede estudiar este problema de manera simplificada.
Primero, solicitamos a un experto en matemáticas que definiera un grafo de esa AD. El grafo del experto se compone de las siguientes seis áreas: aritmética, álgebra, probabilidad y estadística, geometría, trigonometría y cálculo, las cuales incluyen un total de 48 temas (nodos) interrelacionados de acuerdo con su complejidad. Así, el grafo del experto integra solo algunos temas de matemáticas. Los temas representan los nodos del tipo V. En segundo lugar, usamos este grafo del experto como línea base para aplicar diez iteraciones de las tres fases del método propuesto. El estado del grafo, al terminar la iteración 1, es la entrada para la fase 1 de la iteración 2, y así de manera sucesiva.
Finalmente, se establecen diez nodos O, uno por cada iteración, para obtener el GC. Las PA de los diez nodos O se han dispuesto de forma arbitraria al suponer a un estudiante simulado.
RESULTADOS
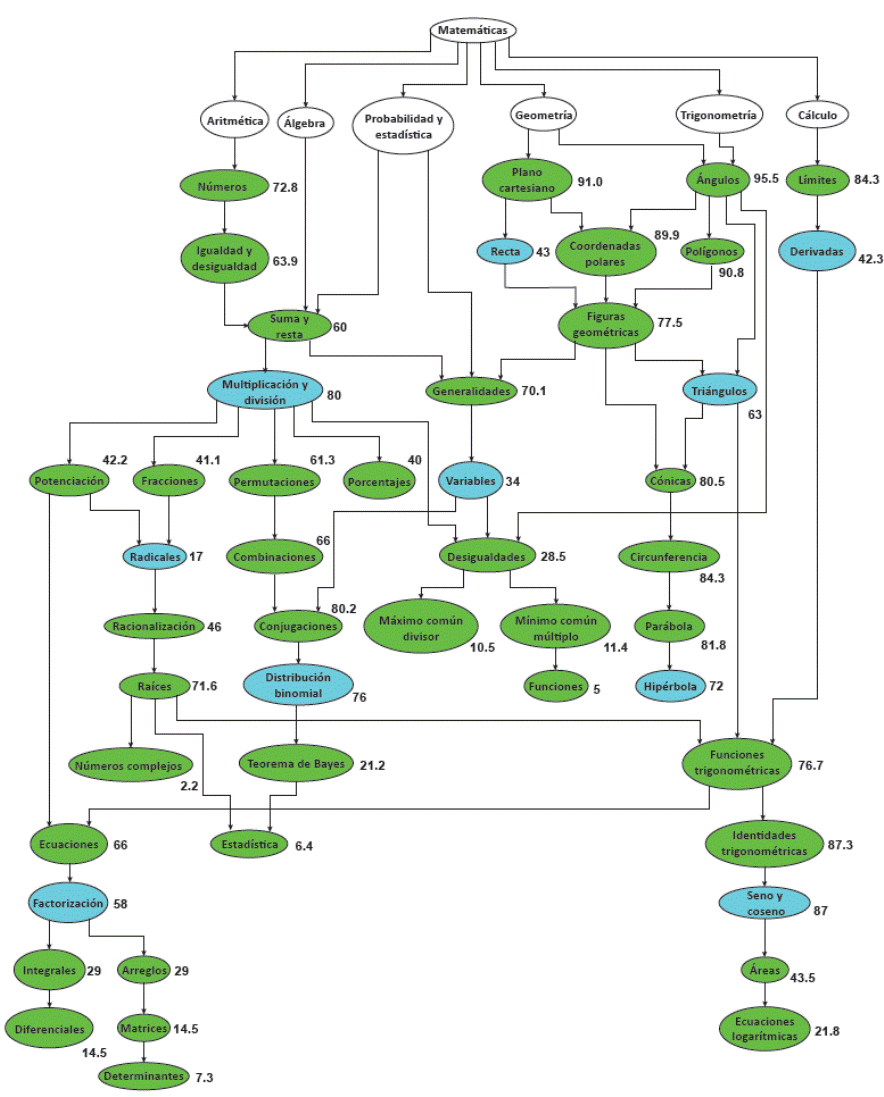
En la tabla 2 se especifican los resultados de las diez iteraciones, el nodo O establecido en la fase 1, la evidencia proporcionada por el estudiante sobre el dominio del tema (nodo O) del AD de matemáticas y los porcentajes de cada tipo de nodo al terminar cada iteración. Al concluir la iteración 10 se obtiene el GC mostrado en la figura 3.
En la tabla 2 se observa que, al finalizar la iteración 1, solo se registró 2.1% de nodos SL, lo cual representa a un nodo; esto se debe a que la estadística es el único nodo a partir del cuarto salto del nodo O variables (figura 3). Además, la PA del nodo O Variables permite clasificar y ponderar 18 nodos interrelacionados de manera subjetiva, a partir de la primera evaluación objetiva sobre el dominio del tema del estudiante. Este enfoque evita la evaluación exhaustiva de los temas del GC y permite ponderar los nodos de forma adecuada porque se fundamenta en la evaluación objetiva, es decir, la PA del nodo O.
Tabla 2 Resultados de las iteraciones del método
| ITERACIÓN | NODO O | % DE DOMINIO DEL ESTUDIANTE | % DE NODOS EN EL GRAFO | |||
|---|---|---|---|---|---|---|
| O | S | SL | SV | |||
| 1 | Variables | 34 | 2.1 | 35.4 | 2.1 | 60.4 |
| 2 | Radicales | 17 | 4.2 | 52.1 | 8.3 | 35.4 |
| 3 | Triángulos | 63 | 6.3 | 62.5 | 20.8 | 10.4 |
| 4 | Multiplicación y división | 80 | 8.3 | 66.7 | 20.8 | 4.2 |
| 5 | Seno y coseno | 87 | 10.4 | 77.1 | 12.5 | 0.0 |
| 6 | Hipérbola | 72 | 12.5 | 77.1 | 10.4 | 0.0 |
| 7 | Derivadas | 91 | 14.6 | 75.0 | 10.4 | 0.0 |
| 8 | Distribución binomial | 76 | 16.7 | 72.9 | 10.4 | 0.0 |
| 9 | Factorización | 58 | 18.8 | 81.3 | 0.0 | 0.0 |
| 10 | Recta | 43 | 20.8 | 79.2 | 0.0 | 0.0 |
Fuente: elaboración propia.
Al concluir, se ha establecido un nodo O por cada iteración. Como resultado, la evaluación de los primeros cinco nodos O ha permitido clasificar y ponderar 100% de los nodos del GC, de los cuales 89.6% ha sido impactado por el efecto causal de los nodos O. En este sentido, al finalizar la iteración del quinto nodo O (Seno y coseno) no existen nodos SV en el GC. La iteración 9 de la tabla 2 muestra la eliminación de los nodos SL, mientras que en la última iteración se especifica que la evaluación objetiva de 20.8% de los nodos del grafo ha impactado de forma subjetiva al resto de los nodos, como se ilustra en la figura 3. Por lo tanto, la figura 3 es el GC que representa el dominio de un estudiante sobre los temas del AD de matemáticas.
Aunque el método propuesto permite clasificar y ponderar los nodos del GC de forma sistemática y acorde a la complejidad de los temas, pareciera que la figura 3 no demuestra la precisión adecuada. Por ejemplo, el nodo Conjunciones tiene una PA mayor que la de sus dos nodos padres combinaciones y variables. En otras palabras, podría resultar confuso porque el estudiante tiene más dominio en un tema (nodo) de mayor complejidad que en un tema (nodo) de menor complejidad.
Lo anterior se debe a que el nodo Conjunciones fue impactado por el efecto causal de tres nodos O. El primero, nodo Variables, tiene una PA baja (34), mientras que el segundo, nodo Multiplicación y división, y el tercero, nodo Distribución binomial, tienen una PA mayor, 80 y 76, respectivamente. Por lo tanto, la PA del nodo Conjunciones (nodo S) es actualizada una vez por cada uno de los caminos que lo contemplen, los cuales se determinan en la fase 2 y fase 3 del método propuesto.
El método se enfoca en clasificar solamente temas. Por esta razón, en la figura 3 el nodo del primer nivel (AD) y los seis nodos del segundo nivel (áreas de la AD), no son clasificados ni ponderados en el GC obtenido. Por último, la cantidad de los tipos de nodos S y SL en cada iteración depende del nodo O establecido. Por lo tanto, si se realizan más evaluaciones con estudiantes diferentes, cada estudiante tendrá una instancia independiente del GC de acuerdo con su grado de dominio de los temas de la AD.
DISCUSIÓN Y CONCLUSIONES
Aunque los GC son ampliamente utilizados y aplicados en investigaciones actuales de diversas áreas, todavía queda trabajo por hacer en el ámbito educativo. En este artículo presentamos nuestra contribución inicial mediante un método que clasifica y pondera los nodos (temas) de un grafo de conocimiento de un área disciplinar. En el método se toma como línea base el grafo del experto para que sea la entrada de las tres fases iterativas. Al finalizar las iteraciones, se obtiene el GC que representa el dominio de un estudiante sobre los temas del AD.
La evaluación exhaustiva de los nodos del GC se evita mediante el efecto causal del nodo tipo O, el cual impacta a los nodos ascendientes y descendientes que tiene interrelacionados. Además de que los nodos interrelacionados son clasificados al tomar ventaja de la evaluación objetiva del nodo tipo O, también son ponderados con una precisión adecuada al considerar como base la PA del nodo tipo O. Para ser justos, el estudio de caso describe la prueba del método con la evidencia de un estudiante simulado. Nuestro propósito es mostrar la aplicación de cada fase del método con sus respectivas reglas para exponer su potencial en el dominio educativo.
El estudio de caso ha demostrado que el método propuesto evita la evaluación exhaustiva de los nodos (temas) de la AD, y consigue una ponderación adecuada. En este sentido, al evaluar objetivamente solo 20.8% de los nodos, el método ha permitido obtener un GC que manifiesta el grado de dominio del estudiante sobre el AD. Con base en este antecedente, el método propuesto puede ser utilizado en otros escenarios educativos. Por ejemplo, en el nivel medio superior y superior en AD como química, física, contabilidad, entre otras. Para hacerlo, se recomienda seguir las fases y reglas establecidas previamente. Sin embargo, en AD complejas y con temas intrínsecamente interrelacionados, se elevaría la dificultad de realizar la ponderación y clasificación de los nodos; esto se debe porque al seguir las reglas mencionadas se tendría que determinar los n caminos que tienen los nodos interrelacionados al nodo O.
Hay varios aspectos por mejorar en este método y su implementación. Primero, el proceso de iteración de las fases aún no es sólido porque no se especifica una pauta de cuántos nodos O establecer. Como un método que evita la evaluación exhaustiva, esperamos implementar un módulo inteligente basado en redes bayesianas que infiere cuándo finalizar las iteraciones. Integraremos diferentes fuentes de datos heterogéneas que mejoren la precisión de la ponderación de los nodos. Por ejemplo, los resultados del examen de los estudiantes antes de ingresar a la universidad y su comportamiento en las plataformas tecnológicas que gestionan el aprendizaje.
En segundo lugar, debido a que cada estudiante tendrá un GC diferente en función de su dominio del AD, es necesario automatizar el proceso mediante un sistema que gestione el conocimiento de los estudiantes sobre un AD, el cual se base en el enfoque del método propuesto. En esta misma dirección, planeamos desarrollar módulos dirigidos a cuatro tipos de usuarios finales: experto, estudiante, profesor y administrador.
En tercer lugar, el método propuesto puede potenciar el aprendizaje en la educación universitaria debido a que el GC representa el dominio de un estudiante sobre un AD. Una vez que se conoce el grado de conocimiento del estudiante, se puede favorecer al desarrollo de sus competencias disciplinarias y profesionales mediante la atención puntual de los temas (nodos) con deficiencia.
Finalmente, pretendemos investigar las formas más efectivas de determinar rutas de aprendizaje de acuerdo con el GC de cada estudiante a partir de las recomendaciones. En particular, la gestión de conocimiento mediante un GC orientado al dominio educativo es nuestra perspectiva de investigación.











 nueva página del texto (beta)
nueva página del texto (beta)