1. Introduction
This study examines a multi-item manufacturing problem with a single machine, an outsourcer, and random defective items. To help production managers decide the most economical lot size, Taft (1918) proposed the economic production quantity model for a single-item fabrication under a perfect fabrication condition. Using mathematical modeling and balancing the setup and stock holding costs, author determined the most economic batch size to minimize long-run average fabrication-related costs. Facing the trend of increasing multiproduct demands from global markets, modern manufacturing firms have focused on making an efficient multi-item fabrication plan to meet customers’ needs. Aggarwal (1984) suggested a simplified common order cycle for subgroups of multi-item inventories and proposed an efficient computational procedure to find the optimal order cycle values. Leachman and Gascon (1988) examined a multiproduct single-machine manufacturing system with time-varying stochastic demands. Based on the results from observing stock status linking to the maintenance of economic production cycles, the authors proposed a dynamic cycle-length heuristic to consolidate the feedback controls to facilitate the production decision making on a period time basis. Bruggemann and Jahnke (1994) considered a two-stage multi-item scheduling and lot-sizing problem. The authors incorporated the partially non-linear constraints into a conventional mixed-integer linear model to deal with their two-stage batch production. Since it turned into NP-complete in positive setup times, the authors used the simulated annealing approach for calculating fabrication schedules on both stages. Khoury et al. (2001) used a common cycle method to explore a multiproduct lot-scheduling problem with insufficient capacity. The authors started examining a problem with two products and extended to problems with multiple products using a common cycle approach with discussions. Rossetti and Achlerkar (2011) assessed segmentation techniques for managing massive scale multi-item inventories. The authors developed two different plans that used statistical clustering, namely (i) grouped multi-item individual policies and (ii) multi-item group policies, and evaluated their performance via a set of experiments to conclude that they can outperform the inventory management result from using ABC analysis. Additional studies (Chiu, Wu & Tseng, 2019; Chiu, Huang, et al., 2019; Chiu, Lin & Wu, 2020; Gallego et al., 1996; Keshavarzfard et al., 2019; Lesmono et al., 2020 Pochet & Wolsey, 1991; Taleizadeh et al., 2019) examined multi-item fabrication systems with diverse features.
For production management to smooth fabrication schedules and avoid machine overloads, outsourcing is an effective option. de Kok (2000) examined allocation and outsourcing strategies for packaging capacity in a process industry, wherein the limited capacity is allocated among various package sizes; each has a targeted fill rate. According to a periodic review ordering policy, the author proposed two separate capacity reservation strategies: one is to postpone excess capacity needs into the future, and the other is to outsource the excessive capacity needs. Then, cost minimized optimal policies were examined, and the best policy was selected. The author also offered managerial insights into the impact of diverse cost variables and processes and strategy selection. Yildirim et al. (2005) examined a multi-period stochastic fabrication planning and sourcing problem under service level constraints. A producer has multiple plants and/or subcontractors, and each source has its own capacity, lead time, and fabrication cost. The firm must satisfy the random demands of multiproduct according to preset service level requirements from its clients. The authors employed mathematical programming to deal with the problem to determine the production quantity, when and where to produce them, and the number of inventories. Lee and Choi (2011) examined a two-stage fabrication scheduling problem incorporating an outsourcing plan, wherein two operations are required in each activity in these stages. Transactions can be completed either by an in-house facility or through an outside contractor. Their purpose was to minimize the weighted sum of the outsourcing expense and the in-house makespan. Due to the problem’s NP-hard nature, the authors proposed an approximation algorithm to solve the problem. Hahn et al. (2016) explored multi-criteria outsourcing decision-making for stochastic manufacturing systems. For determining beneficial outsourcing alternatives at the strategic level, the authors presented a non-parametric ranking method using both non-model-based Key Performance Indicators (KPI) and model-based KPIs. To evaluate strategic outsourcing policy’s performance, the authors offered an improved aggregate planning incorporating a queuing network to handle manufacturing systems’ stochastic conduct. A real case form industry was utilized to demonstrate the potential benefits of their approach. Other studies (Chiu, Zhao et al., 2020; Dan-Asabe et al., 2019; Prajapati et al., 2020) explored the benefits, risks, and different aspects of implementing outsourcing policies in manufacturing firms.
Furthermore, the fabrication of random defective products is inevitable because of unanticipated factors in real manufacturing environments. These products must be identified, separated, and discarded to retain the desired quality of the finished lot. Wee (1993) examined inventory systems with permitted partial backorder for deteriorating products. Modeling and formulation were proposed along with two numerical examples for demonstrating how the author’s policy can lead to minimum cost. Bertsimas and Paschalidis (2001) studied the make-to-order production systems incorporating probabilistic service level requirements. They aimed to determine a fabrication plan to meet customer’s multiproduct demand with minimum cost and under stochastic service level guarantees. Additional studies that addressed fabrication systems with different features of imperfect quality and unreliable issues can also be found (Adazabra et al., 2018; Afshar-Nadjafi et al., 2019; Delgoshaei & Ali, 2019; de Vasconcelos et al., 2019; Fathallah et al., 2019; Gabitov et al., 2020; Mandić et al., 2019; Mustajib et al., 2019; Ortiz-Servin et al., 2019; Sinha et al., 2020; Urrea & Pascal, 2018;). This study examines a multi-item manufacturing problem with a single machine, an outsourcer, and random defective items. Prior research paid little attention to the collective influences of outsourcing and scrap on multi-item systems. The present work aims to bridge the gap.
2. Problem description and assumption
The RHA steel plates of different thicknesses were produced at JINDAL Steel plant, Angul, Orissa. The process layout for the production of steel is shown in Fig. 1. Steel production started with melting directly reduced iron (DRI) in an electric arc furnace. Other raw materials include in plant scrap and the fluxes like lime and dolomite for making slag. The molten metal was transferred to a ladle furnace for final refining and was further subjected to vacuum degassing to minimise Hydrogen and other impurities. Table 1 illustrates the analysed final chemical composition of the steel.
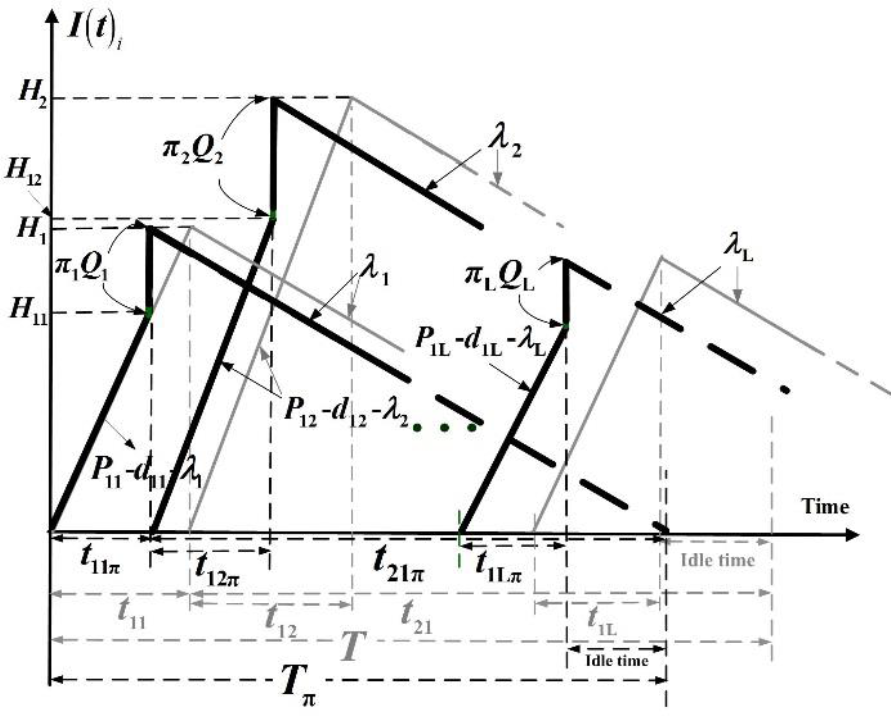
Figure 1 Inventory level of end product i in the proposed multi-item replenishing system considering an outsourcer and random defective items.
Table 1 Assumption of values of parameters for each item and for the proposed system.
| Item # | π i | K i | β 1i | K πi | C i | β 2i | C πi | x i | C Si | h i | P 1i | λi |
| 1 | 0.4 | 10000 | -0.60 | 4000 | 80 | 0.40 | 112.0 | 5% | 20 | 10 | 58000 | 3000 |
| 2 | 0.4 | 11000 | -0.65 | 3850 | 90 | 0.35 | 121.5 | 10% | 25 | 15 | 59000 | 3200 |
| 3 | 0.4 | 12000 | -0.70 | 3600 | 100 | 0.30 | 130.0 | 15% | 30 | 20 | 60000 | 3400 |
| 4 | 0.4 | 13000 | -0.75 | 3250 | 110 | 0.25 | 137.5 | 20% | 35 | 25 | 61000 | 3600 |
| 5 | 0.4 | 14000 | -0.80 | 2800 | 120 | 0.20 | 144.0 | 25% | 40 | 30 | 62000 | 3800 |
A multi-item replenishing system with an outsourcer and random scraps is investigated. Consider L end products are made on a machine obeying a common cycle time discipline, at production rates P 1i (where i = 1, 2, …, L). Demands of these products are λi per year and to cut down the manufacturing cycle time, an outsourcer is used to help supply a π i portion of the lot for each end item i in a cycle and these outsourced items are scheduled to be received at the time in-house production processes end (Figure 1). The relevant costs relating to paying outsourcer for each product i are the fixed cost K πi and unit cost C π. The outsourcer is requested to guarantee product quality and timely delivery of all of its supplies. The outsourced items are to be received at the fabrication finishing point of each product i, which bring the inventory level of end product i from H 1i to H i , before the beginning of depletion time t 2iπ. Then, all finished items of product i are depleted before next fabrication cycle starts (Figure 1). Extra notations utilized in this study are given below:
Q i = |
batch size of product i, |
K i = |
setup cost for manufacturing product i in -house, |
C i = |
unit in-house manufacturing cost, |
β 1i = |
linking parameter between Kπi and Ki, where Kπi = (1 + β1i)Ki and -1 < β1i < 0 is assumed, |
β2i = |
linking parameter between Cπi and Ci, where Cπi = (1 + β2i)Ci and β2 > 0 is assumed, |
C Si = |
unit disposal cost of product i, |
d 1i = |
production rate of defective product i, |
x i = |
random defective rate in the manufacturing process of product i, |
E[x i ] = |
the expected value x i , |
T π = |
common manufacturing cycle time - the decision variable; |
E[T π]= |
the expected value T π, |
H 1i = |
level of end product i in the end of in-house manufacturing process, |
H i= |
level of finished product i in the end of in-house manufacturing process and after the receipt of outside supplies, |
h i = |
unit holding cost of product i, |
I(t)i= |
level of end products at time t, |
I D(t)i = |
level of defective items at time t, |
t 1iπ = |
manufacturing uptime of product i, |
t 2iπ = |
depletion time of product i, |
t 1i = |
manufacturing uptime of product i for the same system without an outsourcer, |
t 2i = |
depletion time of product i for the same system without an outsourcer, |
T = |
the common manufacturing cycle time for the same system without an outsourcer, |
TC(T π) = |
total system cost per cycle, |
E[TCU(T π)] = |
the expected annual system cost, |
|
the average of π i |
|
the average of x i |
|
the average of β 1i , |
|
the average of β2i |
As shortages are not allowed, P 1i - d 1i - λ i must be greater than zero. During the production processes of the other (1 - π i ) portion of product i, an x i proportion of defective items are produced at the rate d 1i randomly (hence, we have d 1i = x i P 1i ). The inventory level of defective product i produced in the proposed multi-item replenishing problem is illustrated in Figure 2.
3. Mathematical modeling and optimal solution
From the description of the proposed multiproduct replenishment system, formulas for batch size Q i, common manufacturing cycle time T π, and additional equations can be identified as follows (where i = 1, 2, …, L):
Plus the following formulas for linking parameters β1i and β2i as described in definition/notation of previous section:
TC(T π) - total system cost per cycle contains the following: in-house setup and variable costs, fixed and variable outsourcing expenses, variable disposal cost for scraps, and holding costs for finished and defective products in a replenishing cycle (see Eq. (10)).
Substitute Eqs. (8) and (9) in Eq. (10), TC(T π) becomes as follows:
Replace Eq. (1) in Eq. (11), and employ E[x i ] and E[T π] to deal with effects of randomness of x i on the expected cost E[TCU(T π)], with extra derivation one has the following:
Where
3.1. The optimal common cycle time
The following are the first- and second-derivative of the expected annual system cost E[TCU(T π)]:
Since (1 + β1i), Tπ, and Ki are all positive,
hence, the second-derivative of E[TCU(Tπ)] (i.e., Eq. (14)) is positive. Therefore,
E[TCU(Tπ)] is convex for all Tπ different from zero.
To locate the optimal Tπ, we set the first-derivative of
E[TCU(Tπ)] = 0 and solve
With extra derivations, the following
4. Numerical illustration
This section offers a numerical illustration to confirm that our research outcomes can be practically used.
Consider five distinct product end items that need to be manufactured by a multi-item single-machine production system with an outsourcer and random defective rate. Assumption of values of parameters for each item (see Eqs. (8) and (9)) and for the proposed manufacturing system is given in Table 1.
For average outsourcing factor
4.1. The impact from variations in
Applying the formulas of the proposed model (see section 3), we can further
reveal the influence of variations in
Table 2 Influence of variations in
Further exploration reveals the effect of variations in
On the other hand, Figure 6 depicts the
effect of changes in
Besides, a benefit is gained regarding the decline in machine utilization. Figure 7 illustrates the effect of variations
in
The analytical result also reveals a piece of important information on
4.2. The effect from the difference in
Another key factor in our study is the average scrap rate
Also, the influence of changes in
Figure 10 depicts the analytical result of
important information on
4.3. Joint impacts from diverse system factors
The collective influences of changes in the average outsourcing setup cost
linking parameter
Figure 12 shows the joint impacts of
variations in
Moreover, the analytical results also reveals important information on
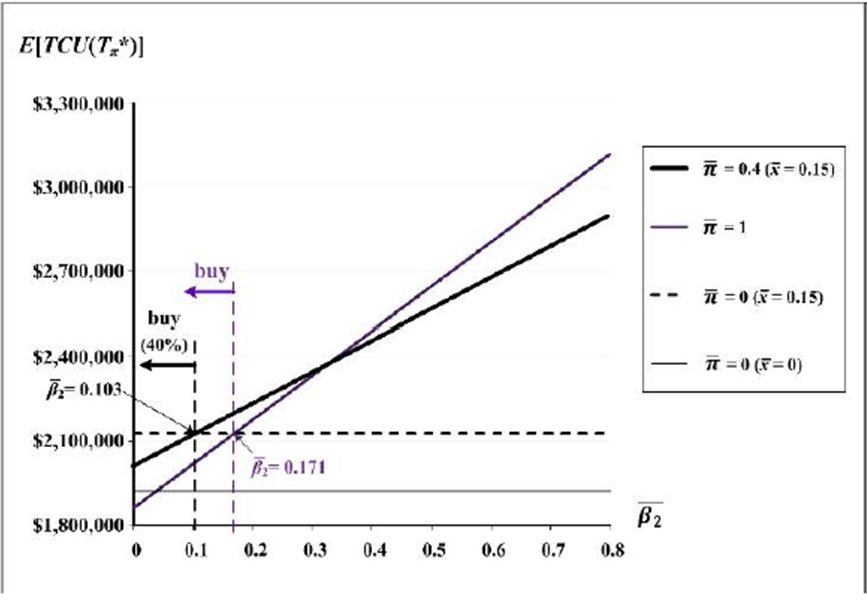
Figure 13 Impact of differences in \overline{\beta_2} on E[TCU(
Additionally, our model can provide the critical
4.4. The managerial insights from the study’s results
From the above research’s results, the production planners/managers can disclose the impact of an outsourcing strategy and random scraps on the optimal replenishing policy (in terms of rotation cycle length) of a multi-item manufacturing system. These include the individual and collective influence of variations in average: (i) outsourcing factor, (ii) scrap rate, and (iii) outsourcing-relevant costs on the optimal system’s rotation cycle time, total costs, and overall machine utilization, etc., to facilitate managerial operational controlling and decision making.
5. Concluding remarks
This study develops a mathematical model representing a multi-item single-machine hybrid stock refilling system with random defective items. We employ mathematical derivations to find long-run average system expenses and uses an optimization technique to derive a closed-form common rotation time for this hybrid system. This study’s main contribution includes (1) Establishing a decision support model for production managers/planners to deal with the specific multi-item single-machine hybrid refilling system with random scrap. (2) Disclosure of crucial individual/collective impacts of variations in outsourcing percentages/ relevant-cost and scrap rates on the optimal replenishing policy, total system cost, overall utilization, and each system’s cost-component (refer to Figures 3 to 13). These findings can facilitate the planning, controlling, and decision making of such a hybrid system. Finally, an important topic for future study is investigating the effect of random multiproduct demand rates on the problem.











 nueva página del texto (beta)
nueva página del texto (beta)














