1. Introduction
Damage in a structure may lead to a decrease in stiffness and stability that can adversely influence the functionality of structural systems during their lifetime. The damage may be due to usual weakening of material properties, overloads, different environmental and human-induced factors, or some unexpected reasons such as earthquakes, thermal effects, and vehicle impact. Accordingly, damage detection can prevent the occurrence of unpredictable failures, reduce the cost of maintenance, and increase the life safety and functionality of structures (Ravanfar et al., 2015 & 2016a). Common recent non-destructive tests (NDTs) for detecting damage are based on visual assessments, X-ray, ultrasonic, acoustic emission and radiography (Hakim et al., 2020; Wu et al., 2020). However, these approaches are inadequate to assess the status of structural components when the defect is deep in and is not observable.
Vibration-based damage detection methods are popular in the area of structural fault diagnosis because they are able to detect damage in large and complicated structures (Chik et al., 2021; Jayasundara et al., 2020; Ravanfar et al., 2016b). These methods are based on the fact that any decrement in the rigidity of a structure, causes an alteration in its vibrational parameters like natural frequencies, damping ratio, and mode shapes (Hakim & Razak, 2011; Padil et al., 2020). Artificial neural networks (ANNs), which parallel the remarkable capability of biological nervous systems to learn in situations with uncertainty and inaccuracy are very useful for solving inverse problems and have strong capabilities to detect damage using vibration data. Therefore, they have been applied for structural health monitoring in the last decade. (Pagani et al., 2021; Tran-Ngoc et al., 2019).
Several comprehensive reviews on vibration-based structural health monitoring methods have been conducted and the damage identification algorithms and both their merits as well as drawbacks were discussed (Avci et al., 2021; Hakim & Razak, 2014a). An Experimental study on the damage detection and localization of a steel truss bridge using the combination of ANN and wavelet transform was presented by Mousavi et al. (2021). Extracted modal parameters from acceleration signals were applied to evaluate the validity of the said approach. The experimental results showed the capability of the method to identify the severity and location of damage.
Detection of delamination as a type of structural damage was subsequently investigated by Maurya et al. (2022). In their study, ANN was applied to determine the delamination damage in carbon fiber reinforced polymer (CFRP) composite beam. A modal analysis was performed to obtain the first three natural frequencies and the results showed that the existence of delamination affected the modal parameters. The researchers also determined that, ANN could predict the location and length of delamination in the CFRP composite beam. Next, Chang et al (2018) employed the dynamic parameters of a steel-frame building to identify the magnitude and location of damage using ANN. Different reductions in stiffness were applied, and subsequently, modal parameters consisted of frame were obtained. Results demonstrated that ANN was able to detect the damaged members with a high level of accuracy.
Moving on, Tan et al. (2017) developed a technique to detect damage in a steel beam using the combination of ANNs and modal strain energy and found that the method used was able to accurately identify defect in beam structures. In another study, Aydin and Kisi (2015) applied modal parameters as the input datasets of ANNs to detect damage in beam structures. The authors, used the first four natural frequencies of the structure as the input parameters of ANN. The results showed that ANN was able to identify cracks in the beam structures with a high level of accuracy.
In recent years, the interest of applying ANNs using modal parameters to structural health monitoring has increased and several attempts have been made to assess damage in civil structures using ANNs trained with vibration data (Chang & Kim, 2016; Hakim et al., 2015; Hakim et al., 2021; Lee et al., 2021; Nguyen et al., 2019). Regardless of the presently available research efforts, there are still remaining needs to diagnose defect in structural systems using an ensemble neural network when multiple point of damage case is applied and to assess both its location and severity. As such, the major concentration of this present study was to investigate the potential of an ensemble neural network as an artificial intelligence method, which is trained with modal parameters, for structural damage detection. Vibration parameters of the structures were considered to identify the magnitude and position of triple-point damage cases in two beam-like structures.
2. Artificial neural networks (ANNs)
ANNs are progressive machine learning method influenced by the human brain, which are capable of nonlinear modeling, pattern recognition and classification. They can develop their own algorithm and provide significant answers using given the input and output data very quickly and with a high level of accuracy when applied to solve real problems (Fan et al., 2020; Hakim & Razak, 2014b). ANNs are constructed with a number of neurons that are interconnected. The structure of an ANN consists of an input layer, output layer, and at least one hidden layer (Liang et al., 2016; Wang et al., 2015). The layers are linked by transfer functions. The architecture of a neural network is demonstrated in Figure 1, which illustrates the signals from the input layer passing through the hidden layer and arriving at the output layer. Backpropagation algorithm is the most appropriate algorithm and is commonly applied in civil engineering applications (Noorzaei et al., 2007; 2008). The least mean square error (MSE) is the performance index of the backpropagation algorithm. In this algorithm, after serving the input datasets to the ANN, the output will be compared with the target datasets to minimize the MSE. The training of the network will stop, when the error is minimized.
One of the main advantages of ANNs is their capability to generalize, which presents them with the ability to handle unseen data, and as such, the performance of ANNs is mostly dependent on their generalization capability. Ensemble neural network is one of the promising methods to develop the generalization ability of a network. Neural network ensembles were formally suggested and established by Hansen and Salamon (1990). They proved that they can perfect the generalization power of ANNs by training a specific number of individual ANNs and merging their outputs (Huang et al., 2020).
In ensemble neural networks, many single networks are used to train and then synthesize the outputs of each single network. Ensemble neural network exhibits improved performance when compared against a single network in most cases. The model of an ensemble neural network is exhibited in Figure 2. In ensemble neural networks, vibration characteristics can be applied as inputs and when the networks are properly trained, damage identification is fast and mathematical models are not required.
3. Experimental modal analysis
Experimental modal analysis is one of the significant methods in structural fault diagnosis. It represents the process of obtaining the modal characteristics of a structure such as natural frequency, damping ratio, and modal shape by exciting the structure artificially (Karaağaçlı & Özgüven, 2021; Mohammad et al., 2011; Saito & Kuno, 2020). In this present research, two steel I-beam shapes with a length of 3.2 m and depth of 150 mm were considered. The width of flange was 75 mm and thickness of both the web and flange were 5 mm and 7 mm, respectively. The beam-like structures were excited using a shaker and responses were measured by accelerometers. A photo of the test specimen is as shown in Figure 3.
Figure 4 illustrates that the test grid had 48 points in three sets between the beam supports. The accelerometers were attached to the structure using a magnet base and had a sensitivity range of 100 mV/g. The time history signals from the accelerometers were amplified and converted by a signal analyzer into digital form. Fast Fourier Transform (FFT) was also used to convert the time domain signals into frequency spectra domain. Signals were assumed to be periodic during the process of FFT, while in reality, there are some undesirable distortions leakage. A technique called windowing was used to overcome the problem of leaking. This technique of windowing is the process of the weighting of the time domain data to decrease the effect of leakage. There are several different window functions to reduce unwanted distortion. In this research, the Hanning window was used to improve the application of FFT.
In this study, two identical beams were tested in its intact and under various damaged scenarios to obtain the modal parameters, consisted of the first five natural frequencies and mode shapes. The results of the intact beams are presented in Table 1. As shown in Table 1, the frequency differences were more substantial in the higher modes than in the lower modes that were simply acquired.
Table 1 Natural frequencies of intact structures.
| Frequency | F1 | F2 | F3 | F4 | F5 |
|---|---|---|---|---|---|
| Beam | |||||
| B1 | 55.16 | 202.48 | 441.16 | 712.09 | 964.8 |
| B2 | 55.04 | 201.94 | 440.18 | 711.84 | 968.8 |
In the experimental modal analysis, diverse damage scenarios consisted of three locations of damage in each beam were created. For each location of damage, 25 levels of severities with depths of 3 to 75 mm with an interval of 3 mm were gradually induced. The width of damage was 5 mm. Modal testing for each case was done, individually. The locations of damages for beam B1 were at 3L/15, 5L/15, and 7L/15 of the span length, while for beam B2, the locations were at 4L/15, 6L/15, and L/2 of the span length. Damage was induced using a saw cut at the above-mentioned locations of the structures. The first five natural frequencies of the undamaged and damaged states for beams B1 and B2 are illustrated in Figures 5 and 6, respectively.
As shown in Figures 5 and 6, when damage occurs, the dynamics of the structure were modified and natural frequencies of all modes reduced. It could be seen that there was a large reduction in the natural frequencies after inducing 75 mm damage in three different locations of the beams. The maximum reductions in the natural frequency in beam B1 were 35.03%, 31.44%, 32.76%, 25.57% and 19.09% for mode 1 to mode 5, respectively. Meanwhile, the reductions in beam B2 were 39.48%, 24.97%, 31.36%, 21.28%, and 16.95% for mode 1 to mode 5, respectively. This indicated that the natural frequencies of mode 1 were the most affected when damage was induced in the three different locations of the beam. In addition, from the results of the first five mode shapes, a big variation in the magnitude of modes for all first five mode shapes was observed.
4. Finite element simulation
In the first step, a finite element analysis of the undamaged structures was performed. In the second step, similar damage scenarios with triple damage points, were modeled to attain the modal parameters. The modal parameters were achieved by implementing a linear modal analysis using the ABAQUS software (ABAQUS, 2014). The mode shapes of the undamaged structure with their values of natural frequencies are shown in Figure 7. It was observed that, the mode shapes of the undamaged structure were smoothed functions, which confirmed the absence of defects.
In this study, the simulation of damage was performed by rectangular openings of the span length as shown in Figure 8.
The variations of the mode shapes after inducing 75 mm damage are shown in Figures 9 and 10 for beams B1 and B2, respectively. From Figures 9 and 10, it was apparent that there was a large reduction in the natural frequencies and very significant variations of mode shapes in both beams B1 and B2 were seen after they were subjected to the 75 mm damage in three locations of the structures. The mode shapes graphs showed very considerable affectability of mode shapes to the local damage. The figures also demonstrated a significant decrease in the stiffness of the structures, and consequently, large differences in the mode shapes.
5. Damage detection using ANN
The development of an ensemble neural network for the damage detection of triple-point damage is presented in this section. The inputs to the neural network were the first five flexural modes and all corresponding mode shape values at the points on the centerline of the beams. Initially, five single networks, representing mode 1 to mode 5, were considered. Secondly, an ensemble neural network was implemented to merge the results of the individual networks into a single network. Three various locations of damage for each beam with 25 levels of cut slot for each location were considered. The damage locations at 3L/15, 4L/15, 5L/15, 6L/15, 7L/15, and L/2 of the span length were corresponded to a damage index for location which was the ratio of the damage location from the support to the length of the beam (ld/L), as shown in Table 2.
Table 2 Damage index for different locations.
| Location of damage (ld) |
Damage index for location (ld/L) |
|---|---|
| 3L/15 | 0.200 |
| 4L/15 | 0.267 |
| 5L/15 | 0.333 |
| 6L/15 | 0.400 |
| 7L/15 | 0.467 |
| L/2 | 0.500 |
In this study, the damage index for severity was considered as the ratio of the damage depth to the height of the beam (dd/h). The damage indices for the different severities of the beam are given in Table 3.
Table 3 Damage index for different severities.
| cut slot (mm) |
damage index for severity (dd/h) |
cut slot (mm) |
damage index for severity (dd/h) |
|---|---|---|---|
| 3 | 0.02 | 42 | 0.28 |
| 6 | 0.04 | 45 | 0.30 |
| 9 | 0.06 | 48 | 0.32 |
| 12 | 0.08 | 51 | 0.34 |
| 15 | 0.10 | 54 | 0.36 |
| 18 | 0.12 | 57 | 0.38 |
| 21 | 0.14 | 60 | 0.40 |
| 24 | 0.16 | 63 | 0.42 |
| 27 | 0.18 | 66 | 0.44 |
| 30 | 0.20 | 69 | 0.46 |
| 33 | 0.22 | 72 | 0.48 |
| 36 | 0.24 | 75 | 0.50 |
| 39 | 0.26 | - | - |
The input layer of the neural network had 15 neurons, representing the first natural frequency and 14 input neurons corresponding to the mode shape values of mode 1 at the points on the center of the structure. The output of the neural network had four neurons, namely the damage index for the severity (dd/h) and damage indices for the three different locations (ld1/L, ld2/L, ld3/L).
The inputs and outputs of the ANN for modeling in the case of triple damage was an array, as follows:
In the above array, f and ϕ denoted the frequency and mode shape values, respectively. The number “1” represented the first mode shape. Also, the numbers 2 to 15 indicated the mode shape values at the points of 2 to 15. Initially, the best possible network for the training datasets from mode 1 was selected, and subsequently, this network was applied to the datasets from modes 2 to 5. Finally, all results from the individual networks were combined into a single network using the ensemble approach. For the preparation of the training datasets, 104 patterns, where each pattern was consisted of 15 input neurons and four output neurons, were used. The training process was continued to produce satisfactory outputs compared to the target values. Finally, a network with the architecture of 15-7-5-4, after approximately 55000 iterations, reached a minimum MSE. The architecture for this network is illustrated in Figure 11. It was observable that, the architecture was consisted of 15 neurons in the input layer that corresponded to the first natural frequency and fourteen mode shape values, two hidden layers with seven and five neurons, and four neurons in the output layer that corresponded to the severity and three locations of damage in the structure. The damage severities and three locations of damage were identified and compared with the actual values, as illustrated in Figure 12.

(d) third location of damage.
Figure 12 . Damage identification through the ANN for mode 1 (triple damages).
The statistics of the selected network are summarized in Table 4. Looking at Figure 12 and Table 4, it was ascertained that the relationship between the inputs and outputs for the network of mode 1 in all damage severities was established with low AE of 0.98%, 1.14%, and 1.24% for training, testing, and validation data, respectively. Also, a very clear correlation value between the damage severity and recognition accuracy was obtained. In addition, Figure 12 also shows a high accuracy of damage severity.
Table 4 Performance of the neural network architecture for mode 1.
| Datasets | Correlation | AE | ||||||
|---|---|---|---|---|---|---|---|---|
| Severity | L1 | L2 | L3 | Severity | L1 | L2 | L3 | |
| All | 0.9914 | 0.9642 | 0.9620 | 0.9621 | 0.01048 | 0.04536 | 0.05139 | 0.05188 |
| TRN | 0.9927 | 0.9706 | 0.9701 | 0.9698 | 0.00986 | 0.02439 | 0.02582 | 0.02597 |
| VLD | 0.9889 | 0.9515 | 0.9522 | 0.9504 | 0.01246 | 0.04012 | 0.04480 | 0.04611 |
| TST | 0.9876 | 0.9487 | 0.9465 | 0.9447 | 0.01138 | 0.01651 | 0.05693 | 0.05784 |
From the outcomes of damage localization, it was observed that a good performance was obtained with validation and testing AE values of (4-4.7%) and (4.65-5.78%), respectively. The performance graph of damage localization for mode 1 is shown in Figure 13. The architecture of 15-7-5-4, which reached to an AE of 0.025 (2.5%) and 0.045 (4.5%) for the training and validation datasets, respectively, after approximately 55000 iterations, gave precise results for damage location.
The same architecture (denoted as 15-7-5-4) was applied for modes 2 to 5 to identify the severity and locations of damages using the data obtained from the extracted vibrational modes. The input-output vectors for the networks of mode 2 to mode 5 are as follows:
Firstly, the datasets were applied separately into the five networks. Then, an ensemble network merged the outputs of the individual networks and brought out the output results. The architecture of the ensemble network had 20 neurons in the input layer and four neurons in the output layer, as shown in Figure 14. In Figure 14, “S” denoted the damage severity, which was dd/h. On the contrary, “L” denoted the location of damage, which was ld/L. In addition, L1, L2, and L3 represented the first, second, and third location of damage, respectively. From the training of the ensemble network, the best possible network was constructed with two hidden layers (ten and six neurons in the first and second hidden layers, respectively). The minimum MSE was found to be 0.000657 and maximum value of the correlation was obtained.
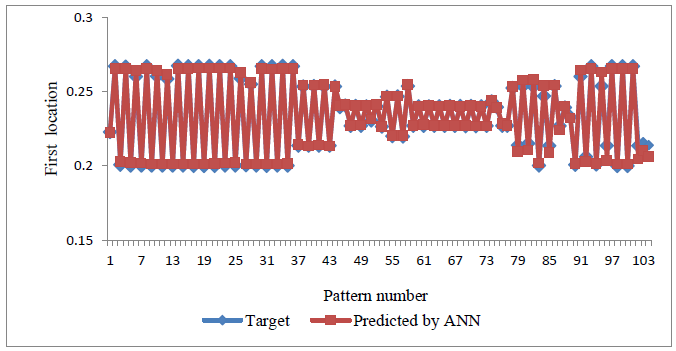
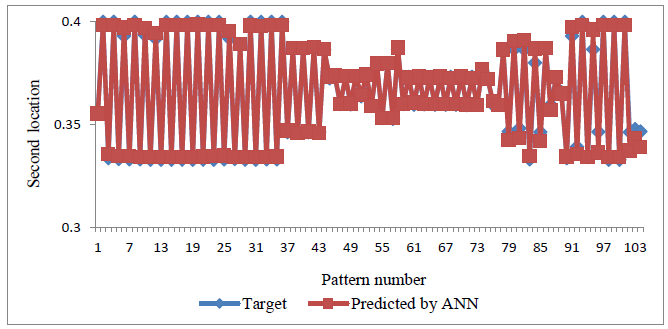
The results of damage severity and three different locations using the ensemble neural network are depicted in Figure 15. It was demonstrated that the ensemble network was very successful in recognizing the severity of damage cases. According to the results, there was a good agreement between the modal characteristics of the structures and location of damage. The damage localization outcomes showed that the ensemble network provided a very good identification for the locations of damage.

(d) Second location of damage.
Figure 15. Damage detection of I-beam structure through the ensemble network.
The performance graph of both damage severity and locations are depicted in Figures 16 and 17, respectively. Based on the figures, the ensemble network had a maximum AE of 0.75%, 1.02, and 0.98% for the training, testing, and validation datasets, respectively, for damage severity. The results were very close with the actual data, and thus demonstrated the feasibility of using the ensemble network to detect damage in the I-beam structures.
A comparison between the individual ANNs and ensemble neural network is summarized in Table 5. Based on Table 5, the outcomes of severity in the ensemble network were better than the individual networks of modes 1, 4, and 5. The ensemble network also identified the severity of all modes with a correlation of 0.9918, which was slightly smaller than the single networks of modes 2 and 3, which was negligible. The outcomes of the single networks in the triple damage cases demonstrated a few inappropriate results for damage localization in the light damage cases, while the severity identifications were accurate for all damage cases. It could be explained that, it was difficult to show any alteration in the modal curvature resulting from the experimental outcomes (for light damage). On the other hand, the ensemble network demonstrated precise results, even for the light damage cases. The results of the ensemble network for damage localization were also much better than all the individual networks. Furthermore, the MSE of the ensemble network was also better.
Table 5 Comparison between individuals and ensemble networks.
| Network | Design | MSE | AE(All data) | Correlation(All data) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Severity | L1 | L2 | L3 | Severity | L1 | L2 | L3 | |||
| M1 (Mode 1) |
15-7-5-4 | 0.0020 | 0.01048 | 0.0454 | 0.0514 | 0.0518 | 0.9914 | 0.9642 | 0.9620 | 0.9621 |
| M2 (Mode 2) |
15-7-5-4 | 0.0015 | 0.011052 | 0.0141 | 0.0143 | 0.0143 | 0.9958 | 0.9615 | 0.9616 | 0.9618 |
| M3 (Mode 3) |
15-7-5-4 | 0.0067 | 0.01011 | 0.0137 | 0.0132 | 0.0134 | 0.9979 | 0.9715 | 0.9718 | 0.9719 |
| M4 (Mode 4) |
15-7-5-4 | 0.0015 | 0.012839 | 0.0142 | 0.0143 | 0.0141 | 0.9912 | 0.9634 | 0.9638 | 0.9639 |
| M5 (Mode 5) |
15-7-5-4 | 0.0068 | 0.015338 | 0.0182 | 0.0184 | 0.0182 | 0.9889 | 0.9533 | 0.9533 | 0.9534 |
| Ensemble | 20-10-6-4 | 0.0006 | 0.008235 | 0.0107 | 0.0108 | 0.0106 | 0.9918 | 0.9785 | 0.9786 | 0.9782 |
Moving on, it was obvious that the individual networks of modes 2 and 3 could identify the severity and locations of damage with high accuracy when compared with the results of the other modes. Despite that, the ensemble network was able to recognize the position of damage for all modes with higher accuracy than the individual modes. In addition, the correlation of all datasets for damage location in the ensemble network reached 0.9785. Finally, results also demonstrated that using the ensemble neural network, the damages were recognized with the highest accuracy level, as compared to the individual networks.
6. Conclusions
In this present research, an ensemble neural network as an artificial intelligence method was developed to detect triple locations of damage in I-beam like structures using the vibration-based damage identification method. In the first step, the experimental modal analysis was implemented and modal data from two I-beam structures were measured.
The results demonstrated that the natural frequencies of the structures decreased with the increasing size of damage and the mode shapes revealed a significant divergence near the damage locations. Simulations of the structures were performed to achieve the vibration data and verify both the validity and effectiveness of the experimental modal analysis results.
The finite element analysis outcomes showed that the numerical simulations for the structures were similar to the test structures and very good correlations were attained. For the detection of the severity and location of damages with triple locations, five single ANNs, representing mode 1 to mode 5, were considered. After that, an approach called ensemble network was introduced to merge the outcomes of the single networks. The results of damage identification in the I-beam structures with triple damage cases in the individual networks demonstrated larger error, while the effectiveness and performance of the ensemble network showed good accuracy, even for the light damage cases. From the results, it was observed that the ensemble network identified most of the triple damage cases in the I-beams with a high level of precision, which reiterated its effectiveness and high accuracy. Accordingly, this method could serve as a reliable technique for the identifications of damage in structures.
Conflict of interest
The authors do not have any type of conflict of interest to declare.
Financing
Communication of this research is made possible through monetary assistance by Universiti Tun Hussein Onn Malaysia and the UTHM Publisher’s Office via Publication Fund E15216.











 nueva página del texto (beta)
nueva página del texto (beta)