1.1. Model identification for the fermentation process

Mathematical models play a crucial role in various scientific disciplines as they enable the description and prediction of system behavior under different conditions by utilizing variables. In this research, the symbolic optimization algorithm known as genetic programming (GP) was employed, following the approach proposed by ^{Madár et al. (2005)}. This method facilitates the identification of both the model's structure and its parameters using experimental data. The key considerations in this approach include the following:

The target vector J(θ)∈Rm represents the adjustment function based on the mean square error (MSE) between the calculated data and the measured output values. Here, θ∈Rn denotes the decision vector. In "Eq. 2," the parameters include N, the number of samples used for model identification; yk, the experimental output; y^(k), the calculated output; k, the sample index; and χ, the vector of regression variables. In "Eq. 3," the parameters consist of nonlinear functions F1,…,FM and model parameters p1,…,pM. genetic programming (GP) is a systematic method that employs natural evolution to automatically generate algorithms and expressions for the identification of mathematical models for specific problems (^{Koza & Poli, 2005}). These expressions are encoded as a tree data structure, with functions as nodes and terminals as leaf nodes, allowing the generation of nonlinear input-output models. An orthogonal least squares algorithm is applied to estimate the contribution of tree branches and create a precise model (^{Brameier & Banzhaf, 2007}). To develop the appropriate model for ethanol fermentation and similar systems, the GP MATLAB™ toolbox (available at http://www.mathworks.com/matlabcentral/fileexchange/47197-genetic-programming-matlab-toolbox) (^{Abonyi, 2005}) was utilized (^{Datta et al., 2019}; ^{Grosman & Lewin, 2004}; ^{Kummer et al., 2019}). The parameters of GP are presented in "Table 1."

In this research, the variables θ=t,T are considered as decision variables. In addition to the results obtained using "Eq. 1," the following adjustment metrics are utilized: the coefficient of determination R2 ("Eq. 4"), which describes the fit between experimental and calculated data; the root mean squared error (RMSE) ("Eq. 5"), and the sum of squared error (SSE) ("Eq. 6"). The objective is to develop a model that can elucidate the impact of temperature on ethanol fermentation productivity, particularly how temperature influences the growth of microorganisms and, consequently, the system's ethanol concentration over time.

The structure of the article is the following: Section 2 shows the experimental and computational methodologies; The results and discussion are shown in Section 3. Finally, some remarks and conclusions are exposed in Section 4.

1.2. Review of multi-objective optimization design procedures

A multi-objective optimization statement without loss of generality is defined as follows:

subject to: g(θ) ≤ 0, h(θ) ≤ 0 and ≤ θ _i ≤ θ _i θi- with i=1,…,n. Where θ∈Rn is defined as the decision vector, J(θ)∈Rm as the objetive vector and g(θ), h(θ) as the inequality and equatilty constraint vectors, respectively; θ _i , θi¯ correspond to the lower and upper bounds in the decision space.

Since there is no single solution that is optimal for all objectives, a set of solutions called the Pareto set is defined. Each solution in the Pareto set represents an objective vector on the Pareto front. All solutions on the Pareto front are considered a set of Pareto-optimal and non-dominated solutions.

A design procedure employing multi-objective optimization techniques typically consists of three fundamental steps: 1) stating the multi-objective problem (MOP), 2) conducting the multi-objective optimization (MOO) process, and 3) performing the multi-criteria decision making (MCDM) stage (^{Meza et al., 2017}).

• MOP statement

At this stage, the designer must make decisions regarding the design concept to address the problem, how to evaluate the performance of design alternatives, and which solutions are relevant, practical, or feasible. In the case of ethanol fermentation, the design concept refers to the operating conditions, while the design alternative pertains to specific time and temperature settings. Performance measurement requires the existence of a parametric model that establishes a correlation between the decision variables (which lead to specific design alternatives) and their performance

• MOO process

During this stage, the multi-objective optimization algorithm is implemented for the multi-objective problem (MOP). The algorithm can be ad-hoc or selected from a suitable pool of algorithms available. An algorithm is considered suitable for the problem at hand if it possesses desirable characteristics such as convergence, diversity, and relevance.

• Decision-making stage

Finally, with the approximate Pareto front, the designer will evaluate the trade-offs between conflicting design objectives and consider the design alternatives. The goal is to select a solution that strikes a preferable balance in performance for the specific problem. Procedures and visualization tools play a crucial role in assisting designers, particularly when dealing with four or more design objectives.

2.1. Microorganism and culture conditions

Saccharomyces cerevisiae CSI-1 (abbreviated as CSI) yeast was used as the microorganism in this study. A vial of CSI stock cultures, stored at -10 °C, was thawed and used to refresh the cells in tubes containing 10 mL of culture medium prepared with 20 g/L of glucose and 5 g/L of yeast extract (YE). The medium, sterilized for 20 minutes at 121°C prior to inoculation, was then incubated at 37°C for 24 h in a Shel Lab Sl incubator. Subcultures were performed monthly.

2.2. Inoculum preparation and fermentation medium

The refreshed culture served as the seed to prepare the inoculum using 200 mL of growth medium composed of 30 g/L of glucose and 5 g/L of YE. The inoculum was cultivated in a Shel Lab Sl incubator at a temperature of 37°C for 24 h. The pre-culture was subsequently centrifuged at room temperature using a high-speed centrifuge (Kubota model CR21G) at a speed of 6000×g for 5 min to harvest the cells. The cell pellet was then resuspended in 100 mL of sterilized water and used as the inoculum. The fermentation medium consisted of 5 g/L of YE and 100 g/L of molasses (70 g/L sucrose and 30 g/L glucose). The molasses contained a low concentration of fructose and were not monitored. The media was autoclaved for 20 min at 121°C.

2.3. Batch fermentation

The harvested cells from the inoculum were transferred to the fermenter to initiate the fermentation process. Ethanol fermentations were conducted in a 1 L fermenter with a working volume of 800 mL. The experiment was initiated at temperatures of 30°C, 33°C, 35°C, and 37°C with an agitation speed set at 100 rpm. The optical density, temperature, and pH were monitored and recorded throughout the fermentation process. Samples were withdrawn every 3 h, except at 12 h and 15 h, as these periods corresponded to the logarithmic phase where the monitored parameters were predictable, stable, and reproducible.

2.4. Analysis

3.1. Experimental dynamics of the fermentation process

The experimental dynamics of the fermentation process are presented using the experimental characteristics DCW, RG, RS, E, and CFU/mL (see "Tables 2-6" and "Figures 1-2").

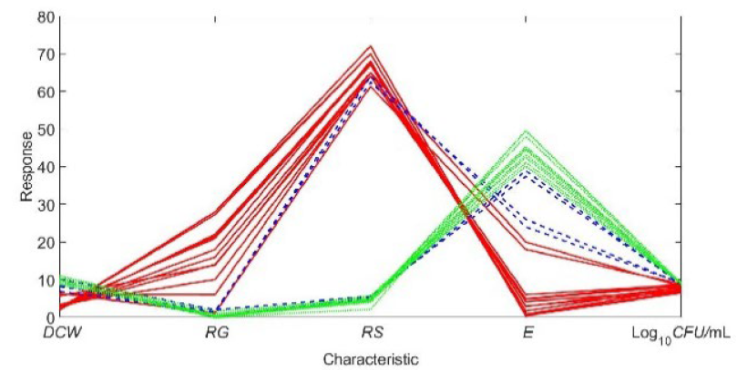
Figure 1 Coupling of the characteristics of the fermentation process. Green lines: E > 40 g/L; blue lines: 20 g/L < E ≤ 40 g/L: red lines: 0 g/L < E ≤ 20 g/L (experimental characteristics). 

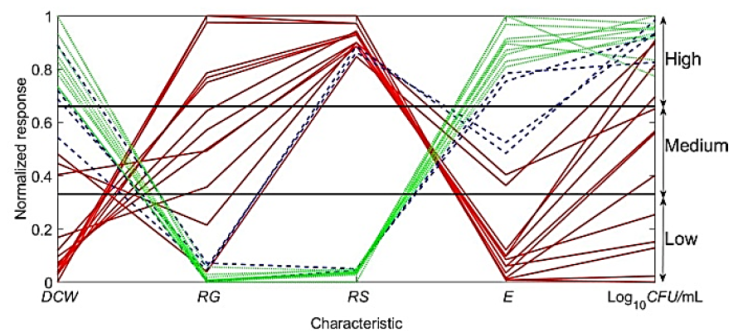
Figure 2 Coupling of the characteristics of the fermentation process. Green lines: E > 40 g/L; blue lines: 20 g/L < E ≤ 40 g/L: red lines: 0 g/L < E ≤ 20 g/L (normalized responses). 

"Table 2" displays the dynamics of DCW as a function of time and temperature. The parameters that are within a limited range are DCW and CFU/mL, which show a strong correlation. It is preferable to have low values of DCW and CFU/mL to achieve high specific productivity. However, DCW or its equivalent CFU/mL correlates with the volumetric productivity, represented by ethanol concentration (E) ("Figure 1"). Ethanol (E) can be considered as a reference for analyzing the coupling of the other parameters. This is the optimal way to track the fermentation kinetics, considering that E is the final product of the substrate metabolism. Three intervals can be identified for E ("Figure 2"): a) E>40 g/L, b) 20 g/L<E≤40 g/L and c) 0 g/L<E≤20 g/L. For the first interval a) E>40 g/L, high values of DCW, low values of RG, low values of RS, and high values of CFU are required and were obtained as expected. This trend is evident since higher CFU production leads to increased ethanol production.

For the second interval (b) 20 g/L<E≤40 g/L, high and medium values of DCW, low values of RG, high values of RS, and high values of CFU are required. In contrast, for the third interval 0 g/L<E≤20 g/L, low and medium values of DCW, high, medium, and low values of RG, high values of RS, and high, medium, and low values of CFU are observed to be required. This trend is also reasonable because lower CFU results in lower production of E. One solution to this situation is to allow the fermentation to continue for a longer time. However, this approach is unfavorable from an industrial perspective. This situation arises since the yeast acts as a biocatalyst, consuming the substrate according to the reaction rate. Glucose is the first substrate to be consumed due to the diauxic phenomenon, and then sucrose is metabolized once the initial glucose present in the molasses is depleted. At the end of fermentation, the desired product, E, is produced consequently correlated with the consumed substrate, the concentration of cells (DCW), and the operating temperature. "Table 3" shows the dynamics of RG as a function of time and temperature. The decrease in RG is inversely proportional to time, with the most drastic results at t>12 h. There are similarities in the RG values, specifically at: (a) RG≅27g/L, (b) RG = 28 g/L, (c) RG = 0.2 g/L and (d) RG = 0 g/L.

For (a) RG≅27g/L, the operating conditions correspond to: T = 33 °C, t = 0 h and T = 35 °C, t = 0 h. For (b) RG = 28 g/L, the operating conditions correspond to: T=30 °C, t = 0 h and T = 37 °C, t = 0 h. For (c) RG = 0.2 g/L, the operating conditions correspond to: T = 30 °C, t = 24 h and T = 35 °C, t = 21 h and T = 37 °C, t = 21 h. Finally, for (d) RG = 0 g/L the operating conditions correspond to: T = 33 °C, t = 24 h and T = 37 °C, t = 24 h. The decrease in glucose concentration is due to the cell's metabolism for cell reproduction, converting glucose into ethanol as a product. Glucose is preferred over sucrose as a substrate because it is thermodynamically favorable.

"Table 4" displays the dynamics of RS as a function of time and temperature. The decrease in RS varies with time, with the most significant changes occurring at t>12 h. This characteristic shows similar values for all operating conditions. However, the operating conditions T = 33 °C, t = 12 h, and T = 37 °C, t = 24 h do not follow the same trend as the other operating conditions. As part of the normal yeast metabolism of glucose and sucrose, the cell undergoes diauxic shift, where glucose is preferred over sucrose (^{Peng et al., 2015}). Only when glucose is depleted does the yeast start to consume sucrose. It is known that Saccharomyces cerevisiae can utilize simple sugars but are unable to use monosaccharides such as xylose. Therefore, this model does not apply when the substrate comes from lignocellulosic fermentable sugars (^{Nawaz et al., 2020}).

"Table 5" presents the dynamics of ethanol (E) as a function of time and temperature. The increase in E is directly proportional to time, with the most notable changes occurring at t>12. For the time interval at at t>12 h, the production of E increases twice that of at t>12 h. Some operating conditions that do not present the same trend as the others are the following: (a) E = 0 g/L, (b) E = 0.8 g/L and (c) E = 6 g/L with T = 35 °C, t = 0 h with; with T = 35 °C, t = 3 h and T = 37 °C, t = 6 h respectively. Again, this small difference is due to slight differences in the initial inoculum to the main fermentation.

"Table 6" displays CFU/mL as a function of time and temperature. The increase in CFU/mL is directly proportional to time, but there is a stationary phase observed at t>12 h. This characteristic exhibits a similar trend across all operating conditions and is often observed in various microorganisms when important nutrients or cofactors are depleted. “Figures 1-2" illustrate the interrelationship among all the fermentation process characteristics in a combined manner.

The characteristics that are in a limited range are DCW and CFU/mL, and their influence on the other characteristics is observed in the production of ethanol ("Figure 1"). Characteristic E (ethanol) can be considered as a reference to analyze the coupling of the other characteristics, for which there are three intervals ("Figure 2"): a) E > 40 g/L, b) 20 g/L<E≤40 g/L and c) 0 g/L<E≤20 g/L. For the first interval a) E>40 g/L, high values of DCW, low values of RG, low values of RS and high values of CFU/mL are observed. For the second interval b) 20 g/L<E≤40 g/L, high and medium DCW values, low RG values, high RS values and high CFU/mL values are observed. Finally, for the third interval 0 g/L<E≤20 g/L, low and medium values of DCW, high, medium, and low values of RG, high values of RS and high, medium, and low values of CFU/mL are observed for the kinetics of the fermentation. The situation is due to the consumption of substrate by the yeast obeying the reaction rate. The first substrate consumed is glucose, then the diauxic phenomenon biases the reaction toward sucrose consumption. At the end of the fermentation, the ethanol produced as desired product is a consequence correlated with the substrate consumed and the temperature.

3.2. Model identification of the fermentation process

The experimental data were used in the GP MATLAB™ toolbox to obtain the mathematical model that describes the behavior of the fermentation process. The parameters of GP are described in "Table 1." The mathematical models are:

where, the parameter models are: DCW is dry cell weight, CFU is colony forming units, RG is residual glucose, RS is residual sucrose, E is ethanol concentration, t is time and T is temperature considering the following restrictions: if DCW < 0 then DCW = 0; if RG=0 if RS<0 then RS=0; if E<0 then E=0 and CFU/mL<0 then CFU/mL=0. The mathematical models are compared with the experimental data ("Figure 3"), and it can be observed that the mathematical model fitted the experimental data values fairly.

Figure 3 Validation of the mathematical model vs. experimental data: a) DCW (g/L); b) RS (g/L); c) log₁₀ CFU/mL; d) RG (g/L); e) E (g/L); experiments were performed by triplicate. 

The fitness is higher than R2≤0.92 as reported in "Table 7." Therefore, "Eqs. 7-11" adequately represent the experimental data and are used to optimize the characteristics of the fermentation process.

3.3. Statement of optimization problem

In this research work, it is considered that the ethanol fermentation process presents the following characteristics: (DCW) g/L, (RG) g/L, (RS) g/L, (E) g/L and (Log₁₀ CFU/mL). These characteristics are considered as dependent variables of the process. The independent variables of the process are time (t) and temperature (T). The relationship between the dependent and independent variables is shown in "Eqs 8-12". Some bibliographic references that consider a methodology like this work is ^{Ramírez-Hernandez et al. (2017)} where they consider: a) set of data obtained experimentally from the dependent variables of independent, b) identification of the structure and parameters of the model and finally c) optimization in numerical simulation of the best operating conditions. For point c) optimization in numerical simulation of the best operating conditions in this research work, the following is considered. The multiobjective optimization problem can be posed by finding the values of X ₁ and X ₂ with Jθ∈R6=J1,J2,  J3,   1J3,   J4,  J5 therefore:

where θ is time (X ₁) and temperature (X ₂) subject to the decision variables are 0<X1<24 and 30<X2<37. The definition of the decision variables allows the optimization algorithm to define the search space for potential solutions. In this work, the search space was determined with respect to a previous experimentation ("Tables 2-6"). To obtain potential solutions the MATLAB ™ optimtool/gamultiobj (multiobjective optimization using genetic algorithm) toolbox was used.

3.4. Optimization

"Figures 4a-4b" present the operating conditions and corresponding characteristics obtained from the model and experimental data, showing a correspondence between them. In contrast, "Figures 4c-4d" display the set and Pareto front of operating conditions obtained through the optimization algorithm, along with the characteristics obtained through simulation. Additionally, the maximum values obtained from both experiments and simulation are also indicated.

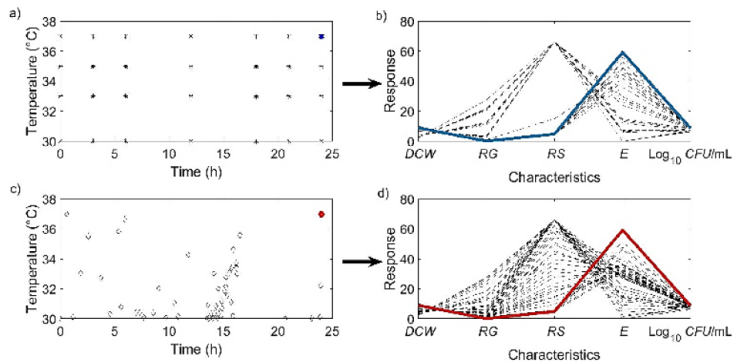
Figure 4 Set and Pareto front of the optimization process: a) Independent variables (t, T) proposed experimentally, b) dependent variables (DCW, RG, RG, E and Log₁₀ CFU/mL) obtained with the mathematical model; c) independent variables (t, T) proposed by means of optimization, d) dependent variables (DCW, RG, RG, E and Log₁₀ CFU/mL) obtained with the mathematical model and c). Blue lines indicate the maximum of E. 

It is observed that there is a highly aggregated set in the region corresponding to a time interval of 10 to 15 h, but the maximum value is found with the operating conditions that meet   t>37°C and t>22 h. One advantage of simulation is that it allows us to observe operating conditions that could lead to better performance of the process, which may include regions that were not explored in experimentation. The model was evaluated through experimentation and yielded satisfactory results.

These results precisely reveal the desired conditions for an exothermic process like ethanol fermentation. Operating ethanol fermentation above 37°C is crucial for tropical countries due to its significant economic advantages. The advantage lies in the fact that if fermentation is conducted at temperatures higher than 37°C, it becomes easier to control using heat exchangers, especially considering that the cooling water temperature in tropical countries typically ranges from 30-35°C. Moreover, operating at temperatures above 37°C is also an economic advantage for processes with a duration of less than 24 h, as it reduces energy consumption required for cooling equipment. Operating at 37°C is a characteristic of the selected microorganism, which can produce ethanol even at temperatures as high as 45°C. However, operating at such elevated temperatures is not advisable as it negatively affects the viability of the microorganism. Maintaining viability is crucial to reuse the microorganism for multiple cycles of operation.