2.1. Data

In this work, we take the data reported and used in the supplementary information of (^{Li et al., 2019}) as a source of information, whose database consists of 333 records of values taken from research articles. The descriptors used are the composition of the absorbing layer, the bandgap, the difference between the highest energy-occupied molecular orbitals (HOMO) of the HTL layer and the absorbing layer (∆HOMO), and the difference between the lowest energy-unoccupied molecular orbitals (LUMO) of the absorbing layer and the ETL layer (∆LUMO). Also, electrical characteristics are included, the open-circuit voltage Voc, the short-circuit current density Jsc and the fill factor FF. To analyze the relevance of thickness, this value was manually extracted from each scientific article. In those cases where this value was not reported, the authors were contacted directly via e-mail. In total, 221 thicknesses were obtained, so our dataset is limited to this number. This dataset is published in (^{Velez Sanchez et al., 2022}).

2.2. Descriptors

Selecting descriptors is a task of significant importance when applying automatic learning methods. Descriptors must have an implicit meaning and be available, which requires that they be easily reportable and universally reported by authors in scientific papers to be considered. Ideally, the number of descriptors should be reduced to avoid over-fitting problems; and not contain redundant information. However, guaranteeing full compliance with the above conditions is difficult. Recent work has used variables such as bandgap, ∆HOMO, and ∆LUMO to represent the information from which cell characteristics could be predicted (^{Li et al., 2019}; ^{Odabaşı et al., 2019}). In addition, in works such as those presented by ^{Gladkikh et al. (2020)}, ^{Pilania et al. (2016)}, ^{Takahashi et al. (2018)}, ^{Zhang et al. (2020)}, characteristics such as electronegativity, the number of atomic orbitals, the Goldschmidt tolerance factor of the elements that make up the absorbing layer are used to perform prediction or classification tasks in machine learning algorithms. However, no works were found in which the thickness of the absorbing layer is included as a descriptor. In the present work, in addition to the variables already mentioned in previous works, it is desired to use the thickness of the absorbing layer as an input characteristic of the model in charge of estimating the performance in the prediction of output electrical variables such as the short circuit voltage Voc, short circuit current Jsc, the filling factor FF and PCE. In addition to the inclusion of the thickness, a modification was made to the database used, which consisted of changing the coding for the compounds that form the Perovskite, which went from 8 to three variables that were as follows: A = MA - FA - Cs, which groups the compounds used in the Perovskite cation A, B = Pb - Sn and X = I - Br - Cl. This modification was made to make the models used in the linear regression more flexible, thus lowering the complexity of the final model and reducing the effects of over-fitting on the results obtained.

2.3. Mutual information as a measure of nonlinear statistical association

The mutual information ́on between two random variables x, y, denoted as I(x, y) measures the mutual dependence between the two variables; that is, it quantifies the amount of information obtained from one random variable through the observation of the other random variable (^{Bishop, 2006}).

Where I(, y) ≥ 0; and I(x, y) = 0 for the case where x, y are independent variables. The units in which this measure is expressed depend on the type of logarithm; in particular, if the logarithm is in base two, the mutual information is in units of bits. There are several methods for estimating I(-, -); however, in the present work, the k-neighbors-based method, reported in (^{Kraskov et al., 2004}; ^{Ross, 2014}), is used. I(-, -) is calculated between each descriptor A, B, X, Eg, ∆HOMO, ∆LUMO, δ and each electric variable of the solar cell Voc,  Jsc,  FF,  PCE. Those descriptors that offer a low value of mutual information are discarded.

2.4. Multiple linear regression

The regression function is assumed to be linear for the inputs in multiple linear regression. In our case for A, B, X, Eg, ∆HOMO, ∆LUMO, and f(δ). To include the possibility of a nonlinear relationship f(-), in the present work, we evaluated several options with the help of δ vs outputs plots of the collected data. We can obtain nonlinear models with a proper transformation of inputs or output. Although linear regression models are simple, they can sometimes give similar or better results than nonlinear models. Especially in models with a small number of training data (^{Hastie et al., 2009}). Two prediction models are proposed for each k = 1, …,4 performance measure (Voc, Jsc, FF, and PCE). In the first one, thickness is not considered,

Furthermore, in a second model, if the thickness is included.

Where Z= [1 A X Eg ∆HOMO ∆LUMO]; Zδ= [1 A X Eg ∆HOMO ∆LUMO f(δ)]; f(-) is some nonlinear transformation ́on of the descriptor δ, and ε-εδ are prediction errors ́on. To estimate the degree of contribution of the variable δ, we compare the performance of the above two models y(k) and yδ(k) for each kth electrical property. The parameters α(k) and β(k) are found using the least-squares criterion

3.1. Estimation of the degree of statistical-linear association of descriptors

Table (1) reports the estimated bitwise values of the statistical association I(-, -) for different pairs of descriptors vs electrical characteristics. This value was calculated for each pair of variables and 20 different subsets of 177 samples out of 221 (80% of the total), where samples were randomly selected without replacement. Each value reported in Table (1) results from the average of the 20 values obtained for each of the 20 subsets. This strategy allowed us to estimate the standard error associated with each of the estimates and thus develop a t-student hypothesis test to determine whether the estimated values are statistically different from zero. That is, to determine if statistically there is an association. As a result, it is obtained that all except 2 are statistically different from zero. The results show that the absorbing layer's thickness helps explain the behaviour of the Jsc inside the cell. They also allow us to infer that the results obtained for B, formed by B = Pb - Cs, are a product of a large amount of data in which B is lead. Because of this, the metric used cannot perceive the importance of B within the linear regression models.

From the results obtained and summarized in Table (1), the following behaviors are observed, among others: i) thickness as a descriptor plays a significant role in describing the behavior of Jsc, being this the descriptor with the most significant contribution to this electrical characteristic. ii) Under this same working model, descriptors A, X and Eg are the ones that have the most significant contribution to Voc. iii) A comparable situation is found for efficiency (PCE), which presents a contribution from descriptors A and X. These results are consistent with the physical explanation of the phenomenon of photoconversion of radiation into electrical energy in a photovoltaic device. The thickness of the Perovskite layer, playing an indispensable role in photogeneration, influences the generation rate G described in the models reported in the literature (^{Le Corre et al., 2019}). Similarly, the thickness of this absorbing layer affects the transport process of photogenerated carriers to the selective transport layers (ETL and HTL). Hence, as a parameter, it influences the carrier recombination rate (^{Le Corre et al., 2019}). Likewise, Voc and PCE as electrical characteristics are strongly affected by the Eg of the absorber layer (^{Jarosz et al., 2020}), which in turn depends strongly on the chemical composition of the Perovskite, which is described by A, B, and X (^{Kato et al., 2017}).

3.2. Estimation of the performance values

Figure (1) shows the comparison graphs of the descriptor δ versus the main electrical characteristics of the devices. Figure (1c) shows the nonlinear relationship between the thickness δ and Jsc. This nonlinear relationship between thickness and parameters such as Jsc or PCE has been previously described in theoretical reports on this type of device (^{Le Corre et al., 2019}; ^{Sha et al., 2015}). When calculating the linear correlation value (Pearson's correlation) between δ and Jsc, 0.28 is obtained; however, when applying the transformation of the form f(δ) =√δ, this linear correlation value becomes 0.35. Therefore, in the present work, it is preferred to use the transformed variable √δ as input.

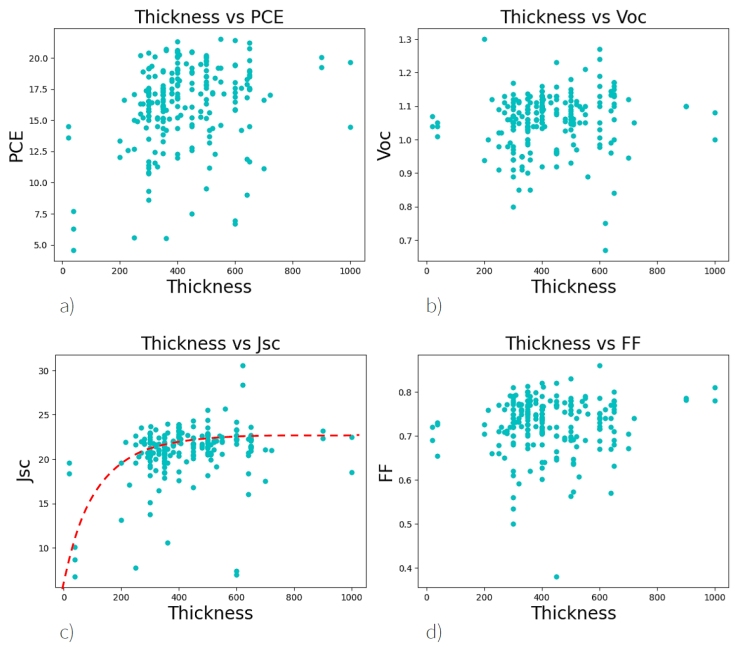
Figure 1 Example of scatter plots of some inputs versus some outputs. a) Thickness vs PCE, b) thickness vs Voc, c) thickness vs Jsc, d) thickness vs FF. 

The Jsc, Voc, FF, and PCE characteristics were estimated using multiple linear regression. For each electrical variable to be estimated, two models were applied by selecting those described in equations 2 and 3 belonging to the Z and Zδ sets, respectively. Due to its low level of nonlinear correlation reported in Table 1, Descriptor B was not considered in any of these models. To estimate the performance of the models, typically measured in terms of root mean square error (RMSE), a cross-validation procedure of 10 partitions is used, where each partition is formed by a training subset of the linear regression model of 199 data, and the remaining 22 are used to measure the performance of the same model. This process is repeated ten times, once for each different participation. Table (2) reports the performance results regarding the mean square error.

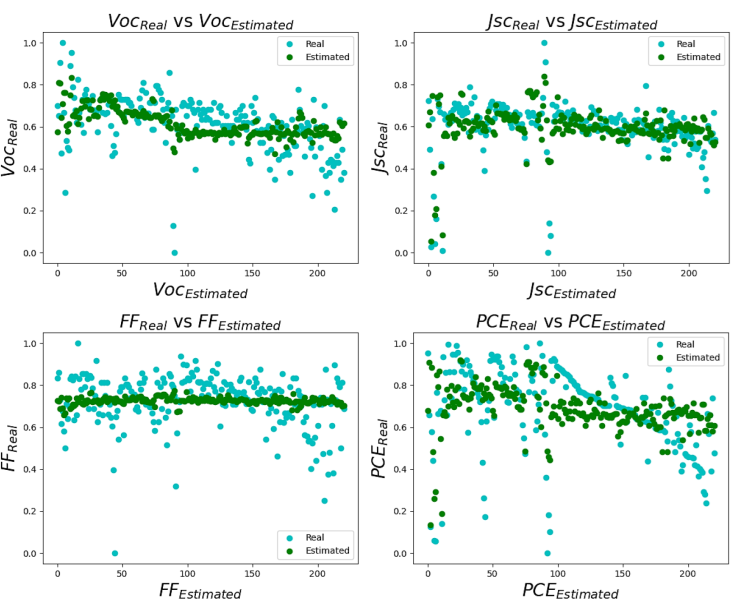
On the other hand, to determine whether the differences in performance in terms of RMSE are statistically significant, a two-sample t-student test is applied. The results show that the inclusion of the thickness of the absorbing layer (√δ) as a descriptor improves the prediction of the Jsc and PCE values. The thickness information, transformed in the √δ form, provides relevant information for Jsc and PCE estimation purposes. As a result, it is found that for the case of Jsc and PCE, the improvement in performance by adding the thickness.

The Jsc, Voc, FF, and PCE characteristics were estimated using multiple linear regression. For each electrical variable to be estimated, two models were applied by selecting those described in equations 2 and 3 belonging to the Z and Zδ sets, respectively. Due to its low level of nonlinear correlation reported in Table 1, Descriptor B was not considered in any of these models. To estimate the performance of the models, typically measured in terms of root mean square error (RMSE), a cross-validation procedure of 10 partitions is used, where each partition is formed by a training subset of the linear regression model of 199 data, and the remaining 22 are used to measure the performance of the same model. This process is repeated ten times, once for each different participation. Table (2) reports the performance results regarding the mean square error.

On the other hand, to determine whether the differences in performance in terms of RMSE are statistically significant, a two-sample t-student test is applied. The results show that the inclusion of the thickness of the absorbing layer (√δ) as a descriptor improves the prediction of the Jsc and PCE values. The thickness information, transformed in the √ δ form, provides relevant information for Jsc and PCE estimation purposes. As a result, it is found that for the case of Jsc and PCE, the improvement in performance by adding the thickness.

To visualize this improvement, we have compared the predictions obtained vs the real values for the four models. Figure 2 shows the behaviors of the estimated values. Of these four models, Jsc's prediction is the best performing.

Figure 2 Estimated values vs real values plot for linear regression model outputs. a) Voc_real vs Voc_estimated, b) Jsc_real vs Jsc_estimated, c) FF_real vs FF_estimated, d) PCE_real vs PCE_estimated.