PACS: 01.50.My; 01.50.P
1. Introducción
En la enseñanza de la física, el laboratorio juega un papel muy importante dentro del aprendizaje significativo como elemento fundamental de interacción del estudiante con las leyes y fenómenos. Hoy en día y gracias al desarrollo tecnológico en los avances de dispositivos móviles como por ejemplo teléfonos celulares inteligentes o Smartphones, tabletas, mini altavoces bluetooth, etc, es cada día más fácil el uso de estos dispositivos para desarrollar experiencias que permiten al estudiante interactuar con los fenómenos y variables físicas 1.
Algunos de los dispositivos móviles que se están construyendo en la actualidad tienen implementado sensores para la medición de variables físicas, como por ejemplo: acelerómetros, sensores hall, giroscopios, barómetros, sensores de luz, termómetros, etc.; además se han desarrollado aplicaciones para Android que utilizan los sensores para medir las respectivas variables físicas. Por lo tanto, estos dispositivos se han convertido en herramientas empleadas por los docentes para diseñar prácticas de laboratorio y al estudiante utilizarlos en la realización de experiencias enfocadas a comprobar leyes o fenómenos físicos.
El presente proyecto muestra cómo implementar experimentos de física de ondas estacionarias en tubos abiertos y cerrados utilizando para ello dos teléfonos celulares inteligentes (smartphones) y un mini altavoz bluetooth. Se emplea en el desarrollo de la experiencia aplicaciones de Android como generador de frecuencias y medidor de espectros.
2. Fundamentos físicos
2.1. Tubos sonoros
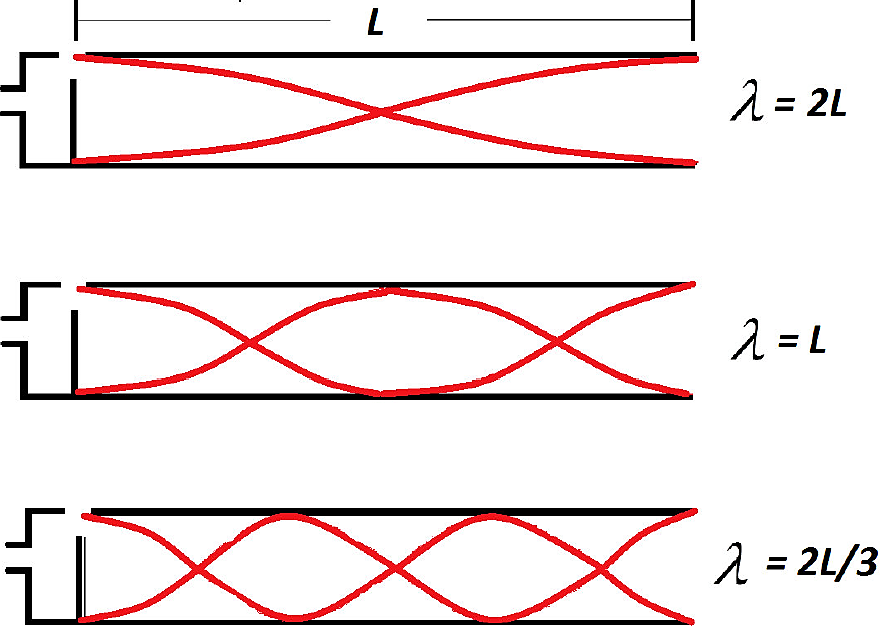
En la Fig. 1 se muestra el esquema de un tubo abierto en ambos extremos el cual tiene longitud L. Cuando el aire entra al tubo se produce una onda de sonido que puede ser descrita mediante el desplazamiento de las moléculas del aire o por la variación de la presión. La onda longitudinal producida viaja en el tubo y se refleja en el extremo abierto produciendo una onda estacionaria. Estas ondas estacionarias producen nodos y antinodos de desplazamiento o de presión. Los nodos de desplazamiento son puntos donde las moléculas de aire no se desplazan mientras que los antinodos de desplazamiento son puntos donde las moléculas de aire tienen máximo desplazamiento. Desde la perspectiva de la expresión de ondas de presión, en el punto donde se forma un nodo de desplazamiento se origina un antinodo de presión y en el punto donde se forma un antinodo de desplazamiento se produce un nodo de presión 2,3,4. En el extremo de un tubo abierto se forma un antinodo de desplazamiento o nodo de presión, por cuanto la presión al interior y en el exterior del tubo es la presión atmosférica.
La relación que existe entre la longitud del tubo abierto y la longitud de onda es:
Donde n es el número del armónico respectivo.
La relación entre la longitud de onda λ y la velocidad del sonido es:
Por lo tanto, la frecuencia es:
Al realizar la gráfica de frecuencia f contra n el resultado es una línea recta con pendiente m = v/2L.
En la Fig. 2 se muestra un tubo cerrado en un extremo y abierto en el otro por donde circula la columna de aire. En el lado cerrado del tubo se origina un nodo de desplazamiento o antinodo de presión por lo que en virtud del fenómeno de superposición de las ondas incidentes y reflejadas se producen ondas estacionarias. La relación entre la longitud de onda y la longitud el tubo cerrado es:
Por tanto, la frecuencia en función del número de armónicos n, correspondiente a los tubos cerrados es:
2.2. Generador de señales
El generador de señales es un instrumento muy utilizado en los laboratorios de física, por cuanto su función es la de generar una señal de voltaje de forma senoidal, cuadrada, diente de sierra o en pulso. Este equipo se puede usar en experimentos de ondas en tubos sonoros, ondas en cuerdas, experimentos de efecto Doppler, etc. Existen diferentes tipos de circuitos de acuerdo al tipo de forma de onda a generar; en el caso de ondas armónicos senoidales se pueden utilizar circuitos operacionales o transistores conectados a circuitos LC sintonizados, pero estos tienen el inconveniente de la variación de frecuencia, entre los que se destacan el Colpitts y el Hartley 5,6, los cuales se utilizan para aplicaciones de radiofrecuencia. Si se desean osciladores de ondas senoidales de baja frecuencia en la gamma del sonido o mayor es común utilizar circuitos osciladores que tienen la forma del diagrama en bloques de la Fig. 3, el cual consiste en un elemento activo: transistor, un mosfet o un amplificador operacional y una red de realimentación positiva constituida por resistores y capacitores. La ganancia del amplificador se encarga de restablecer la energía eléctrica perdida por el sistema. Para que el circuito funcione como un oscilador, la realimentación de lazo cerrado debe producir ganancia mayor que 1, es decir, |Af |>1 y además se satisfagan las condiciones de fase y el criterio de Barkhausen que dice: βA = 1 5,6.
Los osciladores de señales senoidales más utilizados son el de desplazamiento de fase y el de puente de Wien que se muestran en las Figs. 4 y 5 respectivamente. En el primero los circuitos RC producen un corrimiento de fase de 180°, donde la frecuencia y el factor de realimentación β obtenida es:
En el circuito de oscilador en puente de Wien, de la Fig. 5 la realimentación se configura mediante un circuito de resistores y capacitores conectados en puente, donde la frecuencia está dada por:
y la relación
proporciona la ganancia de lazo para que el circuito se mantenga en oscilación.
Para osciladores de onda cuadrada es común utilizar circuitos estables como se muestra en la figura con el circuito integrado LM555 5 donde la frecuencia está dada por:
Además, se fabrican generadores de señal con el circuito integrado XR-2206, el cual consiste en un circuito integrado monolítico capaz de producir una onda senoidal, cuadrada, en rampa y en forma de pulso de alta calidad, con frecuencias de operación entre 0.01 Hz hasta más de 1 MHz, el cual consta de un oscilador controlado por voltaje, multiplicador analógico, conformador de onda y la etapa de amplificación 7.
Para teléfonos celulares inteligentes o Smartphone se han desarrollado aplicaciones en el sistema operativo Android que emulan generadores de funciones. En la Fig. 7 se muestra el generador utilizado para este proyecto, 4.
2.3. Analizador de espectros
Una señal eléctrica se puede analizar o estudiar de dos formas diferentes: en el dominio del tiempo o en el dominio de la frecuencia. El osciloscopio es el instrumento que sirve para visualizar los valores instantáneos de voltaje de la señal eléctrica en el dominio temporal, mientras que el analizador de espectros lo hace en el dominio de la frecuencia. El osciloscopio no separa las señales armónicas presentes, en cambio, el analizador de espectros muestra las diferentes señales presentes en amplitud contra frecuencia. En la Fig. 8 se muestra el diagrama para explicar estos conceptos; en el osciloscopio, en una pantalla (TRC) o display digital se visualizan la mezcla o sumatoria de frecuencias o armónicas, en cambio en el analizador de espectros se observarán las diferentes frecuencias separadas con sus respectivas amplitudes.
Existen diferentes tipos de analizadores de espectros, el analógico, de barrido y el ADS o analizador dinámico de señales el cual utiliza el modelo matemático de la transformada rápida de Fourier.
El analizador de espectros analógico se indica en la Fig. 9, consiste en divisores de potencia que alimentan circuitos pasabanda con su respectivo detector que al final muestra cada señal separada en frecuencia, por lo que a este se le conoce como analizador de tiempo real y tiene el inconveniente de necesitar bancos de filtros para su funcionamiento 10-12.
Otra variante del analizador de espectro es el de barrido, el cual emplea la técnica de heterodinación que utiliza un oscilador local que genera una onda diente se sierra. La señal a estudiar de frecuencia fs se mezcla con la señal del oscilador local fOL produciendo una frecuencia intermedia fFI la cual alimenta un sólo circuito pasabanda para posteriormente ser detectada y mostrada en el TRC o pantalla de estado sólido, Fig. 10.
Actualmente la versión de los analizadores de espectros más utilizada es la que emplea la trasformada de Fourier, para ello la señal es digitalizada mediante microprocesadores o microcontroladores y las visualiza en el dominio de la frecuencia.
Una función periódica se puede representar mediante la serie de Fourier de acuerdo a:
Donde los coeficientes a0, an y bn se denominan coeficientes de Fourier y se definen como:
El primer término de la serie es llamado nivel de continua de la señal y el primer término de las sumatorias se denomina frecuencia fundamental, los demás son los llamados armónicos de orden superior. El número de coeficientes de la serie es infinito, pero si se tiene en cuenta que para los armónicos superiores la amplitud disminuye considerablemente éste se puede reducir 13,14.
La transformada de Fourier, Ec. 14 realiza la función de trasladar la señal en el dominio del tiempo a una función en el dominio de la frecuencia.
En el año 1965 J.W. Cooley y John Turkey desarrollaron el algoritmo matemático denominado FFT o transformada rápida de Fourier con la cual se realizan cálculos más eficientes.
En la Fig. 11 se muestra el diagrama de un ADS, analizador dinámico de señales, el cual consiste en un circuito convertidor análogo a digital, estimación del espectro mediante la transformada rápida de Fourier y la visualización de las señales.
Debido al desarrollo tecnológico actual se pueden desarrollar proyectos de analizadores de espectros utilizando plataformas como: arduino, microprocesadores, raspberry pi, microcontroladores, etc.
Para celulares inteligentes o smartphone que funcionan bajo la plataforma de Android se han desarrollado aplicaciones que utilizan la transformada rápida de Fourier que trabajan como Analizadores de Espectros 15, en la Fig. 12 se muestra una de estas aplicaciones que fue usada en este proyecto.
3. Desarrollo experimental
En la Fig. 13 se muestra una fotografía del minialtavoz bluetooth el cual debe ser vinculado al teléfono celular, este sirve para emitir las ondas de sonido que producen las variaciones de presión en el aire.
En la Fig. 14 se muestra el tubo de cloruro de polivinilo (PVC) de los utilizados en la construcción con diámetro de 5 cm y una longitud de 1.00 m. Se construyeron bases que sostienen el tubo y una mesa donde colocar los dos teléfonos celulares, uno que va enlazado por bluetooh con el mini altavoz que utiliza el generador de ondas senoidales y el otro apuntando directamente su micrófono a la cavidad abierta del tubo, en el caso del tubo cerrado se colocó en un extremo una tapa con un pequeño orificio en el centro y de esta forma detectar las ondas de sonido a través de la aplicación del analizador de espectros.
Para realizar el experimento de las ondas estacionarias con el tubo abierto se varia la frecuencia del generador de ondas comenzando con frecuencias bajas aproximadamente a 100 Hz y aumentando con el ajuste fino hasta que aparezca un pico delgado y alargado que tenga máxima amplitud, como se muestra en la Fig. 15, anotando el valor de frecuencia que marque el generador de señal, este será el primer armónico o frecuencia fundamental. Luego se incrementa la frecuencia hasta encontrar los armónicos superiores deseados, en este caso de ocho (8). En las Tablas I y II, se muestran los resultados obtenidos del número de armónicos y de la respectiva frecuencia para el tubo abierto y cerrado respectivamente.
Tabla I Numero de armónicos n y frecuencia f(Hz). Tubo abierto.
| η | f (Hz) |
| 1 | 168.09 |
| 2 | 337.09 |
| 3 | 504.57 |
| 4 | 672.38 |
| 5 | 840.12 |
| 6 | 1008.29 |
| 7 | 1176.46 |
| 8 | 1348.50 |
4. Resultados y discusión
La Tabla I indica los datos medidos de los primeros ocho armónicos para el tubo abierto, mientras que la Tabla II son para el tubo cerrado.
En la Figs. 16 y 17 muestra la relación de frecuencia contra el número de armónicos para tubos sonoros abiertos y cerrados respectivamente, se observan gráficas lineales con pendiente 168.32 Hz y 85.1 Hz aplicando mínimos cuadrados, de las cuales se calculó la velocidad del sonido en el aire, arrojando como resultado 336.64 m/s para tubos abiertos y 340.4 m/s para tubos cerrados. Tomando como valor teórico de 340 m/s para la velocidad del sonido en el aire, los errores porcentuales de la velocidad del sonido calculada es de 0.988% y 0.118%, lo que permite indicar que los valores obtenidos están muy próximos a los teóricos.
5. Conclusión
Se estudió el comportamiento de las ondas de sonido en tubos abiertos y cerrados utilizando dos teléfonos celulares inteligentes o smartphones y un mini altavoz bluetooth. En uno de los celulares se instaló la aplicación de generador de señales diseñada en Android y en el otro la aplicación de analizador de espectros. Se procedió a vincular el mini altavoz bluetooth el teléfono celular que tiene el generador de señales instalado. Se varió las frecuencias de los armónicos para los dos tipos, se graficaron los datos y realizó el respectivo ajuste por mínimos cuadrados, calculando de la pendiente de la línea recta obtenida la velocidad del sonido en el aire. El resultado de la velocidad fue de 336.64 m/s para el tubo abierto y 340.4 m/s para el tubo cerrado, con porcentajes de errores de 0.988% y 0.118%, que comparados con el valor teórico de 340.0 m/s indica que los valores obtenidos de la ejecución del experimento están muy cercanos a los experimentales reportados.











 nueva página del texto (beta)
nueva página del texto (beta)