Artículos

 

Productos derivados sobre bienes de consumo

 

Francisco Venegas Martínez y Salvador Cruz Ake^1*

 

¹ Escuela Superior de Economía, IPN, E–mail: fvenegas1111@yahoo.com.mx; salcake@yahoo.com, respectivamente.

 

Fecha de recepción: 14/06/2009
Aceptación: 04/05/2010

 

Resumen

Este trabajo de investigación desarrolla un modelo de equilibrio general con expectativas racionales en tiempo continuo útil para la determinación de precios de contratos "forward", contratos futuros, bonos cupón cero y opciones europeas (de compra y venta) sobre bienes de consumo. Para ello, el modelo considera un individuo representativo en una economía con dos bienes, los cuales son producidos con tecnologías estocásticas. Por último, el modelo propuesto permite examinar estrategias para obtener ganancias especulativas mediante el uso de diferentes productos derivados.

Palabras clave: General equilibrium, stochastic optimal control, pricing derivatives on commodities.

Clasificación JEL: E13, C61, G12, G13.

 

Abstract

This paper develops a continuous–time general equilibrium model with rational expectations useful for the determination of prices of forward and future contracts, zero coupon bonds and European (calls and puts) options on consumption goods. To reach this end, the model considers a representative individual in an economy with two goods, which are produced by using stochastic technologies. Finally, the proposed model allows considering strategies aimed in obtaining speculative gains by using different derivative products.

 

Introducción

Un sinnúmero de innovaciones financieras sobre productos derivados, particularmente obligaciones de deuda respaldadas por diversos colaterales con la opción de recompra, y un crecimiento inusual de los montos de operación de estos instrumentos exacerbaron la crisis mundial de principios de 2008 al generar una burbuja especulativa; el resultado, una debacle financiera para la economía más grande del mundo, lo cual sin duda tendría efectos negativos sobre sus socios comerciales y especialmente para México, en donde las secuelas se dejan ver en muchos fundamentales de la economía mexicana.

Los mercados de productos derivados sobre bienes también han mostrado un rápido crecimiento en el mundo. La operación en estos mercados está más ligada a la especulación que a la cobertura y sus potenciales efectos sobre la economía real deberían ser estudiados con más cautela. Es importante destacar que, en la gran mayoría de productos derivados sobre bienes, la entrega nunca es hecha; por lo regular, las posiciones son cerradas antes del vencimiento o, bien, si llegan al vencimiento, sólo se liquidan diferencias, estando presente en la mayoría de los casos la intención de obtener ganancias especulativas. Sin duda, las prácticas en estos mercados deberían ser reguladas de manera más eficiente a fin de evitar catástrofes como las generadas, recientemente, por derivados exclusivamente financieros.

El crecimiento que los mercados de derivados de bienes (o derivados de físicos como una posible traducción de commodities derivatives) han tenido en el mundo es impresionante y se muestra en las Gráficas 1 y 2. Dicho crecimiento se debe en gran medida a la flexibilidad que estos instrumentos proporcionan a sus usuarios para entrar o salir rápidamente del mercado. Asimismo, estos instrumentos presentan un alto grado de liquidez, es decir, un vendedor casi siempre encuentra un comprador y viceversa, De igual forma, los derivados de físicos tienen un alto nivel de apalancamiento, esto es, la inversión inicial es pequeña comparada con el valor del bien subyacente.

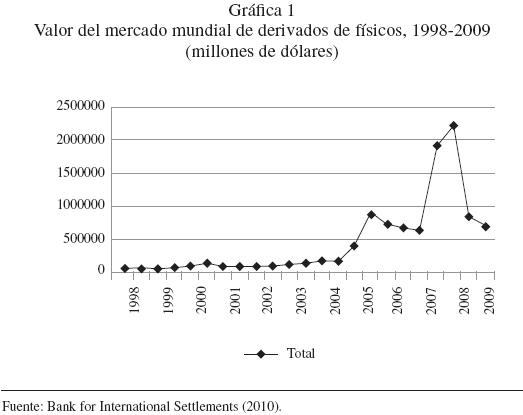
Es importante destacar que el mercado estadounidense de derivados de físicos ha tenido un importante crecimiento en las dos últimas décadas; como se puede apreciar en el Cuadro 1, El Grupo CME (Chicago Mercantile Exchange) es el mercado más grande del mundo y en él se cotiza y negocia una gran diversidad de contratos futuros y opciones de bienes (v.g. trigo, arroz, maíz, sorgo, soya, olivo, canola, café, jugo de naranja, tocino, ganado vivo, leche en polvo, algodón, mantequilla, etc.). Una de las principales causas del crecimiento de este mercado es que el riesgo crédito de estos instrumentos es mínimo debido a la asociación de la bolsa de derivados de físicos con una cámara de compensación y liquidación. Las bolsas internacionales de físicos de mayor crecimiento en el mundo se muestran en el Cuadro 2.

La presente investigación permite un mejor entendimiento sobre la determinación de precios de contratos "forward", futuros, bonos (cupón cero) y opciones (europeas) de compra y venta sobre bienes. Con el fin de determinar los precios de los contratos "forward" y futuros, se desarrolla un modelo de equilibrio general con expectativas racionales en tiempo continuo en una economía con dos bienes, con consumidores idénticos en gustos y dotaciones y con una tecnología que presenta rendimientos constantes a escala. El modelo propuesto presenta y explica en forma precisa y consistente por qué estos contratos son diferentes, cómo se relacionan entre sí y cómo se relacionan con otros precios de la economía, tal como los precios de contado ("spot"). Asimismo, el modelo explica congruentemente cómo el riesgo de mercado se refleja en los precios de los productos derivados.

El modelo determina endógenamente precios de los mencionados contratos utilizando un marco de equilibrio general en el que las preferencias, dotaciones e información de los agentes económicos, así como la tecnología de producción se especifican exógenamente. En consecuencia, los precios de equilibrio están directamente relacionados con las preferencias y con los parámetros asociados al proceso de producción estocástica dentro de la economía. El modelo extiende varios resultados disponibles en la literatura con un único bien. Específicamente se generalizan los modelos de intercambio puro de Rubinstein (1976), Lucas (1978), Johnsen (1978), Brock (1982), Prescott y Mehra (1980) y Cox, Ingersoll y Ross (1985).

Es importante destacar que en el modelo propuesto, un consumidor–inversionista que piensa que el precio del bien subyacente aumentará, con la intención de obtener una ganancia especulativa, toma una posición larga en productos derivados para comprar una unidad del bien subyacente a un precio preestablecido en una fecha futura predeterminada (el vencimiento del contrato). Una propuesta diferente a la de esta investigación para determinar precios consiste en buscar el precio relativo entre dos bienes. Esto es llamado un equilibrio parcial, un modelo bien conocido de este tipo es el modelo de valuación de opciones europeas de Black y Scholes (1973). Mientras que esta propuesta no puede relacionar los precios con las preferencias y con la producción estocástica en una economía, sí permite determinar importantes relaciones sobre los precios relativos o los rendimientos de activos. Al respecto, Breeden (1979), (1980) y Grauer y Litzenberger (1979) examinaron la estructura relativa de los rendimientos de las acciones con procesos estocásticos.

Otra aproximación que explora la relación existente entre derivados y teoría de juegos se puede encontrar, por ejemplo, en Montrucchio y Semeraro (2006) y Grenadier (2000). Aunque esta novedosa relación ha despertado recientemente mucho interés, el objetivo del presente trabajo está más bien alineado con los modelos de equilibrio general que utilizan procesos estocásticos, particularmente el movimiento Browniano (o proceso de Wiener) para examinar el comportamiento de variables financieras y económicas relevantes, en este contexto se señalan, por ejemplo, las investigaciones de: Merton (1971) y (1973), Cox, Ingersoll y Ross (1985) y Venegas–Martínez (2001), (2006a), (2006b), (2008b), (2009) y (2010).

La presente investigación está organizada como sigue. En la siguiente sección se lleva a cabo una breve descripción de productos derivados sobre bienes. En la sección tercera se describen las preferencias de los consumidores, su información y sus dotaciones, asimismo se especifican las posibilidades de producción y de inversión. En la cuarta sección se establece la restricción presupuestal del consumidor representativo y se plantea el problema de decisión de un consumidor racional, adverso al riesgo, sobre consumo y portafolio a lo largo de su vida. En la quinta sección se caracteriza el equilibrio general, en el cual se determinan los precios que continuamente ponen en equilibrio a los mercados. La última sección contiene los principales resultados del presente trabajo de investigación. En esa sección se establecen las principales relaciones funcionales de los precios de equilibrio, los detalles técnicos se trasladan a un apéndice.² Asimismo, se determinan los precios de bonos cupón cero y de opciones europeas sobre una unidad del bien de consumo. Las estrategias para especular con un portafolio de inversión generalizan la propuesta por Cox, Ingersoll y Ross (1981). Se muestra cómo se pueden utilizar contratos futuros para replicar los pagos a partir de un contrato "forward" sobre un número aleatorio de unidades de un bien. Un apéndice contiene los detalles analíticos sobre las condiciones necesarias y suficientes del problema de optimización que resuelven los agentes.

 

Descripción de productos derivados sobre bienes

Antes de entrar de lleno en la descripción del modelo para la determinación endógena de los precios de estos contratos a través de un modelo de equilibrio general, es indispensable definir con precisión los contratos "forward", futuros, bonos y opciones sobre bienes, destacando las similitudes y diferencias.

Contratos "forward" sobre bienes

Un contrato "forward" es un acuerdo entre dos partes (reforzado legalmente con la entrega de garantías por ambas partes) que obliga a una de las partes a comprar y a la otra a vender una unidad de un bien a un precio predeterminado en una fecha futura preestablecida. El precio al cual se llevará a cabo la operación de compra–venta de dicha unidad es llamado precio de entrega y éste se establece (en los términos del contrato) cuando el acuerdo se firma y no se puede cambiar a lo largo de la vida del contrato. Estos contratos son exclusivos de los mercados sobre mostrador, también llamados mercados OTC (por las iniciales en inglés de "Over–The–Counter markets"). Los contratos "forward" son acuerdos hechos a la medida en cuanto a necesidades específicas de las partes: tipo de bien, tamaño del contrato, fecha de vencimiento y lugar y condiciones de entrega.

Un contrato "forward" se firma en dos tantos, uno para cada una las partes. Si, antes del vencimiento, el precio del bien está por arriba del precio pactado, entonces la posición larga puede vender su contrato (su tanto); en caso contrario, la posición corta podrá hacerlo. Para ambas partes, la posibilidad de encontrar compradores dependerá de la demanda por este tipo de contratos. Es importante aclarar que si una posición corta vende su contrato, el contrato no incluye al bien; en consecuencia, si un individuo compra el contrato de una posición corta y dicho individuo llega a la fecha de vencimiento, éste tendrá que comprar el bien para entregarlo a la posición larga; a menos que se especifque en el contrato sólo el pago de diferencias. Como puede observarse, el valor de un contrato "forward" cambia entre el tiempo en que se pacta y la fecha de vencimiento. En el momento en que el contrato se firma, éste carece de valor, pero inmediatamente después, en cuanto el precio del subyacente se mueve, el contrato adquiere un valor diferente de cero que se puede negociar en el mercado.

Los contratos "forward" pueden ser utilizados tanto para especulación como para cobertura. En el primer caso, un agente que cree que el precio del bien subyacente aumentará puede especular tomando una posición larga en un contrato "forward" sobre dicho bien. Similarmente, un agente que piensa que el precio del bien disminuirá puede especular tomando una posición corta en un contrato "forward" sobre dicho bien. Existe una diferencia importante entre especular comprando o vendiendo contratos "forward" sobre el bien y especular comprando o vendiendo el bien. Cuando se compran bienes en el mercado de contado, se requiere de un pago inicial en efectivo igual al valor del bien. Sin embargo, si se utiliza un contrato "forward" sobre el mismo bien, no se requiere de algún pago inicial. Por lo tanto, especular utilizando contratos "forward" proporciona al agente ciertas ventajas. Obviamente, el uso de contratos "forward" para cobertura se puede plantear de manera similar, siendo las intenciones del agente lo que hace la diferencia. Por ejemplo, si un productor requiere comprar, en una fecha futura, un insumo en moneda extranjera y teme que el tipo de cambio se incremente, puede buscar, en el presente, una contraparte que voluntariamente acuerde un tipo de cambio (que cubra al productor sobre futuros incrementos en la divisa) para llevar a cabo la operación de compra de la divisa en la fecha de interés.

Contratos futuros sobre bienes

Los contratos a futuro, contratos futuros o, simplemente, futuros, al igual que los contratos "forward", son acuerdos que obligan a una de las partes a comprar y a la contraparte a vender un activo (financiero) a un precio preestablecido en una fecha futura. Sin embargo, a diferencia de los contratos "forward" que se negocian sobre mostrador, los contratos futuros se cotizan y operan en una bolsa de futuros.³ Este tipo de contratos tiene características estandarizadas, principalmente, en lo que se refiere al tamaño⁴ y a la fecha de vencimiento. Para reforzar el cumplimiento de los contratos, cada una de las partes entrega una cantidad (margen) a un tercero, la cámara de compensación y liquidación, para asegurar el cumplimiento de las obligaciones adquiridas. Los contratos futuros son impersonalizados, es decir, las dos partes que intervienen en el contrato no se conocen entre sí, ya que la cámara de compensación actúa como contraparte de todas las partes. La cámara de compensación también liquida diariamente los contratos, maneja los márgenes y administra el riesgo de incumplimiento, a cambio de una comisión. Es importante destacar que la cantidad que cada una de las partes entrega a la cámara recibe el nombre de margen o aportación inicial para distinguirlo del concepto de garantía, ya que este último se refiere a la entrega de un colateral de por lo menos el valor del activo objeto del contrato.

Por lo anterior, la diferencia de forma entre los contratos "forward" y los contratos futuros es la estandarización de los últimos. La diferencia de fondo es que los contratos futuros se liquidan diario (por una cámara de compensación), mientras que los contratos "forward" se liquidan hasta el vencimiento. El proceso de liquidación diaria es equivalente a pactar todos los días un contrato "forward", de tal manera que un contrato futuro es la suma de contratos "forward" diarios. La distinción entre los pagos de los contratos "forward" y contratos de futuros fue estudiada por Black (1976). Al respecto, Jarrow y Oldfeld (1981) explicaron aún más esta distinción y mostraron que cuando la tasa de interés es constante a todos los plazos, los precios de los contratos "forward" y los contratos futuros coinciden.

Por último observe que, a diferencia de los contratos "forward", en donde sólo se intercambia el bien por efectivo en la fecha de vencimiento, en los contratos futuros cada día (hábil) se revisa si precio del bien está por arriba (debajo) del precio pactado, en cuyo caso la posición larga (corta) recibe la diferencia. Este procedimiento de liquidación diaria se conoce como "mark–to–market". En conclusión, los precios de los contratos "forward" y futuros diferen entre sí porque prometen diferentes pagos, ya que los últimos conllevan un proceso de liquidación diaria.

Bonos cupón cero sobre bienes

Un bono cupón cero sobre un bien es una promesa de pago (impersonalizada) en la que el emisor se compromete a entregar incondicionalmente una unidad de un bien en una fecha futura, la cual será referida como vencimiento del título. El interesado en adquirir este pagaré entrega una cantidad inicial (en términos de bienes) en una fecha previa al vencimiento. Cabe destacar que el propietario de este tipo de instrumentos se encuentra expuesto al riesgo de incumplimiento por parte del emisor. Sin embargo, en todo lo que sigue de la presente investigación se supondrá que todos los bonos sobre bienes son libres de riesgo crédito. Asimismo, si el tenedor de un bono cupón cero requiere liquidez antes del vencimiento y desea vender este certificado, entonces estará sujeto al riesgo de mercado. Por supuesto, si se espera a la fecha de vencimiento para recibir el bien en cuestión, el riesgo de mercado será inexistente.

Contratos de opción sobre bienes

Un contrato de opción de compra es un acuerdo entre dos partes (reforzado legalmente), una de las cuales adquiere el derecho (a cambio de una prima), mas no la obligación, de comprar una unidad de un bien a un precio predeterminado en una fecha futura preestablecida. El vendedor mantiene siempre la obligación de vender si el comprador desea ejercer su derecho (opción) de comprar.

Similarmente, en contrato de opción de venta es un acuerdo entre dos partes, una de las cuales adquiere el derecho, mas no la obligación, de vender un activo, bien o servicio a un precio predeterminado en una fecha futura preestablecida. El comprador mantiene la obligación de comprar si el vendedor desea ejercer su derecho (opción) de vender.

Estos contratos se pueden negociar en los mercados sobre mostrador (mercados OTC) o en bolsas de opciones; en estos últimos, sólo las posiciones cortas (vendedores de derechos de compra y venta) entregan márgenes a la cámara de compensación. Asimismo, la cámara de compensación lleva a cabo el proceso de liquidación diaria. Como en el caso de los contratos "forward" o futuros, los contratos de opción (de compra o venta) también pueden ser utilizados tanto para especulación como para cobertura.

Observe que, en un contrato de opción, sólo la posición larga (comprador del derecho de comprar o vender) puede vender su contrato si el precio del bien está por arriba del precio de ejercicio (para una opción de compra) o si el precio del bien está por debajo del precio de ejercicio (para una opción de venta). No existe incentivo (racional) alguno para que un individuo compre el contrato de opción de una posición corta. Por ejemplo, en el caso de un vendedor de una opción de compra, si el precio del bien se fuera por debajo del precio de ejercicio, la posición corta no podría vender el bien subyacente al precio de ejercicio, ya que la posición larga no ejercería su derecho de comprar. Por último, si el tenedor del derecho sólo puede ejercerlo en la fecha de vencimiento se dice que la opción es europea; si el tenedor del derecho lo puede ejercer en cualquier momento entre las fechas de inicio y vencimiento se dice que la opción es americana. La presente investigación se concentrará en opciones del tipo europeo.

 

Descripción de la Economía

Considere una economía que produce dos bienes y que está poblada por dos consumidores con preferencias y dotaciones idénticas. El supuesto de que los consumidores sean idénticos es mucho menos restrictivo de lo que parece ser, desde el punto de vista de un planeador central (un presidente o un primer ministro) no existe distinción entre sus gobernados cuando se trata de maximizar la satisfacción de la población. El agente representativo desea maximizar su utilidad total esperada a lo largo del tiempo:

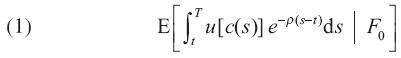
donde c(t) =(c₁(t), c₂(t)) representa el consumo en el tiempo t de los dos bienes existentes en la economía, ρ es la tasa subjetiva de descuento y E es el operador esperanza condicional en toda la información disponible, expresada en F₀. Con el fin de obtener soluciones analíticamente tratables se supondrá que la función de utilidad satisface u[c(t)] = ln(c₁(t) + ln(c₂(t)). De esta manera, el agente representativo es adverso al riesgo. Asimismo, observe que, bajo esta forma funcional, los agentes son adversos al riesgo.

Ambos consumidores tienen dotaciones iguales de los bienes. Supongamos que Y(t) = (Y₁(t), Y₂(t))' es el vector de agregados de cada bien en el tiempo t; entonces Y_i(t) = (y_{i j}(t), y_{i j} (t))' donde y_{i j}(t) representa la dotación del bien i que tiene el consumidor j, donde i = 1, 2 y j = 1, 2. En virtud de que la tecnología de producción presenta rendimientos constantes a escala, cada consumidor tendrá, respectivamente, θY₁(t) y (1 — θ)Y₂(t), 0 < θ < 1, y dado que los agentes son idénticos se debe tomar θ = 1/2. Por último, el consumidor racional tiene que decidir qué cantidad de su dotación consumir y qué cantidad invertir; por lo que es posible definir a y(t) = K(t) + c(t), donde K(t) representa la cantidad total de la dotación invertida por cada consumidor, nuevos bienes destinados a la producción, en el proceso de producción del bien i.

Por otra parte, cada bien es producido por uno y sólo un proceso productivo donde el insumo necesario para la producción del bien i es el mismo bien. Los procesos de producción están dados por una versión estocástica de la tecnología y(t) = AK(t), donde A representa el producto marginal (estocástico) del capital. En virtud de que la tecnología es homogénea de grado uno en K(t), se mantiene el supuesto de rendimientos constantes a escala. El proceso productivo de los bienes de consumo está dado por la siguiente ecuación diferencial estocástica

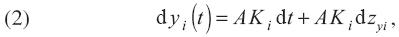
donde y_i (t) representa el nivel de producción de cada bien A=A(t) es el coeficiente estocástico del progreso tecnológico que determina el rendimiento marginal del producto; K_i es el capital invertido en el proceso de producción del bien i, es decir, la producción total destinada a la inversión por parte del consumidor típico; y dz_yi es un proceso de Wiener o movimiento Browniano, el cual se distribuye como una variable aleatoria normal con E[dz_yi] = 0 y Var[dz_yi] = dt. Por lo anterior, la tecnología es estocástica e independiente de las decisiones tomadas por el consumidor. Asimismo, se supone que

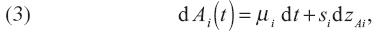
donde el parámetro de tendencia (física) µ_i representa el rendimiento marginal medio esperado del producto y s_i es la volatilidad instantánea del proceso productivo. La economía está entonces caracterizada por el vector de variables tecnológicas A(t) y el vector de niveles de producción y(t). De hecho, es conveniente reescribir (2) y (3) en notación vectorial, de tal forma que:

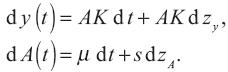
Este sistema de ecuaciones diferenciales estocásticas define el proceso de producción de la economía en cuestión. Se supone la existencia de mercados competitivos para cada uno de los bienes o de los contratos para comprar (o vender) en el futuro dichos bienes con el fin de determinar los precios en el equilibro. En virtud de que las variables de estado resumen el conocimiento del consumidor acerca de la economía, todos los precios de equilibrio pueden ser expresados únicamente como funciones de estas variables de estado. Sea (t) = (y(t), A(t), t) el precio en el tiempo t de algún bien o contrato definido anteriormente. Por el lema de Itô (véanse, por ejemplo, Venegas–Martínez (2008a), Friedman (1975) o Fleming y Rishel (1975) sobre el lema de Itô), la dinámica de (t) satisface:

donde L es el operador diferencial (de cambio marginal en el precio (t) = (y(t), A(t), t) definido por

s = (s ₁, s₂)'. Como una convención en la notación, se definen para cualquier precio los operadores β_π y σ_π dados, respectivamente, por

entonces β_π es la tasa de cambio esperada instantánea en y σ_πσ_π' es la varianza instantánea del cambio en .

Debido a que el modelo está destinado a calcular el precio relativo "spot" de los bienes y el precio de dos tipos generales de contratos definidos anteriormente, se supone que existen mercados "spot" competitivos en los que los bienes disponibles son comercializados continuamente (los mercados nunca cierran). El bien uno es arbitrariamente escogido como el bien numerario, así que su precio en el tiempo t, denotado por P(t), es idéntico a 1 para todo t. El precio relativo "spot" en el tiempo t del otro bien es denotado por P₂(t). Por el Lema de Itô, la dinámica de P(t) está dada por

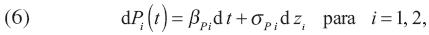
donde β_Pi y σ_{P i} se determinan después de sustituir P_i = en (4) y (5), respectivamente. Si ahora se reescribe (6) bajo notación vectorial, se tiene que

Los consumidores también pueden crear y comercializar contratos en mercados competitivos, los cuales tienen un número de liquidaciones especificadas como función del estado de la economía (y(s), A(s)) para s [t,T], donde el periodo entre t y T es el tiempo de vida del contrato. Se consideran, primero, dos tipos de contratos, los cuales son continuamente comercializados. Los contratos del primer tipo tienen un valor de mercado diferente de cero y tienen su liquidación sólo en el tiempo de maduración, T. Se dirá, en lo que sigue, que estos contratos sólo realizan pagos en la fecha de vencimiento. Ejemplos de este tipo de contratos son los bonos cupón cero sobre bienes (promesas futuras para entregar un bien) y los contratos "forward" que pagan una unidad de un bien al vencimiento. Los contratos del segundo tipo tienen un valor de mercado cero en todos los periodos del tiempo, pero estos contratos tienen liquidaciones continuas. Se dirá que este tipo de contratos realizan pagos continuos. Un ejemplo es el contrato de futuros, el cual tiene un valor cero al inicio, pero sus propietarios obtienen (o pagan) la diferencia entre los precios futuros y pactados a cada instante del tiempo.

El precio del bono de descuento unitario, B₁(t,T), es el precio que deberá ser pagado en el tiempo t, en términos del bien numerario, por la entrega de una unidad del bien numerario en un tiempo futuro T. El bono de descuento unitario tiene asociada una tasa de interés libre de riesgo de incumplimiento e instantánea, r¡, de tal forma que r = – B_x(t,t)/T. Se supone que los consumidores pueden prestar y pedir prestado el bien numerario a una tasa de interés libre de riesgo (de incumplimiento) r.

Los contratos "forward" ya fueron anteriormente definidos. Denote por T el tiempo de vencimiento, t el tiempo actual y F_i(t,T) el precio "forward" (precio justo de entrega) por una unidad del bien i. Asimismo, se denota por V_i(s, T, F_i (t,T)) el valor de mercado en el tiempo s de un contrato "forward" pactado al precio "forward" F_i(t,T). Dado que el contrato "forward" tiene un valor de mercado cero cuando es firmado, se tiene que V_i(t, T, F_i(t,T)) = 0. Observe que en la fecha de vencimiento se cumple que V_i(t, T, F_i(t,T))= P_i(T) — F_i(t,T), lo cual determina las ganancias (o pérdidas) a partir de la compra de una unidad del bien al precio F_i(t,T) cuando el precio "spot" es igual a P_i(T).

Un último tipo de contratos con pago en el vencimiento es una opción europea sobre un bien, es decir, la opción sólo puede ser ejercida en el vencimiento. El tenedor de este contrato sobre el bien i tiene la opción de comprar, es decir, tiene el derecho, mas no la obligación, de comprar una unidad del bien i en un tiempo futuro predeterminado, T, a un precio de ejercicio especificado, Di, en el tiempo t, que será pagado hasta T siempre y cuando se ejerza la opción. Se denotará por G_i(t, T, D_i) el precio (o prima) de una opción sobre un bien, cotizada en el tiempo t, la cual expira en el tiempo T > t.

El único tipo de contratos de pagos continuo que se considera, en esta investigación, es un contrato futuro. En este caso, t denotará el tiempo presente, T la fecha de vencimiento, y f_i(t,T) el precio futuro del bien i. En tiempo continuo, el contrato futuro es firmado a cada instante en el tiempo, t, al nuevo precio futuro f_i(t,T) y, por lo tanto, siempre tiene un valor de mercado igual a cero. Las liquidaciones continuas se determinan por los cambios instantáneos en el precio del futuro.

Sin pérdida de generalidad, se supone que sólo hay un contrato con pago al vencimiento con un valor de mercado denotado por v y un contrato con pago continuo, el cual tiene un valor de mercado cero pero presenta una liquidación estocástica df sobre cada intervalo de tiempo di. Por el lema de Itô, la dinámica de v satisface

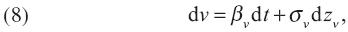
donde β_v y σ_v se encuentran sustituyendo v = en (4) y (5), respectivamente. Similarmente, las liquidaciones estocásticas se determinan mediante

donde β_f y σ_fse obtienen una vez más usando (4) y (5). La principal diferencia entre estos dos tipos de contratos es que un contrato de pagos continuos no requiere de una inversión inicial, sin embargo, presenta liquidaciones continuas de carácter estocástico, mientras un contrato de pago al vencimiento tiene, en general, un valor de mercado diferente de cero, pero provee una única liquidación en la fecha de vencimiento.

 

El problema de optimización del consumo

Frente al conjunto de oportunidades de producción e inversión descrito en la sección anterior, el consumidor debe asignar, en cada momento, proporciones de su riqueza entre invertir en las tecnologías de producción y los dos contratos anteriormente definidos, teniendo también que escoger un vector de consumo, c(t). Sea w(t) la riqueza del consumidor en el tiempo t, es decir, el valor de mercado de todos los bienes y contratos mantenidos por el consumidor. Sea m(t) el número de contratos con pago al vencimiento y n(t) el número de contratos con pagos continuos mantenidos por el consumidor (con valor de mercado cero). Por lo tanto, la riqueza invertida por pedir prestado o prestar a una tasa libre de riesgo está dada por

El cambio en la riqueza del consumidor en el tiempo es la suma de sus ganancias (o pérdidas) debido a la inversión en la producción, contratos con pago en el vencimiento, contratos con pagos continuos o pedir prestado (o prestar) a una tasa de interés constante a todos los plazos y libre de riesgo de incumplimiento. De esta manera, el cambio marginal en la riqueza satisface, por el lema de Itô:

El producto interior en la expresión anterior es tal que dP·dq = tr(σ_PG')dt (esta notación se refiere al producto punto o interior). Por lo tanto,

En la ecuación (12), βw es la tasa de cambio esperado instantánea en la riqueza y σ_wσ_w' es la varianza (matriz de varianzas–covarianzas) de este cambio.

El consumidor (racional) desea maximizar su utilidad esperada, en (1), a lo largo del tiempo sujeto a su restricción presupuestal, dada en (12). De hecho, ya que él toma las funciones de los precios P, v, f y r como dadas, así como las dinámicas del estado de la economía, representadas por las ecuaciones (4) y (5). La teoría estándar de control óptimo (véase, por ejemplo, Venegas–Martínez (2008a)) establece que si las funciones {K_i}, m(w, y, A), n(w, y, A), c(w, y, A) y J(w, y, A) satisfacen la ecuación de Hamilton–Jacobi–Bellman para este problema, entonces m, n y c son decisiones óptimas y J es la función óptima de utilidad (utilidad indirecta, bienestar económico o función de valor). Esto es, J(w, y, A) es la utilidad total esperada por el consumidor a lo largo de su vida generada a partir de su riqueza cuando el estado es igual a (y, A) y sigue este mismo curso en el futuro. La ecuación de Hamilton–Jacobi–Bellman para el problema de un consumidor racional es:

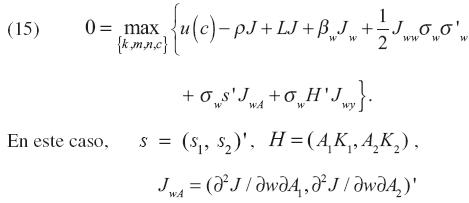
y J _wy=(²J/ wy₁,²J/ wy₂)'. En el apéndice se proporcionan las condiciones necesarias y suficientes (de primer y segundo orden) del problema de optimización del consumidor racional.

Las condiciones de primer orden tienen algunas implicaciones para las demandas por activos de los consumidores en un equilibrio. Su demanda por un activo reflejará no sólo su "trade–off" instantáneo entre riesgo y rendimiento, sino también el uso de los activos como estrategia de especulación aprovechando los cambios en el conjunto de oportunidades de inversión. Por lo tanto, es posible obtener un modelo de determinación de precios de activos de capital con una Beta de acuerdo con Breeden (1979) o un modelo de determinación de activos de capital multifactor como los de Merton (1973) o Richard (1978) y (1979).

 

Equilibrio de mercado

En la sección anterior se vio que, dadas las funciones de precios y las dinámicas del estado de la economía, cada consumidor determina su consumo óptimo y decide cuánto invertir (decisiones de portafolio) al resolver la ecuación (15). En esta sección se especifican las condiciones para el equilibrio de mercado, las cuales permitirán determinar las funciones de precios con las dinámicas del estado de la economía tomadas como dadas por los consumidores. Hay dos tipos de condiciones que definen el equilibrio de mercado, que se describen a continuación.

El primer conjunto de condiciones para el equilibrio de mercado es que los mercados continuamente se vacían en el sentido ordinario de que la oferta se iguala con la demanda. Estas condiciones de equilibrio se cumplen automáticamente en esta economía porque todos los consumidores son idénticos. Por lo tanto, cada consumidor debería invertir la misma proporción q igual del stock agregado de los bienes en todo tiempo t, es decir,

donde η es la constante de proporcionalidad. En virtud de que los consumidores son idénticos, la demanda de equilibrio por contratos con pago al vencimiento y el mercado de bonos para prestar o pedir prestado a la tasa libre de riesgo satisfacen:

Las ecuaciones (16)–(19) implican que, en equilibrio, toda la riqueza se mantiene en los stocks (acervos) de bienes, es decir,

Otra condición para el equilibrio de mercado es que los consumidores tienen expectativas racionales. Por esto se entiende que las funciones de precios y las dinámicas del estado de la economía obtenidas por los consumidores al resolver (15), junto con la restricción presupuestal, son las funciones observadas de precios, las cuales están consideradas en la agregación de las decisiones óptimas de los consumidores. Se ha supuesto de antemano que los consumidores conocen las dinámicas de las variables de estado de la tecnología, (y(t), A(t)), dadas la ecuación (4).

La agregación de la dinámica del stock de riqueza de los consumidores, dada en la ecuación (3), debe ser igual a la dinámica del stock agregado. Un equilibrio con expectativas racionales facilita la búsqueda de las funciones de precios P, v, f y r, así como un valor de la función / y los controles óptimos {K_i}, m, n y c, los cuales satisfacen simultáneamente las ecuaciones (15)–(19).

En el apéndice se proporcionan las fórmulas para las funciones de precios de equilibrio. En la siguiente sección se aplican dichas fórmulas para encontrar los precios de los bonos a descuento sobre bienes (unitario), contratos "forward" y opciones sobre bienes. También se caracteriza el precio de equilibrio de los contratos futuros.

 

Precios de equilibrio de los derivados

En esta sección se presentan las fórmulas generales para determinar los precios de equilibrio de bienes y de contratos sobre bienes. En el apéndice, en las Proposiciones 1 y 2, respectivamente, se obtienen las fórmulas para los contratos con pago al vencimiento y los contratos con pagos continuos. Estos resultados se aplican a continuación para obtener los precios de los contratos en cuestión.

Los precios de todos los contratos sobre bienes que se determinarán en esta sección, excepto por los precios de los futuros, son aplicaciones de una fórmula general para encontrar el valor presente de un flujo riesgoso de bienes. La fórmula general para los contratos es obtenida en la Proposición 1 del Apéndice. A continuación se establece una versión resumida de este resultado:

Teorema 1. Si α_i (T) =α_i (y(T), A(T)) denota una cantidad (posiblemente aleatoria) del bien i para ser recibido en el tiempo T al precio P_i(T), el valor de mercado en el tiempo t de α_i está dado por:

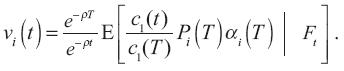
Observe que vi(t) es implícitamente una función del estado actual (y(t), A(t), t) pero esta dependencia ha sido suprimida por conveniencia de notación.

La proposición 1 en el apéndice establece que el valor presente del flujo aleatorio de un bien en el tiempo T se encuentra a partir de los siguientes pasos. Primero se convierte la cantidad aleatoria, α_i(T), al tiempo T, del bien i en una amortización aleatoria del bien 1 al multiplicarlo por P_i(T). Después se transforma la amortización aleatoria del bien numerario en el tiempo T al multiplicarlo por la tasa marginal de sustitución del bien uno entre los tiempos T y t, . Por último, se transforma la amortización del bien numerario en el tiempo aleatorio t a una cantidad determinista al tomar la esperanza condicional en información relevante en t. La proposición 1 extiende los modelos de: Nielsen (1974), Rubinstein (1976), Johnsen (1978), Richard (1978) y (1979), y Cox, Ingersoll y Ross (1985).

El precio de equilibrio en el tiempo t de un bono a descuento, que paga una tasa libre de riesgo (de incumplimiento) sobre una unidad del bien i con vencimiento en el tiempo T, con preferencias logarítmicas, está dado por:

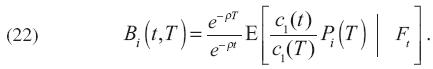
Esto se sigue de la Proposición 1 con α_i 1. En el apéndice también se muestra que

Así, el precio "spot" en el tiempo t del bien i es, por supuesto, la tasa marginal de sustitución entre el bien i y el bien uno, el bien numerario. Si se hace uso de (23), se puede reescribir (22) como:

La expresión anterior proporciona la tasa marginal de sustitución esperada entre el bien 1 al tiempo t y el bien i al tiempo T. En el caso especial del bien numerario se tiene que P₁(T) 1, así que la ecuación (22) se transforma en

Esta fórmula describe el precio del bono real de descuento en el bien numerario y, por lo tanto, puede ser usado para determinar la estructura de plazos de las tasas de interés. De hecho, esta solución generaliza lo encontrado por Cox, Ingersoll y Ross (1985) en una economía de un solo bien. Observe que si la función de utilidad es lineal, se tiene que

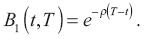
Es decir, el precio del bono sobre el bien numerario se descuenta con la tasa subjetiva de descuento del consumidor representativo.

En lo que sigue, la atención se concentrará en los contratos "forward". El valor de equilibrio de un contrato "forward" sobre el bien i pactado en el tiempo t cuando el precio "forward" es F_i(t, T), con tiempo de madurez T y cotizado al tiempo s, donde t ≤ s ≤ T, está dado por

Lo anterior se sigue a partir de la Proposición 1 con α_i(T)P_i(T) = P_i(T) — F_i(i,T), la diferencia entre el precio spot y el precio futuro del bien /. El valor del contrato en el tiempo T puede ser positivo, cero o negativo según P_i(T) sea mayor, menor o igual que F_i(t,T). En equilibrio, el valor de un nuevo contrato "forward" debería ser cero, es decir, V_i(t,T,F(t,T)) = 0 . Esto implica que

Una vez más, la fórmula para el precio "forward", en equilibrio, tiene una interpretación intuitiva: el valor es igual al costo en el tiempo t de una unidad del bien i para ser entregada en el tiempo T, pero con pagos diferidos hasta el tiempo T. Por último, observe que si se sustituye (27) en (26), se tiene que

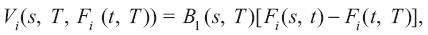
lo cual proporciona el valor de un contrato "forward" obtenido en Jarrow y Oldfield (1981) utilizando un argumento de arbitraje.

Es posible también obtener una expresión alternativa para los precios "forward" utilizando la tasa de interés "forward" observada en el tiempo t, R ^f (t,s) , en términos del bien numerario. En este caso, B₁ (t,T ) puede ser expresado en términos de la tasa de interés "forward" como:

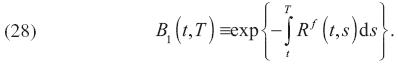
Lo anterior se puede precisar de la siguiente manera. Si se considera un movimiento Browniano 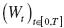definido sobre un espacio fijo de probabilidad con su filtración aumentada, 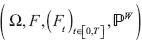donde la filtración representa la información disponible en cada instante t, y se supone que la dinámica de la tasa forward, R^f (t,s), se especifica exógenamente por una ecuación diferencial estocástica con un solo factor de incertidumbre:

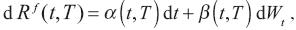
en donde las funciones α y β tienen que satisfacer, casi seguramente con respecto de , las siguientes propiedades:

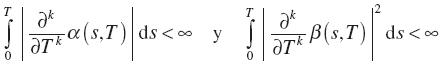
para k = 0,1, en cuyo caso y entonces se puede escribir (28) con la garantía de que la integral allí definida permanezca finita. En este caso, se determina endógenamente el proceso B{t,T) que haga consistentes los supuestos entre la ecuación diferencial estocástica que gobierna la dinámica de R^f(t,s) y la ecuación de valor del bono (28).

Ahora bien, si se sustituyen (22) y (28) en (27), se encuentra que los precios "forward" satisfacen:

Por lo tanto, los precios "forward" dependen de las tasas "forward" de interés. La expresión dada por la ecuación (29) es particularmente útil para comparar los precios futuros y los precios "forward".

El precio futuro de equilibrio cotizado en un contrato de futuros en el tiempo t para el bien i y con un tiempo de entrega T, está dado por⁵

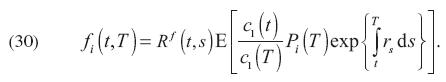
Esta fórmula también se obtiene en el apéndice. En la expresión (30), r_s es la tasa instantánea de interés libre de riesgo (de incumplimiento) del bien numerario.⁶ Esta tasa y su unicidad se definen más precisamente como sigue. Sea {W _t}_{t≥ 0} un movimiento Browniano (proceso de Wiener) definido sobre un espacio fijo de probabilidad ( Ω, F,)I y sea F = {F_t }_t≥0 su filtración aumentada, la cual representa la información del mercado disponible hasta el tiempo t. Se supone que la dinámica estocástica de la tasa corta, r_t, es conducida por una ecuación diferencial estocástica de la forma:

donde µ(r_t ,t) y σ(r_t,t) son procesos adaptados a la filtración F. Como puede observarse, el proceso {W_t }_{t≥ 0} modela el riesgo de mercado. Con el propósito de asegurar que la ecuación diferencial estocástica que conduce la dinámica de la tasa instantánea de interés tenga una solución única, se requiere que µ(r_t,t) y σ(r_t,t) satisfagan la condición global de Lipschitz, a saber,

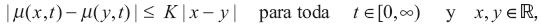
donde K es una constante independiente de x y y, además de la condición de crecimiento

Asimismo, para que la media y la varianza del proceso del proceso de r_t estén bien definidas, se requiere que se satisfagan las siguientes condiciones de integrabilidad, casi dondequiera con respecto de dadas por:

Bajo las condiciones anteriores, existe un único proceso r_t con media y varianza finitas, condicionales en la información en F.

Las ecuaciones (29) y (30) proveen el contraste en cuanto a por qué los precios "forward" y los precios futuros, en general, difieren. Al tiempo t, el precio "forward" es el valor presente de un número conocido, , de unidades del bien i para ser entregadas en el tiempo T. El precio del futuro es el valor presente de un número aleatorio, 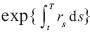, de unidades del bien i para ser entregadas en el tiempo T. Por lo tanto, el precio del contrato futuro representa una especulación simultánea tanto en el precio "spot" del futuro como del número de unidades para ser entregadas, lo cual a su vez es determinado por la tasa de futuros instantánea de interés. En contraste, los precios de los contratos "forward" representan una especulación sobre el precio del futuro "spot". De hecho, el precio futuro, f_i(t,T), es igual al precio "forward", 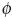_i(t,T), para la entrega de una cantidad aleatoria, 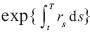, del bien i. Para ver esto, considere un contrato forward firmado en el tiempo t < T, y que en el tiempo T entrega 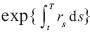unidades del bien i . Observe que la cantidad 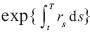es independiente del bien sobre el cual el contrato se firmó y se conoce en el tiempo T. Este contrato "forward" no requiere de pagos en el tiempo t, pero especifica el precio por unidad del bien i, 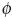_i(t,T), para ser pagado en el tiempo T. Para mostrar que 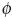_i(t,T) = f_i{t,T) primero observe que los beneficios, Π_i(t,T), realizada en el tiempo T de una posición larga en un contrato "forward" firmado en el tiempo t son

Dado que, en este caso, no se requiere una inversión inicial, se debería tener un equilibrio cuando el valor presente de los beneficios en el tiempo t sea cero. Si se usa α_i(T) P_i(t) = Π_i(t,T) en la Proposición 1 y se multiplica por u₁[c(t)]exp{–ρ(T–t)}, la utilidad marginal del bien numerario descontada subjetivamente, se obtiene

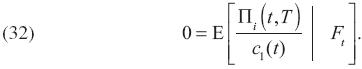
La ecuación anterior dice que el precio "forward", 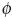_i(t,T), se determina de tal manera que la utilidad marginal esperada de recibir un beneficio, Π_i(t,T), sea igual a P_i(t) – 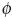_i(t,T) sobre 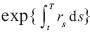unidades del bien i. Asimismo, a partir de la ecuación (32), se encuentra que

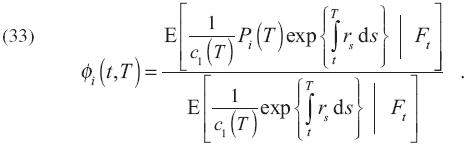
De la misma forma, en el Apéndice, ecuación (A.16), se muestra que

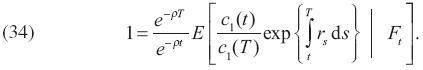
La ecuación anterior dice que el valor presente de las ganancias en el tiempo t de una inversión de una unidad del bien numerario en "rolling–over" bonos de descuento instantáneo, del tiempo t al tiempo T debe ser uno. Si se sustituye (34) en (33), se sigue que

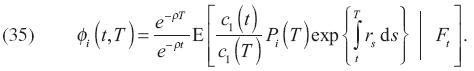
Al comparar (30) con (35), se tiene que (¡)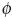_i (t,T) = f_i (t,T).

Si se utiliza una estrategia de portafolio similar a la que en un principio usaron Cox, Ingersoll y Ross (1981), se muestra que sin inversión en el tiempo t, se pueden usar contratos futuros para replicar las amortizaciones en el tiempo T, Π_i(t,T), de los contratos "forward" descritos anteriormente. Si se considera un plan, el cual será llamado "plan forward", de una posición larga en una cantidad 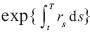de contratos de fufuros con vencimiento en el tiempo T, para cada tiempo entre t y T. Este plan genera en cada tiempo una amortización instantánea

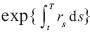d f_i(,T). La reinversión continua de las amortizaciones pasadas y del interés acumulado se lleva a cabo a una tasa de interés instantánea libre de riesgo, r_τ. En este caso, Π_i(,T) denota el valor de este plan en el tiempo . Evidentemente, ya que no fue requerida la inversión, se tiene que Π_i(t,t) = 0 . El cambio en el valor instantáneo, dΠ_i(i,), es la suma de las ganancias de los contratos de futuros y del interés sobre Π_i(i,), de tal forma que

La solución de la ecuación (36), con Π_i(t,t) = 0 , está dada por

Por lo tanto, en el tiempo = T, las ecuaciones (31) y (37) proporcionan expresiones idénticas para Π_i(t,T), ya que f_i(T,T)= P_i(T). Note que el plan "forward" para invertir en un contrato futuro y un contrato "forward" sobre 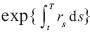unidades de un bien cubre las amortizaciones de manera idéntica en el tiempo T. Esto proporciona la clave para interpretar los precios futuros. Cuando la tasa instantánea spot r es determinista, los precios "forward" y los precios de los futuros coinciden, es decir, F_i(t,T)= f_i (t,T). Este resultado extiende el trabajo de Jarrow y Oldfield (1981), en donde se muestra que F_i(t,T)= f_i (t,T) cuando r es constante.

Por último, se determina la fórmula del precio (prima) de una opción sobre un bien. El precio de equilibrio, G_i (t, T, D_i), de una opción sobre un bien con precio de ejercicio D_i está dado por

Esto se sigue a partir el Teorema 1 con α_i(T)P_i(T) = max {P_i(T) –D_i,0). Intuitivamente, el precio de la opción es el valor descontado de los pagos que serán recibidos en el tiempo T. El factor de descuento es, una vez más, la tasa marginal de sustitución del consumo del bien numerario en el tiempo T y el bien numerario en el tiempo t (véase, al respecto, Venegas–Martínez, 2005). Por último, observe que si la función de utilidad es lineal y r es la tasa de interés libre de riego de incumplimiento y σ es la volatilidad instantánea de P_i(t), la cual se supone constante, entonces

donde la función Φ(d) es la función de distribución acumulada de una variable aleatoria normal estándar, Z ~ N (0,1) , es decir,

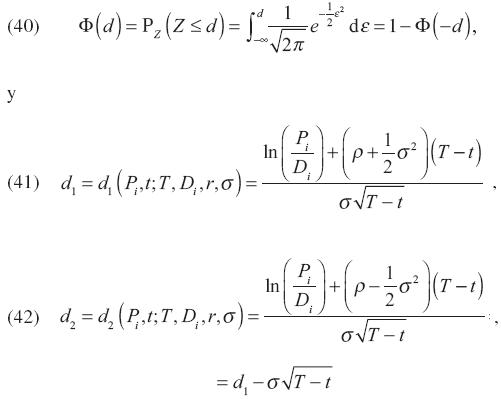
la cual coincide con la fórmula tradicional obtenida por Black–Scholes en (1973), en donde la tasa de descuento es la tasa subjetiva.

 

Conclusiones

En virtud de que, en todo el mundo, los mercados de productos derivados sobre bienes han mostrado incrementos sustanciales en el monto de sus operaciones y la operación en estos mercados está ligada a la generación de ganancias, es indispensable analizar, con más cautela, sus potenciales efectos sobre la economía real. Un buen comienzo para este análisis es contar con una explicación de la determinación de precios de productos derivados sobre bienes, destacando cómo estos derivados se relacionan entre sí y cómo se relacionan con otros precios de la economía.

Mucha investigación se ha realizado sobre valuación de productos derivados financieros y muy poco se ha estudiado sobre derivados de bienes. En este trabajo se ha desarrollado un modelo de equilibrio general con expectativas racionales en tiempo continuo que proporciona una fórmula general del valor presente de un flujo riesgoso de bienes. La aplicación de dicha fórmula a varias situaciones ha permitido la determinación de precios de contratos "forward", contratos futuros, bonos cupón cero y opciones europeas (de compra y venta) sobre bienes de consumo.

Las dinámicas estocásticas de las diferentes variables financieras y económicas (endógenas y exógenas) que se consideran en la economía bajo estudio han sido modeladas a través del movimiento Browniano (o proceso de Wiener). Es importante destacar que el modelo propuesto permite examinar estrategias de especulación con distintos productos derivados.

Por último se debe mencionar que el modelo se puede generalizar en diferentes direcciones, por ejemplo, la inclusión de saltos en los precios de los bienes y la consideración de valores extremos en dichos saltos.

 

Bibliografía

Bank for International Settlements (2010). http://www.bis.org/statistics/derdetailed.htm        [ Links ]

Black, F. (1976). "The Pricing of Commodity Contracts". Journal of Financial Economics, Vol. 3, No. 1–2, pp. 167–179.         [ Links ]

Black, F. y M. Scholes (1973). The Pricing of Options and Corporate Liabilities, Journal of Political Economy, Vol. 3, No. 81, pp.637–659.         [ Links ]

Breeden, D. T. (1979). An Intertemporal Asset Pricing Model with Stochastic Consumption and Investment Opportunities, Journal of Financial Economics, Vol. 7, No. 3, pp. 265–296.         [ Links ]

Breeden, D. T. (1980). Consumption Risks in Futures Markets, Journal of Finance, Vol. 35. No. 2, pp. 503—520.         [ Links ]

Brock, W. A. (1982). Asset Prices in a Production Economy, in J. J. McCall (ed.) The Economics of Information and Uncertainty, University of Chicago Press.         [ Links ]

Cox, J. C., J. E. Ingersoll y S. A. Ross (1981). The Relation between Forward Prices and Futures Prices. Journal of Financial Economics, Vol. 9, No. 4, pp. 321–346.         [ Links ]

Cox, J. C., J. E. Ingersoll y S. A. Ross (1985). A Theory of the Term Structure of Interest Rates. Econometrica, Vol. 53, No. 2, pp. 363–384.         [ Links ]

Fleming, W. H. y R. W. Rishel (1975). Deterministic and Stochastic Optimal Control, Springer Verlag, New York.         [ Links ]

French, K. R. (1981). A Comparison of Futures and Forward Prices. Journal of Financial Economics, Vol. 12, No. 3, pp. 311–342.         [ Links ]

Friedman, A. (1975). Stochastic Differential Equations and Applications. Vol. I, Academic Press, New York.         [ Links ]

Grenadier, S. (2000). Game Choices. The Intersection of Real Options and Game Theory, RiskBooks. Incisive Financial Publishing Limited. England.         [ Links ]

Grauer, F. L. A. y R. H. Litzenberger (1979). The Pricing of Commodity Futures Contracts, Nominal Bonds and Other Risky Assets under Commodity Price Uncertainty, Journal of Finance, Vol. 44, pp. 69–84.         [ Links ]

Jarrow, R. A. y G. S. Oldfield (1981). Forward Contracts and Futures Contracts, Journal of Financial Economics, Vol. 9, No. 4, pp. 373–382.         [ Links ]

Johnsen, T. H. (1978). The risk structure of security prices: Notes on multi–period asset pricing, Working paper, July (Columbia University, New York).         [ Links ]

Lucas, R. F. (1978). Asset Prices in an Exchange Economy. Econometrica, Vol. 46. No. 6, pp. 1429–1445.         [ Links ]

Merton, R. C. (1971). Optimal Consumption and Portfolio Rules in a Continuous–Time Model, Journal of Economic Theory. Vol. 3. No. 4, pp. 373–413.         [ Links ]

Merton, R. C. (1973). An Intertemporal Capital Asset Pricing Model. Econometrica, Vol. 41, No. 5, pp. 867–887.         [ Links ]

Montrucchio, L., Semeraro, P. (2006). Refinement Derivatives and Values of Games, Fundazione Collegio Carlo Alberto, www.collegiocarloalberto.it        [ Links ]

Nielsen, N. C. (1974). The Firm as an Intermediary between Consumers and Production Functions under Uncertainty, Unpublished doctoral dissertation, Jan. Graduate School of Business, Stanford University, Stanford, CA.         [ Links ]

Prescott, E. C. y R. Mehra (1980). Recursive Competitive Equilibrium: The Case of Homogeneous Households, Econometrica, Vol. 48, No. 6, Sept. pp. 1365–1379.         [ Links ]

Richard. S. F. (1978). An Arbitrage Model of the Term Structure of Interest Rates, Journal of Financial Economics, Vol. 6, No. 1, pp. 33–57.         [ Links ]

Richard, S. F. (1979). A generalized capital asset pricing model, in: E. J. Elton and M. J. Gruber, eds. Portfolio theory 25 years after: Essays in honor of Harry Markowitz North–Holland, Amsterdam.         [ Links ]

Rubinstein, M. E. (1976). The Valuation of Uncertain Income Streams and the Pricing of Options, Bell Journal of Economics, Vol. 7, No. 2, pp. 407–425.         [ Links ]

Sundaresan, M. (1980). A Study of Commodity Future Prices, Unpublished doctoral dissertation, Sept. Graduate School of Industrial Administration. Carnegie–Melton University, Pittsburgh, PA.         [ Links ]

Venegas–Martínez, F. (2001). Temporary Stabilization: A Stochastic Analysis. Journal of Economic Dynamics and Control, Vol. 25, No. 9, pp. 1429–1449.         [ Links ]

Venegas–Martínez, F. (2005). Bayesian Inference, Prior Information on Volatility, and Option Pricing: A Maximum Entropy Approach. International Journal of Theoretical and Applied Finance, Vol.8, No. 1, pp. 1–12.         [ Links ]

Venegas–Martínez, F. (2006a). Stochastic Temporary Stabilization: Undiversifable Devaluation and Income Risks. Economic Modelling, Vol. 23, No. 1, pp. 157–173.         [ Links ]

Venegas–Martínez, F. (2006b). Fiscal Policy in a Stochastic Temporary Stabilization Model: undiversifable Devaluation Risk. Journal of World Economic Review, Vol. 1, No. 1, pp. 13–38.         [ Links ]

Venegas–Martínez, F. (2008a). Riesgos financieros y económicos (productos derivados y decisiones económicas bajo incertidumbre, 2da. edición, Cengage Learning Editors (anteriormente International Thomson Editors), México.         [ Links ]

Venegas–Martínez, F. (2008b). Real Options on Consumption in a Small Open Monetary Economy. Journal of World Economic Review, Vol. 3, No. 2, pp. 105–115.         [ Links ]

Venegas–Martínez, F. (2009). Temporary Stabilization in Developing Countries and Real Options on Consumption. International Journal of Economic Research, Vol. 6, No. 2, 237–257.         [ Links ]

Venegas–Martínez, F. (2010). "Fiscal Policy in a Stochastic Model of Endogenous Growth: the Mexican Case". Indian Development Review: An International Journal of Development Economics, Vol. 8, No.1–2, pp. 139–157.         [ Links ]

 

Notas

* Agradecemos los comentarios de los árbitros anónimos.

² Están disponibles previa solicitud a los autores o, bien, pueden ser consultados en el sitio de internet de EconoQuantum, http://econoquantum.cucea.udg.mx/?page_id=13.

³ Un mercado reconocido por las autoridades financieras y organizado y especializado para este tipo de transacciones.

⁴ El tamaño de los contratos ya ha sido estandarizado a una unidad de un bien.

⁵ Cox, Ingersoll y Ross (1985) también presentan una fórmula para el precio futuro sobre un bono a descuento.

⁶ Sundaresan (1980) escoge una clase particular de funciones de utilidad y funciones de producción y derivados acercándose a las soluciones de la forma de (29) y (30). French (1981) compara precios "forward" y precios futuros observados bajo el supuesto de que la utilidad marginal de la riqueza es constante.