Introducción
El uso de la bioimpedancia en aplicaciones médicas es cada vez más habitual, debido a que es una técnica mínimamente invasiva y de bajo costo en comparación a otras técnicas para la detección de carcinomas (Ng et al., 2008), (Zou y Gou, 2003). La Espectroscopia de Impedancia Eléctrica (EIE) y la Tomografía de Impedancia Eléctrica (TIE), han sido empleadas en temas relacionados al cáncer de mama. La EIE permite caracterizar las propiedades dieléctricas de los tejidos biológicos a partir de mediciones de impedancia eléctrica de estos. Los parámetros de la bioimpedancia dependen principalmente de la morfología celular y se han utilizado como medida de contraste para diferenciar patologías (Halter, Hartov y Paulsen, 2008), (Surowiec et al., 1988), (Jossinet y Schmitt, 1999). La TIE permite reconstruir imágenes de la distribución de las conductividades de un dominio de interés a partir de las mediciones de voltaje en electrodos que se encuentran en los límites del dominio (Harikumar, Prabu y Raghavan, 2013). Se han propuesto varios métodos numéricos para resolver el problema inverso de la TIE. En general, se pueden dividir en dos grupos, métodos directos e iterativos. Los métodos directos utilizan un solo paso matemático para calcular la distribución de conductividad a partir de los voltajes medidos y la matriz de sensibilidad. Los métodos iterativos optimizan un conjunto de funciones objetivas de forma iterativa hasta que se alcanzan condiciones estables. En la Tabla 1 se muestran algunos de los principales métodos y algoritmos empleados para la reconstrucción e imágenes (Nombo, Mwambela y Kisangiri, 2016). Así mismo, diversos grupos de investigadores han desarrollado diferentes técnicas en la obtención de imágenes para lograr la localización de carcinomas mamarios (Wang et al., 2001), (Zou y Guo, 2003). La calibración y validación de sistemas biomédicos basados en TIE o EIE se lleva a cabo mediante mediciones de impedancia en emuladores del tejido biológico considerado y en algunos casos se realizan comparaciones con otros sistemas o metodologías (Harikumar, Prabu y Raghavan, 2013), (Sadlier et al., 2013). El trabajo de (Quiao et al., 2007) presenta modelos que emulan los principales tejidos mamarios incluyendo tumoraciones con dimensiones de 2 a 8mm. Las mediciones de impedancia se realizaron mediante el sistema EIM de Montfort MK3 (Wang et al. 2001). Como resultado se observó que al variar la conductividad de la solución salina, ubicada entre los electrodos y los emuladores de agar-agar, es posible reconstruir imágenes que muestran la ubicación de las tumoraciones simuladas.
Tabla 1 Métodos empleados para la reconstrucción de imágenes de TIE.
| Directos | Iterativos |
| Linear Back Projection (LBP): en una sola iteración se obtiene la distribución de conductividad a partir de las mediciones de voltaje en el límite del dominio. La imagen obtenida provee información cualitativa, la cual depende del número de mediciones. | Landweber and Projected Landweber Iteration: es usado para resolver problemas lineales inversos. Requiere de un factor de relajación y un vector de la imagen inicial. A pesar de ser el método iterativo más rápido, requiere muchas iteraciones para alcanzar condiciones estables. Lo que hace a este método inapropiado para reconstrucciones de imágenes on-line o en tiempo real. |
| Singular Value Decomposition (SVD): es un método basado en la factorización matricial que tiene aplicación en el cálculo del inverso generalizado de una matriz no cuadrada, al generar una matriz seudo inversa. Sin embargo, el método reconstruye imágenes con cualidades insatisfactorias. | Iterative Linear Back Projection (ILBP): es una generalización iterativa del método LBP que involucra un factor de ganancia que debe permanecer constante. Solo se emplea un conjunto de datos de medición en cada iteración, generando imágenes que sufren del ruido existente en las mediciones de potencial en el límite del dominio. Esta situación se puede mejorar al utilizar la técnica de reconstrucción de imágenes simultánea. |
| Tikhonov Regularization (TR): en este método el inverso de la matriz sensibilidad se obtiene con la adición de un parámetro regulador, cuyo valor influye directamente en la calidad de la reconstrucción de la imagen. Valores bajos de este parámetro generan una buena aproximación de la distribución de conductividad, pero la solución se verá afectada con el error en las mediciones de potencial. Por otro lado, valores altos en el parámetro de regularización minimizan el error de las mediciones de potencial, pero incrementan el error en la aproximación de la distribución de conductividad. Generalmente, la elección del valor del parámetro de regularización es elegido empíricamente. | Iterative Tikhonov Reconstruction (ITR): este método es una generalización de Tikhonov Regularization. Los resultados son mejores en comparación con muchos de los métodos directos. Sin embargo, este método es computacionalmente ineficiente y solo puede usarse para aplicaciones off-line y de investigación en laboratorios. |
| Model-Based Reconstruction: en este método la diferencia entre las conductividades medidas y estimadas se minimiza al alterar la distribución de la constante dieléctrica aplicada como entrada al modelo del sensor. El proceso se repite hasta que la diferencia entre conductividad simulada y medida es menor que el valor predefinido. Se debe considerar que el algoritmo es lento y por lo tanto se recomienda emplearlo en aplicaciones off-line. | |
| Optimization Reconstruction Methods: existen distintos métodos de optimización (Modelado matemático difuso, algoritmos genéticos, redes neuronales, etc.) que pueden ser utilizados para resolver el problema inverso de la reconstrucción de imágenes. Sin embargo, se debe considerar el ruido computacional y experimental debido a la naturaleza mal planteada del problema inverso. Ya que encontrar una solución basada en la minimización del error de la función del problema directo no garantiza una solución óptima. |
Por otro lado, en (Halter, Hartov y Paulsen, 2008) se reporta la optimización de un sistema de medición de bioimpedancia que utiliza cuatro arreglos circulares de 16 electrodos de Ag/AgCl. Durante la experimentación lograron obtener imágenes para localizar objetos dentro de un tanque con solución salina de conductividad cercana a los tejidos mamarios. Una configuración de electrodos novedosa aparece en (Lee et al., 2012), donde la reconstrucción de TIE se logra mediante cambios de los niveles de voltajes a diferentes frecuencias. Sin embargo, la simulación de la propuesta presenta imágenes de poca precisión.
En (Kantartzis, Abdi y Liatsis 2013) se reporta una evaluación exhaustiva de los sistemas TIE utilizando varios patrones de inyección de corriente, donde numéricamente se demuestra que la variación tanto de la distribución como del número de electrodos utilizado tiene un efecto en la calidad de detección de carcinomas mamarios en las imágenes obtenidas a través del sistema de medición TIE. En (Halter et al., 2014) se reporta la obtención de imágenes TIE de un globo de látex pulsante, que emula la vascularización de un tumor, sumergido en líquido salino dentro de un tanque con electrodos colocados en su periferia. A pesar de que la propuesta utiliza un análisis que requiere un post procesamiento y manipulación de las mediciones obtenidas, los resultados obtenidos son sustancialmente mejores que los reportados en un trabajo anterior sobre imágenes TIE estáticas y absolutas de la mama (Poplack et al., 2007). En la metodología TIE rotativa el sensor gira alrededor del dominio de interés y es capaz de obtener más información que un sistema estático de electrodos. Como resultado se obtienen reconstrucciones más precisas con contraste mejorado y una capacidad para distinguir inclusiones en tanques cilíndricos y en forma de copa (Murphy, Mahara y Halter, 2016). El trabajo publicado por (Murphy et al., 2017) describe una técnica que combina la TIE con la información espacial proporcionada por el ultrasonido. Las imágenes reconstruidas muestran con precisión la conductividad de un emulador de tumor/inclusión dentro de un tanque cilíndrico. Sin embargo, no es posible detectar tumores menores a 1.8 cm. Los trabajos de (Trokhanova, Okhapkin y korjenevsky, 2008) y (Pak et al., 2012) reportan imágenes TIE anatómicamente cercanas a las obtenidas por el ultrasonido en más de 100 mujeres evaluadas. El sistema empleado utiliza 256 electrodos de acero inoxidable montados en una placa y emplea el algoritmo Back Proyection para la reconstrucción de imágenes (Cherepenin, 2002), (Cherepenin, 2001). Se debe considerar que en esta técnica la calidad de las imágenes depende de la destreza del usuario final para manipular la sonda de medición.
Además del uso de la TIE en la localización de carcinomas mamarios, se tiene una amplia gama de aplicaciones clínicas entre las que se han reportado: evaluación dinámica cardiovascular (Kerrouche, McLeod y Lionheart, 2001), (de Gelidi et al., 2020); ventilación pulmonar (Ferichs, 2000), (de Castro Martins et al., 2019); vaciado gástrico (Nakae et al., 1999), (Vaisman et al., 1999); y la respuesta neuronal evocada (Tidswell et al., 2001a), (Tidswell et al., 2001b), (Hannan et al., 2020).
En este trabajo se presenta la reconstrucción de imágenes a partir de la medición de la impedancia empleando el método Linear Back Proyection (LBP) con la finalidad de obtener información de la ubicación de emuladores de carcinoma insertados en modelos experimentales de agar-agar en forma de mama femenina. Los resultados obtenidos se comparan con la posición real de los emuladores del carcinoma y además se contrastan con la localización obtenida con un algoritmo reportado llamado Circulo Rastreador de Anomalías (CRA).
Método
Marco teórico
Para el desarrollo de este trabajo se utilizó la medición bipolar, la cual emplea el mismo par de electrodos para hacer la inyección de corriente y la medición de voltaje. Los valores de las frecuencias de la corriente inyectada se seleccionaron en un rango donde los efectos de los campos magnéticos pueden ser despreciables. Por lo tanto, la ecuación de Poisson, junto con las condiciones de contorno de Neumann, definen la distribución de potenciales dentro del dominio de interés y el comportamiento del límite del dominio respectivamente (Ma et al., 1997).
Donde: J es la densidad de corriente inducida; σ es la conductividad eléctrica; Φ es el potencial eléctrico; Vm el voltaje presente en electrodos de medición; y N es el vector normal al electrodo de interés.
Generalmente, se emplea software de elemento finito para resolver la ecuación 1 y obtener Vm a partir de la densidad de corriente y la distribución de conductividad eléctrica. Lo anterior se le conoce como “el problema directo” y puede representarse de forma lineal y discreta mediante el producto matricial (Holder, 2004):
Donde: B es el vector columna que contiene las M mediciones de voltaje esperadas en los límites del sistema; S es la matriz de sensibilidad; y G es el vector que contiene los valores de conductividad para cada uno de los P píxeles en la imagen que representan una discretización, por elemento finito, de la distribución de la conductividad en el dominio de interés; en este caso P = 1024 pixeles (resolución del campo). El valor de cada P píxel está relacionado con el conjunto de cambios de gradiente de voltaje normalizado (Dikin y Wang, 1996).
Los mapas de sensibilidad son una representación de la respuesta de los electrodos del sistema de medición a un estímulo individual en el área de detección. Los mapas de sensibilidad se pueden medir directamente desde los electrodos, al medir la respuesta de cada uno de estos cuando está presente una señal de excitación. Sin embargo, una forma más práctica y rápida de obtener los mapas de sensibilidad es calcularlos con la ecuación (Zhang, 2011), (Frías y Yang, 2017a), (Frías y Yang, 2017b):
Donde: Φi y Φj son los potenciales presentes en los pixeles P (x,y) de interés; mientras que Ai y Bj son la distribución de las corrientes inyectadas por cada par de electrodos.
Para conocer la distribución de los materiales u objetos dentro del dominio se debe de resolver “el problema inverso”, que consiste en determinar la conductividad a partir de las mediciones de voltaje tomadas en el límite del dominio de interés a través de los electrodos de medición (Holder 2004), esto es:
Sin embargo, como el número de mediciones independientes es considerablemente
menor que el número de pixeles, la matriz de sensibilidad S no
es cuadrada, por lo que se debe emplear la transpuesta de la matriz de
sensibilidad ST. En consecuencia,
se obtiene una aproximación del vector de conductividades
La normalización de la conductividad aproximada
Donde: Bi es el voltaje normalizado en cada par de electrodos i; S es el mapa de sensibilidad para cada par de electrodos; siendo m el número de mediciones independientes.
Experimentación
En este trabajo se utilizó la metodología de medición presentada en (Gutiérrez-López et al., 2019) consistente en: un arreglo anillar de ocho electrodos de Ag/AgCl, los cuales son típicamente empleados en aplicaciones de TIE (Hähnlein et al., 2011), un sistema selector de pares de medición, un analizador de impedancias HIOKI 3532-50 y una computadora para el análisis datos. Este sistema realiza 56 mediciones de impedancia de manera sistemática para cada una de las frecuencias de excitación (500Hz, 1kHz, 5kHz y 10 kHz).
Para la experimentación con emuladores de tejidos se utilizaron modelos de agar-agar con forma de mama femenina. Los cuales representan la distribución anatómica de los principales tejidos que componen una mama femenina: tejido graso, glándula mamaria y carcinoma. Las conductividades empleadas son: 0.023 S/m para el tejido graso, 0.22 S/m para la glándula mamaria y 1.125 S/m para el carcinoma (Jossinet y Schmitt, 1999), (Sadlier et al., 2013). En total se definieron y elaboraron siete modelos experimentales, los cuales fueron utilizados en (Gutiérrez-López et al., 2019) (ver Tabla 2).
Tabla 2 Modelos experimentales con forma de mama femenina.
| Modelo experimental | Descripción |
|---|---|
| 1 | Representa una mama sin carcinoma |
| 2 | Un carcinoma de 1cm frente del electrodo 1 |
| 3 | Un carcinoma frente del electrodo 7 |
| 4 | Un carcinoma de 1.5 cm fragmentado, entre los electrodos 5 y 6 |
| 5 | Un carcinoma de 2 cm detrás del pezón |
| 6 | Un carcinoma de 1 cm con 30 % de la conductividad reportada, colocado frente al electrodo 1 |
| 7 | Un carcinoma de 1 cm con 70% más de la conductividad reportada, colocado frente al electrodo 1 |
Reconstrucción de imágenes TIE
Para la reconstrucción de imágenes a partir de las mediciones de impedancia de los modelos experimentales se utilizó el algoritmo LBP, con el cual se determina el vector de conductividad mediante la ecuación 8. En la TIE 2D cada par de electrodos de conducción crea una distribución de curvas equipotenciales en el domino 2D que termina perpendicularmente en el límite del dominio de interés. Para reconstruir la imagen de conductividad en el método LBP, el gradiente de voltaje normalizado entre dos curvas equipotenciales en el límite se retroproyecta en el valor de conductividad en la región equipotencial encerrada por las dos curvas para todas las combinaciones de medición/inyección (Khalighi y Mikaeili, 2019). Sin embargo, previo a ello se determina la matriz de sensibilidad con los mapas de sensibilidad de cada par de electrodos que componen las 56 mediciones de impedancia.
El modelo computacional de un corte transversal de la mama sin carcinoma y el arreglo anillar de ocho electrodos fueron diseñados mediante el software especializado COMSOL Multiphysics 5.1. La simulación de las propiedades del modelo se llevó a cabo mediante la incorporación de las ecuaciones (1)-(4), con lo que se establecieron las conductividades del tejido graso y glándula mamaria (ver Fig. 1a). A través de la simulación se obtuvieron las distribuciones de potenciales y corrientes para un determinado par de electrodos (ver Fig. 1b). El mapa de sensibilidad para cada par de electrodos se obtuvo aplicando la ecuación 6 a la distribución de potenciales y corrientes obtenida, ello fue realizado en MATLAB.
Resultados
Se obtuvo una matriz de sensibilidad con dimensiones 1024x56, donde cada mapa de sensibilidad tiene 1024 elementos. En la Fig. 2 se muestran las simulaciones en COMSOL de los pares de electrodos consecutivos E2-E5, E2-E6 y E2-E7, donde el electrodo 2 (E2) es la fuente de corriente. Los mapas de sensibilidad muestran las zonas sensibles de cada par de electrodos (ver Fig. 2a) al establecerse un diferencial de potencial (ver Fig. 2b).

Fig. 2 Simulaciones de tres mediciones consecutivas dentro del barrido de electrodos: a) Mapas de sensibilidad; b) Distribución de potenciales.
Posteriormente a la obtención de la matriz de sensibilidad, se utilizaron los datos de las mediciones de impedancias realizadas en los modelos de mama en agar-agar reportadas en (Gutiérrez-López et al., 2019), con el fin de obtener una imagen para la localización de los emuladores de carcinoma insertados en los modelos experimentales. El procesamiento de los datos se realizó en MATLAB versión R2018a, el cual consistió en:
Calcular la diferencia aritmética entre los valores medidos del modelo sin carcinoma y cada uno de los seis modelos restantes.
Obtener el voltaje diferencial mediante la multiplicación de los datos con la corriente suministrada durante el barrido de los electrodos (60 micro amperes).
Calcular la conductividad normalizada G mediante ecuación (8) y la normalización de los voltajes diferenciales obtenidos.
Finalmente, generar la imagen resultante haciendo uso de las funciones propias de MATLAB: reshape para modificar las dimensiones del vector G de 1024x1 a 32x32 y surface para generar la imagen que representa la distribución de la conductividad para cada modelo experimental.
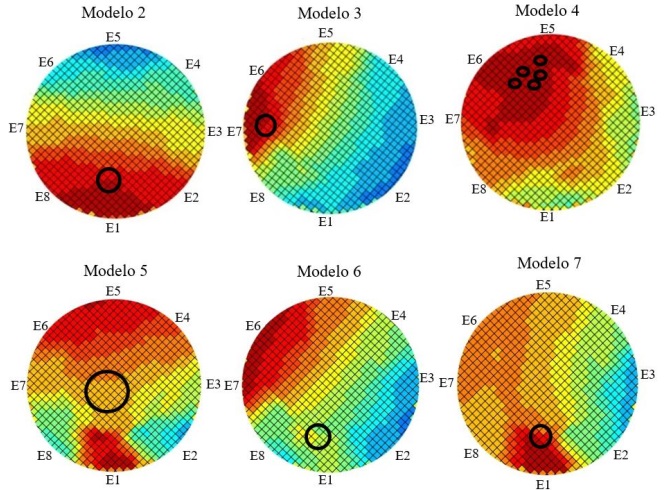
Las imágenes resultantes para los seis modelos en agar-agar se presentan en la Fig. 3, en donde la posición real de los emuladores de carcinoma se representa con un círculo color negro. Mientras que el color rojo obscuro indica la existencia de altas conductividades que corresponden a las zonas de ubicación de los carcinomas emulados. La imagen de conductividad normalizada del modelo 1, que emula una mama sin carcinoma, no se muestra debido al resultado nulo que se genera al momento de realizar la diferencia aritmética. Bajo esta consideración la zona indicada en rojo obscuro representa la posición del emulador. Como puede observarse de las imágenes resultantes que el área roja se aproxima a la posición real de los emuladores de carcinoma para la mayoría de los modelos, no siendo el caso para los modelos 5 y 6. La explicación del modelo 5 se relaciona con la baja sensibilidad que presenta la configuración anillar de los electrodos en el área central, lo que dificulta la detección de emuladores u objetos que se encuentren en el centro del dominio de interés. Sin embargo, debido a las dimensiones del emulador de carcinoma, se manifiestan conductividades altas en las zonas cercanas a los electrodos 1 y 5. La no detección de la posición real del emulador en modelo 6 se debe al bajo valor de conductividad definido para este caso, 30% a la reportada en la literatura, el cual es muy cercano al de la glándula mamaria. Por ello el emulador no genera cambios significativos de impedancia en la zona cercana de su posición real. Por otro lado, la posición resultante de la imagen en modelo 6 se debe a la forma de mama del modelo agar-agar, la cual genera un volumen heterogéneamente distribuido. Por lo que la zona cercana al electrodo 1 tiene mayor volumen y en consecuencia mayor impedancia, en comparación a la zona de los electrodos 5, 6 y 7. Por otro lado cabe destacar que en el modelo 4 todos los fragmentos del emulador se encuentran en la zona resultante de mayor conductividad.
Con la finalidad de comparar los resultados obtenidos con el método LBP descrito, en la Fig. 4 se muestran las posiciones resultantes de los emuladores de carcinoma para los seis modelos utilizando el método Circulo Rastreador de Anomalías (CRA) reportado en (Gutiérrez-López et al., 2019), las cuales se representan por el círculo rojo. Dicho método se basa en determinar la zona de menor impedancia dentro del dominio de interés a partir del cruce de ocho rectas que representan las mediciones de menor impedancia dentro de un subconjunto de siete mediciones de impedancia. Es importante indicar que tanto el método CRA como el LBP hacen uso del mismo conjunto de mediciones de impedancia. Al comparar ambos métodos para detección de emuladores de carcinomas, se observa que los resultados son una aproximación de la posición real de los emuladores. Sin embargo, ninguno de los métodos implementados permite indicar la posición del emulador de carcinoma en el modelo 6, por las razones previamente mencionadas. Cabe destacar que para el método CRA sí se logra obtener la localización correcta del emulador para el modelo 5, lo cual no fue posible con el método LBP. Sin embargo, se puede observar que todos los fragmentos del emulador para el modelo 4 se encuentran en la zona de mayor conductividad resultante del método LBP, siendo ésta una mejor aproximación que la posición obtenida con el método CRA. Es importante resaltar que a diferencia del método CRA, las imágenes TIE permiten mostrar el mapa de las conductividades distribuidas en todo el dominio de interés.

Fig. 4 Localización de emulador mediante método CRA en los modelos considerados (Gutiérrez-López et al., 2019).
No obstante, se ha reportado que los métodos de reconstrucción de imágenes involucran un problema inverso mal planteado (Holder, 2004). Esto explica la resolución moderadamente baja de esta técnica, es decir, la sensibilidad se reduce al alejarse de los electrodos de medición y limita la precisión de la estimación de la propiedad eléctrica. Otro factor que limita la resolución es el número relativamente bajo de mediciones disponibles en los sistemas clínicos de TIE (Murphy, Mahara y Halter, 2016), (Sabatier y Sebu, 2007).
Generalmente los emuladores de carcinomas reportados tienen contornos bien definidos por formas geométricas como una esfera o un cilindro y las dimensiones de estos superan los dos centímetros (Halter, Hartov y Paulsen, 2008), (Murphy et al., 2017). Por otro lado, en este trabajo el tamaño y la forma de los emuladores de carcinoma son más similares a los contornos amorfos de un carcinoma real en estado preclínico, diámetro alrededor de 1 cm. Esta irregularidad del emulador dificulta la reconstrucción de la posición de los emuladores de carcinoma dentro de los modelos experimentales en agar-agar.
Se debe considerar que el algoritmo presentado para la reconstrucción de imágenes TIE consume pocos recursos computacionales al no realizar iteraciones, en comparación a los enfoques estándar empleados para la reconstrucción de imágenes basados en mediciones de impedancia tales como: el algoritmo estándar de Gauss-Newton, suavizado de Laplace (Borisc et al., 2009), método iterativo de Landweber (Yang et al., 1999) y regularización de variación total ( Khan, Manwaring y Halter, 2014), los cuales no pueden detectar con precisión los tumores si no cuentan con información estructural previa.
El método Tikhonov Regularization es similar al algoritmo LBP, ya que se encuentra dentro del grupo de los métodos directos para la reconstrucción de imágenes (Nombo, Mwambela, y Kisangiri, 2016). Pero debe de optimizarse el parámetro regulador para cada sistema de medición, debido a que es sensible a los errores en las mediciones de potencial. Por otra parte, el algoritmo LBP es genérico y no requiere adecuaciones para funcionar correctamente con cualquier sistema de medición. Existe la posibilidad de combinar estos dos métodos y obtener mejores resultados en la imagen reconstruida (Sapuan et al., 2020). Por otra parte, existen modificaciones realizadas al algoritmo LBP que permiten una mejoría en la resolución y sensibilidad de la imagen reconstruida, como es el caso del algoritmo Modified Weighted Back Projection (MWBP), capaz de calcular equipotenciales con mayor precisión al tomar en cuenta la naturaleza de las líneas de campo eléctrico establecidas al momento de inyectar corriente a través de un electrodo, sin embargo este método solo se ha probado en una matriz de 256 electrodos montados en una placa (Khalighi, y Mikaeili, 2019).
Conclusiones
En este trabajo se presentó una metodología para reconstruir imágenes de tomografía basadas en mediciones de impedancia eléctrica, el cual no realiza iteraciones en comparación a los algoritmos iterativos que normalmente se emplean para la detección de carcinomas.
El uso de un modelo computacional para la obtención de la distribución de la conductividad permite que la técnica de reconstrucción sea implementada. Además, los mapas de sensibilidad se calculan una sola vez si la distribución de los electrodos no cambia.
El algoritmo LBP, descrito e implementado en este artículo, solo utiliza un ciclo de ejecución, por esta razón no demanda mayores recursos computacionales con lo cual tiene el potencial de ser utilizado en aplicaciones de tiempo real.
Los modelos experimentales en agar-agar emplearon estructuras complejas para la representación de los tejidos mamarios (carcinomas amorfos y entrelazamiento entre la glándula mamaria y el tejido graso) en contraste a las estructuras geométricas bien definidas empleadas para el mismo objetivo por otros grupos de investigación (Murphy et al., 2017). Por lo que se puede considerar que los modelos empleados son más próximos a la anatomía mamaria.
El análisis del modelo 6, que representa un caso especial de un falso carcinoma, proporciona información adicional sobre el potencial y los desafíos que tiene la técnica TIE para contar con información clínicamente relevante. En este caso, no se localizó la tumoración de manera precisa debido a que la conductividad del emulador era semejante a la de la glándula mamaria. De igual manera se tiene como trabajo a futuro investigar alternativas para aumentar la sensibilidad del método TIE en la zona central de la mama.
Los resultados obtenidos en los modelos considerados tanto con el método CRA como con el basado en TIE descrito en este artículo son de tipo cualitativo. El resultado es una zona en la que se tiene mayor probabilidad de localizar el emulador de carcinoma insertado en el modelo.
Aunque los resultados obtenidos por el método TIE implementado son favorables en la localización de los emuladores de carcinoma en los modelos considerados, es necesario realizar como siguiente etapa la experimentación clínica en pacientes.
En contraste al algoritmo CRA, el método TIE descrito en este trabajo permite obtener una distribución de las conductividades en la zona de estudio a través de una imagen. Lo cual aporta una mejor comprensión del comportamiento de los campos eléctricos dentro del emulador de tejido y cómo se ven afectados por la presencia de emuladores de carcinoma.
Tanto el método TIE desarrollado como el CRA descrito son de mediana complejidad en su implementación y requieren un mínimo de recursos computacionales. Además, podrían en un futuro emplearse de manera complementaria a la mamografía y el ultrasonido para la creación de historiales clínicos, principalmente porque ambas metodologías utilizan energías libres de radiación ionizante, lo que permite su uso de manera regular en humanos.











 nueva página del texto (beta)
nueva página del texto (beta)