Introducción
La idea principal de este trabajo es evaluar el desempeño de un control fraccional tipo PID, en conjunto con un filtro de segundo orden fraccional, en la reducción del acoplamiento cruzado en un modelo matemático no lineal de una central hidroeléctrica reversible. Estas centrales reversibles también llamadas centrales de bombeo, disponen de dos depósitos de agua (embalses) situados a niveles diferentes. En su operación de generación eléctrica, cuando la demanda de energía eléctrica es máxima, estas unidades operan como una central hidroeléctrica convencional: el agua fluye desde el embalse superior hacia el inferior, pasando por túneles haciendo girar turbinas a su paso. Sin embargo, en las horas de menor demanda, el agua se bombea “de regreso” al depósito superior, reiniciando el ciclo productivo. Estos tipos de estaciones utilizan los recursos hídricos de una forma más racional sin embargo consumen energía eléctrica en el ciclo de bombeo.
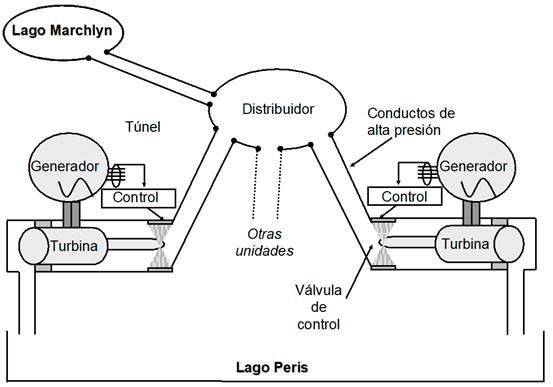
Dinorwig es una planta hidroeléctrica reversible (con almacenamiento por bombeo) ubicada en el norte de Gales, la cual es operada por First Hydro Company, una subsidiaria del corporativo mundial ENGIE, la cual es una de las más grandes generadoras de energía en el Reino Unido con una capacidad instalada de 2,088 MW. La estación cuenta con seis turbinas de 300 MW de potencia, que impulsan generadores síncronos alimentando de energía eléctrica a la red nacional británica. Dinorwig proporciona un control de frecuencia de respuesta rápida cuando se producen picos de demanda. Esta central hidroeléctrica tiene un solo túnel que extrae agua de un embalse superior (lago Marchlyn) hacia un colector, que divide el flujo principal en seis derivaciones de alta presión (tubería forzada), ver Fig. 1. Cada tubería forzada alimenta una turbina que mueve un generador, el caudal se regula mediante una válvula de control. La energía eléctrica generada se controla mediante sistemas de control individuales en cada unidad. La entrada de referencia al lazo de potencia es la desviación de frecuencia de la red desde su punto de ajuste de 50 Hz, formando así un lazo de control de frecuencia exterior.
El modelo de la central hidroeléctrica se basa en los trabajos del Grupo de Control Automático de la Universidad de Bangor, U. K.)1) (2) (3, donde el modelo fue evaluado con respecto al sistema real. De éstos se deriva un modelo de simulación no lineal multivariable de la central. El modelar la planta ha proporcionado una mejor comprensión de sus características, las cuales son: dinámica de fase no mínima (NMP), polos mal amortiguados (asociados con el golpe de ariete en el túnel de suministro y la sincronización eléctrica) y una relación no lineal entre flujo y potencia. También es conocido que existe un acoplamiento hidráulico significativo entre las turbinas, debido al suministro común (interacción de acoplamiento cruzado). Esto hace que la planta sea un buen candidato para la aplicación de controles avanzados. Existen varios ejemplos de controles avanzados que se están aplicando tanto en centrales eléctricas convencionales 4) (5 como en centrales hidroeléctricas 6) (7.
En la búsqueda de mejorar el desempeño dinámico no lineal de sistemas hidroeléctricos, varios autores han reportado casos de éxito. Por ejemplo, Meng y Xue 8 presentan un controlador de orden fraccional, que los autores denominan robusto, para plantas hidroeléctricas, en este trabajo, un compensador de orden fraccionario, con un controlador de estructura flexible, se introduce usando la teoría de retroalimentación cuantitativa (QFT, por sus sigla en inglés) buscando dar una mejor desempeño de lazo abierto óptimo, empleando la carta de Nichols. Por su parte, Lamba et al. 9 presentan un control con integral y derivada de orden fraccional. El regulador fue diseñado para el control de frecuencia en un Sistema de potencia en dos áreas interconectadas.
Rosas-Jaimes et al. 10 han publicado un artículo donde se presenta un Control PID Fraccional. Este control fue diseñado para una central hidroeléctrica con seis unidades de generación. Las características no lineales de dicho conjunto de unidades hidro-generadoras sirven de base para sintonizar el controlador mediante una estrategia que usa modelos lineales a trozos. También ha sido propuesto un Control en tiempo finito de orden fraccional, tolerante a fallas, para un sistema no lineal de turbinas hidráulicas que presenta fallas en el actuador, ha sido presentado por Yang et al. 11. En este trabajo un estimador de fallas en tiempo finito fue propuesto para observar rápidamente cambios de señales que indiquen fallas en el actuador. Lo anterior permite que el controlador actúe y guie al sistema a una recuperación rápida hacia un estado estable. Las propuestas discutidas anteriormente, aunque logran mejorar el desempeño de las centrales hidroeléctricas, no toman en cuenta expresamente la característica de acoplamiento cruzado de dichos sistemas.
Este artículo inicia con una discusión del modelo no lineal multivariable utilizado en este trabajo, seguido de una descripción del control de orden fraccional tipo PID con acción pseudo derivativa, posteriormente se describe la técnica utilizada en este trabajo para reducir la interacción de acoplamiento cruzado mediante un filtro fraccional de segundo orden. Finalmente se discuten algunos resultados y conclusiones.
Descripción del Modelo de la Estación Hidroeléctrica
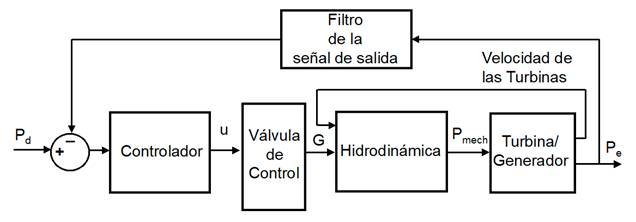
La Fig. 2 muestra los 5 subsistemas que componen el modelo de la central hidroeléctrica. El gobernador es donde se calculan las señales de control. El modelo de las válvulas de control incluye no sólo la dinámica de las válvulas sino también la de los servomecanismos (1) para todas las seis unidades. La hidrodinámica incluye el túnel principal y los seis conductos de alta presión, en inglés se usa el término penstock para referirse a éstas. También se modela el par turbina/generador. Como puede apreciarse, las salidas de este subsistema se filtran antes de que sean retroalimentadas.
El subsistema de válvulas de control emplea un servosistema hidráulico para mover éstas con el fin de controlar el flujo, por lo tanto, se considera un modelo de Segundo orden, el cual incluye dos constantes de tiempo (1).
Donde: u es la señal de control 1)(3).
Para el subsistema que describe la hidrodinámica, se utiliza un modelo no lineal, que incluye características elásticas, para simular cambios de velocidad y potencia 12. La Fig. 3 muestra la interacción entre el túnel principal y una compuerta. El bloque “Túnel principal” se conecta a las otras 5 compuertas formando el modelo hidráulico completo. En la Fig. 3:
Impedancia de sobretensión del conducto, Z0 (2).
Coeficiente de pérdida de cabezal hidráulico en m/(m3/s)2, fp.
Caudal sin carga en m3/s, qnl.
Ganancia de la turbina, At.
Apertura de la válvula de control, ΔG.
Salida de potencia mecánica de la turbina, ΔPm.
Incremento de la potencia eléctrica proporcionada a la red eléctrica ΔPe.
Longitud de los conductos de alta presión en m, l.
Constante de tiempo del flujo de agua en segundos, Tw13.
Constante de tiempo de oleaje en segundos, Te (3) 3
Velocidad del sonido en el agua en m/s, v.
Se considera, para efectos prácticos, al simular este sistema, que los factores At, fp y qnl son idénticos en todas las unidades. Debido a que la central tiene grandes conductos de alta presión; las columnas de agua se modelaron asumiendo un comportamiento elástico 12. El efecto de acoplamiento también se modela al incluir el túnel principal, que se representa también como un conducto de alta presión.
En la Fig. 3, la potencia mecánica ΔPm es la entrada a la turbina-generador, que se modela, para el subsistema Turbina/Generador, asumiendo un estado estacionario mediante las ecuaciones de "oscilación" 13 y la ecuación (4):
Donde:
ΔPe es la alteración de la energía eléctrica aportada a la red.
H es la constante de inercia del subsistema eléctrico.
Δω es la alteración de la velocidad angular del rotor.
Finalmente, para la reducción de ruido se utiliza un filtro de primer orden, denominado subsistema de filtros de ruido en la Fig. 2, el cual tiene la función de transferencia (5).
Acoplamiento cruzado
El túnel común en la planta hidroeléctrica Dinorwig, produce un importante efecto de acoplamiento cruzado. Este acoplamiento tiene un efecto perjudicial sobre el margen de estabilidad en lazo cerrado, dado que las unidades conectadas reaccionan modificando sus señales de control, a través de sus controladores, cuando otras unidades cambian sus puntos de operación. Las unidades que no están conectadas tienen sus válvulas cerradas y por tanto no “perturban” el flujo. En consecuencia, el número de unidades activas determina la estructura del sistema 12, el sistema es, como puede verse, inherentemente multivariable. Para este trabajo, el modelo considera sus valores por unidad (p.u.), estandarizadas a 300MW y 50Hz, asumiendo una red eléctrica con impedancia infinita 3.
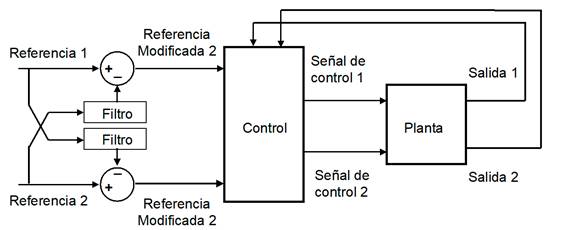
El objetivo de este trabajo es desacoplar la interacción que se produce cuando algunas unidades están regulando una salida de potencia fija y otras están siguiendo una referencia de potencia, buscado reducir el error de frecuencia. Este enfoque puede verse como la aplicación de un filtro, que modifica deliberadamente las referencias de las unidades de potencia fija para compensar los cambios en la referencia de las unidades de control de frecuencia, esto se ilustra, considerando sólo dos unidades, en la Fig. 4 14).
Controlador PID Pseudoderivativo de orden fraccional
Podlubny propuso un PIλDδ (controlador FO-PID) de orden fraccionario 15, en este controlador, el operador integrador (λ) y el diferenciador (δ) son reales. La estructura interna del controlador de orden fraccional consiste en la conexión en paralelo de la parte proporcional, de integración y derivada 16)(17. La función de transferencia de este controlador se muestra en la ecuación (6).
Aquí:
operador real integral, λ > 0
operador real diferencial, δ > 0
ganancia proporcional, Kp
ganancia integral, Ki
ganancia diferencial, Kd.
El operador integral fraccional s-q no se puede implementar directamente cuando q no es un número entero. Un método común es hacer una aproximación. La Fig. 5 muestra un enfoque que se ha sido muy estudiado. Esta implementación simula el operador s-q como un circuito de compensación Adelanto-Atraso (7) 18.
Donde:
El operador de derivada fraccional sq también puede implementarse usando métodos de aproximación, mediante un circuito Adelanto-Atraso (9) 18.
Donde: A está definido por (8).
Si se considera un controlador en tiempo discreto (10).
Empleando la aproximación Adelanto-Atraso, se obtiene (11).
En la ecuación (10) tomando λ=1 y δ=1, se obtiene un controlador PID clásico. Si Ki=0 en la ecuación (10) y (11), se encuentra un controlador PDδ. Todos estos tipos de controladores son casos particulares del controlador de orden fraccional, que es más flexible y brinda la oportunidad de mejorar las propiedades dinámicas de un sistema de control, 19) (20. En algunas aplicaciones, el componente D del controlador PID puede causar algunos problemas. Al alterar la estructura del controlador, es posible obtener los beneficios asociados de la acción derivada, sin tomar la derivada de la función de error sino directamente la derivada de la señal de salida, esto se denomina retroalimentación pseudoderivada. La estructura de este esquema de control se examina en 21, tanto para sistemas multivariables como de entrada y salida únicas. En este trabajo se evalúa un controlador de orden fraccional tipo PID pseudoderivativo con compensación de saturación (anti-windup), Fig. 6. El efecto “windup” ocurre particularmente como una limitación de los sistemas físicos debido a los efectos de saturación 22. Como puede verse en la Fig. 6, el anti-windup puede implicar desconectar el integrador durante períodos de tiempo, los cuales son determinados conforme a la dinámica de recuperación. La estabilidad de los controles fraccionales ha sido abordada por diferentes autores 23) (24), sin embargo dado que la forma en la cual se realiza el diseño, en este trabajo, del control fraccional, éste es visto como un compensador en cascada tanto con la parte integral como la proporcional (11). Si se desarrolla la ecuación (11), el PID de orden fraccionario (FO-PID) puede verse como un filtro de segundo orden, con dos polos reales y un par de ceros conjugados complejos. Por lo tanto, se pueden utilizar técnicas que permitan fijar polos y ceros de compensadores para ajustar los FO-PID y analizar su estabilidad.
Filtro de orden fraccional
Como se explicó anteriormente, el inherente acoplamiento hidráulico entre las unidades de generación de energía puede ser reducido modificando las referencias mediante filtros. En este trabajo se empleó un filtro de orden fraccional, dado que las figuras de mérito de la salida que se pueden lograr, con éste, son mucho mayores a lo alcanzable con filtros de orden entero. La función de transferencia de este filtro se muestra en (12). Como puede verse éste tiene dos ceros y un polo enteros, además de un polo fraccional y un factor de ganancia (G f). La Fig. 7 describe un esquema de este filtro de orden fraccional.
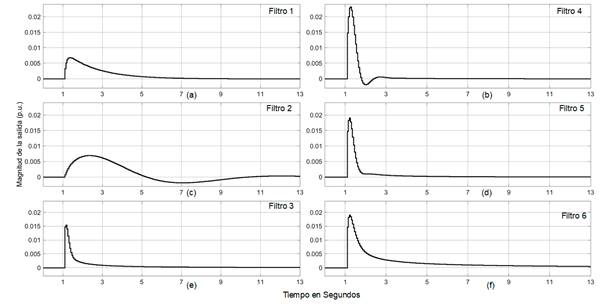
Para demostrar las diferentes formas de salida que se pueden obtener con el filtro de orden fraccional diseñado para este trabajo, se realizaron diferentes simulaciones empleando entradas tipo escalón. Se consideró un filtro sin ceros, por cual Z0 y Z1 se igualaron cero, mientras que Z2 se igualó a uno. La Tabla 1 muestra los diferentes parámetros empleados en las simulaciones, mientras que las formas de las salidas se muestran en la Fig. 8. El filtro 1 es de segundo orden entero con un factor de amortiguamiento (() igual a 2 y una frecuencia natural ((n) igual a 3. En el filtro 2, la potencia integral (() se cambia de 1 a 1.5, puede observarse como la señal de salida es más lenta y presenta una típica oscilación en la respuesta. En los filtros 3 a 6, se mantiene (=0.5, dado que se usan diferentes valores para ( y (n, en cada filtro, es posible regular la amplitud de la salida tipo impulso, al mismo tiempo que se controla la velocidad de caída de la señal.
Tabla 1 Parámetros de los diferentes filtros evaluados.
| Potencia Integral λ | Factor de Amortiguamiento ζ | Frecuencia de Oscilación ωn | |
|---|---|---|---|
| Filtro 1 | 1 | 2 | 3 |
| Filtro 2 | 1.5 | 2 | 3 |
| Filtro 3 | 0.5 | 2 | 3 |
| Filtro 4 | 0.5 | 0.5 | 3 |
| Filtro 5 | 0.5 | 1 | 3 |
| Filtro 6 | 0.5 | 2 | 1.5 |
Respuesta del sistema a cambios en la referencia tipo escalón
Para mostrar las mejoras que el controlador Proporcional, Integral y pseudo-Derivativo con anti-windup, con acciones integral y derivativa de orden fraccional (PDF-AWU-FO), aportaría a una central hidroeléctrica, se realizaron simulaciones de este controlador en el modelo no lineal descrito en secciones anteriores. Dado que los modelos son válidos para cambios pequeños alrededor del punto de operación 1) (2) (3, primero se llevó a todas las unidades del sistema a un punto de operación de 0.86 p.u. Posteriormente a 100 segundos de simulación, ya con el sistema en estado estable, se modifica sólo el punto de operación de la unidad 1 a 0.9 p.u. Las Unidades 2 a 6 siguen la misma referencia, por lo tanto, sus respuestas son iguales. Para establecer un punto de comparación, el modelo no lineal de la hidroeléctrica se simuló también bajo la regulación de un controlador PID con anti-windup (PID-AWU). La Tabla 2 muestra los parámetros de control para cada uno de los controladores, ambos sintonizados buscando una reducción del sobretiro 23. La Fig. 9 muestra el comportamiento del sistema de generación de energía para ambos controles evaluados. Ambas respuestas tienen similares tiempos de subida, sin embargo, se nota una mejoría en el sistema bajo el PDF-AWU-FO al reducir la magnitud de la oscilación en estado estable, aunque esta reducción en porcentaje es considerable, 40%, ambas señales de salida se encuentran muy cerca de la referencia, por lo que estas fluctuaciones se consideran dentro de la región de estado estable (± 5%). De igual forma se nota una ligera reducción de las oscilaciones, entre los 105 y 115 segundos se simulación (Fig. 9), cuando el sistema es controlado mediante el PDF-AWU-FO. Lo anterior es conveniente para el sistema dado que amortigua la oscilación debida al comportamiento no lineal del sistema sin reducir la velocidad de éste. Para las unidades 2 a 6, operando en sincronía, se analizaron sus respuestas al acoplamiento cruzado, Fig. 9. Dado lo anterior, para cuantificar la mejora del sistema controlado, se realizó el cálculo de la integral del error al cuadro (ISE). Se obtuvo, con el PDF-AWU-FO, un valor final de 2.734x10-3 con respecto a 3.144x10-3 del PID-AWU, por lo que se tiene una reducción del 13% cuando se emplea el control PDF-AWU-FO.

Referencia Unidad 1/ Referencia Unidades 2 a 6 / Salida Unidad 1 / Salidas Unidades 2 a 6.
Fig. 9 Respuesta del modelo no lineal de la Planta hidroeléctrica con el controlador PID-AWU (a) y el controlador PDF-AWU-FO (b).
Tabla 2 Parámetros de los controladores.
| Parámetros | PID-AWU | PDF-AWU-FO |
|---|---|---|
| Tiempo de Muestreo | 0.1 s | 0.1 s |
| Ganancia proporcional, Kp | 0.165 | 0.116 |
| Ganancia integral, Ki | 0.667 | 0.9 |
| Ganancia diferencial, Kd | 0.03 | 0.05 |
| Operador real integral, λ > 0 | 1 | 0.9 |
| Operador real diferencial, δ > 0 | 1 | 0.6 |
| Límite de saturación | 0.8929 | 0.8929 |
| Limite de cambio | 0.0833 | 0.0833 |
Respuesta de acoplamiento cruzado con el filtro de orden fraccional en la referencia
Para mostrar los efectos del filtro de referencia en la salida del sistema, se realizó una simulación con los mismos cambios en las señales de referencia, descritos en la sección anterior. Esto es, todas las unidades se llevaron a 0.86 p.u. y a 100 segundos de simulación, excepto la unidad 1 que se ajusta a 0.9 p.u. La Tabla 3 muestra los parámetros del filtro de referencia de orden fraccional propuesto. Para cuantificar la mejora en la respuesta al acoplamiento cruzado (ver Fig. 10), se realizó el cálculo de la integral del error al cuadro (ISE), con el sistema controlado mediante el PDF-AWU-FO, ajustado con los parámetros de la Tabla 2, pero ahora con filtro de orden fraccional en la referencia. Se obtuvo un valor final de 2.432x10-3, por lo que se obtiene una reducción de 11% con respecto a 2.734x10-3 del PDF-AWU-FO.
Tabla 3 Parámetros del filtro fraccional de referencia.
| Tiempo de Muestreo | Potencia Integral λ | Factor de Amortiguamiento ζ | Frecuencia de Oscilación ωn |
|---|---|---|---|
| 0.1 s | 0.75 | 1.75 | 6 |
El análisis de la integral del error al cuadrado permite observar las mejoras en el sistema mediante el uso del control fraccional, el empleo de éste mejora al sistema en un 13% del ISE. Aunado a lo anterior, si se complementa con el uso de los filtros fraccionales la mejora en este indicador es del 11% cuando el sistema se evalúa en la respuesta al acoplamiento cruzado.

Fig. 10. Response of the non-linear model of the hydroelectric plant with the PDF-AWU-FO controller with filter in the reference.
Output Unit 1 / Output Units 2 to 6 / Reference Unit 1 / Reference Units 2 to 6.
Salida Unidad 1 / Salidas Unidades 2 a 6 / Referencia Unidad 1 / Referencias Unidades 2 a 6.
Fig. 10 Respuesta del modelo no lineal de la Planta hidroeléctrica con el controlador PDF-AWU-FO con filtro en la referencia.
Conclusiones
El presente trabajo describe el modelo no lineal estructural y funcional de la planta hidroeléctrica de Dinorwig el cual ha permitido pruebas en simulación de diversos controladores como los de tipo fraccional, validando su aplicación en plantas de premisas similares. Se demuestran y establecen las condiciones teórico-prácticas de los controladores de tipo fraccional mostrando sus capacidades y ajustes que deben ser considerados para su implementación. Los resultados de las simulaciones han demostrado que el PDF-AWU-FO, podría emplearse en un sistema hidroeléctrico para mejorar su rendimiento. Se ha mostrado que sintonizado baja las mismas reglas que un PID-AWU “clásico”, el PDF-AWU-FO reduce oscilaciones en el estado transitorio, mejorando la respuesta en estado estacionario. De igual forma se nota una mejoría en la respuesta de acoplamiento cruzado cuando se emplea este controlador de orden fraccional. La inclusión de un filtro fraccional en las señales de referencia mejora la respuesta de acoplamiento cruzado sin alterar las respuestas directas tanto transitorias como de estado estable. Por lo anterior se puede expresar que el controlador PDF-AWU-FO, con filtro fraccional en la referencia, aportaría ventajas concretas si se aplicara en la regulación de sistemas hidroeléctricos.











 nueva página del texto (beta)
nueva página del texto (beta)