Artículos

 

Guía de densidad para manejo de bosques naturales de Pinus teocote Schlecht. et Cham. en Hidalgo

 

Density management guide for natural Pinus teocote Schlecht. et Cham. fotest in Hidalgo

 

Jonathan Hernández Ramos¹, J. Jesús García Magaña², H. Jesús Muñoz Flores³, Xavier García Cuevas¹, Trinidad Sáenz Reyes³, Celestino Flores López⁴ y Adrián Hernández Ramos⁴

 

¹ Campo Experimental Chetumal, CIR-Sureste. INIFAP. Correo-e: hernandez.jonathan@inifap.gob.mx

² Universidad Michoacana de San Nicolás de Hidalgo.

³ Campo Experimental Uruapan, CIR-Pacífico Centro. INIFAP.

⁴ Universidad Autónoma Agraria Antonio Narro.

 

Fecha de recepción: 9 de febrero de 2012;
Fecha de aceptación: 20 de abril de 2013.

 

RESUMEN

La densidad es un indicador confiable del grado de ocupación del arbolado de un lugar y tiempo específicos, además es una de las pocas variables que representan, de manera sencilla y objetiva la estructura de áreas forestales. En 12 municipios del oriente del estado de Hidalgo se elaboró una guía de densidad para bosques de Pinus teocote. Con la finalidad de desarrollar la metodología de Índice de Densidad de Rodales de Reineke se levantaron 282 sitios de muestreo con dimensiones entre 100 y 1 000 m² en rodales de densidad completa; asimismo, para definir el Factor de Competencia de Copas se midieron 131 árboles individuales aislados. En la construcción de la guía de densidad se determinó la línea de máxima densidad o nivel "A" con el modelo propuesto por Reineke: se obtuvo un índice de 755 árboles a un diámetro cuadrático de 25 cm. Con los árboles aislados se estableció la línea "B" o densidad mínima; bajo la metodología del Factor de Competencia de Copas: el índice registrado fue de 421 árboles para el mismo diámetro cuadrático. A partir de la guía generada se relacionaron índices cuantitativos que permiten comparar el grado de densidad y algunas variables dasométricas en rodales de Pinus teocote, de manera independiente de la edad, la calidad de sitio y dimensiones de los árboles dentro de intervalos de densidad específicos.

Palabras clave: Estado de Hidalgo, Factor de Competencia de Copas, guía de densidad, Índice de Densidad de Rodales de Reineke, manejo forestal, Pinus teocote Schlecht. et Cham.

 

ABSTRACT

Density is a reliable indicator of the degree of occupation of a specific time and place by trees; besides, it is one of the few variables that represent the structure of forests in a simple, objective manner. A density management guide for Pinus teocote was created for 12 municipalities of eastern Hidalgo. In order to develop the methodology of Reineke’s Stand Density Index, 282 sampling sites with a surface between 100 and 1 000 m² in full density stands were evaluated; also, in order to define the Crown Competition Factor, 131 isolated individual trees were measured. During the making of the density management guide, the maximum density line or level "A" was determined according to the model proposed by Reineke: an index of 755 trees to a 25 cm square diameter. Line "B", or minimum density, was established based on the isolated trees, according to the Crown Competiton Factor: the recorded index was 421 trees to the same square diameter. Based on the guide thus generated, a relationship was established between quantitative indices allowing comparison between the density degree and certain dasometric variables in Pinus teocote stands, regardless of their age, the quality of the site and the dimensions of the trees within specific density intervals.

Key words: Hidalgo state, Crown Competition Factor, density guide, Reineke’s Stand Density Index, forest management, Pinus teocote Schlecht. et Cham.

 

INTRODUCCIÓN

Los bosques y las selvas mexicanos han sufrido de fuertes disturbios debido al impacto del cambio de uso del suelo, la tala ilegal, los incendios forestales, las plagas y enfermedades, los fenómenos meteorológicos y el crecimiento demográfico, lo cual, aunado a la deficiente aplicación de prácticas silvícolas, ocasiona la reducción de la cubierta vegetal de los diversos ecosistemas.

En el periodo de 2005-2010, FAO (2010) refiere una tasa de deforestación de 155 mil hectáreas por año y una degradación entre 250 y 300 mil hectáreas por año, en promedio. La pérdida de la cubierta forestal es más acentuada en los bosques irregulares, dado que existe un menor conocimiento de las herramientas de manejo que le permitan al técnico seleccionar una medida silvícola, en función de sus características estructurales (Velásquez et al., 2002).

La estructura de los bosques está determinada por la amplitud de las clases de edad, por el diámetro normal o la posición social de sus copas, características con las cuales se clasifica a la masa como regular o irregular, de acuerdo a la capacidad de subsistir en condiciones de escasa luminosidad y elevada competencia sobre las cuales la interacción entre el hábitat, las condiciones ambientales y el manejo ejercen su influencia (Husch et al., 1982; Cano, 1988).

La ordenación forestal se realiza con base en las condiciones de reproducción, densidad, crecimiento altura-diámetro, auto-poda, raleo natural y capacidad de liberación, según la tolerancia de cada especie (Daniel et al., 1982). La competencia también influye en el arreglo de la vegetación (densidad), pues es el resultado de la demanda de los árboles por el espacio de crecimiento, cuyo resultado es la muerte eventual de otros individuos (Toumey y Korstian, 1947).

En la caracterización de los rodales, la densidad es un indicador confiable del grado de ocupación del arbolado de un lugar específico en un tiempo dado (Zeide, 2004); además, es una de las pocas variables que representan de manera sencilla y objetiva la estructura de áreas forestales. En la actualidad existen varios procedimientos para describirla, pero es evidente que los de uso más frecuente son el Índice de Densidad de Rodales de Reineke (Reineke, 1933), la Relación Área/Árbol propuesta por Chismas y Schumacher (1940), el Factor de Competencia de Copas (Krajicek et al., 1961) y el Índice de Densidad Relativa (Curtis, 1970).

Las guías de densidad son un instrumento eficaz y práctico en la planeación de los tratamientos silvícolas para ser aplicados y define el número de árboles por unidad de superficie en un rodal, debido a que proporcionan información sobre las densidades mínimas y máximas, así como el porcentaje de árboles que se deben eliminar en cada etapa de desarrollo del arbolado; esto permite obtener la mayor productividad de los bosques. Asimismo, estas guías son un elemento importante para el manejo forestal, ya que con ellas se pueden establecer esquemas de manejo silvícola (Reineke, 1933; Chauchard, 2001; Torres y Magaña, 2001). Aguirre et al. (1994) desarrollaron una guía para Pinus pseudostrobus Lindl. en Nuevo León.

En el estado de Hidalgo se han elaborado guías de densidad para Pinus patula Schlecht. et Cham. (Acosta et al., 2007) y para P. montezumae Lamb. (Rodríguez et al., 2009); sin embargo, no existen para P. teocote Schlecht. et Cham., especie relevante por su distribución y abundancia en la entidad y en el país, y porque tiene una madera dura, fuerte y por lo tanto, muy apreciada en la industria. En el presente trabajo se planteó como objetivo generar una guía para el manejo de la densidad en rodales puros de Pinus teocote Schlecht. et Cham. basada en el Índice de Densidad de Rodales de Reineke (IDRR) y en el Factor de Competencia de Copas (FCC).

 

MATERIALES Y MÉTODOS

Descripción del área de estudio

El estudio se realizó en el oriente del estado de Hidalgo, que forma parte de la Cordillera del Eje Neovolcánico Transversal en un intervalo altitudinal de 2 000 a 3 100 m, entre las coordenadas 16°57´ y 20°27´ norte y 98°48´ y 99°12´ oeste.

De acuerdo a la clasificación de Köppen modificada por García (1988), el clima corresponde al tipo C, templado con lluvias en verano.

La forma del terreno se clasifica en plana, ondulada y semi-montañosa con pendientes de 5 a 45%, con una exposición variada. La vegetación está representada, principalmente, por Pinus rudis Endl., P. montezumae, P. patula y algunas especies de Quercus y Alnus.

Los suelos son de tipo Feozem, Andosol, Cambisol y Regosol, característicos de la región que, junto a las condiciones antes mencionadas, favorecen un desarrollo ideal de Pinus teocote (Inegi, 1992).

Esta área pertenece a la Unidad de Manejo Forestal 1303, donde la superficie forestal bajo manejo es de 24 858 ha, de las cuales, y debido a las condiciones dasonómicas de los predios forestales, 78.88% se aplica el Método de Desarrollo Silvícola (MDS); 17.47% en la combinación del MDS y del Método Mexicana de Ordenación de los Bosques Irregulares (MMOBI); 3.52%, está manejado solo con el MMOBI, y 0.12%, con otros métodos (Conafor, 2011).

Diseño de muestreo. La información se extrajo de una superficie de 3 100 ha, en la que se efectuaron dos muestreos selectivos: el primero, con apoyo de ortofotos digitales y recorridos de campo se eligieron rodales de diferentes dimensiones y edades con densidad completa; se levantaron sitios circulares de muestreo con dimensiones fijas entre 100 y 1 000 m², según el estado de desarrollo de la masa; el segundo, para árboles individuales que crecieron aislados, se distribuyeron bajo criterios de exposición y abarcaron todas las categorías diamétricas posibles.

Criterios para la selección de los sitios. Únicamente se tomaron en cuenta rodales de densidad completa, con el criterio de que el arbolado ubicado dentro del sitio tocara sus copas en tres a cuatro lados, y que estuviera libre de daños por plagas, enfermedades, incendios o algún otro factor de disturbio. Se evitó escoger sitios en las orillas de los rodales (a menos de 10 m); asimismo, se seleccionaron rodales libres de aprovechamiento durante los últimos 15 a 20 años. Los datos registrados en cada uno fueron el diámetro normal y el número de árboles existentes.

Criterios para la selección de los árboles aislados. Se consideró el crecimiento sin competencia lateral, copa completa y sin daños por plagas o enfermedades, no bifurcados y que fueran producto de regeneración natural. Se tomó información de diámetro normal y del diámetro de copa en cada uno de los árboles.

Procesamiento de datos de campo. La base de datos se elaboró en Microsoft Excel 2007 y el análisis se realizó mediante el paquete estadístico SPSS Statistics 17.0 (Softonic, s/f), con una base de datos para rodales de densidad completa (sitios) y otra para árboles aislados; se obtuvieron diagramas de dispersión para detectar datos atípicos y ajustar la información.

Obtención del Diámetro cuadrático. Para estimar el Dq se usó la expresión de Clutter et al. (1983):

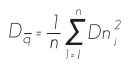
Donde:

= Diámetro cuadrático (cm)

Dn = Diámetro normal (cm)

n = Número de árboles medidos

Diámetro de referencia. Una vez determinado el diámetro cuadrático, se eligió el diámetro de referencia (Dqr) en 25 cm, de acuerdo a lo propuesto por Reineke (1933) y Vega (1995), el cual permite hacer comparaciones entre rodales.

Ajuste del modelo del IDRR. Con el diámetro cuadrático de cada sitio y el número de árboles extrapolados a la hectárea se efectuó un ajuste de los datos a una regresión no lineal, a fin de predecir el número de árboles ha^-1 y por categoría diamétrica; para ello se utilizó la siguiente expresión (Montero et al., 2007; Santiago-García et al., 2013):

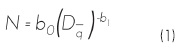
Este modelo general, en forma linealizada, se expresaría así (Clutter et al., 1983):

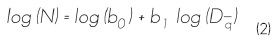
Donde:

N = Número de árboles ha^-1

b₀= Coeficiente de regresión (Intercepto)

b₁= Coeficiente de regresión (pendiente)

log= Logaritmo base 10.

Curva de referencia. Con el objeto de definir la curva de referencia se hizo variar el intercepto al origen y se conservó la pendiente para cualquier índice a partir del modelo general (Gingrich, 1967; Zepeda, 1984; Zepeda y Villarreal, 1997; Aguirre y Jiménez, 1992; Aguirre y Jiménez, 1994; Alonso, 1996) con la siguiente expresión:

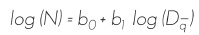
Al despejarse se tiene:

Donde:

N = Valor por donde requiere pasar la curva, denominado "índice de densidad";

K = Constante.

Cálculo del área basal por hectárea. Se logra a través de la ecuación del número de árboles por hectárea para obtener el área basal en metros cuadrados de árboles individuales de un diámetro cuadrático dado; para ello se utiliza la siguiente ecuación:

Donde:

abh^-1 = Área basal por hectárea (m² ha^-1).

Ajuste del modelo del FCC. Bajo el supuesto de que existe una correlación alta entre el diámetro de copa del árbol que creció de forma libre, sin interferencias, y el diámetro normal (Krajicek et al., 1961), con pares de los valores de área de copa (m) y diámetro normal del fuste (cm) medido a 1.3 m de altura de árboles aislados, se generaron los coeficientes de regresión lineal del modelo:

Donde:

dc = Diámetro de copa (m)

d = Diámetro normal promedio (cm)

b₀= Coeficiente de regresión (Intercepto)

b₁= Coeficiente de regresión (Pendiente)

Área de copa. Expresa en términos de porcentaje de una hectárea, el área máxima de terreno que puede ocupar la copa de un árbol de un diámetro normal dado.

Se determinó el área de copa de árboles individuales (ac) en m², mediante la ecuación:

Al sustituir (4) en (5) se tiene:

Donde:

ac = Área de copa de un árbol individual (m²).

Cuando se redefine ac por área máxima de copa individual (amci), se desarrolla el binomio al cuadrado, de acuerdo a Krajicek et al. (1961), Clutter et al. (1983), Zepeda (1984) y Husch et al. (1993).

Para el cálculo de espacios de crecimiento (ec), número de árboles por hectárea (nah-1) y área basal por hectárea (abh) se utilizan las siguientes expresiones:

 

Espacios de crecimiento

Donde:

ec(%) = Espacio de crecimiento en porcentaje de superficie

Número de árboles por hectárea. El número de árboles por hectárea se estima con la siguiente expresión:

Donde:

nah^-1 = Número de árboles por hectárea.

Área basal por hectárea. Por último, para calcular el área basal por hectárea se empleó la siguiente expresión:

Construcción de la guía de densidad. Estimación de valores en la línea "A" o densidad máxima. Se usaron los valores calculados del IDRR en la construcción de la línea, la cual pasa por el máximo número de árboles ha^-1 a un diámetro cuadrático de referencia (Dqr) base de 25 cm.

Con los valores de número de árboles ha^-1 por categoría diamétrica, se estima el área basal ha^-1 para construir la guía de densidad; mediante la unión de los valores que representan el diámetro cuadrático, número de árboles y área basal, se define la posición; el grado de densidad es expresado en porcentaje de la línea "A", tanto en el número de árboles como en área basal ha^-1.

Estimación de valores en la línea "B" o densidad mínima. Para la generación de la línea se emplearon los valores del FCC de la relación del área de copa y el número de árboles. Se obtuvo el número de árboles por categoría diamétrica y los valores del área basal ha^-1, de esto resultó la posición de la línea "B" en la guía por la unión de valores.

Estimación de valores en la línea "C" o densidad mínima aceptable. La posición y tendencia de la línea es definida a partir de incrementos medios por categoría diamétrica, con base en la línea "B" proyectada hacia abajo de esta una línea vertical perpendicularmente al eje de las abscisas, nivel que se quiere alcanzar en los 10 años siguientes. Para ello, el incremento medio en diámetro que resulte en los últimos 10 años se utilizará para que posteriormente cada diámetro normal medio se multiplique por los incrementos calculados con la ecuación (Zepeda y Villarreal, 1987):

 

Al despejar, se obtiene:

Donde:

5 = Amplitud de las clases diamétrica

tp = Tiempo de paso (años número o número de anillos en los últimos 2.5 cm)

id = Incremento corriente anual en diámetro (cm año^-1)

Esto permite generar el diámetro normal y el área basal individual para multiplicarlos por el valor de número de árboles ha^-1 que representan al nivel "B" y así obtener el área basal ha^-1 para, finalmente, unir las variables y definir el nivel "C"

 

RESULTADOS Y DISCUSIÓN

Índice de Densidad de Rodales de Reineke

Se determinó que los valores de los coeficientes de regresión fueron b₀= 105,550.708 y b₁= -1.534711 de la ecuación (1), la cual tuvo un R² = 0.886 y un valor de α< 0.0001. Al sustituir los valores en las ecuaciones:

Donde:

NAH = Número de árboles ha^-1.

IDRR. Con base en este parámetro se determinó el IDRR = 775 para rodales con un diámetro cuadrático de referencia de 25 cm. Se calculó el número máximo de árboles ha^-1 según el índice, con la expresión resultante de la ecuación (1):

IDRR= 105 550708(25)^-1,5347
IDRR = 755.14

Lo anterior generó una serie de valores por categoría diamétrica.

Se observó que a mayor cercanía a la densidad máxima (100 %) o línea "A" y con diámetros más grandes, se cuenta con una menor cantidad de árboles ha^-1. Comportamiento que corresponde a la Ley de Auto-aclareo o curva de Liocourt (Yoda et al., 1963; Gezar et al., 2007; Santiago-García et al., 2013), basada en la competencia entre individuos del rodal.

El valor de b₁, pendiente de la curva, es de -1.535, semejante al señalado por Reineke (1933) con -1.605; Yoda et al. (1963) con -1.5; Zepeda y Villarreal (1987) en Pinus hartwegii Lindl. con -1.669; Valencia (1988) con -1.55 en Pinus douglasiana Martínez; Vega (1995) para Pinus pseudostrobus con -1.54; Alonso (1996) para Pinus rudis, con -1.54; Fernández (1999) para Pinus arizonica Engelm., -1.56; Torres et al. (2000) en una mezcla de Pinus-Pseudotsuga–Alnus y Quercus, con -1.45, -1.80 y -1.51 respectivamente; Andermatt et al. (2000) con -1.60 en Pseudotsuga menziesii (Mirb.) Franco, y Fassola et al. (2004) para Grevillea robusta A. Cunn, ex R. Br. con -1.60.

Las diferencias entre los valores de las pendientes en los estudios mencionados se atribuyen a efectos aleatorios de muestreo y a las características propias de las especies, ya que para cada x (Dq) existe una serie de valores en número de árboles por unidad de superficie bajo una distribución normal, y la muestra no siempre representa el centro de la campana de la distribución normal. Respecto a la variación de la pendiente de la línea, también se adjudica a las diferentes condiciones de desarrollo de los taxa y a la relación con la distribución dentro del rodal y la densidad existente.

El intercepto b₀ para estimar el número de árboles dado por IDRR se refiere al sistema de curvas generadas a partir de la curva referencia, con lo que se definen nuevos interceptos al origen al mover la línea de regresión, pero con la misma pendiente, para cualquier índice de densidad. Al tomar y despejar el modelo para un ejemplo de IDRR de 700 y un diámetro cuadrático de 25 cm, se obtendrá el intercepto, para obtener el número de árboles ha^-1.

log700 = -1.534711 + b₁log(25) + b₀
log700 = + (-1.534711*log25) = b₀
2.84509 + 2.1454 = b₀
4.9905 = b₀

Cálculo del área basal por hectárea. Mediante la ecuación del número de árboles por hectárea y el área basal en metros cuadrados de árboles individuales de un diámetro cuadrático dado; para ello se utiliza la siguiente expresión:

Factor de Competencia de Copas. En la construcción del FCC se emplearon los diámetros de fuste a la altura de 1.3 m y el diámetro promedio de copa de 131 árboles aislados.

Relación diámetro de copa/diámetro normal. Con una regresión lineal a fin de estimar el diámetro de copa (dc) a partir del diámetro normal (d ), para cada categoría diamétrica se generó la siguiente expresión, cuyo ajuste fue satisfactorio (R² = 0.905 y α> 0.0001): 

dc = 1.437445688 + 0.1623921148d

Área de copa individual. Con los valores de los b´s se tiene la siguiente ecuación:

Si se redefine al ac por amci, al sustituir la ecuación para estimar el diámetro de copa por el diámetro de copa de árboles que crecen sin competencia y al desarrollar el binomio cuadrado, se genera la siguiente expresión (Krajicek et al., 1961):

amcf= 07854(1.437445688 + 0.1623921148d)²
amci= 1.62283283 + 0.3666716d + 0.02071194d²

Donde:

amci = Área máxima de copa individual (m²).

Espacios de crecimiento (ec%), número de árboles por hectárea (nah^-1) y área basal por hectárea (abh^-1). Una vez creada la ecuación del amci se estimaron los espacios de crecimiento que teóricamente ocuparían los árboles de categorías diamétricas dadas, cuyo crecimiento estaría libre de competencia, así como el número de árboles y área basal por hectárea.

El número de árboles por hectárea se estima de acuerdo a la siguiente expresión: 

Por último, para calcular el área basal por hectárea, se usó la siguiente expresión:

Donde:

ec% = Espacios de crecimiento (%)

nah = Número de árboles ha^-1

abh = Área basal m²ha^-1

Cálculo del factor de competencia de copas (FCC).

Para i = 1, 2, 3,…… hasta el número de árboles en una hectárea tipo.

Dicha expresión es equivalente a la siguiente:

Donde:

A = Área ocupada por el rodal tipo (1 hectárea)

d_i = Diámetro normal medio de la i-ésima categoría diamétrica

na_i = Número total de árboles en la parcela considerada

Incrementos para la densidad mínima aceptable. La posición y tendencia de la línea "C" que representa la densidad mínima aceptable se definió a partir de incremento corriente anual (ICA) diamétrico extrapolados en 10 años y el tiempo de paso (TP) por categoría diamétrica (Cd), según la expresión: 

Para establecer el diámetro normal de la línea "C" se restó el incremento corriente anual en 10 años a la categoría diamétrica correspondiente a la línea "B"; por tratarse de la densidad deseada en un periodo de 10 años y con esos valores se precisó el diámetro normal para así calcular el área basal ha^-1 y los árboles ha^-1, y mediante la unión de valores se ubicó la posición y tendencia de la línea.

Construcción de la guía de densidad definitiva. Se utilizaron las ecuaciones creadas para el Índice de Densidad de Rodales de Reineke (IDRR), las cuales definen la línea de máxima densidad de 100% ("Línea A") que separa el intervalo de densidad relativa, considerada como plenamente poblada del intervalo sobre-poblado. Se estiman los diversos grados de densidad con base en los resultados consignados para IDRR, de acuerdo a la metodología propuesta por Gingrich (1967).

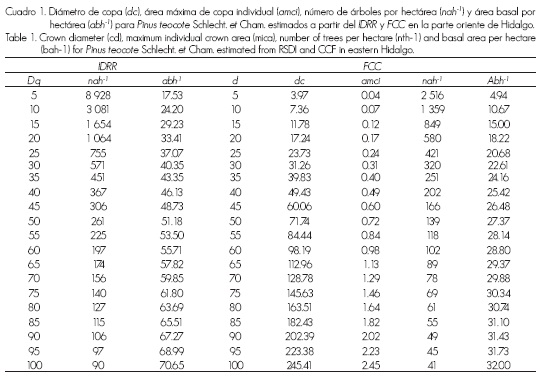
Para la línea de densidad mínima ("B"), dibujada a un porcentaje del IDRR (42.1%) de la densidad máxima (basado en el diámetro cuadrático de referencia de 25 cm) que especifica cuándo un rodal tiene una densidad suficiente o deficiente, se logra según los valores generados con las ecuaciones derivadas del Factor de Competencia de Copas (FCC) para el número de árboles y área basal. Los resultados para el caso del IDRR y el FCC se muestran en el Cuadro 1.

Hacer clic para agrandar

La Línea "C" que representa la densidad mínima aceptable, se obtuvo con base en los incrementos diamétricos promedios por categoría, al dar valores entre 38 y 25% respecto a la densidad máxima aceptable, lo cual expresa los valores del área basal, el diámetro cuadrático promedio y el número de árboles por hectárea, así como de densidad, para el óptimo desarrollo del rodal; se creó la guía de densidad propuesta (Figura 1).

Hacer clic para agrandar

 

Manejo de las guías de densidad

La Figura 1 indica que arriba de la línea "A" existe una sobrepoblación, esto refleja la necesidad de aplicar un tratamiento silvícola para disminuirla y lograr la apertura de espacios.

Entre el área de la línea "A" y la línea "B", donde se utiliza todo el espacio de crecimiento, todos los rodales serán de densidad completa o cerrada.

En relación con la parte baja de la línea "B" se tiene un rodal subpoblado, en el cual se espera que en el transcurso de 10 años alcance la densidad completa mínima o la línea "B". Para el caso de la línea "C", por debajo de ella, el rodal presenta una deficiencia de densidad; en consecuencia, se necesitarían tratamientos para aumentarla.

La guía de densidad se emplea para prescribir tratamientos silvícolas. En la Figura 1 del ejemplo (1), si se tiene un área basal de 37.07 m² y 755 árboles por hectárea, con un diámetro promedio de 25 cm (valor de la máxima densidad aceptada) se puede seguir la línea de 25 cm hacia abajo a un nivel de densidad de 80% y establecer un área basal de 33.36 m²ha^-1 para mantener completa la densidad a ese diámetro promedio; por lo tanto, la aplicación de tratamientos silvícolas permiten remover 3.71m² de área basal o dejar 680 árboles por ha^-1 del mismo diámetro promedio y con ello cambiar el área basal (2) o eliminar 298 árboles de diferentes diámetros para lograr un diámetro promedio de 30 cm con área basal de 32.28 m²ha^-1 en el mismo nivel de densidad (3), a fin de orientar este último al desarrollo y crecimiento de la masa mediante el uso completo del sitio, o producir madera de forma eficiente según los objetivos silvícolas.

Por otra parte, cuando se tiene un área basal y una densidad inferior a la línea de mínima densidad o nivel "B", deberá dejarse más tiempo la masa forestal sin intervención silvícola hasta que alcance la densidad deseada y sobreponga este nivel "B", así como orientar el rodal a ocupar de manera efectiva la superficie en el lugar (4).

 

CONCLUSIONES

La guía de densidad obtenida relaciona índices cuantitativos que permiten comparar el grado de densidad y las variables dasométricas en rodales puros de Pinus teocote dentro de los intervalos de densidad determinados, lo cual hace posible prescribir tratamientos silvícolas y apoyar las decisiones de los silvicultores, sin perder de vista sus limitaciones y su carácter de herramienta de apoyo.

La guías de densidad construidas representan un soporte para planificar diferentes opciones de manejo de la densidad de rodales puros de Pinus teocote en la región oriente del estado de Hidalgo.

La metodología aplicada es confiable para definir los límites de variación natural de la densidad en la especie para la región; los modelos utilizados muestran la capacidad tanto explicativa como predictiva como base para el manejo forestal.

 

REFERENCIAS

Acosta M., M., F. A. Carrillo y O. T. Magaña. 2007. Aplicación práctica de una guía de densidad en rodales naturales y plantaciones forestales del estado de Hidalgo. Folleto Técnico No. 7. INIFAP. Centro de Investigación Regional Centro. Pachuca, Hgo. México. 23 p.         [ Links ]

Aguirre C., O. y J. P. Jiménez. 1992. Índice de densidad del rodal de Reineke para Pinus pseudostrobus Lindl. en Nuevo León. In: II Simposio Regional de Biología. Cd. Victoria, Tamaulipas. México. p. 13.         [ Links ]

Aguirre C., O. y J. P. Jiménez. 1994. Índice de densidad del rodal de Reineke para Pinus teocote Sch. et Cham. en Nuevo León. In: II Simposio Regional de Biología y Ecología, Tampico, Tamps. México. 7 p.         [ Links ]

Aguirre C., O., M. G. Vega y L. P. Jiménez. 1994. Guía de densidad para Pinus pseudostrobus Lindl. en Nuevo León. In: Memorias del Simposio y II Reunión Nacional de Silvicultura y Manejo de los Recursos Forestales, Colegio de Postgraduados. Montecillo, Edo. de Méx. México. p. 43.         [ Links ]

Alonso G., L. 1996. Guía de densidad para Pinus rudis Endl. en Arteaga, Coah. Universidad Autónoma Agraria Antonio Narro. Buenavista, Coah. México. 76 p.         [ Links ]

Andenmatten, E., M. Rey y F. Letourneau. 2000. Índice de Densidad de Rodales de Reineke para Pino oregon (Pseudotsuga menziesii (Mirb) Franco) en la región Andino Patagonia. Informe Técnico 11. Área de Investigación en Recursos Forestales. Centro Regional Patagonia Norte. Bariloche, Río Negro Argentina. pp. 229-233.         [ Links ]

Cano C., J. 1988. El sistema de manejo regular de los bosques en México. Fundamentos de Silvicultura y su aplicación práctica. División de Ciencias Forestales, Universidad Autónoma Chapingo. Texcoco, Edo. de Méx. México. 222 p.         [ Links ]

Chauchard, L. M. 2001. Crecimiento y producción de repoblaciones de Pinus radiata D. Don en el territorio histórico de Guipúzcoa (País Vasco). Tesis doctorales Nº 40 Departamento de Agricultura y Pesca. Gobierno del País Vasco. País Vasco, España. 173 p.         [ Links ]

Chisman, H. H. and F. Schumacher. 1940. On the tree-area ratio and certain of its applications. J. Forest. Vol. 38 (4): 311-317.         [ Links ]

Comisión Nacional Forestal. (Conafor). 2011. Estudio regional forestal. Unidad de Manejo Forestal 1303. Asociación de Productores Forestales de la Región Pachuca-Tulancingo A. C. Tulancingo, Hgo., México. pp. 94-105.         [ Links ]

Clutter, J. L., C. J. Fortson, V. L. Pineaar, H. G. Brister and L. R. Bailey. 1983. Timber management, a quantitative approach. John Wiley and Sons, Inc. New York, NY. USA. 333 p.         [ Links ]

Curtis, R. O. 1970. Stand density measures and interpretation. Forest Sci. 16 (4):403–414.         [ Links ]

Daniel, T. W., A. J. Helms y S. F. Baker. 1982. Principios de Silvicultura. Editorial McGraw-Hill. México, D.F. México. 482 p.         [ Links ]

Food and Agriculture Organization of the United Nations (FAO). 2010. Evaluación de los Recursos Forestales Mundiales 2010. Informe principal. Roma Italia. 346 p.         [ Links ]

Fassola, H. E., A. F. Moscovich, P. Ferrere, M. C. Domecq, H. Hampel, C. Maletti y D. Alegranza. 2004. Regulación de la densidad en rodales de Grevillea robusta A. Cunn. para la producción de madera de calidad y forraje en el sur de la Provincia de Misiones. Revista de Investigaciones Agropecuarias 33 (1):15-37.         [ Links ]

García, E. 1988. Modificación del sistema de clasificación climática de Köppen. Instituto de Geografía. Universidad Nacional Autónoma de México. México, D.F. México. 217 p.         [ Links ]

Gezan, S. A., A. Ortega y E. Andenmatten. 2007. Diagramas de manejo de densidad para renovales de roble, raulí y coigüe en Chile. Bosque. 28:97-105.         [ Links ]

Gingrich, S. F. 1967. Growth and yield in uneven aged silviculture and management in the United States. USDA Forest Service. Washington, DC. USA. pp. 115-124.         [ Links ]

Husch, B., C. Miller and T. Beers. 1982. Forest mensuration. John Wiley and Sons, Inc. New York, NY USA. 402 p.         [ Links ]

Husch, B., C. Miller and T. Beers. 1993. Forest mensuration. Krieger Publishing Co. Malabar, FL USA. 410 p.         [ Links ]

Instituto Nacional de Estadística Geográfica e Informática (Inegi). 1992. Síntesis geográfica del estado de Hidalgo. Secretaría de Programación y Presupuesto. México, D.F. México. 134 p.         [ Links ]

Krajicek, E. J., A. K. Brinkman and S. F. Gingrich. 1961. Crown competition, a measure of density. Forest Sci. 16 (1):5-42.         [ Links ]

Montero M., M., H. M. De los Santos-Posadas y M. Kanninen. 2007. Hyeronima alchorneoides: ecología y silvicultura en Costa Rica. Serie Técnica. Informe Técnico/CATIE No. 354. Turrialba. Costa Rica. 50 p.         [ Links ]

Reineke, L. H. 1933. Perfecting a stand density index for even aged forests. J. Agric. Res. 46 (7): 627-638.         [ Links ]

Rodríguez L., R., R. Z. Razo, D. H. Díaz y J. R. Meza. 2009. Guía de densidad para Pinus montezumae en su área de distribución natural en el Estado de Hidalgo. Folleto Técnico No. 1. Universidad Autónoma del Estado de Hidalgo. Instituto de Ciencias Agropecuarias. Área Académica de Ingeniería Forestal. Tulancingo de Bravo, Hgo. México. 31 p.         [ Links ]

Santiago-García, W., H. M. De los Santos-Posadas, G. Ángeles-Pérez, J. R. Valdez-Lazalde, D. H. Del Valle-Paniagua y J. J. Corral-Rivas. 2013. Auto-aclareo y guías de densidad para Pinus patula mediante enfoque de regresión de frontera estocástica. Agrociencia 47: 75-89.         [ Links ]

Softonic Inc. s/f. IBM SPSS Statistics version 17.0 (http://softonic.com/s/spss-statistics-17-espa%C3%B1ol (octubre, 2011).         [ Links ]

Torres R., J. M. 2000. El área de ocupación promedio: una medida de competencia independiente de la distancia. Agrociencia 34: 485-495.         [ Links ]

Torres R., J. M. y O. S. Magaña. 2001. Evaluación de plantaciones forestales. Editorial Limusa. México, D.F. México. 472 p.         [ Links ]

Toumey, J. W. and F. C. Korstian. 1947. Foundations of silviculture. John Wiley and Sons, Inc. New York, NY. USA. 469 p.         [ Links ]

Velásquez, A., J. F. Mas, J. R. Díaz-Gallegos, R. Mayorga-Saucedo, P. C. Alcántara, R. Castro, T. Fernández, G. Bocco, E. Ezcurra y J. L. Palacio. 2009. Bosques Mexicanos. World Wildlife Fund. México, D.F. México.         [ Links ]

Valencia V., J. 1988. Utilización del Índice de Densidad de Reineke en Pinus douglasiana en Atenquique, Jalisco. Universidad Michoacana de San Nicolás de Hidalgo. Uruapan del Progreso, Mich. México. 39 p.         [ Links ]

Yoda Kira, K. T., H. Ogawa and K. Hozumi. 1963. Self-thinning in overcrowded pure stands Under Cultivated and natural conditions. Journal of Biology. 14: 107-129.         [ Links ]

Zeide, B. 2004. Optimal stand density: a solution. Can. Jour. For. Res. 34: 846-854.         [ Links ]

Zepeda B., E. M. 1984. Ejemplificación de tres procedimientos para caracterizar rodales por su densidad. Serie de Apoyos Académicos No. 34, Universidad Autónoma Chapingo. Departamento de Bosques. Chapingo, Edo. de Mex. México. 57 p.         [ Links ]

Zepeda B., E. M. y E. M. D. Villarreal. 1987. Guía de densidad para Pinus hartwegii Lindl. de Zoquiapan, México. Universidad Autónoma Chapingo. Chapingo, Edo. de Mex. México. 52 p.         [ Links ]